 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Force-dependent elasticity of nucleic acids†
Juan
Luengo-Márquez
*ac,
Juan
Zalvide-Pombo
a,
Rubén
Pérez
 ab and
Salvatore
Assenza
ab and
Salvatore
Assenza
 *abc
*abc
aDepartamento de Física Teórica de la Materia Condensada, Universidad Autónoma de Madrid, 28049 Madrid, Spain. E-mail: juan.luengo@uam.es
bCondensed Matter Physics Center (IFIMAC), Universidad Autónoma de Madrid, 28049 Madrid, Spain. E-mail: salvatore.assenza@uam.es
cInstituto Nicolás Cabrera, Universidad Autónoma de Madrid, 28049 Madrid, Spain
First published on 16th March 2023
Abstract
The functioning of double-stranded (ds) nucleic acids (NAs) in cellular processes is strongly mediated by their elastic response. These processes involve proteins that interact with dsDNA or dsRNA and distort their structures. The perturbation of the elasticity of NAs arising from these deformations is not properly considered by most theoretical frameworks. In this work, we introduce a novel method to assess the impact of mechanical stress on the elastic response of dsDNA and dsRNA through the analysis of the fluctuations of the double helix. Application of this approach to atomistic simulations reveals qualitative differences in the force dependence of the mechanical properties of dsDNA with respect to those of dsRNA, which we relate to structural features of these molecules by means of physically-sound minimalistic models.
1. Introduction
There is an intricate connection between the elasticity of nucleic acids and their biological role,1–8 which affects their organization and functionality over multiple scales.5,7,9–13 Specific motifs, such as A-tracts in double-stranded DNA (dsDNA) and AU-tracts in double-stranded RNA (dsRNA), have been found to confer to the chain mechanical properties significantly departing from sequence-averaged values,14–19 supporting the existence of a mechanical code contained in the sequence of nucleotides along with the genetic code.20,21When stretching forces in the range 5–50 pN are exerted, as is the case e.g. for RNA polymerases,22 the mechanical response of double-stranded nucleic acids lies within the elastic regime,9,23,24 where enthalpic structural deformations dominate while the molecules still retain the double-helical conformation.8,25 The mechanical properties of nucleic acids are theoretically depicted by mapping each sequence of basepairs into a set of elastic parameters describing a suitable functional form of the mechanical energy of the system. For deformations close to the equilibrium conformation of the chain,26 the mechanical energy is approximately harmonic in the deformation modes. At the simplest level, double-stranded nucleic acids can be regarded as homogeneous elastic rods, characterized by their extension and torsion. The Elastic Rod Model (ERM) energy of the system upon pulling thus reads27
 | (1) |
Substantial experimental and theoretical efforts have been made to characterize the elastic response of nucleic acids,8,10,27–34 revealing a number of striking mechanical features of dsDNA, such as the positive correlation between the deformations in the contour length and the torsion angle for forces up to approximately 40 pN.27,31 Conversely, dsRNA has been found to unwind when stretched,32–34 which is the typical behavior of most chiral materials.35
The picture becomes even more complex when one realizes that the elastic parameters of the ERM depend themselves on the mechanical stresses exerted on the molecule.27,34,36–38 Rotor-bead tracking has shown that the change in torsion of pulled dsDNA becomes negative beyond 40 pN,27 which implies a change in sign for g. We conjecture that the change in the elastic response arises from the microscopic distortion of the chain. Given the enormous complexity of DNA, the structure of the chain in equilibrium with external mechanical stress is likely to display different elastic behavior than the unperturbed chain. Therefore, accessing force-dependent elasticity can provide important information on the microscopic conformational changes that take place within the chain.
By its own construction, the ERM with constant parameters39 cannot account even qualitatively for the change in twist–stretch coupling of dsDNA found experimentally.27 This limitation can be important when addressing biologically relevant systems.3 For instance, during transcription, RNA polymerase has been experimentally found to exert forces around 14 pN on the downstream dsDNA,22 whose features affect the advancement of the transcription process.40 Furthermore, the mechanical properties of DNA are relevant when addressing dsDNA-based nanomaterials as DNA origamis,41 and detailed knowledge on structural changes due to mechanical stress is key for related applications.
To address the force-dependent elastic response, a subsequent work assumed a force-dependent twist–stretch coupling, g(f), and determined empirically that g was roughly constant up to 30 pN, after which it increased linearly with the pulling force.36 However, this approach assumes that the whole force-dependence must rely on the twist–stretch coupling, while it would be equally expectable to find a force-dependence on any of the elastic parameters. Moreover, the quantitative details of g(f) depend on the values chosen for S, C and the persistence length lP, often leading to physically-unacceptable imaginary values of g(f) even within the experimentally-observed ranges of values for the three constants (section S1 in the ESI†).
Current theoretical approaches are ill-suited to extract the elastic parameters with force-dependence. The standard practice of fitting the average values by means of formulas derived from the minimization of eqn (1) cannot account by construction for stress-dependent elastic constants, since a stress–strain curve is needed for fitting purposes. Interestingly, for a monotonous change of e.g. S(f), the effective value obtained from fitting lies outside of the range of values spanned by S(f) within the force domain (section S2 ESI†), thus introducing a systematic offset in the estimation of the parameter. Many experimental studies rely on this approach, thus force-dependent elasticity of nucleic acids remains mostly unexplored. Previous studies32,42 have circumvented this limitation of energy minimization procedures to explore a force-dependent twist stretch coupling by imposing a number of turns in addition to the stretching force, not finding a significant variation of g within a limited force range. However, this approach can not split the force-dependency of the several elastic parameters, as only quotients of the kind  or
or  can be accessed through energy minimization. Furthermore, this strategy cannot explore independently the action of a torque and that of a pulling force, as both must be exerted simultaneously in order to extract information.
can be accessed through energy minimization. Furthermore, this strategy cannot explore independently the action of a torque and that of a pulling force, as both must be exerted simultaneously in order to extract information.
On the other hand, fluctuations-based approaches43,44 are widely used,18,25,45 but are based on formulas strictly valid only in the absence of external mechanical stress. However, the potential of fluctuations-based approaches to address the physical behavior of deformed DNA molecules is starting to be recognized, e.g., in the context of plectoneme formation.46
In this study, we present an alternative route to explore the force dependence of the parameters of the ERM based on a novel generalization of the latter approach, which enables the study of fluctuations in the presence of mechanical stresses. Application of our method to atomistic trajectories of dsDNA and dsRNA sequences from literature21,34,47 unveils a hitherto unreported dependence of the stretch and twist moduli on the stretching force, whose physical origin is identified by means of minimalistic toy models. These novel predictions on S(f) and C(f) are found together with a behavior of g(f) in line with experimental observations.
2. Results and discussion
2.1. Force-depending elasticity from fluctuations
The ERM belongs to a class of models attributing a harmonic energetic penalty for each of the deformation modes, including also coupling terms between different modes.44 We denote as Δqi the deformation associated to the generalized coordinate qi, and as γi the generalized force conjugated to qi. The energy for N deformation modes thus reads | (2) |
We first define the work matrix, having elements  , and the covariance matrix with elements
, and the covariance matrix with elements  . From eqn (2) and the generalized equipartition theorem,48
. From eqn (2) and the generalized equipartition theorem,48 , it is possible to show that (see section S3 in ESI†)
, it is possible to show that (see section S3 in ESI†)
 | (3) |
 , kBT is the thermal energy of the system, and
, kBT is the thermal energy of the system, and 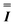 is the Nth order identity matrix. Note that the diagonal elements of the stiffness matrix are the elastic moduli, and the off-diagonal elements are the coupling parameters. Remarkably, eqn (3) establishes a method to compute rigorously the parameters of the ERM from the knowledge of the fluctuations associated to the deformation modes of a perturbed system. Additionally, since
is the Nth order identity matrix. Note that the diagonal elements of the stiffness matrix are the elastic moduli, and the off-diagonal elements are the coupling parameters. Remarkably, eqn (3) establishes a method to compute rigorously the parameters of the ERM from the knowledge of the fluctuations associated to the deformation modes of a perturbed system. Additionally, since  is symmetric, eqn (3) imposes that any system described by eqn (2) must satisfy
is symmetric, eqn (3) imposes that any system described by eqn (2) must satisfy  . The fulfillment of such requirement allows the evaluation of the extent to which a physical system may be correctly described by the harmonic approximation.
. The fulfillment of such requirement allows the evaluation of the extent to which a physical system may be correctly described by the harmonic approximation.
Ultimately, eqn (3) allows the exploration of changes of the elastic parameters with structural deformations imposed by mechanical stress. In this work, we exploit this formalism to examine the response of double-stranded nucleic acids at forces f = 1–20 pN in the absence of an applied torque (τ = 0); these values are well within the region of the force-torque space in which the duplex is experimentally found to be stable, namely for −10 pN nm < τ < 35 pN nm,49 and for pulling forces up to 50–60 pN.28,49 Outside of this regime, it is expected that major conformational rearrangements imply drastic changes of the elastic response. In this regard, we note that eqn (3) is derived for a generalized harmonic-like potential (eqn (2)), so it is apt to address transition-induced elastic variations. Yet, for the present work we decided to focus on the case of double-stranded nucleic acids. We further stress that the applicability of eqn (3) extends well beyond the elasticity of nucleic acids. For instance, we envisage that this formalism will provide novel information on the elasticity of membranes under mechanical stress, e.g. stretching of lipid monolayers in Langmuir balance.50
2.2. Force-dependent elastic parameters of dsDNA and dsRNA
We next exploit this approach by investigating the elastic properties of short dsDNA and dsRNA molecules when a stretching force up to 20 pN is applied, for which the stretched ERM energy with two deformation modes (eqn (1)) should be a sufficient description of the elastic response. We have analyzed the trajectories of 17 dsDNA sequences and 11 dsRNA sequences from all-atoms simulations reported in the literature,21,34,47 based on the parm99 force field51 with the bsc0 modifications52 and, in the case of dsRNA, the χOL3 modifications.53 This force field has been shown to quantitatively account for the different elastic behavior of dsDNA and dsRNA34 and has been employed to inform a coarse-grained model capable of quantitatively recapitulating the experimental findings on dsDNA elasticity.54Fig. 1 shows C(f), S(f) and g(f) of the Transcription Factor Binding Site (TFBS – dsDNA) and of GG (dsRNA) as an example. The error bars result from combining block analysis and bootstrapping. The complete set of sequences can be found in Tables S1 and S2,† while the force-dependent elastic parameters obtained for each sequence by means of eqn (3) can be found in section S5 in the ESI.† | ||
| Fig. 1 Elastic parameters of dsDNA (in blue) and dsRNA (in red) versus stretching force representations. Black lines correspond to the linear fit taken under the linearity assumption. (a) and (b) Twist modulus of TFBS and GG versus force. (c) and (d) Twist-stretch coupling of TFBS and GG versus force, taken as the average between the two off-diagonal entries of the stiffness matrix. (e) and (f) Stretch modulus of TFBS and GG versus force. The error bars were estimated by splitting the data in 5 blocks, computing the elastic constants in each of them, and then applying the bootstrap method.55 | ||
To convey succinctly the information contained in our analysis, we computed the variations C′(f), S′(f) and g′(f) of the elastic constants. Quantitatively, we considered the slopes of linear fits of their force dependence, which account for the sign and magnitude of such variation. This approach implicitly assumes a linear dependence of the form A(f) ≃ A0 + f × A′(f) for each Elastic Parameter A∈{C, S, g}. Black lines in Fig. 1 correspond to the linear fit of each Elastic Parameter of TFBS and of S(f) of CG. The assumption holds acceptably for most sequences (see Fig. S9–S36†). The appropriateness of the linear approximation is accounted for in the error estimation of the slope.
As discussed above, changes in the elastic response emerge from structural modifications of the pulled chains. The following results examine the force-dependent elasticity in the form of A′(f) for each of the elastic parameters, and relate it to deformations of microscopic geometrical quantities of the duplex. In section 2.3 we discuss how the spontaneous curvature of the chain causes a decrease of the twist stiffness, i.e. C′(f) < 0. Section 2.4 shows how alignment and misalignment of the centers of the basepairs cause strengthening (S′(f) > 0) and softening (S′(f) < 0) upon pulling of dsDNA and dsRNA, respectively. Finally, in section 2.5 we show how the twist–stretch correlation decreases with the stretching force (i.e. g′(f) > 0) for both dsDNA and dsRNA.
2.3. The intrinsic curvature of the chain causes the decrease of the twist stiffness
For the twist modulus we find C′(f) ≤ 0 within error for all sequences. Furthermore, in the case of dsDNA, C′(f) displays a strong negative correlation with the crookedness β (Fig. 2a), which quantifies the displacement of the centers of the base pairs from the helical axis.21 To account for this displacement, as β increases, the normals to the base planes must be less aligned with the helical axis. Since the local torsion is mostly determined by the stacking between bases, while the overall twist modulus is obtained by the change in the helical twist, we conjecture that the change in C is due to the progressive alignment of the base pairs and the helical axis imposed by the force.In order to test this hypothesis, we develop a toy model with the minimal components that illustrate this concept (see Fig. 2(b)). We place three vectors, u0, u1 and u2, along the z-axis, which is oriented parallel to the helical axis. Each vector is pointing from one base to the opposite one at a certain basepair of a perfectly straight molecule, i.e. u0, u1 and u2 are all perpendicular to the z axis. The twist angle obtained in this case is the intrinsic torsion angle θ = arccos(u1·u2). To account for the presence of a spontaneous curvature, we rotate the top vector (u2) by an angle β around the x axis, obtaining the rotated vector rβ(u2). To consider a crookedness for this simplified geometry, one can think of the centers of the three vectors as being extracted from a helix with helix angle β, for which a direct identification with the crookedness can be shown formally (see section S4.2 in the ESI†). The torsion angle χ(θ, β) is then the angle formed by the versors of u1 and of the projection of rβ onto the xy plane.
Next, we assume that the energetics of the torsion is determined by the intrinsic torsion angle as  , where the intrinsic twist modulus
, where the intrinsic twist modulus ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) is independent of the force and θ0 is the equilibrium twist angle. By the equipartition theorem,
is independent of the force and θ0 is the equilibrium twist angle. By the equipartition theorem,  . In contrast, the observed twist modulus is obtained as
. In contrast, the observed twist modulus is obtained as  , where the variance 〈Δχ2〉 can be computed by standard Boltzmann statistics considering the functional dependence of χ on θ and β (see section S4.3 in the ESI†). When
, where the variance 〈Δχ2〉 can be computed by standard Boltzmann statistics considering the functional dependence of χ on θ and β (see section S4.3 in the ESI†). When ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) /L0kBT ≫ 1, the twist modulus may be expanded up to
/L0kBT ≫ 1, the twist modulus may be expanded up to
| C(β) = C(β0)[1 + sin(β0)Ω(θ0,β0)(β − β0)], | (4) |
 . Note also that
. Note also that  , where kβ is the stiffness associated to the crookedness.21 Considering that to first order sin(β) ≈ sin(β0), we can thus write
, where kβ is the stiffness associated to the crookedness.21 Considering that to first order sin(β) ≈ sin(β0), we can thus write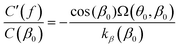 | (5) |
In order to make use of this result, we employ the fit performed by Marin-Gonzalez et al.,21 in which kβ could be expressed as a function of β0 as kβ(β0) = Ae−kβ0 + B, being A = (2.24 ± 1.24) × 106 pN, B = 700 ± 120 pN, and k = 16.2 ± 1.5. We show in Fig. S5† that the previous fit captures the kβ(β0) function for all sequences analyzed in this work, including those of dsRNA.
The analytical result in eqn (5) conveys the variation of the twist modulus with the stretching force, employing as only input the equilibrium intrinsic torsion angle and the equilibrium crookedness. In Fig. 2(a) we display the values of C′(f)/C(β0) from the analysis of the simulations, identifying β(f = 1 pN) with β0. We also show the analytical result of eqn (5) taking the equilibrium intrinsic torsion angle of dsDNA θ0 = 34°. Despite being minimalistic, the toy model provides a prediction (eqn (5)) that captures quantitatively the data obtained for dsDNA without any fitting (Fig. 2(a)). Indeed, as discussed above, the parameters θ0 and kβ in eqn (5) were set a priori to established values. The perturbative approach used to reach eqn (5) is justified considering that for dsDNA ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) /L0kBT ≈ 35. For comparison, in Fig. S6† we also show the curves obtained numerically for dsDNA and dsRNA without the perturbative approximation. The toy model reveals that the observed decrease of the twist modulus with the stretching force can be explained solely by geometrical arguments, being a direct consequence of the intrinsic crookedness of the molecules.
/L0kBT ≈ 35. For comparison, in Fig. S6† we also show the curves obtained numerically for dsDNA and dsRNA without the perturbative approximation. The toy model reveals that the observed decrease of the twist modulus with the stretching force can be explained solely by geometrical arguments, being a direct consequence of the intrinsic crookedness of the molecules.
In the case of dsRNA, the simulation data do not show a clear correlation between C′(f)/C(β0) and β0 (Fig. 2(a)), suggesting that at large curvatures the crookedness might not be the key determinant of the twist response of the molecule. A possible concurring factor might be, for instance, a force-dependent intrinsic twist modulus ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) . Despite not capturing quantitatively the data, the toy model does however account for the sign and order of magnitude of C′(f)/C(β0).
. Despite not capturing quantitatively the data, the toy model does however account for the sign and order of magnitude of C′(f)/C(β0).
2.4. dsDNA becomes stiffer and dsRNA softer upon pulling
We now focus on the stretch modulus S. As shown in Fig. 3(a), we first observe that for most dsDNA sequences the stretch modulus increases, S′(f) > 0, while for most dsRNA sequences S′(f) < 0. A possible microscopic mechanism to which this observation may be ascribed is the strengthening – or weakening – of the stacking interactions between the bases upon stretching. Such effect can be monitored by analyzing the force-variation of the slide, λ, a structural parameter that measures the relative displacement of two consecutive base pairs along the direction of the Watson–Crick hydrogen bonds. The slide is known to have a different evolution with the stretching force for dsDNA and dsRNA.34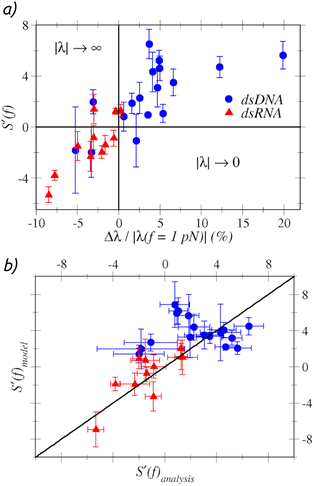 | ||
| Fig. 3 (a – top) Variation of the stretch modulus with the force against the relative slide variation. (b –– bottom) Scatter of S′(f) comparing the predictions of the model in ref. 21 and our analysis. | ||
Fig. 3(a) displays S′(f) against the relative slide variation of each sequence Δλ/|λ(f = 1 pN)|, with Δλ = λ(f = 20 pN) − λ(f = 1 pN). Since λ < 0, a negative slide variation – as found in most dsRNA sequences – implies that λ increases in magnitude, while Δλ > 0 – as found in most dsDNA sequences – implies |λ| → 0. We reason that the magnitude of the slide is expected to be negatively correlated with the strength of the stacking interactions, since |λ| quantifies the degree at which the aromatic rings in the stacking bases are not overlapping with each other. Since the slide is negative for both dsDNA and dsRNA, the points in Fig. 3(a) corresponding to Δλ/|λ(f = 1 pN)| < 0 indicate that the force further reduces the overlap of bases, i.e. it weakens the stacking interactions, hence S′(f) < 0. Conversely, Δλ/|λ(f = 1 pN)| > 0 is indicative of a strengthening of the stacking interactions, so that S′(f) > 0. Microscopically, the opposite change of λ for stretched dsDNA and dsRNA can be traced down to the different way in which it correlates with the h-rise for the two molecules.34 As we discuss in section S4.5 in the ESI,† in dsDNA the magnitude of the slide is negatively correlated with the h-rise, hence the increase of the h-rise upon pulling results in a decrease of |λ|. In contrast, dsRNA is characterized by a positive correlation, so that the slide further increases in magnitude upon pulling. These findings further exemplify the potential of extending the ERM to include force-dependent Elastic Parameters, as inspection of the structural changes correlated to the variations of the elastic response unveils important physical mechanisms that occur in the system when mechanical stresses are exerted.
These data can be further interpreted in terms of the model proposed by Marin-Gonzalez et al. in ref. 21, where the stretch modulus was expressed as the effective spring constant of a harmonic summation of base-pair steps stiffnesses kbp and the crookedness stiffness,  . Assuming kbp not to change upon pulling, one thus finds
. Assuming kbp not to change upon pulling, one thus finds  . Hence, the sign of the variation of the stretch modulus is determined by the sign of k′β(f). The crookedness stiffness estimates the energy cost of reducing the crooked curvature of the molecule, and the stronger the stacking interactions, the larger this energy cost. Fig. 3(b) shows how the predictions of the model match the sign and order of magnitude of S′(f) from the analysis of fluctuations, thus providing a plausible physical interpretation of the results.
. Hence, the sign of the variation of the stretch modulus is determined by the sign of k′β(f). The crookedness stiffness estimates the energy cost of reducing the crooked curvature of the molecule, and the stronger the stacking interactions, the larger this energy cost. Fig. 3(b) shows how the predictions of the model match the sign and order of magnitude of S′(f) from the analysis of fluctuations, thus providing a plausible physical interpretation of the results.
2.5. The twist–stretch correlation decreases with the stretching force
Finally, for the variation of the twist–stretch coupling, we find g′(f) ≥ 0 for virtually all dsDNA and dsRNA sequences (Fig. S10†). This observation matches the experiments for dsDNA,27,36 where it was found that g should switch to a positive sign at approximately 40 pN. In the case of dsRNA, g′(f) > 0 implies an enhancement of the negative correlation between twist and stretch. Ordinary chiral objects are expected to have g(f) > 0.56 In section S4.7 in ESI† we show that a helical object with constant radius has g′(f) < 0, so that the observation of g′(f) > 0 is far from being trivial. It would be interesting to compare this prediction based on all-atom simulations to experimental data. For instance, in a rotor-bead assay the combination g(f) > 0 and g′(f) > 0 would result in a non-linear decrease of torsion with force with negative convexity. To our knowledge, this feature has never been explored experimentally.3. Conclusions
In this study, we have introduced a novel approach that rigorously allows the computation of the stress-dependent elastic constants of the generalized Elastic Rod Model for molecules under the action of external work. We believe that this procedure sets a promising theoretical playground for future works, opening the field to overcome the limitations of the ERM, whose requirement of constant mechanical moduli hampers the full characterization of mechanical phenomena emerging from the complexity of nucleic acids.Our analysis of atomistic simulations of short dsDNA and dsRNA reveals that the twist modulus decreases upon stretching for both double-stranded nucleic acids. We show that this variation arises from the intrinsic curvature of the molecules, and that a toy model depicting this argument can account quantitatively for the simulation data in the case of dsDNA, while capturing the qualitative behavior of dsRNA. Most strikingly, we find that the stretch modulus of dsDNA becomes stiffer upon pulling, while that of dsRNA softens. Based on our analysis, we ascribe this difference to the opposite force-response of stacking interactions in dsDNA and dsRNA. This effect might be relevant for certain nucleic acids nanostructures, whose mechanical stability relies on stacking interactions.41,57 Finally, the twist–stretch coupling is found to increase with force for both dsDNA and dsRNA. This is in line with the experimental observations for dsDNA,27,36 while it gives a novel prediction for dsRNA to be tested in single-molecule setups.
This study provides an important milestone in the quest for the mechanical understanding of nucleic acids. In future developments, we will seek a more direct comparison with experiments by integrating the general framework proposed here with polymer physics models, so as to include the effect of thermally-induced bending characteristic of longer sequences. From a wider perspective, our study establishes new distinctive features of nucleic acids, further enlarging the list of fundamental differences between dsDNA and dsRNA.
Author contributions
JLM and SA designed the work. JLM and JZP performed the theoretical calculations. JLM analyzed the data and wrote the manuscript. JLM, RP and SA discussed the results and their microscopic interpretation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The project that gave rise to these results received the support of a fellowship from “la Caixa” Foundation (ID 100010434) and from the European Union's Horizon Research and Innovation Programme under the Marie Skłodowska-Curie grant agreement no. 847648. The fellowship code is LCF/BQ/PI20/11760019. We acknowledge support from the Ministerio de Ciencia e Innovación (MICINN) through the project PID2020-115864RB-I00 and the “María de Maeztu” Programme for Units of Excellence in R&D (grant no. CEX2018-000805-M). We thank Laura R. Arriaga for helpful discussion.References
- M. Hogan and R. Austin, Nature, 1987, 329, 263–266 CrossRef CAS PubMed.
- R. Rohs, S. M. West, A. Sosinsky, P. Liu, R. S. Mann and B. Honig, Nature, 2009, 461, 1248–1253 CrossRef CAS PubMed.
- R. Rohs, X. Jin, S. M. West, R. Joshi, B. Honig and R. S. Mann, Annu. Rev. Biochem., 2010, 79, 233 CrossRef CAS PubMed.
- G. Da Rosa, L. Grille, V. Calzada, K. Ahmad, J. P. Arcon, F. Battistini, G. Bayarri, T. Bishop, P. Carloni and T. Cheatham III, et al. , Biophys. Rev., 2021, 1–11 Search PubMed.
- J. Šponer, G. Bussi, M. Krepl, P. Banáš, S. Bottaro, R. A. Cunha, A. Gil-Ley, G. Pinamonti, S. Poblete and P. Jurečka, et al. , Chem. Rev., 2018, 118, 4177–4338 CrossRef PubMed.
- J. Yi, S. Yeou and N. K. Lee, J. Am. Chem. Soc., 2022, 144(29), 13137–13145 CrossRef CAS PubMed.
- Q. Vicens and J. S. Kieft, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2112677119 CrossRef CAS PubMed.
- A. Marin-Gonzalez, J. Vilhena, R. Perez and F. Moreno-Herrero, Q. Rev. Biophys., 2021, 54, e8, DOI:10.1017/S0033583521000068.
- S. B. Smith, Y. Cui and C. Bustamante, Science, 1996, 271, 795–799 CrossRef CAS PubMed.
- E. Herrero-Galán, M. E. Fuentes-Perez, C. Carrasco, J. M. Valpuesta, J. L. Carrascosa, F. Moreno-Herrero and J. R. Arias-Gonzalez, J. Am. Chem. Soc., 2013, 135, 122–131 CrossRef PubMed.
- Y. A. G. Fosado, D. Michieletto, J. Allan, C. A. Brackley, O. Henrich and D. Marenduzzo, Soft Matter, 2016, 12, 9458–9470 RSC.
- M. Di Pierro, B. Zhang, E. L. Aiden, P. G. Wolynes and J. N. Onuchic, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 12168–12173 CrossRef CAS PubMed.
- M. Di Pierro, R. R. Cheng, E. L. Aiden, P. G. Wolynes and J. N. Onuchic, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 12126–12131 CrossRef CAS PubMed.
- F. Moreno-Herrero, R. Seidel, S. M. Johnson, A. Fire and N. H. Dekker, Nucleic Acids Res., 2006, 34, 3057–3066 CrossRef CAS PubMed.
- E. Segal and J. Widom, Curr. Opin. Struct. Biol., 2009, 19, 65–71 CrossRef CAS PubMed.
- T. E. Haran and U. Mohanty, Q. Rev. Biophys., 2009, 42, 41–81 CrossRef CAS PubMed.
- A. Marin-Gonzalez, C. L. Pastrana, R. Bocanegra, A. Martín-González, J. Vilhena, R. Pérez, B. Ibarra, C. Aicart-Ramos and F. Moreno-Herrero, Nucleic Acids Res., 2020, 48, 5024–5036 CrossRef CAS PubMed.
- T. Dršata, N. Špačková, P. Jurečka, M. Zgarbová, J. Šponer and F. Lankaš, Nucleic Acids Res., 2014, 42, 7383–7394 CrossRef PubMed.
- A. Marin-Gonzalez, C. Aicart-Ramos, M. Marin-Baquero, A. Martín-González, M. Suomalainen, A. Kannan, J. Vilhena, U. F. Greber, F. Moreno-Herrero and R. Pérez, Nucleic Acids Res., 2020, 48, 12917–12928 CrossRef CAS PubMed.
- B. Eslami-Mossallam, R. D. Schram, M. Tompitak, J. van Noort and H. Schiessel, PLoS One, 2016, 11, e0156905 CrossRef PubMed.
- A. Marin-Gonzalez, J. Vilhena, F. Moreno-Herrero and R. Perez, Phys. Rev. Lett., 2019, 122, 048102 CrossRef PubMed.
- H. Yin, M. D. Wang, K. Svoboda, R. Landick, S. M. Block and J. Gelles, Science, 1995, 270, 1653–1657 CrossRef CAS PubMed.
- C. G. Baumann, S. B. Smith, V. A. Bloomfield and C. Bustamante, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 6185–6190 CrossRef CAS PubMed.
- J. F. Marko and E. D. Siggia, Macromolecules, 1994, 27, 981–988 CrossRef CAS.
- A. Noy and R. Golestanian, Phys. Rev. Lett., 2012, 109, 228101 CrossRef PubMed.
- P. Nelson, Biological physics, WH Freeman New York, 2004 Search PubMed.
- J. Gore, Z. Bryant, M. Nöllmann, M. U. Le, N. R. Cozzarelli and C. Bustamante, Nature, 2006, 442, 836–839 CrossRef CAS PubMed.
- C. Bustamante, Z. Bryant and S. B. Smith, Nature, 2003, 421, 423–427 CrossRef PubMed.
- M. Orozco, A. Pérez, A. Noy and F. J. Luque, Chem. Soc. Rev., 2003, 32, 350–364 RSC.
- M. Orozco, A. Noy and A. Pérez, Curr. Opin. Struct. Biol., 2008, 18, 185–193 CrossRef CAS PubMed.
- J. F. Marko, Europhys. Lett, 1997, 38, 183 CrossRef CAS.
- J. Lipfert, G. M. Skinner, J. M. Keegstra, T. Hensgens, T. Jager, D. Dulin, M. Köber, Z. Yu, S. P. Donkers and F.-C. Chou, et al. , Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 15408–15413 CrossRef CAS PubMed.
- K. Liebl, T. Drsata, F. Lankas, J. Lipfert and M. Zacharias, Nucleic Acids Res., 2015, 43, 10143–10156 CAS.
- A. Marin-Gonzalez, J. Vilhena, R. Perez and F. Moreno-Herrero, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 7049–7054 CrossRef CAS PubMed.
- L. D. Landau, E. M. Lifšic, E. M. Lifshitz, A. M. Kosevich and L. P. Pitaevskii, Theory of elasticity: volume 7, Elsevier, 1986, vol. 7 Search PubMed.
- P. Gross, N. Laurens, L. B. Oddershede, U. Bockelmann, E. J. Peterman and G. J. Wuite, Nat. Phys., 2011, 7, 731–736 Search PubMed.
- X. Shi, D. Herschlag and P. A. Harbury, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E1444–E1451 CAS.
- O. D. Broekmans, G. A. King, G. J. Stephens and G. J. Wuite, Phys. Rev. Lett., 2016, 116, 258102 CrossRef PubMed.
- R. S. Mathew-Fenn, R. Das and P. A. Harbury, Science, 2008, 322, 446–449 CrossRef CAS PubMed.
- M. Noe Gonzalez, D. Blears and J. Q. Svejstrup, Nat. Rev. Mol. Cell Biol., 2021, 22, 3–21 CrossRef CAS PubMed.
- J. Ji, D. Karna and H. Mao, Chem. Soc. Rev., 2021, 50, 11966–11978 RSC.
- T. Lionnet, S. Joubaud, R. Lavery, D. Bensimon and V. Croquette, Phys. Rev. Lett., 2006, 96, 178102 CrossRef PubMed.
- M. Gō and N. Gō, Biopolymers, 1976, 15, 1119–1127 CrossRef PubMed.
- W. K. Olson, A. A. Gorin, X.-J. Lu, L. M. Hock and V. B. Zhurkin, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 11163–11168 CrossRef CAS PubMed.
- V. Velasco-Berrelleza, M. Burman, J. W. Shepherd, M. C. Leake, R. Golestanian and A. Noy, Phys. Chem. Chem. Phys., 2020, 22, 19254–19266 RSC.
- W. Vanderlinden, E. Skoruppa, P. J. Kolbeck, E. Carlon and J. Lipfert, PNAS Nexus, 2022, 1, pgac268 CrossRef PubMed.
- A. Marin-Gonzalez, J. Vilhena, F. Moreno-Herrero and R. Perez, Nanoscale, 2019, 11, 21471–21478 RSC.
- K. Huang, Statistical mechanics, John Wiley & Sons, 2008 Search PubMed.
- F. Kriegel, N. Ermann and J. Lipfert, J. Struct. Biol., 2017, 197, 26–36 CrossRef CAS PubMed.
- L. R. Arriaga, I. López-Montero, R. Rodríguez-García and F. Monroy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 061918 CrossRef PubMed.
- J. Wang, P. Cieplak and P. A. Kollman, J. Comput. Chem., 2000, 21, 1049–1074 CrossRef CAS.
- A. Pérez, I. Marchán, D. Svozil, J. Sponer, T. E. Cheatham III, C. A. Laughton and M. Orozco, Biophys. J., 2007, 92, 3817–3829 CrossRef PubMed.
- M. Zgarbová, M. Otyepka, J. Šponer, A. Mládek, P. Banáš, T. E. Cheatham III and P. Jurecka, J. Chem. Theory Comput., 2011, 7, 2886–2902 CrossRef PubMed.
- S. Assenza and R. Pérez, J. Chem. Theory Comput., 2022, 18, 3239–3256 CrossRef CAS PubMed.
- D. Frenkel and B. Smit, Understanding molecular simulation: from algorithms to applications, Elsevier, 2001, vol. 1 Search PubMed.
- R. D. Kamien, T. C. Lubensky, P. Nelson and C. S. O'Hern, Europhys. Lett, 1997, 38, 237 CrossRef CAS.
- F. Kilchherr, C. Wachauf, B. Pelz, M. Rief, M. Zacharias and H. Dietz, Science, 2016, 353, aaf5508 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr06324g |
| This journal is © The Royal Society of Chemistry 2023 |

