Tuning interfacial two-component superconductivity in CoSi₂/TiSi₂ heterojunctions via TiSi₂ diffusivity

Abstract

We report the observation of enhanced interfacial two-component superconductivity possessing a dominant triplet component in nonmagnetic CoSi₂/TiSi₂ superconductor/normal-metal planar heterojunctions. This is accomplished through the detection of odd-frequency spin-triplet even-parity Cooper pairs in the diffusive normal-metal component of T-shaped proximity junctions. We show that by modifying the diffusivity of the normal-metal part, the transition temperature enhancement can be tuned by a factor of up to 2.3 while the upper critical field increases by up to a factor of 20. Our data suggest that the C49 phase of TiSi₂, which is stabilized in confined geometries, underlies this enhancement. These findings are addressed via a Ginzburg–Landau model and the quasi-classical theory. We also relate our findings to the enigmatic 3-K phase reported in Sr₂ RuO₄.

---

1. Introduction

The interest in novel quantum states of matter and in particular non-conventional superconducting states have been ever increasing. This development is driven by both scientific interest and technological prospects,^1–4 and includes high-temperature and interface superconductivity.^5–7 Of special interest are triplet superconductors which can host Majorana zero modes.^4,8,9 These, in turn, have attracted considerable attention as potential building blocks for fault-tolerant quantum computing. In terms of realizing practical quantum devices, planar heterostructures with spin-triplet pairing compatible with existing silicon-based integrated-circuit technology are particularly desirable. A major challenge, however, is the identification of materials systems hosting triplet superconductivity as well as the utilization of such Cooper pairs at the microscopic scale.

A three-terminal T-shaped proximity structure comprised of a superconductor (S) in contact with a diffusive normal metal (N), schematically shown in Fig. 1(a), had been proposed to phase-sensitively distinguish triplet from singlet superconductors.¹⁰ This T-shaped proximity structure detects triplet pairing through a zero-bias conductance peak (ZBCP) that results from the generation of odd-frequency spin-triplet even-parity pairs in the normal diffusive side of the S/N interface as illustrated in Fig. 1(b).^11–14 This is referred to as the anomalous proximity effect (APE) to distinguish it from the case of a singlet superconductor where a conductance dip ensues.

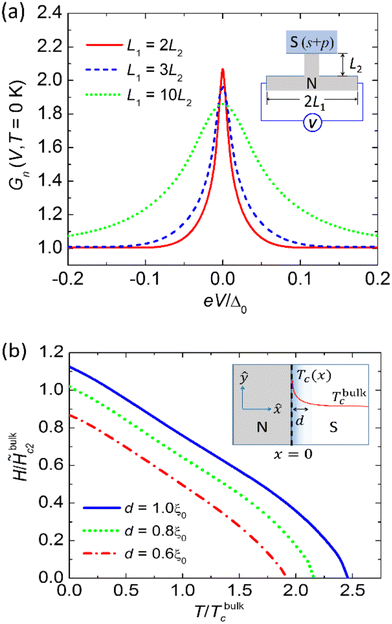
Fig. 1 (a) Illustration of a T-shaped proximity structure proposed in ref. 10 to distinguish a triplet from a singlet superconductor (S) and where S forms the arm of the letter ‘T’. N is the diffusive normal metal component of the structure. This sketch also illustrates the S/N interface (in red) where the interfacial superconductivity with its enhanced onset temperature forms. R_B denotes the barrier resistance of this interface. R_N is the resistance of the N component. (b) The predicted zero-bias conductance peak (dip) for a spin-triplet (spin-singlet) S. (c) SEM image of device B1 together with the schematic 4-probe measurement configuration. The magnetic field direction is indicated. (d) Schematics of our CoSi₂/TiSi₂ T-shaped proximity devices and their various voltage-electrode (VE) pairs. 2L₁ is the voltage-electrode (VE) separation. L₂ is the length of the normal metal (N) segment connecting to superconductor (S).

Yet, the fabrication of such T-shaped structures has proven difficult for many materials including superconductors.^15,16 The successful fabrication of high-quality CoSi₂/TiSi₂ T-shaped proximity structures on silicon was only recently achieved.^17,18 The availability of these structures established the existence of triplet pairing in CoSi₂ on Si(100) via the observation of the APE.¹⁷ CoSi₂ is a superconducting material that is widely used in the semiconductor industry with a superconducting transition temperature (T^bulk_c) of 1.3 K. Bulk specific heat measurements as well as theoretical estimates suggest that CoSi₂ is a phonon-mediated spin-singlet superconductor.^19–21

Generalizing the proposal of Asano et al.¹⁰ to include the effect of spin–orbit coupling (SOC), the findings reported in ref. 17 have been interpreted in terms of two-component superconductivity with a dominant triplet component.²² This interpretation is in line with the finding that the accompanying interface between CoSi₂ and the Si(100) substrate²³ gives rise to a SOC which exceeds the bulk CoSi₂ superconducting energy gap Δ₀ by a factor of ∼30, see ref. 17. We note in passing that yet another route to triplet pairing is based on proximity structures involving ferromagnets.²⁴ These systems too offer a way of realizing odd-frequency pairing states near their superconductor/ferromagnetic metal interfaces.^25,26

In this manuscript, we demonstrate that an enhanced two-component superconductivity emerges in the vicinity of the S/N interface formed by CoSi₂ (S) and TiSi₂ (N) which is reminiscent of the enigmatic ‘3-K phase’ reported in Sr₂RuO₄.²⁷ We establish that the transition temperature and upper critical field can be tuned by the diffusive properties of the normal metal component. This is accomplished via the APE that has been reported in these structures.¹⁷ An SEM image of a typical device is shown in Fig. 1(c) while a sketch of it is provided in Fig. 1(d). Clearly discernible are the various voltage-electrode (VE) pairs which allow us to relate the ZBCP to the proximity of superconducting CoSi₂/Si. The device parameters of all devices used in the present study are compiled in Table 1. Fig. 1(a) also highlights the CoSi₂/Ti₂Si₂ interface (in red) where the interfacial superconductivity forms as we discuss below.

Table 1 Device parameters of CoSi₂/TiSi₂ T-shaped superconducting proximity structures. T_a is the thermal annealing temperature for the formation of the TiSi₂ component. L₁ and L₂ are defined in Fig. 1(d). R_N (ρ_N) is the residual resistance (resistivity) of the TiSi₂ component at 4 K. ΔG_n = G_n − 1 is the increase in normalized differential conductance above the normal-state value (=1). FWHM is the full-width at half-maximum of the ZBCP. Thouless energy is defined by E_Th ≈ ħD/L₁², where D is the electron diffusion constant of the TiSi₂ component. T^onse_c is the onset temperature of the APE (except for B2m), defined by ΔG_n(T = T^onset_c) = 10⁻³ × ΔG_n (T = 0.37 K). G_J,□ is the S/N junction (interface) conductance per unit area. 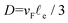The diffusion constant was calculated through the relation , with v_F = ħ(3π²n)^1/3/m* and , where m* was approximated by the free-electron mass. The carrier concentration n for devices B3 and B5 was taken to be that of C54 phase, while n for the rest devices was taken to be that of C49 phase

Device	T a (°C)	L 1 (μm)	L 2 (μm)	R N (Ω)	ρ N (μΩ cm)	ΔGn (at 0.37 K)	FWHM (meV)	E Th (meV)	D (cm^2 s^−1)	T c ^onset (K)	G J,□ (4 K) (Ω^−1 μm^−2)
a T ^onsetc was extracted from Gn(0, T, 0) of the S/N junction geometry to minimize any possible experimental uncertainty. b Device B4 became unstable. Conductance spectra could not be completed.
B1	750	0.42	0.39	57.5	197	112%	0.18	0.0012	3.1	2.94	1.46
B1m	750	0.42	0.39	55.8	191	31%	0.22	0.0012	3.2	2.84	1.47
B2	750	0.20	0.66	12.0	79.8	9.3%	0.04	0.013	7.7	2.33	0.34
B2m	750	0.20	0.66	12.7	84.3	1.0%	0.056	0.012	7.3	2.03^a	0.32
B3	780	0.23	0.10	0.346	2.14	5.9%	0.026	0.13	106	2.14	1.03
B4^b	750	0.34	0.18	73.3	195	1.8%	0.24	0.0019	3.2	1.70	—
B5	800	0.45	0.32	1.31	3.34	0.13%	0.03	0.023	67.9	1.50	5.18
B5m3	800	0.45	0.32	19.1	48.6	66%	0.20	0.004	12.7	2.10	0.93

---

2 Results

In contrast to CoSi₂ in the thermodynamic limit, parity is no longer a good quantum number in the heterostructure due the presence of interfaces. This is reflected in the gap structure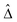:which is a combination of singlet Δ_s and triplet Δ_t components, where is a matrix in spin-space, and d is the d-vector of triplet pairing, σ, σ_y are the Pauli matrices, and 1 is the identity matrix in spin-space. A dominant triplet component, inferred through the APE that drives a ZBCP and a superconducting transition temperature comparable with T^bulk_c was demonstrated in ref. 17 and 22. This is compatible with d along the SOC field.^22,28,29 Otherwise, a suppression of T_c well below T^bulk_c is expected for a dominant triplet component.

We here report our observation of interfacial superconductivity in CoSi₂/TiSi₂ heterostructures with an onset temperature (T^onset_c) that exceeds T^bulk_c by up to a factor 2.3 and that also possesses a dominant triplet component. We present a Ginzburg–Landau (GL) analysis in terms of this two-component superconductivity order parameter that encompasses the T^onset_c enhancement and explores its particular features. Implications and possible applications are also mentioned.

This analysis also sheds light on the different roles played by the CoSi₂/Si(100) and the CoSi₂/TiSi₂ interfaces forming CoSi₂/TiSi₂ heterostructures. The thickness of the CoSi₂/Si films in this work is ≃105 nm while that of the TiSi₂ part is ≃125 nm thick and ≃(0.2–0.4) μm wide. TiSi₂ is a diffusive normal metal and remains metallic down to at least a temperature (T) of 50 mK.¹⁷ The primary quantity of interest of the CoSi₂/TiSi₂ T-shaped proximity junction is the normalized conductance G_n(V, T, B) = G(V, T, B)/G₀ where G denotes the differential conductance, G(V, T, B) = dI(V, T, B)/dV with I the current, V the bias voltage, B the magnetic field, and G₀ is the residual conductance of the device in the absence of superconductivity. Practically, we take G₀ = G(0, 4 K, 0).

Fig. 2(a) illustrates the basic feature of the APE in the representative device B5m3. It depicts G_n(V, 0.365 K, 0) measured by using different VE pairs which define different segments of the TiSi₂ component [cf.Fig. 1(c) and (d)]. In all cases, I was applied through the outermost electrode pair (1,6). Fig. 2(a) reveals large amplitudes of the ZBCPs measured with VE pairs (3,4), (2,5) and (1,6). The inset shows a zoom-in of the ZBCPs measured with the VE pairs (1,2) and (2,3), which are located away from the S/N interface. We see that in this case the amplitudes of the ZBCPs are small. In fact, the G_n curve measured with the VE pair (1,2) is flat. It then follows that the ZBCP must arise from odd-frequency spin-triplet Cooper pairs through the APE^10,17,22 and cannot be of any other origin (cf. additional discussion in ESI†). Owed to the properties of the T-shaped proximity structure, the ZBCP thus serves as a diagnostics for the presence of triplet pairing in CoSi₂/Si and/or CoSi₂/TiSi₂ interface.

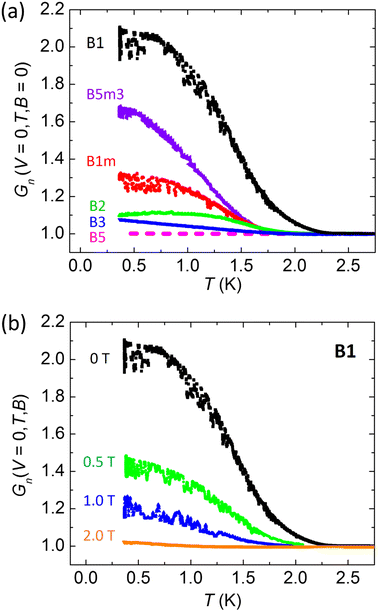
Fig. 2 (a) Normalized conductance spectra G_n(V, 0.365 K, 0) of device B5m3 measured with various voltage-electrode (VE) pairs indicated by the electrode numbers in Fig. 1(d). I was always applied using the electrode pair (1,6). Inset: a zoom-in of G_n(V, 0.365 K, 0) measured with VE pairs (1,2) and (2,3). (b) G_n(V, T, 0) of device B1 recorded at several T values. Inset: a zoom-in of the 2.5 K curve. (c) G_n(V, 0.37 K, B) of device B1 in several B values. Inset: a zoom-in of the 2.0 T curve.

Fig. 2(b) shows G_n(V, T, 0) vs. V for device B1 at several T values. ZBCPs are clearly discernible, which are gradually suppressed with increasing T, thus establishing the presence of dominant triplet pairing in the junction. The inset reveals that the ZBCP persists up to at least 2.5 K. Fig. 2(c) displays G_n(V, 0.37 K, B) of the same device in several B fields and at T = 0.37 K. While the ZBCP is gradually suppressed with increasing B, it persists up to at least 2 T§ (inset).

We find that in a number of devices the highest T at which the ZBCP is discernable is significantly enhanced over T^bulk_c, i.e., T^onset_c > T^bulk_c in these devices. The enhanced T^onset_c value is not only enhanced over those in the T-shaped structures studied in ref. 17 (T^onset_c ≲ 1.4 K), but also with respect to the T_c value (≈1.5 K) of epitaxial CoSi₂/Si films²³ while the amplitude of the ZBCP is strongly enhanced up to ≈210% with respect to G₀. This is illustrated in Fig. 3(a). Devices B1, B2, B3 and B5 were measured as grown (cf. ESI†).

Fig. 3 (a) G_n(0, T, 0) in six devices vs. temperature T. (b) G_n(0, T, B) of device B1 in several B fields.

The upper critical field is significantly enhanced as well. Fig. 3(b) depicts G_n(0, T, B) of device B1 for several B fields. G_n(0, T, B) is gradually suppressed with increasing B. Yet, a small proximity effect is still visible in B = 2.0 T which is much higher than the in-plane upper critical field (≤0.12 T) of CoSi₂/Si films.¹⁷ Additional conductance spectra are provided in the ESI.†

In order to address the origin of this phenomenon the junctions underwent thermal cyclings up to room temperature followed by the cooling down for further measurements, see the ESI† for additional information. (Following thermal cycling, the devices were renamed such that device Bi (i = 1, … 5) became Bim after the first thermal cycling and Bimj (j > 1) after the j^th subsequent thermal cycling.) The G_n (0, T, 0) of device B1 (B1m) increases with decreasing T below T^onset_c = 2.94 K (2.84 K), reaching 212% (131%) at 0.365 K. There are visible conductance fluctuations which are probably induced by dynamical structural defects in this particular device,³⁰ see Fig. 3.

The quasi-classical theory discussed below associates the height of the ZBCP with the ratio of the normal-metal and interface conductances which leads us to study the relation between T^onset_c and the diffusivity of the device. Fig. 4 brings out this relation and reveals that the measured T^onset_c value is strongly correlated with the high residual resistivity ρ_N, i.e., low electron diffusion constant (D) of the N part. By and large, a higher T^onset_c is found in devices with higher ρ_N or in other words systems with lower D. The reason for the variation in ρ_N of TiSi₂ is connected to its occurrence in mainly two phases, a base-centered phase (C49) and a face-centered phase (C54).^31,32 C49 is metastable and contains large amounts of stacking faults³³ which lead to an order of magnitude larger resistivity [ρ(300 K) ≃ (100–200) μΩ cm] than the C54 phase [ρ(300 K) ≃ (17–25) μΩ cm].

Fig. 4 Onset temperature T^onset_cvs. inverse residual resistivity 1/ρ_N of TiSi₂, i.e., the normal-metal component. Devices of the present study are marked by red bullets (). For comparison, the T^onset_c values (■) taken from ref. 17 are also included.

Although C49 is metastable in the thermodynamic limit it can be stabilized in spatial confinement and systems at the microscale due to a lack of nucleation sites for C54. The annealing temperature, T_a, at which the TiSi₂ in the junction forms, see Table 1, affects its composition with respect to C54/C49 such that T_a ≳ 800° C favors formation of C54.^33,34 The C49 structure possesses a slightly larger volume than the C54 structure so that phase changes from C49 to C54 and vice versa are accompanied by strain.³⁵ This gives a qualitative understanding of the effects of T_a and thermal cycling on T^onset_c. Devices primarily composed of C54 such as B5 are transformed into a C49 rich composition and a concomitantly large T^onset_c as in device B1. The changes induced by thermal cycling in devices primarily composed of C49 are less pronounced (see ESI† for details). This leads us to suspect that C49 grains are more stable near the CoSi₂/TiSi₂ interface and that its microscopic properties drive the formation of triplet pairing at the interface at the elevated T^onset_c compared with T^bulk_c (CoSi₂). The data point of Fig. 4 with the largest diffusivity seemingly defies the overall trend between T^onset_c and ρ_N. This outlier may represent an interface whose properties are not well characterized by the diffusivity of the wire or this data point indicates that the onset temperature goes through a minimum as a function of the diffusivity reminiscent of what has been observed in Sr₂RuO₄ under strain.³⁶

We address the experimental findings in terms of a quasi-classical theory for three-terminal proximity structures as formed by the CoSi₂/TiSi₂ heterojunctions. The diffusive character of the N part of our junctions requires a treatment of the transport equations in the Usadel limit³⁷ where the results can differ from those obtained in the weakly disordered limit.³⁸ For the superconducting order parameter, we consider a SOC induced s + p pairing state with a dominant triplet component.²² Within the formulation of the circuit theory,^39–42 an insulating barrier is expressed as a delta function [ZE_Fk_F⁻¹δ(x)] at the S/N interface. The weight of the barrier can be expressed in terms of a dimensionless parameter Z, Fermi energy E_F, and the Fermi wavenumber k_F. A higher ratio of R_N/R_B, i.e., resistance of the N component (R_N) over barrier resistance (R_B), results in an APE over a broader energy range and thus in an increase in the full-width-half-minimum (FWHM) of the ZBCP.¹⁰ The zero-bias value itself, however, is (roughly) independent of R_N/R_B if electron dephasing is ignored in the diffusive N component of the junction.

In Fig. 5(a), we keep R_B, Δ_t, Δ_s and Z fixed, and vary L₁ according to the experiments as shown in Fig. 2(a). Importantly, when VE configuration is changed, the S/N interface properties remain fixed but as L₁ changes so will R_N. We find that the ZBCP becomes broader, in qualitative agreement with Fig. 2(a). While this variation of FWHM with L₁ agrees with the experiment, we find that the inclusion of a small amount of electron dephasing is required to reproduce the experimental behavior of G_n (V = 0), i.e., a suppression of G_n (V = 0) with increasing L₁. In diffusive metals, existence of a finite electron dephasing rate in low-T regimes has been reported for long, but its microscopic origin(s) are yet to be fully identified.⁴³ Magnetic impurities as a source of dephasing however seems unlikely as their presence in our heterojunctions has been ruled out.¹⁷ Thus, the quasi-classical approach supports the interpretation that for the C49 phase, R_N is higher than in the C54 phase, giving rise to a larger ZBCP provided other parameters are kept constant. The higher ρ_N value of the devices indicating the presence of the C49 phase also results in an enhanced T^onset_c as shown in Fig. 4 and a strong proximity-induced odd-frequency pairing in the N part of the junctions. The robustness of ZBCPs in these devices supports the interpretation in terms of the SOC generated two-component superconductivity with a dominant triplet component, which is essential for the ZBCP.

Fig. 5 (a) Calculated G_n(V, T = 0, B = 0) for a T-shaped junction obtained from the quasi-classical theory for a s + p superconductor for various values of L₁. The triplet gap Δ_t = 2Δ₀/√5, the singlet gap Δ_s = Δ₀/√5, Z = 2, and electron dephasing rate ħ/τ_φ = 0.05Δ₀. The value of L₂ is fixed, R_N/R_B = 100L₁/L₂ and Δ₀ is 20ħD/L₂², where D is the diffusion constant of N. Inset: Junction geometry. (b) The H–T phase diagram based on GL theory for the emergent superconductivity due to the enhanced superconducting correlation near the S/N interface for several values of d in units of ξ₀. T and H are expressed in units of T^bulk_c and H̃^bulk_c2, respectively. Inset: Illustration of the S/N interface region of effective width d. The red curve portrays the enhanced T_c(x) near the interface.

3 Discussion

The quasi-classical theory provides a good explanation for the robustness of the ZBCPs in T-shaped junctions. It does, however, not take into account the enhanced superconductivity found in these devices. As the interface plays a vital role in the enhancement of superconductivity, we conclude that somewhere near or at the S/N interface there exists another superconducting phase whose T_c is higher than T^bulk_c. The microscopic origin of such an enhancement could be changes in the electronic structure or the softening of phonon modes near the interface, driven by the C49 phase of TiSi₂. As in the cases of YIr₂–Ir and EuIr₂–Ir eutectic systems, the strain induced by large volume C49 grains can cause the softening of the phonon mode, which can likely result in a region with stronger pairing correlations near the interface.^44,45 Correlation effects due to a possible band narrowing of Co-derived 3d bands at the interface might also contribute to the observed enhancement. Independent of the microscopic mechanism, our results indicate that the interface superconductivity is stable against interface-induced disorder and possesses a dominant triplet component.

Here we resort to a GL approach to understand this phenomena qualitatively. This Rashba SOC causes a band splitting that gives rise to two bands with opposite helicities and mixing of singlet and triplet pairing channels in the superconducting state. The free energy for such a system in a one-dimensional representation reads,⁴⁶, here 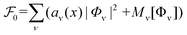is the usual GL free energy for each individual component, the subscript ν = ± represents the two components of the order parameter, and M[Φ] contains all higher order and gradient terms (technical details are relegated to the ESI†). The coefficient a_v is α_v(T − T_cv). We take the superconductor to be in the clean limit. is the coupling between the two components, a negative value of the coefficient c ensures that both order parameter have identical phases and is the free energy density of the non-superconducting state in the absence of a magnetic field (H). is the contribution from the magnetic field ( denotes the total magnetic field while refers to the external field as is common in the GL literature. H has to be identified with B of Fig. 2 and 3). is a Lifshitz invariant term that leads to s magneto-electric coupling and determines the effect of superconducting order on spin-polarization (cf. ESI†).

We take the S/N interface at x = 0 and assume the system to be homogeneous along the other directions. We restrict ourselves to the experimental field configuration, i.e., along the interface in the plane (ŷ). The coefficients of the quadratic terms are taken to be spatially varying to model the enhanced superconductivity near the interface. The information about the interface is embedded in the spatial dependence of these quadratic coefficients.^47,48a_±(x) is α_±[T − T_c±(x)], where and . Here η_±/c are the dimensionless parameters determining the amount of T_c enhancement, and d is the width of the effective interface. Minimizing the free energy leads to a set of differential equations (see ESI† for details). At the S/N interface we apply the De Gennes's boundary conditions,^49,50, where the extrapolation length is a characteristic length scale associated with the induced superconducting correlations. Note, in contrast to conventional superconductors, here cannot be identified with the dirty limit of the superconducting correlation length in the N segment, because it does not account for the physics of odd-frequency pairs, which are vital in the present case. We therefore treat as a phenomenological parameter.

Fig. 5(b) shows the temperature and magnetic field phase diagram for appearance of onset order at the interface for various d values. The onset temperature and magnetic field are obtained by minimizing the free energy with De Gennes's boundary conditions with extrapolation , where ξ₀ is the coherence length at T = 0 for the bulk superconductor. Within the GL formalism, T^onset_c exceeds T^bulk_c in the low-field limit, and the T^onset_c decreases with increasing field. In our calculations, we find that the onset magnetic field in the low-T limit is comparable to H̃^bulk_c2 ≡ Φ₀/(2πξ₀²), which is a magnetic field scale of the order of orbital upper critical fields. However, quantitatively the onset magnetic field is much smaller compared to the experiment, despite a reasonable T^onset_c obtained from theoretical calculations.

The experiment finds that in the low T limit, the onset magnetic field exceeds the upper critical field of the bulk superconductor by a factor ∼100, see ref. 19 and that of CoSi₂/Si films by ∼20, see ref. 17. The experimentally observed critical magnetic field is higher than 2 T and this value is comparable to the Pauli-limited field for the bulk superconductor (∼2.4 T). The interface induced order survives up to (10–12) ξ₀ from the surface (cf. ESI†). As shown in Fig. 5(b), T^onset_c for the appearance of such order above T^bulk_c is very sensitive to the width of the interface. As the interface region becomes thinner, T^onset_c drops rapidly. In the devices with C49 phase, the interface region is expected to be relatively more disordered and its effective width is expected to be high compared to the low-ρ_N devices, due to smaller grain sizes or possible incomplete C49–C54 transformation (see ESI† for additional information).

Thus, the GL functional provides an effective model for the CoSi₂/TiSi₂ heterojunctions, which can guide future investigations. is the magneto-electric coupling term. The presence of this term suggests that the (CoSi₂/Si)/TiSi₂ system is an ideal system to explore, e.g., the superconducting diode effect and charge transport effects.^51,52 Consequences of this term with respect to the magnetic field direction are currently explored. Our results also demonstrate the stability of triplet dominant pairing, and thus the prevalence of odd-frequency pairs in heterostructures.^13,22,53,54 There is however a noticeable difference between its earlier realizations and the present case. The formation of odd-frequency pairs in (CoSi₂/Si)/TiSi₂ junctions does not require the proximity of magnetic order.

The enhanced superconductivity in CoSi₂/TiSi₂ is reminiscent of the elusive ‘3-K phase’ in the enigmatic transition metal compound Sr₂RuO₄.^27,55–57 In fact, a similar model to our GL functional has originally been used to address the 3-K phase.^47,48 There, it has been speculated that superconducting Ru islands are responsible for the 3-K phase. In contrast, here the highly diffusive C49 phase appears to drive the interface superconductivity while the C49 and C54 TiSi₂ phases remain metallic down to lowest temperatures (see Fig. S2 of the ESI†). Moreover, here, the interface superconductivity possesses a dominant triplet component which is robust with regard to external magnetic fields.

4 Conclusions

T-shaped proximity structures have established the existence of a dominant triplet component in superconducting films on Si(100) due to the large Rashba spin–orbit coupling. Here, we have shown that the CoSi₂/TiSi₂ interface of such T-shaped proximity devices develops two-component superconductivity with a dominant triplet component at an enhanced onset temperature compared to that of CoSi₂ films on Si(100). This onset temperature enhancement by a factor of up to 2.3 is accompanied by an upper critical field increase of up to a factor of 20. We demonstrated that the diffusivity of TiSi₂ which forms the normal metal component of the junction determines the enhancement and related this to the highly diffusive C49 phase of TiSi₂ which appears to be stabilized near the interface. Triplet superconductivity in the T-shaped proximity devices is inferred from the observation of a zero-bias conductance peak that is caused by the anomalous proximity effect. In-depth studies of the interface, e.g., via electron-energy loss spectroscopy is left for future investigations. A quasi-classical theory was presented to understand the conductance spectra of the T-shaped proximity structures and a phenomenological Ginzburg–Landau theory was used to model the enhanced interface superconductivity.

Unconventional and functional properties of superconductivity near interfaces and in confined systems are of considerable interest. In part this is fueled by potential future applications. The silicon-based heterojunctions with dominant triplet pairing reported here are amenable to existing microfabrication techniques and are promising building blocks for the fabrication of superconducting devices and thus for quantum technology applications.

Author contributions

S. P. C. conducted the experiment, V. M. performed the calculations, J. J. L., S. K. and F. Z. conceived and supervised the research. All authors discussed the results and reviewed the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank S. S. Yeh for experimental help. This work was supported by the National Science and Technology Council of Taiwan through grant numbers MOST 106-2112-M-009-007-MY4 and 110-2112-M-A49-015, and by the Ministry of Education of Taiwan through the Higher Education Sprout Project. V. M., Y. L. and F. C. Z. are partially supported by NSFC grants 11674278 and 11920101005 and by the priority program of the Chinese Academy of Sciences grant no. XDB28000000, and by the China Postdoctoral Science Foundation under grant no. 2020M670422 (Y. L.). S. K. acknowledges support by Yushan Fellowship Program of the Ministry of Education, Taiwan.

References

1. N. Read and D. Green, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 10267–10297.
2. C. Nayak, S. H. Simon, A. Stern, M. Freedman and S. Das Sarma, Rev. Mod. Phys., 2008, 80, 1083–1159.
3. X.-L. Qi and S.-C. Zhang, Rev. Mod. Phys., 2011, 83, 1057–1110.
4. J. Alicea, Rep. Prog. Phys., 2012, 75, 076501.
5. G. R. Stewart, Adv. Phys., 2017, 66, 75–196.
6. J. Pereiro, A. Petrovic, C. Panagopoulos and I. Božović, Interface superconductivity: History, development and prospects, cond-mat/1111.4194, 2011.
7. C.-L. Song, X.-C. Ma and Q.-K. Xue, MRS Bull., 2020, 45, 366–372.
8. A. Huxley, I. Sheikin, E. Ressouche, N. Kernavanois, D. Braithwaite, R. Calemczuk and J. Flouquet, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 144519.
9. J. Yang, J. Luo, C. Yi, Y. Shi, Y. Zhou and G.-Q. Zheng, Sci. Adv., 2021, 7, eabl4432.
10. Y. Asano, Y. Tanaka, A. A. Golubov and S. Kashiwaya, Phys. Rev. Lett., 2007, 99, 067005.
11. Y. Tanaka, Y. Asano, A. A. Golubov and S. Kashiwaya, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 140503.
12. Y. Tanaka, Y. Asano, A. A. Golubov and S. Kashiwaya, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 059901.
13. Y. Tanaka and A. A. Golubov, Phys. Rev. Lett., 2007, 98, 037003.
14. S.-I. Suzuki, A. A. Golubov, Y. Asano and Y. Tanaka, Phys. Rev. B, 2019, 100, 024511.
15. H. Courtois, P. Charlat, P. Gandit, D. Mailly and B. Pannetier, J. Low Temp. Phys., 1999, 116, 187–213.
16. A. P. Mackenzie, T. Scaffidi, C. W. Hicks and Y. Maeno, npj Quantum Mater., 2017, 2, 40.
17. S.-P. Chiu, C. C. Tsuei, S.-S. Yeh, F.-C. Zhang, S. Kirchner and J.-J. Lin, Sci. Adv., 2021, 7, eabg6569.
18. S.-P. Chiu, W.-L. Lai and J.-J. Lin, Jpn. J. Appl. Phys., 2021, 60, 088002.
19. B. T. Matthias and J. K. Hulm, Phys. Rev., 1953, 89, 439–441.
20. K. Tsutsumi, S. Takayanagi and T. Hirano, Phys. B, 1997, 237–238, 310–311.
21. L. F. Mattheiss and D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 10623–10627.
22. V. Mishra, Y. Li, F.-C. Zhang and S. Kirchner, Phys. Rev. B, 2021, 103, 184505.
23. S.-P. Chiu, S.-S. Yeh, C.-J. Chiou, Y.-C. Chou, J.-J. Lin and C.-C. Tsuei, ACS Nano, 2017, 11, 516–525.
24. A. I. Buzdin, Rev. Mod. Phys., 2005, 77, 935–976.
25. F. S. Bergeret, A. F. Volkov and K. B. Efetov, Rev. Mod. Phys., 2005, 77, 1321–1373.
26. A. Pal, J. A. Ouassou, M. Eschrig, J. Linder and M. G. Blamire, Sci. Rep., 2017, 7, 40604.
27. Y. Maeno, T. Ando, Y. Mori, E. Ohmichi, S. Ikeda, S. NishiZaki and S. Nakatsuji, Phys. Rev. Lett., 1998, 81, 3765–3768.
28. L. P. Gor'kov and E. I. Rashba, Phys. Rev. Lett., 2001, 87, 037004.
29. P. A. Frigeri, D. F. Agterberg, A. Koga and M. Sigrist, Phys. Rev. Lett., 2004, 92, 097001.
30. S.-S. Yeh, W.-Y. Chang and J.-J. Lin, Sci. Adv., 2017, 3, e1700135.
31. L. F. Mattheiss and J. C. Hensel, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 7754–7759.
32. M. Ekman and V. Ozoliņš, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 4419–4424.
33. Z. Ma and L. H. Allen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 13501–13511.
34. H. Jeon, C. A. Sukow, J. W. Honeycutt, G. A. Rozgonyi and R. J. Nemanich, J. Appl. Phys., 1992, 71, 4269–4276.
35. C. Colinet, W. Wolf, R. Podloucky and A. Pasturel, Appl. Phys. Lett., 2005, 87, 041910.
36. C. W. Hicks, D. O. Brodsky, E. A. Yelland, A. S. Gibbs, J. A. N. Bruin, M. E. Barber, S. D. Edkins, K. Nishimura, S. Yonezawa, Y. Maeno and A. P. Mackenzie, Science, 2014, 344, 283–285.
37. K. D. Usadel, Phys. Rev. Lett., 1970, 25, 507–509.
38. T. Löthman, C. Triola, J. Cayao and A. M. Black-Schaffer, Phys. Rev. B, 2021, 104, 094503.
39. Y. V. Nazarov, Superlattices Microstruct., 1999, 25, 1221–1231.
40. Y. Tanaka, Y. V. Nazarov and S. Kashiwaya, Phys. Rev. Lett., 2003, 90, 167003.
41. Y. Tanaka, Y. V. Nazarov, A. A. Golubov and S. Kashiwaya, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 144519.
42. Y. Tanaka, Y. V. Nazarov, A. A. Golubov and S. Kashiwaya, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 219907.
43. J. J. Lin and J. P. Bird, J. Phys.: Condens. Matter, 2002, 14, R501–R596.
44. B. T. Matthias, G. R. Stewart, A. L. Giorgi, J. L. Smith, Z. Fisk and H. Barz, Science, 1980, 208, 401–402.
45. H. Suhl, B. T. Matthias, S. Hecker and J. L. Smith, Phys. Rev. Lett., 1980, 45, 1707–1708.
46. M. Sigrist, AIP Conf. Proc., 2009, 1162, 55–96.
47. M. Sigrist and H. Monien, J. Phys. Soc. Jpn., 2001, 70, 2409–2418.
48. H. Kaneyasu, Y. Enokida, T. Nomura, Y. Hasegawa, T. Sakai and M. Sigrist, Phys. Rev. B, 2019, 100, 214501.
49. P. G. De Gennes, Rev. Mod. Phys., 1964, 36, 225–237.
50. A. Samoilenka and E. Babaev, Phys. Rev. B, 2020, 101, 134512.
51. F. Ando, Y. Miyasaka, T. Li, J. Ishizuka, T. Arakawa, Y. Shiota, T. Moriyama, Y. Yanase and T. Ono, Nature, 2020, 584, 373–376.
52. R. Wakatsuki, Y. Saito, S. Hoshino, Y. M. Itahashi, T. Ideue, M. Ezawa, Y. Iwasa and N. Nagaosa, Sci. Adv., 2017, 3, e1602390.
53. Y. Tanaka, M. Sato and N. Nagaosa, J. Phys. Soc. Jpn., 2012, 81, 011013.
54. J. Linder and A. V. Balatsky, Rev. Mod. Phys., 2019, 91, 045005.
55. T. Ando, T. Akima, Y. Mori and Y. Maeno, J. Phys. Soc. Jpn., 1999, 68, 1651–1656.
56. Z. Q. Mao, K. D. Nelson, R. Jin, Y. Liu and Y. Maeno, Phys. Rev. Lett., 2001, 87, 037003.
57. H. Wang, J. Luo, W. Lou, J. E. Ortmann, Z. Q. Mao, Y. Liu and J. Wei, New J. Phys., 2017, 19, 053001.

---

Footnotes

† Electronic supplementary information (ESI) available: Additional data, technical details, auxiliary discussions supporting the main conclusions. See DOI: https://doi.org/10.1039/d2nr05864b

‡ These authors contributed equally to this work.

§ In this work, the B field was applied in the CoSi₂/Si plane and parallel to the S/N interface.

---