Growth pathways of exotic Cu@Au core@shell structures: the key role of misfit strain

Abstract

The CuAu system is characterized by a large lattice mismatch which causes a misfit strain in its core@shell architectures. Here we simulate the formation of Cu@Au core@shell nanoparticles by Au deposition on a preformed seed, and we study the effect of the shape and composition of the starting seed on the growth pathway. Three geometric shapes of the starting seed are considered: truncated octahedra, decahedra and icosahedra. For each shape, we consider two compositions, pure Cu and CuAu, at equicomposition and intermixed chemical ordering. Our results show that the shape and composition of the seed have significant effects on the growth pathways of Cu@Au core@shell nanoparticles. When starting with icosahedral seeds, the growing structure stays in that motif always. When starting with truncated octahedral and decahedral seeds, we have observed that there is a clear difference between the pure and intermixed seeds. For pure seeds, the growth often leads to exotic structures that are obtained after some structural transformations. For mixed seeds, the growth leads to quite regular structures resembling those obtained for pure metals. These growth pathways originate from strain relaxation mechanisms, which are rationalized by calculating the atomic level stress.

---

1 Introduction

In the recent past, bimetallic nanoparticles (NPs) have become of great interest in different areas because of the variety of their structures and properties. Bimetallic NPs can display various chemical arrangements of the constituent elements, which include intermixing patterns, core@shell and Janus structures.¹ Core@shell nanoparticles composed of a supporting core and a noble metal shell are of particular interest for their applications in catalysis. In core@shell NPs, the lattice mismatch between the core and shell regions may indeed either enhance or suppress surface strain.² Strained surfaces exhibit electronic properties that influence the adsorption energy of molecules and their reactivity, allowing the fine-tuning of their catalytic performance.^3–8

Previous works showed that the strain in core@shell nanoparticles depends both on the shell thickness and the lattice mismatch.^2,9–11 Because core@shell nanocrystals can only sustain a limited magnitude of strain, continuous shell growth will trigger structural deformation processes to release the excess strain energy.¹² Depending on the magnitude of the misfit, strain relaxation in the core@shell nanocrystals can be achieved through different mechanisms. Gamler et al. have investigated the strain in core@shell nanocubes as a function of lattice mismatch and shell thickness.⁹ Using geometric phase analysis combined with molecular dynamics simulations, they have shown that an increase in shell thickness results in more lattice relaxation leading to a significant expansive deformation at the surface of the core@shell nanoparticles. On the other hand, Nathanson and co-workers¹¹ have revealed the atomic stress-release mechanisms in cubic Au@Pd core@shell nanoparticles. They have found that the lattice strain in the Au@Pd core@shell nanoparticles caused many deformations such as arc-like bending of atomic rows along the faces and edges of the nanoparticle, a bulging deformation of the Pd shell, and stacking faults in the Pd shell at the corners of the particle.

Cu–Au bimetallic nanoparticles have attracted extensive interest due to their higher specific catalytic activity.¹³ The catalytic performance of Cu–Au nanoparticles outperformed their individual components in terms of oxidation of CO, benzyl alcohol, and propene,¹³ and reduction of CO₂.¹⁴ However, the lattice mismatch between Cu and Au is about 11.4%, which may prevent the epitaxial growth during the formation of core@shell structures. This makes the synthesis of the CuAu core@shell nanoparticles quite complex and needs a reliable strategy. Recently, CuAu core@shell nanoparticles have been successfully produced both in wet-chemistry synthesis^15–19 and in gas phase growth experiments by the cluster beam technique.^20,21 For example, in the study carried out by Wang et al., Au@Cu nanorods with high shape anisotropy were successfully produced using a seed-mediated method through the localized epitaxial mechanism of Cu shells on a single-crystalline Au seed.¹² They demonstrated, theoretically and experimentally, that the strain energy due to the large lattice mismatch between the Au core and the Cu shell has a significant impact on the epitaxial growth and can induce the formation of twin planes on single-crystalline seeds and subsequently promote the anisotropic growth into nanorods. The aggregation of Cu-rich CuAu clusters in the gas phase has been simulated by Molecular Dynamics (MD)²² focusing on the size dependence of the composition of the final aggregates. The shapes of CuAu nanoparticles have been very recently studied under a hydrogen atmosphere.²³

In the literature, there are several examples showing the presence of different types of defects in core@shell nanoparticles, that are attributed to strain relaxation mechanisms. However, the mechanisms themselves by which strain arises during the growth and by which it is finally released are, to a large extent, unknown. In this respect, MD simulations can be very useful as they allow one to follow the atomic trajectories step by step.

In this paper, we study the growth pathways of CuAu nanoparticles by MD simulations, focusing on the deposition of Au atoms on the preformed seeds. We consider seeds of different shapes and compositions. The shapes are icosahedral, decahedral and fcc truncated octahedral. The compositions are either pure Cu or 50% Cu–50% Au.

We aim at dealing with the following points: (i) how misfit strain builds up in the growing structure while depositing on different starting seeds and (ii) how strain relaxation influences the growth pathways and the final shapes of core@shell nanoparticles.

Our results show that the shape and composition of the seed play a pivotal role in the growth pathways of the growing nanoparticles, leading in some cases to the formation of exotic structures, which are unlikely to form in the growth of pure nanoparticles. This behaviour is rationalized by atomic-level stress calculations. The different growth pathways are triggered by the stress distribution at the core–shell interface, which heavily depends on the shape and composition of the core.

2 Model and methods

The interactions between atoms are modelled using an atomistic model for CuAu developed on the basis of the second-moment approximation to the tight-binding model.²⁴ This potential was previously tested against density functional theory calculations and experimental data. Specifically, the comparison with DFT was about the energetics of clusters in the size range of 200–300 atoms and the comparison with the experiments was about the dissolution enthalpies of impurities, mixing enthalpies and the lattice parameters of ordered phases in the bulk. A good agreement was obtained.²⁵ In this semi-empirical potential, the total energy E is written as a sum of a bonding (E^b_j) and repulsive (E^r_j) part as:whereand

Here the parameter r_ij represents the distance between atoms i and j. s (w) refers to the chemical species of the atom i (j). If s = w, r⁰_sw is the nearest-neighbor distance in the corresponding bulk crystal lattice, whereas for s ≠ w, r⁰_sw is taken as the arithmetic mean of the distances of pure metals. Cutoff distances on the interactions are imposed by replacing the exponentials in eqs. (2) and (3) by fifth-order polynomials, of the form a₃(r − r_c2)³ + a₄(r − r_c2)⁴ + a₅(r − r_c2)⁵, between distances r_c1 and r_c2. The parameters a₃, a₄, and a₅ are fitted in each case to obtain a function which is always continuous, with the first and second derivative for all distances, and goes to zero at r_c2. The parameter sets of this CuAu system can be found in ref. 25. In our MD simulations the classical equations of motion are solved using the velocity Verlet algorithm with a time step of 5 fs. The growth simulations begin with a few hundred-atom clusters and proceed by the deposition of a single Au atom every 10 ns, and end up when the size of 1000 atoms is reached (total simulation time of about 8 μs). Simulations on this time scale have been favorably compared with experiments on the growth of other metal clusters.^26,27 Growth is performed at constant temperature by the procedure described in ref. 26.

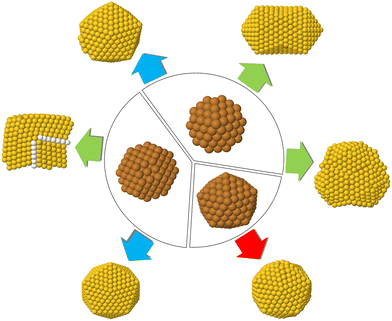
Our simulations can be classified into two types, which differ according to the composition of the initial seed. As shown in Fig. 1, the seed can either be pure Cu or intermixed CuAu. For each simulation type, three different shapes of the seeds are considered – fcc truncated octahedra (TO), decahedra (Dh) and icosahedra (Ih) on which the Au atoms are deposited. In type I simulations, we deposit Au atoms on pure Cu seeds, whereas in type II simulations, the Au atoms are deposited on intermixed CuAu seeds of 50%–50% composition. For both simulation types, the total number of atoms in the seed is 201 for TO, 192 for Dh and 309 for Ih, corresponding to ∼2 nm diameter. These sizes are in the range of the typical nucleation seed sizes in experiments.^12,27,28 We simulate at three different temperatures (300, 400 and 500 K), and in all cases, we perform five independent simulations.

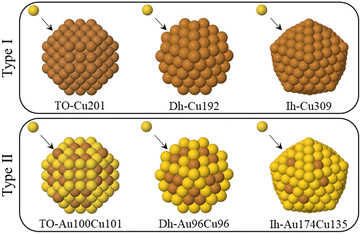Fig. 1 The two simulation types made in this work. In type I simulations Au atoms are deposited on pure Cu seeds. In type II, Au atoms are deposited on CuAu seeds. The columns show the different starting seeds of the simulations. From left to right: TO seeds of 201 atoms, Dh seeds of 192 atoms, Ih seeds of size 309 atoms. All the CuAu seeds are at equi-composition with intermixed chemical ordering, which corresponds to the lowest-energy chemical ordering.²⁵ Au and Cu atoms are represented by yellow and brown spheres, respectively.

The chemical ordering of the seeds of type II simulations is obtained by global optimization searches using exchange moves.²⁵ From the second row of Fig. 1, we can see that the chemical ordering is intermixed in all shapes with a rather clear tendency of Au atoms to enrich the surface layer. The Au surface enrichment looks stronger in the Ih shape than in the Dh and TO shapes. Correspondingly, the cores are enriched with Cu atoms, with some Au atoms being sparsely distributed.

3 Evolution of chemical ordering

In order to understand the core@shell chemical ordering of type I and type II simulations at the atomic level, we have analysed the final structures of the two simulation types. In all cases, we found qualitatively the same core@shell chemical ordering, i.e. the minority Cu atoms are located in the core while the outer shell is exclusively formed by Au atoms. The distribution of minority Cu atoms within the nanoparticles has been characterized by calculating their gyration radius with respect to their geometric centre during the kinetic growth process.²⁹ The results are shown in Fig. S1 in the ESI.† The interdiffusion of Cu atoms depends on the temperature. As expected, the diffusion of Cu atoms is more activated at higher temperature but it is limited to the inner part of the nanoparticles so that Cu atoms are not able to reach the cluster surface. Diffusion of Cu atoms depends also on the shape of the starting seed – it is much weaker in Ih structures than in TO and Dh ones³⁰ due to the tendency of the smaller Cu atoms to fill the central part of icosahedra. Results on the interdiffusion of Au and Cu inside the growing nanoparticles are reported in the ESI (Fig. S2†).

In summary, a perfect core@shell arrangement is always obtained, with the surface layer almost completely made of Au atoms. In contrast, we obtained a wide variety of NP shapes, as discussed in the following section.

4 Evolution of shapes during growth

Let us now discuss the geometric structures of the NPs obtained at the end of the growth simulations. The results are summarized in Table 1.

Table 1 Final shapes of type I and type II simulations at different temperatures T (in K) and with different starting structures. For each seed and temperature, five independent simulations were performed. All results represent the shape of the final nanoparticle grown up to 1000 atoms. N_multitwins is the number of simulations in which the multi-twin structure is obtained, N_fcc is the number of simulations in which the fcc structure is grown, N_Ih is the number of simulations in which the icosahedral shape is achieved, N_Dh is the number of simulations in which the decahedral structure is obtained and N_PolyIh is the number of simulations in which double or triple icosahedra are obtained. Surface views of all these structures are shown in Fig. S3–S5 in the ESI†

Starting structure	T (K)	N multitwins	N fcc	N Ih	N Dh	N PolyIh
TO, pure Cu	300	3	2	0	0	0
	400	3	2	0	0	0
	500	2	0	3	0	0
Dh, pure Cu	300	0	0	3	0	2
	400	0	0	4	0	1
	500	0	0	2	0	3
Ih, pure Cu	300	0	0	5	0	0
	400	0	0	4	0	1
	500	0	0	4	0	1
TO, mixed CuAu	300	0	5	0	0	0
	400	0	4	0	1	0
	500	0	1	3	1	0
Dh, mixed CuAu	300	0	0	2	2	1
	400	0	0	0	5	0
	500	0	0	4	0	1
Ih, mixed CuAu	300	0	0	5	0	0
	400	0	0	5	0	0
	500	0	0	5	0	0

---

When starting with icosahedral seeds, the growing clusters always keep that motif at any growth temperature. In the case of pure Cu seeds (type I simulations), the surface of these Ih structures is often irregular on one of its sides and smooth with a chiral stacking on the other side. Surface reconstructions are often found in Ih structures since they can allow the release of the strain which is naturally associated with that structure.^2,31 In particular, the formation of the chiral icosahedral overlayer is started by the nucleation of anti-Mackay islands on all the (111)-like facets of the initial Mackay Cu seed (see Fig. S6 in the ESI†), and by their subsequent rotation³² which allows the release of the strong in-plane compression of atoms in the anti-Mackay facets.¹

In type II simulations, growth is more regular. The Au atoms cover the starting Ih seeds in a shell-by-shell way, leading to the formation of perfect Mackay Ih structures with smooth surfaces.

At variance with the case of Ih seeds, when starting with TO and Dh seeds there is a clear difference between type I and type II simulations. In type I simulations, the growth very often leads to structures that are completely different from those of the seeds. In some cases, icosahedra are grown, but also more complex structures, referred to as exotic structures in the following, are grown. The possible outcomes of type I simulations are schematically shown in Fig. 2. Exotic structures can be classified into three classes: irregular fcc double twins, double icosahedra and triple icosahedra. Representative growth sequences of these three classes will be described in the following. With regard to the transformation into icosahedra, we note that Cu@Au icosahedra are generally more favourable than Cu@Au fcc structures for the sizes and compositions considered here.^25,30

Fig. 2 Representative structures obtained during the deposition of Au atoms on pure Cu seeds of three different shapes. The red arrow indicates the growth within the motif of the initial seed. Blue arrows indicate the growth pathways with structural transformations of the initial structures into the icosahedral ones. Green arrows indicate the growth towards exotic structures.

For type II simulations, growth often proceeds within the same motif of the seed, thus resembling the growth sequences obtained for pure metals or for bimetallic systems with a small lattice mismatch^26,29,33,34 (see the final structures reported in the ESI†). However, at the highest temperature (500 K), the more energetically favourable icosahedral structures are often grown from both TO and Dh seeds.

4.1 Pathway to irregular double twins

Depending on the growth temperature (see Table 1), type I simulations starting from a truncated octahedral seed produce different structures such as tetrahedra, irregular double twins and icosahedra. Here we focus on the growth pathway to the double twin structures, while the transitions to tetrahedra and icosahedra, which have been already discussed elsewhere,^26,29 are shown in the ESI (Fig. S7†).

The growth pathway to double twins is presented in Fig. 3. This pathway is made of three main stages referred to as A, B and C, corresponding to the different average nearest-neighbour distances (d_nn) between the Cu atoms (see the top right plot of Fig. 3, where a simulation at 300 K is shown). Fig. 3 shows also several simulation snapshots that are observed from the [110] direction. In these snapshots, the Cu atoms of the TO seed are represented by larger spheres and Au deposited atoms are shown by smaller dots.

Fig. 3 Growth pathway of the irregular double-twin nanoparticle starting from a TO copper seed. Snapshots are taken for a growth simulation at 300 K with a deposition rate of 0.1 atom per ns. Au atoms are represented by smaller dots and Cu by larger spheres. The colors green, red and blue correspond to the fcc, hcp and bcc character of the core atoms, respectively. The surface atoms are colored in gray. The top right figure shows the variation of the nearest-neighbour-distance d_nn between Cu atoms during Au deposition. A, B and C represent the first, middle and last growth steps, respectively, of the double-twin growth pathway. The bottom right inset shows the surface view of a double-twin structure of size 1000 atoms.

In the first growth stage A (snapshots of the first row in Fig. 3) some Au atoms are exchanged with Cu ones, especially with those of the (100) surfaces and edges. This slightly increases d_nn, so that it becomes larger than the nearest-neighbour distance in the Cu fcc bulk crystal.

When the first Au layer is completely formed (stage B in Fig. 3), the Cu–Cu bonds become even more stretched, as observed in the top right graph in Fig. 3. The increase of d_nn is a clear indication that tensile strain is building up in the growing clusters. The effect of an Au layer for what concerns the atomic-level strain and stress of a TO Cu seed will be better analysed in section 5. In order to relieve this strain, the Cu core undergoes some atomic rearrangements, in which local hcp and bcc environments are formed. These environments are shown in the snapshots of the second row of Fig. 3. These rearrangements slow down the increase of d_nn.

In the last stage of growth (C), shown in the third row of Fig. 3, the strong internal strain caused by the deposited Au atoms induces the formation of two non-parallel twin planes (which are marked by red arrows in the snapshots of the third row) within the growing cluster. This process reduces the tensile strain of Cu atoms and stabilize d_nn expansion (as shown in regime C of the plot in the figure).

4.2 Pathways to polyicosahedra

Let us now discuss the growth pathways of the exotic shapes obtained during the growth on a pure Dh seed.

In these simulation series, the majority of NPs transform from decahedra to icosahedra during growth. This transformation is indeed naturally expected in the growth from decahedra as it was already observed in the growth of pure Ag and Au NPs.^33,35

However, besides the icosahedral structures, other less common growth shapes are obtained, such as double and triple icosahedra.

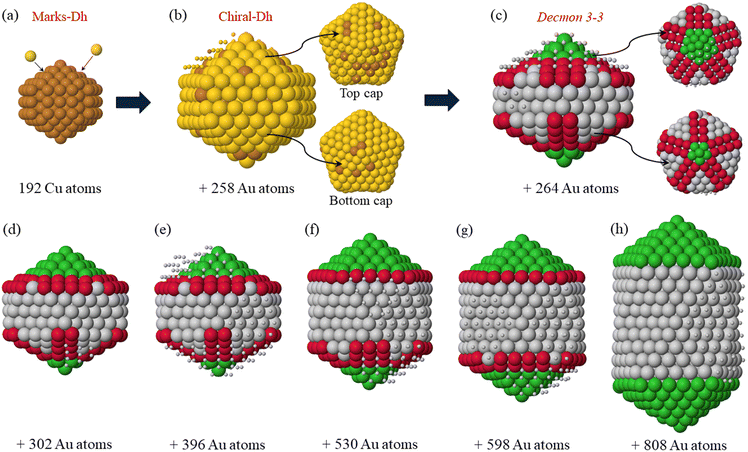
Let us first analyze the growth pathway of a double icosahedron, whose key steps are reported in Fig. 4. In the initial stages (Fig. 4(b)), we observe the formation of the first Au-rich shell on the initial Dh seed, leading to the formation of a chiral decahedral Cu@(CuAu) structure in which all facets are close-packed. This structure is metastable so its formation induces a global restructuring of the NPs. As a result, a Decmon 3-3 structure with an anti-Mackay cap is formed as shown in Fig. 4(c). This chiral-Dh → Decmon transformation is explained in the following by means of Fig. 6. Indeed, this Decmon nanoparticle shape was produced for the first time in ref. 36 by the inert gas condensation method for the Co@Au core@shell structure and its thermal stability was proved in ref. 37 for pure Au by molecular dynamics simulations.

Fig. 4 Growth sequence of a double icosahedron starting from a pure Cu Dh seed in a simulation at 500 K and a deposition rate of 0.1 ns⁻¹. (a) Starting Marks Dh seed of size 192 atoms. (b) Chiral decahedral structure with a complete growing shell in which all facets are close-packed. (c) Decmon 3-3 structure with an island on hcp stacking on the bottom cap. This structure presents many (100) sites on both caps where new atoms are favorably adsorbed. This facilitates the growth of the structure along its fivefold axis by a self-replicating process (d)–(h). In (a) and (b), brown and yellow spheres represent Cu and Au atoms, respectively. In (c)–(h), atoms colored in gray correspond to the close-packed facets, while red atoms are those of the (100) facets. Atoms in green represent those in the caps of the growing structure. Additional atoms are shown by small balls.

As shown in Fig. 4(c), the Decmon motif exposes (111) and (100) facets. It is well known that the adsorption of atoms on the (100) facets is energetically more favourable than that on the (111) facets, because the former present fourfold adsorption sites while the latter present threefold adsorption sites. The (100) sites are located on the top and bottom caps of the structure (atoms in red) and absent in the lateral facets.

The caps of the Decmon structure present a peculiar atomic pattern. There is a central part of the cap (represented by green atoms in Fig. 4(c–h)) with Mackay icosahedral arrangement, on which the adsorption sites are threefold. This is surrounded by an anti-Mackay part with (111)-like (grey atoms) and (100)-like (red atoms) nanofacets. The (100) facets present fourfold adsorption sites which are more favourable for the adsorption of incoming atoms during growth. For this reason, atoms deposited on the NPs diffuse around and finally accommodate on one of the caps, to nucleate atomic islands and finally forming a new layer on the cap. In the new layer, the central Mackay part (in green) is enlarged by a ring of atoms, while the (111)-like facets shrink and the (100)-like facets become more and more rectangular, i.e. they become thinner in the radial direction but longer in the direction along the cap border (compare the snapshots in Fig. 4(e–h)). This process replicates until the Mackay part enlarges to fully occupy the cap (Fig. 4(h)), thus completing the growth of the double icosahedron.

In Fig. 5, we give the representative snapshots of the growth of the triple icosahedral structure starting from a pure Dh seed. The formation of this structure is less common than that of the double icosahedron, so we have a very limited set of examples.

Fig. 5 Growth pathway of a triple icosahedron from a pure Dh seed at a temperature of 500 K. (a) Decmon motif on the top part of the nanocluster and a reconstructed decahedron on the bottom part sharing the same fivefold axis. (b) Transformation of the reconstructed decahedron part into a second Decmon structure. (c) and (d) Double decmon showing the two growing grooves. (e)–(g) Completed icosahedra on two caps and a lateral icosahedron with different truncation. (h) Complete growth of triple icosahedra. White dashed lines show the nearby triangular (111) facet of the growing grooves. White solid lines highlight facet evolution in the structural rearrangement process.

In the first stage of the growth, we observed the formation of a nanocluster with an Au-rich shell (see Fig. 5(a)). The top part of this structure is Decmon and the bottom one is a reconstructed Dh. The formation of the Decmon part at the early stage of the growth might be attributed to the presence of a large number of mixed Cu–Au bonds (compared to the simulations where the double icosahedron is grown), which makes the structure less stable and leads to the structural rearrangements.

After some Au deposition, the reconstructed Dh part transforms into a Decmon as well, which leads to the double-Decmon as presented in Fig. 5(b). As a result, the formation of (100)-like facets on both caps of the growing nanostructure is observed, which can lead to the growth of an icosahedral motif on each cap at a later stage of the growth in the same way as Fig. 4.

This double-Decmon structure is made of two Decmon motifs which meet at an internal pentagon and are symmetric about it. This leads to the formation of grooves on the lateral surfaces of the nanocluster between the two Decmon structures. These grooves, which do not form in the growth pathway of double-icosahedra (see Fig. 4), are of two types: (111)-groove and (100)-groove as shown in Fig. 5(b). The adsorption energy of Au adatoms on these grooves differs from one groove to another and it depends on the presence of Cu atoms in the groove. More precisely, Au adsorption on the top of facets containing Cu atoms is more energetically favourable than on pure Au facets. Thus, Au islands are therefore likely to nucleate in the grooves with mixed CuAu facets than the pure Au ones as shown in Fig. 5(c) (small balls on cyan facets).

The growth of the first layer on these mixed grooves triggers the nucleation of an island on nearby triangular (111) facets (dashed triangle in Fig. 5(c)) which leads to the formation of new (100)-like fourfold adsorption sites (Fig. 5(d)). Adatoms adsorbed on these sites drive the formation of a second layer above the first one with quite small (111) facets and large (100) facets as shown in Fig. 5(e). These (100) facets promote the lateral growth and lead to an almost complete Ih motif as shown in Fig. 5(f), which presents a large (100) surface. After that, the (100)-like facet rearranges into a rhombic (111) one, finally giving a third icosahedron on the lateral side of the double icosahedron (see Fig. 5(g) and (h)).

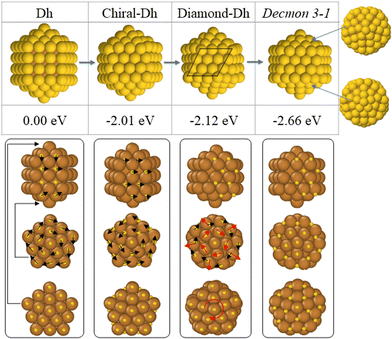
Finally, let us elucidate the transition mechanisms from a Dh to a Decmon structure observed during the Dh → double-Ih growth pathway. To this end, we performed some MD simulations at a fixed temperature for a Cu@Au Ino decahedral nanoparticle of size 147 atoms. In this configuration, the core is pure Cu and the shell is a pure Au monolayer. The mechanisms are explained in Fig. 6. The solid–solid structural transition is initiated by the rearrangement of the Au atoms of the (100) surfaces which transforms the Ino Dh into a chiral-Dh, as shown in the second column of Fig. 6. Subsequently, the Au atoms belonging to the chiral-Dh caps rotate with respect to the other fragment of the surface shell, resulting in a Diamond-Dh structure as shown in the third column of Fig. 6. By twisting the atoms in the caps of the chiral Au shell, a Cu core with an anti-Mackay cap can be formed, leading to the formation of a Decmon 3-1 structure with an anti-Mackay stacking of the top cap as presented in the last column of Fig. 6.

Fig. 6 Transformation from Ino Dh to Decmon of a Cu@Au core@shell cluster of size 147 atoms at a temperature of 500 K. Black and red arrows represent the displacement directions of the Au atoms of the outer shell and of the Cu atoms of the subsurface shell, respectively.

5 Discussion of stress effects

In order to understand the driving force causing the structural transformations and the formation of the exotic shapes during the growth on pure Cu TO and Dh seeds, we analyse here the atomic level stress. This is done by means of the local stress tensor which is defined for each atom i by the following formula:³⁸

V _i and E_i represent the atomic volume and the energy of atom i, respectively. r^a_ij and r^b_ij (with a, b = x, y, z) are the cartesian components of the vector r_ij, which joins atoms i and j. The isotropic local pressure P_i is proportional to the trace of the tensor:

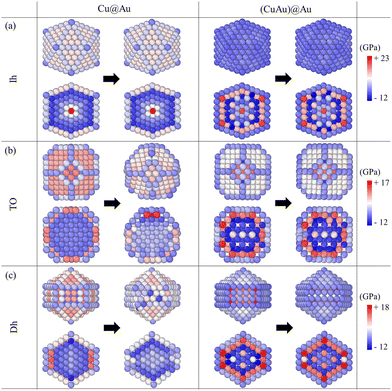
Here, we calculate the atomic pressure for perfect core@shell configurations with either a pure Cu or a mixed CuAu core covered by pure Au shells with monolayer thickness (Au-skin) for Ih, TO and Dh shapes. Our results are reported in Fig. 7, where we show the pressure maps, and in Table 2, where we report the average deviation from zero pressure 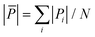for the structures of Fig. 7. We will use the same notation as before: Cu@Au when the core is pure Cu and (CuAu)@Au when it is mixed. For each geometry, the pressure map is given for both Cu@Au and (CuAu)@Au arrangements. We note that positive values of the pressure on a given atom indicate that the atom is compressed, while negative values show that the atom suffers from tensile stress.

Fig. 7 Pressure maps of Ih (a), TO (b) and Dh (c) for Cu@Au (left part) and (CuAu)@Au (right part) core@shell configurations. In all cases, the Au shell is one layer thick. For both Cu@Au and (CuAu)@Au cases, we show the pressure maps of the perfect initial structures (to the left of the arrows), and those of the structures obtained after evolving by MD for 0.3 μs at 500 K. In all cases, the structure is shown in two views: surface view and cross section. Blue and red colors correspond, respectively, to the negative and positive pressure values. Pressure scales (in GPa) are shown for all shapes.

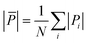Table 2 Average deviation from zero pressure in the initial and final configurations of Fig. 7

Structure	System	|P̄|in (GPa)	|P̄|fi (GPa)
TO	Cu@Au	4.97	3.17
	(CuAu)@Au	5.67	5.58
Dh	Cu@Au	4.93	3.86
	(CuAu)@Au	5.94	5.32
Ih	Cu@Au	5.07	5.07
	(CuAu)@Au	6.29	6.29

---

For Cu@Au configurations (see the left column of Fig. 7), we observe that the pressure values on the surface are mostly positive (especially those on the (111) and (100) facets) and they are negative at the sub-surface sites for all three motifs. This means that the perfect Au skin covering the pure Cu core generates a compressive stress on surface atoms and tensile stress on sub-surface atoms. This stress pattern is strongly different from what is found for Au and Cu pure nanoparticles, in which surface atoms suffer from tensile stress and subsurface atoms are compressed.

On the other hand, the pressure in the inner part of the cluster is quite different for the three structures. For Ih, the pressure values of the inner atoms go from strongly positive at the central site to strongly negative at the subsurface ones. For TO and Dh shapes, all inner atoms (Cu atoms) have a negative pressure which means that all atoms suffer from tensile stress. In the case of TO, the pressure within the core is homogeneous and atomic sites are almost equivalent. In the case of Dh, inner sites are not equivalent: pressure is higher at the subvertex and subsurface sites and lower for atoms belonging to the fivefold axis.

This pressure pattern is a destabilizing factor, as the natural pressure pattern in a metal NP is the opposite, i.e. negative pressure for surface atoms and positive pressure for inner atoms. As stated in the literature, the surface strain in these structures for perfect core-skin configurations can be alleviated by surface rearrangements,^2,39,40 which may lead to the formation of some peculiar shapes during the kinetic growth process as observed in our simulations. We verified this point directly for the structures of Fig. 7 by evolving them by MD for 0.3 μs at T = 500 K. The Cu@Au TO and Dh structures underwent significant surface reconstruction leading to irregular shapes with lowered pressure deviation |P̄| (see Table 2). In contrast, (CuAu)@Au structures presented smaller surface reconstruction and changes in |P̄|.

During the growth on the Ih seed, this surface stress is reduced by the formation of an anti-Mackay layer in the first stage of the growth. Actually, at small sizes, this configuration has been proved to be more energetically favorable for several systems with a large lattice mismatch such as Cu@Ag, Co@Ag, Ni@Ag and Ni@Au.³² As the number of Au atoms increases, this anti-Mackay structure becomes energetically unstable which leads to the transformation to a chiral configuration and the formation of an Ih structure with chiral and/or irregular surfaces at a later stage of the growth.

During the growth process on the TO seed, we observed different types of structural arrangements depending on the amount of Au atoms. For a low amount of Au, the surface stress is released by rearranging the (111) facets into either hcp or mixed fcc/hcp stacking. As the number of Au atoms increases on the surface, the interatomic Cu–Cu distances in the core expand (compared to the bulk Cu metal) to better adapt to the Au shell. This makes the defects extend to the inner part, in order to reduce the tensile stress of the core. This finally leads to the creation of twin planes and then to the formation of peculiar shapes like the one described in subsection 4.1.

For (CuAu)@Au (see the right column of Fig. 7), the compressive stress at the surface is smaller than in the Cu@Au core, because the core is more expanded due to the presence of Au atoms. For TO and Dh structures, the pressure values at the surface decrease from 8 GPa to less than 1 GPa for the (111) facets and from 9 GPa to less than −1 GPa for the (100) surfaces. On the other hand, for the Ih structure, the pressure in (CuAu)@Au is negative at the surface. Therefore, Au atoms at the surface suffer from tensile stress instead of compressive stress, as in the case of pure systems. In summary, these results show that the replacement of a pure seed with a mixed one very well relaxes the stress of the additional Au shell, so the continuation of the growth within the initial motif is possible, in analogy with pure nanoparticles.

6 Conclusions

In this work we have investigated the growth of CuAu bimetallic nanoparticles in the gas phase by different types of molecular dynamics simulations. Our results show that core@shell chemical ordering arrangements are always achieved, i.e. Cu@Au configurations in type I simulations and (CuAu)@Au configurations in type II simulations. In all cases, the purity of the Au surface layer is perfect. The cores are pure Cu in the Cu@Au arrangement and mixed in the (CuAu)@Au configuration. In these growth pathways, we have observed that the interdiffusion of the Cu atoms of the initial seed is partially activated as the temperature increases. Indeed, this interdiffusion behavior is observed to be limited to the layers of the core@shell interface and cannot reach the surface within our simulation time scale and temperature range. Interdiffusion is nearly blocked when the growing nanoparticles undergo structural transformations towards icosahedra.

Regarding the nanoparticle shapes, we have observed that the final shapes are strongly dependent on the geometry and composition of the initial seed. In both simulation types, when depositing Au atoms on Ih seeds the structure stays in that motif always until the end of the simulations. When starting with Dh and TO seeds, there is a clear difference in the final structures of type I (Cu@Au configurations) and type II simulations ((CuAu)@Au configurations). These shapes are regular in the case of (CuAu)@Au structures and resemble those obtained for pure metals. Cu@Au NPs often undergo structural transformations during the growth, leading to Ih and exotic structures. For TO seeds, the greatest part of the Cu@Au NPs presents multi-twin structures with the exception of a few icosahedra grown at 500 K. In the case of Dh seeds, Ih shapes together with some poly-Ih structures were grown for this Cu@Au core@shell configuration.

Growth is characterized by the building up of atomic level stress at the interface between the core and the growing Au shell, which is stronger in the case of pure Cu seeds because of larger lattice mismatch and associated misfit strain. Stress relaxation is achieved by different types of structural transformations, leading to the formation of a wide variety of NP shapes.

Author contributions

EE performed and analyzed the MD simulations. RF assisted in the analysis of the simulations and supervised the work. Both authors contributed to the drafting of the paper.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge support from the PRIN 2017 project UTFROM of the Italian MIUR and from the Progetto di Eccellenza of the Physics Department of the University of Genoa. The authors acknowledge networking support from the IRN Nanoalloys of CNRS. The authors are grateful to Diana Nelli and Cesare Roncaglia for useful discussions and a critical reading of the paper.

References

1. R. Ferrando, Structure and Properties of Nanoalloys, Elsevier, 2016.
2. D. Nelli, C. Roncaglia and C. Minnai, Adv. Phys.: X, 2023, 8, 2127330.
3. L. Xu, H.-W. Liang, Y. Yang and S.-H. Yu, Chem. Rev., 2018, 118, 3209–3250.
4. D. Hudry, I. A. Howard, R. Popescu, D. Gerthsen and B. S. Richards, Adv. Mater., 2019, 31, 1900623.
5. J. Liu and J. Zhang, Chem. Rev., 2020, 120, 2123–2170.
6. Z. Xia and S. Guo, Chem. Soc. Rev., 2019, 48, 3265–3278.
7. J. Liang, F. Ma, S. Hwang, X. Wang, J. Sokolowski, Q. Li, G. Wu and D. Su, Joule, 2019, 3, 956–991.
8. K. D. Gilroy, X. Yang, S. Xie, M. Zhao, D. Qin and Y. Xia, Adv. Mater., 2018, 30, 1706312.
9. J. T. L. Gamler, A. Leonardi, X. Sang, K. M. Koczkur, R. R. Unocic, M. Engel and S. E. Skrabalak, Nanoscale Adv., 2020, 2, 1105–1114.
10. J. Zhao, B. Chen and F. Wang, Adv. Mater., 2020, 32, 2004142.
11. M. Nathanson, K. Kanhaiya, A. Pryor, J. Miao and H. Heinz, ACS Nano, 2018, 12, 12296–12304.
12. Z. Wang, Z. Chen, H. Zhang, Z. Zhang, H. Wu, M. Jin, C. Wu, D. Yang and Y. Yin, ACS Nano, 2015, 9, 3307–3313.
13. C. L. Bracey, P. R. Ellis and G. J. Hutchings, Chem. Soc. Rev., 2009, 38, 2231–2243.
14. Z. Xu, E. Lai, Y. Shao-Horn and K. Hamad-Schifferli, Chem. Commun., 2012, 48, 5626–5628.
15. J. Zhang, X. Xu, C. Yang, F. Yang and X. Yang, Anal. Chem., 2011, 83, 3911–3917.
16. Y. Yoshida, K. Uto, M. Hattori and M. Tsuji, CrystEngComm, 2014, 16, 5672–5680.
17. W. Xue, H. Yin, Z. Lu, Y. Feng, A. Wang, S. Liu, L. Shen and X. Jia, Catal. Lett., 2016, 146, 1139–1152.
18. M. Tang, B. Sun, D. Zhou, Z. Gu, K. Chen, J. Guo, L. Feng and Y. Zhou, Org. Electron., 2016, 38, 213–221.
19. J. Gunlazuardi, A. D. Kurniawan, P. K. Jiwanti, Y. Einaga and T. A. Ivandini, Anal. Methods, 2022, 14, 726–733.
20. A.-X. Yin, X.-Q. Min, Y.-W. Zhang and C.-H. Yan, J. Am. Chem. Soc., 2011, 133, 3816–3819.
21. F. Yin, Z. W. Wang and R. E. Palmer, J. Exp. Nanosci., 2012, 7, 703–710.
22. I. V. Chepkasov, V. S. Baidyshev, A. A. Golubnichiy, I. S. Zamulin, A. G. Kvashnin and S. M. Kozlov, Aggregate, 2022, e273.
23. Q. Wang, A. Nassereddine, D. Loffreda, C. Ricolleau, D. Alloyeau, C. Louis, L. Delannoy, J. Nelayah and H. Guesmi, Faraday Discuss., 2022.
24. F. Cyrot-Lackmann and F. Ducastelle, Phys. Rev. B: Solid State, 1971, 4, 2406–2412.
25. J.-Q. Goh, J. Akola and R. Ferrando, J. Phys. Chem. C, 2017, 121, 10809–10816.
26. Y. Xia, D. Nelli, R. Ferrando, J. Yuan and Z. Y. Li, Nat. Commun., 2021, 12, 3019.
27. P. Andreazza, A. Lemoine, A. Coati, D. Nelli, R. Ferrando, Y. Garreau, J. Creuze and C. Andreazza-Vignolle, Nanoscale, 2021, 13, 6096–6104.
28. D. Nelli, A. Krishnadas, R. Ferrando and C. Minnai, J. Phys. Chem. C, 2020, 124, 14338–14349.
29. E. y. El koraychy, D. Nelli, C. Roncaglia, C. Minnai and R. Ferrando, Eur. Phys. J.: Appl. Phys., 2022, 97, 28.
30. D. Nelli, C. Mottet and R. Ferrando, Faraday Discuss., 2022.
31. D. Nelli, Eur. Phys. J.: Appl. Phys., 2022, 97, 18.
32. D. Bochicchio and R. Ferrando, Nano Lett., 2010, 10, 4211–4216.
33. E. y. El koraychy, C. Roncaglia, D. Nelli, M. Cerbelaud and R. Ferrando, Nanoscale Horiz., 2022, 7, 883–889.
34. D. Nelli, C. Roncaglia, S. Ahearn, M. Di Vece, R. Ferrando and C. Minnai, Catalysts, 2021, 11, 718.
35. F. Baletto, C. Mottet and R. Ferrando, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 155408.
36. A. Mayoral, D. Llamosa and Y. Huttel, Chem. Commun., 2015, 51, 8442–8445.
37. J. P. Palomares-Báez, J. M. Montejano-Carrizales, G. Guisbiers, M. José-Yacamán and J. L. Rodríguez-López, Nanotechnology, 2019, 30, 425701.
38. V. Vitek and T. Egami, Phys. Status Solidi B, 1987, 144, 145–156.
39. E. Panizon and R. Ferrando, Nanoscale, 2016, 8, 15911–15919.
40. M. Settem, P. Kumar, I. Adlakha and A. K. Kanjarla, Acta Mater., 2022, 234, 118038.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr05810c

---