Nanoscale friction of biomimetic hair surfaces

Abstract

We investigate the nanoscale friction between biomimetic hair surfaces using chemical colloidal probe atomic force microscopy experiments and nonequilibrium molecular dynamics simulations. In the experiments, friction is measured between water-lubricated silica surfaces functionalised with monolayers formed from either octadecyl or sulfonate groups, which are representative of the surfaces of virgin and ultimately bleached hair, respectively. In the simulations, friction is monitored between coarse-grained model hair surfaces with different levels of chemical damage, where a specified amount of grafted octadecyl groups are randomly replaced with sulfonate groups. The sliding velocity dependence of friction in the simulations can be described using an extended stress-augmented thermally activation model. As the damage level increases in the simulations, the friction coefficient generally increases, but its sliding velocity-dependence decreases. At low sliding velocities, which are closer to those encountered experimentally and physiologically, we observe a monotonic increase of the friction coefficient with damage ratio, which is consistent with our new experiments using biomimetic surfaces and previous ones using real hair. This observation demonstrates that modified surface chemistry, rather than roughness changes or subsurface damage, control the increase in nanoscale friction of bleached or chemically damaged hair. We expect the methods and biomimetic surfaces proposed here to be useful to screen the tribological performance of hair care formulations both experimentally and computationally.

---

1 Introduction

A detailed understanding of the tribology of human hair is essential to develop new shampoos and conditioners that leave hair untangled and feeling smooth.¹ In particular, maintaining low friction between hairs is important for satisfactory sensory perception during touching, brushing and combing.^2–7 Consequently, the kinetic friction of hair has been studied using a wide range of experimental techniques from the macroscale to the nanoscale.^8–30 The friction between nanoscale tips and single hairs,^{10–14,18,22,26} as well as crossed hair–hair contacts,^23–25 have been investigated using atomic force microscopy (AFM) and high-load nanotribometers.²⁷ Understanding the friction between hairs is crucial since this dominates the overall resistance felt during combing and brushing.²⁵

Friction forces on hairs are anisotropic due to the overlapping nature of the outer cuticle cells.⁹ Friction is much higher when hairs are rubbed in the tip-to-root direction, where the cuticles lock together, than in the root-to-tip direction, where they are able to slide over one another more easily.⁹ A monolayer of 18-methyleicosanoic acid (18-MEA) is covalently bonded to the protein layer below, mostly through thioester bonds with cysteine residues in the cuticle of the hair. This protective 18-MEA monolayer is commonly known as the fatty acid layer (F-layer). The F-layer makes hair surfaces hydrophobic and also provides low friction.^12,29 Previous AFM experiments have consistently found an increase of the coefficient of friction (CoF) for bleached hair compared to virgin hair.^{10,12–14,22,24} During bleaching, the 18-MEA layer is partially removed by oxidation of the cysteine, which leads to the formation of negatively charged cysteic acid groups, making the hair surface more hydrophilic.^19,31–33 From experiments in humid air environments (relative humidity, RH ≈ 50%), capillary condensation has been proposed as a possible mechanism for the increase in adhesion and friction from bleaching hair.¹² Indeed, capillary condensation is known to increase friction on hydrophilic surfaces more than on hydrophobic ones.³⁴ However, more recent investigations showed that even in dry environments (RH ≈ 4%) increases in the CoF are observed for bleached and chemically damaged hair compared to virgin hair.²² The relative increase in the CoFs on chemically damaged hair was found to be largest for measurements with a nanoscale AFM tip, as compared to microscopic and macroscopic methods, where cuticle edge effects and probe size can perturb the friction signals.¹⁵ This motivates an investigation of hair friction phenomena at the smallest scales, where effects due to changes in surface chemistry can be isolated from topological effects.

Environmental factors also affect hair friction. For example, hairs undergo swelling when soaked in water,¹⁶ which has been found to lead to increased friction forces. It has been suggested that the hair surface softens in water, leading to larger contact areas and thus higher friction.^22,24 The application of cationic surfactant/polymer-based hair conditioners on damaged hair can partially recover the hydrophobic character of virgin hair.²⁹ Conditioners also lower the CoF compared to chemically damaged hair¹⁴ by restoring the boundary layer that was partially lost when 18-MEA molecules were removed.²⁴

As with most natural materials, the structure and friction of hair shows considerable variability between individuals and populations.¹³ The development of synthetic biomimetic surfaces with reproducible properties would therefore be useful for the screening of the tribological performance of different hair care formulations.¹ Artificial hair mimics have been constructed to reproduce the microscale roughness features of overlapping cuticles³⁵ and the F-layer has been represented by a gold AFM tip coated with a thiol monolayer.¹⁸ However, the friction of biomimetic surfaces for chemically damaged hair has not yet been investigated. The use of atomically-smooth, biomimetic surfaces in nanotribology tests allows for reduced variability compared to real hair and for the detailed investigation of the effects of surface chemistry and treatments, while eliminating the influence of microscale roughness, which otherwise leads to friction anisotropy.⁹

Confined nonequilibrium molecular dynamics (NEMD) simulations have been used to study the friction behaviour of a wide range of systems.³⁶ Surfactant monolayers adsorbed on solid surfaces are one of the most widely studied systems with NEMD simulations due to their importance in engineering and biological systems. These studies have investigated a wide range of applications from organic friction modifier (OFM) lubricant additives^37,38 to synovial joints.^39,40 While most of these studies have employed all-atom force fields,³⁶ the large, heterogeneous surfaces and macromolecules commonly encountered in biological systems are more suited to the use of coarse-grained representations.⁴¹ Coarse-grained force fields have already been used to study, for example, the intermonolayer friction of lipid bilayer membranes^42,43 the friction of protein translocation through nanopores,⁴⁴ and the adsorption and desorption of polymers on heterogeneous substrates that are representative of the surface of the hair under shear flow.⁴⁵

In this study, we use NEMD simulations and chemical colloidal probe (CCP) AFM to study the kinetic friction between model hair surfaces. In the AFM experiments, we study the friction of water-lubricated biomimetic surfaces that are representative of virgin and ultimately bleached hair. In the NEMD simulations, we employ our recently developed and validated coarse-grained (CG) model of the surfaces of virgin and bleached hair³³ within the MARTINI framework.⁴⁶ Both dry and wet contacts are considered under a wide range of sliding velocities. Both the experimental and simulation frameworks will serve as a useful benchmark for the high-throughput screening of the tribological performance of potential hair care formulations.^1,47 The methodology presented in this work is also expected to be applicable to investigate the nanotribology of other heterogeneous biological surfaces such as natural textiles and skin.¹¹

2 Methodology

2.1 MD system setup

Coarse-grained molecular models of hair surfaces at different degrees of damage, as introduced in our previous study,³³ are used to describe the contact interface. Here, the MARTINI 2.0 force field^46,49 is used in conjunction with a polarizable water model.⁵⁰ The polarizable water model was selected because electrostatic screening is believed to play an important role for interactions between the damaged (charged) model hair surfaces. This model employs a 4 : 1 mapping for non-hydrogen atoms to coarse-grained beads. Full details of the parameters chosen can be found in our previous study.³³ The systems were constructed using the Moltemplate software.⁵¹

In the MARTINI model, a shifted Lennard-Jones (LJ) potential⁵² is used to describe the non-bonded interactions. Switching to zero is performed between the cut-off radius r_LJ,cut = 0.9 and r_LJ,shift = 1.2 nm.⁴⁶ Coulomb potentials are added for interactions between charged beads. Long-range electrostatic interactions are considered using the Yeh–Berkowitz slab implementation⁵³ of the particle–particle particle-mesh (PPPM) method.⁵⁴ A coulombic switching radius of r_C,cut = 1.2 nm and a relative energy tolerance of 10⁻⁵ are applied. Bonds and angles are treated using weak harmonic potentials as in the original MARTINI framework.⁴⁶ For wet systems, bonds between polarizable water beads of a single water unit are constrained using the SHAKE⁵⁵ algorithm.

Fig. 1 shows a representative example of a dry and wet system (pristine hair) during compression and sliding. A graphene sheet is used as an impenetrable substrate for grafting the lipid monolayer at a separation distance d_graft = 0.65 nm. This separation distance reproduces the experimentally-measured thickness of the F-layer.^33,56 Harmonic bonds are added between the coarse-grained carbon chain beads (C₁).⁴⁶ Deformation of the graphene beads in the z (surface-normal) direction is possible, but they are constrained in the x and y directions. As in our previous study,³³ the lipid grafting positions are independent from the graphene beads at a nominal grafting distance of d_graft = 0.65 nm in a hexagonal lattice (surface coverage = 2.7 molecules per nm²), which is achieved using ghost beads in the same plane as the hexagonal sheet. The ghost beads are coupled to the motion of the graphene sheet during compression and shearing. The hexagonal arrangement of the molecules is motivated by experimental observations.⁵⁷

Fig. 1 CG-MD configurations of squeeze-out systems in (a) dry, (b) wet contacts and sliding contacts for (c) dry and (d) wet contacts. Sliding contacts are shown in the unwrapped state as opposed to the periodic, wrapped bead coordinates to indicate the relative motion. Beads are coloured by type: C₁ (gray), C₅ (cyan), P₅ (lime) and water (central red, satellite cyan opaque). Rendered with VMD.⁴⁸

The surface dimensions are 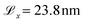and . Given that the thickness of a human hair is typically 50–100 μm and each cuticle cell is approximately 5–10 μm long,¹⁹ this represents a small patch of a single cuticle. We tested the effect of surface size on the convergence of the thermodynamic and friction properties of interest in preliminary simulations. No statistically significant differences were found between the selected surface size and simulations with an increase in the box length of 50% in x and y. We advise against using smaller surfaces to ensure that characteristic damage patterns are properly resolved, particularly at low degrees of hair damage, where only a few damage islands exist on the surface.³³

We consider an idealized contact between the cuticle F-layers of two hair fibers. The contact is treated as macroscopically flat, which is an adequate simplification at the length scales of the simulation box compared to the diameter of a hair (curvature = 0.02° at for d_hair = 50 μm). The lipids are representative of 18-MEA chains covalently bonded to the underlying protein layers via thioester bonds to cysteine groups. In the MARTINI framework,^46,49 this consists of a surface-grafted P₅ bead bonded to a C₅ bead (representative of the thioester and amine/carboxyl groups in cysteine) bonded to five C₁ beads (representative of the eicosane chain).⁵⁸ The oxidised cysteic acid groups formed by damage from chemical treatments or bleaching are represented by sulfonate groups that are covalently bound to the underlying protein.³² The sulfonate groups are represented by Q_a beads (replacing the neutral C₅ bead) with a charge of −1.⁵⁹

The surface damage is quantified by the number damage ratio χ_N, i.e., the ratio of the number of eicosane chains randomly replaced by sulfonate groups to the number of eicosane chains in a pristine monolayer.³³ We consider such pristine hair monolayers (χ_N = 0), as well as those we showed previously to be representative of the surface of virgin hair (χ_N = 0.25) and medium bleached hair (χ_N = 0.85),³³ as well as ultimately bleached (χ_N = 1.0) and other intermediate degrees of damage. The degree of damage was calibrated to the different hair types through comparison to experimental contact angle data using water and n-hexadecane.³³ For the damaged surfaces, sodium counterions (Na⁺) are added to the systems to maintain charge neutrality, which is a requirement for stable simulations of partially periodic systems when considering long-range electrostatic forces.⁵³ The Na⁺ cations and hydration shells (three water molecules) are represented by the Q_d beads with a charge of +1.⁴⁹ The contacts studied in the NEMD simulations consist of two surfaces with an equal degree of damage. Excluding the screening effect of the counterions, the damaged surfaces carry a surface charge density reaching from ρ_q = −11.0 μC cm⁻² to ρ_q = −37.2 μC cm⁻² for virgin and medium bleached hair, respectively. These values are somewhat larger than those from previous experimental measurements of the surface charge of virgin (−1.5 μC cm⁻²) and bleached (−8.0 to −10.0 μC cm⁻²) hair.⁶⁰ This discrepancy is probably due to partial screening of the negative hair surface charges by the K⁺ counterions present in the experimental solutions. This effect is not considered in the simulations surface charge values in Table 1. The surface coverage of SO₃⁻ groups in the medium bleached hair case (χ_N = 0.85) of 2.3 nm⁻², is very close to the value estimated from experiments (2.2 nm⁻²).³²

Table 1 Properties of single coarse-grained molecular and experimental model surfaces

Property	Unit	Simulations		Experiments
		Pristine hair	Ultimately bleached	C18-functionalised	SO3^−-functionalised
a Inferred from the difference between the measured thickness and that expected for a close-packed monolayer.
Monolayer thickness	nm	1.96 ± 0.01	0.47 ± 0.08	2.12 ± 0.09	0.52 ± 0.08
Grafting density	nm^−2	2.73	2.73	3.95^a	1.65^a
Surface energy	mJ m^−2	21.4	31.1	26.4	76.7

---

2.2 MD simulation details

Classical MD simulations are performed using the LAMMPS software.⁶¹ The velocity-Verlet⁶² integration scheme is used with a timestep of 5 fs. First, the systems are energy minimized using the conjugate gradient algorithm, before being equilibrated at T = 298 K with a global Nosé–Hoover thermostat.^63,64 During this phase, the position of the graphene sheets is fixed in the z-direction. Next, a constant normal force (F_N = 4.9 nN) equivalent to a pressure of 10 MPa is added to all of the beads in the top graphene sheet (A = 490 nm²), while the beads in the bottom graphene sheet remain fixed. The chosen pressure is based on an estimate of the Hertz pressure in previous AFM experiments of friction in hair–hair contacts.^24,25 Here, the applied load, F_N ≈ 0.1 mN, and the Young’ modulus of virgin and chemically damaged hair were taken as E = 0.9 GPa or E = 0.5 GPa, which is representative of virgin and chemically damaged soaked hair, respectively.⁶⁵ Further details are shown in the ESI (Fig. S1†).

In the dry systems, the force is maintained until the average pressure reaches the target value. The dry systems are periodic in the x and y directions and finite in the z direction. In the wet systems, the normal force is maintained until the number of water molecules remaining in the contact and corresponding contact thickness reach a steady state value, to simulate the squeeze-out process at the target pressure.³⁸ For these squeeze-out simulations, a fully periodic system is used, as shown in Fig. 1(b). Water beads are initially distributed randomly in the contact using PACKMOL⁶⁶ with additional reservoir space added around the contact. The number of water units in the system is fixed throughout the squeeze-out simulations. The initial surface-normal separation distance between the two graphene layers of the surfaces is set at d = 11.5 nm. Before the compression phase, the system is equilibrated at 298 K and atmospheric pressure (1 atm) is followed using a Parrinello–Rahman barostat acting in the z-direction.⁶⁷ Once the system volume reached a steady state value, the dimensions were fixed again for the compression phase. For the sliding phase of the wet contacts, new systems are constructing containing the steady state number of water beads from the squeeze-out simulations and the additional space in the x-direction is removed. The simulation boxes for the dry and wet NEMD simulations are periodic in the x and y directions and finite in the z direction. These systems are energy minimised, equilibrated at 298 K, and then compressed to 10 MPa prior to the sliding phase. The chosen pressure for the MD simulations is consistent with that calculated using Hertz theory for two crossed hair fibres using measured values of the Young's modulus of virgin and chemically damaged hair⁶⁵ and the load range used in previous AFM experiments of hair–hair friction (Fig. S1†).^24,25 The chosen pressure is also representative of the CCP AFM experiments using the biomimetic surfaces (Fig. S2†).

For the sliding phase, at sustained normal force, the upper graphene surface is moved in the x-direction at a constant sliding velocity, v_s, while the bottom slab remains stationary. The motion of individual graphene beads in the other directions (y and z) is rigidly constrained. Sliding velocities between 10⁻² and 10⁰ m s⁻¹ are considered, which are several orders of magnitude higher than typical velocities in AFM experiments using hair that typically operate in the 10⁻⁶ to 10⁻³ m s⁻¹ range.^16,18,24 The v_s values considered in the NEMD simulations are, in fact, closer to realistic scenarios of hair manipulations such as brushing and combing (v_s ≈ 10⁻¹ m s⁻¹)^68,69 or rubbing with a finger.⁷⁰ The requirement to sample a sufficient fraction of each surface in contact at reasonable computation times imposes a lower limit on the sliding velocity.

During the sliding phase, thermostatting is applied only to the P₅ beads of the hair surfaces in the direction lateral (y) to compression and sliding⁷¹ to act as a heat sink for thermal dissipation from frictional heating close to the sliding graphene sheets. This is a more physically realistic thermostatting strategy compared to thermostatting the entire system, which prevents thermal gradients from developing.⁷² For this purpose, a Langevin thermostat⁷³ is applied to the P₅ beads at T = 298 K and a time relaxation constant τ_t = 0.1 ps. Production sliding simulations are run for at least 200 ns. At the lowest sliding velocities considered here (v_s = 0.01 m s⁻¹), simulations are run up to 500 ns to sample at least 5 nm of surface displacement.

2.2.1 Water model viscosity. Since the viscosity of fluids is important to their tribological behaviour of soft contacts,⁷⁴ we validated the pressure–viscosity response of the polarizable MARTINI water model against experimental data. Viscosity calculations with the MARTINI force field have been performed in few instances,^{42,43,75–77} but the viscosity of the polarizable MARTINI water models have not been previously reported. Here, we employ the Green–Kubo method^78,79 to determine the dynamic viscosity η of polarizable MARTINI bulk water⁵⁰ at ambient conditions (T = 298 K, p = 1 atm) in the NVT ensemble after equilibration using a Nosé–Hoover thermostat.^63,64 A value of η = 54.8 ± 1.5 mPa s is found, which underestimates the experimental value⁸⁰ by ∼39%. 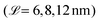The magnitude of this deviation is comparable to that of other atomistic water models,⁸¹ such as SPC/E⁸² or TIP5P.⁸³ The size of the simulation cell did not significantly affect the viscosity for the three tested box lengths shown in the ESI (Fig. S3(a)†). Furthermore, we evaluated the dynamic viscosity at system pressures of p = 0.1, 100, 200, 300 MPa using a Nosé–Hoover thermostat and barostat.^63,64 The corresponding viscosity–pressure plots are shown in the ESI (Fig. S3(b)†). Unlike for experimental water, the viscosity of the polarizable MARTINI model strongly increases with pressure. At high pressure, the model overestimates viscosity compared to experimental values. This is believed to result from the well-known attribute of MARTINI water to be prone to strong reordering,⁴⁹ thus transitioning to a solid-like behaviour at significantly lower bulk pressures than real water. We also observe this behaviour at elevated temperatures (T = 323 K), although shifted towards slightly higher bulk pressures. Thus, we conclude that the range of system pressures should be limited to p < 100 MPa to remain in a realistic viscosity regime. Such pressures are generally sufficient to match those observed experimentally inside the soft contacts found in biological systems.⁸⁴

2.3 Experimental details

We performed CCP AFM⁸⁵ experiments in a liquid cell to study the friction of atomically-smooth hair mimic surfaces in a water-lubricated environment. Biomimetic hair surfaces were produced by silanizing silicon wafers and 5 μm silica colloidal AFM probes with either octadecyl (C₁₈) or sulfonate (SO₃⁻) groups. The silicon wafers (Silicon Valley Microelectronics, Inc., California) had dimensions of 12 × 12 mm² with a 1.2 nm thick native oxide layer and 0.2 nm root-mean-square (RMS) roughness. We used custom-ordered 5 μm radius colloidal silica NovaScan (Boone, Iowa) AFM probes attached to Si₃N₄ cantilevers with a nominal spring constant of 0.35 N m⁻¹. The radius (5.0 ± 0.1 μm) and smoothness (0.2 nm RMS roughness) of the CCP probes were confirmed using scanning electron microscopy (SEM). The extremely small roughness of both experimental substrates enables the use of atomically-smooth surfaces in the simulations. Considering the large radius of the probe and accounting for its deformation during contact results in negligible curvature (<1°) on the scale of the NEMD simulation box, which justifies the use of flat surfaces. Tipless reference cantilevers were used to calibrate the normal spring constant and microscopic geometrical calculations were used to calculate the torsional spring constants.⁸⁶

The pristine hair mimic was represented by silica surfaces functionalised with octadecyltrimethoxysilane (OTMS), while ultimately bleached hair was represented by silica surfaces functionalised with a p-sulfonated phenylalkylsilane. Similar functionalised substrates were applied recently to study the wettability of biomimetic hair surfaces.³³ Proprietary methods were used to produce the functionalised surfaces, but similar methods have been described previously for alkylsilanes⁸⁷ and p-sulfonated phenylalkylsilanes.⁸⁸ Piranha solutions were used to prepare the silica surfaces prior to functionalisation. The same functionalisation methods were used for the silicon wafer and the silica colloidal probe. Time-of-flight secondary ion mass spectrometry (ToF-SIMS) measurements (TOF.SIMS 4, IONTOF, Germany) were applied to investigate the chemical composition of the monolayers. They confirmed that the expected species were present on the surfaces. For the SO₃⁻ systems, TOF-SIMS was used to confirm almost complete (91%) conversion of chlorosulfonyl precursor groups into SO₃H groups. Sulfonic acid is a very strong acid, so the SO₃H groups will be mostly deprotonated in water at neutral pH. Despite the use of deionised water in the friction experiments, it is reasonable to assume the presence of sodium counterions to ensure local electroneutrality (as in the NEMD simulations) from external contamination, for example the glassware⁸⁹ used during the functionalisation process.⁸⁸

Comparisons of the surface properties from the experiments and simulations are shown in Table 1. Uniform monolayer formation was confirmed using spectroscopic ellipsometry (M-2000DI/EC-400, J. A. Woollam Co., Inc., Nebraska), which was used to measure the film thickness across nine different locations on each surface. These measurements spanned a 18 mm² area of the substrate. Table 1 shows that the monolayer thickness values for both surfaces are in excellent agreement between the experiments and simulations. The thickness measured for pristine hair is also consistent with previous experimental measurements of the F-layer on real hair.⁵⁶ The experimental grafting densities were estimated by comparing the film thicknesses measured using ellipsometry to the expected thicknesses for upright molecules in close-packed monolayers.⁹⁰ The expected thickness is 2.7 nm for OTMS⁹¹ and 0.8 nm for the p-sulfonated phenylalkylsilane.⁸⁸ Based on the difference in thickness, the calculated packing efficiency for OTMS was 79% of the theoretical maximum, while for the p-sulfonated phenylalkylsilane it was 65%. The theoretical maximum coverage was estimated from the cross-sectional area of the molecules: for OTMS, this was taken as 0.2 nm²,⁹² while for the larger p-sulfonated phenylalkylsilane a value of 0.4 nm² was used.⁹³ This rough calculation resulted in the experimental grafting densities shown in Table 1. Due to the nature of the way that the damaged surfaces for the NEMD surfaces were prepared (random replacement of C₁₈ groups with SO₃⁻ groups) to match experimental wetting data,³³ both groups have an equal grafting density. From the ellipsometry measurements, it seems that the packing density of the C₁₈ groups is somewhat higher in the experiments than the simulations, while the packing density of the SO₃⁻ groups is higher in the simulations than the experiments. Thus the selected packing density for the simulations represents a reasonable compromise between the two experimental systems. The SO₃⁻ group coverage for ultimately bleached hair in the experiments and simulations is in reasonable agreement with previous experimental estimates for bleached hair (2.2 nm⁻²).³² The differences in packing density between the experiments and simulations may have a minor effect on friction. Previous experiments⁹⁰ and NEMD simulations³⁸ using different surfaces and surfactants containing C₁₈ groups have shown that higher surface coverages generally lead to lower friction. Therefore, it might be expected that friction in the C₁₈ system will be somewhat overestimated in the NEMD simulations compared to the experiments. For the SO₃⁻-functionalised surfaces, the main effect of the higher surface coverage in the simulations than the experiments will be an increased charge density, which may also affect friction. Given the major differences in surface chemistry and thus friction mechanisms between the C₁₈ and SO₃⁻ systems, the differences in packing density between the simulations and experiments are expected to have only a small effect on friction.

The surface energies (polar + nonpolar) shown in Table 1 were calculated using the Owens–Wendt method.⁹⁴ The contact angle measurements of polar (water) and nonpolar (n-hexadecane or diiodomethane) liquids were reported previously from experiments and simulations using the same surfaces.³³ Both the simulations and experiments show a higher surface energy for the SO₃⁻ system than the C₁₈ system. This is in agreement with previous wetting experiments, which showed that the surface energy is higher for bleached hair (29.8 mJ m⁻²) than virgin hair (18.9 mJ m⁻²).⁹⁵ AFM experiments also suggested higher surface energies for bleached hair (44 mJ m⁻²) than virgin hair (24 mJ m⁻²) from adhesion measurements.³² The surface energy of both surfaces is higher in the current experiments than the simulations. This can mainly be attributed to the lower surface tension values in the simulations due to the systematically lower water–vapor surface tension of the polarizable MARTINI water model.^33,50

The CCP AFM experiments were performed using a Bruker (Billerica, Massachusetts) MultiMode 8 scanning probe microscope in contact mode. The contact was immersed in deionised water medium. A scan angle of 90 deg. was used with respect to the cantilever long axis. The typical scan length during the lateral (friction) force measurements was 30–100 nm at a scanning frequency of 1 Hz. The friction forces were measured at applied normal loads between 1–3000 nN. The lateral deflection signal (cantilever twist) was converted to a friction force from the cantilever geometry and torsional spring constant.⁸⁶ The use of smooth biomimetic surfaces eliminates any damage-induced change in microscale surface topography⁹⁶ or porosity⁹⁷ from the friction measurements, which is not the case with real hairs.^13,24 Separate CCP AFM measurements were made without sliding to quantify the repulsion in the SO₃⁻ system (−20 nN) and adhesion in the C₁₈ system (+450 nN). This is consistent with previous AFM measurements that have shown reduced hair–hair adhesion following chemical damage¹³ or bleaching.²⁴ The larger adhesion for the C₁₈ system in water is due to hydrophobic interactions.⁹⁸

Given the difference in the contact area between the experiments and simulations, our aim was to match the contact pressure rather than the load. The graphene sheet used for functionalisation in the CG-MD simulations is fully periodic in the x- and y-directions and is therefore considered macroscopically inelastic. Elastic deformation in the simulations is thus limited to the functionalised molecules. The pressure can be calculated simply by dividing the force applied in the z-direction by the area of the surfaces. Conversely, in the experiments, the elasticity of the substrate and the functionalised molecules both need to be considered. Using the Johnson–Kendall–Roberts (JKR)⁹⁹ contact theory modified by Reedy¹⁰⁰ for thin coatings with experimentally measured adhesion and elastic properties of the silica (substrate)¹⁰¹ and surfactant monolayers (coating),¹⁰² we estimate that the contact pressure in these experiments varies between 5–79 MPa over the chosen load range (1–3000 nN). Further details on this calculation and comparison to other methods that do not account for adhesion and/or thin coatings are provided in the ESI (Fig. S2†). It is worth noting though that for previous AFM experiments using hair–hair contacts, the load had no effect on the coefficient of friction over a range of 10 to 1000 nN.²³ High-load nanotribometer experiments of hair–hair contacts showed that the CoF decreased from 10 to 100 mN, at which point wear began to occur.²⁷ Thus, we consider our chosen baseline pressure in the NEMD simulations (10 MPa) to be representative of the current CCP AFM experiments using biomimetic surfaces and previous AFM experiments of nanoscale hair friction where no wear occurred. We also performed a subset of squeeze-out and NEMD simulations over a wider range of pressures (5–50 MPa) to enable more direct comparison with the CCP AFM experiments. The variable-pressure NEMD simulations were all performed a sliding velocity of v_s = 0.1 m s⁻¹.

3 Results and discussion

3.1 Dry contacts

To investigate the molecular-scale origins of the friction behaviour, we first study the structure of the hair surfaces during compression and sliding at different degrees of damage. Fig. 2 shows the surface-normal (z) mass density and through-film velocity profiles (v_x) for dry contacts from the NEMD simulations. At low damage levels, the thickness of the F-layer on each surface is approximately 2 nm, which is consistent with previous experimental measurements.⁵⁶ It is also similar to the thickness measured by ellipsometry for the pristine hair biomimetic surface (Table 1). At all damage levels, there is clear layering, which is strongest close to the sliding surfaces, but extends into the centre of the contact (z = 0 nm). The mass density profiles are insensitive to the sliding velocity, which is consistent with previous atomistic NEMD simulations of stearic acid monolayers adsorbed on iron oxide surfaces.³⁷ The monolayers on the opposing surfaces are interdigitated with each other, as shown by the overlap in mass density profiles. There is a general increase in the amount of interdigitation with increasing damage ratio. The outer layers of the lipids move at the same velocity as the graphene surfaces to which they are grafted and the velocity changes linearly between the two extremes in the interdigitated region. This observation is also consistent with previous atomistic NEMD simulations of surfactant monolayers adsorbed on iron oxide surfaces.³⁸ There do not appear to be any velocity slip planes between the layers shown in the mass density profiles, which would appear as discontinuous changes in the velocity profiles.

Fig. 2 Dry contact monolayer mass density (top) and velocity (bottom) profiles at v_s = 1 m s⁻¹ and σ = 10 MPa for different damage ratios, χ_{N (a-e)}. The damage ratio increases from left to right. The densities of the lower surface (solid black), upper surface (solid green), sodium counterions (orange) and graphene sheets (black dashed) are shown.

The CoF (μ) in the single-pressure NEMD simulations is obtained using the Amontons friction law by dividing the lateral force (F_L) by the normal force (F_N) acting on the outer layer of beads.¹⁰³ Previous nanoscale AFM hair friction experiments have shown a linear relationship between F_L and F_N, with a negligible intercept.^13,24 The mean CoF between dry surfaces from the NEMD simulations is shown in Fig. 3 as a function of sliding velocity for the various levels of damage considered. At the lowest sliding velocity considered (v_s = 0.01 m s⁻¹), the CoF increases monotonically with damage ratio, which is consistent with previous experimental measurements of virgin, chemically damaged and bleached hair.^10,13,22 At low sliding velocity, the NEMD simulations show a difference in CoF of almost two orders of magnitude between the virgin (χ_N = 0.25) and medium bleached hair (χ_N = 0.85). Experiments in a dry nitrogen atmosphere (RH ≈ 4%) showed that compared to virgin hair, the CoF was approximately three times higher for chemically damaged (KOH-treated) hair and twice as high for bleached hair.²² There are several differences between these previous experiments and the current simulations that may explain the larger difference between virgin and damaged hair in the simulations compared to the experiments. Firstly, due the hair samples in the AFM experiments would have still contained some residual water molecules, despite the low relative humidity. Secondly, the experiments used silicon nitride tip–hair contacts, rather than hair–hair contacts. Finally, the sliding velocity used in the experiments (4 × 10⁻⁶ m s⁻¹) is well below those that can be directly simulated using the current CG-MD framework (1 × 10⁻² m s⁻¹).

Fig. 3 Dry CoF as a function of sliding velocity v_s and monolayer damage at σ = 10 MPa in double logarithmic plots. Eqn (1) (dashed lines) is fitted to the data for all damage ratios except χ_N = 1.³⁷ Uncertainty bars are omitted in (a) to improve clarity. (b) Shows the same data as a nondimensional representation, collapsed by the fitting parameters v₀ and μ₀. Vertical bars show one standard deviation. Insets in (a) show raw friction vs. time signals at the same x and y axis scale.

For low and moderately damaged hair (χ_N < 0.85), the CoF increases rapidly with sliding velocity, as expected for liquid-like systems.¹⁰⁴ For higher damage levels, the friction dynamics are more solid-like, showing only moderate increases in friction force with sliding velocity, as well as stick-slip behaviour.¹⁰⁵ The transition from liquid-like, smooth friction towards a more solid-like, stick-slip regime (insets in Fig. 3a and Fig. S4†) can be observed by an increase in the standard deviation of the CoF around the mean (shown in Fig. 3(b)). This is attributed to the reduction in the number of flexible lipids on each surface and increase in the number of inflexible charged groups, which leads to increasingly stiff and heterogeneous surfaces. At high sliding velocity, a crossover is observed where the CoF at moderate damage exceeds that at higher damage. The ultimately bleached (χ_N = 1.0) surfaces have a higher CoF by one order of magnitude compared to the medium bleached (χ_N = 0.85) case. At this degree of damage, CoF is completely insensitive to sliding velocity, as expected for solid–solid friction.¹⁰⁵ The much higher friction for the damaged surfaces is mainly due to the strong electrostatic interactions between the negatively charged sliding surfaces and the positively charged confined counterions. Similarly high CoFs have also been observed for negatively charged surfaces with strongly confined ionic liquid cations.¹⁰⁶

For all systems with χ_N ≤ 0.85, the CoF increases logarithmically with sliding velocity, v_s. This behaviour is indicative of a stress-augmented thermal activated (SATA) process,¹⁰⁷ similar to the Eyring model for liquid viscosity.¹⁰⁸ Such behaviour has been observed in many boundary-lubricated contacts protected by adsorbed or grafted monolayers in both experiments^104,109,110 and NEMD simulations.^{37,38,111,112} The logarithmic dependency of the CoF on v_s predicted by SATA models generally only holds for intermediate v_s. At very low sliding velocities, a linear relationship is more common, because thermal fluctuations dominate the activation process, as opposed to the external shear stress.^104,105,110 An extended SATA model describing both the v ∝ ln(v_s) behaviour at high v_s and the v ∝ v_s at low has been applied to CoF data from NEMD simulations using both all-atom³⁷ and CG¹¹² force fields:

where the reference coefficient of friction, μ₀, and reference sliding velocity, v₀, are fitting parameters. The applicability of this model to our data is confirmed for dry hair contacts by means of the dimensionless representation in Fig. 3(b). The fitting parameters μ₀ and v₀ are shown in Fig. 4(a) and (b) as a function of surface damage. The ultimately bleached case (χ_N = 1.0) has been excluded from this fitting since the CoF is insensitive to sliding velocity for this system. The fitting parameters μ₀ = k_BT/(p_Nd₀³) and v₀ = k₀·d₀ from the SATA model can be related to physical quantities. Specifically, d₀ represents the distance between the molecular-scale energy barriers, while k₀ is the hopping rate constant. In these systems, the barriers are likely related to the molecular-scale roughness due to the lipid islands that form on the damaged surfaces.³³ The reference CoF and reference velocity both decrease with increasing damage ratio. Fig. 4(c) and (d) shows that there is an increase in the distance between barriers, d₀, and a decrease in the hopping rate constant, k₀, with increasing damage. These changes in d₀ and k₀ indicate that energy hopping events occur more infrequently and with a larger energy barrier distance as the damage ratio increases. This is because, as the damage level increases, the number of lipid islands decreases, while their physical separation increases.³³ The transition towards smaller, more widely spaced lipid islands is consistent with the appearance of stick-slip friction at high damage levels (inset in Fig. 3a and Fig. S4†).

Fig. 4 Reference (a) coefficient of friction μ₀, (b) velocity v₀ and corresponding (c) barrier distance d₀ and (d) hopping rate constant k₀ from thermal activation model fits³⁷ as a function of monolayer damage.

The molecular-scale roughness from the lipid islands imposes a physical barrier to overcome during sliding. The d₀ value correlates with the interdigitation between the lipid monolayers on the opposing sliding surfaces (Fig. 2). We quantify the degree of interdigitation by means of the average volume available per bead in the region of direct interdigitation between the two contacts. We find the available volume per bead to increase monotonically from 〈V_i〉 ≈ 0.1 nm³ for pristine hair monolayers to 〈V_i〉 ≈ 0.14 nm³ for χ_N = 0.85 (Fig. S5(a)†). Therefore, more space per CG bead is available at higher damage. This is in contrast to the interdigitation distance, which reaches its peak at intermediate degrees of damage, consistent with a maximum in the expected degree of heterogeneity.³³ We observe that the volume per bead (rather than the interdigitation distance) is highly correlated with the barrier distance d₀ from the fits to eqn (1) (Fig. S5(b)†).

The orientation of the lipid molecules may also affect the friction behaviour. Absolute tilt angles of the vector from the lipid root bead (P₅) to the terminal bead (C₁) relative to the xy-plane are shown in the ESI (Fig. S6(a)†). For the dry contacts, the absolute tilt angle decreases from ≈50° for pristine hair surfaces, to ≈25° for medium bleached hair. This suggests that the lipids go from a mostly upright conformation to lying more parallel to the surface as the damage level increases. There is a slight decrease in the absolute tilt angle with increasing sliding velocity.

We also quantified the orientational tilt angle, which is measured between the projection of the P₅–C₁ vector in the xz-plane and the x unit vector, as shown in the ESI (Fig. S6(b)†). The lipids move from being aligned parallel to the z-direction (perpendicular to the hair surface and sliding direction) at low sliding velocity, to being almost completely aligned with the sliding direction at high sliding velocity. Friction is often reported to increase as a function of monolayer alignment in the direction of sliding, which is generally attributed to higher commensurability between the interacting monolayers.^113,114 In the current study, however, the monolayers are relatively loosely packed (maximum lipid coverage = 2.7 nm⁻²)^38,115 and the interface does not form a crystalline, commensurate interface, even when the molecules are aligned with the sliding direction. Indeed, at low damage levels, where high commensurability is most likely due to the highest lipid coverage, there is no stick-slip behaviour evident in the friction versus sliding distance signals (Fig. S4†). Molecular alignment does not seem to have a significant effect on the friction behaviour.

The absence of water in biological systems is rare, even in dry environments. The presence of residual water in the cuticle,¹¹⁶ absorbed water from ambient humidity,¹¹⁷ and the frequent contact of hair with water during washing¹¹ mean that the addition of water molecules at the interface is an essential component of realistic NEMD simulations.

3.2 Wet contacts

3.2.1 Squeeze-out simulations. Squeeze-out simulations are performed at various degrees of chemical hair damage to establish an equilibrium film thickness at the target pressure (10 MPa) for subsequent sliding NEMD simulations.³⁸ The equilibrium number of water units and examples of temporal evolution of the number of polarizable water units (N_w) and contact thickness at p = 10 MPa are shown in Fig. 5. A steady-state thickness between 4–6 nm is reached after 13–20 ns, depending on the degree of damage. A decrease in the equilibrium thickness and increase in the number of water units is observed with increasing damage. As the damage level increase, the number of hydrophobic lipids decreases and hydrophilic sulfonate groups become more prevalent on the surface. Stronger intermolecular interactions between the sulfonate groups and the water beads keep more water trapped inside the contact.⁹⁸ The steady state contact thickness decreases until reaching a constant value (d = 4.2 nm) at χ_N > 0.5 due to the combined effects of a reduced number of lipids and an increase in water content. The equilibrium contact thickness is largest at low damage levels due to the increased physical separation caused by the higher density lipid monolayers.

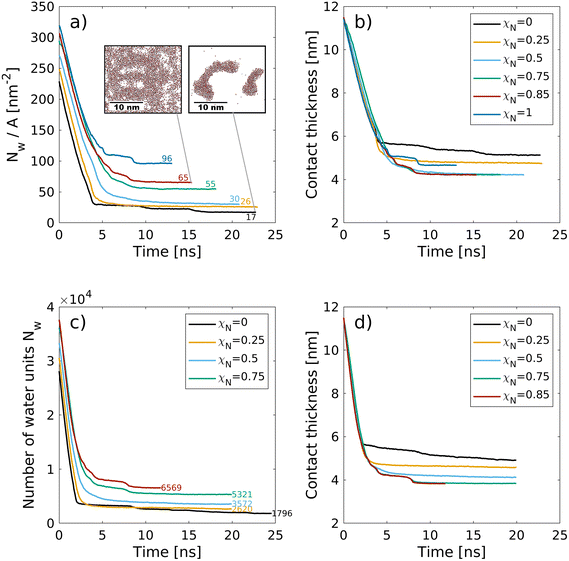Fig. 5 Change in the number of water molecules (4·N_w,CG) per surface area N_w/A (a) and the contact thickness between the graphene sheets (b) with time during the squeeze-out simulations at a pressure, σ = 10 MPa for hair surfaces with different degrees of χ_N. The molecule number densities per unit area at equilibrium are shown as text labels in (a). Insets in (a) show snapshots of the confined water beads at the end of the squeeze-out simulations rendered with VMD.⁴⁸ The contact thickness in (b) includes the monolayer thickness.

Recent small-angle neutron scattering (SANS) experiments suggest that the cell membrane complex of the hair cuticles in healthy hair contains water clusters with a size of 40 Å (correlation length, estimated from a Debye–Bueche model).¹¹⁶ For formic acid treatment, which removes internal lipids from the hair, the number of such clusters was reduced.¹¹⁶ While this transition takes place below the exposed F-layer, the proposed mechanism is comparable to the contacts modeled in this work. In the cell membrane complex, the contact between the 18-MEA monolayers on two neighbouring cuticles is essentially the same as between the outer cuticles of two virgin hairs. In our NEMD simulations, we observe the formation of water clusters of similar size as those observed experimentally¹¹⁶ for the pristine hair systems (χ_N = 0). Droplets are energetically favored over thin film formation due to the hydrophobic nature of the two monolayer surfaces. The formation of droplets between hydrophobic monolayers was also observed in previous NEMD simulations.¹¹⁸ At higher damage levels, water progressively attaches to regions where the lipids have been removed, which is consistent with our previous CG-MD simulations³³ and AFM experiments.¹¹⁹ For the ultimately bleached hair surfaces (χ_N = 1.0), an equivalent atomistic water number density per unit area of N_w/A = 96 nm⁻² is obtained, which is distributed within six hydration layers normal to the two surfaces. This value is in good agreement with the largest value used in atomistic NEMD simulations that studied the friction of water confined between hydrophilic alkylsilane monolayers (N_w/A = 85 nm⁻²).¹²⁰ For the fully funtionalised surfaces (χ_N = 0.0), the final water coverage (N_w/A = 17 nm⁻²) is in good agreement with the plateau value (N_w/A = 20 nm⁻²) obtained from previous atomistic Monte Carlo simulations of water adsorption between hydrophobic graphene surfaces separated by 1.6 nm.¹²¹

3.2.2 NEMD simulations. We used systems containing the equilibrium number of water molecules from the squeeze-out simulations to investigate the friction between the wet hair surfaces with different damage levels. We first looked at the structure of the water-containing systems. Mass density profiles at v_s = 1 m s⁻¹ and σ = 10 MPa are shown in Fig. 6 for all damage levels where χ_N ≤ 0.85. As for the dry systems, the density profiles are insensitive to the sliding velocity. Strong layering is observed at the solid–liquid interface for both the grafted monolayers and water molecules. Strong layering has also been noted in several previous molecular simulation studies of water confined between hydrophobic and hydrophilic surfaces.^121,122 Ordered water layers have also been observed experimentally between adsorbed cetyltrimethyl-ammonium bromide (CTAB) surfactant monolayers and have been shown to facilitate low friction.¹²³

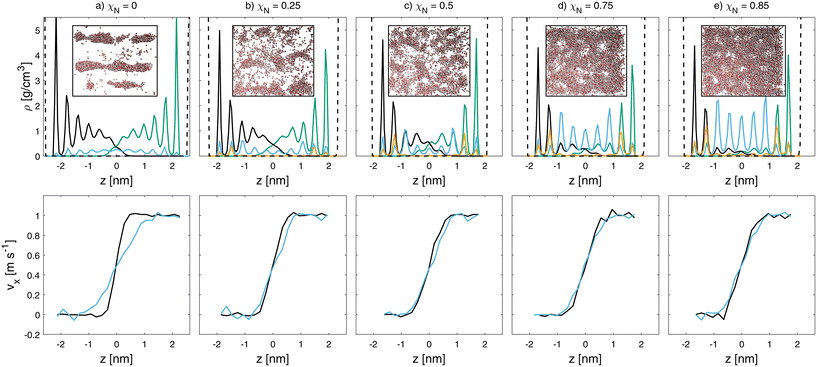Fig. 6 Mass density (top) and velocity (bottom) profiles for wet sliding simulations at v_s = 1 m s⁻¹ and σ = 10 MPa at different degrees of monolayer damage (a-e). Water (blue), lower hair (black), upper hair surface (green), Na⁺ counterions (orange) and base graphene sheets (dashed black) density profiles are shown. Velocity profiles of lipids (black) and water (blue) are shown. Insets show top view snapshots of water inside the contacts. Rendered with VMD.⁴⁸

The hydrophobic nature of the pristine hair surfaces (χ_N = 0.0) favors the formation of water droplets over thin films.³³ The droplets are stretched in the direction of sliding, as is evident from the inset in Fig. 6(a). Additional snapshots at different sliding velocities are shown in the ESI (Fig. S7 and S8†). For these undamaged systems, the water droplets penetrate around 2 nm into the lipid monolayers and adhere to the hydrophilic P₅ beads at their base. At higher damage levels, thin water films form that are interspersed with lipid islands, as shown by the top view snapshots in Fig. 6. Even at χ_N = 0.85, we observe interdigitation between the lipid monolayers on the two opposing surfaces. This is due to swelling of the monolayers,³³ which results in mostly upright conformations, even at high damage levels. At χ_N = 1 (not shown), there are no lipids remaining on the surface and thus no interdigitation. In this case, there is a complete thin (4 nm) water film between the sulfonate-covered surfaces. Fig. 7 shows the velocity profiles of the lipids among both surfaces and water at the interface. In the pristine hair case, there is a slip plane between the lipid monolayers on the opposing surfaces, while the water beads are sheared to the depth that they penetrate the lipid monolayer. This is attributed to the pinning of the water droplets to the lower regions of the displaced monolayers. In all other cases, the water beads move at the same velocity as the neighbouring lipid beads.

Fig. 7 Wet CoF as a function of sliding velocity, v_s, for the different damage ratios at σ = 10 MPa in double logarithmic representation. Dashed lines indicate fits eqn (1).³⁷ Open symbols represent data not included in the fits. (b) Friction–velocity data normalized by the fitting parameters.

For the wet contacts, the absolute tilt angle (Fig. S9(a)†) tends to be invariant to damage at a value of ≈50°. This confirms that swelling of the monolayer occurs in water under confinement, with the lipids retaining an upright conformation even at high damage levels. This observation is consistent with our previous single-surface CG-MD simulations.³³ As for the dry contacts, there is a slight decrease in the absolute tilt angle at higher sliding velocities. At low sliding velocity, the orientational tilt angle decreases more in the dry systems (Fig. S6(b)†) than the wet systems (Fig. S9(b)†). This suggests that the lipids align with the sliding direction more readily in the dry systems than the wet ones. As with the dry systems, molecular alignment seems to have a negligible effect on the friction behaviour in wet contacts.

Fig. 7(a) shows the CoF in the wet contacts as a function of sliding velocity for the different damage levels at 10 MPa. At χ_N = 0.75 and below, smooth, liquid-like friction signals are observed. Despite the presence of water in the contact, stick-slip friction is observed at χ_N = 0.85 and above, as evident from the inset in Fig. 7(a) for χ_N = 1.0. The water film thickness is insufficient to provide complete surface separation, even at the relatively low pressure simulated. Interdigitation is confirmed by the overlapping lipid density profiles in Fig. 6(e). In contrast, the ultimately bleached systems (χ_N = 1.0) are fully separated by a water film with a thickness of ≈2.6 nm, distributed among six hydration layers. Nonetheless, stick-slip is observed in this system, as indicated by the standard deviation of the friction force signal of 37% around the mean CoF. Stick-slip friction was also observed in previous experiments using wet bleached hair–hair contacts.³⁰ The highest CoFs in Fig. 7(a) are obtained for the ultimately bleached system across all sliding velocities. In this case, stick-slip is promoted by interlayer sliding of commensurate surface-bound hydration layers on the highly hydrophilic surfaces. High stick-slip friction was also observed in previous atomistic NEMD simulations of water confined between hydrophilic surfaces.¹²⁴

At low sliding velocity, the CoF increases monotonically with damage ratio. Here, the CoF for bleached hair (χ_N = 0.85) is much higher than for virgin hair (χ_N = 0.25), which is consistent with previous AFM experiments using real hair.¹³ At high velocities, a crossover is observed where the CoF for virgin hair exceeds that for medium bleached hair.

For v_s > 0.1 m s⁻¹, the CoF data is fitted to eqn (1).³⁷Fig. 7(b) shows the non-dimensional representation of the CoF included in the fits normalized by the fitting constants μ₀ = k_BT/(p_N·d³) and v₀ = k₀d.³⁷ The changes in fitting constants as a function of surface damage are shown in the ESI (Fig. S10†). At high v_s, the model accurately describes the observed friction behaviour. At v_s < 0.1 m s⁻¹, the CoFs strongly deviate from the fits on the high sliding velocity data. The CoFs become almost independent of sliding velocity below v_s = 0.1 m s⁻¹ for all degrees of damage and clearly no longer follow the typical SATA behaviour. The corresponding data points are therefore omitted from the fitting, as indicated by open symbols in Fig. 7(a).

One mechanism by which the CoF could exceed that expected from eqn (1) at low sliding velocities is capillary condensation. Previous AFM experiments using nanoscale silica–silica contacts at moderate relative humidity showed that friction decreased logarithmically with increasing sliding velocity before levelling off.¹²⁶ Although there are no water–vapour interfaces in our NEMD simulations, this are water–lipid interfaces. Increased adhesion forces have been reported previously due to capillary forces at water–oil interfaces.¹²⁷ In the low-velocity regime, nanoscale water droplets (low damage) could give rise to additional cohesive forces through the presence of well-defined phase boundaries. Indeed, previous AFM experiments have shown that water nanodroplets in n-hexadecane can increase friction.¹²⁸ Snapshots of these water structures in the pristine hair contacts are shown at different sliding velocities in the ESI (Fig. S7†). At full surface damage, no such phase boundary is present in the lateral direction because a thin water film forms.

We quantified the area of contact-bridging water–lipid interface by tracing the perimeter of the water droplet (low damage) or lipid islands (high damage) and multiplying by the average thickness of those structures in the surface-normal direction (Fig. S11†). There is a clear transition between intermediate (χ_N = 0.5) and high (χ_N = 0.75) damage where there is a large increase in the interfacial area. However, the interfacial area weakly increases with sliding velocity and thus cannot be linked to increased capillary adhesion at low velocities, where a higher interfacial area would be expected.¹²⁷ Moreover, capillary condensation would be expected to increase friction on hydrophilic surfaces more than hydrophobic ones,³⁴ which is the opposite to the trend we observe in our NEMD simulations.

Related to capillary effects, freezing of the confined water bridges is another possible explanation for elevated friction at low sliding velocities. Indeed, previous AFM experiments of the phenomenon have observed higher than expected friction at low sliding velocities,¹²⁹ as shown in Fig. 7(a). To investigate this effect, the diffusion and structure of the confined water molecules were studied at different sliding velocities and damage levels. The mean-square displacement (MSD) and radial distribution function (RDF) of the central water beads were analysed, as shown in Fig. 8. While the lateral MSD increases linearly with time for highly damaged systems, it approaches a plateau at low degrees of damage, which is indicative of subdiffusion. The more pronounced subdiffusive behaviour at low degrees of damage is partially due to a decrease in confinement lengthscale (Fig. 6). The majority of the surfaces are covered by lipids and water resides within small droplet-like regions. This is in agreement with previous studies of water confined by soft materials,¹³⁰ where the lengthscale of confined water was found to play a role in the tendency of water to show subdiffusion.

Fig. 8 Mean-square displacement (MSD) of the central polarizable water beads perpendicular to the direction of sliding (y: left; z: middle) at different sliding velocities and for pristine hair surfaces (top row), virgin (middle row) and medium bleached hair (bottom row). Here, t = 0 ns indicates a time at which the contact has long reached dynamic equilibrium. Approximate diffusion coefficients for subdiffusive configurations are obtained from linear fits for t > 10 ns. Right side: radial distribution function (RDF) of central water beads compared to the RDF in bulk.¹²⁵

The diffusion coefficients, D in Fig. 8 are generally larger in the lateral direction (y) than the direction perpendicular to the surfaces (z). This suggests that the water molecules move more freely along the surface plane than between the confined water layers shown in Fig. 6. An increase of the lateral diffusion coefficient, D_y, is observed with increasing damage ratio. For the medium bleached model hair surfaces (χ_N = 0.85), water diffusion coefficients perpendicular to the direction of sliding increase at higher sliding velocity, from D_y = 2.2 × 10⁻⁹ to 3.8 × 10⁻⁹ m² s⁻¹. These values are similar to those obtained previously for bulk polarizable MARTINI water (D = 2.5 × 10⁻⁹ m² s⁻¹)⁵⁰ and liquid water from experiments (D = 2.3 × 10⁻⁹ m² s⁻¹).¹³¹ For the virgin model hair surfaces (χ_N = 0.25), long-time lateral diffusion is much slower than for bulk water (D_y = 5.9 × 10⁻¹⁰). This reduction is similar to that observed in previous atomistic MD simulations of water inside lipid bilayers.¹³² For pristine hair (χ_N = 0.0), the lateral diffusion coefficient is more than two orders of magnitude lower (D_y = 1.2 × 10⁻¹¹) than in the bulk. This reduction in lateral diffusion is similar to that observed previously for confined bilayer ice by atomistic MD simulations (D_y ≈ 10⁻¹² m² s⁻¹).¹³³ This implies that the confined water dynamics are solid-like in the pristine hair systems. It has also been suggested that surface hydrophobicity might be crucial to confinement-induced liquid–solid water phase transitions¹³⁴ since freezing has not been observed for hydrophilic surfaces in either experiments¹³⁵ or simulations.^136,137 Indeed, we note that the lateral diffusion coefficient increases as the damage level (and thus surface hydrophilicity) is increased. In our NEMD simulations, the water mobility is more sensitive to damage than sliding velocity and, at low damage, the lateral diffusion coefficients suggest that the water remains in the same state at both low and high sliding velocity.

Structural ordering of the confined water molecules as shown in the RDFs in Fig. 8 is consistent with bulk ordering of polarizable MARTINI water as shown by Sergi et al.¹²⁵ Although the peak intensities increase somewhat at lower sliding velocity, there are only small shifts in the peak positions for a given degree of surface damage. Additional peaks do not appear at larger distances, which would be indicative of long-range order. This suggests that the reduction in water diffusion at low damage levels is due to a confinement-induced liquid–amorphous transition, rather than crystallisation. This is consistent with previous atomistic MD simulations of water confined between hydrophobic surfaces.¹³⁶

We also investigated the structure and mobility of the hydrated sodium counterions (Na⁺) that are adsorbed near the damaged regions of the surfaces of virgin (χ_N = 0.25) and medium bleached (χ_N = 0.85) hair. These results are shown in the ESI (Fig. S12†). For both surfaces, the counterion RDF is similar to the bulk RDF for cations⁵⁰ and is independent of the sliding velocity. We observe similar changes in counterion diffusion with surface damage and sliding velocity as seen for water. The mobility of the counterion beads is generally lower than the water beads due to the stronger electrostatic interactions with the SO₃⁻ surface groups. Immobilisation of counterions on charged substrates has also been observed in previous simulations.¹³⁸ The higher friction in damaged hair could therefore arise from overcoming attractive electrostatic interactions between the negatively-charged sulfonate groups on the surfaces and the strongly adsorbed sodium cations confined between them during sliding. Kagata et al.¹³⁹ made a similar hypothesis to explain the high friction of like-charged gels in the presence of counterions. The proposed electrofriction mechanism could be investigated further by changing the size and charge of the counterions.

The CoF in wet systems are now compared to the dry counterparts discussed in the previous section. The ratio between the wet and dry contact CoF as a function of sliding velocity at equal pressure is shown in Fig. 9. At sliding velocities of v_s = 0.1 m s⁻¹ and above, wet contacts render a friction reduction for all of the systems. The largest reduction at all sliding velocities is for the ultimately bleached (χ_N = 1.0) system. At low sliding velocities, wet friction forces exceed dry friction forces for the systems with low damage levels (χ_N < 0.85). This is attributed to increased adhesive contributions of solid-like interfacial water droplets confined between the surface-bound lipids. Conversely, large friction reductions are found for the ultimately bleached surfaces at all sliding velocities because the thin water film provides sufficient separation to lubricate the contact interface.

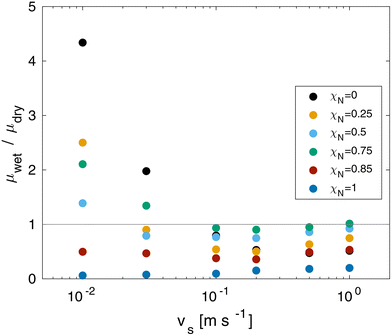Fig. 9 Ratio between wet and dry CoF as a function of sliding velocity v_s and monolayer damage χ_N at σ = 10 MPa.

Previous experiments have also shown higher friction for wet hair than dry hair.⁸ Previously, this has been attributed to microscale effects, specifically the swelling of the cuticles leading to increased contact area and rougher surfaces.¹¹ Such mechanisms are not captured by our CG-MD model, apart from swelling within the lipid monolayer.³³ Our NEMD simulations suggest that solidification of confined water droplets¹²⁹ is an additional nanoscale mechanism that could lead to increased adhesion and friction between wet hairs.

3.2.3 Comparison between NEMD simulations and AFM experiments. As a final step, the friction behaviour from the NEMD simulations of the wet systems is compared to previous AFM experiments on real hair in humid air¹³ and new CCP AFM experiments with the biomimetic surfaces in water. The shear and normal forces for virgin and damaged hair obtained in the previous AFM experiments¹³ were converted to stresses τ₀ using JKR theory⁹⁹ with previously measured surface energies for virgin and bleached hair.⁹⁵ The CCP AFM shear stress and normal stress values are converted from the measured forces using the extension to JKR theory⁹⁹ for thin coatings due to Reedy.¹⁰⁰ The experimentally-measured normal and friction forces from the CCP AFM experiments, prior to conversion to stresses, are shown in the ESI (Fig. S13†).

In the NEMD simulations (Fig. 7), a monotonic increase of the CoF with the damage ratio is observed at the lowest sliding velocity (v_s = 1 × 10⁻² m s⁻¹). For the pristine hair surfaces (χ_N = 0.0) at 10 MPa, we obtain a CoF (σ/τ, i.e. ratio of shear stress to normal stress) of μ = 0.11 ± 0.04, which increases to a maximum of μ = 0.54 ± 0.21 in the case of ultimately bleached surfaces (χ_N = 1.0). The biomimetic surfaces using CCP AFM functionalised with C₁₈ (pristine hair) and SO₃⁻ (ultimately bleached) yield CoFs of μ = 0.023 ± 0.002 and μ = 0.67 ± 0.03, respectively. This means that the CoF of the ultimately bleached contact is ∼29 times greater than the pristine hair contact. Therefore for surfaces representative of ultimately bleached hair, the agreement in the CoF from the experiments and NEMD simulations at a single pressure is excellent (−19%). For the pristine hair surfaces, the CoF is around five times larger higher in the simulations than the experiments. One source of this difference could be the higher C₁₈ surface coverage in the experiments than the NEMD simulations (Table 1), which has been shown previously to lead to higher friction.^38,90 In the C₁₈ systems, the CCP AFM experiments show a non-negligible load-independent adhesive contribution to the friction force, known as the Derjaguin offset.^103,115 To quantify this contribution in the simulations, we performed additional squeeze-out and NEMD simulations at a wider range of pressures (σ = 5–50 MPa). A summary of the amount of water after squeeze-out for all configurations is given in the ESI (Table S1†). In all of the variable-pressure NEMD simulations, a sliding velocity of v_s = 0.1 m s⁻¹ was applied. While this is much larger than in the CCP AFM experiments (v_s = 10⁻⁷ m s⁻¹), it is within the regime of approximately constant μ ≠ μ(v_s) behaviour (Fig. 7) in the simulations. Thus, only relatively small reductions in the CoF would be expected were the CoF–velocity results to be extrapolated to experimental velocity. Since additional datapoints in the low-velocity regime would be required to enable accurate extrapolation, we directly compare the CoFs obtained for the virgin and damaged hair from the experiments and simulations conducted at higher sliding velocities. It is worth noting that similarly high sliding velocities to those applied in the NEMD simulations are encountered physiologically during hair brushing and combing (v_s ≈ 0.1 m s⁻¹).^68,69

Fig. 10 shows the shear stress, τ, as a function of normal stress, σ, for (a) the NEMD simulations and (b) CCP AFM experiments. In both the experiments and NEMD simulations, there is a linear increase in τ with σ, as expected from the Amontons friction law.¹⁰³ However, in some cases, there is a non-negligible intercept, which is indicative of an adhesive contribution that can be quantified though the Derjaguin offset.^103,115 The CoFs (gradient) and Derjaguin offsets (intercept) shown in Table 2 are extracted from the linear fits shown in Fig. 10 to the equation: τ = (σ·μ) + τ₀, where τ₀ is the Derjaguin offset.^103,115

Fig. 10 Shear stress, τ, as a function of normal stress, σ, from (a) wet NEMD simulations and (b) biomimetic CCP AFM experiments in water. Experiments for C₁₈ (χ_N = 0) and SO₃⁻ (χ_N = 1) functionalised surfaces. Experiments (v_s ≈ 10⁻⁷ m s⁻¹) were conducted at lower sliding velocities than the simulations (v_s = 10⁻¹ m s⁻¹). Vertical bars for the NEMD data represent the standard deviation of the friction signals. The inset in (b) shows the magnified C₁₈ friction data. Linear fits for NEMD and experimental data are shown as dashed lines. Corresponding prediction intervals on the experimental data with 95% confidence are shown as shaded areas. Experimental pressures are obtained from the extension to JKR theory⁹⁹ for thin coatings due to Reedy.¹⁰⁰

Table 2 CoF, μ, and Derjaguin offset, τ₀, results from wet NEMD simulations (σ = 5–50 MPa) in pristine hair (χ_N = 0.0), virgin hair (χ_N = 0.25), damaged (medium bleached) hair (χ_N = 0.85) and ultimately bleached hair (χ_N = 1.0) contacts. Experimental results from CCP AFM using C₁₈ (pristine hair) or SO₃⁻ (ultimately bleached) contacts (σ = 1–60 MPa) and previous AFM results for silicon nitride tips on virgin and damaged hairs (σ = 6–47 MPa) in humid air (RH ≈ 50%).¹³ Experiments (v_s = 10⁻⁶ to 10⁻⁷ m s⁻¹) were conducted at lower sliding velocities than the simulations (v_s = 10⁻¹ m s⁻¹)

	Exp. μ	Sim. μ	Exp. τ0 [MPa]	Sim. τ0 [MPa]
Pristine hair mimic (wet)	0.023 ± 0.002	0.028 ± 0.018	0.52 ± 0.1	1.5 ± 0.5
Ultimately bleached hair mimic (qet)	0.67 ± 0.03	0.227 ± 0.223	−0.5 ± 1.8	1.1 ± 6.5
Virgin hair (air)^13	0.03 ± 0.01	0.054 ± 0.010	2.3	1.7 ± 0.3
Damaged hair (air)^13	0.13 ± 0.05	0.20 ± 0.08	5.7	1.3 ± 2.4

---

In the CCP AFM experiments, the Derjaguin offset is small and negative for the ultimately bleached system, suggesting negligible adhesion. For the pristine hair system, the Derjaguin offset is small and positive (τ₀ = 0.52 ± 0.1 MPa), suggesting some adhesion. Quantifiable adhesion is expected in water for the pristine hair and moderately damaged systems due to hydrophobic interactions between the lipid monolayers.⁹⁸ The NEMD simulations also give a non-negligible Derjaguin offset for the equivalent systems, but the high uncertainties do not allow for a quantitative distinction between the damage levels. The Derjaguin offsets seen in the previous AFM experiments with real hair¹³ were much larger than those found in both our NEMD simulations and CCP AFM experiments. Moreover, the Derjaguin offset was observed to be larger for damaged hair than virgin hair,¹³ which is the opposite trend to that observed in the CCP AFM experiments. This suggests that there are other contributions to adhesion in real hairs than are captured by the biomimetic surfaces, which is likely related to the microscale roughness of the cuticles.¹⁴⁰

The trends between the CoF values for the different damage levels from the NEMD simulations are in qualitative agreement with the CCP AFM experiments, as shown in Fig. 10. For the pristine hair surfaces, the CoF is slightly overestimated (+22%) by the simulations compared to the experiments, while for the ultimately bleached surfaces, the CoF is underestimated (−66%). The differences for pristine hair likely originate from lower surface coverage of the C₁₈ groups in the simulations,^38,90 while the difference for ultimately bleached hair could be due to differences in the counterions,¹³⁹ the exact nature of which are not known in the experiments. Previous simulations with MARTINI, the intermonolayer friction of lipid bilayers was underestimated by around an order of magnitude compared to experiment.⁴³ Thus, the level of agreement with experimental friction results achieved here with a CG force field can be considered acceptable.

The CoF of the pristine hair mimic surfaces in CCP AFM (μ = 0.023 ± 0.002) is in excellent agreement with that obtained with a silicon nitride AFM tip on hair (μ = 0.03 ± 0.01).¹³ However, the CoF for the ultimately bleached hair mimic (μ = 0.67 ± 0.03) was much higher than that between a silicon nitride AFM tip and damaged hair (μ = 0.13 ± 0.05).¹³ This is probably due to the fact that only the substrate was charged in the previous AFM experiments, rather than both contacting surfaces, as in the current CCP AFM experiments, leading to weaker counterion trapping and thus lower friction.¹³⁹

For the single-pressure NEMD simulations of the intermediate systems, which are representative of virgin (χ_N = 0.25) and medium bleached (χ_N = 0.85) hair contacts (Fig. 7), CoFs of μ = 0.14 ± 0.05 and μ = 0.39 ± 0.12 were respectively obtained at 10 MPa and the lowest sliding velocity (v_s = 1 × 10⁻² m s⁻¹). Thus, the CoF for medium bleached hair is more than twice that of virgin hair. For the variable-pressure (5–50 MPa) NEMD simulations (Fig. 10), the CoFs were μ = 0.054 ± 0.010 for virgin hair and μ = 0.20 ± 0.08 for medium bleached hair. Thus, the CoFs for both systems are somewhat overestimated in the NEMD simulations compared to the previous AFM experiments.¹³ However, the trends between the different damage levels are in excellent agreement with the experiments,¹³ where the CoF of damaged hair was approximately four times higher than virgin hair (Table 2). The fourfold increase in the CoF compared to virgin hair is also consistent with several other previous AFM experiments in humid air and water environments for both medium bleached and KOH-damaged hair.^10,22

Overall, there is good agreement between the friction results from the nanoscale AFM on hair,¹³ the CCP AFM experiments with biomimetic surfaces, and the NEMD simulations (Table 2). The CoF is generally higher in the simulations than the experiments (other than the ultimately bleached system). This is probably due to the higher sliding velocity necessary in the NEMD simulations (v_s = 1 × 10⁻² m s⁻¹) than the CCP AFM (v_s = 2 × 10⁻⁷ m s⁻¹) and hair–tip AFM (v_s = 2 × 10⁻⁶ m s⁻¹) experiments.¹³ The agreement of the NEMD data with experiments suggests that nanoscale friction increases associated with hair damage are primarily induced by the changes in surface chemistry rather than changes in microscale surface roughness, as suggested from previous experimental results.¹³ In support of this hypothesis, it has recently been shown using an AFM relocation method that the nanoscale roughness of hair does indeed not change significantly for a single 10-minute bleaching treatment.¹⁴¹ The NEMD simulations suggest that confinement-induced solidification of water¹²⁹ and counterion trapping¹³⁹ respectively lead to elevated nanoscale friction in virgin hair and bleached hair.

We expect that the biomimetic surfaces proposed here will be useful to screen the tribological performance of hair care formulations both experimentally and computationally.⁴⁷ Moreover, the methodology presented in this work could be readily extended to study the nanotribology of other biological surfaces such as natural textiles and skin.¹¹

4 Conclusion

We have investigated the nanoscale friction between biomimetic hair surfaces at different degrees of damage using coarse-grained NEMD simulations and CCP AFM experiments. In the experiments, the silica surfaces were functionalised with either octadecyl groups, to represent the outer 18-MEA monolayer on pristine hair, or sulfonate groups, to represent the oxidised cysteic acid groups that form on the surface of ultimately bleached hair. In the CCP AFM experiments, we observed much higher CoFs for the ultimately bleached hair model surfaces than the pristine hair model surfaces. This observation is in agreement with previous AFM experiments of silicon nitride tips sliding on virgin and damaged hair.

In the NEMD simulations, we measured the friction between surfaces representative of pristine, virgin, medium bleached, and ultimately bleached hair, as well as intermediate degrees of damage. Both dry and wet contacts were considered over a wide range of sliding velocities. For dry and wet contacts at high sliding velocities, we find a near-logarithmic dependency of friction on sliding velocity, which is indicative of a SATA process. We successfully applied an Eyring-like extended SATA model to our NEMD simulation data. For wet contacts, we observe a departure from the SATA behaviour at low sliding velocities as the CoF levels off and approaches a constant value. A reduction in CoF due to the presence of water in the contact is observed at all sliding velocities for hydrophilic bleached hair, but only at high sliding velocity for hydrophobic pristine and virgin hair. For pristine and virgin hair, the confined water molecules become more solid-like at low sliding velocities, which explains the increase in friction compared to the dry systems.

We observed a monotonic increase of friction forces with increasing chemical damage at low sliding velocities in the NEMD simulations. This observation is in good agreement with previous AFM experiments on real hair surfaces and the new CCP AFM measurements with biomimetic surfaces. We also performed additional NEMD simulations at varied pressure to quantify the adhesive contribution to the shear stress, known as the Derjaguin offset. In both the NEMD simulations and CCP AFM experiments, a non-negligible Derjaguin offset was observed for pristine and virgin hair, which is due to hydrophobic interactions. This adhesive contribution was underestimated in both the CCP AFM experiments and NEMD simulations compared to previous AFM experiments with real hair, which is due to the absence of microscale roughness from the overlapping cuticles. A fourfold increase in the CoF was observed in the variable-pressure NEMD simulations moving from the virgin to medium bleached hair models, which is in excellent agreement with previous AFM experiments with real hair. We identify the role of counterion trapping on charged surfaces as a potential nanoscale mechanism for the elevated CoF on chemically damaged hair. Our observations demonstrate that friction increases of bleached or chemically damaged hair at the nanoscale are controlled by the modified surface chemistry, rather than roughness changes or subsurface damage.

Data availability

Additional figures are provided in the ESI,† as referenced in the main text. NEMD input files and initial configurations for LAMMPS have been deposited on a dedicated repository, available at https://github.com/erikweiand/cg-hair-nemd.

Author contributions

E. W.: methodology, investigation, data curation, formal analysis, visualization, writing – original draft; J. P. E.: conceptualization, methodology, supervision, writing – original draft; Y. R.: conceptualization, methodology, investigation, data curation, formal analysis, writing – review & editing; P. H. K.: conceptualization, project administration, writing – review & editing; S. H. P.: methodology, writing – review & editing; F. R. R.: project administration, writing – review & editing; S. A. U.: conceptualization, supervision, writing – review & editing; D. D.: conceptualization, funding acquisition, resources, supervision, project administration, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

E. W. thanks the Engineering and Physical Sciences Research Council (EPSRC) and Procter and Gamble for PhD funding through an iCASE studentship (EP/T517690/1). J. P. E. was supported by the Royal Academy of Engineering (RAEng) through their Research Fellowships scheme. D. D. thanks Shell and the RAEng for support via a Research Chair in Complex Engineering Interfaces as well as the EPSRC for funding through an Established Career Fellowship (EP/N025954/1). We acknowledge the use of the Imperial College London Research Computing Service (https://doi.org/10.14469/hpc/2232) and the UK Materials and Molecular Modelling Hub, which is partially funded by the EPSRC (EP/P020194/1 and EP/T022213/1). We thank Sumanth Jamadagni and Andrei Bureiko (Procter and Gamble) for useful discussions.

Notes and references

1. G. S. Luengo, A.-L. Fameau, F. Léonforte and A. J. Greaves, Adv. Colloid Interface Sci., 2021, 290, 102383.
2. F.-J. Wortmann and A. Schwan-Jonczyk, Int. J. Cosmet. Sci., 2006, 28, 61–68.
3. C. Thieulin, R. Vargiolu and H. Zahouani, Wear, 2019, 426–427, 186–194.
4. X. Zeng, H. Yang, D. Han, C. Liu, X. Chang, M. Zhang and L. Zhang, Measurement, 2021, 179, 109499.
5. L. D. Bloch, N. Y. Valente, C. C. Escudeiro, F. D. Sarruf and M. V. R. Velasco, J. Sens. Stud., 2021, 36, e12621.
6. A. Galliano, M. Fougere, L. Wolfram, H. I. Maibach and G. S. Luengo, Sking Res. Technol., 2021, 27, 607–617.
7. L. Skedung, E. S. Collier, K. L. Harris, M. W. Rutland, M. Applebaum, A. J. Greaves and G. S. Luengo, Perception, 2021, 50, 728–732.
8. A. M. Schwartz and D. C. Knowles, J. Soc. Cosmet. Chem., 1963, 14, 455–463.
9. M. J. Adams, B. J. Briscoe and T. K. Wee, J. Phys. D: Appl. Phys., 1990, 23, 406–414.
10. R. L. McMullen and S. P. Kelty, Scanning, 2001, 23, 337–345.
11. B. Bhushan, G. Wei and P. Haddad, Wear, 2005, 259, 1012–1021.
12. S. Breakspear, J. R. Smith and G. S. Luengo, J. Struct. Biol., 2005, 149, 235–242.
13. C. LaTorre and B. Bhushan, Ultramicroscopy, 2005, 105, 155–175.
14. C. LaTorre and B. Bhushan, J. Vac. Sci. Technol., A, 2005, 23, 1034–1045.
15. C. LaTorre and B. Bhushan, Ultramicroscopy, 2006, 106, 720–734.
16. G. Wei and B. Bhushan, Ultramicroscopy, 2006, 106, 742–754.
17. C. La Torre, B. Bhushan, J. Z. Yang and P. M. Torgerson, J. Cosmet. Sci., 2006, 57, 37–56.
18. M. Sadaie, N. Nishikawa, S. Ohnishi, K. Tamada, K. Yase and M. Hara, Colloids Surf., B, 2006, 51, 120–129.
19. B. Bhushan, Prog. Mater. Sci., 2008, 53, 585–710.
20. S. Lee, S. Zürcher, A. Dorcier, G. S. Luengo and N. D. Spencer, ACS Appl. Mater. Interfaces, 2009, 1, 1938–1945.
21. A. Dussaud and L. Fieschi-Corso, J. Cosmet. Sci., 2009, 60, 261–271.
22. N. Nikogeorgos, I. W. Fletcher, C. Boardman, P. Doyle, N. Ortuoste and G. J. Leggett, Biointerphases, 2010, 5, 60.
23. E. Max, W. Häfner, F. Wilco Bartels, A. Sugiharto, C. Wood and A. Fery, Ultramicroscopy, 2010, 110, 320–324.
24. H. Mizuno, G. S. Luengo and M. W. Rutland, Langmuir, 2010, 26, 18909–18915.
25. H. Mizuno, G. S. Luengo and M. W. Rutland, Langmuir, 2013, 29, 5857–5862.
26. J. R. Smith, J. Tsibouklis, T. G. Nevell and S. Breakspear, Appl. Surf. Sci., 2013, 285, 638–644.
27. J. Bowen, S. A. Johnson, A. R. Avery and M. J. Adams, Surf. Topogr.: Metrol. Prop., 2016, 4, 024008.
28. Y. Aita and Y. Nonomura, J. Oleo Sci., 2016, 65, 493–498.
29. S. Tokunaga, H. Tanamachi and K. Ishikawa, Cosmetics, 2019, 6, 31.
30. T. Miyamoto, N. Yamazaki, A. Tomotsuka, H. Sasahara, S. Watanabe and S. Yamada, J. Surfactants Deterg., 2021, 24, 501–510.
31. M. Okamoto, K. Ishikawa, N. Tanji and S. Aoyagi, Surf. Interface Anal., 2012, 44, 736–739.
32. M. Korte, S. Akari, H. Kühn, N. Baghdadli, H. Möhwald and G. S. Luengo, Langmuir, 2014, 30, 12124–12129.
33. E. Weiand, J. P. Ewen, P. H. Koenig, Y. Roiter, S. H. Page, S. Angioletti-Uberti and D. Dini, Soft Matter, 2022, 18, 1779–1792.
34. A. A. Feiler, J. Stiernstedt, K. Theander, P. Jenkins and M. W. Rutland, Langmuir, 2007, 23, 517–522.
35. T. Kawasoe, M. Kakizawa and H. Shimizu, Tribol. Online, 2008, 3, 127–130.
36. J. P. Ewen, D. M. Heyes and D. Dini, Friction, 2018, 6, 349–386.
37. M. Doig, C. P. Warrens and P. J. Camp, Langmuir, 2014, 30, 186–195.
38. J. P. Ewen, C. Gattinoni, N. Morgan, H. A. Spikes and D. Dini, Langmuir, 2016, 32, 4450–4463.
39. C. Klein, C. R. Iacovella, C. McCabe and P. T. Cummings, Soft Matter, 2015, 11, 3340–3346.
40. A. Chatterjee, D. K. Dubey and S. K. Sinha, Langmuir, 2021, 37, 46–62.
41. M. G. Saunders and G. A. Voth, Annu. Rev. Biophys., 2013, 42, 73–93.
42. W. K. Den Otter and S. A. Shkulipa, Biophys. J., 2007, 93, 423–433.
43. A. Zgorski, R. W. Pastor and E. Lyman, J. Chem. Theory Comput., 2019, 15, 6471–6481.
44. Z. Liu, X. Shi and H. Wu, Nanotechnology, 2019, 30, 165701.
45. T. I. Morozova, N. A. García, J.-L. Barrat, G. S. Luengo and F. Léonforte, ACS Appl. Mater. Interfaces, 2021, 13, 30086–30097.
46. S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. De Vries, J. Phys. Chem. B, 2007, 111, 7812–7824.
47. B. J. Coscia, J. C. Shelley, A. R. Browning, J. M. Sanders, R. Chaudret, R. Rozot, F. Léonforte, M. D. Halls and G. S. Luengo, Phys. Chem. Chem. Phys., 2023, 25, 1768–1780.
48. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics Modell., 1996, 14, 33–38.
49. S. J. Marrink and D. P. Tieleman, Chem. Soc. Rev., 2013, 42, 6801–6822.
50. S. O. Yesylevskyy, L. V. Schäfer, D. Sengupta and S. J. Marrink, PLoS Comput. Biol., 2010, 6, e1000810.
51. A. I. Jewett, D. Stelter, J. Lambert, S. M. Saladi, O. M. Roscioni, M. Ricci, L. Autin, M. Maritan, S. M. Bashusqeh, T. Keyes, R. T. Dame, J.-E. Shea, G. J. Jensen and D. S. Goodsell, J. Mol. Biol., 2021, 433, 166841.
52. S. J. Marrink, A. H. De Vries and A. E. Mark, J. Phys. Chem. B, 2004, 108, 750–760.
53. I. C. Yeh and M. L. Berkowitz, J. Chem. Phys., 1999, 111, 3155–3162.
54. R. W. Hockney and J. W. Eastwood, Computer Simulation Using Particles, CRC Press, New York, 1989.
55. J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
56. J. A. Swift and A. W. Holmes, Text. Res. J., 1965, 35, 1014–1019.
57. L. Coderch, M. A. Oliver, V. Martínez, A. M. Manich, L. Rubio and M. Martí, Sking Res. Technol., 2017, 23, 479–485.
58. Y. Atsmon-Raz and D. P. Tieleman, J. Phys. Chem. B, 2017, 121, 11132–11143.
59. M. Vögele, C. Holm and J. Smiatek, J. Chem. Phys., 2015, 143, 243151.
60. F. M. Maddar, D. Perry, R. Brooks, A. Page and P. R. Unwin, Anal. Chem., 2019, 91, 4632–4639.
61. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in ‘t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171.
62. L. Verlet, Phys. Rev., 1967, 159, 98.
63. S. Nosé, Mol. Phys., 1984, 52, 255–268.
64. W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697.
65. I. P. Seshadri and B. Bhushan, Acta Mater., 2008, 56, 774–781.
66. L. Martinez, R. Andrade, E. G. Birgin and J. M. Martinez, J. Comput. Chem., 2009, 30, 2157–2164.
67. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182.
68. S. New, G. Daniels and C. L. Gummer, Int. J. Cosmet. Sci., 2018, 40, 461–466.
69. W. Newman, G. L. Cohen and C. Heyes, J. Soc. Cosmet. Chem., 1973, 24, 773–782.
70. S. Derler and G.-M. Rotaru, Wear, 2013, 301, 324–329.
71. D. Toton, C. D. Lorenz, N. Rompotis, N. Martsinovich and L. Kantorovich, J. Phys.: Condens. Matter, 2010, 22, 074205.
72. R. Khare, J. de Pablo and A. Yethiraj, J. Chem. Phys., 1997, 107, 2589.
73. T. Schneider and E. Stoll, Phys. Rev. B: Solid State, 1978, 17, 1302–1322.
74. N. Selway, V. Chan and J. R. Stokes, Soft Matter, 2017, 13, 1702–1715.
75. F. Liu, W. Zhou, D. Liu, F. Chen and J. Wei, J. Mol. Liq., 2018, 265, 572–577.
76. S. D. Peroukidis, D. G. Tsalikis, M. G. Noro, I. P. Stott and V. G. Mavrantzas, J. Chem. Theory Comput., 2020, 16, 3363–3372.
77. H. Alasiri, Energy Fuels, 2019, 33, 2408–2412.
78. M. S. Green, J. Chem. Phys., 1954, 22, 398–413.
79. R. Kubo, J. Phys. Soc. Jpn., 1957, 12, 570–586.
80. K. R. Harris and L. A. Woolf, J. Chem. Eng. Data, 2004, 49, 1064–1069.
81. M. A. González and J. L. F. Abascal, J. Chem. Phys., 2010, 132, 096101.
82. H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271.
83. M. W. Mahoney and W. L. Jorgensen, J. Chem. Phys., 2000, 114, 363.
84. E. Liamas, S. D. Connell, S. N. Ramakrishna and A. Sarkar, Nanoscale, 2020, 12, 2292–2308.
85. W. A. Ducker, T. J. Senden and R. M. Pashley, Nature, 1991, 353, 239–241.
86. C. P. Green, H. Lioe, J. P. Cleveland, R. Proksch, P. Mulvaney and J. E. Sader, Rev. Sci. Instrum., 2004, 75, 1988–1996.
87. S. Karamdoust, B. Yu, C. V. Bonduelle, Y. Liu, G. Davidson, G. Stojcevic, J. Yang, W. M. Lau and E. R. Gillies, J. Mater. Chem., 2012, 22, 4881–4889.
88. P. Pacher, A. Lex, V. Proschek, O. Werzer, P. Frank, S. Temmel, W. Kern, R. Resel, A. Winkler, C. Slugovc, R. Schennach, G. Trimmel and E. Zojer, J. Phys. Chem. C, 2007, 111, 12407–12413.
89. Y. Tran and P. Auroy, Eur. Phys. J. E, 2001, 5, 65–79.
90. B. M. Fry, G. Moody, H. A. Spikes and J. S. S. Wong, Langmuir, 2020, 36, 1147–1155.
91. K. Bierbaum, M. Kinzler, C. Woll, M. Grunze, G. Hähner, S. Heid and F. Effenberger, Langmuir, 1995, 11, 512–518.
92. P. Fontaine, M. Goldmann and F. Rondelez, Langmuir, 1999, 15, 1348–1352.
93. J.-G. Ma, B. J. Boyd and C. J. Drummond, Langmuir, 2006, 22, 8646–8654.
94. D. K. Owens and R. C. Wendt, J. Appl. Polym. Sci., 1969, 13, 1741–1747.
95. T. Gao, Y. He, P. Landa and J.-M. Tien, J. Cosmet. Sci., 2011, 62, 127–137.
96. N. Wang, R. Barfoot, M. Butler and C. Durkan, ACS Biomater. Sci. Eng., 2018, 4, 3063–3071.
97. Y. Z. Hessefort, B. T. Holland and R. W. Cloud, J. Cosmet. Sci., 2008, 59, 303–315.
98. J. Israelachvili, Acc. Chem. Res., 1987, 20, 415–421.
99. K. L. Johnson, K. Kendall and A. D. Roberts, Proc. R. Soc. London, Ser. A, 1971, 324, 301–313.
100. E. D. Reedy, J. Mater. Res., 2006, 21, 2660–2668.
101. S. Inaba, S. Fujino and K. Morinaga, J. Am. Ceram. Soc., 1999, 82, 3501–3507.
102. V. V. Tsukruk, V. N. Bliznyuk, J. Hazel, D. Visser and M. P. Everson, Langmuir, 1996, 12, 4840–4849.
103. J. P. Gao, W. D. Luedtke, D. Gourdon, M. Ruths, J. N. Israelachvili and U. Landman, J. Phys. Chem. B, 2004, 108, 3410–3425.
104. S. Campen, J. Green, G. Lamb, D. Atkinson and H. Spikes, Tribol. Lett., 2012, 48, 237–248.
105. M. H. Müser, Phys. Rev. Lett., 2002, 89, 224301.
106. A. M. Smith, K. R. Lovelock, N. N. Gosvami, T. Welton and S. Perkin, Phys. Chem. Chem. Phys., 2013, 15, 15317–15320.
107. H. Spikes, Friction, 2018, 6, 1–31.
108. H. Eyring, J. Chem. Phys., 1936, 4, 283–291.
109. B. J. Briscoe and D. C. Evans, Proc. R. Soc. London, Ser. A, 1982, 380, 389–407.
110. C. Drummond, J. Israelachvili and P. Richetti, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 066110.
111. G. He and M. O. Robbins, Tribol. Lett., 2001, 10, 7–14.
112. M. R. Farrow, A. Chremos, P. J. Camp, S. G. Harris and R. F. Watts, Tribol. Lett., 2011, 42, 325–337.
113. R. M. Overney, H. Takano, M. Fujihira, W. Paulus and H. Ringsdorf, Phys. Rev. Lett., 1994, 72, 3546.
114. A. Jabbarzadeh, Tribol. Int., 2016, 102, 600–607.
115. S. J. Eder, A. Vernes and G. Betz, Langmuir, 2013, 29, 13760–13772.
116. A. Ishihara, Y. Tsukamoto, H. Inoue, Y. Noda, S. Koizumi and K. Joko, Int. J. Cosmet. Sci., 2021, 43, 653–661.
117. C. Barba, M. Martí, A. M. Manich, J. Carilla, J. L. Parra and L. Coderch, Thermochim. Acta, 2010, 503–504, 33–39.
118. J. M. D. Lane, M. Chandross, M. J. Stevens and G. S. Grest, Langmuir, 2008, 24, 5209–5212.
119. V. Dupres, T. Camesano, D. Langevin, A. Checco and P. Guenoun, J. Colloid Interface Sci., 2004, 269, 329–335.
120. C. D. Lorenz, M. Chandross, J. M. D. Lane and G. S. Grest, Model. Simul. Mater. Sci. Eng., 2010, 18, 034005.
121. A. Striolo, A. A. Chialvo, P. T. Cummings and K. E. Gubbins, Langmuir, 2003, 19, 8583–8591.
122. C. Sendner, D. Horinek, L. Bocquet and R. R. Netz, Langmuir, 2009, 25, 10768–10781.
123. N. Dhopatkar, A. P. Defante and A. Dhinojwala, Sci. Adv., 2016, 2, e160076.
124. W. Chen, A. S. Foster, M. J. Alava and L. Laurson, Phys. Rev. Lett., 2015, 114, 095502.
125. D. Sergi, G. Scocchi and A. Ortona, J. Chem. Phys., 2012, 137, 094904.
126. R. Szoszkiewicz and E. Riedo, Phys. Rev. Lett., 2005, 95, 135502.
127. H. K. Christenson, J. N. Israelachvili and R. M. Pashley, SPE Reservoir Eng., 1987, 2, 155–165.
128. C. Cafolla and K. Voïtchovsky, Nanoscale, 2020, 12, 14504–14513.
129. K. B. Jinesh and J. W. M. Frenken, Phys. Rev. Lett., 2008, 101, 036101.
130. S. Hanot, S. Lyonnard and S. Mossa, Nanoscale, 2016, 8, 3314–3325.
131. K. Krynicki, C. D. Green and D. W. Sawyer, Faraday Discuss. Chem. Soc., 1978, 66, 199–208.
132. F. Y. Hansen, G. H. Peters, H. Taub and A. Miskowiec, J. Chem. Phys., 2012, 137, 204910.
133. R. Zangi and A. E. Mark, J. Chem. Phys., 2003, 119, 1694–1700.
134. S. Han, M. Y. Choi, P. Kumar and H. E. Stanley, Nat. Phys., 2010, 6, 685–689.
135. U. Raviv, P. Laurat and J. Klein, Nature, 2001, 413, 51–54.
136. K. Koga, H. Tanaka and X. C. Zeng, Nature, 2000, 408, 564–567.
137. N. Giovambattista, P. J. Rossky and P. G. Debenedetti, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 041604.
138. R. R. Netz, Phys. Rev. Lett., 2003, 91, 138101.
139. G. Kagata, J. P. Gong and Y. Osada, J. Phys. Chem. B, 2003, 107, 10221–10225.
140. T. R. Cristiani, N. A. Cadirov, Z. Zhang, Z. Shi, A. Bureiko, R. C. A. Eguiluz, K. Kristiansen, J. Scott, K. Meinert, P. H. Koenig and J. N. Israelachvili, Langmuir, 2019, 35, 15614–15627.
141. R. Humphry, N. Wang and C. Durkan, J. Mech. Behav. Biomed. Mater., 2022, 126, 105001.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr05545g

---