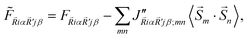Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Regulating the thermal conductivity of monolayer MnPS3 by a magnetic phase transition†
Dingbo
Zhang‡
ab,
Ke
Wang‡
c,
Shuai
Chen
 b,
Lifa
Zhang
d,
Yuxiang
Ni
b,
Lifa
Zhang
d,
Yuxiang
Ni
 *a and
Gang
Zhang
*a and
Gang
Zhang
 *b
*b
aSchool of Physical Science and Technology, Southwest Jiaotong University, Chengdu 610031, China. E-mail: yuxiang.ni@swjtu.edu.cn
bInstitute of High Performance Computing, A*STAR, 138632, Singapore. E-mail: zhangg@ihpc.a-star.edu.sg
cSchool of Automation, Xi'an University of Posts & Telecommunications, Shaanxi 710121, China
dNNU-SULI Thermal Energy Research Center, and Center for Quantum Transport and Thermal Energy Science (CQTES), School of Physics and Technology, Nanjing Normal University, Nanjing 210023, China
First published on 6th December 2022
Abstract
In this study, based on ab initio calculations and the phonon Boltzmann transport equation, we found that magnetic phase transitions can lead to a significant change in the thermal conductivity of monolayer MnPS3. Around the Néel temperature (78 K) with the antiferromagnetic–paramagnetic (AFM–PM) phase transition, its thermal conductivity increases from 14.89 W mK−1 (AFM phase) to 103.21 W mK−1 (PM phase). Below 78 K, the thermal conductivity of monolayer MnPS3 can be doubled by applying a magnetic field of 4 T, this value has been reported in a previous experiment for the antiferromagnetic–ferromagnetic (AFM–FM) phase transition. Above 78 K, the thermal conductivity of PM phase can be greatly reduced through the PM–AFM magnetic phase transition. In addition to the value of thermal conductivity, the relative contribution ratio between acoustic and optical modes changes with different magnetic phases. The subsequent analyses demonstrate that this regulation originates from the change in lattice parameter, bonding interaction and phonon anharmonicity. In addition, the different effect on the thermal conductivity between the FM and AFM phases was identified by comparing the corresponding phonon scattering characteristics. This study should shed light on the understanding of phonon thermal conductivity in 2D magnets, and provide a practical method for the realization of 2D thermal switching devices, which would enable a broad range of novel applications including energy conversion and thermal management.
1 Introduction
Two-dimensional (2D) magnetic materials retain long-range magnetic ordering in the individual monolayer.1–3 By manipulating the spin degree of freedom of the electron, the data processing speed and integration densities of 2D magnetic materials can be largely enhanced.4,5 Thus, 2D magnetic materials act as a good playground to explore future information technologies. One significant challenge that magnetic-based devices are facing is the heat dissipation issue, which directly affects the working state and operational stability.6,7 In this regard, it is imperative to obtain fundamental understanding of the thermal conductivity of 2D magnetic materials.8–10In recent years, progress has been made in understanding the magnetic ordering impact on the thermal transport of 2D magnetic materials. For instance, semi-hydrogenated graphene bears a higher thermal conductivity in its FM phase (55.7 W mK−1) than in the paramagnetic (PM) phase (24.5 W mK−1).6 For monolayer CrI3, the magnetic state enhances the thermal conductivity because it induces a more symmetric structure with weaker phonon anharmonicity.7 It should be mentioned that antiferromagnets have drawn more attention than ferromagnets,11–13 owing to their several advantages including spin superfluidity,14 ultrafast dynamics15 and the negligible spin–dipole interaction.16 Unfortunately, little is known about the thermal conductivity in 2D antiferromagnetic materials.
Recently, 2D MnPS3, one novel antiferromagnet, was obtained through chemical exfoliation.17 The unit cell of monolayer MnPS3 is composed of two Mn2+ ions and one [P2S6]4−, forming a hexagonal honeycomb lattice, as shown in Fig. 1.18 So, the antiferromagnetic configuration in the MnPS3 unit cell is described as one Mn atom which is spin-up and the other one is spin-down. In addition, 2D MnPS3 is one direct bandgap semiconductor, sharing ultrafast domain-wall dynamics and the spin photogalvanic effect.15,19 Excitons in MnPS3 are bound by an energy of more than 1 eV, exceeding the values in transition-metal dichalcogenides, advancing this 2D antiferromagnet as a new platform for exploring the magnetic and phononic properties.20
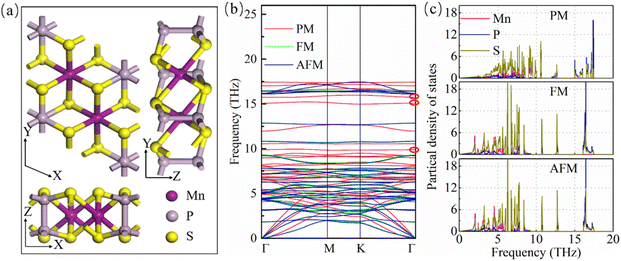 | ||
| Fig. 1 The structure and phonon behaviors. (a) Atomic structure of monolayer MnPS3. (b) Phonon dispersions and (c) phonon density of states of monolayer MnPS3 with PM/FM/AFM phases. | ||
In this work, we investigated the structures, lattice vibrations and thermal conductivities of monolayer MnPS3 with PM, ferromagnetic (FM) and antiferromagnetic (AFM) phases. We found that, through the PM–AFM phase change, the phonon anharmonicity of monolayer MnPS3 obviously increased and the thermal conductivity decreased by one order of magnitude. Meanwhile, the AFM phase has lower thermal conductivity compared with its FM counterpart. The phonon mean free path (MFP), group velocity and phonon scattering strength were analyzed to reveal the underling physical mechanism.
2 Computational methods
The first-principles calculations were performed using Density Functional Theory (DFT) as implemented in the Vienna Ab initio Simulation Package (VASP).21 The Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional was used.22 A Hubbard U correction was included.23 When the exchange parameter for Mn 3d-electrons was fixed as U = 5 eV, the calculated electronic band-gap (2.70 eV) of MnPS3 is close to the experimental value of 2.96 eV.17 Therefore, the same value of U was used to compute all the properties of the PM, FM and AFM phases. As DFT is a ground state theory, in principle, it cannot deal with the PM phase. In our DFT calculations, the PM phase is in fact a nonmagnetic phase, i.e., the spin-polarization is switched off and no spin or magnetism exists in the calculations. In the structural optimization, the convergence criteria for the electronic and ionic relaxations are 10−8 eV and 10−4 eV Å−1, respectively. The K-mesh of 25 × 25 × 1 and cut-off energy of 500 eV are used. A vacuum length of 20 Å is adopted to eliminate the interaction between neighboring layers. Before calculating the phononic properties, the magnetic ground state of monolayer MnPS3 was determined by the energy difference between possible magnetic configurations (FM, AFM-zigzag, AFM-stripy, and AFM-Néel) as shown in Fig. S1 in the ESI,† and we find that the AFM-Néel state is the magnetic ground state because of its lowest energy. In the following, the AFM state means AFM-Néel state. Calculations of the second- and third-order force constants were carried out by using Phonopy and thirdorder.py, respectively.24,25 Additionally, it was found that the higher-order force constants have little impact on the thermal conductivity of 2D materials at low temperatures (<200 K), as shown in Table S2.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26,27 Therefore, in our work, only second- and third-order force constants are considered. The thermal conductivity was calculated by solving the phonon Boltzmann transport equation as implemented in ShengBTE.28 After structure optimization, 10.67, 7.69 and 7.76 Å are used as the thickness of the monolayer MnPS3 with PM, FM and AFM phases, respectively. The thickness of the monolayer is equal to the height of a bulk cell in the Z direction divided by the corresponding number of atomic layers. Details of the calculation can be found in ESI.†
26,27 Therefore, in our work, only second- and third-order force constants are considered. The thermal conductivity was calculated by solving the phonon Boltzmann transport equation as implemented in ShengBTE.28 After structure optimization, 10.67, 7.69 and 7.76 Å are used as the thickness of the monolayer MnPS3 with PM, FM and AFM phases, respectively. The thickness of the monolayer is equal to the height of a bulk cell in the Z direction divided by the corresponding number of atomic layers. Details of the calculation can be found in ESI.†
3 Results and discussion
3.1 Structure, phonon dispersion and phonon density of states
We firstly investigated the influence of magnetic ordering on the structural parameters. As shown in Fig. 1, the phonon dispersions are located in a frequency range of 0–18 THz and there appear no imaginary frequencies throughout the entire Brillouin zone, suggesting the dynamical stability of all these three phases. The optimized lattice constants and bond lengths of the FM and AFM phases are quite close but both are larger than those of the PM phase (Table 1). The calculated structural parameters of the AFM phase are consistent with previous reports.29,30 To identify the accuracy of our calculation, we did a comprehensive review on the experimental and theoretical lattice constants of MnPS3 at various magnetic states and the lattice constants are summarized in Table S1.†| Properties | PM | FM | AFM |
|---|---|---|---|
| Lattice constant (Å) | 5.70 | 6.14 | 6.15 |
| Mn–S bond length (Å) | 2.45 | 2.61 | 2.63 |
| P–S bond length (Å) | 3.26 | 3.38 | 3.40 |
| Layer thickness (Å) | 10.67 | 7.69 | 7.76 |
Based on the frozen magnon method, the relationship of the harmonic IFCs between FM (AFM) and PM structures is described by the following formula:
![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) and F are the harmonic IFCs in the FM(AFM) and PM phases, respectively. J′′ stands for the second derivative of magnetic exchange interaction J. The movement of atom i is marked by
and F are the harmonic IFCs in the FM(AFM) and PM phases, respectively. J′′ stands for the second derivative of magnetic exchange interaction J. The movement of atom i is marked by 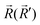 lattice vector along the α(β) Cartesian direction. S is equal to half of the spin number in a magnetic atom. The J′′ of FM and AFM phases can be calculated via the interatomic force constants (Fig. 2). It is obvious that the IFCs of AFM and FM states are similar, while the difference in IFCs between PM and AFM states is quite significant, resulting in the difference in the lattice constant between PM and AFM states is up to 0.45 Å. This is similar to the previous theoretical results about the difference in lattice constant between the PM31,32 and AFM states.31 Similar phenomena were also observed in bulk MnPS3.31,33
lattice vector along the α(β) Cartesian direction. S is equal to half of the spin number in a magnetic atom. The J′′ of FM and AFM phases can be calculated via the interatomic force constants (Fig. 2). It is obvious that the IFCs of AFM and FM states are similar, while the difference in IFCs between PM and AFM states is quite significant, resulting in the difference in the lattice constant between PM and AFM states is up to 0.45 Å. This is similar to the previous theoretical results about the difference in lattice constant between the PM31,32 and AFM states.31 Similar phenomena were also observed in bulk MnPS3.31,33
With 10 atoms in the unit cell, monolayer MnPS3 has 3 acoustic and 27 optical phonon modes. To better observe the difference in phonon dispersions among PM, FM and AFM phases, we presented them in Fig. 1(b), while more details are presented in Fig. S2.† The phonon branches in the FM and AFM phases are similar, which are different from that in the PM phase. Next, we mainly focused on the three optical branches of the PM structure, which are located in the gap of the FM/AFM phases (marked by red circle). The corresponding vibration modes are presented in Fig. S3† and their irreducible representations are A1g, A2g and A2u modes, respectively. These three lattice vibration modes are identified in the FM/AFM phases. The frequencies of these three optical branches are 9.90, 15.09 and 15.76 THz at Γ point in the PM phase, while these values are 5.18 (5.21), 16.11 (16.12) and 16.15 (16.15) THz in the FM (AFM) phase, respectively. The appearance of the large splitting between PM and FM/AFM phases for the three optical branches is mainly due to the sensitivity of the atoms in MnPS3 to the magnetic ordering, which induces the down- and up-shift of optical phonon modes mainly contributed by Mn atoms and other atoms, respectively. The phonon projected density of states (pDOS) shown in Fig. 1(c) confirms the shift of optical phonons, which also demonstrates the redshift of acoustic phonon modes in the AFM/FM phases compared with the PM phase. These results indicate significant coupling between spin and phonon in the FM and AFM monolayer MnPS3.
3.2 The magnetic ordering-dependent thermal conductivity
In order to explore the impact of magnetic ordering on the thermal conductivity, the thermal conductivities of monolayer MnPS3 with PM, FM and AFM phases were calculated, respectively. As shown in Fig. 3(a) on a log–log scale, the thermal conductivity of monolayer MnPS3 decreases as temperature (T) increases, following a 1/T dependence, confirming that the phonon–phonon anharmonic scattering plays a major role in the thermal conductivity of monolayer MnPS3. Near the Néel temperature (78 K) of MnPS3, the thermal conductivity of the PM phase is 103.21 W mK−1, seven times as large as that of the AFM phase (14.89 W mK−1). For FM ordering, the thermal conductivity (27.35 W mK−1) is only 26% of that of the PM phase. The magnetic ordering effectively changes the thermal conductivity of monolayer MnPS3, which has never been reported in the literature. The ratio between the thermal conductivity of different phases (κPM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) κAFM = 6.93 and κPM
κAFM = 6.93 and κPM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) κFM = 3.77) is comparable to those of reported theoretical works such as RuCl3 (κFM
κFM = 3.77) is comparable to those of reported theoretical works such as RuCl3 (κFM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) κPM = 6.23), RuBr3 (κFM
κPM = 6.23), RuBr3 (κFM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) κPM = 6.87) and RuI3 (κFM
κPM = 6.87) and RuI3 (κFM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) κPM = 1.59).9 In experiments, below 78 K, the thermal conductivity of monolayer MnPS3 can be doubled by applying an magnetic field perpendicular to the layer, where the critical value of the magnetic field for the AFM–FM phase transition is about 4 T.17 Above 78 K, the thermal conductivity can be greatly reduced through external magnetic fields, this method has been demonstrated to induce a PM–AFM magnetic phase transition.1,34 Thus, the large modulation of the thermal conductivity of monolayer MnPS3 provides a practical method for the realization of 2D thermal switching devices.
κPM = 1.59).9 In experiments, below 78 K, the thermal conductivity of monolayer MnPS3 can be doubled by applying an magnetic field perpendicular to the layer, where the critical value of the magnetic field for the AFM–FM phase transition is about 4 T.17 Above 78 K, the thermal conductivity can be greatly reduced through external magnetic fields, this method has been demonstrated to induce a PM–AFM magnetic phase transition.1,34 Thus, the large modulation of the thermal conductivity of monolayer MnPS3 provides a practical method for the realization of 2D thermal switching devices.
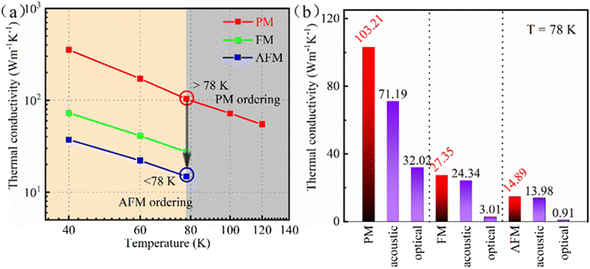 | ||
| Fig. 3 The thermal conductivity. (a) The magnetic ordering-dependent thermal conductivities and (b) contribution of acoustic and optical modes to the thermal conductivities at 78 K. | ||
In these three magnetic phases, acoustic phonons are still the major contributors to the thermal conductivity but the relative contribution ratio between acoustic and optical modes changes with different magnetic phases (Fig. 3(b)). This behavior also occurs in hydrogenated graphene.6 Recently, the impact of the four-phonon scattering process on the thermal conductivity of solids have attracted extensive research attention.35,36 Compared with the relaxation time of phonons in the low frequency range, the relaxation time of phonons in the high frequency range (i.e., optical modes) will be reduced more significantly by the four-phonon scattering processes.37 For PM/AFM/FM MnPS3, the thermal conductivity contributed by the optical phonons is low. Thus, the four-phonon scattering process is not considered in our work. To understand the underlying physical mechanism of the tunable thermal conductivity, we analyzed the phonon mean free path, group velocity and phonon scattering strength.
3.3 The magnetic ordering-dependent phonon properties
It is obvious from Fig. 4(a) that the normalized cumulative thermal conductivity increases as the phonon mean free path (MFP) increases until it reaches a limit length, which is 1835.58, 3125.71 and 16681.01 nm for the AFM, FM and PM phases, respectively. This suggests that the MFP of the PM phase is longer than that of FM and AFM phases, which results in a larger thermal conductivity. Fig. 4(b) presents the group velocities of three acoustic branches (ZA: out-of-plane acoustic, TA: transverse acoustic and LA: longitudinal acoustic) and optical branches varying with frequency. Specifically, the impact of magnetic ordering on phonon velocity is more remarkable for the three acoustic branches. The maximum phonon group velocities of acoustic phonon modes gradually decrease from PM to FM to AFM phases, as shown in Table S3.† Therefore, the reduced group velocity in the FM and AFM phases is also responsible for the lower thermal conductivity. However, compared with the large change in MFP, the change in group velocity is slight, revealing the remarkable impact of magnetic ordering on phonon anharmonicity in monolayer MnPS3.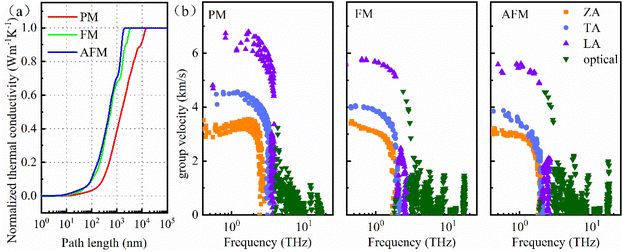 | ||
| Fig. 4 The magnetic ordering-dependent phonon behaviors. (a) Mean free paths and (b) frequency-resolved phonon group velocities of the PM/FM/AFM phases. | ||
Phonon scattering strength and phonon anharmonicity of these three magnetic phases were evaluated by calculating the scattering rate, the scattering phase space and the Grüneisen parameter.38,39 These parameters reflect the scattered possibility in unit time, the number of channels available for a phonon to be scattered and the phonon anharmonicity, respectively.40 As presented in Fig. 5(a) and Fig. S4,† the phonon–phonon anharmonic scattering rate and phonon-isotope scattering rate in AFM/FM phases are obviously higher than that in the PM phase, which implies that the phonon relaxation time is shortened. Fig. 5(b) shows that the AFM/FM phases have a greater value of scattering phase space than the PM phase at the same frequency, which implies that the former phases hold more scattering channels than the latter one. The scattering phase space gradually decreases with the increase of phonon frequency, which was also observed in 2D group-IV materials.41 This is a consequence of the fact that the phonon branches at low frequencies are denser (Fig. 1(b)), which causes more phonon scattering possibility in accordance with the requirement of energy and momentum conservation.
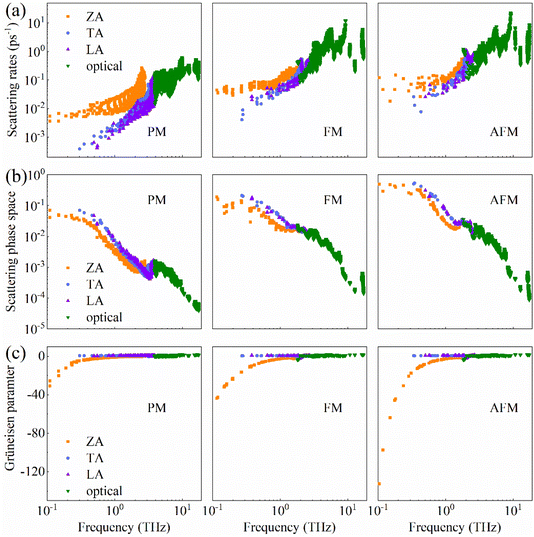 | ||
| Fig. 5 The magnetic ordering-dependent phonon scattering characteristics. (a) Anharmonic scattering rates, (b) scattering phase spaces and (c) Grüneisen parameters for the PM/FM/AFM phases. | ||
As shown in Fig. 5(c), the Grüneisen parameters of the AFM/FM phases are smaller than that of the PM structure. These results show that the phonon scattering and anharmonicity in FM/AFM monolayer MnPS3 are enhanced significantly. Moreover, the Grüneisen parameter varies inversely with the bond strength of the material.42,43 Therefore, the FM/AFM phases have weaker bonding interaction compared with the PM phase, which is in agreement with our aforementioned simulation results.
4 Conclusions
In conclusion, we systematically investigated the structural deformation, lattice vibration and thermal conductivity of monolayer MnPS3 with PM/FM/AFM phases. The structural parameters of monolayer MnPS3 with different magnetic ordering were analyzed, and the order of bonding strength is PM > FM > AFM phase. Remarkable impact of magnetic ordering on phonon spectrum were also observed. The thermal conductivity of the FM/AFM phases is lower than the PM one. The magnetic ordering-dependent phonon properties were further analyzed to explain the obtained results. Our study provides an insight into magnetic ordering-dependent phonon behavior and suggests a possibility for MnPS3-based thermal switching devices.Conflicts of interest
The authors have no conflicts to disclose.Acknowledgements
We gratefully acknowledge the use of computing resources at the Agency for Science, Technology and Research (A*STAR) and NSCC, Singapore. D. B. Zhang gratefully acknowledges the financial support from the China Scholarship Council (grant no. 202107000030). GZ is supported in part by RIE2020 Advanced Manufacturing and Engineering (AME) Programmatic (A1898b0043) and A*STAR Aerospace Programme (M2115a0092). KW acknowledges the support from National Natural Science Foundation of China (NNSFC) (12204373).References
- C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang and Y. Wang, Nature, 2017, 546, 265–269 CrossRef CAS PubMed.
- J. Cenker, B. Huang, N. Suri, P. Thijssen, A. Miller, T. Song, T. Taniguchi, K. Watanabe, M. A. McGuire and D. Xiao, Nat. Phys., 2021, 17, 20–25 Search PubMed.
- C. Gong and X. Zhang, Science, 2019, 363, eaav4450 CrossRef CAS PubMed.
- S. Wolf, D. Awschalom, R. Buhrman, J. Daughton, S. von Molnár, M. Roukes, A. Y. Chtchelkanova and D. Treger, Science, 2001, 294, 1488–1495 CrossRef CAS PubMed.
- J. Ma, X. Xi, Y. Li and X. Sun, Nat. Nanotechnol., 2021, 16, 576–583 CrossRef CAS PubMed.
- H. Li, P. Zhang, T. Ouyang, H. Wang, J. Li, C. He, C. Zhang and C. Tang, Appl. Phys. Lett., 2022, 120, 092403 CrossRef CAS.
- G. Qin, H. Wang, L. Zhang, Z. Qin and M. Hu, J. Mater. Chem. C, 2020, 8, 3520–3526 RSC.
- K. Wang, X. Xu, Y. Cheng, M. Zhang, J.-S. Wang, H. Wang and G. Zhang, Appl. Phys. Lett., 2021, 118, 023102 CrossRef CAS.
- Y. Liu, Q. Liu, Y. Liu, X. Jiang, X. Zhang and J. Zhao, Nanoscale, 2021, 13, 7714–7722 RSC.
- K. Wang, W. Zhou, Y. Cheng, M. Zhang, H. Wang and G. Zhang, Nanoscale, 2021, 13, 10882–10890 RSC.
- V. Baltz, A. Manchon, M. Tsoi, T. Moriyama, T. Ono and Y. Tserkovnyak, Rev. Mod. Phys., 2018, 90, 015005 CrossRef CAS.
- D. Torelli, H. Moustafa, K. W. Jacobsen and T. Olsen, npj Comput. Mater., 2020, 6, 1–12 CrossRef.
- L. Jin, L. Wang, X. Zhang, Y. Liu, X. Dai, H. Gao and G. Liu, Nanoscale, 2021, 13, 5901–5909 RSC.
- Y. M. Bunkov, E. Alakshin, R. Gazizulin, A. Klochkov, V. Kuzmin, V. L'vov and M. Tagirov, Phys. Rev. Lett., 2012, 108, 177002 CrossRef PubMed.
- I. M. Alliati, R. F. Evans, K. S. Novoselov and E. J. Santos, npj Comput. Mater., 2022, 8, 1–9 CrossRef.
- V. Ivády, T. Simon, J. R. Maze, I. Abrikosov and A. Gali, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 235205 CrossRef.
- G. Long, H. Henck, M. Gibertini, D. Dumcenco, Z. Wang, T. Taniguchi, K. Watanabe, E. Giannini and A. F. Morpurgo, Nano Lett., 2020, 20, 2452–2459 CrossRef CAS PubMed.
- M. Birowska, P. E. F. Junior, J. Fabian and J. Kunstmann, Phys. Rev. B, 2021, 103, L121108 CrossRef CAS.
- R.-C. Xiao, D.-F. Shao, Y.-H. Li and H. Jiang, npj Quantum Mater., 2021, 6, 1–6 CrossRef.
- J. Yang, Y. Zhou, Q. Guo, Y. Dedkov and E. Voloshina, RSC Adv., 2020, 10, 851–864 RSC.
- J. Hafner, J. Comput. Chem., 2008, 29, 2044–2078 CrossRef CAS PubMed.
- M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS.
- A. Rohrbach, J. Hafner and G. Kresse, J. Phys.: Condens. Matter, 2003, 15, 979 CrossRef CAS.
- D. Zhang, Y. Hu, H. Zhong, S. Yuan and C. Liu, Nanoscale, 2019, 11, 13800–13806 RSC.
- D. Zhang, S. Hu, Y. Sun, X. Liu, H. Wang, H. Wang, Y. Chen and Y. Ni, ES Energy Environ., 2020, 10, 59–65 CAS.
- Y. Ouyang, C. Yu, J. He, P. Jiang, W. Ren and J. Chen, Phys. Rev. B, 2022, 105, 115202 CrossRef CAS.
- F. Eriksson, E. Fransson and P. Erhart, Adv. Theory Simul., 2019, 2, 1800184 CrossRef.
- W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747–1758 CrossRef CAS.
- M. Jiang, K. Xu, N. Liao and H. Zhou, Appl. Surf. Sci., 2021, 543, 148846 CrossRef CAS.
- Y. Zhang, W. Wang, M. Huang, P. Liu, G. Hu, C. Feng, X. Lei, M. Gu, H. Yang and K. Liu, Nanoscale, 2020, 12, 23266–23273 RSC.
- B. L. Chittari, Y. Park, D. Lee, M. Han, A. H. MacDonald, E. Hwang and J. Jung, Phys. Rev. B, 2016, 94, 184428 CrossRef.
- I. Cabria and A. A. El-Meligi, Int. J. Hydrogen Energy, 2018, 43, 5903–5912 CrossRef CAS.
- D. H. Luong, T. L. Phan, G. Ghimire, D. L. Duong and Y. H. Lee, APL Mater., 2019, 7, 081102 CrossRef.
- M. Gibertini, M. Koperski, A. F. Morpurgo and K. S. Novoselov, Nat. Nanotechnol., 2019, 14, 408–419 CrossRef CAS PubMed.
- Y. Yin, Y. Hu, S. Li, G. Ding, S. Wang, D. Li and G. Zhang, Nano Res., 2022, 15, 3818–3824 CrossRef CAS.
- J. Chen, J. He, D. Pan, X. Wang, N. Yang, J. Zhu, S. A. Yang and G. Zhang, Sci. China: Phys., Mech. Astron., 2022, 65, 117002 Search PubMed.
- X. Yang, T. Feng, J. Li and X. Ruan, Phys. Rev. B, 2019, 100, 245203 CrossRef CAS.
- Y. Xia, Appl. Phys. Lett., 2018, 113, 073901 CrossRef.
- J. Yu, T. Li, G. Nie, B.-P. Zhang and Q. Sun, Nanoscale, 2019, 11, 10306–10313 RSC.
- Y. Ni, D. Zhang, X. Liu, H. Wang, Y. Chen, Y. Xia and H. Wang, J. Chem. Phys., 2021, 155, 204701 CrossRef CAS PubMed.
- B. Peng, H. Zhang, H. Shao, Y. Xu, G. Ni, R. Zhang and H. Zhu, Phys. Rev. B, 2016, 94, 245420 CrossRef.
- X. Su, N. Zhao, S. Hao, C. C. Stoumpos, M. Liu, H. Chen, H. Xie, Q. Zhang, C. Wolverton and X. Tang, Adv. Funct. Mater., 2019, 29, 1806534 CrossRef.
- Z.-F. Cheng and R.-L. Zheng, Chin. Phys. Lett., 2016, 33, 046501 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr04709h |
| ‡ Authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |