Disordered spin gapless semiconducting CoFeCrGa Heusler alloy thin films on Si (100): experiment and theory†
Vireshwar
Mishra‡
a,
Amar
Kumar‡
a,
Lalit
Pandey
a,
Nanhe Kumar
Gupta
a,
Soumyarup
Hait
a,
Vineet
Barwal§
a,
Nikita
Sharma
a,
Nakul
Kumar
a,
Sharat
Chandra
b and
Sujeet
Chaudhary
 *a
*a
aThin Film Laboratory, Department of Physics, Indian Institute of Technology Delhi, New Delhi-110016, India. E-mail: sujeetc@iitd.ac.in
bIndira Gandhi Centre for Atomic Research, HBNI, Kalpakkam, Tamilnadu-603102, India
First published on 12th December 2022
Abstract
Spin gapless semiconductors (SGSs) are an intriguing class of quantum materials that bridge the gap between half-metallic ferromagnets and semiconductors. The presence of a semiconducting bandgap for one spin channel and zero band gap for other spin channels, together with the possibility of four different band structure configurations, makes them one of the most desirable candidates to be used in tunable spin transport based spintronics devices. Here, we have performed various structural, magnetic and transport measurements on an optimized CoFeCrGa (CFCG) Heusler alloy thin film (∼50 nm) grown over a Si(100) substrate using an industry-viable magnetron sputtering technique. The grown film showed B2-ordering under the given set of X-ray diffraction measurement conditions with a saturation magnetization (Ms) of 1.86μB per f.u. (at 5 K) and a Curie temperature of ∼595 K. Nearly linearly varying longitudinal resistivity with a negative temperature coefficient was observed. A fitted longitudinal conductivity curve through a “two-carrier model” shows a slight band overlap in the gapless channel for one spin channel and a small energy gap (ΔE) of 167 meV for other spin channels. A negative and linear out-of-plane magnetoresistance response was observed in these films. The temperature dependent anomalous Hall effect measurement gives nearly temperature independent carrier concentration (and/or) mobility with an anomalous Hall conductivity of 91.35 S cm−1 at 5 K. The first principles calculations have also been performed for bulk and (220) CFCG surfaces to correlate the various structural, electronics and magnetic properties of the optimized CFCG Heusler alloy thin film. The DFT derived results, viz. lattice parameter and MS exhibit a good match with the experimentally observed results. All these properties collectively imply that the grown film possesses disordered-SGS like behaviour. It is remarkable to note that CFCG films with the (022) surface possess a very high electronic spin polarization of 91%. The results of the study suggest that CFCG is a potential candidate to be used in spintronics-based devices such as spin-injectors.
1. Introduction
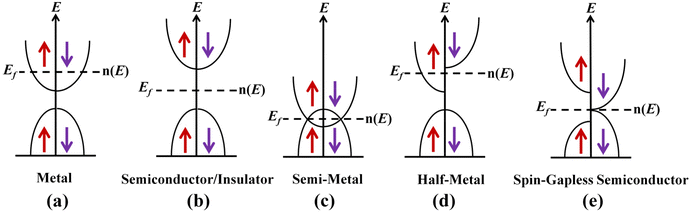
Based on the electronic band structure, materials in nature are broadly classified into metals, semiconductors/insulators and semi-metals with the energy band schematics as shown in Fig. 1(a), (b), and (c), respectively. In the current era, spintronics has captivated immense attention in the field of research from both applied and fundamental points of view. The presence of spin-polarization at the Fermi level is the key requirement for a material to be used for spin manipulation in spintronics-based devices. Half-metallic ferromagnets (HMFs) are thus considered as an ideal candidate for spintronics applications as they possess 100% spin polarization at the Fermi level [as shown in Fig. 1(d)] and hence are capable of producing considerable spin polarized current.1–3 The current spintronics technology can potentially use HMFs in devices like magnetic tunnel junctions (MTJs), non-local spin-valve (NLSV), current perpendicular to plane giant magnetoresistance (CPP-GMR), spin-transfer torque (STT) oscillators,4–8etc.A very new class of materials namely spin-gapless semiconductors (SGSs) in the family of HMFs has recently come into existence which is anticipated to play a crucial role in the semiconductor spintronics industry.9–11 The SGS behaviour was first predicted in Co-doped PbPdO2 through first principles electronic and band structure calculations using density functional theory.9 These materials possess a semiconducting bandgap for the minority spin channel and a zero bandgap for the majority spin channel at the Fermi level [see Fig. 1(e)] and hence act as a bridge between HMFs and semiconductors.9 Their unique band structure leads to some specific properties like generation of spin-polarized current from both electrons and holes, ability to switch from n-type to p-type spin polarized current by inducing some external field and need for almost negligible energy for exciting electrons from a valence band to a conduction band. The unique band structure of SGS materials thus makes them an ideal replacement for diluted magnetic semiconductors (DMS) with a Curie temperature (TC) in excess of 300 K. The presence of the SGS characteristic in Heusler alloys makes them more prominent over DMS because of their relatively high TC.12
Recently, many Heusler compounds have been reportedly found to exhibit the SGS characteristic as confirmed by ab initio calculations.11,13–15 However, very few of them have been confirmed experimentally, e.g. Mn2CoAl, CoFeMnSi, Ti2MnAl and CoFeCrGa.10,16–19 CoFeCrGa (CFCG) is an alloy, an equiatomic quaternary Heusler alloy (EQHA), with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry. These compounds have the general formula AA′BC and interestingly, the spin diffusion length of such compounds is remarkably higher than those of pseudo ternary alloys of the chemical formula A2A′1−xBxC, hence resulting in low dissipation power based spintronics devices.20,21
1 stoichiometry. These compounds have the general formula AA′BC and interestingly, the spin diffusion length of such compounds is remarkably higher than those of pseudo ternary alloys of the chemical formula A2A′1−xBxC, hence resulting in low dissipation power based spintronics devices.20,21
Gao et al. first investigated the half-metallic nature of the CFCG alloy through first principles calculations22 and then Bainsla et al. probed its SGS characteristic theoretically (through first principles calculations) and experimentally (in a polycrystalline bulk CFCG alloy grown by arc melting).19 Rani et al. have further studied the effect of excess Co-atom concentration (replacing the Fe atom) on the structural, magnetic and magnetotransport properties of bulk Co1+xFe1−xCrGa samples grown by arc melting.23 However, the literature still lacks reports on the thin film growth of the CFCG alloy, which is the need of the hour. Moreover, the literature also misses the detailed study of magnetotransport properties like the anomalous Hall effect (AHE) and the linear magnetoresistance (MR) of this particular quaternary alloy. These factors motivated us to grow CFCG thin films and study their detailed structural, magnetic and magnetotransport properties.
In the present work, we have grown ordered CFCG thin films over a Si(100) substrate through an industry-friendly magnetron sputtering technique. The structural, morphological, magnetic and transport (electron-transport and magneto-transport) measurements are performed in detail for the investigation of SGS behaviour and the quality of thin CFCG films. DFT calculations are also performed for one of the most stable structures among three different types of CFCG structures for both bulk and thin film morphology. These first principles DFT results have been correlated with the experimentally obtained results. The presence of SGS like characteristics in CFCG thin films indicates that this material can be used as a promising candidate for future spintronics-based devices.
2. Experimental methodology
2.1. Sample preparation
A set of four different CFCG thin films namely B-250, B-350, B-450 and B-550 of optimal thickness (∼50 nm) were grown over Si(100) substrates using a pulsed DC magnetron sputtering system. Here, the number attached to the sample names represents the post annealing temperature, TA = 250 °C, 350 °C, 450 °C and 550 °C, for the films, respectively. Before loading to a vacuum chamber, all the substrates were cleaned with acetone and isopropyl alcohol using an ultrasonication method. Prior to the deposition process, the chamber was pumped to the base pressure less than 2 × 10−7 Torr by employing a cryo pump, a turbomolecular pump and a rotary-pump. The deposition process was carried out at a fixed working pressure of 3 × 10−3 Torr by applying a pulsed-DC power of 90 Watt to the composite CFCG target (diameter 2′′) at a fixed argon gas flow rate of 64 sscm. Prior to starting the deposition, the Si(100) substrates were pre-heated in a UHV chamber at 650 °C for 1 hour. All of the layers were deposited at room temperature (RT) and then post-annealed in situ for 2 hours at the respective TA at 2 × 10−7 Torr. The structural features of the CFCG films were then investigated. The magnetic and transport characteristics for only the structurally refined CFCG optimal phase (B-550) were studied.2.2. Film characterization
The crystal structures of all the film samples and the thickness, roughness and density of the optimized samples were investigated by performing X-ray diffraction (XRD) and X-ray reflectivity (XRR) measurements, respectively, using a PANalytical make model – X'pert-PRO-diffractometer equipped with a Cu-Kα (l = 1.541 Å) X-ray source. All further measurements were performed over optimized CFCG film samples. Atomic force microscopy (AFM) was used to probe the surface morphology and roughness of the CFCG films using a Bruker make (model – Dimension Icon) microscope. The elemental composition was determined by Energy Dispersive X-ray analysis (EDAX) measurement performed in a Hitachi High Tecnol (Model-TM3000). The XRR and AFM measurements are described in ESI section S1† while EDAX measurement is described in section S2.† Magnetization measurements were performed using a superconducting quantum interference device (SQUID) magnetometer. All the transport measurements (temperature-dependent longitudinal resistivity (ρxx), the anomalous Hall effect and magnetoresistance) were performed in the DC transport module of the Quantum Design Inc. make PPMS (model Evercool-II).3. Results and discussion
3.1 Structural characterization
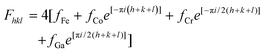 | (1) |
| F111 = 4[(fFe − fCo)2 + (fCr − fGa)2]1/2 | (2) |
| F200 = 4|(fCo + fFe) − (fCr + fGa)| | (3) |
| F220 = 4(fCo + fFe + fCr + fGa) | (4) |
For the Cu-Kα radiation source, the atomic scattering factors for Co and Fe atoms are almost similar (fCo ∼ fFe) and hence it is challenging to distinguish between Y and L21 structures. Thus, the structure factor for (111) superlattice reflection, in this case, reduces to
| Fhkl = 4|(fCr − fGa)| | (5) |
From eqn (2)–(5), we can assess that the complete randomization between Co and Fe as well as Cr and Ga elements results in the vanishing of (111) superlattice reflection and therefore the resulting structure corresponds to full B2 disorder. On the other hand, the complete randomization among Co, Fe, Cr and Ga elements i.e., each element occupies all the four Wyckoff positions with the equal probability, leads to the A2 disordered structure with the absence of both (111) and (200) reflections. Moreover, in EQHAs, the disorder only among tetrahedral site atoms (i.e., Co and Fe) gives an L21 disordered structure. It is worth noting that even the presence of (111) and (200) peaks do not guarantee the complete B2 or L21 ordering. With finite A2 disordering the intensities of these peaks are expected to be lowered accordingly. The presence of fundamental (220) reflection is, however, independent of the L21, B2 or A2 structure.
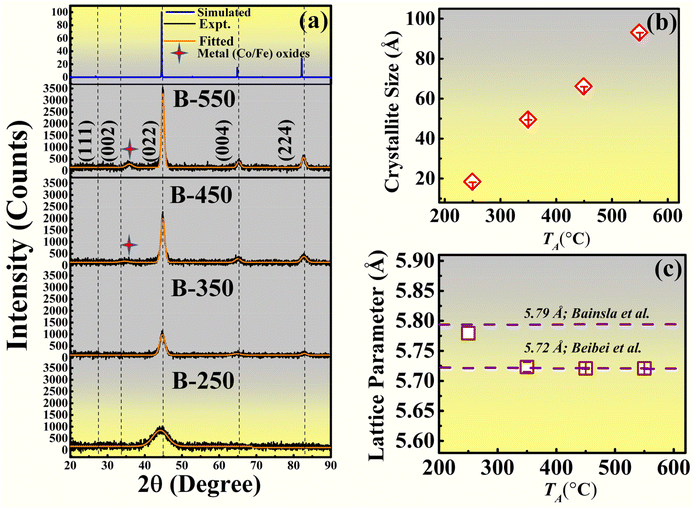
Fig. 2(a) shows the grazing incidence XRD (GIXRD) spectra of all samples at room temperature, collected at a fixed glancing angle (GA) of 1° together with the simulated XRD curve (using Powder Cell, version 2.4) for the CFCG Type-I structure (shown by a solid blue line). The details regarding the different types of CFCG Heusler structures depending on the occupancy of various Wyckoff positions by different elements are mentioned in the theoretical section 3.4.1.2. The intensities of diffraction peaks [Fig. 2(a)] and crystallite sizes [Fig. 2(b)] both increase with the TA, owing to the agglomeration of nucleated stable islands via enhanced thermal surface diffusivity with increased TA.25,26 The small intensity of XRD reflections and lesser crystallite size for TA ≤ 350 °C infer the nanocrystalline film growth at lower TA. Both the B-450 and B-550 films exhibit three fundamental reflections ((022), (004), and (224)) and one impurity reflection at ∼36°. The intensities of all these reflections are relatively stronger in the B-550 film due to the improvement in the crystallinity. The impurity reflection is attributed to the formation of an oxide of Fe (Fe3O4) and/or Co (Co3O4) elements as the peak position of this reflection matches well with the (311) reflection of the oxides.27,28 The (111) and (002) superlattice reflections, which are the typical characteristics of a well ordered quaternary Heusler structure, are absent in the data obtained from conventional X-ray diffractometers. This could be either due to nearly similar scattering factors of the constituent elements Co, Fe, Cr and Ga, or the very low intensity of the (111) and (002) superlattice reflections compared to the fundamental reflections (see the simulated curve in Fig. 2(a)) or the presence of other antisite disorders (B2, DO3 or A2). Deepika et al. and Bainsla et al. also failed to observe (200) and (111) reflections even for bulk CFCG samples through a conventional diffractometer. While Rani et al. succeeded in observing these reflections through synchrotron radiation based XRD, Bainsla et al. established the claim of L21 ordering based on differential thermal analysis.29 Therefore, it should be noted that our B-550 sample exhibits the A2-structrure based on the limited measurement capability of the diffractometer. Thus, the possibility of partial crystallization of the L21 structure is not fully ruled out. The well-known Debye–Scherrer's relationship, 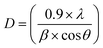 , was used to calculate the crystallite size (D) of the samples, where β and θ are the full width of half maxima (FWHM) and Bragg's angle, respectively, corresponding to the principal (220) reflection and λ (= 1.5406 Å) is the wavelength of the Cu-Kα radiation X-ray source. Whereas the lattice parameter (a) was evaluated using Bragg's diffraction formula, 2d
, was used to calculate the crystallite size (D) of the samples, where β and θ are the full width of half maxima (FWHM) and Bragg's angle, respectively, corresponding to the principal (220) reflection and λ (= 1.5406 Å) is the wavelength of the Cu-Kα radiation X-ray source. Whereas the lattice parameter (a) was evaluated using Bragg's diffraction formula, 2d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = nλ with the interplanar spacing
θ = nλ with the interplanar spacing  which for B-250, B-350, B-450 and B-550 samples are found to be 5.779 (±0.012) Å, 5.723 (±0.007) Å, 5.720 (±0.002) and 5.721 (±0.001) Å, respectively, and these values are very close to the experimentally and theoretically reported values for the CFCG alloy as shown by the dashed lines in Fig. 2(c).24,30
which for B-250, B-350, B-450 and B-550 samples are found to be 5.779 (±0.012) Å, 5.723 (±0.007) Å, 5.720 (±0.002) and 5.721 (±0.001) Å, respectively, and these values are very close to the experimentally and theoretically reported values for the CFCG alloy as shown by the dashed lines in Fig. 2(c).24,30
3.2 Magnetization measurements
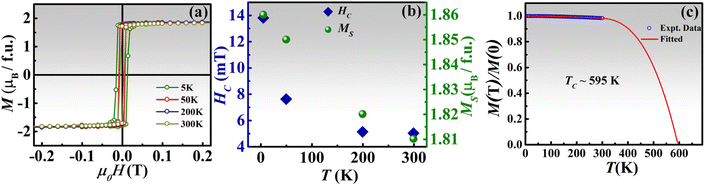
Temperature-dependent isothermal magnetization hysteresis (MH) curves traced at different temperatures (T = 5 K, 50 K, 200 K and 300 K) for the B-550 film sample under an applied magnetic field parallel to the film plane are shown in Fig. 3(a). In Fig. 3(b), the temperature dependences of the coercivity (HC) and saturation magnetization (MS) inferred from the MH-loops are plotted. From Fig. 3(b), it is evident that the HC decreases from 13.8 mT (at 5 K) to 5 mT (at 300 K), suggesting that the film is magnetically soft over the entire temperature range. The decrease in HC with temperature is accompanied by a reduction in the anisotropy field with temperature and also in part due to the weakening of the strength of pinning of the domain walls in the intergranular regions, which is typical in polycrystalline films, like the one in the present study.31 The value of MS is found to vary from 1.86μB per f.u. (at 5 K) to 1.81μB per f.u. (at 300 K, i.e., room temperature) as shown in Fig. 3(b). The experimentally obtained values of MS here are slightly smaller than the earlier reported values for bulk samples (2.1μB per f.u.) and also the theoretically predicted value (1.97μB per f.u.).23,29,30 Some of the Co-atoms occupying the tetrahedral vacancy and/or the swapping of the atoms between Co–Fe and Co–Cr might be causing this observed drop in the overall magnetic moment.24,32The thermal magnetization curve [M(T)] for the B-550 sample was recorded within the temperature range of 5–300 K as shown in Fig. 3(c). The sample was first cooled to 5 K in the presence of an applied magnetic field (μ0H) of 500 mT applied parallel to the film and then the data were recorded during heating while maintaining the magnetic field at a constant value (i.e., the field cool warming procedure). Various half-metallic Heusler compounds have been reported to have T2 dependent magnetization.33–35 In view of this, we used the following empirical formula for an itinerant type FM material to fit the experimentally observed M(T) curve, as illustrated by the solid red line in Fig. 3(c):
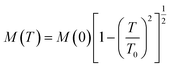 | (6) |
Here M(0) is the zero-temperature value of magnetization which is here considered to be the same as the value at 5 K. The fitted curve was extrapolated to the zero-magnetization value so as to infer the TC, which is found to be ∼595 K. This value is less than the earlier reported value for bulk samples (690 K).23 The key parameters that influence a material's TC are the 3d exchange interaction between the transition metal elements and the lattice parameter in crystallites.36 Moreover, the properties of the specimen, such as magnetic moment, exchange coupling, and crystal anisotropy, are greatly affected during the transition from 3D (bulk) to 2D (thin film), resulting in a weakening of interatomic exchange interactions and, as a result, a lower ordering temperature (TC) in thin films compared to the bulk sample.10
3.3 Transport measurement
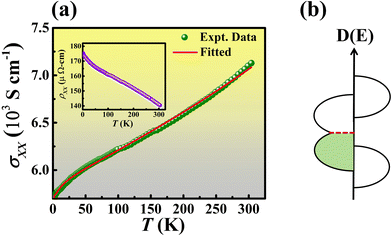 | ||
| Fig. 4 (a) Longitudinal conductivity variation with the temperature under a zero external field together with the fit (shown by the solid red line) using the two carrier model [employing eqn (7)] for the CFCG B-550 thin film. The inset depicts the variation of longitudinal resistivity with temperature. (b) Schematic of the density of states for disordered-SGSs. The band edges of the diagram follow the 3D Van Hove singularity.44 | ||
In order to explain the temperature dependence of resistivity we have considered CFCG here as a disordered-SGS and adopted the two-carrier model used by Kharel et al.40 Kharel et al. modelled the conductivity of the majority spin channel for spin narrow-gap semiconductors, spin gapless semiconductors and disordered spin-gapless semiconductors. The model assumes that one spin channel for disordered-SGSs has a band overlap while another channel has a semiconducting band gap, the schematic of which is shown in Fig. 4(b). The conductivity for the disordered SGS according to this model is thus expressed as a combination of conductivity through the overlapped channel (σSGS) and the semiconducting channel (σSC),37,43i.e.
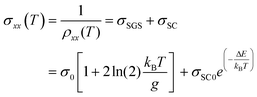 | (7) |
| ρXY = ρOHEXY + ρAHEXY = R0H + RAHEMZ | (8) |
| n(T) = 1/eR0 and μ(T) = R0/ρXX | (9) |
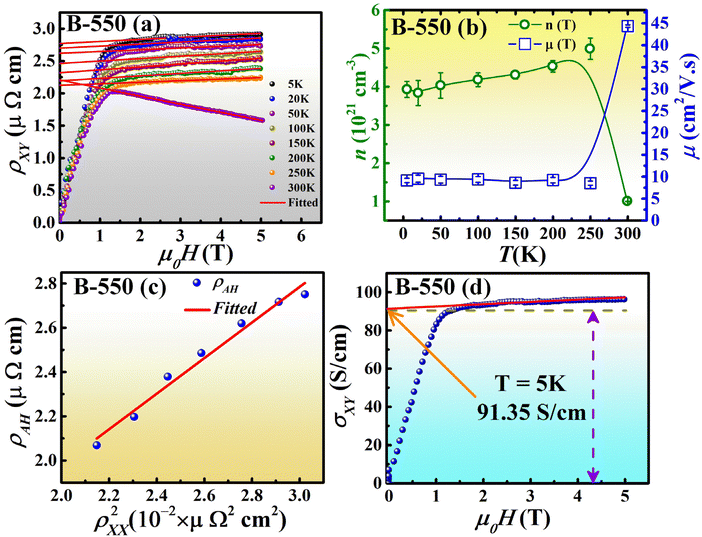 | ||
| Fig. 6 (a) Variation of the Hall resistivity (ρXY) with the magnetic field (μ0H) traced at different temperatures ranging from 5 K to 300 K. The solid red lines show the linearly fitted OHE contribution to transverse resistivity, the intercept of which gives the value of the AHE resistivity, i.e., ρAH and (b) the corresponding plot of carrier concentration (and/or mobility) at the respective temperatures, obtained through the fitted OHE curves. (c) ρAH variation with ρ2XX fitted with eqn (11) as shown by the solid red line. (d) Plot of the Hall conductivity curve for the B-550 sample at 5 K. The value of σAH, obtained by extrapolating the OHE data to the zero field, is shown in the main panel. | ||
The plot of the variation of n and μ with respect to the temperature is shown in Fig. 6(b) through which it can be observed that these parameters are nearly temperature-independent up to the temperature range of 5 K to 250 K, which is typically a characteristic of SGSs. However, at 300 K, an increase in the value of μ while a drop in the value of n are observed, which is attributed to the change from p-type to n-type carriers as mentioned above. The values of n[μ] at 5 K and 300 K are found to be (3.92 ± 0.21) × 1021 cm−3 [(9.15 ± 0.48) cm2 V−1 s−1] and (0.99 ± 0.01) × 1021 cm−3 [(44.37 ± 0.28) cm2 V−1 s−1], respectively, which are quite higher than those expected for normal semiconductors. This is expected in the SGSs since they possess zero band gap near the Fermi level of the majority spin channel. Due to this, carriers are readily available to conduct even at a very low temperature similar to the case of semimetals and metals. Several reports confirmed the range of carrier concentration of SGS materials.16,31,48
The AHE resistivity, i.e., ρAH majorly arises because of two contributions: (I) intrinsic contribution and (II) extrinsic contribution. The intrinsic contribution particularly relies upon the band structure of the system and is highly independent of impurity induced or SOC-induced scattering, while the reverse is true for the extrinsic contribution.47 The intrinsic contribution to ρAH(ρint) was first explained theoretically by Karplus and Luttinger where they considered that the spin orbit interaction (SOI) and inter-band mixing effectively induce an anomalous velocity contribution to the carriers in the direction perpendicular to the applied field, according to which ρintαρ2XY.49 Lately, this theory has been revised by considering the Berry phase as an essential parameter.50 During an adiabatic motion of an electron (in which the electron cannot interchange its band), its wave function is associated with an extra phase part, called the Berry phase. This phase depends on the curvature of the band and associates with something called the Berry curvature (bn). The Berry curvature is basically a pseudo magnetic field whose magnitude depends on the Berry phase or band curvature. By the effects of an electric field and this pseudo magnetic field, the conduction electrons experience an anomalous velocity perpendicular to both the electric field and Berry curvature giving rise to the AHE. On the other hand, the extrinsic contribution to ρAH(ρext) is explained by the (I) skew scattering51 and (II) side-jump scattering52 mechanisms. The skew scattering arises due to the asymmetric scattering of a conduction electron because of an effective spin orbit interaction. According to Smit, this SOI results in a transverse spin orbit force.51 In a pure periodic crystal, this force can only polarize the charge distribution but cannot accelerate the electron as the periodicity of the transverse force and the crystal are identical. But in the presence of disorder or impurity, the periodicity is disturbed, and the transverse force can slightly scatter the electron. As the electron is scattered slightly, the direction of its velocity changes which in turn changes the direction of the resulting relativistic magnetic field. The dependency of scattering cross section on the transverse component of spin and orbital magnetic moments of the electron results in the asymmetric scattering of the electron.
The side-jump phenomenon is however explained by the local distortion of the wavefunction by an impurity and creation of a local current density. This contribution to the AHE can be understood in terms of localized electrons or wave packets (but not in terms of plane waves or momentum representation) where the center of mass of the conduction electron undergoes a sideways displacement (Δy) on scattering by an impurity or a phonon in the presence of spin–orbit interaction.53 This displacement is also spin dependent i.e., an electron with opposite spin will experience displacement along the opposite direction.
We employed here an expanded scaling model proposed by Tian et al.54 to estimate the extrinsic and intrinsic contributions to the AHE. According to this model, the ρAH is expressed as
| ρAH(T) = αρXX0 + βρ2XX0 + bρ2XX(T) | (10) |
After merging the temperature independent term, the above equation reduces to
| ρAH(T) = a′ρXX0 + bρ2XX(T) | (11) |
3.4 Electronic-structure analysis
3.4.1.1 Computational methodology. To gain more insight into the structural, electronic, and magnetic properties of the CFCG film, density functional theory (DFT) calculations were performed as implemented within the QUANTUM ESPRESSO code with a projected augmented wave (PAW) basis set.55,56 To deal with the electronic exchange and correlation interactions, we have used the Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA).57 For all the calculations, a plane wave energy cut-off of 350 Ry and a 15 × 15 × 15 k-mesh are used. For the Brillouin zone integration, the optimized tetrahedron method is used.58 The SCF calculations were stopped when the variation in the total energy was less than 10−6 Ry. All the crystal structures for CFCG were generated using the VESTA program.59
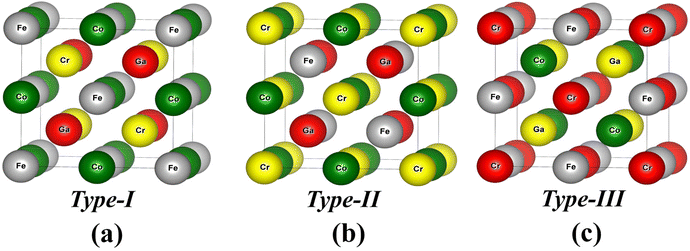
3.4.1.2 Structural properties. The EQHAs are found to exist in an ordered cubic structure of space group No. 216 with the LiMgPdSn prototype (Y-type),60 with four formula units (f.u.) per unit cell. The constituent atoms can occupy different Wyckoff positions 4a (0, 0, 0), 4b (0.5, 0.5, 0.5), 4c (0.25, 0.25, 0.25) and 4d (0.75, 0.75, 0.75). Therefore, here for the CFCG alloy, we have considered three non-degenerate atomic configurations depending on the arrangement of these four kinds of elements (Co, Fe, Cr and Ga) randomly occupying the Wyckoff positions (4a, 4b, 4c and 4d). The three possible atomic arrangements are noted as Type-I (Fe at 4a, Co at 4b, Cr at 4c and Ga at 4d), Type-II (Cr at 4a, Co at 4b, Fe at 4c and Ga at 4d) and Type-III (Cr at 4a, Fe at 4b, Co at 4c and Ga at 4d). The 16 atoms’ conventional unit-cells for all different kinds of arrangements are shown in Fig. 7.
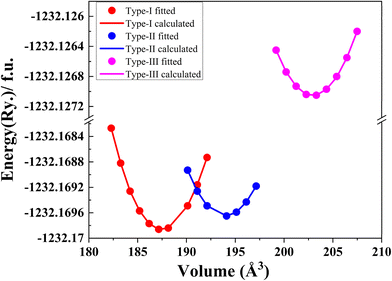
To have an idea about the ground state structural properties, we have calculated the total energy per formula unit (f.u.) vs. volume curves for all kinds of arrangements, as shown in Fig. 8, which shows that CFCG is structurally more stable with the Type-I structure. To determine the optimized lattice parameter and ground state energy, total energy per f.u. vs. lattice volume has been fitted using the Murnaghan equation of state.61
All the fitted parameters – the optimized lattice parameter, minimum total energy, bulk modulus (B0) and its derivative (B′0) for all the structures are tabulated in Table 1. The optimized lattice parameter for the Type-I structure, which is the most stable structure, is found to be 5.72 Å, similar to the earlier reported value62 and also agrees with the experimental value of 5.721 (±0.001) Å obtained from the XRD data of Fig. 2(c).
| Structure | Optimized volume (Å3) | Optimized lattice parameter (Å) | Total energy (Ry per f.u.) | B 0 (GPA) | B′0 |
|---|---|---|---|---|---|
| Type-I | 187.46 | 5.72 | −1232.1698 | 182.5 | 5.63 |
| Type-II | 193.93 | 5.79 | −1232.1696 | 162.0 | 5.04 |
| Type-III | 202.92 | 5.88 | −1232.1270 | 150.4 | 2.27 |
3.4.1.3 Electronic structure and magnetic properties. We have calculated the spin-resolved density of states (DOS) and the band structure for the Type-I CFCG structure, as shown in Fig. 9. The calculated total and atomic magnetic moments for CFCG are given in Table 2. From the DOS and band structure, it is obvious that for the spin up electrons, valence band maxima and conduction band minima touch each other, and for the spin down electrons, there is a finite gap. As seen from Table 2, the calculated magnetic moment on the unit cell (Mtot) for CFCG is 2μB per f.u., which is consistent with the Slater Pauling Rule, which is one of the prerequisites for SGS.60 Therefore, CFCG is a spin gapless semiconductor in nature. The major contribution to the Mtot of CFCG comes from the Cr and Co atomic moments, while the Fe atoms are antiferromagnetically coupled with the Cr and Co moments. Ga atoms have a negligible moment, as also reported in another reference.62
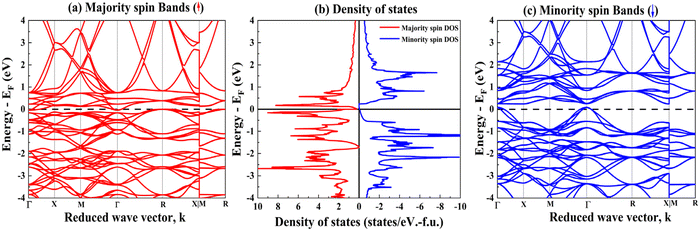 | ||
| Fig. 9 Spin resolved band structures for (a) the majority and (c) minority spins and (b) DOS per f.u. for the Type-I CFCG alloy. | ||
| M tot (μB per f.u.) | M Co (μB) | M Fe (μB) | M Cr (μB) | M Ga (μB) | Nature | |
|---|---|---|---|---|---|---|
| This work | 2.00 | 0.99 | −0.70 | 1.68 | −0.03 | SGS |
| Shi et al.62 | 1.97 | 0.94 | −0.74 | 1.81 | −0.04 | SGS |
Although the calculated lattice parameter is matched well with the experimental lattice parameter, the calculated magnetic moment, however, exceeds the experimentally measured value. Possibly, this discrepancy could be due to the consideration of CFCG in the bulk geometry in the DFT calculations. In the next section, therefore, we present the results of DFT calculations for the case of the CFCG alloy in the thin film form where the film surface, as opposed to bulk, dominantly governs the physical properties of the thin films.
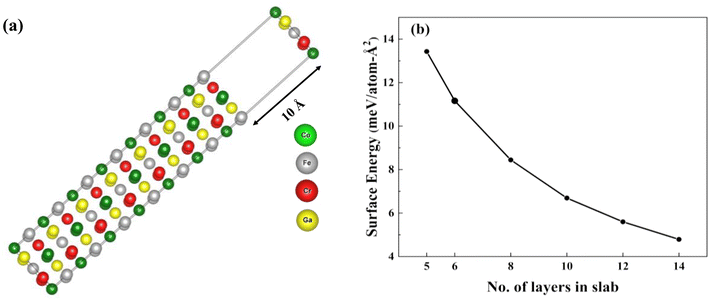 | ||
| Fig. 10 (a) A slab with 14 monolayers for electronic calculations. (b) Convergence of surface energy with respect to the number of layers in the CFCG slab for the (022) surface. | ||
In Fig. 11(a)–(c), the plots of the band structure and density of states are presented. As observed from these band structure and DOS plots for the CFCG thin film geometry, the spin up channel is metallic with several electronic states crossing EF; whereas in the spin down channel, there are very small and negligible electronic states (∼0.13486 states per eV per f.u.). As a result, it is concluded that the SGS nature of CFCG is lost for the (022) surface, and such a slab of CFCG with the (022) surface is expected to have nearly half-metallic nature, which is in contrast to the experimentally observed non-metallic behavior in the transport measurements (see Fig. 4).
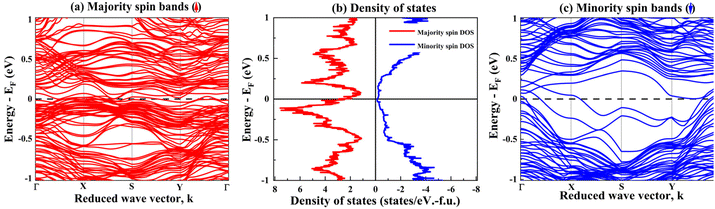 | ||
| Fig. 11 (a) Spin-up band structure, (b) density of states and (c) spin-down band structure plots for a slab with 14 monolayers of the (022) CFCG alloy. | ||
The electronic spin polarization is calculated from the DOS plot (Fig. 11(b)). It is quite remarkable to note that the (022) surface of the CFCG thin film possesses a very high spin polarization of 91%, in contrast to other Co-based equiatomic quaternary Heusler alloys which show a low value for electronic spin polarization in thin films.22,63,64 Thus, it turns out that CFCG thin films could have several potential spintronics applications.
On the other hand, the total magnetic moment for the (022) surface is found to be 1.75μB per f.u. which is much closer to the experimentally measured value (∼1.86μB per f.u.), compared to the magnetic moment value for the bulk structure (2μB per f.u.). The difference in the experimentally observed magnetic moment and electronic transport from the DFT findings can be attributed to the presence of other (hkl) planes on the surface and also the point-defects (site and antistites disorders, and vacancies) present in the thin films.65–69 Consideration of such disorder for DFT-calculations for the thin film geometry in the CFCG alloy is beyond the scope of the present investigations.
4 Conclusion
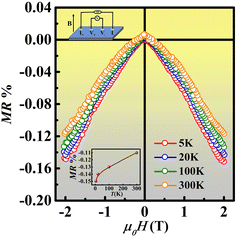
The polycrystalline thin films of the CoFeCrGa (CFCG) Heusler alloy were grown over Si(100) substrates using the pulsed DC magnetron sputtering technique. The various structural, magnetic and transport measurements were performed to characterize the optimized B-550 CFCG thin film. The structural measurement revealed that the grown film possesses A2-ordering under the limit of measurement. However, the possibility of B2 and L21-ordering still persists as the (200) and (111) superlattice reflections can be traced by implying a higher resolution X-ray source such as synchrotron radiation. The magnetic measurements give saturation magnetization and Curie temperature values of 1.81μB per f.u. and ∼595 K, respectively. An almost linear variation of longitudinal resistivity (and/or conductivity) with temperature was observed with a negative temperature coefficient. Fitting of the conductivity curve through a two carrier model reveals that the gapless channel of the CFCG B-550 film has some band overlap which corresponds to the presence of some structural disorder in the system. The isothermal magnetoresistance curves recorded at different temperatures (5–300 K) are found to exhibit negative and linear behaviour up to 2 T magnetic field. The temperature-dependent anomalous Hall effect measurement gives a nearly temperature-independent carrier concentration (mobility) with a room temperature value of 3.9 ± 0.04 × 1021 cm−3 (9.15 ± 0.48 cm2 V−1 s−1). The expanded scaling mechanism performed over the AHE data reveals that both extrinsic and intrinsic factors contribute to the AHE; however, the phonon-induced skew scattering has a greater extrinsic contribution compared to impurity induced skew scattering and also the intrinsic Berry phase has a considerable contribution to the AHE. The positive slope of high field AHE curves up to 250 K suggests that holes are the majority carriers which agrees with the results of resistivity measurement. The anomalous Hall conductivity obtained by extrapolating the AHE curve at a cryogenic temperature (T = 5 K) is found to be 91.35 S cm−1. Irrespective of the absence of B2 and L21-ordering, our experimental findings such as a positive temperature coefficient of resistivity, a nearly temperature independent carrier concentration (and/or mobility) and linear MR justify the presence of SGS like behaviour within our film. To correlate the obtained structural, electronic, and magnetic properties, DFT calculations were performed for bulk and the thin film CFCG alloy. The structural and magnetic properties are in well agreement with the experimentally obtained results, while the electronic nature is not consistent and needs further investigation. The experimental and theoretical studies suggest that the CFCG alloy is a desirable candidate for spintronics based devices and has further scope to be studied for dynamic and device-based studies.Author contributions
Vireshwar Mishra: conceptualization (lead), data curation (lead), formal analysis (lead), investigation (lead), methodology (lead), validation (lead), visualization (lead), writing original draft (lead), and writing – review and editing (lead). Amar Kumar: conceptualization (supporting), data curation (equal), formal analysis (supporting), methodology (supporting), writing original draft (supporting) and writing – review and editing (supporting). Lalit Pandey: conceptualization (supporting), data curation (supporting), formal analysis (supporting), and methodology (supporting). Nanhe Kumar Gupta: conceptualization (supporting) and formal analysis (supporting). Soumyarup Hait: data curation (supporting), formal analysis (supporting), and writing – review and editing (supporting). Vineet Barwal: data curation (supporting) and formal analysis (supporting). Nikita Sharma: data curation (supporting) and formal analysis (supporting). Nakul Kumar: data curation (supporting), formal analysis (supporting), and methodology (supporting). Sharat Chandra: data curation (supporting), formal analysis (supporting), and validation (supporting). Sujeet Chaudhary: conceptualization (equal), formal analysis (equal), funding acquisition (lead), investigation (equal), project administration (lead), validation (equal), and writing – review and editing (equal).Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the Central Research Facility (CRF), IIT Delhi for EDAX and VSM measurements, IIT Delhi HPC facility for computational resources and the Ministry of Education, Government of India and the Council of Scientific and Industrial Research (CSIR) India for financial assistance throughout this work.References
- C. Felser, G. H. Fecher and B. Balke, Angew. Chem., Int. Ed., 2007, 46, 668–699 CrossRef CAS PubMed.
- K. Inomata, N. Ikeda, N. Tezuka, R. Goto, S. Sugimoto, M. Wojcik and E. Jedryka, Sci. Technol. Adv. Mater., 2008, 9, 014101–014119 CrossRef.
- M. Oogane and S. Mizukami, Philos. Trans. R. Soc., A, 2011, 369, 3037–3053 CrossRef CAS PubMed.
- H.-xi Liu, Y. Honda, T. Taira, K. Matsuda, M. Arita, T. Uemura and M. Yamamoto, Appl. Phys. Lett., 2012, 101, 132418–132422 CrossRef.
- A. You, M. A. Y. Be and I. In, Appl. Phys. Lett., 2010, 122504, 1–4 Search PubMed.
- Y. Sakuraba, M. Ueda, Y. Miura, K. Sato, S. Bosu, K. Saito, M. Shirai, T. J. Konno and K. Takanashi, Appl. Phys. Lett., 2012, 101, 2–6 CrossRef.
- B. A. Frandsen, Z. Gong, M. W. Terban, S. Banerjee, B. Chen, C. Jin, M. Feygenson, Y. J. Uemura and S. J. L. Billinge, Phys. Rev. B, 2016, 94, 1–8 CrossRef.
- A. You, M. A. Y. Be and I. In, Appl. Phys. Lett., 2016, 042405, 1–5 Search PubMed.
- X. L. Wang, Phys. Rev. Lett., 2008, 100, 1–4 Search PubMed.
- S. Ouardi, G. H. Fecher, C. Felser and J. Kübler, Phys. Rev. Lett., 2013, 110, 2–6 CrossRef.
- S. Skaftouros, K. Özdoǧan, E. Şaşoǧlu and I. Galanakis, Appl. Phys. Lett., 2013, 102, 022402–022405 CrossRef.
- H. Ohno, Science, 1998, 281, 951–956 CrossRef CAS.
- G. Z. Xu, E. K. Liu, Y. Du, G. J. Li, G. D. Liu, W. H. Wang and G. H. Wu, EPL, 2013, 102, 17007–17012 CrossRef.
- K. Özdoǧan, E. Şaşioǧlu and I. Galanakis, J. Appl. Phys., 2013, 113, 193903–193907 CrossRef.
- G. Y. Gao and K. L. Yao, Appl. Phys. Lett., 2013, 103, 1–6 Search PubMed.
- L. Bainsla, A. I. Mallick, M. M. Raja, A. K. Nigam, B. S. D. Ch. S. Varaprasad, Y. K. Takahashi, A. Alam, K. G. Suresh and K. Hono, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 4–9 CrossRef.
- W. Feng, X. Fu, C. Wan, Z. Yuan, X. Han, N. Van Quang and S. Cho, Phys. Status Solidi RRL, 2015, 9, 641–645 CrossRef CAS.
- K. Ueda, S. Hirose and H. Asano, Appl. Phys. Lett., 2017, 110, 202405–202408 CrossRef.
- L. Bainsla, A. I. Mallick, M. M. Raja, A. A. Coelho, A. K. Nigam, D. D. Johnson, A. Alam and K. G. Suresh, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 045201, 1–5 Search PubMed.
- H. S. Goripati, T. Furubayashi, Y. K. Takahashi and K. Hono, J. Appl. Phys., 2013, 113, 043901–043905 CrossRef.
- L. Bainsla and K. G. Suresh, Appl. Phys. Rev., 2016, E75-B, 82–86 Search PubMed.
- G. Y. Gao, L. Hu, K. L. Yao, B. Luo and N. Liu, J. Alloys Compd., 2013, 551, 539–543 CrossRef CAS.
- D. Rani, Enamullah, L. Bainsla, K. G. Suresh and A. Alam, Phys. Rev. B, 2019, 99, 104429–104438 CrossRef CAS.
- L. Bainsla, R. Yilgin, J. Okabayashi, A. Ono, K. Suzuki and S. Mizukami, Phys. Rev. B, 2017, 96, 1–9 CrossRef.
- S. Hait, S. Husain, V. Barwal, N. K. Gupta, L. Pandey, P. Svedlindh and S. Chaudhary, J. Magn. Magn. Mater., 2021, 519, 167509 CrossRef CAS.
- S. Hait, V. Barwal, N. K. Gupta, L. Pandey, V. Mishra and S. Chaudhary, Appl. Surf. Sci., 2022, 572, 151423–151433 CrossRef CAS.
- A. Kumar, D. K. Pandya and S. Chaudhary, J. Appl. Phys., 2012, 111, 3–8 Search PubMed.
- Z. Lendzion-Bielun, U. Narkiewicz and W. Arabczyk, Materials, 2013, 6, 2400–2409 CrossRef CAS PubMed.
- L. Bainsla, A. I. Mallick, M. M. Raja, A. A. Coelho, A. K. Nigam, D. D. Johnson, A. Alam and K. G. Suresh, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 1–5 CrossRef.
- B. Shi, J. Li, C. Zhang, W. Zhai, S. Jiang, W. Wang, D. Chen, Y. Yan, G. Zhang and P. F. Liu, Phys. Chem. Chem. Phys., 2020, 22, 23185–23194 RSC.
- V. Mishra, V. Barwal, L. Pandey, N. K. Gupta, S. Hait, A. Kumar, N. Sharma, N. Kumar and S. Chaudhary, J. Magn. Magn. Mater., 2021, 547, 168837 CrossRef.
- K. Özdoğan, E. Şaşıoğlu and I. Galanakis, J. Appl. Phys., 2013, 113, 193903–193907 CrossRef.
- A. You, M. A. Y. Be and I. In, Appl. Phys. Lett., 2016, 242408, 1–5 Search PubMed.
- L. Ritchie and G. Xiao, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 1–6 Search PubMed.
- K. Sato, T. Naka, M. Taguchi, T. Nakane, F. Ishikawa, Y. Yamada, Y. Takaesu, T. Nakama and A. De Visser, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 1–8 CAS.
- V. Barwal, N. Behera, S. Husain, N. K. Gupta, S. Hait, L. Pandey, V. Mishra and S. Chaudhary, J. Magn. Magn. Mater., 2021, 518, 167404 CrossRef.
- G. M. Stephen, C. Lane, G. Buda, D. Graf, S. Kaprzyk, B. Barbiellini, A. Bansil and D. Heiman, Phys. Rev. B, 2019, 99, 1–8 CrossRef.
- J. H. Mooij, Phys. Status Solidi, 1973, 17, 521–530 CrossRef CAS.
- K. Kudo, A. Masago, S. Yamada, L. S. R. Kumara, H. Tajiri, Y. Sakuraba, K. Hono and K. Hamaya, Phys. Rev. B, 2021, 103, 1–9 CrossRef.
- P. Kharel, W. Zhang, R. Skomski, S. Valloppilly, Y. Huh, R. Fuglsby, S. Gilbert and D. J. Sellmyer, J. Phys. D: Appl. Phys., 2015, 48, 245002–245007 CrossRef.
- L. Bainsla, A. I. Mallick, A. A. Coelho, A. K. Nigam, B. S. D. Ch. S. Varaprasad, Y. K. Takahashi, A. Alam, K. G. Suresh and K. Hono, J. Magn. Magn. Mater., 2015, 394, 82–86 CrossRef CAS.
- Z. X. Chen, Y. Sakuraba, K. Masuda, X. D. Xu, L. S. R. Kumara, H. Tajiri, Y. Kotani, V. Kushwaha, A. Perumal and K. Hono, Acta Mater., 2022, 232, 0–10 CAS.
- G. M. Stephen, C. Lane, G. Buda, D. Graf, S. Kaprzyk, B. Barbiellini, A. Bansil, D. Heiman, N. High and M. Field, Phys. Rev. B, 2019, 99, 224207 CrossRef CAS.
- P. Y. Yu and M. Cardona, Fundamentals of Semiconductors, 1996 Search PubMed.
- Y. Du, G. Z. Xu, X. M. Zhang, Z. Y. Liu, S. Y. Yu, E. K. Liu, W. H. Wang and G. H. Wu, EPL, 2013, 103, 0–6 CrossRef.
- G. Z. Xu, Y. Du, X. M. Zhang, H. G. Zhang, E. K. Liu, W. H. Wang and G. H. Wu, Appl. Phys. Lett., 2014, 104, 1–5 Search PubMed.
- N. Nagaosa, Rev. Mod. Phys., 2010, 82, 1539–1592 CrossRef.
- H. Fu, Y. Li, L. Ma, C. You, Q. Zhang and N. Tian, J. Magn. Magn. Mater., 2019, 473, 16–20 CrossRef CAS.
- R. Karplus and J. M. Luttinger, Phys. Rev., 1954, 95, 1154–1160 CrossRef.
- S. Ganesh and Q. Niu, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1–11 CrossRef.
- J. Smit, Physica, 1958, 24, 39–51 CrossRef CAS.
- L. Berger, Phys. Rev. B: Solid State, 1972, 5, 1862–1870 CrossRef.
- L. berger, Phys. Rev. B: Condens. Matter Mater. Phys., 1970, 2, 4559–4566 CrossRef.
- Y. Tian, L. Ye and X. Jin, Phys. Rev. Lett., 2009, 087206, 1–4 Search PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. De Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502–395520 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. De Gironcoli, P. Delugas, R. A. Distasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H. Y. Ko, A. Kokalj, E. Kücükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H. V. Nguyen, A. Otero-De-La-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901–465930 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, 1996 Search PubMed.
- M. Kawamura, Y. Gohda and S. Tsuneyuki, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 094515–094522 CrossRef.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658 CrossRef CAS.
- T. Graf, C. Felser and S. S. P. Parkin, Prog. Solid State Chem., 2011, 39, 1–50 CrossRef CAS.
- B. F. D. Murnaghan, The Compressibility of Media Under Extreme Pressures, Univ. Texas Public, 1915, vol. 18 Search PubMed.
- B. Shi, J. Li, C. Jin, J. Yang, C. Zhang, Y. Yan, Y. Wang and G. Zhang, J. Magn. Magn. Mater., 2021, 517, 167383–167392 CrossRef CAS.
- J. M. K. Al-zyadi, A. A. Kadhim and K. Yao, J. Electron Spectrosc. Relat. Phenom., 2018, 226, 17–21 CrossRef CAS.
- R. Paudel, J. Zhu, M. K. Hussain, M. Batouche, M. Waqas and D. Paudyal, J. Magn. Magn. Mater., 2021, 539, 168425–168433 CrossRef CAS.
- S. Kurdi, Y. Sakuraba, K. Masuda, H. Tajiri, B. Nair, G. F. Nataf, M. E. Vickers, G. Reiss, M. Meinert, S. S. Dhesi, M. Ghidini and Z. H. Barber, J. Phys. D: Appl. Phys., 2022, 55, 185305–185314 CrossRef.
- J. Kudrnovský, V. Drchal and I. Turek, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 1–8 CrossRef.
- S. Biswas, S. Chaudhuri, N. Kander, S. Mitra, S. Guchhait and A. K. Das, ACS Appl. Electron. Mater., 2021, 3, 4522–4534 CrossRef CAS.
- B. Pradines, R. Arras, I. Abdallah, N. Biziere and L. Calmels, Phys. Rev. B, 2017, 95, 1–13 CrossRef.
- Y. Miura, K. Nagao and M. Shirai, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 1–7 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr03424g |
| ‡ These authors contributed equally. |
| § Present Address: Centre for Magnetic and Spintronics Materials (CMSM), National Institute for Materials Science (NIMS), 3050047 (Japan). |
| This journal is © The Royal Society of Chemistry 2023 |