A comprehensive method to study the DNA's association with lamin and chromatin compaction in intact cell nuclei at super resolution

Abstract

Super-resolution fluorescence microscopy has revolutionized multicolor imaging of nuclear structures due to the combination of high labeling specificity and high resolution. Here we expanded the recently developed fBALM (DNA structure fluctuation-assisted binding activated localization microscopy) method by developing a stable methodological sequence that enables dual-color imaging of high-resolution genomic DNA together with an immunofluorescently labeled intranuclear protein. Our measurements of the nuclear periphery, imaging DNA and LaminB1 in biologically relevant samples, show that this novel dual-color imaging method is feasible for further quantitative evaluations. We were able to study the relative spatial signal organization between DNA and LaminB1 by means of highly specific colocalization measurements at nanometer resolution. Measurements were performed with and without the antifade embedding medium ProLong Gold, which proved to be essential for imaging of LaminB1, but not for imaging of SytoxOrange labeled DNA. The localization precision was used to differentiate between localizations with higher and lower amounts of emitting photons. We interpret high intensity localizations to be renatured DNA sections in which a high amount of Sytox Orange molecules were bound. This could give insight into the denaturation kinetics of DNA during fBALM. These results were further complemented by measurements of γH2AX and H3K9me3 signal organization to demonstrate differences within the chromatin landscape, which were quantified with image processing methods such as Voronoi segmentation.

---

1 Introduction

The spatial organization of chromosomes in the nucleus is central to our understanding of gene regulation in normal and abnormal development but is yet poorly understood.^1–3 The possibility to visualize chromosomes with fluorescence in situ hybridization (FISH)⁴ provided initial evidence that chromosome territories are not randomly organized in the nucleus,^5–7 but are positioned either closer to the nuclear periphery or interior, depending on the gene density along each chromosome.^8–12 The nuclear lamina plays an important role in maintaining this radial arrangement, as it tethers chromatin, defining its position relative to the nuclear envelope.¹³ Genome-wide mapping showed that lamina-associated domains (LADs), defined as genomic regions that make molecular contact with the nuclear lamina, cover more than one third of the genome.¹⁴ The large size of LADs and their presence throughout the genome implies that they have an important role in chromosome architecture. Most LADs have low levels of gene expression, a low gene density and are enriched in heterochromatin related histone marks H3K9me2 and H3K9me3, suggesting that they play a role in the control of gene repression.¹⁵ Dysregulation of LaminB1 expression has been associated with neurological disorders and the malignant development of several cancer types.^16–18 Chromatin interaction with the nuclear lamina is known to mediate the repression of gene transcription and chromatin accessibility.^19,20 Furthermore, reduced LaminB1 expression was shown to induce chromatin instability and to modulate the DNA damage response.^21,22 Recent studies demonstrated the high-resolution topology of nuclear lamins and the spatial localization of DNA damage.^23–25 Considering the involvement of LaminB1 in the modulation of gene expression and DNA damage repair, we aimed to develop a method that would allow to better understand the effect of LaminB1 dysregulation on chromatin organization and DNA damage at a nanoscale level.

A fuller understanding of nuclear lamina mediated gene regulation calls for enhanced resolution approaches to analyze the spatial distribution of both the chromatin and lamina proteins in the same cell. Although genome-wide mapping techniques have revealed a lot of information about LAD characteristics and their size, they cannot detect and directly analyze nanoscale structures on the level of individual molecules in single cell nuclei. Electron microscopy offers atomic resolution. However, it requires destructive and highly complex sample fixation, including the cutting of samples in ultra-thin sections. Furthermore, it is in general difficult to achieve specific contrast in biological samples. The advantage of super-resolution optical microscopy methods is that fluorescent molecule-specific labeling allows multicolor imaging within the same sample. In addition, super-resolution microscopy provides a resolution far better than conventional optical microscopy, also in 3D conserved specimens, and omits mechanical sectioning.

Single molecule localization microscopy (SMLM)²⁶ belongs to the family of novel super-resolution optical methods that can circumvent the Abbe diffraction limit.^27,28 It is based on the idea that the spatial positions of individual fluorescent molecules (fluorophores) in a diffraction-limited image can be computationally determined with high precision if their signals (which are determined by the microscope's point spread function) are spatially and temporally separated.²⁹ The separation is achieved by exploiting the photophysical properties of the fluorophores to switch between an active “bright” state, where they emit fluorescent light when excited, and one or more inactive “dark” states in which they do not fluoresce.^30–32 This stochastic process leads to fluorophore “blinking”, which is recorded as an image sequence and can be used to reconstruct a super-resolution map of the positions of the labeled molecules within a nucleus.³³

To conduct measurements with statistical relevance of at least hundreds of cells, it is necessary to develop a stable and reproducible method that works on the specimens of interest. Therefore, we tested our dual-color SMLM method directly on samples of LaminB1-depleted nuclei to assess its potential of revealing differences compared to control nuclei. Dual-color super-resolution microscopy has already been successfully implemented to study e.g. changes in chromatin organization together with nuclear lamina and nuclear pore complex formation during bovine preimplantation development³⁴ and to study changes in chromatin condensation during model ischemia³⁵ or in cancer cells.³⁶ DNA labeling methods determine the efficiency and precision of SMLM. Immunolabeling chromatin-associated proteins (histones)^24,33,37 gives rise to a linkage error caused by the large size of the antibodies and in addition only labels specific histone modifications of the DNA. In comparison, DNA-binding dyes have a very small molecular weight, can label the DNA directly³⁸ and are less influenced by diffusion and penetration related constraints.³⁹ In previous dual-color SMLM studies DNA dyes such as DAPI³⁴ and Vybrant Violet^35,40 were used. Here, we utilized Sytox Orange, a small DNA intercalator which can bind both to the accessible DNA and also to the inaccessible and compact DNA.⁴¹ In addition, when bound Sytox Orange has a very high fluorescence enhancement (450×) compared to its unbound state.⁴²

Using the method of structure fluctuation-assisted binding activated localization microscopy (fBALM),^43–45 Sytox Orange dynamically interacts with the DNA, binding and unbinding to the double-stranded structure. This happens in a carefully adjusted chemical environment, which induces local reversible transitions between single-stranded (ssDNA) and double-stranded DNA (dsDNA). Since Sytox Orange has a fluorescence enhancement when bound to dsDNA, the cycle of unbinding during denaturation and binding during renaturation of DNA leads to a blinking behaviour that can be used to detect localizations as in the original SMLM method. The method of fBALM strongly minimizes the effect of background which is otherwise caused by unspecifically bound fluorophores because the unbound state of Sytox Orange essentially does not emit fluorescence.

Here, we present how fBALM, with its advantages of enhanced structural resolution and efficient labeling of DNA, can be used for dual-color SMLM imaging of chromatin with another intranuclear protein, in this case LaminB1. We outline the methodology for dual-color fBALM imaging in B cell lymphoma cells. Using quantitative methods, we demonstrate that this dual-color SMLM method can also be used for additional analysis such as detection of nanometer-scaled changes in chromatin structure in single cells. We compare Sytox Orange DNA labeling with conventional histone immunolabeling and visualize the double-strand break (DSB) marker γH2AX to show the possibilities of investigating DNA accessibility and DNA damage in relation to the labeled nuclear lamina. To further characterize the DNA labeling during fBALM dual-color imaging, we finally compare the effect of different chemical environments and investigate the DNA denaturation kinetics at the nuclear nanoscale.

2 Experimental

2.1 Single molecule localization microscopy

BL-2 cells (Burkitt lymphoma, ACC 625, DSMZ-German Collection of Microorganisms and Cell Cultures GmbH) were cultured as described previously⁴⁶ and LMNB1 (LaminB1 protein coding gene) expression was reduced by 60–70% by using a suitable shRNA construct. A stable shLMNB1 cell line was generated by transducing BL-2 cells with lentiviral particles containing shRNA (Dharmacon, clone ID: V3IHSMCG_4721111) targeting LMNB1 mRNA. The trans-lentiviral shRNA packaging kit with calcium phosphate transfection reagents (Dharmacon, catalogue number TLP5913) was used to transduce BL-2 cells according to the manufacturer's protocol. Transduced cells were positively selected with puromycin and incubated with 500 ng mL⁻¹ of doxycycline for 72 hours to induce shRNA against LMNB1. Transduction efficiency was assessed by flow cytometry analysis of GFP positive (shLMNB1-containing) BL-2 cells, which revealed that around 90% of the cells express shLMNB1 (Fig. S1a†). The targeting of LaminB1 by shRNAs was validated by western blotting, which confirmed a 60% reduction of the total LaminB1 protein level (Fig. S1b†). Western blotting was performed as previously described.⁴⁶ Furthermore, confocal microscopy confirmed depletion of LaminB1 incorporation particularly around the nuclear periphery (Fig. S2†). In contrast to experiments inducing DSBs by external treatment,^24,25 the cell model used in this study is a highly proliferative and aggressive lymphoma cell line which continuously undergoes spontaneous DSBs. Images ofBL-2 nuclei stained against LaminB1 and γH2AX taken prior to SMLM can be found in the ESI (Fig. S3†). Cells were immunostained as described⁴⁷ with rabbit-anti-LaminB1 antibodies labeled with Alexa 594 or mouse-anti-LaminB1 antibodies labeled with Alexa 647 to mark LaminB1. Mouse-anti-γH2AX antibodies labeled with Alexa 647 marked DNA damage sites and rabbit-anti-H3K9me3 antibodies labeled with Alexa 594 marked heterochromatin. The exact catalogue numbers and applied dilutions can be found in Table S1.† Immunolabeled samples were all fixated and embedded in ProLong Gold (Thermo Fischer Scientific) prior to imaging. To directly label DNA for fBALM, the cells were first treated with RNase A (1 : 1000 in PBS) at 37 °C for 15 min and then stained with Sytox Orange (Thermo Fisher Scientific, 1 μg mL⁻¹) for 30 min, followed by three washings with PBS and 0.1% Tween-20. For the cells labeled with Sytox Orange, the fBALM buffer was applied before imaging, which contains 40 μg mL⁻¹ catalase, 0.5 mg mL⁻¹ glucose oxidase and 10% glucose, all in PBS.⁴³

The microscope used was built by W. Schaufler⁴⁸ and is situated at the Light Microscopy Facility of the German Cancer Research Center in Heidelberg. Its setup has been previously described in detail by M. Krufczik et al.⁴⁷ Enhanced thermo-mechanical stability was provided by the setup⁴⁸ and ensured a localization precision of ±10 nm with temperature fluctuations below 10 mK.²⁵ For excitation of Alexa 647, we used the 642 nm laser at 0.8 kW cm⁻² laser intensity in the sample plane and for excitation of Alexa 594, we used the 561 nm laser at an intensity of 1.2 kW cm⁻² (for single-colored LaminB1 samples) or 1.87 kW cm⁻² (all other samples). Sytox Orange was excited with the 561 nm laser at an intensity of 1.01 kW cm⁻². The exposure time for immunofluorescently stained samples was 100 ms per frame and we collected 2000–5000 frames for each cell. For samples stained with Sytox Orange, we typically acquired 2000–40 000 frames at an exposure time of 50 ms per frame. For the long acquisition of Sytox Orange, we imaged a single nucleus at 40 ms exposure time at 1.01 kW cm⁻² laser intensity until no visible blinking could be observed anymore (after 455 987 and 256 056 frames for a control and a shLMNB1 nucleus, respectively). The long acquisition consisted of several consecutive measurements, between which the initial laser flash (at 1.87 kW cm⁻²), which is applied prior to every measurement to push fluorophores to their reversible dark state, was reapplied (a total of 12 and 20 times for control and shLMNB1, respectively) as this led to maximal blinking. In addition, the focus was re-adjusted, and for the shLMNB1 nucleus the intensity was decreased over time from 1.41, to 1.01, to 0.62 kW cm⁻² and then increased back to 1.01 kW cm⁻².

2.2 SMLM data analysis

Images were reconstructed by localizing fluorophores with the in-house program SMLM.py⁴⁹ and the open-source program ThunderSTORM.⁵⁰ The output of the programs is a results table including information on the x- and y-positions of the blinking fluorophores, the standard deviations and localization precision, and signal intensity.⁵¹ A representative localization precision distribution of LaminB1 (imaged with the original SMLM method, in ProLong Gold) is shown in Fig. S4a† and is comparable for the γH2AX and H3K9me3 measurements (data not shown). The localization precision of a representative dual-color fBALM measurement is shown for Sytox Orange (Fig. S4b†) and LaminB1 (Fig. S4c†), both imaged in ProLong Gold and fBALM buffer. This shows that the mean localization precision remains good for LaminB1 (12 ± 10 nm) and Sytox Orange (21 ± 11 nm) despite imaging in fBALM buffer. In SMLM.py a threshold of 3 was used to reduce noise and the first 30 frames were omitted. In ThunderSTORM the following settings were applied: a wavelet filter for image filtering (B-spline order: 3 and B-spline scale: 2), detection of local maxima with 8-neighborhood connectivity and a threshold of one times the standard deviation of the intensity values from the first wavelet deviation for the approximate localization of fluorophores, and the integrated form of a symmetric 2D Gaussian function for the sub-pixel localization, approximated with the weighted least-squares method (fitting radius: 5 px, initial Sigma: 0.5 px). For post-processing analysis, the method of cross-correlation was used for drift correction with the default settings (bin number and magnification set to 5), as well as merging of molecules. Since for dual-color data the two channels were measured sequentially, we had to perform a drift correction on each channel separately. The reference frame for the drift correction was selected as the last frame for the first channel and the first frame for the second channel. In addition, artifacts caused by the algorithm from fitting an incorrect drift were avoided by drift-correcting a region of interest containing dominant features and applying its drift correction to the total dataset. Since the focus of this investigation lied in its methodological feasibility, the acquisition of an appropriately high number of data sets fulfilling statistical requirements for evaluation will be the subject of future experiments.

2.3 Colocalization analysis

The algorithm by Malkusch et al.⁵² is available in ThunderSTORM and was used to calculate a colocalization value for each localization A_i of molecule species A and each localization B_i of species B. This was done by determining the distribution of localizations from both species A and B around A_i and around B_i. For species A around A_i this would bewhere ρ_Ai,_A(r) is the density of localizations N_Ai of species A in the circular area of radius r. The distribution was normalized by the density of localizations within the circular area where the radius is the largest observed distance R_max of A_i to A. A uniform distribution would therefore give an expected value of D(r) = 1. From these distributions, Spearman's rank correlation coefficient S_Ai, which takes values between −1 and +1, was calculated between the distribution functions of both molecule populations in the neighborhood of each localization A_i. To avoid false positive correlation values due to localizations with nearest neighbors that are further away, S was weighted with the nearest neighbor distances E_Ai,_B, resulting in the colocalization value

A colocalization value of −1 indicates an anti-correlation between the two molecules species, while 0 indicates non-correlated distributions, and +1 perfectly correlated distributions.

2.4 Cluster analysis and Voronoi segmentation

Clusters were detected and segmented using a cluster analysis based on the DBSCAN algorithm.⁵³ For defining clusters, suitable cluster parameters were determined iteratively. LaminB1 clusters had to have a minimum number of 10 localizations within a radius of 70 nm (for control) or 100 nm (for shLMNB1). H3K9me3 clusters had to have a minimum number of 80 localizations within a radius of 150 nm. The convex hull of the cluster was determined using the function ConvexHull from scipy.spatial. The area of the cluster is enclosed by the convex hull and was calculated with the shoelace formulawhere (x₀, y₀), (x₁, y₁),…, (x_N, y_N) are the points of the convex hull and (x₀, y₀) = (x_N, y_N). The density of a cluster was calculated by dividing the number of localizations belonging to the cluster by the cluster area.

Voronoi cell areas were calculated for each locus and inverted to receive the absolute single molecule position (SMP) Voronoi density. For absolute SMP Voronoi densities, the histogram bins were computed such that the bar heights summed to 1. Dividing each density value by the total number of localizations in the nucleus gave the normalized Voronoi density. Here, the bins were computed such that the area of the histogram was 1. To average over multiple measurements from the same sample, the corresponding probability density function was applied to the data frame containing the Voronoi densities of all localizations.

In addition, the xy-positions of the localization data were transformed into polar coordinates, with the center of mass of the nucleus being the coordinate system's origin. This enabled the Voronoi analysis as a function of the nucleus's radius r.

2.5. Line profile analysis

1. As input data, the density image with its pixel intensities that are proportional to the amount of localizations was used. Depending on the desired resolution, the xy-position data can also be used directly. However, the density image was more suitable as the intensity values are continuous and not discretized. To reproject the intensity values given in the Cartesian image into a polar coordinate system, the origin was first selected manually as a (x,y) point and the Cartesian coordinates were transformed to polar coordinates with and θ = arctan2(x, y).

2. In contrast to a Cartesian grid, pixel areas increase radially in a polar grid. To account for this, the pixel intensity was normalized to the new area. A radial coordinate spacing of 1 pixel was chosen for the grid interpolation.

3. Next, the maximal intensity within each angular interval dθ was determined. Since we were only interested in the intensity along the periphery, intensities present in the nuclear interior were set to zero with a manual mask. A value of dθ = 0.01 radians was chosen, which corresponds to 0.57°.

4. The corresponding radial position r of the maximal intensity was calculated. The intensity was then summed over the interval [r − dr, r + dr] to account for the finite thickness of the LaminB1 line. A value of dr = 10 pixel was chosen. The resulting intensities were plotted as a function of the angle θ. To reduce noise, the resulting function was smoothened by applying a Savitzky–Golay filter with a window size of 25 and a polynomial order of 3.

3 Results

3.1 Determination of optimal imaging conditions for dual-color SMLM

In BL-2 nuclei with both normal and reduced LaminB1 expression, LaminB1 was labeled immunofluorescently with Alexa 647 and DNA was labeled with the DNA-binding dye Sytox Orange. To achieve an efficient photoswitching behavior of Sytox Orange and in turn precise, high-density labeling of nuclear DNA, the pH had to be gradually decreased. This was done using the previously developed fBALM buffer^43,44to create a denaturing environment for the DNA without destroying the chromatin configuration.

Although the fBALM buffer enabled the blinking of Sytox Orange, in some of our experiments Alexa 647 immediately lost its blinking behavior after fBALM buffer was added. However, in samples additionally embedded in ProLong Gold, Alexa 647 showed blinking. To test how the addition of ProLong Gold affected both channels quantitatively, the number of LaminB1 and Sytox Orange localizations were measured in dual-colored samples containing both ProLong Gold and the fBALM buffer. These measurements were conducted as a function of time to determine the influence of the decreasing pH on the number of localizations. Fig. 1 shows the detected fluorophore numbers in both the Alexa 647 and Sytox Orange channel. Adding buffer to LaminB1 labeled with Alexa 647 decreased the number of localizations by half (Fig. 1a). A further linear decrease with progressing time was observed. This shows that although the fBALM buffer has an effect on the number of Alexa 647 localizations, a sufficiently high number for the data analysis performed here is still detected, even over long periods of time (up to 5 h). The temporal trend of Sytox Orange localizations (Fig. 1b) shows that the numbers reach a maximum at approximately 1–3 h after applying the buffer when samples were additionally embedded in ProLong Gold. We found out that to get maximum signal from both channels it is critical that Alexa 647 is imaged first and immediately after buffer application while the signal from Sytox Orange should be imaged 1–3 h after buffer application.

Fig. 1 Influence of ProLong Gold and fBALM buffer on the blinking behavior of Alexa 647 (a) and Sytox Orange (b). BL-2 cells were immunostained with antibodies against LaminB1 and DNA was stained with Sytox Orange. The resulting localizations in one nucleus acquired in the first 2000 frames are presented as a function of time. Each data point represents a different nucleus. All samples were embedded in ProLong Gold and after time t = 0, the fBALM buffer was added. Nuclei measured at t = 0 were not exposed to the buffer yet. The experiment was performed on three identically prepared sample sets (distinguished by the marker shape). The marker color distinguishes between control and LaminB1-depleted nuclei.

3.2 Dual-color SMLM high-resolution imaging of DNA and LaminB1

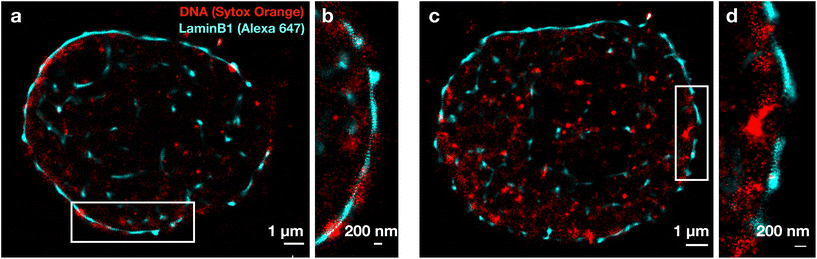
After determining the correct sequence and optimal imaging time for Alexa 647 and Sytox Orange, dual-color SMLM images were collected. Fig. 2 shows an exemplary dual-color image for a control (a and b) and LaminB1-depleted (c and d) nucleus. The expected lining of LaminB1 (cyan) along the nuclear periphery was used as a reference structure, as it could be seen also without fBALM buffer. This clearly demonstrates that the imaging of LaminB1 worked despite the sample being in the fBALM buffer. The images in Fig. 2 show that the LaminB1-labelled nuclear lamina varies in thickness (both inserts show the envelope with gaps). In addition, small clusters of LaminB1 can be seen in the nuclear interior. Sytox Orange (red) is distributed in small condensed clusters and shows increased concentration along the nuclear periphery.

Fig. 2 Merged dual-color SMLM images of Sytox Orange (red) and LaminB1 (cyan) of a control (a) and shLMNB1 (c) nucleus with inserts (b and d) magnifying the nuclear periphery from rectangular regions. The images were reconstructed with ThunderSTORM, using Gaussian rendering and a magnification of 50×. Both images were reconstructed from 5000 frames and were drift-corrected as described in Methods.

3.3 Colocalization of LaminB1 and DNA

To quantify the association of LaminB1 localizations with the chromatin distribution in the nucleus, we studied the colocalization between the two channels. A nearest neighbor analysis was applied, for which the distances of fluorophores from one channel to the nearest fluorophores of the other channel were calculated. In addition, a coordinate-based colocalization (CBC) analysis was used, which is based on the calculation of a colocalization value for each fluorophore.⁵² In contrast to the nearest neighbor analysis, the colocalization value from the CBC analysis should not be prone to detect false positive colocalizations. The colocalization can take values between −1 and +1, as it is based on Spearman's rank correlation coefficient (see Methods). A value of +1 indicates perfect alignment, while a value of −1 indicates anti-correlation. A value of 0 represents a low probability for colocalization. The nearest neighbor histograms (Fig. 3a) show that the nearest distances between the two molecule species are below 20 nm. Specifically, the histograms peak at even smaller distances (below 10 nm) when only nearest LaminB1 neighbors around Sytox Orange localizations are considered, compared to vice versa. This is expected due to higher occurrence of LaminB1 localizations compared to Sytox Orange. In the CBC analysis (Fig. 3b) the control nuclei (blue histograms) have a larger peak at positive colocalization values near +1 than the shLMNB1 nuclei (red histograms). Conversely, the shLMNB1 nuclei have a larger peak at negative colocalization values near −1 than the control nuclei. This suggests a decrease in colocalization between LaminB1 and DNA after LaminB1 depletion.

Fig. 3 Nearest neighbor distance frequency distributions (a) and histograms of colocalization values (b) for control and shLMNB1 nuclei. The distributions were averaged over all measured nuclei (4 control and 8 shLMNB1 nuclei) and normalized. We distinguish between LaminB1 to Sytox Orange (SO) localization distances and vice versa.

As a next step, the colocalization values (Fig. 3b) were mapped onto the position data of the super-resolution images. This enabled a direct visualization of the spatial distribution of (anti-)correlations in the nucleus. Fig. 4 shows representative images of both cell types where each locus was assigned a colocalization value that is indicated by the color. The control nucleus (Fig. 4a and b) exhibits more correlations (shown in red) than the shLMNB1 nucleus (Fig. 4c and d). These correlations appear most prominently at the nuclear periphery, while the color blue (anti-correlations) occurs mostly in the interior. The images in Fig. 4 were created by converting the interactive stack that is made in ThunderSTORM into a summed RGB image.

Fig. 4 Spatial visualization of colocalization values in nuclei. The calculated colocalization values of LaminB1 and Sytox Orange are shown both for a representative control (a and b) and shLMNB1 (c and d) nucleus. The colocalization values of all LaminB1 molecules (a and c) and all Sytox Orange molecules (b and d) are shown for each nucleus separately. The colorbar in (c) is valid for all images and indicates the colocalization value. A value of +1 (red) indicates perfect alignment, while a value of −1 (blue) indicates anti-correlation. A value of 0 (green) represents a low probability for colocalization. The scale bars all show 2 μm.

3.4 Cluster analysis and Voronoi segmentation

To investigate changes in the chromatin landscape after reducing the incorporation of LaminB1 in the nucleus, we studied the distribution of DNA and other DNA associated proteins in relation to the nuclear lamina. Our experiments showed that the LaminB1 knockdown resulted in more H3K9me3 localizations per unit area in the nucleus (Fig. 5a). It should be noted that the LaminB1 knockdown affected the lamina in cells and batches differently, resulting in distinct large holes in the lamina or a globally disintegrated structure (Fig. S5†).

Fig. 5 H3K9me3 signal density (a) and number of clusters (b) per nucleus, measured for 37 control and 45 shLMNB1 nuclei. The mean is indicated by a red cross, and the median by a red line. The box shows the interquartile range (IQR), which has values ranging from the first quartile (Q1) to the third quartile (Q3). The end of the lower whisker is defined by Q1 − 1.5·IQR, and the upper end is defined by Q3 + 1.5·IQR. The circles are outliers. A representative localization image of H3K9me3 signal with the result of the cluster analysis in a control (c) and shLMNB1 nucleus (d) is shown. Each white pixel represents a localization. Localizations in a cluster are colored red and the area enclosed by the convex hull is colored green. Here, a mask of the nucleus was used to set localizations outside the nucleus to zero.

In wide-field and localization images we observed clusters (Fig. 5c and d). These clusters were identified as high-density subsets in the SMLM positional data. Here, appropriate cluster parameters were chosen for each marker (see Methods). The heterochromatin marker H3K9me3 was found with higher probability in clusters in shLMNB1 nuclei (Fig. 5b). Heterochromatin clusters in shLMNB1 nuclei were of slightly higher density than in control nuclei. LaminB1 data was also segmented into clusters to quantify the continuity of the LaminB1 envelope. In shLMNB1 nuclei, these clusters were smaller in size and density compared to those in control nuclei.

An alternative segmentation method was applied to complement these data. The Voronoi analysis allows the segmentation of points without the choice of parameters that would define clusters. This avoids a bias towards known structures. For each locus, an inverted area was calculated that gives a measure for the point's density with respect to its surrounding points. The absolute SMP Voronoi density distributions of LaminB1 in units of [1 nm⁻²] (Fig. 6a) show that control samples have higher densities than shLMNB1 samples. These calculated densities were normalized to account for the varying number of localizations in each nucleus (Fig. 6b) and still show a clear difference between control and shLMNB1 density distributions. To expand the analysis and additionally reveal density differences between the nuclear periphery and interior, the Voronoi densities were plotted as a function of nuclear radius (Fig. 6c and d). Here, a radius of zero corresponds to the center of mass of the nucleus. We see that in control nuclei (Fig. 6c), densities of highest probability (shown with the colorbar) are in close proximity to the nuclear periphery. In comparison, for shLMNB1 nuclei the densities with highest probability are further away from the maximal radius value (Fig. 6d).

Fig. 6 Voronoi analysis of LaminB1 for control and shLMNB1 nuclei. The absolute SMP (a) and normalized (b) Voronoi density distributions are plotted as histograms. The bold curves show the distribution considering all measurements and the faint curves show the individual measurements of 37 control and shLMNB1 nuclei each. The radial density distributions of control (c) and shLMNB1 nuclei (d) are shown, considering localizations from all measurements. Each point represents one localization with its radial position and Voronoi density.

The Voronoi density distribution of γH2AX on the other hand shows a bimodal distribution (Fig. 7a and b). This could indicate a strong segregation between two densities: the very high-density γH2AX foci and the low-density background consisting of individual localizations. The smaller, high-density peak (Fig. 7a and b) reaches higher probabilities for shLMNB1 nuclei. This shows the increased probability of clustering. The radial density distributions (Fig. 7c and d) visualize the radial position of these high-density foci. As shown in Fig. 7b, the high-density γH2AX foci have a normalized Voronoi density value of about −6 log(1 nm⁻²). The corresponding radius for this value is 3–5 μm for control nuclei and 5–6 μm for shLMNB1 nuclei. This means that in both cell types the high-density foci seem to be situated closer to the nuclear periphery than the low-density γH2AX background signals.

Fig. 7 Voronoi density distributions of γH2AX for control and shLMNB1 nuclei. The difference is shown between the absolute SMP (a) and normalized (b) Voronoi densities. The bold curves show the distribution considering all measurements and the faint curves show the individual measurements of 37 control and shLMNB1 nuclei each. The normalized radial distribution of Voronoi densities is shown for control (c) and shLMNB1 (d) nuclei.

The density distributions of heterochromatin in control and shLMNB1 nuclei are almost identical after normalization (Fig. 8a and b). This is not surprising since cluster analysis showed that only a small percentage of the total H3K9me3 signal is arranged in clusters (data not shown), which means that the rest of the signal is the main contributor to the distribution. This rest of the signal is of similar density in control and shLMNB1 nuclei and therefore the distributions are very similar. Nonetheless, the shLMNB1 distribution is slightly shifted to higher densities, even after normalization. The radial density distributions in Fig. 8c and d show that at larger radii (4–6 μm) there is an increased probability of clustering. For control nuclei, this probability is increased compared to shLMNB1 nuclei. Despite the shLMNB1 nuclei being bigger in size, the highest probability for clustering is also at radii of 4–6 μm, as in the case of control nuclei. This shows that these clusters are situated further away from the nuclear periphery than the clusters in control nuclei.

Fig. 8 Voronoi density distributions of H3K9me3 for control and shLMNB1 nuclei. The difference is shown between the absolute SMP (a) and normalized (b) Voronoi densities. The bold curves show the distribution considering all measurements and the faint curves show the individual measurements of 37 control and 45 shLMNB1 nuclei each. The normalized radial distribution of Voronoi densities is shown for control (c) and shLMNB1 (d) nuclei.

Additionally, we compared the heterochromatin data with Voronoi density distributions of Sytox Orange (Fig. 9a and b).

Fig. 9 Voronoi density analysis of various DNA labeling techniques. The absolute SMP (a) and normalized (b) Voronoi density distributions of heterochromatin and Sytox Orange are compared, with Sytox Orange imaged with and without ProLong Gold and considering many (250 000) or few (10 000) imaging frames. Sytox Orange and ProLong Gold are abbreviated with SO and PG, respectively. The corresponding radial Voronoi density distributions are shown for Sytox Orange with ProLong Gold in control (c) and shLMNB1 nuclei (d), Sytox Orange without ProLong Gold considering 10 000 frames in control (e) and shLMNB1 nuclei (f), and considering 250 000 frames in control (g) and shLMNB1 nuclei (h). Plot (c) considers 4 nuclei, (d) 8 nuclei and (e)–(h) 1 nucleus.

Here, we differentiated between probes prepared with and without ProLong Gold. Without ProLong Gold, we also compared densities obtained from 10 000 and 250 000 frames. We observed a difference between all control and shLMNB1 pairs shown in Fig. 9a and b. The shLMNB1 curves (Fig. 9a and b) have peaks that are always shifted towards higher Voronoi densities compared to the control curve. All normalized plots peak at a Voronoi density value of about −8 log(1 nm⁻²) with the exception of Sytox Orange samples without ProLong Gold obtained from 10 000 frames. The latter plots peak at Voronoi density values of about −7 log(1 nm⁻²). This change in density agrees with what we observed from the images (Fig. 11, compare 10 000 with 250 000 frames). When considering only the first 10 000 frames we could see a larger amount of high-density localizations as compared to the more homogeneously distributed localizations (250 000 frames). The curves are all nearly Gaussian in shape, except for Sytox Orange with ProLong Gold (control). However, the additional bumps in this curve (Fig. 9a and b) are not present in every nucleus and arise from a superposition of the relatively diverse control measurements. Since there were only 4 control measurements, these differences between measurements did not get averaged out.

The radial density distributions of Sytox Orange are shown in Fig. 9c–h. Comparing the previously shown heterochromatin radial density distribution (Fig. 8c and d) to all Sytox Orange distributions (Fig. 9c–h), we see that heterochromatin resembles the distribution of Sytox Orange with ProLong Gold (Fig. 9c and d) the most. This is because they both have a homogeneously smeared distribution. In contrast, Sytox Orange imaged without ProLong Gold (Fig. 9e–h) shows distinct radial regions with an increased density. The regions are more discrete if considering only the first 10 000 (Fig. 9e and f) versus 250 000 frames (Fig. 9g and h).

3.5 Line profile analysis

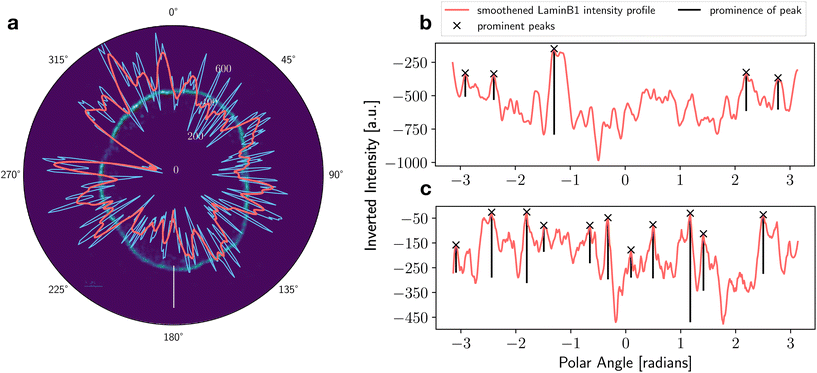
The density distribution of LaminB1 was also studied as a line profile along the nuclear periphery to visualize disruptions within the LaminB1-labelled nuclear lamina. Previous studies demonstrated that γH2AX foci occur in significantly higher numbers and more often in shLMNB1 nuclei than in control nuclei.²¹ The radial Voronoi analysis (Fig. 7c and d) showed that γH2AX clusters occur with increased probability at the nuclear periphery for both cell types. However, colocalization analysis of all LaminB1 and γH2AX localizations in the nucleus (data not shown) revealed a random correlation of γH2AX to LaminB1. One possible explanation for this surprising result, that γH2AX occurs in high numbers at the nuclear periphery, but is not correlated with LaminB1, could be that γH2AX clusters occur in LaminB1 gaps. These observations suggest that, in order to investigate the correlation of γH2AX positioning in the nucleus to the occurrence of LaminB1, we must first investigate and quantify the presence of gaps in the LaminB1-labelled nuclear lamina.

The calculated intensity of the LaminB1 line is shown exemplary for a control nucleus in Fig. 10a. We see that the original profile (plotted in blue) shows regular interruptions. These fluctuations can be magnified by selecting a smaller dθ to increase the angular resolution. Unfortunately, increasing angular resolution also increases the noise. Hence, the choice of dθ and the additional smoothening was guided by the goal to achieve LaminB1 intensities that match the visible gaps. To further quantify the occurrence of gaps in the LaminB1 line, a data processing method that selects the intensity minima (the gaps) was applied. The peaks were inverted and selected based on a combination of their prominence (prominence >100) and their height (height >−400). Fig. 10b and c show the LaminB1 line profile of a control and a shLMNB1 nucleus, respectively. The peaks marked with a cross denote LaminB1 gaps that fit the selection criteria.

Fig. 10 Line profile analysis for quantifying LaminB1 gaps. The LaminB1 intensity profile is plotted in a polar plot and overlayed with the original density image of LaminB1 in an exemplary control nucleus (a). The original intensity profile is plotted in blue, and the smoothened profile in red. For further analysis, the smoothened LaminB1 intensity profile is inverted (b and c). Inverted intensity profiles are shown for the control nucleus (b) and for a shLMNB1 nucleus (c). Peaks in the profile denote LaminB1 gaps and their prominence is used as a measure to quantify LaminB1 gaps. The peaks that fit the selection criteria are marked with a black cross. Their corresponding prominence is shown by the black line.

3.6 Long acquisition of Sytox Orange without ProLong Gold

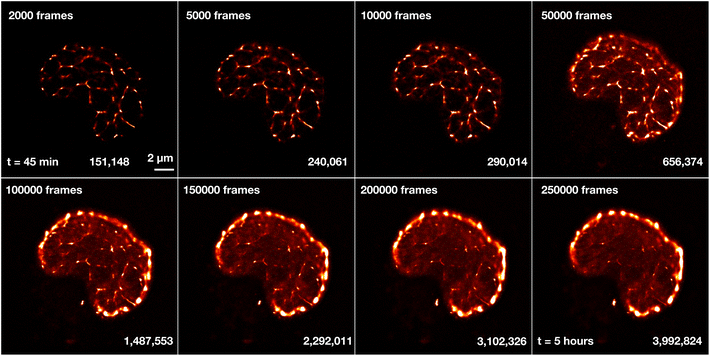
As a reference to the dual-color images of Sytox Orange imaged in ProLong Gold, we also imaged Sytox Orange without ProLong Gold. A single nucleus was measured over the course of several hours to investigate the limits of the fBALM method and its time dependency (Fig. 11). A higher number of frames leads to a higher number of localizations and results in higher structural resolution images. However, this also requires longer acquisition times in which the chemical environment is changing.

Fig. 11 Reconstructed images of Sytox Orange for different number of imaging frames. A shLMNB1 nucleus was measured in fBALM buffer (without ProLong Gold). The measurement started 45 min and ended 5 hours after fBALM buffer was added. The number of frames and the number of localizations are displayed next to each snapshot image. For reference, the time at 50 000 frames corresponds approximately to t = 1.5 h. All images are displayed on the same scale and the scale bar shown next to the first image corresponds to 2 μm. In all the images a drift correction using cross-correlation and merging of molecules was applied after detection of localizations in ThunderSTORM.

Fig. 11 shows reconstructed images of Sytox Orange for different numbers of imaging frames, demonstrating a significant change in structural details during long acquisition times. For better visualization of intensity and density differences without enhancing or suppressing signals in a non-linear way, the perceptually uniform Lookup Table “CET-L3” was applied.⁵⁴ Using localizations from only the first 2000–50 000 frames, a network-like structure was reconstructed. But 3 hours (100 000 frames) after applying the fBALM buffer, the structure changed. The intensity around the nuclear periphery increased while in the nuclear interior the intensity distribution became more homogeneous, albeit with small remaining condensed regions.

To study the origin and properties of the high-intensity periphery and the small condensed clusters, we examined the localization precisions, σ_loc. The distribution of the precisions as a function of their frequency (Fig. 12a) identified localizations with higher and lower precisions. We separated the distribution at σ_loc = 12 nm and reconstructed images using only localizations with σ_loc > 12 nm or only with σ_loc < 12 nm. This filtering of localizations was performed for the two different structures, at 50 000 (Fig. 12c) and 250 000 frames (Fig. 12d). Looking only at high localization precision data (σ_loc < 12 nm), a large amount of signal inside the nucleus is filtered out (Fig. 12g and h). What remains are the Sytox Orange molecules at the periphery and small clusters inside the nucleus. When considering the first 50 000 frames (Fig. 12g), some non-clustered signals remain in the nucleus, causing a homogeneous background. However, when considering 250 000 frames (Fig. 12h), high localization precision data give an image that consists almost only of the peripheral outline and the condensed regions. The lower precision data set (σ_loc > 12 nm) shows less contrast between the peripheral and interior Sytox Orange (Fig. 12e and f). Instead, additional localizations making up the network-like structure are visible.

Fig. 12 Filtering of localizations based on localization precision. The normalized localization precision distribution changes with frame number (a) but always has at least one peak below 12 nm and a broader peak above 12 nm. The shLMNB1 nucleus was imaged in fBALM buffer (without ProLong Gold) (c–h). For comparison, filtering was performed both on an image constructed from 50 000 frames and from 250 000 frames. The corresponding number of localizations is listed for both cases. Images of the category “all σ_loc” include all signals with all localization precisions (c and d). Images of the category “σ_loc > 12 nm” (e and f) and “σ_loc < 12 nm” (g and h) are filtered by only considering localizations with a precision higher or lower than 12 nm. The intensity of the localizations from these categories are shown in the photon number distribution for 250 000 frames (b).

As a measure to determine the amount of bound Sytox Orange molecules in the DNA giving rise to the strong signals seen in σ_loc < 12 nm, the number of emitted photons per localization was considered. For 250 000 frames, the high precision image had a 2.7 times higher mean number of photons than the unfiltered image (Fig. 12b). The same analysis was done also for a control nucleus. In this case, the 250 000 framed image had 5.6 times higher intensity than the unfiltered image.

4. Discussion

Precise chromatin labeling poses a major obstacle in super-resolution microscopy. Recently, a new SMLM technique called fBALM was developed, which is based on the temporary fluorescence emission of DNA-binding dyes in presence of DNA undergoing structure fluctuations in decreased pH. Since the fBALM method relies on the binding mechanisms and not on the photophysics of the dye, DNA dyes with the most advantageous properties (such as Sytox Orange) can be used. However, the major limitation of the fBALM method is the requirement of low pH. In contrast, standard photoswitchable dyes operate best at neutral pH. Hence, since the two methods require different pH environments, we aimed to address the challenge of working with both dyes within one sample. Here, we developed and demonstrated a stable methodological sequence that allows the combination of imaging genomic DNA at enhanced resolution with the fBALM method and imaging an immunofluorescently labeled nuclear lamina protein, LaminB1. Dual-color SMLM was achieved by embedding samples in ProLong Gold prior to fBALM buffer application, optimizing the imaging protocol to achieve maximal amount of blinking events in both channels, and applying drift correction to rectify drift caused by the necessary waiting time between imaging both channels.

Due to the gradual decrease in pH over a period of a few hours, the instabilities caused to the double-stranded DNA structure were only slowly introduced and hence did not substantially change the native chromatin configuration.⁴³ Besides LaminB1 staining, the same methodology can be applied to image any other immunofluorescently labeled protein in the nucleus to study its association to DNA. In addition to the fBALM experiments with ProLong Gold, Sytox Orange was also imaged without ProLong Gold. In both experiments, an average localization precision of 23 nm was achieved in the first 2000 frames. But without ProLong Gold, a stronger blinking behavior was observed which led to a higher number of localizations and thus additional structural detail. When imaged over a longer period of time, the number of detected localizations remained stable with time and allowed the detection of almost 4 million localizations in a single nucleus. Due to the stochastic reconstruction, it is clear that first the densest regions become prominent and gradually the less dense regions do, too. We observed this as a modification of the fBALM image after about 50 000 frames. However, the possibility that further modifications were caused by small changes in the nanostructure of the nucleus due to prolonged exposure to the low pH environment cannot be excluded.

Further, we investigated the kinetics of the denaturation and renaturation process of the DNA during fBALM by studying the localization precision. An ideally precise localization of a single emitter would require the detection of an infinite number of photons with no photonic background. By differentiating between lower and higher precisions, a separation between higher and lower fluorescence intensity localizations was achieved. Localizations with a high number of photons translate to renatured DNA sections in which a high amount of Sytox Orange molecules were bound. This could mean that these renatured sections were longer (consisted of more base pairs) compared to others. The longer renatured sections seemed to be about 3–6 times longer than the average length of a renatured DNA section.

We observed an enhanced localization precision in dense chromatin clusters, which has been observed in other cell types using fBALM and Sytox Orange as well.⁴⁵ Interestingly, using only the signals with enhanced localization precision (σ_loc < 12 nm) and using a large signal number, the peripheral heterochromatin was exceptionally well highlighted, with a number of clear gaps of much lower signal density.

Several quantitative analyses were applied to the data. The cluster analysis revealed that H3K9me3 signals in shLMNB1 nuclei were found with higher frequency in clusters than in control nuclei. However, this only showed a global picture, without revealing structural differences between the nuclear periphery and interior. The radial organization was therefore analyzed with alternative methods such as the Voronoi density analysis and the line profile analysis. The Voronoi analysis proved to be a good alternative to the cluster analysis, as it was able to segregate high-density clusters from background signals without the use of cluster parameters. γH2AX clusters were shown to occur with increased probability at the nuclear periphery for both cell types. However, colocalization analysis revealed a random correlation of γH2AX to LaminB1, which gave rise to the hypothesis that the clusters occur in LaminB1 gaps. A line profile analysis was developed which could be used to investigate this question in future studies. The radial distribution of heterochromatin showed that after LaminB1 knockdown, heterochromatin loses its concentration at the periphery. This observation agrees with previous studies.^55,56 Colocalization analysis between DNA and LaminB1 showed a strong anti-correlation. A more pronounced anti-correlation was observed in LaminB1-depleted nuclei. Nearest neighbor distances were also larger in shLMNB1 nuclei.

The analysis showed changes in the distribution of relevant proteins (γH2AX and LaminB1), as well as the compaction of DNA after LaminB1 depletion. The fBALM method with simultaneous imaging of immunofluorescently labeled proteins was successfully implemented. In combination with the appropriate analysis tools presented here, this provides the means to answer biological questions about DNA–protein association and compaction. Further elucidating the correlation between functional pathways and chromatin architecture in cells responding to environmental influences will be a future challenge.^3,57

Author contributions

Conceptualization, V. W., M. H. and C. C.; methodology, K. C., M. G., M. H. and C. C.; measurement and validation, K. C.; formal analysis, K. C.; specimen preparation, F. F.; resources, M. G., M. H. and C. C.; data curation, K. C.; writing—original draft preparation, K. C.; writing—review and editing, C. C. and M. H.; visualization, K. C.; supervision, M. H.; project administration, M. H.; all authors have read and agreed to the published version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Felix Bestvater, German Cancer Research Center (DKFZ), Heidelberg, for instrumental support and stimulating discussions. We also thank Margund Bach, David Ridinger, Ruth Winter, Arslan Saleem, Wladimir Schaufler and Kim Küntzelmann for experimental advice and support and Jan Neumann, Ole Kröger and Filip Sadlo for support in data analysis tools. Parts of the work were supported by grant (FKZ 02NUK058A) of the German Federal Ministry of Education and Research (BMBF) and grant 19001 of Blood Cancer UK.

References

1. T. Cremer, M. Cremer and C. Cremer, Biochemistry, 2018, 83, 313–325.
2. J. Krigerts, K. Salmina, T. Freivalds, P. Zayakin, F. Rumnieks, I. Inashkina, A. Giuliani, M. Hausmann and J. Erenpreisa, Biophys. J., 2021, 120, 711–724.
3. J. Erenpreisa, J. Krigerts, K. Salmina, B. I. Gerashchenko, T. Freivalds, R. Kurg, R. Winter, M. Krufczik, P. Zayakin, M. Hausmann and A. Giuliani, Cells, 2021, 10, 1582.
4. M. Hausmann, J.-H. Lee and G. Hildenbrand, Epigenetics Methods, Academic Press, 2020, vol. 18, pp. 399–418.
5. T. Cremer and C. Cremer, Eur. J. Histochem., 2006, 50, 161–176.
6. T. Cremer and C. Cremer, Eur. J. Histochem., 2006, 50, 177–222.
7. T. Cremer and C. Cremer, Eur. J. Histochem., 2006, 50, 223–272.
8. L. Manuelidis, Hum. Genet., 1985, 71, 288–293.
9. C. Lanctôt, T. Cheutin, M. Cremer, G. Cavalli and T. Cremer, Dynamic genome architecture in the nuclear space: Regulation of gene expression in three dimensions, 2007.
10. A. Bolzer, G. Kreth, I. Solovei, D. Koehler, K. Saracoglu, C. Fauth, S. Müller, R. Eils, C. Cremer, M. R. Speicher and T. Cremer, PLoS Biol., 2005, 3, 0826–0842.
11. T. Cremer and C. Cremer, Nat. Rev. Genet., 2001, 2, 292–301.
12. T. Cremer, M. Cremer, B. Hübner, H. Strickfaden, D. Smeets, J. Popken, M. Sterr, Y. Markaki, K. Rippe and C. Cremer, FEBS Lett., 2015, 589, 2931–2943.
13. W. F. Marshall, A. F. Dernburg, B. Harmon, D. A. Agard and J. W. Sedat, Mol. Biol. Cell, 1996, 7, 825–842.
14. B. van Steensel and A. S. Belmont, Cell, 2017, 169, 780–791.
15. L. Guelen, L. Pagie, E. Brasset, W. Meuleman, M. B. Faza, W. Talhout, B. H. Eussen, A. De Klein, L. Wessels, W. De Laat and B. Van Steensel, Nature, 2008, 453, 948–951.
16. K. M. Sakthivel and P. Sehgal, Oncol. Rev., 2016, 10, 65–71.
17. C. Denais and J. Lammerding, Cancer biology and the nuclear envelope, advances in experimental medicine and biology, Springer, New York, 2014, pp. 435–470.
18. C. Evangelisti, I. Rusciano, S. Mongiorgi, G. Ramazzotti, G. Lattanzi, L. Manzoli, L. Cocco and S. Ratti, Cell. Mol. Life Sci., 2022, 79, 1–11.
19. K. L. Reddy, J. M. Zullo, E. Bertolino and H. Singh, Nature, 2008, 452, 243–247.
20. L. Pascual-Reguant, E. Blanco, S. Galan, F. Le Dily, Y. Cuartero, G. Serra-Bardenys, V. Di Carlo, A. Iturbide, J. P. Cebrià-Costa, L. Nonell, A. G. de Herreros, L. Di Croce, M. A. Marti-Renom and S. Peiró, Nat. Commun., 2018, 9, 3420.
21. V. Butin-Israeli, S. A. Adam, N. Jain, G. L. Otte, D. Neems, L. Wiesmüller, S. L. Berger and R. D. Goldman, Mol. Cell. Biol., 2015, 35, 884–898.
22. L. Etourneaud, A. Moussa, E. Rass, D. Genet, S. Willaume, C. Chabance-Okumura, P. Wanschoor, J. Picotto, B. Thézé, J. Dépagne, X. Veaute, E. Dizet, D. Busso, A. Barascu, L. Irbah, T. Kortulewski, A. Campalans, C. Le Chalony, S. Zinn-Justin, R. Scully, G. Pennarun and P. Bertrand, Sci. Adv., 2021, 7, 1–18.
23. M. Kittisopikul, L. Virtanen, P. Taimen and R. D. Goldman, Cells, 2019, 8, 361.
24. D. Varga, H. Majoros, Z. Ujfaludi, M. Erdélyi and T. Pankotai, Nanoscale, 2019, 11, 14226–14236.
25. M. Hausmann, E. Wagner, J. H. Lee, G. Schrock, W. Schaufler, M. Krufczik, F. Papenfuß, M. Port, F. Bestvater and H. Scherthan, Nanoscale, 2018, 10, 4320–4331.
26. C. Cremer, R. Kaufmann, M. Gunkel, S. Pres, Y. Weiland, P. Müller, T. Ruckelshausen, P. Lemmer, F. Geiger, S. Degenhard, C. Wege, N. A. Lemmermann, R. Holtappels, H. Strickfaden and M. Hausmann, Biotechnol. J., 2011, 6, 1037–1051.
27. C. Cremer and B. R. Masters, Eur. Phys. J. H, 2013, 38, 281–344.
28. M. Lelek, M. T. Gyparaki, G. Beliu, F. Schueder, J. Griffié, S. Manley, R. Jungmann, M. Sauer, M. Lakadamyali and C. Zimmer, Nat. Rev. Methods Primers, 2021, 1, 1–27.
29. P. Lemmer, M. Gunkel, D. Baddeley, R. Kaufmann, A. Urich, Y. Weiland, J. Reymann, P. Müller, M. Hausmann and C. Cremer, Appl. Phys. B: Lasers Opt., 2008, 93, 1–12.
30. P. Lemmer, M. Gunkel, Y. Weiland, P. Müller, D. Baddeley, R. Kaufmann, A. Urich, H. Eipel, R. Amberger, M. Hausmann and C. Cremer, J. Microsc., 2009, 235, 163–171.
31. D. Sinnecker, P. Voigt, N. Hellwig and M. Schaefer, Biochemistry, 2005, 44, 7085–7097.
32. J. Hendrix, C. Flors, P. Dedecker, J. Hofkens and Y. Engelborghs, Biophys. J., 2008, 94, 4103–4113.
33. J. P. Eberle, A. Rapp, M. Krufczik, M. Eryilmaz, M. Gunkel, H. Erfle and M. Hausmann, Methods in Molecular Biology, 2017, vol. 1663, pp. 1–13.
34. J. Popken, A. Graf, S. Krebs, H. Blum, V. J. Schmid, A. Strauss, T. Guengoer, V. Zakhartchenko, E. Wolf and T. Cremer, PLoS One, 2015, 10, 1–22.
35. I. Kirmes, A. Szczurek, K. Prakash, I. Charapitsa, C. Heiser, M. Musheev, F. Schock, K. Fornalczyk, D. Ma, U. Birk, C. Cremer and G. Reid, Genome Biol., 2015, 16, 1–19.
36. F. Lang, M. F. Contreras-Gerenas, M. Gelléri, J. Neumann, O. Kröger, F. Sadlo, K. Berniak, A. Marx, C. Cremer, H. A. Wagenknecht and H. Allgayer, Cancers, 2021, 13, 1–22.
37. M. Vancurova, H. Hanzlikova, L. Knoblochova, J. Kosla, D. Majera, M. Mistrik, K. Burdova, Z. Hodny and J. Bartek, DNA Repair, 2019, 78, 114–127.
38. K. Günther, M. Mertig and R. Seidel, Nucleic Acids Res., 2010, 38, 6526–6532.
39. A. Bancaud, S. Huet, N. Daigle, J. Mozziconacci, J. Beaudouin and J. Ellenberg, EMBO J., 2009, 28, 3785–3798.
40. D. Zurek-Biesiada, A. T. Szczurek, K. Prakash, G. K. Mohana, H. K. Lee, J. Y. Roignant, U. J. Birk, J. W. Dobrucki and C. Cremer, Exp. Cell Res., 2016, 343, 97–106.
41. X. Yan, R. C. Habbersett, T. M. Yoshida, J. P. Nolan, J. H. Jett and B. L. Marrone, Anal. Chem., 2005, 77, 3554–3562.
42. X. Yan, R. C. Habbersett, J. M. Cordek, J. P. Nolan, T. M. Yoshida, J. H. Jett and B. L. Marrone, Anal. Biochem., 2000, 286, 138–148.
43. A. Szczurek, L. Klewes, J. Xing, A. Gourram, U. Birk, H. Knecht, J. W. Dobrucki, S. Mai and C. Cremer, Nucleic Acids Res., 2017, 45, 1–11.
44. A. Szczurek, U. Birk, H. Knecht, J. Dobrucki, S. Mai and C. Cremer, Nucleus, 2018, 9, 182–189.
45. M. Gelléri, S.-Y. Chen, A. Szczurek, B. Hübner, M. Sterr, J. Neumann, O. Kröger, F. Sadlo, J. Imhoff, Y. Markaki, M. J. Hendzel, M. Cremer, T. Cremer, H. Strickfaden and C. Cremer, bioRxiv, 2022, preprint, bioRxiv:2022.03.23.485308,  DOI:10.1101/2022.03.23.485308.
46. T. Klymenko, J. Bloehdorn, J. Bahlo, S. Robrecht, G. Akylzhanova, K. Cox, S. Estenfelder, J. Wang, J. Edelmann, J. C. Strefford, T. K. Wojdacz, K. Fischer, M. Hallek, S. Stilgenbauer, M. Cragg, J. Gribben and A. Braun, Leukemia, 2018, 32, 364–375.
47. M. Krufczik, A. Sievers, A. Hausmann, J. H. Lee, G. Hildenbrand, W. Schaufler and M. Hausmann, Int. J. Mol. Sci., 2017, 18, 1–16.
48. W. Schaufler, Ph.D. thesis, Karlsruhe Institute of Technology, 2017.
49. F. Grüll, M. Kirchgessner, R. Kaufmann, M. Hausmann and U. Kebschull, 21st International Conference on Field Programmable Logic and Applications, 2011, pp. 1–5.
50. M. Ovesný, P. Křížek, J. Borkovec, Z. Švindrych and G. M. Hagen, Bioinformatics, 2014, 30, 2389–2390.
51. M. Hausmann, N. Ilić, G. Pilarczyk, J. H. Lee, A. Logeswaran, A. P. Borroni, M. Krufczik, F. Theda, N. Waltrich, F. Bestvater, G. Hildenbrand, C. Cremer and M. Blank, Int. J. Mol. Sci., 2017, 18, 1–21.
52. S. Malkusch, U. Endesfelder, J. Mondry, M. Gelléri, P. J. Verveer and M. Heilemann, Histochem. Cell Biol., 2012, 137, 1–10.
53. M. Ester, H.-P. Kriegel, J. Sander and X. Xu, Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining, 1996, pp. 226–231.
54. P. Kovesi, arXiv, 2015, preprint, arXiv:1509.03700v1, https://arxiv.org/abs/1509.03700.
55. M. Sadaie, R. Salama, T. Carroll, K. Tomimatsu, T. Chandra, A. R. Young, M. Narita, P. A. Pérez-Mancera, D. C. Bennett, H. Chong, H. Kimura and M. Narita, Genes Dev., 2013, 27, 1800–1808.
56. A. Reilly, J. P. Creamer, S. Stewart, M. Stolla, Y. Wang, J. Du, R. Wellington, S. Busch, E. Estey, P. Becker, M. Fang, S. Keel, J. Abkowitz, L. Soma, J. Ma, Z. Duan and S. Doulatov, Cell Stem Cell, 2022, 29, 577–592.
57. Nuclear, Chromosomal, and Genomic Architecture in Biology and Medicine, ed. M. Hausmann, G. Hildenbrand and G. Pilarczyk, M. Kloc and J. Z. Kubiak, Springer, 2022.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr02684h

‡ These authors contributed equally as first authors.

§ These authors contributed equally as last authors.

---