 Open Access Article
Open Access ArticleKinetic and thermodynamic sorption studies of Fe(III) and Zr(IV) by DFO@Purolite, a desferrioxamine B based chelating resin†
Giancarla
Alberti
 *a,
Camilla
Zanoni
a,
Vittorio
Losi
a,
Sara
Rovertoni
a,
Lisa Rita
Magnaghi
*a,
Camilla
Zanoni
a,
Vittorio
Losi
a,
Sara
Rovertoni
a,
Lisa Rita
Magnaghi
 a,
Osian
Fonquernie
b,
Stéphane
Brandès
b,
Agnese
Amati
c,
Jean-Claude
Chambron
a,
Osian
Fonquernie
b,
Stéphane
Brandès
b,
Agnese
Amati
c,
Jean-Claude
Chambron
 c,
Nicolas
Maudoux
d,
Raffaela
Biesuz
c,
Nicolas
Maudoux
d,
Raffaela
Biesuz
 a and
Michel
Meyer
a and
Michel
Meyer
 *b
*b
aDipartimento di Chimica – Università degli Studi di Pavia, via Taramelli 12, 27100 Pavia, Italy. E-mail: galberti@unipv.it
bInstitut de Chimie Moléculaire de l’Université de Bourgogne (ICMUB), UMR 6302, CNRS, Université de Bourgogne, 9 avenue Alain Savary, BP 47870, 21078 Dijon Cedex, France. E-mail: michel.meyer@u-bourgogne.fr
cInstitut de Chimie de Strasbourg, UMR 7177, CNRS, Université de Strasbourg, 1 rue Blaise Pascal, BP 296 R 8, 67008 Strasbourg Cedex, France
dTrisKem International, 3 rue des Champs Géons, ZAC de l’Éperon, 35170 Bruz, France
First published on 12th June 2023
Abstract
This paper presents the characterization of a novel solid-phase sorbent for iron(III) and zirconium(IV) obtained by the functionalization of a commercial epoxy methacrylate resin (Purolite® ECR8209) with desferrioxamine B (DFO). The sorption properties of the solid material, named DFO@Purolite, towards Fe(III) and Zr(IV) were investigated in detail. In particular, the sorption kinetics, isotherms and sorption profiles as a function of the solution's pH were studied. The stoichiometry and the complexation constants of both cations with the active sites of the sorbent were determined by applying the Gibbs–Donnan model, i.e., the model used to explain the protonation and the metal sorption on ion exchange resins. While the chelating properties of the solid material investigated herein are in good agreement with those of Fe(III)/DFO and Zr(IV)/DFO previously determined in homogeneous aqueous solutions, the solid/liquid extraction studies further allow to ascertain the speciation model for the latter system that is still subjected to controversy in the literature.
Introduction
Iron is one of the most abundant metals on earth, and it plays an important role in human metabolism since it is involved in essential mechanisms such as the oxygen transport system, the electron transfer chain (respiration), and enzymatic reactions.1 In blood, iron is mostly bound to proteins, named ferritin and transferrin, and its presence has to be strictly regulated, as either deficiencies or overloads can induce various biological disorders. Iron overload promotes the generation of harmful hydroxyl free radicals, while low iron(III) levels result in reduced concentrations in hemoglobin and generate pathologies like thrombocytosis or hypoxia. Frequently transfused patients accumulate iron, especially in the liver, because there is no efficient elimination mechanism for iron in the human body.1 To overcome this problem, patients who receive transfusions also undergo iron-chelation therapy. This treatment maintains a correct Fe(III) level in the organism by using a specific drug that forms a highly-stable and easily eliminated iron(III) complex.2 The classical drug employed in iron or aluminium chelation therapy is the mesylate salt of desferrioxamine B (DFO), commercialised under the trade name Desferal®. DFO (Fig. 1) is a linear trihydroxamic bacterial siderophore produced by Streptomyces strains.3Recently, the chemistry of Zr(IV) has raised interest since the 89Zr4+ radioisotope can be proficiently employed for positron emission tomography (PET), a non-invasive molecular imaging diagnostic method that provides quantitative physiological data. To prevent free radionuclide accumulation in living tissues and bones after delivery of the 89Zr-based agents, it is necessary to chelate the radioisotope with a high-affinity and selective ligand that, moreover, exhibits fast binding kinetics. The ligand should also be biocompatible and able to complex the radioisotope even at very low concentration levels, typically lower than 100 nM.4,5 Desferrioxamine B, the above-cited Fe(III) ligand employed in chelating therapy, fulfils these criteria pretty well and has so far been used in clinical trials.6 Unfortunately, DFO-based drugs also have a number of drawbacks. They are not orally active and have to be injected intramuscularly; long-term treatments cause damage and depletion of essential transition metals when not bound to iron(III), while the in vivo affinity for 89Zr(IV) is not high enough to prevent partial dissociation of the complex, the release of radioactive zirconium in the bloodstream and its ultimate bone accumulation. These reasons lead to the development and research of new drugs for chelation therapy or imaging applications.7–9
Moreover, DFO's complexation ability can be efficiently exploited in other research fields, especially for developing metal ion sensors.10 Several studies reported desferrioxamine B-based optical and electrochemical sensors for probing but also quantifying different cations, such as Fe(III), V(V), or Ga(III), in various aqueous media.11–23 The successful implementation of DFO in practical analytical devices rests on its high affinity for hard Lewis acid cations, on the appearance of rather intense charge-transfer absorption bands in the visible range upon complex formation with ions like Fe3+ or UO22+,24 but also on the ease to immobilize the chelator on a surface or to incorporate it into a solid matrix.25,26 Thanks to the terminal primary amino group of DFO, several strategies have been proposed to functionalize different solid supports, such as nylon,27 cellulose,11,18,28 sepharose,29 acrylate polymers,30,31 or silica-based materials.12,13,16,17,20,32
This paper presents the sorption properties of a novel DFO-based resin towards Fe(III) and Zr(IV). The sorbent coined DFO@Purolite, was obtained by grafting DFO on the beads of the commercially available Epoxy Purolite® resin. The sorption properties of the solid material towards Fe(III) and Zr(IV) have been investigated in detail. In particular, sorption kinetics, isotherms, and sorption profiles were studied as a function of the solution's pH. The stoichiometry and the complexation constants of both cations with the active sites of the DFO@Purolite were determined by applying the Gibbs–Donnan model, i.e., the model we have used in the past to analyse the protonation and the metal sorption properties of various chelating resins.33–35
As shown hereafter, this approach also offers an appealing alternative to the classical potentiometric and/or spectrophotometric titration methods for unravelling the complex formation equilibria of unbound DFO in homogeneous aqueous media. Despite the medical relevance of the Zr4+/DFO3− system,4,5,7,8 the first reports on the coordination chemistry in aqueous solutions date back to 2019, but no consensus has been reached so far regarding the number, stoichiometry, and stability of the complexes formed at equilibrium in water over a wide pH range.36–39 This situation prompted us to focus herein on two cations, Fe3+ and Zr4+, in an attempt to shine new light on the conflicting results appearing in the literature for the latter cation.
Moreover, the luminescence properties of the terbium-loaded resin were investigated to check the feasibility of applying biphotonic microscopy for imaging the DFO distribution throughout the beads and to ascertain the uniform grafting of the chelator both in the core and on the outer surface.
The Gibbs–Donnan model
The thermodynamic model is based on the Gibbs–Donnan description of ion exchange and complexing resins.34,35,40,41 The resin is represented as a concentrated solution phase, separated from the bulk solution by an interface through which water, neutral molecules, and ions can diffuse, whereas the active groups, permanently linked to the resin, cannot. Due to the different mobilities of ions, a potential difference occurs at the interface, named Donnan potential.42 Accordingly, for each couple of ions diffusing through the interface, the following equations hold at equilibrium. | (1) |
In eqn (1), ai stands for the activity of the species i and the overbar (here and throughout the text) represents a species in the solid phase. The activity of any ion inside the resin cannot be measured, but it can be evaluated from eqn (1), which is the basis for the model.
The sorption experiments are carried out by equilibrating a given mass of solid phase with a metal salt solution, ensuring that the active sites of the sorbent are always in large excess with respect to the targeted metal ion. Under these conditions, it can be assumed that any process other than the formation of complexes in the resin phase is negligible and that the concentration of active sites does not depend on the concentration of the complexes formed.34,35,40,41
The general exchange equilibrium is given by eqn (2), where charges are omitted for the sake of clarity.
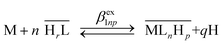 | (2) |
The corresponding conditional biphasic exchange coefficient βex1np is defined by eqn (3).
 | (3) |
By combining eqn (1) and (3), exchange coefficients (βex1np) can be expressed according to eqn (4) as a function of the corresponding intrinsic complexation constants (βi1np) that are independent of the solution composition.34,35,40,41 While characterising surface complex formation equilibria with a bound ligand, they can be directly compared with the thermodynamic equilibrium constants in aqueous phase (βo1np) corresponding to the reaction of the metal ion with the unbound or free analogue of the functional group/chelator L immobilized in the resin.
 | (4) |
In eqn (4), m is the charge of the metal ion, and γi is the activity coefficient of the species i. C is the counter-ion of the active sites of the resin (here considered as monovalent); for a cation-exchange chelating resin, C is a cation. The counter-ion concentration in the resin phase can be determined experimentally or calculated by an iterative procedure.35
Experimentally, the stoichiometry of the resin-bound complexes and the values of the exchange coefficients βex1np can be determined by fitting the sorption profiles, expressed as the variation of the sorbed fraction (f) of the analyte on the solid phase, as a function of the equilibrium pH values of the solution. The relationship between f and the exchange coefficients is given by eqn (5), where w is the mass of dry sorbent, V is the volume of the solution, [M]tot and [![[M with combining macron]](https://www.rsc.org/images/entities/char_004d_0304.gif) ] are the total metal concentration and the concentration of the metal ion sorbed on the solid phase, respectively. K* (eqn (6)) represents the partitioning coefficient of the resin, defined as the ratio of the total metal ion concentration in the solid phase over the free metal ion concentration remaining in solution. In the expression of K* (eqn (6)), the sum is extended to all the complexes formed with the considered metal ion with the active groups of the resin.
] are the total metal concentration and the concentration of the metal ion sorbed on the solid phase, respectively. K* (eqn (6)) represents the partitioning coefficient of the resin, defined as the ratio of the total metal ion concentration in the solid phase over the free metal ion concentration remaining in solution. In the expression of K* (eqn (6)), the sum is extended to all the complexes formed with the considered metal ion with the active groups of the resin.
 | (5) |
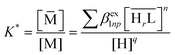 | (6) |
In practice, [![[M with combining macron]](https://www.rsc.org/images/entities/char_004d_0304.gif) ] and thus the fraction f of metal taken up by the resin are calculated from the mass-balance equation (eqn (7)) after measuring [M]eq, the total concentration of all soluble metal-containing species remaining in solution at equilibrium, by AA, ICP-OES, or any other appropriate analytical method.
] and thus the fraction f of metal taken up by the resin are calculated from the mass-balance equation (eqn (7)) after measuring [M]eq, the total concentration of all soluble metal-containing species remaining in solution at equilibrium, by AA, ICP-OES, or any other appropriate analytical method.
[![[M with combining macron]](https://www.rsc.org/images/entities/char_004d_0304.gif) ] = [M]tot − [M]eq ] = [M]tot − [M]eq | (7) |
By introducing the reaction coefficient αM, also known as the Ringbom coefficient,43 [M]eq can be expressed as a function of the free aqua metal ion concentration [Mm+] according to eqn (8). In the absence of a competitive ligand, αM is computed from the global hydrolysis constants of the metal cation (βx0z). Otherwise, when a competing ligand (L′)l− is added to the solution, αM values take into account both the hydrolysis constants of Mm+ and the stability constants (βxyz) of the soluble [Mx(L′)yHz](xm−yl+z)+ complexes formed in the liquid phase between the cation and (L′)l−.
 | (8) |
Knowing the concentration of the active sites in the solid phase and measuring experimentally both f and the pH of the solution, the values of αM can be easily computed for a given chemical model. Hence, the corresponding βex1np values can be refined according to eqn (5) by nonlinear least squares (NLLS) minimization. The number of protons released during complexation can be estimated through a logarithmic form of eqn (5).34 From the refined set of βex1np values, the corresponding βi1np equilibrium constants are calculated using eqn (4).
The success of this approach relies on a trial-error search of the optimal set of sorption reactions that best reproduces the experimental data points. To that end, the best strategy is to assume first that all sorption reactions and stoichiometries of surface complexes are the same as those occurring in a homogenous aqueous phase with model ligands or monomeric units mimicking the functional groups of the resin. In some cases, this set of reactions is not sufficient to model appropriately the sorption profile, and a good fit can only be obtained by considering other stoichiometries.
To select the appropriate set of sorption equilibria, the contribution of the ionic medium on the exchange coefficients (eqn (4)) has to be considered. Consequently, different experiments at various ionic strengths have to be performed in order to check the consistency of the calculated βi1np equilibrium constants. Further indications can be obtained from the evolution of the profiles in the presence of a competitive ligand in solution (see eqn (5)). After combining the results of all these experiments, it is possible to define the reactions and the relative intrinsic complexation constants that describe univocally the sorption under any experimental conditions.
Experimental
Equipment
Compounds were characterised at the “Plateforme d’Analyses Chimiques et de Synthèse Moléculaire de l’Université de Bourgogne” (PACSMUB, https://www.wpcm.fr). Centesimal CHN contents were obtained with a Flash EA 1112 (Thermo Scientific) CHNS analyser. Iron and terbium contents were determined in duplicate by ICP-OES with an iCAP 7400 (Thermo Scientific) spectrometer. Prior to the analyses, the resin samples were mineralized in 4 mL concentrated nitric acid (TraceMetal™ Grade, Fisher Scientific) in a single reaction chamber microwave digestion system (UltraWAVE, Milestone).Fourier-transform mid-infrared (400–4000 cm−1) spectra (FTIR) were recorded at 4 cm−1 resolution on a Bruker Alpha spectrophotometer fitted with a diamond attenuated total reflectance (ATR) accessory (Bruker) and a DTGS (deuterated triglycine sulfate) detector.
Thermogravimetric analyses (TGA) were performed on a Netzsch STA 409 PC Luxx thermoanalyser. Samples purged in an N2 (30 mL min−1)/O2 (10 mL min−1) stream were heated up to 800 °C in alumina crucibles with a heating rate of 10 °C min−1. Data were corrected for buoyancy effects. Onset temperatures (Tonset) were calculated according to the norm ISO 11357-3 as the intersection between the tangent in the inflection point and the selected baseline.
Luminescence spectra of pristine and terbium(III)-loaded DFO@Purolite resin samples were recorded between 450 and 650 nm on a Fluorolog (Jobin-Yvon Horiba) spectrofluorimeter, using an excitation wavelength of 355 nm. Beads were placed in a sample holder for powders and covered with a Suprasil® (Hellma) slide.
Two-photon imaging microscopy was performed with a Nikon A1-MP scanning microscope fitted with a Plan Apo IR ×60 objective (NA: 1.27, water immersion, Nikon, Japan). Dry resin samples were deposited on a microscope glass slide. Two-photon excitation was provided at 750 nm by an infrared laser (Chameleon Vision II, Coherent). Fluorescence emission was collected on four detection channels equipped with FF01-492/SP (400–492 nm), FF03-525/50 (500–550 nm), FF01-575/25 (563–588 nm), and FF01-629/56 (601–657 nm) band-pass filters (Semrock). The images were obtained by merging these four detection channels without any other spectral selection.
Scanning electron microscope (SEM) images were acquired under high vacuum (30 Pa) on a Hitachi SU1510 microscope equipped with a back-scattering electron detector. The instrument operated at an acceleration voltage of 15.0 kV with a working distance ranging between 8.0 and 16.2 mm. The magnification was set at ×95 or ×130. Gold metalized resin samples were prepared using a Scancoat (Edwards) sputtering system.
Chemicals for synthesis
All chemicals were of analytical grade and used as received. The mesylate salt of desferrioxamine B (Desferal®, [(DFO)H4]CH3SO3) was obtained from Apollo Scientific Ltd, Manchester, UK.Pristine Purolite® ECR8209 resin was purchased from Purolite Ltd, Llantrisant, UK (batch number 15S/19/0). It is a highly cross-linked epoxy methacrylate resin with dangling epoxy functional groups (1.5 mmol g−1 of dry resin). Textural characteristics provided by the manufacturer are the mean bead diameter (72 μm) and the mean pore diameter (846 Å). Found elemental analysis: C, 57.95; H, 7.58; N, 0.0%. FTIR (ATR, cm−1): νmax = 3500 (vbr, w), 2949 (CH, w), 2904 (CH, w), 1727 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O ester, s), 1452 (w), 1389 (w), 1256 (m), 1146 (C–O ester, s), 964 (w), 908 (C–O epoxy, w) 859 (C–O epoxy, w), 753 (w), 518 (w), 466 (w).
O ester, s), 1452 (w), 1389 (w), 1256 (m), 1146 (C–O ester, s), 964 (w), 908 (C–O epoxy, w) 859 (C–O epoxy, w), 753 (w), 518 (w), 466 (w).
Synthesis of DFO@Purolite
A 16.90 g batch of DFO@Purolite was synthesized by reacting 14.58 g (22.2 mmol) of Desferal® with 14.80 g of Purolite® resin (22.2 mmol of epoxy group) and 14.87 g of N,N-diisopropyl-ethylamine (DIPEA, 115.0 mmol) in 800 mL methanol in a round-bottom flask. The reactor was sealed with a glass stopper, kept in an oven for four days at 60 °C and shaken manually from time to time. The resin was then recovered by filtration, washed several times successively with water, methanol, water, acetic acid (1 M in water), water, and methanol before drying in vacuo at room temperature. Found elemental analysis: C, 56.10; H, 7.75; N, 1.69%, corresponding to 112.8 mg of DFO per gram of modified DFO@Purolite or 0.201 mmol g−1. FTIR (ATR, cm−1): νmax = 3500 (vbr, w), 2949 (CH, w), 2904 (CH, w), 1727 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O ester, s), 1656 (C
O ester, s), 1656 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O amide and hydroxamic acid, w), 1452 (w), 1389 (w), 1256 (m), 1146 (C–O ester, s), 964 (w), 908 (C–O epoxy, w) 859 (C–O epoxy, w), 753 (w), 518 (w), 466 (w).
O amide and hydroxamic acid, w), 1452 (w), 1389 (w), 1256 (m), 1146 (C–O ester, s), 964 (w), 908 (C–O epoxy, w) 859 (C–O epoxy, w), 753 (w), 518 (w), 466 (w).
Synthesis of Fe(DFO)@Purolite
A small sample of DFO@Purolite (30 mg) was suspended in a saturated solution of Fe(NO3)3 in methanol for 15 min. The resin was washed thoroughly with water and methanol before being dried in vacuo at room temperature. The iron content (1.19%), as determined by ICP-OES, allowed estimating the amount of grafted DFO (119.5 mg g−1 or 0.213 mmol g−1 of DFO), assuming the formation of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Fe/DFO complex.
1 Fe/DFO complex.
Synthesis of Tb(DFO)@Purolite
A 50 mg sample of DFO@Purolite was added to 3 mL of a Tb(acac)3 (5.1 mg, 11.2 μmol) solution in methanol. The reaction mixture was kept at 60 °C for 24 h in an oven. The resin was recovered by filtration, washed with methanol, and dried under vacuum before microscopic analysis. ICP-OES analysis of the mineralized sample gave 1.41% (0.089 mmol g−1) of Tb.Chemicals for sorption experiments
Na2H2(EDTA), NaCl, HCl, and NaOH were purchased from Sigma-Aldrich, Italy. Desferrioxamine B mesylate salt from NOVARTIS FARMA S.p.A, Italy, was purchased in a pharmacy. Iron and zirconium ICP standards (1000 mg L−1 in 2% HNO3) from Sigma-Aldrich, Italy, were used to prepare the metal ion solutions at an appropriate concentration. All aqueous solutions were prepared in volumetric glass flasks with ultrapure water (18.2 MΩ cm) produced by a Milli-Q® Academic A10® cartridge system. Immediately after their preparation, they were transferred to polyethylene bottles. All sorption experiments were conducted in polypropylene tubes with low-density polyethylene caps.Acid–base titrations of resins
A Mettler-Toledo DL 53 titrator fitted with a combined DG-115-SC (Mettler-Toledo) glass electrode was used to perform the acid–base titrations of the active groups of DFO@Purolite resin suspended in aqueous 0.1 M or 1 M NaCl solution. The detailed procedure has been reported elsewhere.33,44 Briefly, titrations were conducted in a double-jacketed titration vessel connected to a water circulator (Julabo FP40) in order to maintain a constant temperature of 298.2(2) K. A small overpressure of nitrogen was applied to exclude CO2 from the headspace. Prior to each experiment, the potentiometric cell was standardized in H+ concentration units (hence, pH is defined as pH = −log [H+]) by titrating previously standardized HCl amounts diluted in the selected supporting electrolyte solution with a standardized, CO2-free NaOH solution. The equivalent point was determined by the method of Gran, thus obtaining the standard potential ( ) and the apparent ionic product of water (Kw).
) and the apparent ionic product of water (Kw).
A weighted amount of dry resin (around 0.5 g) in its completely protonated form was dispersed in 70 mL of supporting electrolyte solution of fixed composition, containing a known amount of NaCl to which HCl was added to reach a pH of around 2.2. The suspension was titrated by adding 0.02 mL increments of standardized 0.2 M NaOH. A minimum of 0.5 h was found to be the time needed for the equilibrium to be reached. The equilibrium condition was considered to be obtained when the drift of the glass electrode was lower than 0.1 mV min−1. The maximum time between two additions of NaOH was fixed at 3 h. Each titration lasted approximately 48 h until pH 11 was reached and included about 40–50 points. The capacity was obtained from the milliequivalents of NaOH required to neutralize the resin. From the titration curves, the protonation equilibrium constants were derived by applying the Gibbs–Donnan formalism.33
Instrumentation used for sorption studies
An iCAP 7400 (Thermo Scientific) ICP-OES spectrometer was used to determine Fe (λ = 259.94 nm, axial mode) and Zr (λ = 339.198 nm, radial mode). The method detection limit (MDL) was 5 μg L−1 for Fe and 4 μg L−1 for Zr.Sorption isotherm: discontinuous procedure
A fixed amount of resin (50.0 mg) was contacted with 0.1 M NaCl solutions at pH 2 (V = 5 mL) containing increasing amounts of Fe(III) or Zr(IV) (from 5 × 10−6 to 5 × 10−3 M). From 10 to 15 tubes were prepared. Samples were gently stirred overnight on a shaking plate. After equilibration, a small amount of solution was collected, appropriately diluted in new disposable test tubes, and analysed by ICP-OES to determine the metal ion concentration. The amount of sorbed metal ion was deduced according to eqn (7) from the difference between the total initial concentration and the concentration remaining in solution. Isotherms were obtained by plotting the sorbed quantity, q (mmol g−1), versus the equilibrium metal–ion concentrations still present in solution, [M]eq (M).Kinetics profiles: discontinuous procedure
A fixed amount of resin (50.0 mg) was contacted with 0.1 M NaCl solutions at pH 2 (V = 5 mL) at fixed Fe(III) or Zr(IV) concentrations. For each experiment, 10 to 15 tubes were prepared. At a given time, a small amount of solution was collected, appropriately diluted in new disposable test tubes, and analysed by ICP-OES to determine the unsorbed metal ion concentration remaining in the supernatant. In this case, the variable studied was the fraction of sorbed metal ion (f) as a function of the stirring duration on the shaking plate.Sorption profiles as a function of pH: discontinuous procedure
A constant mass of resin (50.0 mg) was contacted with a mixture of 1 M NaCl and 1 M HCl to obtain solutions with a total ionic strength of 0.1 or 1.0 M (V = 10 mL) at fixed Fe(III) or Zr(IV) concentrations. The amount of resin over metal–ion concentration ratio was selected to have a large excess of active groups as compared to the number of mmol of metal ions. At least 20 tubes were prepared by setting the initial pH value with HCl or NaOH that varied in the 1–11 range. Samples were gently stirred overnight on a shaking plate. The sample's pH was measured after equilibration, and a small amount of solution was collected, diluted adequately in new disposable test tubes, and analysed by ICP-OES to determine the metal ion concentration. Additional experiments were carried out in the presence of a competing ligand (desferrioxamine B or EDTA) in solution. The sorption profiles were obtained by plotting the fraction of the sorbed metal ion (f) vs. pH.Desorption profiles: discontinuous procedure
A known amount of Fe(III) or Zr(IV) (the number of mmol being always much lower than that of the active sites of the resin) was sorbed at pH ≈ 3 on DFO@Purolite (about 1 g) in 0.1 M NaCl media. The solution was removed, and the solid phase was washed several times with ultrapure water, then filtered and dried. The Fe(DFO)@Purolite and Zr(DFO)@Purolite materials thus obtained were divided into 10 equal portions of 50 mg each introduced into disposable tubes. Each sample was suspended in 10 mL of a 0.1 M (H,Na)Cl solution at pH ≈ 2 and left to equilibrate for 2 h before different quantities of the competitive ligand (desferrioxamine B or EDTA) were added. The suspensions were left to equilibrate overnight on a shaking plate. Then, a small amount of each solution was collected in a new disposable test tube and analysed by ICP-OES to determine the cation content. The desorption profiles were obtained by plotting f vs. the total ligand concentration.Results
Synthesis and characterisation of the DFO@Purolite resin
The DFO@Purolite hybrid material was obtained by covalent grafting of the commercially available mesylate salt of desferrioxamine B (Desferal®) onto the polymethacrylate resin Purolite ECR8209 (Fig. 2). The reaction was conducted at 60 °C in methanol in the presence of an organic base (DIPEA). Functionalization of the solid support relies on the nucleophilic and ring-opening reaction of the N-terminal primary amine of DFO on the dangling epoxy groups of the resin. This neutral support was chosen because of its high loading of reactive epoxy groups (1.5 mmol g−1) and sharp size distribution of the particles. Moreover, no ion-exchange sites other than the hydroxamates are formed upon the attachment of DFO.The successful grafting was clearly attested by comparing the FTIR-ATR spectra of pristine and modified Purolite® (Fig. S1 in the ESI†). Despite their close resemblance, two distinct features at 1656 and 908 cm−1 allow ascertaining the incorporation of DFO onto the resin matrix. The first band that grows in after functionalization is assigned to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretches of the amide and hydroxamic acid groups belonging to DFO. In turn, the intensity decrease of the epoxy C–O stretching mode centred at 908 cm−1 upon grafting clearly supports the covalent attachment of DFO through the epoxy-ring opening reaction. Noteworthy, a similar spectral change occurred in the 800–1000 cm−1 range when the native resin was treated with a large excess of propylamine, which ascertains the appropriate assignment of the 908 cm−1 band.
O stretches of the amide and hydroxamic acid groups belonging to DFO. In turn, the intensity decrease of the epoxy C–O stretching mode centred at 908 cm−1 upon grafting clearly supports the covalent attachment of DFO through the epoxy-ring opening reaction. Noteworthy, a similar spectral change occurred in the 800–1000 cm−1 range when the native resin was treated with a large excess of propylamine, which ascertains the appropriate assignment of the 908 cm−1 band.
The thermal behaviour of the resin before and after chemical modification was investigated by thermogravimetry (TGA) between 25 and 800 °C with a heating rate of 10 °C min−1 in a synthetic air gas flow (Fig. S2 in the ESI†). A small weight loss (1.1% for Purolite® and 3.7% for DFO@Purolite) occurred at 69 and 80 °C, respectively, corresponding to the evaporation of the residual water trapped in the pores of the resins. The unmodified polymer shows three consecutive degradation steps in the 252–516 °C range (Tonset = 252, 291, and 457 °C), while only two are seen for DFO@Purolite between 279 and 528 °C (Tonset = 279 and 454 °C). The first decomposition process occurring in the range 279–351 °C produces a weight loss of 78%, while the second one parallels the third degradation step recorded for pristine Purolite®. Complete calcination is achieved for both materials at around 600 °C. The shift to higher temperatures of up to ca. 45 °C clearly reveals a thermal stabilization of the modified polymer as compared to the native one and provides further evidence that DFO is covalently grafted on the support and not simply adsorbed on the surface or entrapped in the cavities of the material. As both DFO and the methacrylate polymer degrade simultaneously, the amount of grafted chelator could not be determined from the TGA curve.
Hence, the loading of DFO on the resin was deduced from elemental CHN analysis by considering that each molecule of siderophore contains 6 nitrogen atoms, whereas the support is nitrogen-free. Experimentally, the nitrogen content was indeed found to be nil for the bare Purolite® sample but reached 1.69% for the modified material, corresponding to a DFO loading of 0.201 mmol g−1. This value was confirmed by measuring the iron(III) loading capacity of the DFO@Purolite resin. Based on the %Fe determined by ICP-OES (1.19%) and on the assumption that each immobilized DFO molecule binds a single Fe3+ cation, the capacity was found to be 0.213 mmol g−1, which agrees well with the DFO loading estimated from the nitrogen content.
According to scanning electron microscopy (SEM) images, the bead size of bare Purolite® ECR8209 resin ranges approximately from 50 to 130 μm (Fig. S3 in the ESI†), in agreement with the average diameter of 72 μm claimed by the manufacturer. Owing to the mild conditions employed (60 °C, no mechanical stirring), the chemical modification of the polymer by treatment with the mesylate salt of DFO in the presence of DIPEA in methanol did not alter the spherical shape of the beads which retained their smooth aspect, nor their average size, as exemplified by the SEM image shown in Fig. S4 (ESI†).
Finally, the chemical distribution of DFO within the beads was probed by two-photon optical fluorescence microscopy by taking advantage of the fact that two-photon absorption mainly occurs in the focal plane. Hence, the excitation beam is weakly absorbed in the out-of-focus planes, which allows a good penetration even in thick and opaque samples. Emitted light intensity profiles along the cross-section of a bead can be recorded simply by moving step-by-step through the motorized microscope stage without changing the focus. The thereby obtained curve will reflect the distribution profile of the fluorophore across the particle and will enable checking if grafting occurred only at the outer surface of the beads or also in the core. The success of this method relies on the complete penetration of the excitation light beam across the translucent beads, which was clearly achieved by using a NIR (λex = 750 nm) laser source.
However, prior to the biphotonic studies, classical single-photon emission spectroscopy investigations were carried out to check for feasibility. As an emission probe, we have selected terbium(III), which forms a stable [Tb(DFO)H]+ trishydroxamato complex with DFO3− in neutral or weakly alkaline aqueous solutions.45 Moreover, this cation of 4f8 electronic configuration is well known to emit green light upon direct one-photon excitation into the Laporte forbidden f → f transition at 455 nm (ε < 1 M−1 cm−1).46 The emission spectrum of the DFO terbium complex shows the typical four-line 5D4 → 7FJ (J = 3–6) manifold of the Tb3+ aqua ion, with emission maxima at 490, 547, 585, and 621 nm (Fig. S5 in the ESI†). In contrast, pristine Purolite® ECR8209 is a non-emissive material upon excitation at 455 nm, while DFO@Purolite gives rise to a weak but featureless fluorescence signal over the entire 470–670 nm range, like pure [(DFO)H4]CH3SO3. In contrast, the emission spectrum of dry Tb(DFO)@Purolite resin coincides perfectly with that of [Tb(DFO)H]+ recorded in aqueous solution (Fig. S6 in the ESI†). In light of these results, two-photon images of bare Purolite®, DFO@Purolite, and Tb(DFO)@Purolite were recorded with an optical microscope at λex = 750 nm. While the two first materials were non- or weakly fluorescent, allowing nevertheless the collection of high-quality images of DFO@Purolite particles (Fig. S7 in the ESI†), those recorded for the terbium-loaded resin were much brighter. Emission profiles (Fig. 3) revealed a homogenous distribution of Tb3+ across the beads, suggesting that the reaction time (4 d) was long enough to allow DFO to diffuse inside the core and react equally well with either the superficial or the nested epoxy groups born by the cross-linked methacrylate chains.
Acid–base properties of DFO@Purolite
Prior to thermodynamic and kinetic iron(III) and zirconium(IV) uptake studies by DFO@Purolite, potentiometric acid–base titrations of the resin suspended in a 0.1 or 1.0 M NaCl background electrolyte solution were carried out in order to determine the number of active sites. The average value of the capacity (0.23(3) mmol g−1) calculated for the three titrations (Table 1) agrees well with that evaluated by elemental analyses (0.201 and 0.213 mmol g−1 based of %N and %Fe, respectively, vide supra) but also with the maximum sorption capacity derived from the sorption isotherms of Zr(IV) and Fe(III) (vide infra).| Medium | Mass of dry resin (g) | Capacity (mmol g−1) | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kex014 Kex014 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ki014 Ki014 |
|---|---|---|---|---|
| 0.1 M NaCl | 0.5158 | 0.24 | 8.7(1) | 8.49(6) |
| 0.1 M NaCl | 0.4481 | 0.20 | 8.80(9) | 8.65(9) |
| 1.0 M NaCl | 0.4673 | 0.25 | 8.61(8) | 8.58(8) |
Although each molecule of DFO covalently bound to the resin framework possesses four protonation sites, three hydroxamates and one secondary amine in the linker, the refinement of the titration data according to the Gibbs–Donnan formalism allowed us to estimate only the value of the last stepwise protonation constant or first pKa (eqn (9)).
 | (9) |
The refined values of the exchange coefficient (Kex014), which depends on the experimental conditions, are also reported in Table 1, together with the corresponding intrinsic constants Ki014. The average log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ki014 value of 8.57(8) is slightly higher but overall in very good agreement, with the thermodynamic protonation constant of (DFO)H3 in aqueous media reported by Février et al. (log Ko014 = 8.36).24
Ki014 value of 8.57(8) is slightly higher but overall in very good agreement, with the thermodynamic protonation constant of (DFO)H3 in aqueous media reported by Février et al. (log Ko014 = 8.36).24
Stability studies of Zr(IV) and Fe(III) solutions in the absence of resin
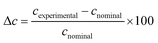
When working with trace amounts of metal ions prone to hydrolyse, such as Fe3+ and Zr4+, it is of paramount importance to verify that no contamination and/or loss of analyte occur. Table 2 compares the nominal metal ion concentrations for all solutions prepared at pH 2 to the experimental value measured by ICP-OES after 1 d storage. With relative differences not exceeding 10%, these results were considered as fully acceptable, considering the used instrumentation and analytical procedures.| c nominal (M) | c experimental (M) | Δca (%) |
|---|---|---|
a
 . .
|
||
| Zr(IV) | ||
| 4.38 × 10−5 | 3.95 × 10−5 | −9.8 |
| 5.48 × 10−6 | 4.67 × 10−6 | −14.8 |
| 3.29 × 10−4 | 3.63 × 10−4 | 10.3 |
| 6.58 × 10−5 | 6.87 × 10−5 | 4.4 |
| 1.10 × 10−4 | 1.22 × 10−4 | 10.9 |
| 1.10 × 10−4 | 1.14 × 10−4 | 3.6 |
| 4.39 × 10−5 | 4.10 × 10−5 | −6.6 |
| 5.49 × 10−5 | 5.72 × 10−5 | 4.2 |
| Fe(III) | ||
| 1.43 × 10−4 | 1.49 × 10−4 | 4.2 |
| 8.95 × 10−5 | 9.07 × 10−5 | 1.3 |
| 8.95 × 10−5 | 8.58 × 10−5 | −4.1 |
| 7.16 × 10−5 | 7.47 × 10−5 | 4.3 |
Zr(IV) and Fe(III) uptake kinetics
Fig. 4 shows the kinetic profiles obtained for three different initial concentrations of Zr(IV) in 0.1 M NaCl solution at pH = 2. In each case, equilibrium was reached in less than 1 h, the required time becoming, as expected, shorter with increasing Zr(IV) concentrations. It is generally accepted that the metal uptake process can be decomposed into three steps, namely, external diffusion, internal diffusion within the polymeric matrix of the particles, and the binding or chelation of the analyte by the active sites of the resin. As illustrated in Fig. 4, the molar fraction of sorbed zirconium over time follows the pseudo-first-order rate law given by eqn (10), indicating that the adsorption dynamics is most-likely controlled by the diffusion process rather than complex formation.47| f = 1 − e−kobst | (10) |
 | ||
| Fig. 4 Kinetic profiles of Zr(IV) uptake by DFO@Purolite. Discontinuous procedure: 0.05 g of resin was contacted with 0.1 M NaCl solutions acidified at pH 2 with HCl (V = 5 mL) at fixed Zr(IV) concentrations (red dots: 550 μM; yellow dots: 55 μM; blue dots: 5.5 μM). The lines represent the best-fitted curves of the experimental data points by the pseudo-first-order rate law expressed by eqn (10). | ||
This result is in line with the lability of zirconium(IV) species in aqueous media, as the first-order exchange rate constant of a water molecule bound to [Zr(H2O)8]4+, [Zr(H2O)7OH]3+, and [Zr(H2O)6(OH)2]2+ in the first solvation sphere with one from the bulk has been estimated to be close to 4.8 × 104, 6 × 105, and 107 s−1, respectively.48 Moreover, Savastano et al. also noticed short equilibration times in the 3–5 min time range when 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 1
1 or 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Zr to free [(DFO)H4]CH3SO3 mixtures were titrated from pH around 2 to 5.36
2 Zr to free [(DFO)H4]CH3SO3 mixtures were titrated from pH around 2 to 5.36
The continuous curves shown in Fig. 4 were computed by NLLS fitting. The values of the adjusted pseudo-first-order rate constant kobs are 0.068(4), 0.085(9), and 0.324(9) min−1 for initial Zr(IV) concentrations of 5.5, 55, and 550 μM, respectively. Regarding Fe(III), the sorption on the resin was found to be much faster than that of Zr(IV), as the equilibrium was reached in less than 20 min.
Zr(IV) and Fe(III) sorption isotherms
Once the rather fast metal uptake by the DFO@Purolite resin at pH 2 was established, its sorption capacity at equilibrium was investigated at the same pH value over a large total metal concentration range that spanned three decades from 5 μM up to 5 mM. Fig. 5 shows the sorption isotherm of Zr(IV) in 0.1 M NaCl containing 0.01 M HCl. The amounts of sorbed metal per gram of resin (q) were best reproduced by the classical Langmuir model given by eqn (11).47,49 A NLLS fit returned KL = 2.5(9) × 103 M−1 and qmax = 0.20(3) mmol g−1. These parameters were used to draw the continuous line of Fig. 5. Accordingly, the maximum sorption capacity (qmax) of Zr(IV) on the resin at pH 2, is in pretty good agreement with the DFO loading determined both by elemental analyses and acid–base titrations (Table 1). | (11) |
 | ||
| Fig. 5 Sorption isotherm of Zr(IV) onto DFO@Purolite. Discontinuous procedure: 0.05 g of resin was contacted with 0.1 M NaCl solutions acidified at pH 2 with HCl (V = 5 mL) containing increasing amounts of Zr(IV) ([Zr]tot = 5 × 10−6 to 5 × 10−3 M). The line represents the best-fit curve of the experimental data points using the Langmuir equation (eqn (11)). | ||
A similar experiment was also performed for Fe(III) using the same experimental conditions as for Zr(IV). Again, the Langmuir model appropriately describes the experimental isotherm. In Fig. 6, the continuous line was drawn with the following parameters of eqn (11): KL = 2.0(2) × 103 M−1 and qmax = 0.200(5) mmol g−1. Whereas the refined qmax values are identical for both metal cations, the slightly higher affinity of the surface-bound DFO chelator for Zr4+ over Fe3+ is reflected by a 25% higher KL value.
 | ||
| Fig. 6 Sorption isotherm of Fe(III) onto DFO@Purolite. Discontinuous procedure: 0.05 g of resin was contacted with 0.1 M NaCl solutions acidified at pH 2 with HCl (V = 5 mL) containing increasing amounts of Fe(III) ([Fe]tot = 5 × 10−6 to 4 × 10−3 M). The line represents the best-fit curve of the experimental data points using the Langmuir equation (eqn (11)). | ||
Sorption profiles as a function of pH for the Zr(IV)/DFO@Purolite system
Next, the effect of pH on the DFO@Purolite complexing properties towards Zr(IV) and Fe(III) has been investigated. To that end, it is fundamental to accurately define the partitioning coefficient K* value for assessing the free metal concentration remaining in solution at equilibrium. Instead of determining an operational value of K*, strictly valid only for a particular set of experimental conditions, we followed the strategy already reported for chelating resins.50–53 Once the sorption reactions and the complexation constants have been defined, it is possible to calculate the K* value under any conditions.As a rough but reasonable estimate, it was assumed that the protonation constants of DFO3− once covalently attached to the DFO@Purolite resin are the same as for the unbound ligand solubilized in aqueous solutions. This assumption is supported by the very good agreement between the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ki014 value of 8.57(8) derived herein by glass-electrode potentiometry for the modified material and the literature datum (log
Ki014 value of 8.57(8) derived herein by glass-electrode potentiometry for the modified material and the literature datum (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ko014 = 8.36) reported by Février et al. for the protonation of unbound (DFO)H3.24 Unfortunately, analysis of the acid–base titration curves of DFO@Purolite did not allow determination of the other three protonation constants pertaining to the secondary amine and two hydroxamate groups of grafted DFO. Nevertheless, if the complexation constants of Zr(IV) on the solid did not significantly differ from those in solution (vide infra), the approximation could be accepted.
Ko014 = 8.36) reported by Février et al. for the protonation of unbound (DFO)H3.24 Unfortunately, analysis of the acid–base titration curves of DFO@Purolite did not allow determination of the other three protonation constants pertaining to the secondary amine and two hydroxamate groups of grafted DFO. Nevertheless, if the complexation constants of Zr(IV) on the solid did not significantly differ from those in solution (vide infra), the approximation could be accepted.
As already demonstrated, desferrioxamine B efficiently complexes Zr(IV) at a very acidic pH (<2).37 Because one purpose is to apply the material in biological fluids or environmental waters, the characterisation was extended to higher pH values. Even under moderately acidic conditions, the study of the sorption profile requires the addition of a competitive ligand to avoid the Zr(IV) hydrolysis and precipitation of Zr(OH)4. Moreover, the binding strength is too high to allow an accurate measurement of the partitioning coefficient K*. Hence, in the presence of a competing chelator L′ in solution, the sorption profile curve is shifted towards the alkaline region, which facilitates the accurate measurement of the total metal concentration remaining in the supernatant liquid phase at equilibrium. Moreover, the exchange properties are thus also determined at pH values closer to those expected for real samples. The sorption profiles of Zr(IV), in the absence and in the presence of DFO and EDTA used as competitive ligands, are displayed in Fig. 7 and 8, respectively. The competition effect is evident since the sorption profiles recorded in the presence of either DFO or EDTA in the liquid phase are shifted towards higher pH values as compared to the profiles obtained in the absence of the competing ligand.
 | ||
| Fig. 7 Sorption profiles of Zr(IV) onto DFO@Purolite. Discontinuous procedure: 0.05 g of resin was contacted with 10 mL of 50 μM Zr(IV) solutions in 0.1 M NaCl (blue dots), 1.0 M NaCl (yellow dots), 1.0 M NaCl containing 0.1 mM DFO (red dots), and 1.0 M NaCl containing 1 mM DFO (green dots). The lines represent the best-fit curves of the experimental data points using eqn (5) and the sorption equilibria given by eqn (12). | ||
Data were processed by applying the Gibbs–Donnan model (eqn (5)). The auxiliary equilibrium constants summarized in Table S1 (ESI†) were used for calculating the reaction coefficient αZr with the MEDUSA program.54 They include the hydrolysis constants of zirconium (βx0z), the protonation (β01z) and stability (βxyz) constants of the zirconium complexes formed in aqueous solution with L′ = EDTA4− and DFO3−. Regarding the speciation of the Zr4+/DFO3− system, the literature provides so far conflicting results. In 2018, Savastano et al. suggested the formation in 0.1 M NMe4Cl of both mono- and binuclear species with [Zr(DFO)Hz](z+1)+ (z = −1, 0 and 2), [Zr2(DFO)2Hz](z+2)+ (z = 1–3) and [Zr2(DFO)3Hz](z−1)+ (z = 5, 6) stoichiometries, respectively.36 The same year, Toporivska and Gumienna-Kontecka published a similar study, carried out in 1.0 M NaClO4, in which they found only the three mononuclear [Zr(DFO)H]2+, [Zr(DFO)]+, and [Zr(DFO)(OH)] species.37 Hence, both models were considered herein; but it also prompted us to use EDTA4− as another competing ligand to check the consistency of the derived intrinsic binding constants βi1np.
To avoid over-parametrization and divergence during the NLLS refinement cycles, the first important step in numerical data analysis of sorption data is to make a reasonable initial guess about the stoichiometry of the complexes that form on the solid phase. This turns out to be a trial-error approach during which the sorption profiles are tentatively adjusted using different chemical models. To set up the most plausible starting model, we first considered the binding equilibria in homogeneous solutions reported for the Zr4+/DFO3− system. We assumed that complexes of identical or similar stoichiometry are also encountered when DFO is attached to a solid support; this is a rational reasoning, considering the high flexibility of the siderophore and its tether. If one assumes that the distance between neighbouring DFO molecules grafted on the polymeric chains of Purolite® is in the range or larger than their total length, the formation of  and even more
and even more  surface complexes seems unrealistic but, nevertheless, cannot be excluded a priori.
surface complexes seems unrealistic but, nevertheless, cannot be excluded a priori.
As shown in Fig. 7 when DFO3− was used as the competing ligand L′ and in Fig. 8 when L′ was EDTA4−, the fractions of sorbed metal could be reasonably well reproduced by assuming only the three sorption reactions given by eqn (12), which turned out to correspond to the solution equilibrium model proposed by Toporivska and Gumienna-Kontecka.37
 | (12) |
 | ||
| Fig. 8 Sorption profiles of Zr(IV) onto DFO@Purolite. Discontinuous procedure: 0.05 g of resin was contacted with 10 mL of 50 μM Zr(IV) solutions in 0.1 M NaCl (blue dots), 1.0 M NaCl (yellow dots), 0.1 M NaCl containing 0.5 mM EDTA (black dots), and 0.1 M NaCl containing 5 mM EDTA (violet dots). The lines represent the best-fit curves of the experimental data points using eqn (5) and the sorption equilibria given by eqn (12). | ||
The introduction of additional sorption equilibria involving either 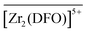 ,
,  , or
, or  complexes did not improve the quality of the fit and/or returned unrealistic parameters. Moreover, the great consistency of the intrinsic complexation constants returned by the NLLS refinement procedure for the six independent data sets acquired at two different ionic strengths (I = 0.1 and 1 M NaCl) and for two competitors L′ taken at concentration levels differing by a factor of up to 10 (Table 3), provides a high degree of confidence on the accuracy of both the selected model and the thermodynamic parameters.
complexes did not improve the quality of the fit and/or returned unrealistic parameters. Moreover, the great consistency of the intrinsic complexation constants returned by the NLLS refinement procedure for the six independent data sets acquired at two different ionic strengths (I = 0.1 and 1 M NaCl) and for two competitors L′ taken at concentration levels differing by a factor of up to 10 (Table 3), provides a high degree of confidence on the accuracy of both the selected model and the thermodynamic parameters.
| Medium | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βi111 βi111 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βi110 βi110 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βi11−1 βi11−1 |
|---|---|---|---|
| a T = 298.2(2) K. b Thermodynamic complexation constant of Zr4+ by DFO3− roughly approximated by extrapolation to infinite dilution with the Davies equation55 of the experimental data reported in ref. 37. The latter was determined by potentiometric titrations in 1.0 M NaClO4 aqueous solution at 298.2 K. | |||
| 0.1 M NaCl | 47.8 | 41.5 | 31.0 |
| 1.0 M NaCl | 47.8 | 41.7 | 31.0 |
| 1.0 M NaCl + 0.1 mM DFO | 47.3 | 41.7 | 30.8 |
| 1.0 M NaCl + 1.0 mM DFO | 47.8 | 41.9 | 30.8 |
| 0.1 M NaCl + 0.5 mM EDTA | 47.8 | 41.9 | 31.0 |
| 0.1 M NaCl + 5.0 mM EDTA | 48.1 | 41.9 | 31.0 |
| Average | 47.8(2) | 41.8(1) | 30.9(1) |
| H2O, I = 0 | 48.5b | 42.5b | 31.5b |
Of note, these solid–liquid extraction experiments also allow selecting indirectly the most plausible Zr4+/DFO3− speciation model among the two proposed so far for homogeneous aqueous phases. Indeed, consistency in the βi1np values determined for L′ = DFO3− and EDTA4−, as reported in Table 3, could only be achieved by combining the three-equilibrium solution model of Toporivska and Gumienna-Kontecka37 for calculating αZr with the three related solid–liquid extraction reactions of eqn (12). It is furthermore gratifying to notice a good agreement between the stoichiometry and the stability constant of each complex formed both in aqueous solution (βo11z, z = −1, 0, 1) and on the modified Purolite® resin (βi11p, p = −1, 0, 1), considering that only rough estimates could be obtained for the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βo11z values. Indeed, extrapolation to infinite dilution of the experimental log
βo11z values. Indeed, extrapolation to infinite dilution of the experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β11z values measured in 1 M NaClO4 was achieved by applying the Davies equation,55 which does not necessarily hold at such a high ionic strength.
β11z values measured in 1 M NaClO4 was achieved by applying the Davies equation,55 which does not necessarily hold at such a high ionic strength.
To infer some structural information about the three species, it is valuable to discuss the pKa values or stepwise protonation constants of the bound complexes. As proposed for [Zr(DFO)H]2+,37 all three hydroxamate functions are also most likely bound to Zr4+ in  , the proton being located on the secondary ammonium group of the tether. With a first pKa of 6.0(2),
, the proton being located on the secondary ammonium group of the tether. With a first pKa of 6.0(2), 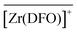 should be better formulated as
should be better formulated as  in which one hydroxide anion has replaced a water molecule in the first coordination shell. Owing to proton ambiguity, it turns out that both formulations are equivalent as they give rise to the same pH change and thus cannot be distinguished from one another. Finally, the occurrence of
in which one hydroxide anion has replaced a water molecule in the first coordination shell. Owing to proton ambiguity, it turns out that both formulations are equivalent as they give rise to the same pH change and thus cannot be distinguished from one another. Finally, the occurrence of  above pH 9 is most likely associated with the neutralization of the secondary ammonium site, as the pKa of 10.9(1) is close to the one estimated for the free ligand at infinite dilution (11.7).24 It is noteworthy that the same protonation scheme has been proposed for the solution species.37
above pH 9 is most likely associated with the neutralization of the secondary ammonium site, as the pKa of 10.9(1) is close to the one estimated for the free ligand at infinite dilution (11.7).24 It is noteworthy that the same protonation scheme has been proposed for the solution species.37
Desorption profiles for Zr(IV)
A desorption profile of Zr(IV) loaded resin was recorded, both to further confirm the sorption reaction model and to evaluate the feasibility of regenerating the extracting material. Fig. 9 shows the static (batch mode) desorption profile obtained at a constant pH of 2 by adding, to the supernatant, increasing amounts of [(DFO)H4]CH3SO3 used here as a scavenger. The graph clearly indicates that complete removal of Zr(IV) from the resin is difficult to achieve at pH 2, as ca. 10% of the metal remains bound even at 0.01 M or slightly higher [(DFO)H4]CH3SO3 concentration levels. | ||
| Fig. 9 Desorption profiles of Zr(IV) at pH 2 as a function of [(DFO)H4]CH3SO3 concentration. Discontinuous procedure: 0.05 g of Zr(IV) loaded DFO@Purolite resin was contacted with 10 mL of 0.1 M NaCl acidified with HCl. The line represents the best-fit curve of the experimental data points using eqn (5). | ||
The line in Fig. 9 corresponds to the best-fit curve of the experimental data points according to eqn (5) for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K* = 8.93. For desorption data modelling, NLLS refinement of K* requires no assumption about the stoichiometry and stability of the complexes formed on the resin surface. Hence, comparison of this value with that computed under similar conditions by means of eqn (6) and the sorption equilibrium constants of Table 3 (log
K* = 8.93. For desorption data modelling, NLLS refinement of K* requires no assumption about the stoichiometry and stability of the complexes formed on the resin surface. Hence, comparison of this value with that computed under similar conditions by means of eqn (6) and the sorption equilibrium constants of Table 3 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K* = 8.95) is a convenient way to ascertain the internal consistency of the entire model. Most gratifyingly, the remarkable agreement provides strong confidence in the accuracy of the proposed sorption equilibria (eqn (12)) and the associated mean log
K* = 8.95) is a convenient way to ascertain the internal consistency of the entire model. Most gratifyingly, the remarkable agreement provides strong confidence in the accuracy of the proposed sorption equilibria (eqn (12)) and the associated mean log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βi11p values reported in Table 3.
βi11p values reported in Table 3.
Sorption profiles as a function of pH for the Fe(III)/DFO@Purolite system
The sorption profiles of Fe(III), in the absence and in the presence of EDTA (0.5 and 5 mM) as a competitive ligand, are displayed in Fig. 10 as a function of pH. The competitive effect of EDTA is evident since the sorption profiles are significantly shifted towards higher pH values by the addition of the chelator to the aqueous phase. In Fig. 10, it can also be observed from the profile corresponding to a 1.0 M NaCl solution containing no EDTA, that the sorption of Fe(III) onto the resin is not quantitative below pH 6, despite the extremely high affinity of DFO3− for iron (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β111 = 41.39, I = 0.1 KCl, T = 298.2 K).56 This behaviour can be explained by the formation of iron(III) chloro complexes in aqueous solutions: FeCl2+ (log
β111 = 41.39, I = 0.1 KCl, T = 298.2 K).56 This behaviour can be explained by the formation of iron(III) chloro complexes in aqueous solutions: FeCl2+ (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β110 = 1.48), FeCl2+ (log
β110 = 1.48), FeCl2+ (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β120 = 2.13), FeCl3 (log
β120 = 2.13), FeCl3 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β130 = 1.13), and FeCl4− (log
β130 = 1.13), and FeCl4− (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β140 = −0.92).54 Accordingly, for a 1.0 M NaCl solution, the Cl− anion becomes an effective competitor (αFe = 1 + β110[Cl−] + β120[Cl−]2 +β130[Cl−]3 + β140[Cl−]4 = 179.9) that lowers the apparent iron binding constants by ca. 2.3 logarithmic units.
β140 = −0.92).54 Accordingly, for a 1.0 M NaCl solution, the Cl− anion becomes an effective competitor (αFe = 1 + β110[Cl−] + β120[Cl−]2 +β130[Cl−]3 + β140[Cl−]4 = 179.9) that lowers the apparent iron binding constants by ca. 2.3 logarithmic units. | (13) |
 | ||
| Fig. 10 Sorption profiles of Fe(III) onto DFO@Purolite. Discontinuous procedure: 0.05 g of resin was contacted with 10 mL of 50 μM Fe(III) solutions in 0.1 M NaCl (blue dots), 1.0 M NaCl (yellow dots), 0.1 M NaCl containing 0.5 mM Na2H2EDTA (black dots), and 0.1 M NaCl containing 5 mM Na2H2EDTA (violet dots). The lines represent the best-fit curves of the experimental data points using eqn (5) and the sorption equilibria given by eqn (13). | ||
The experimental iron sorption data of Fig. 10 were processed as described in the case of zirconium by implementing the sorption equilibria (13) in the Gibbs–Donnan equation (eqn (5)). As for zirconium(IV), three reactions had to be considered to reproduce appropriately the variation of the sorbed iron(III) fraction as a function of pH. For each of the four experiments, the best fit (solid lines in Fig. 10) was again obtained by assuming a chemical model identical to that commonly accepted for the Fe3+/DFO− system in water, namely [Fe(DFO)], [Fe(DFO)H]+, and [Fe(DFO)H2]2+.37,56Table 4 summarizes the four sets of intrinsic sorption equilibrium constants together with their arithmetic means, which are quite similar to the values reported for Fe(DFO)@cellulose (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βi110 = 32.8(7)18). Accordingly, the protonation of the amino tether is characterised by log
βi110 = 32.8(7)18). Accordingly, the protonation of the amino tether is characterised by log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ki111 = 10.8(3), while the conversion of the trishydroxamato
Ki111 = 10.8(3), while the conversion of the trishydroxamato 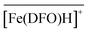 species to the bishydroxamato complex
species to the bishydroxamato complex  occurs only at very low pH, with log
occurs only at very low pH, with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ki112 = 0.7(3). Furthermore, the average βi11p (p = 0–2) values also match perfectly well with the complex formation constants reported by Evers et al. for 0.1 M KCl solutions,56 once corrected for medium effects24 using the Davies equation55 (Table 4).
Ki112 = 0.7(3). Furthermore, the average βi11p (p = 0–2) values also match perfectly well with the complex formation constants reported by Evers et al. for 0.1 M KCl solutions,56 once corrected for medium effects24 using the Davies equation55 (Table 4).
| Medium | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βi110 βi110 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βi111 βi111 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βi112 βi112 |
|---|---|---|---|
| a T = 298.2(2) K. b Thermodynamic complexation constant of Fe3+ by DFO3− (ref. 24), calculated by extrapolation to infinite dilution with the Davies equation55 of the experimental data reported by Evers et al. in ref. 56. The latter were determined by potentiometric titrations in 0.1 M KCl aqueous solution at 298.2 K. | |||
| 0.1 M NaCl | 32.8 | 43.3 | 44.4 |
| 1.0 M NaCl | 32.7 | 43.8 | 44.0 |
| 0.1 M NaCl + 0.5mM EDTA | 32.8 | 43.5 | 44.4 |
| 0.1 M NaCl + 5.0 mM EDTA | 33.0 | 43.8 | 44.4 |
| Average | 32.8(1) | 43.6(2) | 44.3(2) |
| H2O, I = 0 | 32.9b | 43.3b | 44.0b |
Desorption profiles for Fe(III)
Fig. 11 shows the desorption profiles obtained by contacting Fe(III) loaded DFO@Purolite resin with aqueous EDTA solutions (c = 0–0.01 M) at pH 3.5 and 6.5. Under such conditions, quantitative desorption of Fe(III) is impossible, as at best, only 15% of iron is released into solution at pH 3.5, while this amount does not even reach 5% at the higher pH value of 6.5, confirming the strong interaction between the cation and the hydroxamate active sites of the resin. NLLS processing of both data sets by eqn (5) returned a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K* value equal to 21.6 at pH 6.5 and to 14.4 at pH 3.5 by taking into account, for the computation of αFe, the hydrolysis and the complexation constants of Fe(III) with EDTA implemented in the MEDUSA database (Table S1 in the ESI†).54 These values are in good agreement with those computed from the complexation constants obtained by fitting the sorption profiles described in the previous paragraph (log
K* value equal to 21.6 at pH 6.5 and to 14.4 at pH 3.5 by taking into account, for the computation of αFe, the hydrolysis and the complexation constants of Fe(III) with EDTA implemented in the MEDUSA database (Table S1 in the ESI†).54 These values are in good agreement with those computed from the complexation constants obtained by fitting the sorption profiles described in the previous paragraph (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K* = 21.76 and 14.41 for pH 6.5 and 3.5, respectively). Therefore, all results are consistent with the set of reactions (eqn (13)) proposed for the Fe(III)/DFO@Purolite system. From a practical point of view, regeneration of the iron-loaded resin could be achieved by treating it 2–3 times with a more concentrated EDTA solution (0.1 M or more) over several days, until the solid recovered its original white colour.
K* = 21.76 and 14.41 for pH 6.5 and 3.5, respectively). Therefore, all results are consistent with the set of reactions (eqn (13)) proposed for the Fe(III)/DFO@Purolite system. From a practical point of view, regeneration of the iron-loaded resin could be achieved by treating it 2–3 times with a more concentrated EDTA solution (0.1 M or more) over several days, until the solid recovered its original white colour.
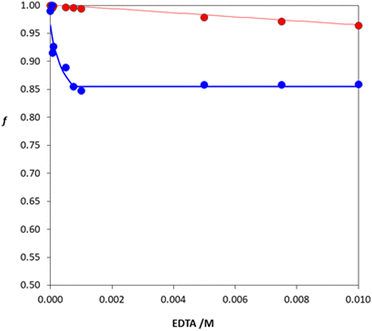 | ||
| Fig. 11 Desorption profiles of Fe(III) at pH 3.5 (blue circles) and at pH 6.5 (red circles) as a function of Na2H2EDTA concentration. Discontinuous procedure: 0.05 g of Fe(III)-loaded DFO@Purolite resin was contacted with 10 mL of 0.1 M NaCl acidified with HCl. The lines represent the best-fit curves of the experimental data points using eqn (5). | ||
Possible analytical applications of the DFO@Purolite resin
The performances of the DFO@Purolite resin pave the way towards numerous analytical applications of this material whenever a preconcentration of the analyte in highly diluted samples or a preliminary separation from other interfering species is required before analysis. Considering the chemical analogy between Fe(III) and Zr(IV) with tetravalent actinides, the former cations being often used as non-radioactive surrogates of the latter, the DFO@Purolite material offers new perspectives in environmental chemistry, e.g., for monitoring the migration of such radionuclides in contaminated soils or their content in natural waters at trace or even ultra-trace levels. Despite the high propensity of actinides to undergo hydrolysis even at very low pH, the diffusive gradients in thin-films (DGT) technology proved to be a convenient way to preconcentrate in situ these toxic elements, which are efficiently accumulated by the chelating resin incorporated in the binding gel layer.57Conclusions
In this paper, the sorption process of Zr(IV) and Fe(III) on a novel hydrophilic chelating resin has been unravelled by applying the Gibbs–Donnan formalism. The polymer, coined DFO@Purolite, was obtained at a multigram scale by functionalizing the commercial epoxy resin Purolite® ECR8209 with desferrioxamine B, a ubiquitous bacterial siderophore and well-known drug used in chelation therapy for treating iron or aluminium overloads and in 89Zr-based immuno-imaging by positron emission tomography. With a DFO loading of 0.20 mmol g−1, the uniform distribution of the organic chelator within the spherical particles was successfully assessed by recording the Tb(III) emission profile of complexed resin under biphotonic excitation with an optical microscope.The thorough characterisation of the sorption properties of the modified resin involved both the modelling of kinetic and thermodynamic data collected under different experimental conditions and ionic strengths of the supernatant liquid phase (I = 0.1 and 1.0 M NaCl). For each element, the sorption rate depends on the initial total metal concentration in solution, but equilibrium is reached much faster in the case of Fe(III) than Zr(IV). Under the experimental conditions adopted herein, the maximum equilibration time is about 30 min for iron versus 2 h for zirconium. The best description of the solid/liquid extraction profile versus time was achieved by considering a pseudo-first-order model, suggesting that the film diffusion, and not the complexation event, is the rate-limiting step of the uptake process.
The sorption isotherms recorded for both cations at pH 2 were shown to follow the Langmuir model. A maximum sorption capacity of qmax ∼ 0.2 mmol g−1 was obtained in both cases, in good agreement with the DFO loading determined by elemental analyses (% N and Fe) and acid–base titrations. This result suggests that all molecules of grafted chelator are accessible to the metal cations diffusing in and staying active for quantitative metal sorption on the solid phase.
Since a possible application of this innovative hybrid material is the uptake of Zr(IV) or Fe(III) from biological or environmental samples, a thorough knowledge of its behaviour at neutral and alkaline media is desired. To that end, sorption profiles collected as a function of pH in the 1–11 range were analysed by applying the Gibbs–Donnan model, which allowed evaluating the sorbed fraction under different conditions and for defining the complexation reactions in the solid phase.
In chloride media, the three identified Purolite-bound zirconium complexes were  ,
, 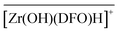 , and
, and  with Cl− as a counter anion. The associated complexation constants do not differ significantly from those reported in homogeneous aqueous solutions by Toporivska and Gumienna-Kontecka.37 For Fe(III), also three complexes were formed with the active sites of DFO immobilized on the solid phase, namely
with Cl− as a counter anion. The associated complexation constants do not differ significantly from those reported in homogeneous aqueous solutions by Toporivska and Gumienna-Kontecka.37 For Fe(III), also three complexes were formed with the active sites of DFO immobilized on the solid phase, namely 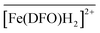 ,
, 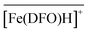 , and
, and  . These stoichiometries and stability constants are in good agreement with the commonly accepted Fe3+/DFO3− speciation model in aqueous solutions.
. These stoichiometries and stability constants are in good agreement with the commonly accepted Fe3+/DFO3− speciation model in aqueous solutions.
According to the metal-uptake performances of the DFO@Purolite resin, numerous analytical applications can be envisaged whenever separation or preconcentration steps before metal ion analyses are required.
Author contributions
Conceptualization: Giancarla Alberti and Michel Meyer; formal analysis: Giancarla Alberti and Camilla Zanoni; methodology: Raffaela Biesuz, Giancarla Alberti, Stéphane Brandès, Nicolas Maudoux, and Jean-Claude-Chambron; investigation: Osian Fonquernie, Stéphane Brandès, Agnese Amati, Vittorio Losi, and Sara Rovertoni; writing – original draft: Giancarla Alberti, Camilla Zanoni, Vittorio Losi, and Sara Rovertoni. Writing – review & editing: Michel Meyer, Raffaela Biesuz, Lisa Rita Magnaghi, and Jean-Claude Chambron.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The Agence Nationale de la Recherche (ANR project PLUTON, grant no. ANR-17-CE08-0053), the Centre National de la Recherche Scientifique (CNRS), the Conseil Régional de Bourgogne-Franche-Comté (CRBFC), the SATT SAYENS, and the European Regional Development Fund (FEDER) are gratefully acknowledged for their financial support. The authors wish to thank the DImaCell Imaging Facility for the use of the two-photon microscope and Pascale Winckler for technical assistance. DImaCell equipements were funded by the CRBFC and FEDER. Osian Fonquernie is indebted to the CRBFC and the FEDER for granting him a PhD fellowship. Camilla Zanoni and Lisa Rita Magnaghi are grateful to the Italian Ministero dell’Università e della Ricerca and to the University of Pavia for funding their PhD and post-doctoral grant, respectively.References
- N. Abbaspour, R. Hurrell and R. Kelishadi, J. Res. Med. Sci., 2014, 19, 164–174 Search PubMed.
- G. Crisponi and M. Remelli, Coord. Chem. Rev., 2008, 252, 1225–1240 CrossRef CAS.
- A. M. Albrecht-Gary and A. L. Crumbliss, in Metal Ions in Biological Systems. Iron Transport and Storage in Microorganisms, Plants, and Animals, ed. A. Sigel and H. Sigel, Marcel Dekker, New York, 1998, vol. 35, pp.239–327 Search PubMed.
- W. Wei, Z. T. Rosenkrans, J. Liu, G. Huang, Q.-Y. Luo and W. Cai, Chem. Rev., 2020, 120, 3787–3851 CrossRef CAS PubMed.
- J. R. Dilworth and S. I. Pascu, Chem. Soc. Rev., 2018, 47, 2554–2571 RSC.
- Y. W. S. Jauw, C. W. Menke-van der Houven van Oordt, O. S. Hoekstra, N. H. Hendrikse, D. J. Vugts, J. M. Zijlstra, M. C. Huisman and G. A. M. S. van Dongen, Front. Pharmacol, 2016, 7, 131 Search PubMed.
- S. Heskamp, R. Raavé, O. Boerman, M. Rijpkema, V. Goncalves and F. Denat, Bioconjugate Chem., 2017, 28, 2211–2223 CrossRef CAS.
- I. V. J. Feiner, M. Brandt, J. Cowell, T. Demuth, D. Vugts, G. Gasser and T. L. Mindt, Cancers, 2021, 13, 4466 CrossRef CAS.
- R. Raavé, G. Sandker, P. Adumeau, C. B. Jacobsen, F. Mangin, M. Meyer, M. Moreau, C. Bernhard, L. Da Costa, A. Dubois, V. Goncalves, M. Gustafsson, M. Rijpkema, O. Boerman, J.-C. Chambron, S. Heskamp and F. Denat, Eur. J. Nucl. Med. Mol. Imaging, 2019, 46, 1966–1977 CrossRef.
- G. Alberti, C. Zanoni, L. R. Magnaghi and R. Biesuz, Chemosensors, 2022, 10, 468 CrossRef CAS.
- Y. Takagai, H. Yamaguchi, T. Kubota and S. Igarashi, Chem. Lett., 2006, 36, 136–137 CrossRef.
- E. G. Roy, C. Jiang, M. L. Wells and C. Tripp, Anal. Chem., 2008, 80, 4689–4695 CrossRef CAS PubMed.
- B.-L. Su, N. Moniotte, N. Nivarlet, L.-H. Chen, Z.-Y. Fu, J. Desmet and J. Li, J. Colloid Interface Sci., 2011, 358, 136–145 CrossRef CAS PubMed.
- R. K. Shervedani and Z. Akrami, Biosens. Bioelectron., 2013, 39, 31–36 CrossRef CAS.
- N. Cennamo, G. Alberti, M. Pesavento, G. Agostino, F. Quattrini, R. Biesuz and L. Zeni, Sensors, 2014, 14, 4657–4671 CrossRef CAS.
- R. Biesuz, G. Emma, C. Milanese, G. Dacarro, A. Taglietti, V. M. Nurchi and G. Alberti, Analyst, 2014, 139, 3932–3939 RSC.
- G. Alberti, G. Emma, R. Colleoni, M. Pesavento, V. M. Nurchi and R. Biesuz, Analyst, 2014, 139, 3940–3948 RSC.
- G. Alberti, F. Quattrini, R. Colleoni, V. M. Nurchi and R. Biesuz, Chem. Pap., 2015, 69, 1024–1032 CAS.
- P. Galinetto, A. Taglietti, L. Pasotti, P. Pallavicini, G. Dacarro, E. Giulotto and M. S. Grandi, J. Appl. Spectrosc., 2016, 82, 1052–1059 CrossRef CAS.
- G. Alberti, G. Emma, R. Colleoni, V. M. Nurchi, M. Pesavento and R. Biesuz, Arabian J. Chem., 2019, 12, 573–579 CrossRef CAS.
- G. Alberti, C. Zanoni, L. R. Magnaghi, M. A. Santos, V. M. Nurchi and R. Biesuz, Chemosensors, 2020, 8, 111 CrossRef CAS.
- S. Faham, H. Golmohammadi, R. Ghavami and G. Khayatian, Anal. Chim. Acta, 2019, 1087, 104–112 CrossRef CAS PubMed.
- M. Pawlaczyk and G. Schroeder, ACS Omega, 2021, 6, 15168–15181 CrossRef CAS PubMed.
- L. Février, F. Coppin, S. Pierrisnard, M. Bourdillon, L. V. Nguyen, N. Zaiter, S. Brandès, V. Sladkov, J.-C. Chambron and M. Meyer, J. Environ. Radioact., 2021, 235–236, 106645 CrossRef PubMed.
- M. L. Rahman, M. S. Sarjadi, S. M. Sarkar, D. J. Walsh and J. J. Hannan, Coord. Chem. Rev., 2022, 471, 214727 CrossRef CAS.
- A. K. Sockwell and M. Wetzler, Chem. – Eur. J., 2019, 25, 2380–2388 CrossRef CAS PubMed.
- Y. Takagai, A. Takahashi, H. Yamaguchi, T. Kubota and S. Igarashi, J. Colloid Interface Sci., 2007, 313, 359–362 CrossRef CAS.
- J. Wenk, A. Sabiwalsky, J. Dissemond, C. Meewes, P. Brenneisen, M. Wlaschek, K. Scharffetter-Kochanek, A. Foitzik, V. Achterberg, A. Reitz and W. Meyer-Ingold, J. Invest. Dermatol., 2001, 116, 833–839 CrossRef CAS.
- Z. Yehuda, Y. Hadar and Y. Chen, J. Agric. Food Chem., 2003, 51, 5996–6005 CrossRef CAS.
- N. A. A. Rossi, Y. Zou, M. D. Scott and J. N. Kizhakkedathu, Macromolecules, 2008, 41, 5272–5282 CrossRef CAS.
- Y. Takagai, M. Abe, C. Oonuma, M. Butsugan, W. Kerlin, K. Czerwinski and R. Sudowe, Ind. Eng. Chem. Res., 2019, 58, 17928–17936 CrossRef CAS.
- J. D. Glennon, M. R. Woulfe, A. T. Senior and N. NiChoileain, Anal. Chem., 1989, 61, 1474–1478 CrossRef CAS.
- M. Pesavento, R. Biesuz, M. Gallorini and A. Profumo, Anal. Chem., 1993, 65, 2522–2527 CrossRef CAS.
- M. Pesavento and R. Biesuz, React. Funct. Polym., 1998, 36, 135–147 CrossRef CAS.
- M. Pesavento, R. Biesuz, G. Alberti and F. D. Riva, React. Funct. Polym., 2001, 46, 233–246 CrossRef CAS.
- M. Savastano, C. Bazzicalupi, G. Ferraro, E. Fratini, P. Gratteri and A. Bianchi, Molecules, 2019, 24, 2098 CrossRef CAS.
- Y. Toporivska and E. Gumienna-Kontecka, J. Inorg. Biochem., 2019, 198, 110753 CrossRef CAS PubMed.
- K. L. Summers, E. K. Sarbisheh, A. Zimmerling, J. J. H. Cotelesage, I. J. Pickering, G. N. George and E. W. Price, Inorg. Chem., 2020, 59, 17443–17452 CrossRef CAS.
- R. Imura, H. Ida, I. Sasaki, N. S. Ishioka and S. Watanabe, Molecules, 2021, 26, 4977 CrossRef CAS.
- Y. Merle and J. A. Marinsky, Talanta, 1984, 31, 199–204 CrossRef CAS PubMed.
- Ö. Szabadka, E. Varga and L. Nagy, Talanta, 2003, 59, 1081–1088 CrossRef PubMed.
- F. G. Helfferich, Ion exchange, McGraw-Hill, New York, 1962 Search PubMed.
- A. Ringbom and E. Still, Anal. Chim. Acta, 1972, 59, 143–146 CrossRef CAS.
- R. Biesuz, A. A. Zagorodni and M. Muhammed, J. Phys. Chem. B, 2001, 105, 4721–4726 CrossRef CAS.
- G. Tircsó, Z. Garda, F. K. Kálmán, Z. Baranyai, I. Pócsi, G. Balla and I. Tóth, J. Inorg. Biochem., 2013, 127, 53–61 CrossRef PubMed.
- J.-C. G. Bünzli and C. Piguet, Chem. Soc. Rev., 2005, 34, 1048–1077 RSC.
- G. Alberti, V. Amendola, M. Pesavento and R. Biesuz, Coord. Chem. Rev., 2012, 256, 28–45 CrossRef CAS.
- S. Yamada, I. Yamauchi and A. Murata, Anal. Sci., 1995, 11, 903–908 CrossRef CAS.
- I. Langmuir, J. Am. Chem. Soc., 1916, 38, 2221–2295 CrossRef CAS.
- M. Pesavento, R. Biesuz, G. Alberti and M. Sturini, Anal. Bioanal. Chem., 2003, 376, 1023–1029 CrossRef CAS PubMed.
- G. Alberti, R. Biesuz, A. Profumo and M. Pesavento, J. Inorg. Biochem., 2003, 97, 79–88 CrossRef CAS PubMed.
- R. Biesuz, G. Alberti, G. D’Agostino, E. Magi and M. Pesavento, Mar. Chem., 2006, 101, 180–189 CrossRef CAS.
- G. Alberti, M. Pesavento and R. Biesuz, React. Funct. Polym., 2007, 67, 1083–1093 CrossRef CAS.
- I. Puigdomenech, MEDUSA – Chemical Equilibrium Diagrams Program, Royal Institute of Technology, Stockholm, Sweden, 2010 Search PubMed.
- C. W. Davies, Ion association, Butterworths, London, 1962 Search PubMed.
- A. Evers, R. D. Hancock, A. E. Martell and R. J. Motekaitis, Inorg. Chem., 1989, 28, 2189–2195 CrossRef CAS.
- R. Cusnir, M. Jaccard, C. Bailat, M. Christl, P. Steinmann, M. Haldimann, F. Bochud and P. Froidevaux, Environ. Sci. Technol., 2016, 50, 5103–5110 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: FTIR spectra, TGA, SEM images, emission spectra, two-photon fluorescence microscopy images of pristine and modified Purolite resin, and a table of auxiliary equilibrium constants. See DOI: https://doi.org/10.1039/d3nj00903c |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2023 |



