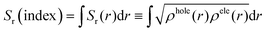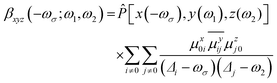Open Access Article
Open Access ArticleBis-TTF-Ge derivatives: promising linear and nonlinear optical properties, a theoretical investigation†
Dalila
Kamli
ab,
Douniazed
Hannachi
 *ac,
Djamila
Samsar
d and
Henry
Chermette
*ac,
Djamila
Samsar
d and
Henry
Chermette
 *e
*e
aLaboratoire d’Électrochimie, d’Ingénierie Moléculaire et de Catalyse Redox (LEIMCR), Département d’Enseignement de Base en Technologie, Faculté de Technologie, Université Ferhat Abbas, Sétif-1, Algérie. E-mail: h_douniazed@yahoo.fr
bDépartement des sciences de la matière, Faculté des Sciences, Université de Khenchela, Algérie
cDépartement de Chimie, Faculté des Sciences, Université Ferhat Abbas, Setif-1, Algérie
dInstitut D’Hygiène et Sécurité Industrielle, Département de Socle commun Hygiène et Sécurité Industrielle, Université de Batna-2, Algérie
eUniversité de Lyon, Université Claude Bernard Lyon 1, Institut des Sciences Analytiques, UMR CNRS 5280, 69622 Villeurbanne Cedex, France. E-mail: henry.chermette@univ-lyon1.fr
First published on 6th December 2022
Abstract
In this work, based on bis(tetrathiafulvalenyldithio)-germane (bis-TTF-Ge), 37 compounds (denoted T0–T36) are designed by the introduction of donor and acceptor groups at different substituent positions. The ground state electronic structures, reactivity indices, electronic transition, charge transfer properties (charge, distance and dipole moment), hyper-Rayleigh scattering and depolarization ratios (static and dynamic) of these compounds are fully investigated using DFT and TD-DFT calculations. The quantum calculations were performed at the CAM-B3LYP/6-311g(d,p) level and using the sum-over-states (SOS) approach in both static and dynamic cases. The chemical hardness (η) of the two substituted bis-TTF-Ge derivatives at the b position has a smaller value than those with the same substituent at positions d, e, a and c. In both static and dynamic regimes the investigations show that the bis-TTF-Ge derivatives substituted with donor or acceptor groups have larger first hyperpolarizability than T0. Our work predicts that the introduction of the substituent group at the b position can increase the hyperpolarizability values more than those at the other positions, and the NO2, NO and COCN acceptor groups lead to the largest values. For example, the dynamic βλ=1064HRS value of T25 is about 145 times larger than that of T0 and about 11 times that in the static regime. Interestingly, the βλ=1064HRS of bis-TTF-Ge substituted with the NO2 group increases with the number of NO2 in the TTF fragment. The large nonlinear optical (NLO) origin of bis-TTF-Ge substituted with NO2, NO and COCN is attributed to charge transfer from the TTF to the acceptor group at the second TTF fragment (overlap Sr index = 0). The studied bis-TTF-Ge substituted with NO2 compounds exhibits the possibility of being an excellent second-order NLO material.
Introduction
Nonlinear optics (NLO) is the study of the interaction of high intensity light with matter. In linear optics the relation between polarization (P) and electric field (E) is linear and the frequency is kept. For an intense laser light, this linearity no longer holds and one gets different kinds of frequencies; this frequency transformation has been observed experimentally by Franken,1 and the intense light induces a change in the refraction index of the material (optical Kerr effect), which leads to a phenomenon called the self-phase modulation.2 The induced polarization at the macroscopic level is generally written as3| ΔP = χ(1)E + χ(2)E2 + χ(3)E3 + ⋯ |
Since the discovery of lasers by Maiman and Collins in 19604,5 great interest has been devoted to the discovery and design of new materials with excellent nonlinear optical properties. This is due to their important applications in different areas such as in photonic devices such as molecular switching, frequency doubling, telecommunications and optical information processing.6–12
Numerous techniques for developing new high-performance NLO materials have been proposed, including diradical characterization,13 synthesis of molecular structures of electron-donor (D)–π–electron-acceptor (A) (D–π–A),14 reinforcing push–pull effects,15,16 designing octupolar compounds,17,18 multidecker sandwich complexes,19 asymmetric coordination complexes,20–23 excess electrons,24–29etc. Among the studied NLO materials the inorganic compounds have attracted exceptional interest because of their physicochemical stability and thermal stability.30,31 For example, tetrathiafulvalene (TTF) derivatives present excellent second- and third-order nonlinear optical responses, and they are a very active field in contemporary chemistry since shortly after their first synthesis in the early 1970s by Wudl and co-workers.32,33 These properties are derived from the large π conjugated systems, the strong electron-donor character and the existence of polarizable sulfur atoms, leading to charge density redistribution within the molecule.34–36
The combination of the TTF group and electron acceptor (A) units that are covalently linked by a π-conjugated bridging group is highly desirable and classified as excellent push–pull organic molecules (D–π–A). So far, TTF–π–A as promising NLO materials have been widely studied by many scientific researchers, because these compounds exhibit intramolecular charge transfer (ICT) and have low energy-gaps.37–39
On the other hand, the binding of the TTF group with transition metals (TM) through covalent linkages or via electrostatic interactions allows the development of new metal complexes with π-conjugated ligands and can present a respectable class of NLO materials.36,40–42 For example, in 2015, Liu and coworkers studied static and dynamic HRS hyperpolarizability of a series of extended tetrathiafulvalene (exTTF) and TTF derivatives of metal cations (TM: Ni2+, Cu2+, Mg2+, Zn2+ and Cd2+) and they found that the TM complexes containing the redox-active TTF unit and the pyridine group exhibit large hyperpolarizability values.43 In addition, the nonlinear optical responses of several square-planar metal TTF complexes44,45 have been studied theoretically and experimentally and have shown the important role of the ligand in perturbing the electron distribution in these complexes and its effect on both the ground and the excited states and, thus, on the linear and nonlinear optical properties.46–51 In recent years growing attention has been expressed concerning germanium, and this interest is due to its high carrier mobility, good stability so that Ge is the most logical candidate to substitute carbon; moreover, it has also potential applications in photodetectors and nonlinear optical fields.52–60
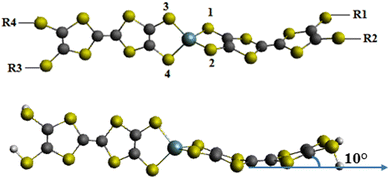
Ueda et al.61 reported spiro molecules: bis(tetrathiafulvalenyldithio)-germane (here named bis-TTF-Ge T36, see Fig. 1). This asymmetric compound which contains large π systems should be a potential second-order NLO material. In this work, our aim is to study the effects of acceptor/donor substituents (NO, CN, COCN, CHO, NO2, NH2 and NMe2) and the substituent positions (a, b, c, d and e; see Fig. 1) on the reactivity indices, and the linear and nonlinear optical properties of bis-TTF-Ge compounds. Also in this study, we focus to offer new perspectives with respect to the origin of nonlinear optical materials for title compounds. Furthermore, to the best of our knowledge, there are no computational studies that address in detail the effect of the number and the nature of substituent groups in compounds made of two TTF groups linked by spiro germanium on the NLO properties.
Computational details
The geometries of the bis-TTF-Ge derivatives were fully optimized using Coulomb-attenuating exchange–correlation density functional method CAM-B3LYP62 using the 6-311g(d,p)63,64 basis set. CAM-B3LYP is a long-range corrected functional developed to handle the inaccuracies of the non-Coulomb part of the exchange functional at long distances. Quantum chemical calculations were performed using the Gaussian 09 program with the TIGHT SCF convergence and ultra-fine integration grid.65–67 No symmetry constraints were applied and the local minima were confirmed on potential energy surface by frequency calculations of the ground state for bis-TTF-Ge compounds at the same level.Chemical reactivity analysis takes advantage of its ground in DFT through a functional Taylor expansion of energy that introduces several reactivity descriptors from energy derivatives of chemical significance.68 According to finite difference approximation and Koopmans’ theorem69–71 the electronic chemical potential (μ) and global hardness (η) can be evaluated from the frontier orbital energies HOMO and LUMO (εH and εL, respectively).
Electronic chemical potential (μ) is the tendency of an atom or molecule to attract electrons; it is given by the following equation:
 | (1) |
The chemical hardness (η) expresses the resistance of a system to change its number of electrons; it is calculated using the relation
| η = εL − εH | (2) |
Global electrophilicity index (ω), introduced by Parr et al.,72 is calculated from the hardness and chemical potential:
 | (3) |
This index expresses the ability of a molecule to accept electrons from the environment.
Furthermore, to investigate and understand the electronic transition and optical properties, the electron excitation energies, oscillator strengths, for the studied compounds were calculated at the TD-CAM-B3LYP level.
The hyper-Rayleigh scattering (HRS) technique involves the detection of the incoherent scattering second harmonic generation at frequency 2ω from a laser with frequency ω incidence. In HRS, we can evaluate the first hyperpolarizability βHRS and its depolarization ratios DR, through the relation6,73,74
 | (4) |
 | (5) |
Previous works have pointed out that CAM-B3LYP, adopted in this work, can provide an absorption spectrum close to experimental results and has been proven to be efficient in calculating the static and dynamic NLO responses.7,75–77 Frequency-dependent hyperpolarizabilities were calculated using an incident wavelength of 1064 nm.
The electron density difference maps (EDDM) corresponding to the crucial excited states can be accurately evaluated as follows:
| Δρ(r) = ρex(r) − ρGS(r) |
Following the procedure proposed by Bahers et al.78 the excited states of interest were examined using charge-transfer indices (CT) including charge-transfer distance (dCT). The product of these quantities dCT and qCT (transferred charge) gives the variation in the dipole moment between the ground and the excited states (Δμ0→n = dCT × qCT).
On the other hand, the overlap distribution between the holes and electrons can be expressed as
In our work, the crucial excited state wavefunctions have been obtained by natural transition orbitals (NTOs) in terms of “excited particle” to “empty hole” of the electronic transition density matrix. The CT indices have been determined using the MULTIWFN program.79
Results and discussion
The optimized geometries of bis-TTF linked by a germane noted Ti (i = 0–36) compounds obtained from DFT quantum chemical calculations is shown in Fig. 2 along with the atom numbering schemes. As can be seen from the figure, the optimized structure of the bis-TTF-Ge is tetrahedral, in which the Ge–S (S is S1, S2, S3 and S4) average length is 2.259 Å and the ∠S3–Ge–S4 and ∠S1–Ge–S2 angles are ∼97° whereas ∠S1–Ge–S3 and ∠S2–Ge–S4 are about 115°. On the other hand, the TTF groups deviate slightly from the perfect planar geometry by 10°, showing a slightly distorted geometry. One of the reasons for this distortion is a steric repulsion between the sulphur atoms and the d orbitals from the germanium atom.On the other hand we can observe that the TTF fragments in the title compounds are distorted into a boat conformation as shown in Fig. 2 in their ground state and this shape agrees well with the available studies. For instance, Demiralp et al. in their study of organic donors (X) containing the TTF group found that X+ always has a planar TTF region but that the neutral is distorted into a boat conformation.80 They suggested that the off-planar geometry is caused by ring strain, which is developed when the H atoms of TTF are substituted by bulky ligands.48 Furthermore, Linker et al. in their study of ethylenedioxy-TTF (EDO-TTF) indicated that a neutral derivative has a boat-shaped conformation, whereas the positively charged EDO-TTF is planar.81
Reactivity
The values of the HOMO and LUMO frontier orbital energies (EHOMO and ELOMO, respectively), the electronegativity (χ), the chemical hardness (η) and the electrophilicity index (ω), calculated for each bis-TTF-Ge compound, are given in Table 1.| Ti | E HOMO | E LUMO | η | χ | ω | |
|---|---|---|---|---|---|---|
| T0 | −5.311 | −2.577 | 2.733 | 3.944 | 2.845 | |
| a | T1 | −5.329 | −3.495 | 1.834 | 4.412 | 5.307 |
| b | T2 | −5.341 | −3.776 | 1.564 | 4.558 | 6.644 |
| c | T3 | −5.361 | −3.505 | 1.855 | 4.433 | 5.296 |
| d | T4 | −5.374 | −3.790 | 1.583 | 4.582 | 6.631 |
| e | T5 | −5.430 | −3.798 | 1.631 | 4.614 | 6.523 |
| a | T6 | −5.388 | −2.708 | 2.680 | 4.048 | 3.057 |
| b | T7 | −5.429 | −2.786 | 2.642 | 4.107 | 3.192 |
| c | T8 | −5.670 | −2.838 | 2.832 | 4.254 | 3.195 |
| d | T9 | −5.710 | −2.914 | 2.795 | 4.312 | 3.326 |
| e | T10 | −5.860 | −2.985 | 2.874 | 4.423 | 3.402 |
| a | T11 | −5.377 | −2.957 | 2.419 | 4.167 | 3.589 |
| b | T12 | −5.429 | −3.374 | 2.054 | 4.401 | 4.715 |
| c | T13 | −5.600 | −3.000 | 2.600 | 4.300 | 3.555 |
| d | T14 | −5.701 | −3.416 | 2.284 | 4.559 | 4.548 |
| e | T15 | −5.855 | −3.437 | 2.418 | 4.646 | 4.463 |
| a | T16 | −5.361 | −2.657 | 2.703 | 4.009 | 2.973 |
| b | T17 | −5.400 | −2.728 | 2.672 | 4.064 | 3.091 |
| c | T18 | −5.527 | −2.738 | 2.788 | 4.132 | 3.062 |
| d | T19 | −5.528 | −2.746 | 2.782 | 4.137 | 3.076 |
| e | T20 | −5.710 | −2.878 | 2.831 | 4.294 | 3.256 |
| a | T21 | −5.382 | −3.009 | 2.373 | 4.195 | 3.708 |
| b | T22 | −5.412 | −3.790 | 1.622 | 4.601 | 6.523 |
| c | T23 | −5.624 | −3.054 | 2.570 | 4.339 | 3.663 |
| d | T24 | −5.653 | −3.834 | 1.819 | 4.744 | 6.184 |
| e | T25 | −5.838 | −3.798 | 2.039 | 4.818 | 5.691 |
| a | T26 | −5.247 | −2.576 | 2.671 | 3.912 | 2.864 |
| b | T27 | −5.019 | −2.450 | 2.569 | 3.734 | 2.714 |
| c | T28 | −5.199 | −2.502 | 2.697 | 3.851 | 2.749 |
| d | T29 | −4.996 | −2.413 | 2.583 | 3.704 | 2.656 |
| e | T30 | −4.971 | −2.363 | 2.607 | 3.667 | 2.578 |
| a | T31 | −5.203 | −2.536 | 2.667 | 3.870 | 2.807 |
| b | T32 | −5.031 | −2.451 | 2.579 | 3.741 | 2.713 |
| c | T33 | −5.179 | −2.495 | 2.684 | 3.837 | 2.743 |
| d | T34 | −4.989 | −2.409 | 2.580 | 3.699 | 2.651 |
| e | T35 | −4.964 | −2.323 | 2.641 | 3.644 | 2.513 |
| e | T36 | −5.291 | −2.715 | 4.003 | 2.575 | 3.111 |
The electronegativities (χ = −μ) of the T1 to T25 bis-TTF-Ge which are substituted with the acceptor group increases with the number of acceptor groups in the title compounds. These results indicate that the trend of the electrons to leave the equilibrium systems increases from the four-acceptor substituted (e) to one-substituted (a) bis-TTF-Ge. The reverse trend is observed for the bis-TTF-Ge with the electron donor R (NH2 and NMe2), so it can be concluded that the bis-TTF-Ge with four electron donors (e) have the largest tendency to donate electrons than d, b, c and a, respectively.
On the other hand, we observe that the substituent position and the number of the substitution play an important role in the stability of studied bis-TTF-Ge. In each group with the same substituent, the substituent position b has a smaller hardness than the d, e, a and c substituent positions. The CHO and CN substituents in bis-TTF-Ge compounds show a decrease according to the following order: a, d, c and e. The ordering of the chemical hardness at the a position is T1 (NO) < T21 (NO2) < T11 (COCN) < T31 (NMe2) < T26 (NH2) < T6 (CN) < T16 (COH). The smallest η values are obtained for acceptor substituents and similar trends for the substituent positions b, c, d and e. Therefore, the hardness of bis-TTF-Ge can be effectively reduced when substituent positions are substituted with acceptor groups. According to the theoretical scale of electrophilicity proposed by Domingo et al.82 of global electrophilicity power (ω) the title compounds can be assigned to a strong electrophile class (2.51 to 6.70 eV).
Electronic transitions
The TD-DFT calculation results of absorption spectra parameters such as excitation energy (ΔE), absorption wavelength (λ) and corresponding oscillator strength (f), charge transfer parameters (qCT, dCT, and Δμ0→i) and Sr index are calculated at the CAM-B3LYP/6-311g(d,p) level and summarized in Table S1 (ESI†).The simulated spectra and the electron density difference maps (EDDMs) are provided in Fig. 3 and Fig. S1, S2 (ESI†), respectively. In general, the absorption spectra of the title compounds are characterized by a strong band (B3) at 267 nm, two weak bands (B1 and B2) and two moderate absorption shoulders (S1 and S2).
The bis-TTF-Ge with NO electron acceptor substituents have five absorption bands, and their absorption wavelength range extends to 750 nm. T1, T2 and T3 show electronic transitions at 727, 680–637 and 654 nm, respectively, with small oscillator strength (f ≤ 0.001), mainly arising from TTF rings 1, 2, and 3 to NO, from TTF rings 1–3 to NO (at positions R1 and R2) and from rings 5 and 6 to NO (at position R3) respectively. The HOMO → LUMO excitations of T1, T2 and T3 are located at 307, 456 and 418 nm, respectively, mainly ascribed to a π → π* charge transfer (CT) character. The electronic transitions of T5 are assigned as a CT from rings 1, 2, 5, and 6 to four NO units (677, 637 and 455 nm) and from rings 1, 2, 5, and 6 to the 4S–Ge unit (at 400 and 289 nm). For T4, the electronic transition appears in the 676, 455 and 316 nm from rings 1–2 to NO (at positions R1 and R2) and from rings 5–6 to S–NO (positions R1 and R2) π → π* CT character, besides the electronic transition at 290 nm (f = 0.132) from rings 5–6 to NO (at position R3) and to the 4S-Ge unit.
For the T6 to T10 compounds, the HOMO → LUMO transition at ∼399 nm is a charge transfer from rings 6 and 5 to 4S-Ge. The bis-TTF-Ge T6 is also ascribed to the same CT character at 292 nm (f = 0.141). For T8 the absorption bands located at 304 and 243 nm, with large oscillator strength, mainly arise from rings 1 and 2 to 4S-Ge and CN (at position R3). For bis-TTF-Ge T10, it involves three CT characteristic bands at 363, 279 and 241 nm from rings 1–3 to C–S–COCN units attached to ring 1, from TTF rings to 4S-Ge (f = 0.198) and from ring 6–5 to C–S–COCN (at R1 and R2 positions) and C3–C4 atoms attached to ring 6 (f = 0.129), respectively. For T7 and T9, the absorption at 276 nm (f = 0.234 and 0.191, respectively) have a mixed character of charge transfer from rings 5 and 6 to S–CN units at the R1 and R2 positions of type n → π* and π → π* electronic transition.
For T14 and T15, the electronic transition at 374 and 351 nm, respectively, is mainly ascribed to the n → π* and π → π* CT mixed character from rings 4, 5 and 6 to S–COCN unit at position R3. The transition at 400 nm of T14 and T15 mainly comes from rings 1–3 to S-COCN (at R1 and R2 positions). The electronic transition of T13 at 398 and 359 nm arises from rings 5 and 6 to 4S-Ge and from rings 1, 2, 5 and 6 to two COCN units CT, respectively.
For T16, T17 and T19 the HOMO → LUMO transition at ∼401 nm is CT from rings 6 and 5 to the 4S-Ge unit. For T16 and T19 the HOMO−2 → LUMO and HOMO−1 → LUMO+4 excitations are CT from rings 1 and 2 to 4S-Ge unit and from rings 1–3 to 4–6, respectively (see Table S1 and Fig. S2, ESI†). Bis-TTF-Ge T18 exhibits absorption at 398 nm (HOMO → LUMO) with a charge transfer from rings 1, 2, 5 and 6 to the 4S-Ge unit. The T20 compound has three absorption bands at 397, 304 and 278 nm with a charge transfer character from rings 6 and 5 to 4S-Ge, from rings 6 and 5 to the four units S–CHO and from rings 1, 2, 5 and 6 to the 4S-Ge unit, respectively.
The bis-TTF-Ge with NH2 and NMe2 electron donors show three main absorption bands. The most intense absorption band of Ti (i = 26 to 35) is at 269 nm, with the largest oscillator strength, mainly coming from intra-rings charge transfer (ICT). The band at ∼404 nm is formed by a charge transfer from rings 1 and 2 to 4S-Ge unit from HOMO → LUMO. The absorption band at ∼310 nm shows that the electronic transitions have a mixed character of charge transfer from rings 1–3 to rings 4–6 of type n → π* and π → π* electronic transition.
For T21, the electronic transition at 434 and 295 nm is assigned as a CT from rings 1 and 2 to S–NO2 and from rings 5 and 6 to S–NO2, respectively. For T23, there is a charge transfer from rings 1, 2, 5 and 6 to S–NO2 (at the R4 position) and to the 4S-Ge unit.
For T25, it is interesting to find that there is a CT from rings 2 and 3 to two units C–S–NO2 (at R1 and R2 positions), from rings 1–2 and 5–6 to the 4S-Ge unit and from rings 4–6 to the C–S–NO2 unit (at R1 and R2 positions) at 524, 394 and 325 nm, respectively; besides n, π → π* mixed CT from 1–3 to 4–6 rings and from rings 2–3 and 5–6 to C–S–NO2 (at ring 6). For T22, the electronic transition arises from rings 1–2 to S–NO2 and from rings 4–6 to S–NO2 (at R1 and R2 positions), from rings 5–6 to 4S-Ge and from rings 1–2 to 4S-Ge. For bis-TTF-Ge T24, the electronic transition is mainly ascribed to a n, π → π* mixed character from rings 2–3 to S–NO2 (at R1 and R2 position), from rings 4–6 to S–NO2 (at R1 and R2 positions) and to S–NO2 at the R3 position.
TD-DFT calculations on bis-TTF-Ge T0–T36 compounds show that the wavelength of the largest oscillator strength located at ∼266 nm, are due to n → π* and π → π* mixed character type intra-TTF electron transition (see Table S1 and Fig. S1, ESI†). Furthermore, these excitations show a relatively small dCT and a large Sr index, indicating that the hole and electron are very close. For example, for T0, T36, T13, T18, T23 and T16 the electron density difference maps (EDDM) of this transition, shown in Fig. 4, reveals a significant intramolecular CT (ICT) and, for all compounds, is reported in the ESI† in Fig. S2.
On the other hand, the TD-DFT results show that the electronic transition HOMO → LUMO for T2, T4, T11, T12, T21, T22 and T24 (R = NO, COCN and NO2; position is a, b and d) is a strong non-local excitation as indicated by the overlapping index between the hole and the electron which is zero (Sr = 0, Table S1, ESI†).
Overall, T22, T24 and T25 show red-shift wavelength absorption compared to T23 and T12. On the other hand, the absorption wavelengths of T6 to T10 are close to T16 to T20. Furthermore, this study displays that the bis-TTF-Ge with electron-acceptor substituents (NO2 and NO) shows a red-shift wavelength absorption compared to the Ti with donor electron substituents. In general, from this calculation, we can conclude that the electronic transition characters and the absorption wavelength of Ti compounds can be tuned through the introduction of the electron donors or electron acceptor substituents at different positions.
Nonlinear optical properties
In current years, quantum chemical calculations have become a widely accepted method for predicting new NLO materials.20,21 For the NLO calculation we carried out a test on T36 with the 6-311++G and 6-311G(d,p) basis set, but did not find significant differences (see Fig. S3, ESI†). This is no surprise because of the quasi linear shape of the molecules and the 6-311G(d,p) basis is a good choice for the title compounds. On the other hand, we calculated the dynamic hyperpolarizabilities at the λ value of 1064 nm (ω = 0.04282 a.u.), which is sufficiently apart from the observed lowest-energy absorption of the title compounds (the λMax values are in the range 250–270 nm). It is known that it is difficult to compare the calculated dynamic first hyperpolarizabilities to the experimental data measured under resonance conditions.83 However the tendency is very similar between experimental and theoretical values,77 and one has hyperpolarizabilities (experimental) > hyperpolarizabilities (dynamic) > hyperpolarizabilities (static) and our calculation shows the same tendency: hyperpolarizabilities (dynamic) > hyperpolarizabilities (static).The second-order nonlinear responses calculated in the static (λ = ∞) and dynamic (λ = 1064 nm) regimes for the 37 derivatives are summarized in Table 2. The reported quantities include the hyper-Rayleigh scattering (βHRS) hyperpolarizabilities and the associated depolarization ratio (DR).
| Ti | μ | DRλ=∞ | β λ=∞HRS | DRλ=1064 | β λ=1064HRS | |
|---|---|---|---|---|---|---|
| T0 | 2.048 | 1.503 | 75 | 1.407 | 137 | |
| a | T1 | 0.797 | 3.817 | 440 | 4.629 | 1266 |
| b | T2 | 0.955 | 5.247 | 782 | 7.147 | 3397 |
| c | T3 | 0.014 | 1.862 | 314 | 1.720 | 1015 |
| d | T4 | 0.702 | 3.505 | 464 | 5.108 | 2469 |
| e | T5 | 1.005 | 2.34 | 317 | 1.541 | 1140 |
| a | T6 | 4.492 | 3.679 | 263 | 4.278 | 501 |
| b | T7 | 7.508 | 5.729 | 416 | 6.576 | 742 |
| c | T8 | 1.436 | 2.053 | 152 | 1.812 | 246 |
| d | T9 | 4.290 | 3.907 | 231 | 3.067 | 383 |
| e | T10 | 5.674 | 1.781 | 173 | 1.407 | 390 |
| a | T11 | 4.271 | 4.731 | 644 | 5.215 | 1566 |
| b | T12 | 6.626 | 5.387 | 627 | 7.022 | 1374 |
| c | T13 | 1.070 | 2.316 | 371 | 2.322 | 858 |
| d | T14 | 3.643 | 1.915 | 324 | 1.859 | 807 |
| e | T15 | 3.440 | 2.739 | 234 | 1.845 | 629 |
| a | T16 | 3.294 | 2.693 | 180 | 3.256 | 360 |
| b | T17 | 5.625 | 3.913 | 265 | 5.131 | 576 |
| c | T18 | 1.829 | 1.688 | 116 | 1.676 | 206 |
| d | T19 | 2.623 | 2.633 | 150 | 3.137 | 331 |
| e | T20 | 1.501 | 1.633 | 104 | 1.326 | 271 |
| a | T21 | 4.106 | 3.92 | 713 | 4.27 | 2859 |
| b | T22 | 6.091 | 4.499 | 800 | 1.145 | 9638 |
| c | T23 | 2.939 | 2.378 | 709 | 1.902 | 2726 |
| d | T24 | 2.583 | 2.527 | 829 | 1.754 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
| e | T25 | 2.836 | 1.952 | 761 | 0.749 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 810 810 |
| a | T26 | 4.838 | 2.447 | 103 | 1.942 | 185 |
| b | T27 | 3.384 | 4.077 | 327 | 3.741 | 602 |
| c | T28 | 1.694 | 2.793 | 118 | 1.914 | 194 |
| d | T29 | 2.717 | 4.596 | 295 | 4.054 | 581 |
| e | T30 | 4.024 | 1.538 | 115 | 1.422 | 183 |
| a | T31 | 4.919 | 2.813 | 110 | 2.158 | 189 |
| b | T32 | 2.567 | 4.724 | 192 | 4.061 | 369 |
| c | T33 | 0.912 | 4.829 | 110 | 2.265 | 173 |
| d | T34 | 2.014 | 6.843 | 185 | 5.122 | 364 |
| e | T35 | 1.388 | 3.059 | 111 | 2.779 | 158 |
| e | T36 | 4.024 | 1.538 | 116 | 1.422 | 183 |
For bis-TTF-Ge T26, T28, and T30 their βλ=∞HRS values are close to the value of T31, T33 and T35 (∼111 a.u.) which indicates that when the NH2 (at a, c and e positions) is replaced by the NMe2 group the effect on the βHRS value is not significant. On the other hand, the βλ=∞HRS value calculated for T26, T28, T30–T31, T33 and T35 are relatively close to the value of T0 (75 a.u.). We can observe that the dynamic regime has the same behavior as the static regime for NH2 and NMe2 donor groups. Furthermore, the hyperpolarizability βλHRS (λ = ∞, 1064 nm) of T27 and T29 are three times larger than that of the T26, T28 and T30. For T32 and T34 the βλHRS values are about twice that of T31, T33 and T35. We can observe that the introduction of donor substituents (NH2 and NMe2) at b and d positions can increase the hyperpolarizability of bis-TTF-Ge. For T1–T5 (acceptor NO unit) the βλHRS (static and dynamic) of T2 is found to be about twice larger than that of T1, T3, T4, and T5.
For bis-TTF-Ge T11–T12, the βλHRS values are larger than those of T13, T14 and T15, respectively. Comparing βλ=1064HRS values of T11–T12 and T0, it can be seen that the T11–T12 values are about 11 times larger than that of T0. For bis-TTF-Ge substituted by CN and CHO units, the βHRS (static and dynamic) values are also larger in the substitution at b and a positions than for d, c and e. For T6–T10, T11–T15 and T16–T20 compounds, we observe that the βλ=∞HRS and βλ=1064HRS values of bis-TTF-Ge substituted by the acceptor COCN group are larger than that of bis-TTF-Ge substituted by CN and COH group at the same substituent position, respectively.
In static and dynamic regimes, the compounds T21–T25 exhibit larger hyperpolarizability values than the other bis-TTF-Ge compounds, which show that the introduction of the acceptor NO2 group can effectively enhance βλHRS values. This observation is in line with Gong et al.'s study of helicenes84 and linear [3]spirobifluorenylene.85 On the other hand, the βλ=∞HRS decreases slightly from T29 ≈ T27 to T25, T21 and T23, respectively, indicating that the substituent position (number) of NO2 substitutions in bis-TTF-Ge have little effect on the βλ=∞HRS values. On the other hand, the βλ=1064HRS values decrease in the order T25 > T24 > T22 > T21 ≈ T23, indicating that the βλ=1064HRS increases with the number of NO2 groups in the bis-TTF-Ge compound (see Fig. 5). The βλ=1064HRS value of T25 is about 7 times larger than that of T23. Furthermore, the βλ=∞HRS value calculated for T0 (and T36) is about 11 times smaller than that of T21–T25 and βλ=1064HRS of T25, T24, T22 and T21 is 145, 92, 70 and 20 times larger than that of T0, respectively.
 | ||
| Fig. 5 Static and dynamic hyperpolarizability values for T21–T25 calculated at the CAM-B3LYP/6-311g(d,p) level. | ||
From this study, we observed that the substituent position b has a stronger effect on the enhancement the βλHRS value than the a, c, d and e substituent positions. Comparing T0 and the bis-TTF-Ge substituent position b, it is found that the βλ=∞HRS values of T2, T12, T7, T17, T27 and T32 is about 10, 8, 6, 4, 4 and 3 times larger than that of T0, respectively, and the βλ=1064HRS value of these compounds is about 25, 10, 5, 4, 4 and 3 times larger than that of T0, respectively. We conclude that the highest hyperpolarizability value can be obtained by the introduction NO2, NO or COCN acceptor groups at the b position for bis-TTF-Ge.
The experimental study of Bao et al.,86 shows that the different numbers (mono-, di-, tri-, and tetra-) of ester substituents as well as their position (trans and cis) have a significant influence on the NLO properties of tetraphenylporphyrins. They indicate that the compounds with four ester groups present a small value of hyperpolarizability. In the static regime, the same results are observed for title compounds, excepting the bis-TTF-Ge substituted with NO2 group (see Fig. 5 and Table 2).
Generally, in the dynamic regime, the hyperpolarizability is 2–5 times larger than that in the static regime, excepting T22, T24 and T25, where βλ=1064HRS is about 26, 15 and 12 times larger than the βλ=∞HRS, respectively. The static hyperpolarizability of T1 to T35 is about 2–11 times larger than that of T0.
On the other hand, the TD-DFT results of T22, T24 and T25 show that the λ0→1 (between 524 and 554 nm) corresponds to the two-photon resonance value (1048–1108 nm). This value is very close to near-resonant wavelength (1064 nm) causing resonance. The two-photon resonance value of T25 is 1048 nm and that of T22 and T24 is 1108 and 1096 nm, respectively. The resonance value of T25 is the closest to the near-resonant wavelength of 1064 nm and that of T22 and T24 is the most shifted from the near-resonant wavelength. This is the reason why the value of βλ=1064HRS of T25 is larger than the value of βλ=1064HRS of T24 and T22, respectively. Accordingly, the wavelength resonance is one of the reasons why the value of βλ=1064HRS is much larger than that of βλ=∞HRS.
On the other hand, the urea molecule is one of the prototypical compounds used in the study of the second-order NLO response of molecules. Therefore it is used frequently as a threshold value for comparative purposes.87,88 The HRS hyperpolarizability of urea was calculated at the same level of theory. From our results we observe that the all bis-TTF-Ge derivative showed values for the static and dynamic HRS hyperpolarizability higher than the T0 (βλ=∞HRS = 75 a.u. and βλ=1064HRS = 137 a.u.) and urea (βλ=∞HRS = 38 a.u. and βλ=1064HRS = 40 a.u.).
The depolarization ratio (DR) is an essential parameter for displaying the contribution of the hyper-Rayleigh scattering response. As revealed by the static and dynamic DR values collected in Table 2, the NLO responses of T1, T2, T4, T6, T7, T9, T11, T12, T17, T21, T22, T27, T29, T32, T33 and T34 compounds display a dominant dipolar character, with the exception of T9, T33 compounds (λ = 1064 nm) dominated by their octupolar component. On the other hand, in our studied bis-TTF-Ge T3, T5, T8, T10, T13, T15, T18, T20, T23, T24, T25, T26, T28, T30, T31, T35 and T36 the octupolar component is dominant. From this study we observed that the (static and dynamic) DR values are more strongly sensitive to the substitution positions than to the nature of the substituent (donor and acceptor). This reveals that the a, b and d substitution positions lead to a dominant dipolar nature of the NLO response; the b substitution positions show a larger DR value in the static and dynamic regimes. On the other hand, the title compounds with c and e substitution positions are octupolar molecules. For the e substitution positions, the DR value (λ = ∞, 1064 nm), close to 1.5 (T10, T18, T20, T30, T36 and T0) characterizes typical octupolar systems. Furthermore, we observed that the DR value at λ = 1064 nm of T0, T10, T20, T22, T25, T30 and T36 is less than 1.5, indicating that those compounds are close to resonance.
On the other hand, we studied the correlation between the energy gaps (hardness) of the title compounds and their hyperpolarizability in the static regime. The results show that β∞HRS values are increased with the decrease of the bis-TTF-Ge energy gaps (the correlation factor is 0.832, see Fig. S4, ESI†). Taking T24 as an example, the energy gap of T24 is the smallest (1.819 eV) but its hyperpolarizability value is the largest (β∞HRS = 829 a.u.), which is in good agreement with the literature.89,90
In order to understand the nonlinear optical origins of studied compounds, the excitation energy (ΔE0→n) and wavelength (Δλ0→n), oscillator strengths (f0→n), transfer distance charges (dCT), charge transfer (qCT) and transition dipole moment (Δμ0→n) calculated for the crucial singlet excited states are summarized in Table 3, with more details in Table S1 (ESI†), and the corresponding electron density difference maps (EDDMs) are shown in Fig. S2 (ESI†).
| Ti | S0→n | ΔE0→n | Δλ0→n | f 0→n | q CT | d CT | Δμ0→n |
|---|---|---|---|---|---|---|---|
| T0 | S0→1 | 3.096 | 400 | 0.003 | 0.821 | 0.035 | 0.054 |
| T1 | S0→1 | 1.706 | 727 | 0.001 | 0.891 | 8.636 | 36.946 |
| S0→7 | 3.218 | 385 | 0.079 | 0.707 | 9.586 | 32.559 | |
| T2 | S0→13 | 3.892 | 318 | <0.001 | 0.999 | 16.977 | 81.427 |
| S0→16 | 4.303 | 307 | 0.126 | 0.618 | 6.649 | 19.741 | |
| T3 | S0→1 | 1.896 | 654 | 0.001 | 0.888 | 11.586 | 49.439 |
| S0→13 | 3.999 | 310 | 0.162 | 0.508 | 2.906 | 7.095 | |
| T4 | S0→17 | 3.921 | 316 | <0.001 | 0.997 | 17.038 | 81.612 |
| S0→20 | 4.010 | 309 | 0.125 | 0.576 | 6.199 | 17.151 | |
| T5 | S0→1 | 1.831 | 677 | <0.001 | 0.805 | 6.489 | 25.050 |
| S0→5 | 2.725 | 455 | 0.046 | 0.794 | 1.452 | 5.526 | |
| T6 | S0→1 | 3.070 | 404 | 0.003 | 0.872 | 6.729 | 28.067 |
| S0→7 | 4.003 | 307 | 0.167 | 0.631 | 7.18 | 20.478 | |
| T7 | S0→1 | 3.051 | 406 | 0.002 | 0.871 | 6.634 | 27.747 |
| S0→7 | 4.028 | 308 | 0.163 | 0.623 | 5.961 | 17.829 | |
| T8 | S0→1 | 3.132 | 396 | 0.004 | 0.792 | 1.963 | 7.467 |
| S0→7 | 4.074 | 304 | 0.429 | 0.513 | 0.320 | 0.784 | |
| T9 | S0→5 | 3.421 | 362 | 0.042 | 0.781 | 4.721 | 17.702 |
| S0→12 | 4.304 | 288 | 0.178 | 0.593 | 3.380 | 9.545 | |
| T10 | S0→1 | 3.086 | 402 | 0.005 | 0.747 | 6.418 | 23.035 |
| S0→13 | 4.305 | 288 | 0.204 | 0.594 | 4.507 | 12.859 | |
| T11 | S0→13 | 4.238 | 293 | 0.141 | 0.601 | 4.082 | 11.783 |
| T12 | S0→20 | 4.200 | 295 | 0.205 | 0.708 | 7.483 | 25.392 |
| T13 | S0→17 | 4.309 | 288 | 0.764 | 0.575 | 1.699 | 4.684 |
| T14 | S0→9 | 3.790 | 327 | 0.100 | 0.752 | 4.598 | 16.609 |
| T15 | S0→8 | 3.528 | 351 | 0.041 | 0.912 | 6.937 | 30.399 |
| T16 | S0→1 | 3.082 | 402 | 0.003 | 0.838 | 6.540 | 26.862 |
| S0→7 | 4.020 | 308 | 0.221 | 0.610 | 3.628 | 10.635 | |
| T17 | S0→1 | 3.065 | 404 | 0.003 | 0.869 | 6.778 | 28.212 |
| S0→7 | 4.032 | 307 | 0.173 | 0.650 | 8.709 | 27.195 | |
| T18 | S0→1 | 3.119 | 398 | 0.003 | 0.800 | 1.281 | 4.946 |
| S0→7 | 4.018 | 309 | 0.295 | 0.558 | 0.723 | 1.945 | |
| T19 | S0→1 | 3.117 | 398 | 0.004 | 0.831 | 5.726 | 22.867 |
| S0→8 | 4.091 | 303 | 0.172 | 0.669 | 5.704 | 18.314 | |
| T20 | S0→1 | 3.125 | 397 | 0.004 | 0.786 | 3.243 | 4.816 |
| S0→7 | 4.074 | 304 | 0.386 | 0.581 | 0.315 | 0.879 | |
| T21 | S0→1 | 2.854 | 434 | 0.083 | 0.831 | 5.372 | 21.438 |
| S0→14 | 4.207 | 295 | <0.001 | 0.999 | 15.939 | 76.256 | |
| T22 | S0→6 | 3.421 | 362 | <0.001 | 0.969 | 15.746 | 73.084 |
| S0→11 | 3.971 | 312 | 0.113 | 0.883 | 6.229 | 26.408 | |
| T23 | S0→1 | 2.867 | 432 | 0.123 | 0.829 | 3.650 | 14.512 |
| T24 | S0→2 | 2.869 | 432 | 0.034 | 0.828 | 5.318 | 22.476 |
| S0→8 | 3.603 | 344 | <0.001 | 0.999 | 15.685 | 75.300 | |
| T25 | S0→2 | 2.366 | 524 | 0.036 | 0.383 | 7.626 | 30.538 |
| S0→9 | 3.811 | 325 | <0.001 | 0.916 | 13.204 | 58.126 | |
| T26 | S0→1 | 3.083 | 402 | 0.003 | 0.875 | 6.448 | 26.428 |
| S0→7 | 4.030 | 308 | 0.332 | 0.536 | 4.420 | 11.286 | |
| T27 | S0→1 | 3.020 | 411 | 0.002 | 0.877 | 6.741 | 28.401 |
| S0→7 | 3.993 | 311 | 0.135 | 0.744 | 8.137 | 29.066 | |
| T28 | S0→1 | 3.050 | 406 | 0.002 | 0.852 | 6.211 | 25.277 |
| T29 | S0→1 | 3.026 | 410 | 0.002 | 0.874 | 6.746 | 28.277 |
| S0→7 | 4.002 | 309 | 0.151 | 0.738 | 8.838 | 31.299 | |
| T30 | S0→1 | 3.039 | 408 | 0.002 | 0.873 | 6.537 | 27.177 |
| S0→7 | 4.016 | 309 | 0.146 | 0.734 | 6.854 | 24.012 | |
| T31 | S0→1 | 3.081 | 402 | 0.003 | 0.870 | 6.972 | 29.120 |
| S0→7 | 4.023 | 308 | 0.319 | 0.593 | 7.924 | 22.565 | |
| T32 | S0→1 | 3.027 | 410 | 0.002 | 0.893 | 7.276 | 31.218 |
| S0→7 | 3.998 | 310 | 0.201 | 0.749 | 9.054 | 32.562 | |
| T33 | S0→1 | 3.089 | 401 | 0.003 | 0.843 | 4.628 | 18.658 |
| S0→7 | 4.021 | 308 | 0.420 | 0.522 | 3.447 | 8.593 | |
| T34 | S0→1 | 3.026 | 410 | 0.003 | 0.896 | 7.178 | 30.898 |
| S0→7 | 3.981 | 311 | 0.219 | 0.689 | 8.247 | 27.285 | |
| T35 | S0→1 | 3.055 | 406 | 0.003 | 0.869 | 5.083 | 21.208 |
| S0→7 | 3.989 | 311 | 0.315 | 0.568 | 2.059 | 5.619 | |
| T36 | S0→1 | 3.083 | 401 | 0.003 | 0.843 | 4.578 | 18.492 |
The charge transfer involves both n → π* and π → π* transitions, the main factor being the conjugation of the p electrons through the delocalization domain.
From the EDDM of bis-TTF-Ge substituted with acceptor groups (T1–T5 (R: NO), T11–T15 (R: COCN) and T21–T25 (R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NO2)), it can be observed that there is obvious CT from the TTF fragment to the substituted groups (R) at the other TTF fragment. These transitions are dominated by an electronic excitation from the HOMO to the LUMO and have high charge transfer parameters (qCT, dCT and Δμ0→n) character which is the necessary condition to obtain a high NLO response. On the other hand, the CT characters of T6–T10, T16–T20 and T26–T36 are from the TTF fragment (rings) to the 4S-Ge unit and these transitions are also associated with a HOMO → LUMO excitation with fewer charge transfer parameters than the other compounds (see Table 3, Fig. S2 and Table S1, ESI†). For instance, the dipole moment variation of T21 (76.26 D) is due to a transferred excitation charge qCT = 0.999 |e| and a larger associated CT distance (dCT = 15.94 Å, Sr = 0) than that of T31 (qCT = 0.87 |e|, dCT = 6.97 Å; Sr = 0.367 and Δμ0→1 = 29.12 D). The relatively small dCT and Δμ0→n values are obtained for bis-TTF-Ge with the substitution donor or acceptor at position c. This can be attributed to the CT from the TTF to the substituted group on the same fragment; see for example T23 in Fig. 6. In contrast, T0 undergoes a moderate CT excitation (qCT = 0.821 |e|) with a weak CT distance and small dipole moment variation (dCT = 0.035 Å and Δμ0→1 = 0.054 D) (see Fig. 6). Furthermore, the title compounds show a nice correlation between HRS hyperpolarizability and the largest dipole moment variation (Fig. 7). Also, there is a good correlation between βλ=∞HRS and βλ=1064HRS, except for T2, T4 and T5 (Fig. 8).
NO2)), it can be observed that there is obvious CT from the TTF fragment to the substituted groups (R) at the other TTF fragment. These transitions are dominated by an electronic excitation from the HOMO to the LUMO and have high charge transfer parameters (qCT, dCT and Δμ0→n) character which is the necessary condition to obtain a high NLO response. On the other hand, the CT characters of T6–T10, T16–T20 and T26–T36 are from the TTF fragment (rings) to the 4S-Ge unit and these transitions are also associated with a HOMO → LUMO excitation with fewer charge transfer parameters than the other compounds (see Table 3, Fig. S2 and Table S1, ESI†). For instance, the dipole moment variation of T21 (76.26 D) is due to a transferred excitation charge qCT = 0.999 |e| and a larger associated CT distance (dCT = 15.94 Å, Sr = 0) than that of T31 (qCT = 0.87 |e|, dCT = 6.97 Å; Sr = 0.367 and Δμ0→1 = 29.12 D). The relatively small dCT and Δμ0→n values are obtained for bis-TTF-Ge with the substitution donor or acceptor at position c. This can be attributed to the CT from the TTF to the substituted group on the same fragment; see for example T23 in Fig. 6. In contrast, T0 undergoes a moderate CT excitation (qCT = 0.821 |e|) with a weak CT distance and small dipole moment variation (dCT = 0.035 Å and Δμ0→1 = 0.054 D) (see Fig. 6). Furthermore, the title compounds show a nice correlation between HRS hyperpolarizability and the largest dipole moment variation (Fig. 7). Also, there is a good correlation between βλ=∞HRS and βλ=1064HRS, except for T2, T4 and T5 (Fig. 8).
 | ||
| Fig. 7 Correlation between HRS hyperpolarizability (βλ=∞HRS) and dipole moment variation (Δμ0→i), (T3, T4, T11, T13 and T23 are exceptions). | ||
Two-level model analyses for hyperpolarizability
The sum-over-states (SOS) method is one of the most commonly used methods for theoretical estimation of hyperpolarizability.91–96 The full form of the SOS formula of component ABC of hyperpolarizability is defined aswhere
 ω is the energy of external fields, and ω = 0 corresponds to the static electric field; Δi stands for excitation energy of state i with respect to the ground state (0).
ω is the energy of external fields, and ω = 0 corresponds to the static electric field; Δi stands for excitation energy of state i with respect to the ground state (0). ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) is the permutation operator that acts on the xyz indices of the β-components. μxij is the x component of the transition dipole moment between state i and state j.
is the permutation operator that acts on the xyz indices of the β-components. μxij is the x component of the transition dipole moment between state i and state j.
Molecular NLO responses of material is intimately related to the electronic absorption properties and through the two-level model established by Oudar and Chemla the static hyperpolarizabilities β can be expressed as97,98
Furthermore, it is well known that the molecular NLO properties calculated using the SOS method are closely related to the number of excited states;99 therefore in our study we plotted the relationship between the first hyperpolarizability (βSOS) and 100 excited states (Fig. S5, ESI†). Generally, these graphs demonstrate that 100 excited states are sufficient for the convergence of the βSOS value. As shown in Table S2 and Fig. S5 (ESI†) the introduction of the substituent group at the b position can increase the hyperpolarizability values more than at the other positions, and the NO2, NO and COCN acceptor groups, lead to the largest values. This prediction agrees well with hyperpolarizability calculated by CAM-B3LYP/6-311g(d,p).
In addition, the two-level analysis discloses that the excited state S7 makes a dominant contribution to the hyperpolarizability value of compounds T6, T7, T8, T16–T18, T20 and T26–T35; the crucial excited states S12, S13, S12, S13, S20 and S17 with largest hyperpolarizability in compounds T9, T10, T19, T11, T12, and T13 respectively; these transitions can be assigned to the CT from TTF fragment (rings) to the 4S-Ge unit (see Tables S1 and S2, ESI†). For systems T1–T5 the dominant contribution to hyperpolarizability values can be assigned to S7, S18, S23, S22 and S5, respectively, and are mainly made up of CT from TTF fragment to the NO groups at the other TTF fragment. For compounds T21 to T25 the excited states S1, S11, S1, S2 and S2, respectively, with CT from the TTF fragment to NO2 groups make large contributions to the hyperpolarizability value. For compounds, T14 to T15 the crucial excited state is S9 and S8 respectively, with CT from the TTF fragment to COCN groups have (see Tables S1, S2 and Fig. S2, ESI†). On the other hand, SOS calculations show that the local excitation transition at ∼266 nm of title compounds (noted in italic in Table S2, ESI†) exhibit a small hyperpolarizability value and a large dipole moment variation. These results agree well with the character of the electronic transition that we have noted before (in the section of nonlinear optical properties and Table 3).
As can be seen from Table S2 and Fig. 9, as a whole, the hyperpolarizability βSOSHRS and ratio DRSOS values (calculated DRSOS ratio and βSOSHRS based on the hyperpolarizability tensor derived by the SOS formula) qualitatively reproduce the general trend of the HRS hyperpolarizabilities and DR character (Table 2) with a few exceptions resulting from the limitation of the SOS method. On the other hand, it is worth stressing that the SOS method obviously overestimates the hyperpolarizability and DR value of Ti compounds (Fig. 9(I) and (II)).
Furthermore, the frequency dispersion factor (FDF) between static and dynamic at a definite wavelength λ = 1064 nm depicted by the ratio β1064/β∞, namely FDFHRS and FDFHRS,SOS, are calculated from the results in the Table 2 and Table S2 (ESI†), respectively and are presented in Fig. 10. From this Fig. 10, as expected, both FDFHRS and FDFHRS,SOS follow the same trend and in addition, the FDFHRS values are quite close to the FDFHRS,SOS values, with the exception of T2, T4, T12, T22 and T25. On the other hand, we can observe that the dispersion of optical nonlinearity of T24, T25 and T22 have maximum frequency dispersion factor at λ = 1064.8 nm, confirming their great nonlinear optical properties, in contrast to the other compounds (dispersion factor from ∼1 to 5.5). It is important to highlight that the SOS method consistently produces large hyperpolarizability and small FDF values of compound bis-TTF-Ge. Indeed, all the compounds containing NO2 substituent(s) (and, to a smaller extent, containing NO) are much more hyperpolarizable at 1064 nm frequency than in static regime, whereas with other substituents, the difference is not significant. This may be related to the NO2 lone pairs, which may be more mobile through the molecular systems.
 | ||
| Fig. 10 Variation of the frequency dispersion factor of bis-TTF-Ge derivatives calculated by SOS method and at the CAM-B3LYP/6-311g(d,p) level. | ||
To summarize, the large HRS hyperpolarizabilities origin of bis-TTF-Ge substituted with acceptor groups come from the CT from the TTF fragment towards the acceptor group located on the second TTF unit. In the meantime, the values of the CT from the TTF to the acceptor group located on the same TTF fragment are weak, whereas the NLO origin of bis-TTF-Ge substituted with donor originates a CT from TTF fragment to the 4S-Ge unit.
Conclusions
The structural properties, reactivity parameters, and linear and nonlinear optical properties of 37 bis-TTF-Ge derivatives differing by a donor and acceptor substitution on the TTF fragment have been investigated by using DFT and TD-DFT calculations. These calculations were performed at the CAM-B3LYP/6-311g(d,p) level and using the sum-over-states (SOS) approach in both static and dynamic regimes.Our results indicate that the bis-TTF-Ge hardness can effectively be reduced when substituent positions are substituted with an acceptor group (NO, NO2, and COCN). Furthermore, the b substituent position leads to a smaller hardness than the d, e, a and c substituent positions. The electronic excitation properties of the title compounds can be described as a mixed transition of intra-TTF charge transfer (ICT) and charge transfer (CT) from TTF to the 4S-Ge unit, TTF to the acceptor group (NO2, NO and COCN) and TTF to TTF. For example, the electronic transition at ∼266 nm is a local excitation with a relatively small dct and large Sr indexes. The transition HOMO → LUMO of bis-TTF-Ge with the acceptor substituent (R = NO, COCN and NO2) at positions a, b and d is a non-local excitation with large dipole moment variation and a small Sr index (Sr ∼ 0). In the case of bis-TTF-Ge with a donor substituent (R: NH2 and NMe2) at positions a, b and d, the transition HOMO → LUMO from the TTF fragment to 4S-Ge shows moderate values of the transition dipole moment and Sr indexes (Sr = ∼0.3) when we compare it with the results of an acceptor substituent.
All bis-TTF-Ge derivatives showed values for the static and dynamic HRS hyperpolarizability higher than T0 and urea.
The quantum chemical calculations indicate that the position and the nature (donor/acceptor) of the substituent have strong effects on the NLO responses. The introduction of a substituent group at the b position induces a greater increase of the first hyperpolarizability and the acceptor NO2, NO and COCN groups show a large value of HRS hyperpolarizability which indicate that the acceptor group has a stronger effect on the second order NLO than the donor group. On the other hand, the compounds with c and e substitution positions are octupolar molecules and a, b and d substitution positions lead to a dominant dipolar nature of the NLO response.
The large first hyperpolarizability origin comes from the CT from the TTF fragment towards the acceptor group located on the second TTF unit. On the other hand, the βλ=∞HRS values of compounds T21–T25 are high and relatively close, indicating that the introduction of the acceptor NO2 group at any substituent position can effectively enhance the first hyperpolarizability. Interestingly, the βλ=1064HRS of bis-TTF-Ge substituted with the NO2 group increases with the number of NO2 in the TTF fragment.
Finally, it is important to emphasize that the intrinsic asymmetric geometry of the bis-TTF-Ge can tune the second order NLO response through the nature, position and number of the substituent group at the TTF fragment, as well as by the Sr index.
On the other hand, our study suggests that these compounds can be used as new materials for developing nonlinear second order photonic devices. Furthermore, the bis-TTF-Ge compounds substituted with the an acceptor group may become excellent candidates for second order NLO materials, which will also promote the evolution of high technology applications.
Author contributions
All the authors discussed the results. Dalila Kamli: calculations achievements, data interpretation, draft writing. Douniazed Hannachi: project initiation, conceptualization, calculations supervision, data interpretation, draft writing. Djamila Samsar: calculations, data interpretation, draft writing. Henry Chermette: calculations, data interpretation, draft writing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the GENCI/CINES for HPC resources/computer time (Project cpt2130), and the PSMN of the ENS-Lyon for computing resources.Notes and references
- P. A. Franken, A. E. Hill, C. W. Peters and G. Weinreich, Phys. Rev. Lett., 1961, 7, 118–119 CrossRef
.
-
Y. R. Shen and G. Z. Yang, The Supercontinuum Laser Source: The Ultimate White Light, 1989, pp. 1–32 Search PubMed
.
- C. Andraud and O. Maury, Eur. J. Inorg. Chem., 2009, 4357–4371 CrossRef CAS
.
- T. H. Maiman, Nature, 1960, 187, 493–494 CrossRef
.
- R. J. Collins, D. F. Nelson, A. L. Schawlow, W. Bond, C. G. B. Garrett and W. Kaiser, Phys. Rev. Lett., 1960, 5, 303–305 CrossRef CAS
.
- M. S. Kodikara, R. Stranger and M. G. Humphrey, Coord. Chem. Rev., 2018, 375, 389–409 CrossRef CAS
.
- Y. Y. Liang, B. Li, X. Xu, F. Long Gu and C. Zhu, J. Comput. Chem., 2019, 40, 971–979 CrossRef CAS PubMed
.
- N. Baggi, E. Garoni, A. Colombo, C. Dragonetti, S. Righetto, D. Roberto, J. Boixel, V. Guerchais and S. Fantacci, Polyhedron, 2018, 140, 74–77 CrossRef CAS
.
- C. Andraud, F. Cyril, B. Olivier, H. Chermette and P. L. Baldeck, Adv. Polym. Sci., 2008, 214, 149–203 CrossRef CAS
.
- Z. R. Khan, M. Shkir, V. Ganesh, S. AlFaify, I. S. Yahia and H. Y. Zahran, J. Electron. Mater., 2018, 47, 5386–5395 CrossRef CAS
.
- K. Iliopoulos, O. Krupka, D. Gindre and M. Salle, J. Am. Chem. Soc., 2010, 132, 14343–14345 CrossRef CAS PubMed
.
- M. Homocianu, A. Airinei, C. Hamciuc and A. M. Ipate, J. Mol. Liq., 2019, 281, 141–149 CrossRef CAS
.
- M. Nakano, R. Kishi, N. Nakagawa, S. Ohta, H. Takahashi and S. Furukawa, J. Phys. Chem. A, 2006, 110, 4238–4243 CrossRef CAS PubMed
.
- E. Cariati, C. Dragonetti, E. Lucenti, F. Nisic, S. Righetto and E. Tordin, Chem. Commun., 2014, 50, 1608–1610 RSC
.
- F. Ricci, F. Elisei, P. Foggi, A. Marrocchi, A. Spalletti and B. Carlotti, J. Phys. Chem., 2016, 120, 23726–23739 CAS
.
- W. Feng, K. Liu, J. Zang, J. Xu, H. Peng, L. Ding, T. Liu and Y. Fang, J. Phys. Chem. B, 2021, 125, 11540–11547 CrossRef CAS PubMed
.
- Y. Lee, S. Jeon and M. Cho, J. Am. Chem. Soc., 1998, 120, 10921–10927 CrossRef CAS
.
- F. Ibersiene, D. Hammoutène, A. Boucekkine, C. Katan and M. Blanchard-desce, J. Mol. Struct., 2008, 866, 58–62 CrossRef CAS
.
- S. Wang, Y. Wang and C. Cai, J. Phys. Chem. C, 2015, 119, 5589–5595 CrossRef CAS
.
- D. Hannachi, M. F. Haroun, A. Khireddinea and H. Chermette, New J. Chem., 2019, 43, 14377 RSC
.
- M. Zaidi, D. Hannachi and H. Chermette, Inorg. Chem., 2021, 60, 6616–6632 CrossRef CAS PubMed
.
- M. Fontani, A. Colombo, C. Dragonetti, S. Righetto, D. Roberto and D. Marinotto, Inorganics, 2020, 8, 1–12 CrossRef
.
- A. Yasin, V. S. Nair, M. H. Ab Rahim, Y. Yamaoka, C. S. Yelleswarapu and R. Jose, J. Mater. Chem. C, 2021, 9, 17461–17470 RSC
.
- A. Ahsin and K. Ayub, J. Nanostruct. Chem., 2022, 12, 529–545 CrossRef CAS
.
- A. Ahsan and K. Ayub, Opt. Laser Technol., 2020, 129, 106298 CrossRef CAS
.
- A. Ahsan, S. Sarfaraz, F. Fayyaz, M. Asghar and K. Ayub, J. Mol. Liq., 2022, 350, 118504 CrossRef CAS
.
- A. Ahsan and K. Ayub, J. Mol. Liq., 2020, 297, 36–40 CrossRef
.
- C. Katan, P. Savel, B. M. Wong, T. Roisnel and V. Dorcet, Phys. Chem. Chem. Phys., 2014, 16, 9064–9073 RSC
.
- L. Ji, R. Edkins, L. Sewell, A. Beeby, A. S. Batsanov, K. Fucke, M. Drafz, J. A. K. Howard, O. Moutounet, L. Ji, R. Edkins, L. Sewell, A. Beeby and A. S. Batsanov, Chem. – Eur. J., 2014, 20, 13618–13635 CrossRef CAS PubMed
.
- A. Ahsin, A. B. Shah and K. Ayub, RSC Adv., 2021, 12, 365–377 RSC
.
- P. S. Halasyamani and W. Zhang, Inorg. Chem., 2017, 56, 12077–12085 CrossRef CAS PubMed
.
- F. Wudl, G. M. Smith and E. J. Hufnagel, J. Chem. Soc. D, 1970, 1453–1454 RSC
.
- F. Wudl, D. Wobschall and E. J. Hufnagel, J. Am. Chem. Soc., 1972, 94, 670–672 CrossRef CAS
.
- C. Marcovicz, R. C. Ferreira, A. B. S. Santos, A. S. Reyna, C. B. De Araújo, I. Malvestiti and E. H. L. Falcão, Chem. Phys. Lett., 2018, 702, 16–20 CrossRef CAS
.
- K. Iliopoulos, R. Czaplicki, H. El Ouazzani, J. Y. Balandier, M. Chas, S. Goeb, M. Sallé, D. Gindre, K. Iliopoulos, R. Czaplicki, H. El Ouazzani, J. Y. Balandier, M. Chas, S. Goeb and M. Sallé, Appl. Phys. Lett., 2010, 97, 101104 CrossRef
.
- C. Liu, W. Guan, P. Song, L. Yan and Z. Su, Inorg. Chem., 2009, 48, 6548–6554 CrossRef CAS PubMed
.
- A. Ayadi, A. Szukalski, A. El-ghayoury, K. Haupa, N. Zouari, J. Myśliwiec, F. Kajzar, B. Kulyk and B. Sahraoui, Dyes Pigm., 2016, 138, 255–266 CrossRef
.
- A. Jana, M. Ishida, J. S. Park, J. O. Jeppesen and J. L. Sessler, Chem. Rev., 2017, 117, 2641–2710 CrossRef CAS PubMed
.
- S. Muhammad, J. Mol. Graphics Modell., 2015, 59, 14–20 CrossRef CAS PubMed
.
- O. Oms, P. Mialane, I. Ledoux, L. Ruhlmann, D. Lorcy and A. Dolbecq, Inorg. Chem., 2018, 57, 3742–3752 CrossRef PubMed
.
- C. Goze, N. Dupont, E. Beitler, C. Leiggener, H. Jia, P. Monbaron, S. Liu, A. Neels, A. Hauser, S. Decurtins, C. Suisse and D. Microtechnique, Inorg. Chem., 2008, 47, 11010–11017 CrossRef CAS PubMed
.
- C. Goze, C. Leiggener, S. Liu, L. Sanguinet, E. Levillain, A. Hauser and S. Decurtins, ChemPhysChem, 2007, 8, 1504–1512 CrossRef CAS PubMed
.
- C. Liu, M. Gao, S. Liu and D. Zhang, RSC Adv., 2015, 5, 42311–42321 RSC
.
- H. Tanaka, Science, 2001, 291, 285–287 CrossRef CAS PubMed
.
- L. Valade, J. Legros, M. Bousseau and P. Cassoux, J. Chem. Soc., Dalton Trans., 1985, 783–794 RSC
.
- K. Miwa, H. Ikuta, H. Hinode, T. Uchida and M. Wakihara, J. Solid State Chem., 1996, 125, 178–181 CrossRef CAS
.
- C. J. Calzado, B. Rodríguez-García, J. R. Galán Mascarós and N. C. Hernández, Inorg. Chem., 2018, 57, 7077–7089 CrossRef CAS PubMed
.
- A. Avramopoulos, H. Reis, G. A. Mousdis and M. G. Papadopoulos, Eur. J. Inorg. Chem., 2013, 4839–4850 CrossRef CAS
.
- A. Avramopoulos, H. Reis, N. Otero, P. Karamanis, C. Pouchan and M. G. Papadopoulos, J. Phys. Chem. C, 2016, 120, 9419–9435 CrossRef CAS
.
- M. Majumder and A. Misra, Phys. Chem. Chem. Phys., 2018, 20, 19007–19016 RSC
.
- A. Avramopoulos, N. Otero, H. Reis, P. Karamanis and M. G. Papadopoulos, J. Mater. Chem. C, 2018, 6, 91–110 RSC
.
- A. Ahsin and A. B. Shah, RSC Adv., 2022, 12, 365–377 RSC
.
- M. T. Baei and M. Koohi, Heteroat. Chem., 2018, 1–14 Search PubMed
.
- E. Tahmasebi, E. Shakerzadeh and Z. Biglari, Appl. Surf. Sci., 2016, 363, 197–208 CrossRef CAS
.
- C. C. Fonkem, G. W. Ejuh, F. T. Nya, R. A. Y. Kamsi, Y. T. Assatse and J. M. B. Ndjaka, Chin. J. Phys., 2019, 4, 207–212 Search PubMed
.
- M. Kurban and M. Kurban, J. Alloys Compd., 2019, 802, 25–35 CrossRef
.
- E. Shakerzadeh, N. Barazesh and S. Zargar, Superlattices Microstruct., 2014, 76, 264–276 CrossRef CAS
.
- A. Slodek, G. Schnurpfeil and D. Wöhrle, J. Porphyrins Phthalocyanines, 2017, 21, 1–13 CrossRef
.
- S. Soleimani-amiri, J. Chin. Chem. Soc., 2018, 65, 1–12 CrossRef
.
- X. Li, S. Li, H. Ren, J. Yang and Y. Tang, Nanomater. Artic., 2017, 1, 1–15 Search PubMed
.
- K. K. Ueda Kazumasa, Y. Masaru, S. Toyonari, F. Hideo, U. Akito and Y. Kyuya, Chem. Lett., 1997, 461–462 CrossRef
.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS
.
- G. A. Petersson and A.-L. Mohammad, J. Chem. Phys., 1991, 9, 6081–6090 CrossRef
.
- G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193–2218 CrossRef CAS
.
-
M. J. Frisch, et al., Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed
.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS
.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed
.
- H. Chermette, J. Comput. Chem., 1999, 20, 129–154 CrossRef CAS
.
- P. K. Chattaraj and R. G. Parr, Struct. Bonding, 1993, 80, 151–174 CrossRef
.
- P. Mondal, K. K. Hazarika and R. C. Deka, PhysChemComm, 2003, 6, 24–27 RSC
.
- P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1873 CrossRef CAS PubMed
.
- R. G. Parr, L. V. Szentpály and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS
.
- R. Bersohn, P. A. O. Yoh-Han and H. L. Frisch, J. Chem. Phys., 1966, 45, 3184–3198 CrossRef CAS
.
- A. Plaquet, M. Guillaume, B. Champagne, F. Castet, L. Ducasse, J. L. Pozzo and V. Rodriguez, Phys. Chem. Chem. Phys., 2008, 10, 6223–6232 RSC
.
- W. Sun, L. Fan, Y. Li, J. Liu, D. Wu and Z. Li, Inorg. Chem., 2014, 12, 6170–6178 CrossRef PubMed
.
- Y. Arshad, S. Khan, M. A. Hashmi and K. Ayub, New J. Chem., 2018, 42, 6976–6989 RSC
.
- L. M. G. Abegaõ, R. D. Fonseca, F. A. Santos, J. J. Rodrigues, K. Kamada, C. R. Mendonca, S. Piguel and L. De Boni, RSC Adv., 2019, 9, 26476–26482 RSC
.
- T. Le Bahers, C. Adamo and I. Ciofini, J. Chem. Theory Comput., 2011, 7, 2498–2506 CrossRef CAS PubMed
.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed
.
- E. Demiralp and W. A. Goddard, J. Phys. Chem. A, 1997, 101, 8128–8131 CrossRef CAS
.
- G. J. Linker, P. T. Van Duijnen, P. H. M. Van Loosdrecht and R. Broer, J. Phys. Chem. A, 2012, 116, 7219–7227 CrossRef CAS PubMed
.
- L. R. Domingo, M. J. Aurell, P. Pérez and R. Contreras, Tetrahedron, 2002, 58, 4417–4423 CrossRef CAS
.
- L. Lescos, S. P. Sitkiewicz, P. Beaujean, M. Blanchard-Desce, B. Champagne, E. Matito and F. Castet, Phys. Chem. Chem. Phys., 2020, 22, 16579–16594 RSC
.
- L. Gong, C. Liu, C. Ma, W. Lin, J. Lv and X. Zhang, RSC Adv., 2019, 9, 17382–17390 RSC
.
- L. Gong, C. Ma, C. Li, J. Lv and X. Zhang, New J. Chem., 2020, 44, 10484–10491 RSC
.
- C. Bao, Y. Li, Y. Li, Z. Si, Y. Zhang, C. Chen, L. Wang and Q. Duan, New J. Chem., 2021, 45, 16030–16038 RSC
.
- N. Ghichi, A. Djedouani, D. Hannachi, C. Bensouici, A. Benboudiaf, H. Merazig and H. Stoeckli-Evans, J. Mol. Struct., 2023, 1271, 134014 CrossRef CAS
.
- A. A. Yahiaoui, N. Ghichi, D. Hannachi, A. Djedouani, S. Meskaldji, H. Merazig and D. Harakat, J. Mol. Struct., 2022, 1263, 133161 CrossRef CAS
.
- K. S. Thanthiriwatte and K. M. Nalin de Silva, J. Mol. Struct., 2002, 617, 169–175 CrossRef CAS
.
- L. Wang, J. Ye, H. Wang, H. Xie and Y. Qiu, Sci. Rep., 2017, 7, 1–11 CrossRef PubMed
.
- B. Champagne and B. Kirtman, J. Chem. Phys., 2006, 125, 024101 CrossRef PubMed
.
- J. P. Coe and M. J. Paterson, J. Chem. Phys., 2014, 141, 124118 CrossRef CAS PubMed
.
- E. Rtibi, M. Abderrabba, S. Ayadi and B. Champagne, Inorg. Chem., 2019, 58, 11210–11219 CrossRef CAS PubMed
.
- Y. Y. He, J. Chen, X. L. Zheng, X. Xu, W. Q. Li, L. Yang and W. Q. Tian, ACS Appl. Nano Mater., 2019, 2, 1648–1654 CrossRef CAS
.
- J. M. F. Custodio, G. D. C. D’Oliveira, F. Gotardo, L. H. Z. Cocca, L. de Boni, C. N. Perez, H. B. Napolitano, F. A. P. Osorio and C. Valverde, Phys. Chem. Chem. Phys., 2021, 23, 6128–6140 RSC
.
- Y. Liu, Y. Yuan, X. Tian, J. Yuan and J. Sun, Int. J. Quantum Chem., 2020, 120, 1–13 Search PubMed
.
- J. L. Oudar and D. S. Chemla, J. Chem. Phys., 1977, 66, 2664–2668 CrossRef CAS
.
- J. L. Oudar, J. Chem. Phys., 1977, 67, 446–457 CrossRef CAS
.
- B. Li, P. Sathishkumar and F. L. Gu, Phys. Chem. Chem. Phys., 2021, 23, 8489–8499 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nj03671a |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2023 |