Intrinsic exchange bias state in silicene and germanene materials EuX2†
Dmitry V.
Averyanov
,
Ivan S.
Sokolov
 ,
Alexander N.
Taldenkov
,
Oleg E.
Parfenov
,
Igor A.
Karateev
,
Oleg A.
Kondratev
,
Andrey M.
Tokmachev
and
Vyacheslav G.
Storchak
,
Alexander N.
Taldenkov
,
Oleg E.
Parfenov
,
Igor A.
Karateev
,
Oleg A.
Kondratev
,
Andrey M.
Tokmachev
and
Vyacheslav G.
Storchak
 *
*
National Research Center “Kurchatov Institute”, Kurchatov Sq. 1, Moscow 123182, Russia. E-mail: vgstorchak9@gmail.com
First published on 23rd March 2023
Abstract
2D magnets have recently emerged as a host for unconventional phases and related phenomena. The prominence of 2D magnetism stems from its high amenability to external stimuli and structural variations. The low dimensionality facilitates competition between magnetic orders which may give rise to exchange bias, in particular in magnetic heterostructures. Here, we propose a strategy for the search of exchange bias state in 2D individual compounds. We track the evolution of magnetic orders driven by the number of monolayers in a system exhibiting antiferromagnetism in the multilayer and ferromagnetism in the monolayer limit. The material, EuSi2, has the structure of multilayer silicene intercalated by Eu. A strong intrinsic exchange bias effect accompanies the dimensional crossover. Comparison with silicene-based GdSi2 and germanene-based EuGe2 suggests the competition between magnetic orders to be a common property of this class of materials that may be useful in spintronic applications.
New conceptsThe recent discovery of intrinsic 2D magnets has initiated a flurry of studies on fundamentals of magnetism, magnetic quantum phases, and spintronic applications. The interest in 2D magnets stems from their high amenability to external stimuli. In the 2D realm, the number N of monolayers (MLs) is a critical variable capable to profoundly alter electronic and magnetic structure to produce fundamentally new states with coexisting/competing magnetic orders. Coupling of different magnetic phases gives rise to the exchange bias (EB) state attracting both fundamental and technological interest. We suggest a coherent strategy to design 2D magnets with significant EB. Our conceptual approach is to seek the EB state in materials exhibiting crossover from 3D antiferromagnetism in the bulk to 2D ferromagnetism when N counts a few MLs. In this regard, we probe an emerging class of 2D magnetic materials, metalloxenes, layered compounds EuX2 formed by alternating silicene or germanene (Si or Ge analogues of graphene) and Eu layers. In these materials, the EB state is intrinsic, in contrast to that in heterostructures. We establish an entire class of EB materials seamlessly integrated with the mature semiconducting platforms of Si or Ge that may be useful in spintronic applications. |
1. Introduction
Layered materials brought to the 2D limit produce unconventional electron states and related functionalities. Magnetism, a recent newcomer to the field of 2D research, is currently gaining ground.1,2 Nowadays, the material landscape of 2D magnetism involves a collection of rather diverse systems. Most of the 2D magnets acquire their magnetic moments from open d-shells.3–6 However, less common f-orbital 2D magnets7–10 are also gaining interest. Special efforts are initiated to imprint magnetism into graphene11,12 and related systems.13 The research is aiming at new quantum phases with potential for applications in ultra-compact spintronics. In particular, heterostructures of 2D materials promise complex behaviors.1,14 The main advantage brought about by low dimensionality is high amenability of magnetic states to external stimuli such as magnetic fields,4 electric fields15 or pressure.16 On the one hand, low dimensionality leads to strong response of materials such as colossal tunneling17 or lateral18 magnetoresistance; on the other hand, it promotes coexistence and competition between different electronic phases and/or magnetic orders.Exchange bias (EB), a state manifesting itself as a shift of the hysteresis loop along the magnetic field axis,19,20 is usually detected in heterostructures combining materials with different magnetic orders. Thus, the natural ability of layered materials to form heterostructures feeds the interest to the 2D limit of EB.20 On the other hand, EB makes an operating principle of magnetic memory technologies, from spin valve readback heads to MRAM circuits.19,20 Most of the research on 2D EB involves Fe3GeTe2 (FGT), a metallic ferromagnet which is relatively easy to handle. In particular, significant EB effects have been found in heterostructures of FGT with layered transition metal antiferromagnets – FePS3,21 CrCl3,22 CrOCl,23 MnPS3 and MnPSe3.24 However, EB is a rather general phenomenon; it can be induced by different magnetic interfaces such as molecule/FGT25 or those driven by chemical modification of FGT, either by surface oxidation26 or proton intercalation.27,28 These chemically induced effects suggest the possibility of intrinsic EB caused by different magnetic orders within an individual compound.
Our aim is to devise a strategy for the search of individual compounds (rather than heterostructures) revealing the EB state. In this regard, it is natural to look for systems with coexisting magnetic orders. Manganite materials provide a classical example of systems with instability of magnetic ordering towards the formation of phase separated droplet structures.29 The phase separation results in the EB state.30,31 On the other hand, EB has been detected in a disordered magnetic system with coexisting antiferromagnetic (AFM) and spin-glass orders.32 In a 2D system, coexisting ferromagnetic (FM) and AFM states can be engendered by different ways such as chemical modification,27 twisting the layers33 or external pressure.16 Here we turn our attention to materials that do not require any external modification. A recent example is GdSi2, a material exhibiting a particularly strong EB effect at the 3D AFM-to-2D FM crossover region.34
One of the peculiar features of 2D magnetism is that the magnetic order in a monolayer (ML) may be fundamentally different from that in the bulk. The most common scenario is transformation of 3D AFM into 2D FM, demonstrated in RESi2 (RE = rare-earth)7 and REGe2,8 CrCl3,6 MnBi2Te4,35 CrSBr,36,37 and oxide systems Fe2O35 and NiO.38 Surely, this situation carries significant potential for implementation of competing magnetic states. In this respect, gradual change of the magnetic state is particularly interesting. This sort of AFM/FM crossover is characteristic to magnetic metalloxenes REX2 (including the above-mentioned GdSi2) – compounds combining atomic layers of silicene or germanene (Si or Ge counterparts of graphene) with rare-earths Gd or Eu.7,8 The materials can also be viewed as intercalated multilayer silicene or germanene. Their important advantage is seamless integration with the mature semiconducting platforms of Si and Ge. Ultrathin REX2 are suggested to host both FM and AFM states39 – a strong prerequisite for an intrinsic EB state. It is noteworthy that EB in GdSi2 is an emerging property: it is not detected in the ML limit, in contrast to EB in a single ML of NiO38 or MnSb2Te4.40
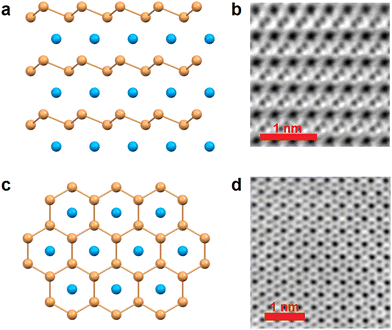
The question is whether the intrinsic EB state constitutes a general phenomenon triggered by competing magnetic states at the crossover region. In this respect, replacement of Gd with Eu can be instructive: 2D systems with ionic lattices of Eu often exhibit strong magnetic properties.12,41,42 The atomic structure of EuSi2 is provided in Fig. 1 employing ball-and-stick models and high-resolution electron microscopy: the side view demonstrates a stack of buckled silicene layers separated by flat layers of Eu. The buckled layers of silicene are stable, in contrast to flat silicene layers in GdSi2 requiring stabilization by a significant amount of Si vacancies. The top view (Fig. 1) demonstrates superimposition of the honeycomb lattice of silicene on the triangular lattice of Eu. Silicene-based EuSi2 exhibits layer-dependent magnetic order7,43 but differs from GdSi2 in terms of the RE oxidation state (2+ instead of 3+) and the silicene structure (buckled instead of flat).
Here, we follow layer-dependent magnetic transformations in silicene-based EuSi2. We synthesize a series of EuSi2 films with different number of MLs N on silicon, attest their structural quality and probe their electron transport and magnetic properties. Based on the pronounced EB effect, we establish a competition of magnetic states at the crossover between 3D AFM and 2D FM. To demonstrate the general character of the phenomenon, we provide a complementary study of magnetism in germanene-based EuGe2.
2. Results and discussion
2.1. Synthesis and structure
Our goal is to synthesize and study Eu-intercalated multilayer silicene. The problem is that the stable polymorphs of Eu silicides do not support this layered structure, in contrast to germanene-based EuGe2.8,44 In particular, EuSi2 crystallizes into a tetragonal polymorph with a 3D net of covalently bound Si atoms.45 However, there is a significant difference between syntheses of bulk materials and thin films. In the latter case, a metastable phase can be stabilized via strong bonding with a suitable substrate. The substrate should have both lattice match and proper bonding with the film. Originally, silicene-based (trigonal) EuSi2 was stabilized via synthesis on silicene-based SrSi2.46 However, studies of intrinsic properties of a film require synthesis without templates. Fortunately, it has been demonstrated that trigonal EuSi2 can be produced directly on Si(111).7,18 This Si surface can be viewed as a covalently bound stack of silicene sheets; thus, it is conducive to the growth of the silicene-based polymorph. In contrast, synthesis of EuSi2 on Si(001) results in the tetragonal polymorph.45We synthesized a series of silicene-based EuSi2 films with different N. We define one monolayer of EuX2 as a combination of 2D-Xene (silicene or germanene) and Eu sheets, i.e. the minimal layer of the EuX2 stoichiometry. For instance, N = 2 for EuSi2 denotes Si–Eu–Si–Eu-substrate. For synthesis we employed molecular beam epitaxy (MBE), a versatile technique suitable to synthesis of films with required N. In particular, MBE has been successfully applied to studies of N-dependent properties in silicene-based SrSi246 and GdSi2.34 The binary compound EuSi2 is synthesized via direct reaction between elementary Eu and Si:
| Eu + 2Si = EuSi2, |
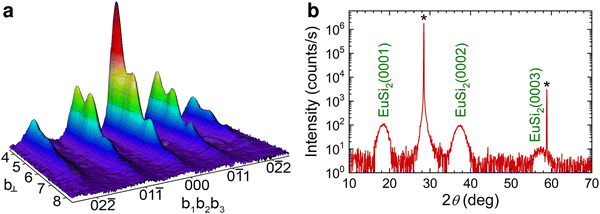
The structural quality of the films was attested by a combination of diffraction techniques. Fig. 2 shows characteristic results for N = 9, the thickness that best illustrates the competition between magnetic states (see below). Reflection high-energy electron diffraction (RHEED) provides in situ characterization of the film surface. The system of reflexes (Fig. 2a) corresponds to trigonal EuSi2 with silicene layers oriented parallel to the surface. θ–2θ X-ray diffraction (XRD) scan (Fig. 2b) confirms this conclusion. The XRD scan is free of signals from the tetragonal polymorph and other potential side phases. As expected, the peaks are rather broad for the ultrathin film. The calculated lattice parameters (lateral from RHEED and out-of-plane from XRD) for EuSi2 on Si(111) agree with those in EuSi2 on SrSi2.43 In particular, the lateral lattice parameters of EuSi2 and Si(111) differ by 3%; this degree of lattice match is sufficient to seed synthesis of the trigonal polymorph. High-resolution electron microscopy was employed to calibrate the number N in the films.
The presence of defects may affect magnetic properties of EuSi2. Ideally, we should compare two EuSi2 films with different amount of defects. Here, we synthesize EuSi2 directly on Si(111). In Ref. 43 we used another approach, synthesis of EuSi2 on a template of SrSi2, to attenuate lattice mismatch and diminish the number of defects. The two films, EuSi2/Si(111) and EuSi2/SrSi2/Si(111), exhibit very similar FM signals as long as the EuSi2 layer is of the same thickness.7 Alternatively, we can compare EuSi2 with its analogue GdSi2 exhibiting a significant number of defects – a Rutherford backscattering study suggests the stoichiometry GdSi1.84.7 Magnetic properties of EuSi2 and GdSi2 are rather similar;7 also, non-trivial magnetoresistance in EuSi2 and GdSi2 reveals strong similarities.18 Therefore, we expect exchange coupling in the films to be rather robust with respect to defects.
2.2. Electron transport and magnetism
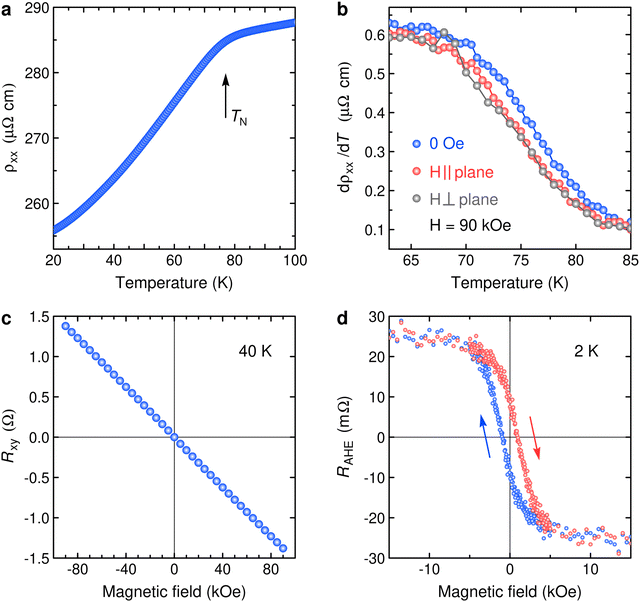
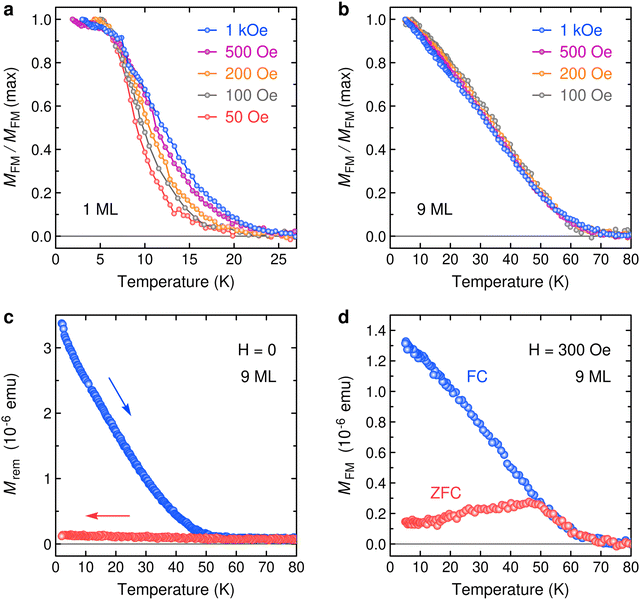
The present work aims at finding fingerprints of competing magnetic states. Different techniques can be employed to detect such competition in 2D materials via EB: magneto-optical Kerr effect,21,24,26 reflectance magnetic circular dichroism23,24 or anomalous Hall effect.22,23,25,28 Here, we study electron transport and magnetization properties with accent on films of intermediate thickness, from N = 5 to N = 12. Fig. 3 demonstrates electron transport in 9 ML EuSi2 bearing features of AFM and FM states. Temperature dependence of resistance (Fig. 3a) exhibits a change of slope at about 80 K corresponding to a magnetic transition. In magnetic fields, both in-plane and out-of-plane, this feature shifts to lower temperatures (Fig. 3b) suggesting the transition to an AFM state. FM states often reveal themselves in anomalous Hall effect. At 40 K, only an ordinary Hall effect shows up (Fig. 3c). However, at low temperature, an anomalous Hall effect with a hysteretic loop becomes evident (see Fig. 3d). (This effect is difficult to employ in studies of EB because strong magnetic anisotropy in EuSi2 orients magnetic moments in-plane.) Thus, in EuSi2, both AFM and FM states manifest themselves at N = 9.The competition of magnetic states is then probed by magnetization measurements (Fig. 4 and 5). In thin films, ferromagnetism affects the magnetic signals more distinctly than antiferromagnetism. A major manifestation of the AFM state is the reduced FM moment with respect to 7 μB per Eu atom expected for a fully spin-polarized Eu2+. Temperature dependence of magnetization demonstrates an upturn at low temperature as the FM order sets in. However, the characteristics of the FM transition depend strongly on the number N in the EuSi2 film. This point is illustrated by N = 1 and N = 9 samples in Fig. 4a and b. Two details catch the eye. First, the transition temperatures are very different – in the N = 9 film it is several times higher although TC is still lower than TN (≈ 80 K) determined by electron transport measurements. Another noticeable feature is the dependence of M(T) curves on weak magnetic fields. In 2D magnets, emergence of FM may require opening a (pseudo)gap in the spin-wave excitation spectrum by a magnetic field. In practice, it looks as if TC is a function of the external magnetic field. In ML EuSi2 (Fig. 4a), the dependence is strong; such phenomenon is a manifestation of 2D nature of the ferromagnetism. In contrast, the dependence is negligible at N = 9 (Fig. 4b), suggesting that the spin-wave excitation spectrum approaches that of a 3D ferromagnet. Thus, it looks as if concurrent dimensional crossover and AFM/FM crossover take place. Other characteristics usually accompanying FM states also show up. In particular, EuSi2 at N = 9 demonstrates remnant magnetization (Fig. 4c) and bifurcation of the field-cooled (FC) and zero-field-cooled (ZFC) magnetization (Fig. 4d).
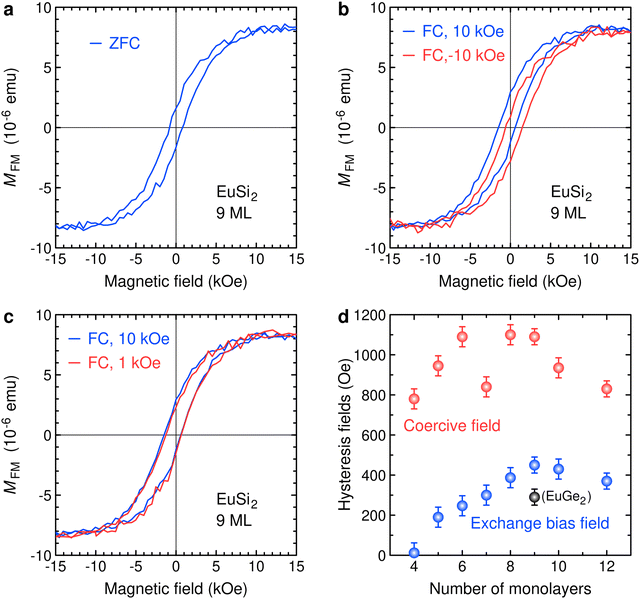
The competing magnetic states can be probed by M–H measurements employing the EB effect (Fig. 5). Following ZFC, the hysteresis loop is symmetric (Fig. 5a), i.e. the rare phenomenon of spontaneous EB, observed in a magnetic alloy,48 FGT,27 and a magnetic kagome lattice,49 does not show up in EuSi2. In contrast, significant shifts of the hysteresis loop take place following FC in a magnetic field of 10 kOe (Fig. 5b). As expected for an EB state, the sign of the shift depends on the sign of the external magnetic field. A difference between the absolute values of the shifts would point at multiple magnetic interfaces;50 in contrast, in EuSi2, the absolute values are the same within the experimental error. The value is about 450 Oe; it does not change much if the FC field is reduced 10 times, from 10 kOe to 1 kOe (Fig. 5c). The EB field is about 3 times lower than that detected in the silicene-based GdSi2;33 however, it is on par with the typical EB fields recorded for heterostructures of magnetic 2D materials.21–23,25 The strong EB effect evidences the presence of competing magnetic states. However, their interplay depends on the number N, as demonstrated by Fig. 5d. EB requires the presence of both FM and AFM domains. In the AFM bulk, FM domains are absent resulting in zero EB field; in the FM limit, EB field does not show up due to a lack of AFM domains (see Fig. S1, ESI† for N = 4). Therefore, dependence of EB field on N is expected to have a maximum between the two limits, naturally in the crossover region where both FM and AFM domains are present. In EuSi2, the EB field reaches maximum at N = 9 (Fig. 5d). Fig. S2 and S3, ESI† provide evidence of EB in EuSi2 films with other values of N. Tuning of N can be considered a rather general way to induce an intrinsic EB.
As mentioned above, the EB phenomenon has been reported for other individual compounds – for instance, it has been observed in ultrathin NiO and attributed to exchange coupling of coexisting FM and AFM domains.38 EB is exhibited by manganites,30,31 materials particularly famous for the magnetic phase separation. It is likely that the situation in EuSi2 is rather similar: phase separation appears as a result of thickness-dependent crossover from the AFM state in the bulk to the FM state in ultrathin films. A simple model to describe EB in antiferromagnets containing FM clusters has been proposed in Ref. 51.
EuX2 magnetism stems from the triangular lattice of Eu atoms. Layered compounds alternating such cationic Eu layers and covalent anionic layers typically demonstrate a particular type of spin configuration – A-type AFM structure with in-plane magnetic moments, formed by FM layers coupled antiferromagnetically along the c-axis.52–54 The in-plane FM interactions in such layered structures are expected to be much stronger than the interlayer magnetic interactions.53,55 It suggests that the magnetic ordering along the c-axis is not robust with respect to change of the spin configuration. The situation is best illustrated by EuCd2As2, another layered material with triangular Eu lattices. In this material, the magnetic order, A-type in-plane AFM or in-plane FM, depends on the level of band filling;56 a relatively low pressure drives the AFM/FM magnetic phase transition;57 in calculations, the sign of the interplane coupling changes in the process of lattice relaxation.55 Similarly, as the number of MLs in EuSi2 diminishes, the A-type in-plane AFM order is driven towards in-plane FM order by structural changes arising from reduced dimensionality. Microscopically, it means that in the crossover region FM clusters appear in the AFM matrix. Within this scenario, the FM moments of the adjacent ab-planes in the clusters are not anti-parallel (as in the A-type AFM environment) but align in parallel. Such spin configuration provides a seamless FM/AFM interface resulting in EB.
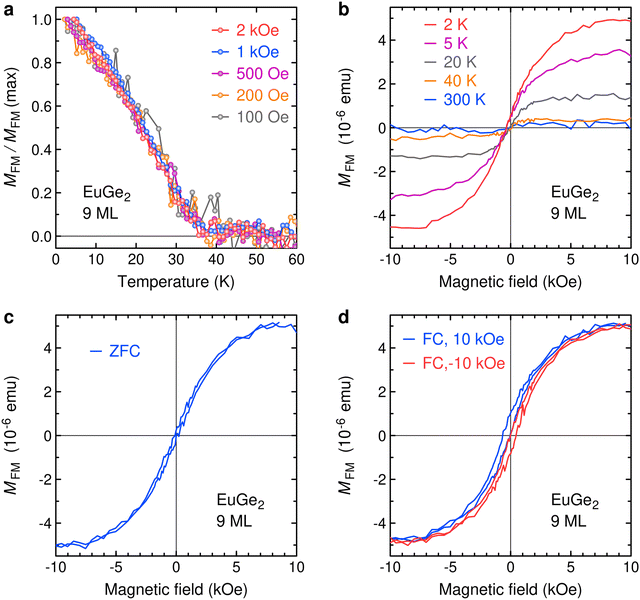
The magnetic properties are largely determined by the lattice of rare-earth ions. Therefore, it is natural to test whether replacement of the covalent anionic layer would affect the appearance of the EB state. We carried out a limited scope study of EuGe2, Eu intercalated germanene. This material has been studied in the bulk44 and ML8 forms demonstrating AFM and FM properties, respectively. In the latter case, a competition between magnetic orders has been suggested, taking into account that the FM moments are far from their maximal values.39 We synthesized 9 ML EuGe2 on Ge(111) following the recipe of Ref. 8. Both temperature (Fig. 6a) and magnetic field (Fig. 6b) dependences of the magnetic moment demonstrate emergence of an FM state in EuGe2. However, the magnetic transition temperature and the saturation moment are lower than those in 9 ML EuSi2. The hysteresis loop following ZFC (Fig. 6c) does not demonstrate any shift along the x-axis. However, significant shifts of the hysteresis loop occur following FC in 10 kOe (Fig. 6d). The absolute values of the shifts for FC in magnetic fields of opposite sign are very close; the effect is comparable to that in EuSi2 (see Fig. 5d). The result supports the idea that EB is a general phenomenon in rare-earth metalloxenes of intermediate thickness.
3. Conclusions
In summary, we carried out a study of layer dependence of electron transport and magnetic properties in the silicene-based material EuSi2 integrated with silicon. The study focuses on the crossover region between the mono- and multilayer limits dominated by ferro- and antiferromagnetic states, respectively. This region is a stage for competition between the magnetic orders, evidenced by pronounced EB effects. Similar behavior has been observed in the multilayer silicene intercalated by Gd,34 another lanthanide forming cations with half-filled 4f shell. It may well be that silicene-based EuSi2 and GdSi2 seed a class of compounds with unconventional magnetic structures based on competing magnetic orders. In the present study we demonstrate that this class spreads to germanene-based compounds, EuGe2 in particular. The reasons for the N-driven competition of magnetic states are yet to be established. For instance, can the triangular lattice of Eu/Gd supporting magnetic frustration be responsible? Probably not, because Eu lattices with rectangular unit cells also show reduced magnetic moments suggesting mixed magnetic states.58 The reduction of the magnetic moment is difficult to capture theoretically as demonstrated by recent studies of EuSi259 and germanene-based metalloxenes.60,61 Further experimental studies of magnetic metalloxenes may shed some light on the problem. In a similar manner, the graphene-based monolayer EuC6 exhibits competition between AFM and FM states.62 In addition, metalloxenes with other than 4f7 lanthanide ions can be considered as promising candidates for search of intrinsic EB. In that case, orbital contributions are also likely to play an important role. The search may lead to materials with particularly advantageous properties for spintronic applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by NRC “Kurchatov Institute”, the Ministry of Science and Higher Education of Russia [Agreement No. 075-15-2021-1351 (structural characterization)], and the Russian Science Foundation [grants No. 22-13-00004 (synthesis), No. 19-19-00009 (magnetism studies), and No. 20-79-10028 (electron transport studies)]. D. V. A. acknowledges support from the President's scholarship (SP 3111.2022.5). The measurements have been carried out using equipment of the resource centers of electrophysical, laboratory X-ray, and electron microscopy techniques at NRC “Kurchatov Institute”.References
- M. Gibertini, M. Koperski, A. F. Morpurgo and K. S. Novoselov, Nat. Nanotechnol., 2019, 14, 408–419 CrossRef CAS PubMed.
- K. F. Mak, J. Shan and D. C. Ralph, Nat. Rev. Phys., 2019, 1, 646–661 CrossRef.
- C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Nature, 2017, 546, 265–269 CrossRef CAS PubMed.
- B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Nature, 2017, 546, 270–273 CrossRef CAS PubMed.
- A. P. Balan, S. Radhakrishnan, C. F. Woellner, S. K. Sinha, L. Deng, C. De Los Reyes, B. M. Rao, M. Paulose, R. Neupane, A. Apte, V. Kochat, R. Vajtai, A. R. Harutyunyan, C. W. Chu, G. Costin, D. S. Galvao, A. A. Martí, P. A. Van Aken, O. K. Varghese, C. S. Tiwary, A. M. M. R. Iyer and P. M. Ajayan, Nat. Nanotechnol., 2018, 13, 602–609 CrossRef PubMed.
- A. Bedoya-Pinto, J.-R. Ji, A. K. Pandeya, P. Gargiani, M. Valvidares, P. Sessi, J. M. Taylor, F. Radu, K. Chang and S. S. P. Parkin, Science, 2021, 374, 616–620 CrossRef CAS PubMed.
- A. M. Tokmachev, D. V. Averyanov, O. E. Parfenov, A. N. Taldenkov, I. A. Karateev, I. S. Sokolov, O. A. Kondratev and V. G. Storchak, Nat. Commun., 2018, 9, 1672 CrossRef PubMed.
- A. M. Tokmachev, D. V. Averyanov, A. N. Taldenkov, O. E. Parfenov, I. A. Karateev, I. S. Sokolov and V. G. Storchak, Mater. Horiz., 2019, 6, 1488–1496 RSC.
- H. You, N. Ding, J. Chen, X. Yao and S. Dong, ACS Appl. Electron. Mater., 2022, 4, 3168–3175 CrossRef CAS.
- A. M. Tokmachev, D. V. Averyanov, I. S. Sokolov, A. N. Taldenkov, O. E. Parfenov, I. A. Karateev and V. G. Storchak, in Xenes: 2D Synthetic Materials beyond Graphene, ed. A. Molle and C. Grazianetti, Woodhead Publishing (Elsevier), Cambridge, US, 2022, ch. 14, pp. 353–375 Search PubMed.
- J. Tuček, P. Błoński, J. Ugolotti, A. K. Swain, T. Enoki and R. Zbořil, Chem. Soc. Rev., 2018, 47, 3899–3990 RSC.
- I. S. Sokolov, D. V. Averyanov, O. E. Parfenov, I. A. Karateev, A. N. Taldenkov, A. M. Tokmachev and V. G. Storchak, Mater. Horiz., 2020, 7, 1372–1378 RSC.
- J. X. Lin, Y.-H. Zhang, E. Morissette, Z. Wang, S. Liu, D. Rhodes, K. Watanabe, T. Taniguchi, J. Hone and J. I. A. Li, Science, 2022, 375, 437–441 CrossRef CAS PubMed.
- B. Huang, M. A. McGuire, A. F. May, D. Xiao, P. Jarillo-Herrero and X. Xu, Nat. Mater., 2020, 19, 1276–1289 CrossRef CAS PubMed.
- S. Jiang, J. Shan and K. F. Mak, Nat. Mater., 2018, 17, 406–410 CrossRef CAS PubMed.
- T. Song, Z. Fei, M. Yankowitz, Z. Lin, Q. Jiang, K. Hwangbo, Q. Zhang, B. Sun, T. Taniguchi, K. Watanabe, M. A. McGuire, D. Graf, T. Cao, J.-H. Chu, D. H. Cobden, C. R. Dean, D. Xiao and X. Xu, Nat. Mater., 2019, 18, 1298–1302 CrossRef CAS PubMed.
- D. R. Klein, D. Macneill, J. L. Lado, D. Soriano, E. Navarro-Moratalla, K. Watanabe, T. Taniguchi, S. Manni, P. Canfield, J. Fernández-Rossier and P. Jarillo-Herrero, Science, 2018, 360, 1218–1222 CrossRef CAS PubMed.
- O. E. Parfenov, A. M. Tokmachev, D. V. Averyanov, I. A. Karateev, I. S. Sokolov, A. N. Taldenkov and V. G. Storchak, Mater. Today, 2019, 29, 20–25 CrossRef CAS.
- S. Giri, M. Patra and S. Majumdar, J. Phys.: Condens. Matter, 2011, 23, 073201 CrossRef CAS PubMed.
- M.-H. Phan, V. Kalappattil, V. O. Jimenez, Y. T. H. Pham, N. W. Y. A. Y. Mudiyanselage, D. Detellem, C.-M. Hung, A. Chanda and T. Eggers, J. Alloys Compd., 2023, 937, 168375 CrossRef CAS.
- L. Zhang, X. Huang, H. Dai, M. Wang, H. Cheng, L. Tong, Z. Li, X. Han, X. Wang, L. Ye and J. Han, Adv. Mater., 2020, 32, 2002032 CrossRef CAS PubMed.
- R. Zhu, W. Zhang, W. Shen, P. K. J. Wong, Q. Wang, Q. Liang, Z. Tian, Y. Zhai, C. W. Qiu and A. T. S. Wee, Nano Lett., 2020, 20, 5030–5035 CrossRef CAS PubMed.
- T. Zhang, Y. Zhang, M. Huang, B. Li, Y. Sun, Z. Qu, X. Duan, C. Jiang and S. Yang, Adv. Sci., 2022, 9, 2105483 CrossRef CAS PubMed.
- H. Dai, H. Cheng, M. Cai, Q. Hao, Y. Xing, H. Chen, X. Chen, X. Wang and J.-B. Han, ACS Appl. Mater. Interfaces, 2021, 13, 24314–24320 CrossRef CAS PubMed.
- J. Jo, F. Calavalle, B. Martín-García, D. Tezze, F. Casanova, A. Chuvilin, L. E. Hueso and M. Gobbi, Adv. Mater., 2022, 34, 2200474 CrossRef CAS PubMed.
- H. K. Gweon, S. Y. Lee, H. Y. Kwon, J. Jeong, H. J. Chang, K.-W. Kim, Z. Q. Qiu, H. Ryu, C. Jang and J. W. Choi, Nano Lett., 2021, 21, 1672–1678 CrossRef CAS PubMed.
- G. Zheng, W.-Q. Xie, S. Albarakati, M. Algarni, C. Tan, Y. Wang, J. Peng, J. Partridge, L. Farrar, J. Yi, Y. Xiong, M. Tian, Y.-J. Zhao and L. Wang, Phys. Rev. Lett., 2020, 125, 047202 CrossRef CAS PubMed.
- S. Albarakati, W.-Q. Xie, C. Tan, G. Zheng, M. Algarni, J. Li, J. Partridge, M. J. S. Spencer, L. Farrar, Y. Xiong, M. Tian, X. Wang, Y.-J. Zhao and L. Wang, Nano Lett., 2022, 22, 6166–6172 CrossRef CAS PubMed.
- E. Dagotto, T. Hotta and A. Moreo, Phys. Rep., 2001, 344, 1–153 CrossRef CAS.
- E. Fertman, S. Dolya, V. Desnenko, L. A. Pozhar, M. Kajňaková and A. Feher, J. Appl. Phys., 2014, 115, 203906 CrossRef.
- D. Niebieskikwiat and M. B. Salamon, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 174422 CrossRef.
- E. Maniv, R. A. Murphy, S. C. Haley, S. Doyle, C. John, A. Maniv, S. K. Ramakrishna, Y.-L. Tang, P. Ercius, R. Ramesh, A. P. Reyes, J. R. Long and J. G. Analytis, Nat. Phys., 2021, 17, 525–530 Search PubMed.
- T. Song, Q.-C. Sun, E. Anderson, C. Wang, J. Qian, T. Taniguchi, K. Watanabe, M. A. McGuire, R. Stöhr, D. Xiao, T. Cao, J. Wrachtrup and X. Xu, Science, 2021, 374, 1140–1144 CrossRef CAS PubMed.
- D. V. Averyanov, I. S. Sokolov, A. N. Taldenkov, O. E. Parfenov, I. A. Karateev, O. A. Kondratev, A. M. Tokmachev and V. G. Storchak, ACS Nano, 2022, 16, 19482–19490 CrossRef CAS PubMed.
- C. X. Trang, Q. Li, Y. Yin, J. Hwang, G. Akhgar, I. Di Bernardo, A. Grubišić-Čabo, A. Tadich, M. S. Fuhrer, S.-K. Mo, N. V. Medhekar and M. T. Edmonds, ACS Nano, 2021, 15, 13444–13452 CrossRef CAS PubMed.
- K. Lee, A. H. Dismukes, E. J. Telford, R. A. Wiscons, J. Wang, X. Xu, C. Nuckolls, C. R. Dean, X. Roy and X. Zhu, Nano Lett., 2021, 21, 3511–3517 CrossRef CAS PubMed.
- E. J. Telford, A. H. Dismukes, R. L. Dudley, R. A. Wiscons, K. Lee, D. G. Chica, M. E. Ziebel, M.-G. Han, J. Yu, S. Shabani, A. Scheie, K. Watanabe, T. Taniguchi, D. Xiao, Y. Zhu, A. N. Pasupathy, C. Nuckolls, X. Zhu, C. R. Dean and X. Roy, Nat. Mater., 2022, 21, 754–760 CrossRef CAS PubMed.
- J. Wang, L. Ma, X. Wang, X. Wang, J. Yao, Q. Yi, R. Tang and G. Zou, Angew. Chem., Int. Ed., 2021, 60, 25020–25027 CrossRef CAS PubMed.
- D. V. Averyanov, I. S. Sokolov, M. S. Platunov, F. Wilhelm, A. Rogalev, P. Gargiani, M. Valvidares, N. Jaouen, O. E. Parfenov, A. N. Taldenkov, I. A. Karateev, A. M. Tokmachev and V. G. Storchak, Nano Res., 2020, 13, 3396–3402 CrossRef CAS.
- Z. Zang, M. Xi, S. Tian, R. Guzman, T. Wang, W. Zhou, H. Lei, Y. Huang and Y. Ye, ACS Appl. Electron. Mater., 2022, 4, 3256–3262 CrossRef CAS.
- F. Huttmann, N. Rothenbach, S. Kraus, K. Ollefs, L. M. Arruda, M. Bernien, D. Thonig, A. Delin, J. Fransson, K. Kummer, N. B. Brookes, O. Eriksson, W. Kuch, T. Michely and H. Wende, J. Phys. Chem. Lett., 2019, 10, 911–917 CrossRef CAS PubMed.
- S. Schulz, I. A. Nechaev, M. Güttler, G. Poelchen, A. Generalov, S. Danzenbächer, A. Chikina, S. Seiro, K. Kliemt, A. Y. Vyazovskaya, T. K. Kim, P. Dudin, E. V. Chulkov, C. Laubschat, E. E. Krasovskii, C. Geibel, C. Krellner, K. Kummer and D. V. Vyalikh, npj Quant. Mater., 2019, 4, 26 CrossRef.
- A. M. Tokmachev, D. V. Averyanov, I. A. Karateev, O. E. Parfenov, O. A. Kondratev, A. N. Taldenkov and V. G. Storchak, Adv. Funct. Mater., 2017, 27, 1606603 CrossRef.
- O. E. Parfenov, D. V. Averyanov, A. M. Tokmachev, I. S. Sokolov, I. A. Karateev, A. N. Taldenkov and V. G. Storchak, Adv. Funct. Mater., 2020, 30, 1910643 CrossRef CAS.
- D. V. Averyanov, A. M. Tokmachev, C. G. Karateeva, I. A. Karateev, E. F. Lobanovich, G. V. Prutskov, O. E. Parfenov, A. N. Taldenkov, A. L. Vasiliev and V. G. Storchak, Sci. Rep., 2016, 6, 25980 CrossRef CAS PubMed.
- O. E. Parfenov, A. N. Taldenkov, D. V. Averyanov, I. S. Sokolov, O. A. Kondratev, M. M. Borisov, S. N. Yakunin, I. A. Karateev, A. M. Tokmachev and V. G. Storchak, Mater. Horiz., 2022, 9, 2854–2862 RSC.
- N. Onda, J. Henz, E. Müller, K. A. Mäder and H. von Känel, Appl. Surf. Sci., 1992, 56–58, 421–426 CrossRef CAS.
- B. M. Wang, Y. Liu, P. Ren, B. Xia, K. B. Ruan, J. B. Yi, J. Ding, X. G. Li and L. Wang, Phys. Rev. Lett., 2011, 106, 077203 CrossRef CAS PubMed.
- E. Lachman, R. A. Murphy, N. Maksimovic, R. Kealhofer, S. Haley, R. D. McDonald, J. R. Long and J. G. Analytis, Nat. Commun., 2020, 11, 560 CrossRef CAS PubMed.
- Y. Wu, W. Wang, L. Pan and K. L. Wang, Adv. Mater., 2022, 34, 2105266 CrossRef CAS PubMed.
- M. L. Pankratova and A. S. Kovalev, Low Temp. Phys., 2018, 44, 1161–1167 CrossRef CAS.
- J. M. Cadogan, D. H. Ryan, R. Rejali and C. D. Boyer, J. Alloys Compd., 2016, 688, 51–54 CrossRef CAS.
- M. C. Rahn, J.-R. Soh, S. Francoual, L. S. I. Veiga, J. Strempfer, J. Mardegan, D. Y. Yan, Y. F. Guo, Y. G. Shi and A. T. Boothroyd, Phys. Rev. B, 2018, 97, 214422 CrossRef CAS.
- S. Pakhira, T. Heitmann, S. X. M. Riberolles, B. G. Ueland, R. J. McQueeney, D. C. Johnston and D. Vaknin, Phys. Rev. B, 2021, 103, 024408 CrossRef CAS.
- J.-Z. Ma, S. M. Nie, C. J. Yi, J. Jandke, T. Shang, M. Y. Yao, M. Naamneh, L. Q. Yan, Y. Sun, A. Chikina, V. N. Strocov, M. Medarde, M. Song, Y.-M. Xiong, G. Xu, W. Wulfhekel, J. Mesot, M. Reticcioli, C. Franchini, C. Mudry, M. Müller, Y. G. Shi, T. Qian, H. Ding and M. Shi, Sci. Adv., 2019, 5, eaaw4718 CrossRef CAS PubMed.
- N. H. Jo, B. Kuthanazhi, Y. Wu, E. Timmons, T.-H. Kim, L. Zhou, L.-L. Wang, B. G. Ueland, A. Palasyuk, D. H. Ryan, R. J. McQueneey, K. Lee, B. Schrunk, A. A. Burkov, R. Prozorov, S. L. Bud’ko, A. Kaminski and P. C. Canfield, Phys. Rev. B, 2020, 101, 140402 CrossRef CAS.
- E. Gati, S. L. Bud’ko, L.-L. Wang, A. Valadkhani, R. Gupta, B. Kuthanazhi, L. Xiang, J. M. Wilde, A. Sapkota, Z. Guguchia, R. Khasanov, R. Valentí and P. C. Canfield, Phys. Rev. B, 2021, 104, 155124 CrossRef CAS.
- A. M. Tokmachev, D. V. Averyanov, A. N. Taldenkov, I. S. Sokolov, I. A. Karateev, O. E. Parfenov and V. G. Storchak, ACS Nano, 2021, 15, 12034–12041 CrossRef CAS PubMed.
- G. Yang, J.-S. Chai, K. Bu, L.-F. Xu and J.-T. Wang, Phys. Chem. Chem. Phys., 2022, 24, 6782–6787 RSC.
- Z. Gao, Y. Wang, J. Gao, Z. Cui, X. Zhang, J. Shi and X. Fan, Comput. Mater. Sci., 2022, 213, 111611 CrossRef CAS.
- Y. Wang, Z. Cui, H. Zeng, Z. Wang, X. Zhang, J. Shi, T. Cao and X. Fan, J. Mater. Chem. C, 2022, 10, 1259–1269 RSC.
- I. S. Sokolov, D. V. Averyanov, F. Wilhelm, A. Rogalev, O. E. Parfenov, A. N. Taldenkov, I. A. Karateev, A. M. Tokmachev and V. G. Storchak, Nano Res., 2022, 15, 408–413 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nh00009e |
| This journal is © The Royal Society of Chemistry 2023 |