Superlattice deformation in quantum dot films on flexible substrates via uniaxial strain†
Julian E.
Heger
 a,
Wei
Chen
a,
Wei
Chen
 ab,
Huaying
Zhong
ab,
Huaying
Zhong
 a,
Tianxiao
Xiao
a,
Tianxiao
Xiao
 a,
Constantin
Harder
ac,
Fabian A. C.
Apfelbeck
a,
Constantin
Harder
ac,
Fabian A. C.
Apfelbeck
 a,
Alexander F.
Weinzierl
a,
Regine
Boldt
d,
Lucas
Schraa
a,
Alexander F.
Weinzierl
a,
Regine
Boldt
d,
Lucas
Schraa
 d,
Eric
Euchler
d,
Eric
Euchler
 d,
Anna K.
Sambale
d,
Anna K.
Sambale
 d,
Konrad
Schneider
d,
Konrad
Schneider
 d,
Matthias
Schwartzkopf
d,
Matthias
Schwartzkopf
 c,
Stephan V.
Roth
c,
Stephan V.
Roth
 ce and
P.
Müller-Buschbaum
ce and
P.
Müller-Buschbaum
 *af
*af
aTechnical University of Munich, TUM School of Natural Sciences, Department of Physics, Chair for Functional Materials, James-Franck-Str. 1, 85748 Garching, Germany. E-mail: muellerb@ph.tum.de
bCollege of Engineering Physics, Shenzhen Technology University (SZTU), Lantian Road 3002, Pingshan, 518118 Shenzhen, China
cDeutsches Elektronen-Synchrotron DESY, Notkestraße 85, 22607 Hamburg, Germany
dLeibniz-Institut für Polymerforschung Dresden e.V., Institut für Polymerwerkstoffe, Hohe Straße 6, 01069 Dresden, Germany
eRoyal Institute of Technology KTH, Teknikringen 34-35, 100 44 Stockholm, Sweden
fTechnical University of Munich, Heinz Maier-Leibnitz Zentrum (MLZ), Lichtenbergstraße 1, 85748 Garching, Germany
First published on 23rd January 2023
Abstract
The superlattice in a quantum dot (QD) film on a flexible substrate deformed by uniaxial strain shows a phase transition in unit cell symmetry. With increasing uniaxial strain, the QD superlattice unit cell changes from tetragonal to cubic to tetragonal phase as measured with in situ grazing-incidence small-angle X-ray scattering (GISAXS). The respective changes in the optoelectronic coupling are probed with photoluminescence (PL) measurements. The PL emission intensity follows the phase transition due to the resulting changing inter-dot distances. The changes in PL intensity accompany a redshift in the emission spectrum, which agrees with the Förster resonance energy transfer (FRET) theory. The results are essential for a fundamental understanding of the impact of strain on the performance of flexible devices based on QD films, such as wearable electronics and next-generation solar cells on flexible substrates.
New conceptsSolution-processible thin-film technology offers attractive applications for next-generation optoelectronics, such as devices on flexible substrates. In these systems, performance and morphology are inherently correlated. The morphological deformation by external strain and its impact on the functionality of devices on flexible substrates is essential to consider. However, it is hard to access the desired information on the necessary length scales by real-space microscopy. Grazing-incidence small-angle X-ray scattering (GISAXS) is a powerful tool for investigating the structure of thin films with high statistical significance. The non-trivial experimental conditions may be why the literature barely covers GISAXS on thin films and flexible substrates during deformation by strain. In this work, we report the superlattice deformation in lead sulfide colloidal quantum dot (PbS CQD) thin films on a flexible substrate via in situ GISAXS upon uniaxial strain, that is enabled by a specially designed sample environment. The concept of thin-film deformation revealed by GISAXS has strong potential to expand to other material classes and benefit the nanoscience community. |
Introduction
Modern technology builds on advanced materials that fulfill three properties: smart, suitable, and sustainable. Advanced materials are smart when they respond to some external triggers of various origins. The stimuli-and-response cycle is fundamental for sensors, robotics, coatings, and electronics. Moreover, they display a certain degree of autonomy, for instance, the feasibility of self-assembling and self-powering. Advanced materials are suitable when they match the expected operating conditions and optimize performance. The race for outperforming next-generation solar cells demonstrates the urgent demand for suitability. Advanced materials are sustainable when produced from abundant precursors, with low energy costs, and with high stability upon operation to reduce the environmental impact. Ideally, they are easily fabricated on a large scale to benefit economic and ecological interests.The material class of colloidal quantum dots (QDs) features promising properties in this context.1,2 They consist of nanocrystals showing strong quantum confinement in all dimensions due to their small sizes of 2–20 nanometers. Hence, they are commonly referred to as artificial atoms, reflecting their high versatility.3 For instance, when deposited into a thin film, colloidal QDs self-assemble into superlattices with long-range order, similar to atoms in a solid.4 Accordingly, unit cells periodically build up the QD superlattice (Fig. 1). From separated to close-packed QDs in superlattices, the wavefunctions of neighboring QDs start to overlap due to the short inter-dot distances, and the energy levels split up. The consequent formation of bands offers new possibilities for charge transport and energy transfer between the QDs. The possibility of either band-like or hopping transport is given, depending on inter-dot distance and the energetic disorder. The disorder is introduced by, e.g., size-polydisperse QDs and influences the energetic landscape by bandtail and midgap states.5,6 Non-radiative energy transfer, e.g., via dipole–dipole interactions sensitive to the distance between neighboring QDs becomes more efficient in superlattices.7,8 The distance between neighboring QDs dominates the electronic coupling within these QD superlattices and influences the optoelectronic properties.5,9,10 Hence, external stimuli that change the inter-dot distance can cause a response.11 For instance, QDs embedded in flexible polydimethylsiloxane (PDMS) matrices showed enhanced luminescence when the samples were stretched.9 This response makes QD superlattices encouraging for smart applications.2,12 Moreover, the feasibility of a controlled synthesis features controlled quantum confinement and thereby controlled optoelectronic properties, e.g., a broadly tunable emission or absorbance spectrum.13 Together with high charge carrier mobilities by state-of-the-art ligand engineering, the aspect of tunability makes QDs suitable, e.g., for next-generation solar cells.14–17 The optimized synthesis of colloidal QDs has a high yield from a reasonable amount of precursor materials.18,19 Surface-attached ligands result in solubility for numerous solvents, increase the environmental stability and give QDs the appearance of semi-soft materials.20–22 Solution processability opens the door to industrial-scale fabrication via printing, spray-deposition, or spin-coating with low energy costs and high compatibility for use in integrated circuits.4,23,24 QDs deposited into thin films dramatically reduce material usage in applications. Recent techno-economic cost analyses have shown that under consideration of synthesis yield optimization, process automatization, and solvent recycling, the fabrication costs of colloidal QD films have the potential to decrease to 3 $ m−2. These aspects make QD films also a sustainable material.25,26
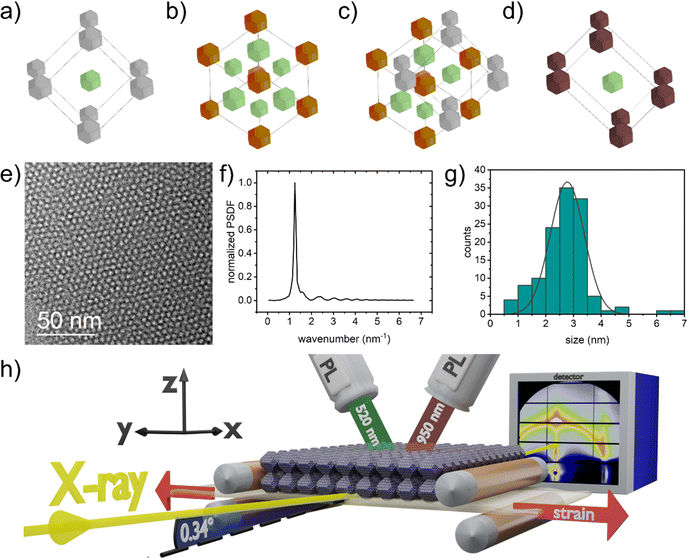
As mentioned before, the electronic and spectral performance of QD films depends on the inter-dot distance and, hence, on the QD superlattice structure. Repeating blocks of unit cells build up the QD superlattice structure and contain information about inter-dot distance and packing density.27 Superlattices made of QDs with different sizes and size distributions, shapes, and ligand conditions can show different kinds of unit cells. For example, spray-coated large-sized lead sulfide (PbS) QDs form superlattices based on a body-centered cubic (BCC) unit cell (Fig. 1(a)).23 In contrast, printed small-sized PbS QDs show face-centered cubic (FCC) symmetry (Fig. 1(b)) in early stages, which eventually form a superposition of cubic unit cells to a nested FCC/BCC structure (Fig. 1(c)) due to the ligand condition shift.4 This nested structure also forms the QD superlattice in films of spin-coated PbS QDs. There are various strategies to tailor the inter-dot distance, e.g., polymer matrix-induced spacing and ligand engineering.9,28–30 Typically, using different-sized ligand molecules, a controlled spacing between QDs is achieved.3,31 Post-treatment techniques, such as ligand exchange or temperature and solvent annealing, are practical tools to change the QD arrangement in a given superlattice configuration after deposition.32–34 Furthermore, Gong et al. suggested that external strain changes the inter-dot distance by tearing neighboring QDs apart, explaining changes in the corresponding photoluminescence (PL) emission.9
The influence of strain on the spatial configuration of QDs becomes essential for applications on flexible substrates, such as wearable electronics and printed photovoltaic foils, since flexibility inherently allows for mechanical deformations of the related devices. However, detailed studies on the correlation between QD superlattice deformation and optoelectronic coupling in QD films upon strain are rarely reported. Winslow et al. recently investigated QD superlattices with grazing-incidence small-angle X-ray scattering (GISAXS) and reported a unit cell phase transition from FCC to body-centered tetragonal (BCT) (Fig. 1(d)) upon sample cooling to 100 K.35 GISAXS is a powerful method to study the superlattice deformation in QD films during strain with X-rays.16,23,36–38 It is sensitive to the desired length scales and probes a large sample volume with the grazing beam's footprint effect. In contrast, probing thin QD films with conventional small-angle X-ray scattering (SAXS) in transmission geometry typically does not yield a sufficient scattering signal. However, GISAXS requires precise sample alignment with respect to the incoming X-ray beam since it is highly surface sensitive. A bent surface could result in multiple reflection conditions and, hence, ill-defined alignment conditions. This circumstance makes the study on flexible films during uniaxial strain challenging, as the freestanding, flexible substrate deforms under tension and thus changes the sample alignment. To overcome this challenge, we introduce a sample environment based on four cylindrical rolls. Two rolls act as support from the bottom and two as fixation from the top, acting together to guide the substrate and balance strain-induced substrate bending (Fig. S1, ESI†). With this approach, we establish a controlled sample alignment for successful GISAXS measurements on freestanding, flexible substrates.
Given the possibility of performing GISAXS, this work aims to complement the understanding of QD superlattice deformation via uniaxial strain and its influence on the respective luminescence. We focus on PbS QD thin films prepared by spin-coating on flexible PDMS substrates, which exhibit a superlattice assembly. Moreover, PbS QDs have also developed into a representative role model for understanding QD superlattices. Fig. 1(e) shows the transmission electron microscopy (TEM) image of the close-packed FCC (111) plane formed by the PbS QDs capped with oleic acid (OA) ligands which we used in this work. The high degree of spatial order and the mean inter-dot spacing are reflected in the radial power spectral density function (Fig. 1(f)). The first order peak at 1.25 nm−1 corresponds to a mean inter-dot spacing of about 5 nm. The PbS QDs have a mean size of 2.7 nm, and a size dispersity with a standard deviation of 21% (Fig. 1(g)). More details about the QD size and size distribution can be found in the Experimental part of this work. Uniaxial strain applied to the sample deforms the QD superlattice. In situ GISAXS probes this QD superlattice deformation, and in situ PL records the optoelectronic coupling as a function of applied strain. Fig. 1(h) sketches the experimental setup.
In this work, we observe superlattice deformation and a unit cell phase transition by strain. Furthermore, the PL signal has strong dependence on strain and follows the evolution of the unit cell. We see a correlation to the changing unit cell isotropy and suggest interpreting the results in the framework of Förster resonance energy transfer (FRET).39 Experimental details for sample fabrication and measurements are given in the Experimental part.
Results
Superlattice deformation upon strain
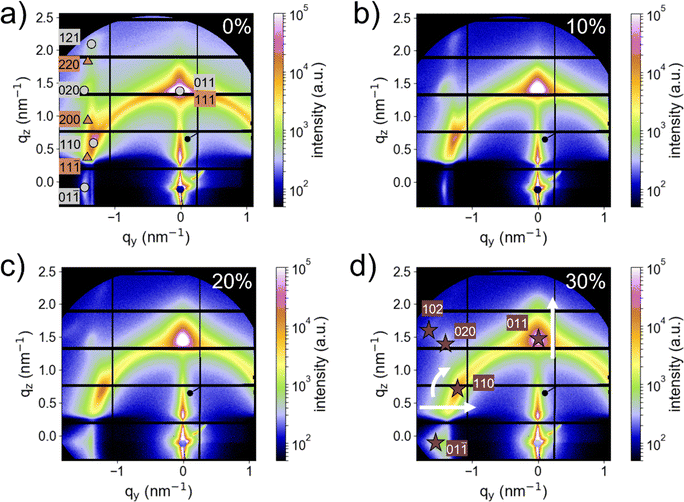
The 2D GISAXS data in Fig. 2 obtained from the in situ uniaxial stretching experiment gives an overview of the QD superlattice deformation process with increasing substrate elongation Δlsub/lsub0 from 0% to 30%, where Δlsub is the difference to initial substrate length lsub0. The 2D data shows the direct beam blocked by a beam stop and typical GISAXS features, such as the sample horizon that separates reflected from transmitted signals and the material characteristic Yoneda peak. In the ESI,† the GISAXS features are displayed in the vertical line cut along qy = 0 nm−1 (Fig. S2, ESI†). Moreover, we observe a change in the vertical density profile in these line cuts, first towards higher and then lower density. The scattering pattern for the relaxed sample at 0% substrate elongation in Fig. 2(a) shows prominent Bragg reflexes arranged in a bow-like intensity distribution characteristic for PbS QDs. Additional reflexes are arranged vertically along qy = 1.3 nm−1. We identify the unit cell by matching the indices of the respective Bragg reflexes. It turns out that the superlattice consists of FCC and BCT unit cells, forming a nested FCC/BCT structure. The (011), (01![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ), (110), (020), and (121) superlattice planes correspond to the BCT part and are labeled with grey boxes in Fig. 2(a). The (011) reflex is aligned vertically to the direct beam position at qy = 0 nm−1. Hence, the BCT unit cell is in edge-on orientation with respect to the substrate plane. The (111), (11
), (110), (020), and (121) superlattice planes correspond to the BCT part and are labeled with grey boxes in Fig. 2(a). The (011) reflex is aligned vertically to the direct beam position at qy = 0 nm−1. Hence, the BCT unit cell is in edge-on orientation with respect to the substrate plane. The (111), (11![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ), (200), and (220) reflexes correspond to the FCC unit cell and are labeled with orange boxes in Fig. 2(a). Since the FCC's (111) reflex is located at qy = 0 nm−1, the FCC unit cell is present in the corner-on orientation.
), (200), and (220) reflexes correspond to the FCC unit cell and are labeled with orange boxes in Fig. 2(a). Since the FCC's (111) reflex is located at qy = 0 nm−1, the FCC unit cell is present in the corner-on orientation.
At 10% substrate elongation (Fig. 2(b)), the GISAXS data deviates from the relaxed state, and the (11![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ), (200), and (220) reflexes related to the FCC phase diminish. At 20% substrate elongation (Fig. 2(c)), the (121) reflex related to the BCT phase diminishes, and the BCT (102) reflex appears (labeled in Fig. 2(d)). With increasing substrate elongation from 0% to 30%, the BCT (110) reflex shifts towards lower and the BCT (011) reflex towards higher q-values. These shifts indicate an anisotropic deformation and, hence, suggest a change in unit cell symmetry. The shifted reflex positions and the additionally appearing reflex match the following superlattice indices of the BCT unit cell symmetry (Fig. 2(d)): (011), (01
), (200), and (220) reflexes related to the FCC phase diminish. At 20% substrate elongation (Fig. 2(c)), the (121) reflex related to the BCT phase diminishes, and the BCT (102) reflex appears (labeled in Fig. 2(d)). With increasing substrate elongation from 0% to 30%, the BCT (110) reflex shifts towards lower and the BCT (011) reflex towards higher q-values. These shifts indicate an anisotropic deformation and, hence, suggest a change in unit cell symmetry. The shifted reflex positions and the additionally appearing reflex match the following superlattice indices of the BCT unit cell symmetry (Fig. 2(d)): (011), (01![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ), (110), (020), and (102). Interestingly, this QD superlattice deformation again relaxes when reducing the substrate elongation to 20% and 10%, respectively (Fig. S3, ESI†). In conclusion, the 2D GISAXS data identifies a complex unit cell evolution from nested FCC/BCT at 0% to BCT with increasing deformation.
), (110), (020), and (102). Interestingly, this QD superlattice deformation again relaxes when reducing the substrate elongation to 20% and 10%, respectively (Fig. S3, ESI†). In conclusion, the 2D GISAXS data identifies a complex unit cell evolution from nested FCC/BCT at 0% to BCT with increasing deformation.
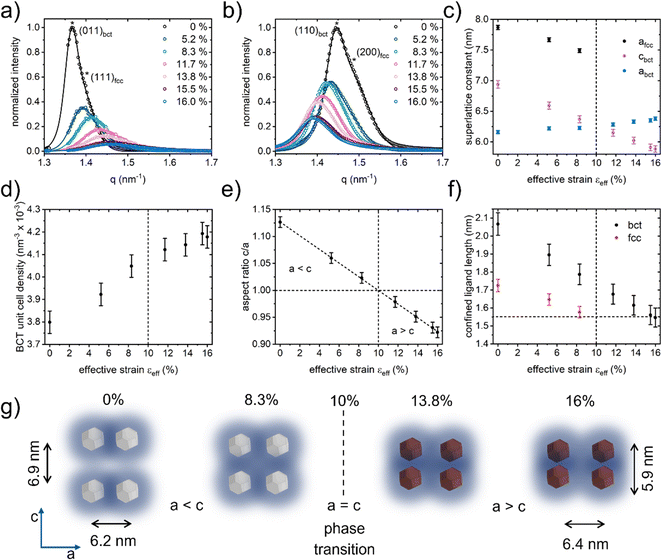
Unit cell evolution
The prominent (011) and (110) superlattice reflexes contain information about the BCT unit cell evolution upon strain, and the (111) and (200) superlattice reflexes about the FCC unit cell evolution. For analysis, we azimuthally integrate the respective peaks to one-dimensional intensity curves that are fitted with Gaussian functions (Fig. 3(a) and (b)). From the respective center q-values, we extract the superlattice constants a, b, and c that represent the lengths of the unit cell edges. For the tetragonal symmetry, the unit cell consists of a squared base area of side length a and a height c, with a = b ≠ c, and for the cubic symmetry, with a = b = c. Hence, the aspect ratio c/a helps to understand the unit cell evolution.It is essential to highlight that the applied strain via uniaxial substrate elongation does not distribute uniformly but mainly along three different length scales of deformation on the PbS QD film: (1) 3D superlattice deformation by changing the superlattice constants a = b and c on the nanoscale. (2) Grain boundary formation on the mesoscale of several tens to hundreds of nanometers. (3) Crack formation on the microscale. In this work, we focus on the superlattice deformation on the nanoscale, which we obtain directly from GISAXS analysis. To account for the inhomogeneous distribution of applied strain, we introduce an effective strain εeff with the equivalent strain magnitude:40,41
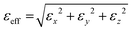 | (1) |
![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/b_char_e107.gif) :
: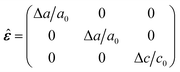 | (2) |
To qualitatively estimate the effect of grain boundary and crack formation on the distribution of the applied strain, we compare the effective strain εSLeff for the superlattice and εSubeff for the substrate as a function of uniaxial substrate elongation (Fig. S4a, ESI†). Whereas the effective strain on the substrate per definition linearly follows the uniaxial elongation, the effective strain on the superlattice deviates after 10% of substrate elongation from εSubeff with increasing magnitude until it approaches a value of εSLeff = 16% at εSubeff = 30%. Scherrer analysis of the superlattice planes’ peak broadening yields an estimation for the evolution of the average grain size (Fig. S4b, ESI†).42 The grain size shrinks from about 165 nm to about 75 nm with increasing effective strain to 10%. After that, the grain size decreases slightly and approaches about 62 nm at 16% effective strain. The disintegration of larger grains to smaller grains upon strain is accompanied by the formation of grain boundaries. Since this effect is strongly suppressed after 10%, we suggest that the evolution of granular interfaces plays a minor role in the observed strain distribution compared to superlattice deformation and crack propagation. We attribute the increasing deviation of effective strain to the beginning crack formation. After 30% of substrate elongation, i.e., 16% of effective strain on the superlattice, the applied strain fully disseminates on the cracks. Optical microscopy reveals the cracks, which are orthogonal to the direction of uniaxial strain, with a width of about 1 μm and with a distance of about 5–10 μm in the relaxed PbS QD film after the stretching experiment (Fig. S4c, ESI†).
The superlattice constants afcc, abct, cbct of the respective unit cells are shown against the effective strain in Fig. 3(c). The FCC unit cell shrinks along afcc from (7.87 ± 0.03) nm to (7.49 ± 0.03) nm and the FCC phase vanishes after 8.3% of effective strain. The BCT unit cell deforms via shrinking cbct from (6.94 ± 0.06) nm to (5.98 ± 0.05) nm and slightly extending abct from (6.16 ± 0.03) nm to (6.38 ± 0.03) nm (Fig. 3(c)). At 10% of effective strain the lattice constants abct = cbct match, indicating a cubic phase transition. The changing superlattice dimensions result in an increasing BCT unit cell density, which is given by the inverse product a−2c−1 of base area and height, respectively (Fig. 3(d)). The density increases from (3.80 ± 0.05) × 10−3 nm3 to (4.12 ± 0.05) × 10−3 nm3, which remains constant within the error bars after the phase transition. The aspect ratio provides an understanding of the BCT unit cell's symmetry evolution as a function of the effective strain (Fig. 3(e)). A horizontally dashed line at the aspect ratio of 1.00 represents the cubic phase line. With increasing effective strain from 0% to 16%, the aspect ratio reduces linearly from 1.13 to 0.91, passing the cubic phase line at 10% of effective strain. The evolution of the aspect ratio reveals an FCC/BCT–BCC–BCT phase transition with a < c from 0% to 10% and a > c after 10% to 16%. A vertically dashed line indicates the phase transition at a = c at 10% of effective strain, separating both BCT phases. Notably, the aspect ratio changes linearly along the effective strain range, demonstrating continuous superlattice deformation until 16%. To further understand the phase transition and the vanishing FCC phase in the nested FCC/BCT structure with the phase transition, it is helpful to consider the spacing between the nearest PbS QD neighbors in the superlattice. The nearest-neighbor spacing nn = DQD − dnn is given by the average QD size DQD and the average nearest-neighbor center-to-center distance dnn. It describes the available free space between the closest QDs, which measures the degree of intercalation and compression of the OA ligands.43 Fig. S5 (ESI†) shows the nearest-neighbor spacing of the FCC and BCT phase against effective strain for mean QD size DQD = 2.7 nm. At 0%, the two spacings of both phases nnfcc = nnbct = (2.86 ± 0.05) nm match because of the nested FCC/BCT structure. With increasing strain, the BCT nearest-neighbor spacing decreases to (2.68 ± 0.05) nm and remains constant within the error bars after the phase transition at 10%. The FCC nearest-neighbor spacing, however, shows a stronger decrease to (2.60 ± 0.05) nm at 8.3%. The reduced nearest-neighbor spacing is close to half of the spacing of about 5 nm that two ligands would induce with relaxed chain lengths of llig0 = 2.5 nm. This result indicates a high degree of ligand intercalation close to the maximum, high ligand compression along the nearest-neighbor distances, and dominating repulsive interactions between the neighboring QDs.43,44 To quantify the ligand compression, the interface between adjacent ligand-capped QDs needs to be considered. This interface is given by the wall of the unit cell's Wigner–Seitz cell and confines the ligand length. The confined ligand length in the superlattice lligSL varies from the relaxed ligand length llig0 and is given by the difference:45
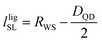 | (3) |
Photoluminescence upon strain
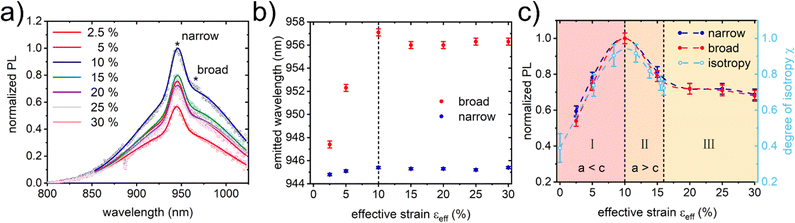
To understand the influence of the superlattice deformation on the optoelectronic coupling upon phase transition, additional in situ PL measurements are performed while increasing the effective substrate strain εSubeff from 2.5% to 30%. The overall PL spectrum shows an inhomogeneous broadening, which redshifts with increasing strain (Fig. 4(a)). Such inhomogeneous broadening is known for polydisperse QD solids with a single mean size and becomes more pronounced with a larger QD size distribution, such as the QDs investigated in this work.7 A reason for the inhomogeneous broadening in polydisperse assemblies is a resonant energy transfer from larger QDs to neighboring smaller QDs via dipole–dipole interactions. After radiative relaxation, the smaller QDs having a smaller bandgap emit a redshifted photon compared to the donor emission. As a result, the acceptor emission intensity is enhanced.46 The energy transfer between neighboring donor and acceptor QDs via dipole–dipole interactions and the characteristic redshift is described in the theory of FRET.7,39 The FRET efficiency is proportional to d−6, where d is the inter-dot distance. Due to the power of 6 exponent, FRET efficiency is very sensitive to changing distances.47 The influence of FRET on the PL spectrum is often observed in polydisperse QD assemblies upon varying distances, e.g., from solution to deposited film.48,49 Spatial sensitivity and enhanced acceptor emission intensity make FRET also essential in fluorescence-based microscopy broadly used in life sciences.50,51 The appearance of the PL spectra in Fig. 4(a) as a function of strain strongly suggests the interpretation of the changing emission in the framework of FRET theory.Inspired by the pioneering work of Kagan et al., we describe the inhomogeneously broadened PL profile as the sum of a narrow and a broad emission band.7 By fitting the PL profiles with two Gaussian functions, we extract the PL intensities, the center values for the emitted wavelength, and the line broadening of the full width at half maximum (FWHM). The normalized intensity substantially boosts to about 185% of the initial magnitude at 2.5% when increasing the strain towards 10%. After the phase transition, the intensity decreases at 30% strain to about 125% of the initial magnitude. This PL intensity behavior is in good agreement with the findings of Gong et al. for perovskite QDs in bulk PDMS matrices.9 Besides the changing intensity, the broad peak experiences a continuing redshift from (947.4 ± 0.3) nm to (957.1 ± 0.3) nm towards the phase transition. After the phase transition, the peak slightly blueshifts to (956.0 ± 0.3) nm and remains constant within the error bars (Fig. 4(b)). The narrow peak only slightly redshifts from (944.8 ± 0.1) nm to (945.4 ± 0.1) nm. In addition to the redshift, the broad peak first slightly narrows in the full width at half maximum (FWHM) from (124.1 ± 0.7) nm to (122.1 ± 0.7) nm and then broadens slightly to (125.6 ± 0.7) nm with respect to the phase transition (Fig. S6, ESI†). In contrast, the FWHM of the narrow peak remains constant at (16.9 ± 0.4) nm across the phase transition.
Discussion
Isotropy-dependent FRET efficiency
The results show that the PbS QD superlattice deforms upon sample elongation and eventually passes an FCC/BCT–BCC–BCT phase transition (Fig. 3(e)). At the same time, the PL intensity and emission spectrum change with respect to the phase transition (Fig. 4(a) and (b); Fig. S6, ESI†). We suggest that the PL behavior observed in this work results from changing dipole–dipole interactions of adjacent QDs in the framework of FRET. In this context, the increasing BCT unit cell density shown in Fig. 3(d) favors FRET as inter-dot distances become shorter. However, the BCT unit cell density does not increase isotropic, which affects the arrangement of adjacent QDs and needs to be considered for the dipole–dipole coupling. To quantitatively estimate the degree of isotropy upon superlattice deformation, we first introduce the anisotropy parameter![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) as the following:
as the following: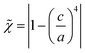 | (4) |
Expression (4) reflects the unit cell anisotropy for a given aspect ratio c/a to the power of 4, considering the 4-fold rotational symmetry of the tetragonal unit cell. The degree of anisotropy becomes minimal with ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) = 0 as the aspect ratio becomes 1 in the cubic phase of maximal isotropy. The degree of isotropy
= 0 as the aspect ratio becomes 1 in the cubic phase of maximal isotropy. The degree of isotropy ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) is then given by:
is then given by:
χ = 1 − ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) | (5) |
By comparing the degree of isotropy χ with the normalized PL emission intensities of the narrow peak and the broad peak as a function of the corresponding effective strains εSLeff and εSubeff, respectively, we identify three distinct stages of optoelectronic coupling with increasing uniaxial substrate elongation (Fig. 4(c)): (I) Increasing isotropy towards the cubic phase with a < c that is followed by increasing PL intensity with the maximum in the isotropic cubic phase a = c. (II) Decreasing isotropy with a > c towards the maximum εSLeff = 16% that is followed by decreasing PL intensity. (III) Constant PL intensity from 16% to 30% of substrate elongation.
Besides the changes in unit cell symmetry discussed in this work, reorientations of QDs on individual superlattice sites are possible contributions to the varying optoelectronic coupling. Especially in BCC configuration, an improved facet–facet alignment of {111} and {100} QD facets, respectively, compared to the FCC is commonly observed.27,42,52–55 We propose further investigations of QD orientation on the superlattice sites as a function of applied uniaxial strain for future studies.
Alternatively, the degree of disorder in the QD film introduced by the size polydispersity and the increasing grain boundaries with strain is a possible explanation for the observed redshift and the inhomogeneous broadening.6 While disorder certainly contributes, we see strong evidence for FRET in the perfect match of PL intensity and unit cell isotropy based on inter-dot distances together with the characteristic redshift and FWHM narrowing of the inhomogeneously broadened peak. A more quantitative verification and analysis of strain-induced PL changes in the framework of FRET could be achieved by time-resolved photoluminescence, which is not the focus of this work.48
Stage I: increasing PL emission from 0% to 10%
In the first stage, FRET benefits from the resulting higher density of adjacent QDs and higher isotropy for dipole–dipole interactions so that it becomes more efficient and mitigates emission losses that otherwise would occur via non-radiative recombinations.8,56 This is reflected in the increasing PL intensity from 0% to 10% (Fig. 4(c)). Further increase of the strain beyond 10% would cause a compression of the confined ligand chains beyond the critical value of lligSL = 1.55 nm, which is energetically unfavorable (Fig. 3(f)). Instead, the FCC/BCT superlattice transforms into a BCC phase at 10%. The ligands relax upon phase transition to the BCC phase, providing a longer confined ligand length of about 1.75 nm, which is in good effective strain. The FCC/BCT–BCC transition takes place via slipping in 〈110〉 directions on the close-packed {111} FCC planes that are in parallel alignment with the {011} BCT planes and is similar to the Nishiyama–Wassermann path known from the martensite transition in iron.57,58 Consequently, neighboring QDs get locally rearranged during the FCC/BCT–BCC phase transition and with the increasing isotropy, more dipole–dipole interactions between the QDs are likely to form. This rearrangement in adjacent QD coupling is reflected in the slightly redshifted wavelengths of the inhomogeneous broadening (Fig. 4(b)) and its reduced FWHM towards the cubic phase (Fig. S6, ESI†).7 Moreover, the decreasing nearest-neighbor spacing (Fig. S5, ESI†) agrees well with the observed redshift of the first excitonic peak in the absorbance spectra (Fig. S7, ESI†). A similar redshift in absorbance was observed by reducing nearest neighbor distances, e.g., by ligand exchange in PbSe thin films.59Stage II: decreasing PL emission from 10% to 16%
Further increase of strain after the unit cell phase transition leads to the decreasing unit cell isotropy followed by decreasing PL intensity. Isotropy and emission intensity vary symmetrically with respect to the maximum at the cubic phase line. Whereas the nearest-neighbor distances in the (011) BCT plane (Fig. S5, ESI†) and the absorbance spectra remain constant (Fig. S6, ESI†), the lattice continuously shrinks along cbct. The FRET efficiency, however, is reduced by the slightly increasing distance along abct since twice as many inter-dot distances along the unit cell edges are affected by abct than by cbct. The reduced isotropy of QD coupling also shifts the dipole–dipole interactions, as seen from the slightly blueshifted wavelength with respect to the phase transition (Fig. 4(b)). The blueshift is less pronounced than the redshift in stage I. We see the reason for this hysteresis in no slipping of the densest planes being involved in stage II. At 16%, the confined ligand length compresses to the same size that formerly caused the FCC/BCT–BCC phase transition via slipping (Fig. 3(f)). In the BCT phase, however, there is no unit cell symmetry left to access via phase transition that would allow for ligand relaxation. This missing relaxation pathway causes the beginning of microscopic crack formation that conserves a constant superlattice configuration with increasing strain. Hence, the FCC/BCT–BCC–BCT phase transition is considered as a ductile-to-brittle transition.Stage III: constant PL emission from 16% to 30%
In the final stage, the strain introduced by substrate elongation is entirely focused on the formation and widening of microscopic cracks (Fig. S4a, ESI†). The superlattice remains under tension in the configuration of isotropy, and inter-dot distances given at the maximum to the superlattice applied effective strain of 16%. Consequently, the optoelectronic coupling remains unchanged regarding constant PL emission intensity and wavelength. We attribute the observed slightly increasing FWHM of the inhomogeneous broadening to the loose interfaces upon crack propagation. This effect also reflects in the blueshift and the broadening at FWHM of the first excitonic peak in the absorbance spectra at 30% of effective strain (Fig. S6, ESI†). A slight decrease of PL intensity within the error bars hints increasing contribution of the arising voids on the area illuminated by the excitation laser, causing increasing light leakage at higher strains.Conclusions
Uniaxial strain applied to the substrate of OA-capped PbS QD thin films introduces three stages of superlattice deformation linked by the ligand shells’ compression to a critical value. This critical value is about 10% for the investigated QDs with a core-to-shell ratio of about 1.08 and corresponds to a confined ligand length of about 1.55 nm. The first two stages are linked by an FCC/BCT–BCC–BCT unit cell phase transition that relaxes the confined ligand length. The varying unit cell isotropy upon phase transition results in changed optoelectronic coupling and explains observed changes in PL emission within the framework of FRET. The third stage introduces crack propagation in the QD thin film because the critical ligand compression cannot be relaxed via unit cell phase transition. Here, the unit cell isotropy remains unchanged with increasing strain, leading to constant PL emission. Given the impact on superlattice deformation and optoelectronic coupling, the external strain on optoelectronic QD devices is necessary to account for real-world applications, e.g., on flexible substrates. Since FRET is a resonant energy transfer, its efficiency varying with strain plays a crucial role, e.g., in the figure of merit for QD solar cells.In summary, we report in situ GISAXS measurements on thin films on freestanding, flexible substrates upon uniaxial strain. By comparing the results of superlattice deformation and PL, we provide a connection between strain and optoelectronic coupling. This connection is given by the variation of the unit cell isotropy upon phase transition that affects the inter-dot coupling and complements the findings from the literature on a fundamental level.
Experimental
Synthesis of flexible PDMS substrates
The PDMS substrates were synthesized by mixing base and curing agent of SYLGARD 184 in a ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The mixture was poured into a rectangular mold and stored in a vacuumed desiccator for outgassing of remaining air. Subsequently, the resulting PDMS slides were cut into substrates with dimensions of 10 mm × 60 mm and a thickness of 1 mm.
1. The mixture was poured into a rectangular mold and stored in a vacuumed desiccator for outgassing of remaining air. Subsequently, the resulting PDMS slides were cut into substrates with dimensions of 10 mm × 60 mm and a thickness of 1 mm.
Fabrication of QDs and QD thin films
The QDs were synthesized following our previous work with slight modifications as follows.60 1.20 g lead oxide (PbO) was dissolved in 3 mL oleic acid (OA) and 10 mL octadecene (ODE) as Pb-precursor. 0.5 mL bis(trimethylsilyl)sulfide ((TMS)2S) was diluted in 2 mL ODE as S-precursor. After the purification of Pb-precursor solvent at 100 °C under vacuum conditions for 6 hours, the solvent was further shifted to an argon atmosphere. The S-precursor was injected into Pb-precursor swiftly and the temperature of the mixture remained at 95 °C for 3 min for the QD crystallization reaction. Afterwards, the reaction was terminated by an ice bath. The resulting PbS QD solution was washed twice with a solvent mixture of acetone and methanol (volume ratio 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), in which the QDs were precipitated by centrifugation at 5000 rpm and dried with nitrogen to obtain a powder. For further use, the powder was redispersed in octane with a concentration of 80 mg mL−1. The films for the in situ GISAXS and PL measurements are deposited from 50 μL of the final solution on the PDMS substrates by spin-coating at 3000 rpm. It is noteworthy that the PDMS surface quality affects the degree of long-range order so that smooth and homogenous surfaces are beneficial to form PbS QD superlattices. The influence of different substrates on morphology and PL is discussed briefly in Fig. S8 (ESI†).
1), in which the QDs were precipitated by centrifugation at 5000 rpm and dried with nitrogen to obtain a powder. For further use, the powder was redispersed in octane with a concentration of 80 mg mL−1. The films for the in situ GISAXS and PL measurements are deposited from 50 μL of the final solution on the PDMS substrates by spin-coating at 3000 rpm. It is noteworthy that the PDMS surface quality affects the degree of long-range order so that smooth and homogenous surfaces are beneficial to form PbS QD superlattices. The influence of different substrates on morphology and PL is discussed briefly in Fig. S8 (ESI†).
Size and size distribution of the QDs
Two PbS QD batches were synthesized according to the same protocol. The first was used for the in situ GISAXS and in situ PL measurements. The second batch was used for TEM and in situ absorbance measurements (Fig. S7, ESI†). The average QD size of the first batch was obtained by optical absorption measurements with a UV-vis-IR spectrometer (Lambda 35, PerkinElmer), with a wavelength range of 190–1100 nm and an interval of 1 nm. The average size of (2.70 ± 0.02) nm of the first PbS QD batch used in the stretching GISAXS and PL experiments was obtained from the absorbance spectrum in Fig. S9 (ESI†). The long-range order, inter-dot distance, average size, and size distribution (Fig. 1(e)–(g)) were confirmed by TEM measurements (Tecnai G2 F30) based on the second batch of PbS QDs. The average size obtained from TEM was (2.8 ± 0.1) nm with a standard deviation of 21% and agrees with the results from absorbance measurements in Fig. S7 and S9 (ESI†). All QD batches had an oleic acid ligand capping that was synthesized according to the literature and had a relaxed chain length llig0 of about 2.5 nm.61Application of uniaxial strain
The PDMS substrate supporting the PbS QD film was mounted in a custom-built stretching apparatus by clamping the sample edges along the strain axis (Fig. S1 (ESI†)).62,63 The clamps were connected to two stepping motors for controlled elongation of Δlsub from the initial sample length lsub0. The ratio Δlsub/lsub0 measures the value of the applied strain to the substrate. Four cylindrical rolls guided the sample during the in situ GISAXS experiments to prevent deformation-induced sagging of the sample (Fig. S1, ESI†). This setup ensured controlled sample alignment with respect to the incident X-ray beam.In situ GISAXS
We performed in situ GISAXS measurements at the beamline P03 at DESY.64 A sample-to-detector distance of 3.8 m was chosen to probe the PbS QD superlattice scattering signal. The signal was captured with a Pilatus 2M detector (Dectris, pixel size 172 × 172 μm2). The wavelength was set to 1.05 Å, corresponding to 11.8 keV photon energy. The incidence angle was adjusted to 0.34°. During the in situ experiments, the sample was moved perpendicular to the incident X-rays to probe a larger sample volume and avoid radiation damage by the highly brilliant beam.GISAXS data analysis
The QD superlattice Bragg reflexes were indexed in the 2D GISAXS data with the software GIXSGUI.65 A detailed step-by-step guide using GIXSGUI for index matching is provided in the ESI† (Fig. S10–S15). The (011)bct, (110)bct, and (111)fcc reflexes were reduced to 1D intensity cuts by azimuthal integration with the software environment DPDAK and fitted with Gaussian functions.66 From the extracted q011, q110, and q111 values, we obtained the superlattice spacing d011, d110, and d111 and consequently the unit cell axes abct, cbct, and afcc.In situ PL measurements
In situ PL measurements were performed in reflection mode during uniaxial stretching. For this, a laser diode with 520 nm wavelength (CPS520, Thorlabs, typical power output 4.5 mW) and a spot size of 4.6 × 1.7 mm2 was aligned on the sample. A finger detector made up of a long-pass filter (Thorlabs FEL0600, cut-on wavelength 600 nm), an achromatic doublet (Thorlabs AC254-075-A, focus 75 mm), and a collimator (Thorlabs F240SMA-780) captured the PL emission. The signal was read out with the software environment SpecWin Pro (Instrument Systems) via a spectrometer with 1000 ms integration time (CAS140CT-154, Instrument Systems).Author contributions
J. E. H. and P. M. B. designed the experiments. W. C., H. Z., C. H., F. A. C. A., A. W., R. B., L. S., E. E., K. S., and J. E. H performed the experiments. W. C., H. Z., C. H., T. X., and J. E. H. synthesized the materials and fabricated the samples. R. B., L. S., E. E., A. K. S., and K. S. designed and developed the stretching apparatus and the GISAXS sample holder. W. C., H. Z., P. M. B., and J. E. H. provided data analysis and interpretation methods. M. S. and S. V. R. supervised and supported the beamtime and the instrumental environment at DESY. S. V. R., K. S., and P. M. B. supervised the project. All authors discussed and approved the final manuscript.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This work was supported by funding from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) project MU1487/32 and Germany's Excellence Strategy—EXC 2089/1—390776260 (e-conversion), TUM.solar in the context of the Bavarian Collaborative Research Project Solar Technologies Go Hybrid (SolTech), the Center for NanoScience (CeNS) and the International Research Training Group 2022 Alberta/Technical University of Munich International Graduate School for Environmentally Responsible Functional Hybrid Materials (ATUMS). W. C. acknowledges financial support from Guangdong Basic and Applied Basic Research Foundation (2021A1515110535). H. Z. and T. X. acknowledge the China Scholarship Council (CSC). The GISAXS measurements were performed at the third-generation synchrotron source PETRA III at DESY in Hamburg, Germany, a member of the Helmholtz Association (HGF). The Authors thank Christian L. Weindl for the graphical artwork of Fig. 1(h) and Lennart K. Reb for helpful discussions about the analysis of the 2D GISAXS data.References
- C. R. Kagan, L. C. Bassett, C. B. Murray and S. M. Thompson, Colloidal Quantum Dots as Platforms for Quantum Information Science, Chem. Rev., 2021, 121, 3186–3233 CrossRef CAS PubMed.
- M. Liu, N. Yazdani, M. Yarema, M. Jansen, V. Wood and E. H. Sargent, Colloidal quantum dot electronics, Nat. Electron., 2021, 4, 548–558 CrossRef.
- J. J. Choi, J. Luria, B.-R. Hyun, A. C. Bartnik, L. Sun, Y.-F. Lim, J. A. Marohn, F. W. Wise and T. Hanrath, Photogenerated exciton dissociation in highly coupled lead salt nanocrystal assemblies, Nano Lett., 2010, 10, 1805–1811 CrossRef CAS PubMed.
- W. Chen, H. Tang, N. Li, M. A. Scheel, Y. Xie, D. Li, V. Körstgens, M. Schwartzkopf, S. V. Roth, K. Wang, X. W. Sun and P. Müller-Buschbaum, Colloidal PbS quantum dot stacking kinetics during deposition via printing, Nanoscale Horiz., 2020, 5, 880–885 RSC.
- C. R. Kagan and C. B. Murray, Charge transport in strongly coupled quantum dot solids, Nat. Nanotechnol., 2015, 10, 1013–1026 CrossRef CAS PubMed.
- P. Guyot-Sionnest, Electrical Transport in Colloidal Quantum Dot Films, J. Phys. Chem. Lett., 2012, 3, 1169–1175 CrossRef CAS PubMed.
- C. R. Kagan, C. B. Murray and M. G. Bawendi, Long-range resonance transfer of electronic excitations in close-packed CdSe quantum-dot solids, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 8633–8643 CrossRef CAS PubMed.
- M. S. Kodaimati, C. Wang, C. Chapman, G. C. Schatz and E. A. Weiss, Distance-Dependence of Interparticle Energy Transfer in the Near-Infrared within Electrostatic Assemblies of PbS Quantum Dots, ACS Nano, 2017, 11, 5041–5050 CrossRef CAS PubMed.
- Y. Gong, J. Shen, Y. Zhu, X. Yang, L. Zhang and C. Li, Stretch induced photoluminescence enhanced perovskite quantum dot polymer composites, J. Mater. Chem. C, 2020, 8, 1413–1420 RSC.
- A. A. Chistyakov, M. A. Zvaigzne, V. R. Nikitenko, A. R. Tameev, I. L. Martynov and O. V. Prezhdo, Optoelectronic Properties of Semiconductor Quantum Dot Solids for Photovoltaic Applications, J. Phys. Chem. Lett., 2017, 8, 4129–4139 CrossRef CAS PubMed.
- P. Siffalovic, L. Chitu, K. Vegso, E. Majkova, M. Jergel, M. Weis, S. Luby, I. Capek, J. Keckes, G. A. Maier, A. Satka, J. Perlich and S. V. Roth, Towards strain gauges based on a self-assembled nanoparticle monolayer-SAXS study, Nanotechnology, 2010, 21, 385702 CrossRef CAS PubMed.
- M. K. Choi, J. Yang, T. Hyeon and D.-H. Kim, Flexible quantum dot light-emitting diodes for next-generation displays, npj Flexible Electron., 2018, 2, 10 CrossRef.
- D. M. Kroupa, M. Vörös, N. P. Brawand, B. W. McNichols, E. M. Miller, J. Gu, A. J. Nozik, A. Sellinger, G. Galli and M. C. Beard, Tuning colloidal quantum dot band edge positions through solution-phase surface chemistry modification, Nat. Commun., 2017, 8, 15257 CrossRef CAS PubMed.
- S. Lee, M.-J. Choi, G. Sharma, M. Biondi, B. Chen, S.-W. Baek, A. M. Najarian, M. Vafaie, J. Wicks, L. K. Sagar, S. Hoogland, F. P. G. de Arquer, O. Voznyy and E. H. Sargent, Orthogonal colloidal quantum dot inks enable efficient multilayer optoelectronic devices, Nat. Commun., 2020, 11, 4814 CrossRef CAS PubMed.
- M.-J. Choi, F. P. García de Arquer, A. H. Proppe, A. Seifitokaldani, J. Choi, J. Kim, S.-W. Baek, M. Liu, B. Sun, M. Biondi, B. Scheffel, G. Walters, D.-H. Nam, J. W. Jo, O. Ouellette, O. Voznyy, S. Hoogland, S. O. Kelley, Y. S. Jung and E. H. Sargent, Cascade surface modification of colloidal quantum dot inks enables efficient bulk homojunction photovoltaics, Nat. Commun., 2020, 11, 103 CrossRef CAS PubMed.
- W. Chen, R. Guo, H. Tang, K. S. Wienhold, N. Li, Z. Jiang, J. Tang, X. Jiang, L. P. Kreuzer, H. Liu, M. Schwartzkopf, X. W. Sun, S. V. Roth, K. Wang, B. Xu and P. Müller-Buschbaum, Operando structure degradation study of PbS quantum dot solar cells, Energy Environ. Sci., 2021, 14, 3420–3429 RSC.
- S. Zheng, J. Chen, E. M. J. Johansson and X. Zhang, PbS Colloidal Quantum Dot Inks for Infrared Solar Cells, iScience, 2020, 23, 101753 CrossRef CAS PubMed.
- J. Yang, T. Ling, W.-T. Wu, H. Liu, M.-R. Gao, C. Ling, L. Li and X.-W. Du, A top-down strategy towards monodisperse colloidal lead sulphide quantum dots, Nat. Commun., 2013, 4, 1695 CrossRef PubMed.
- F. Li, Y. Liu, G. Shi, W. Chen, R. Guo, D. Liu, Y. Zhang, Y. Wang, X. Meng, X. Zhang, Y. Lv, W. Deng, Q. Zhang, Y. Shi, Y. Chen, K. Wang, Q. Shen, Z. Liu, P. Müller-Buschbaum and W. Ma, Matrix Manipulation of Directly-Synthesized PbS Quantum Dot Inks Enabled by Coordination Engineering, Adv. Funct. Mater., 2021, 31, 2104457 CrossRef CAS.
- G. Shi, H. Wang, Y. Zhang, C. Cheng, T. Zhai, B. Chen, X. Liu, R. Jono, X. Mao, Y. Liu, X. Zhang, X. Ling, Y. Zhang, X. Meng, Y. Chen, S. Duhm, L. Zhang, T. Li, L. Wang, S. Xiong, T. Sagawa, T. Kubo, H. Segawa, Q. Shen, Z. Liu and W. Ma, The effect of water on colloidal quantum dot solar cells, Nat. Commun., 2021, 12, 4381 CrossRef CAS PubMed.
- Z. Ning, O. Voznyy, J. Pan, S. Hoogland, V. Adinolfi, J. Xu, M. Li, A. R. Kirmani, J.-P. Sun, J. Minor, K. W. Kemp, H. Dong, L. Rollny, A. Labelle, G. Carey, B. Sutherland, I. Hill, A. Amassian, H. Liu, J. Tang, O. M. Bakr and E. H. Sargent, Air-stable n-type colloidal quantum dot solids, Nat. Mater., 2014, 13, 822–828 CrossRef CAS PubMed.
- J. Zhou, F. Fang, W. Chen, M. Mei, P. Liu, J. Hao, H. Tang, S. Liang, W. Lei, R. Pan, J. Cheng, P. Müller-Buschbaum, X. W. Sun, W. Cao, K. Zheng and K. Wang, Luminescent perovskite nanocrystal composites via in situ ligand polymerization towards display applications, J. Mater. Chem. C, 2021, 9, 14740–14748 RSC.
- W. Chen, H. Tang, Y. Chen, J. E. Heger, N. Li, L. P. Kreuzer, Y. Xie, D. Li, C. Anthony, Z. Pikramenou, K. W. Ng, X. W. Sun, K. Wang and P. Müller-Buschbaum, Spray-deposited PbS colloidal quantum dot solid for near-infrared photodetectors, Nano Energy, 2020, 78, 105254 CrossRef CAS.
- E. Georgitzikis, P. E. Malinowski, Y. Li, J. Maes, L. M. Hagelsieb, S. Guerrieri, Z. Hens, P. Heremans and D. Cheyns, Integration of PbS quantum dot photodiodes on silicon for NIR imaging, IEEE Sens. J., 2020, 20, 6841–6848 CAS.
- C. J. Wrasman, C. Zhou, A. Aitbekova, E. D. Goodman and M. Cargnello, Recycling of Solvent Allows for Multiple Rounds of Reproducible Nanoparticle Synthesis, J. Am. Chem. Soc., 2022, 144, 11646–11655 CrossRef CAS PubMed.
- A. R. Kirmani, M. Woodhouse and J. M. Luther, Technoeconomic Model Suggests Scaling-Up Perovskite Quantum Dots for Optoelectronics Warrants Improved Synthesis Yield, Solvent Recycling, and Automation, ACS Energy Lett., 2022, 7, 1255–1259 CrossRef CAS.
- R. Li, K. Bian, T. Hanrath, W. A. Bassett and Z. Wang, Decoding the superlattice and interface structure of truncate PbS nanocrystal-assembled supercrystal and associated interaction forces, J. Am. Chem. Soc., 2014, 136, 12047–12055 CrossRef CAS PubMed.
- M. C. Weidman, K. G. Yager and W. A. Tisdale, Interparticle Spacing and Structural Ordering in Superlattice PbS Nanocrystal Solids Undergoing Ligand Exchange, Chem. Mater., 2015, 27, 474–482 CrossRef CAS.
- J. Zhou, Y. Liu, J. Tang and W. Tang, Surface ligands engineering of semiconductor quantum dots for chemosensory and biological applications, Mater. Today, 2017, 20, 360–376 CrossRef CAS.
- J.-C. Cheng, L.-Y. Pan, X.-L. Huang, Y.-P. Huang, Y.-H. Wang, S.-P. Xu, F.-F. Li, Z.-W. Men and T. Cui, Interparticle Spacing Effect among Quantum Dots with High-Pressure Regulation, Nanomaterials, 2021, 11, 325 CrossRef CAS PubMed.
- M. C. Weidman, Q. Nguyen, D.-M. Smilgies and W. A. Tisdale, Impact of Size Dispersity, Ligand Coverage, and Ligand Length on the Structure of PbS Nanocrystal Superlattices, Chem. Mater., 2018, 30, 807–816 CrossRef CAS.
- J. Zhang, J. Tolentino, E. R. Smith, J. Zhang, M. C. Beard, A. J. Nozik, M. Law and J. C. Johnson, Carrier Transport in PbS and PbSe QD Films Measured by Photoluminescence Quenching, J. Mater. Chem. C, 2014, 118, 16228–16235 CAS.
- H. Tang, J. Zhong, W. Chen, K. Shi, G. Mei, Y. Zhang, Z. Wen, P. Müller-Buschbaum, D. Wu, K. Wang and X. W. Sun, Lead Sulfide Quantum Dot Photodetector with Enhanced Responsivity through a Two-Step Ligand-Exchange Method, ACS Appl. Nano Mater., 2019, 2, 6135–6143 CrossRef CAS.
- Z. Lingley, S. Lu and A. Madhukar, A high quantum efficiency preserving approach to ligand exchange on lead sulfide quantum dots and interdot resonant energy transfer, Nano Lett., 2011, 11, 2887–2891 CrossRef CAS PubMed.
- S. W. Winslow, D.-M. Smilgies, J. W. Swan and W. A. Tisdale, Reversible Temperature-Induced Structural Transformations in PbS Nanocrystal Superlattices, J. Phys. Chem. C, 2020, 124, 13456–13466 CrossRef CAS.
- M. C. Weidman, D.-M. Smilgies and W. A. Tisdale, Kinetics of the self-assembly of nanocrystal superlattices measured by real-time in situ X-ray scattering, Nat. Mater., 2016, 15, 775–781 CrossRef CAS PubMed.
- Y. Xia, W. Chen, P. Zhang, S. Liu, K. Wang, X. Yang, H. Tang, L. Lian, J. He, X. Liu, G. Liang, M. Tan, L. Gao, H. Liu, H. Song, D. Zhang, J. Gao, K. Wang, X. Lan, X. Zhang, P. Müller-Buschbaum, J. Tang and J. Zhang, Facet Control for Trap-State Suppression in Colloidal Quantum Dot Solids, Adv. Funct. Mater., 2020, 30, 2000594 CrossRef CAS.
- A. Hexemer and P. Müller-Buschbaum, Advanced grazing-incidence techniques for modern soft-matter materials analysis, IUCrJ, 2015, 2, 106–125 CrossRef CAS PubMed.
- K. F. Chou and A. M. Dennis, Förster Resonance Energy Transfer between Quantum Dot Donors and Quantum Dot Acceptors, Sensors, 2015, 15, 13288–13325 CrossRef PubMed.
- P. L. Rosendahl, M. Drass, J. Felger, J. Schneider and W. Becker, Equivalent strain failure criterion for multiaxially loaded incompressible hyperelastic elastomers, Int. J. Solids Struct., 2019, 166, 32–46 CrossRef CAS.
- Y. Staudt, C. Odenbreit and J. Schneider, Failure behaviour of silicone adhesive in bonded connections with simple geometry, Int. J. Adhes. Adhes., 2018, 82, 126–138 CrossRef CAS.
- J. Novák, R. Banerjee, A. Kornowski, M. Jankowski, A. André, H. Weller, F. Schreiber and M. Scheele, Site-Specific Ligand Interactions Favor the Tetragonal Distortion of PbS Nanocrystal Superlattices, ACS Appl. Mater. Interfaces, 2016, 8, 22526–22533 CrossRef PubMed.
- S. W. Winslow, W. A. Tisdale and J. W. Swan, Prediction of PbS Nanocrystal Superlattice Structure with Large-Scale Patchy Particle Simulations, J. Phys. Chem. C, 2022, 126, 14264–14274 CrossRef CAS.
- B. A. Korgel, S. Fullam, S. Connolly and D. Fitzmaurice, Assembly and Self-Organization of Silver Nanocrystal Superlattices: Ordered “Soft Spheres”, J. Phys. Chem. B, 1998, 102, 8379–8388 CrossRef CAS.
- B. W. Goodfellow, Y. Yu, C. A. Bosoy, D.-M. Smilgies and B. A. Korgel, The Role of Ligand Packing Frustration in Body-Centered Cubic (bcc) Superlattices of Colloidal Nanocrystals, J. Phys. Chem. Lett., 2015, 6, 2406–2412 CrossRef CAS PubMed.
- B. Zhang, I. Lyskov, L. J. Wilson, R. P. Sabatini, A. Manian, H. Soleimaninejad, J. M. White, T. A. Smith, G. Lakhwani, D. J. Jones, K. P. Ghiggino, S. P. Russo and W. W. H. Wong, FRET-enhanced photoluminescence of perylene diimides by combining molecular aggregation and insulation, J. Mater. Chem. C, 2020, 8, 8953–8961 RSC.
- A. J. Mork, M. C. Weidman, F. Prins and W. A. Tisdale, Magnitude of the Förster Radius in Colloidal Quantum Dot Solids, J. Phys. Chem. C, 2014, 118, 13920–13928 CrossRef CAS.
- S. W. Clark, J. M. Harbold and F. W. Wise, Resonant Energy Transfer in PbS Quantum Dots, J. Phys. Chem. C, 2007, 111, 7302–7305 CrossRef CAS.
- K. Tai, W. Lü, I. Umezu and A. Sugimura, Inter-Dot Distance Dependence of Photoluminescence Properties in CdSe Quantum Dot Systems, Appl. Phys. Express, 2010, 3, 35202 CrossRef.
- F. Gordon, S. Elcoroaristizabal and A. G. Ryder, Modelling Förster resonance energy transfer (FRET) using anisotropy resolved multi-dimensional emission spectroscopy (ARMES), Biochim. Biophys. Acta, Gen. Subj., 2021, 1865, 129770 CrossRef CAS PubMed.
- R. B. Sekar and A. Periasamy, Fluorescence resonance energy transfer (FRET) microscopy imaging of live cell protein localizations, J. Cell Biol., 2003, 160, 629–633 CrossRef CAS PubMed.
- J. J. Choi, C. R. Bealing, K. Bian, K. J. Hughes, W. Zhang, D.-M. Smilgies, R. G. Hennig, J. R. Engstrom and T. Hanrath, Controlling nanocrystal superlattice symmetry and shape-anisotropic interactions through variable ligand surface coverage, J. Am. Chem. Soc., 2011, 133, 3131–3138 CrossRef CAS PubMed.
- K. Bian, Z. Wang and T. Hanrath, Comparing the structural stability of PbS nanocrystals assembled in fcc and bcc superlattice allotropes, J. Am. Chem. Soc., 2012, 134, 10787–10790 CrossRef CAS PubMed.
- I. A. Zaluzhnyy, R. P. Kurta, A. André, O. Y. Gorobtsov, M. Rose, P. Skopintsev, I. Besedin, A. V. Zozulya, M. Sprung, F. Schreiber, I. A. Vartanyants and M. Scheele, Quantifying Angular Correlations between the Atomic Lattice and the Superlattice of Nanocrystals Assembled with Directional Linking, Nano Lett., 2017, 17, 3511–3517 CrossRef CAS PubMed.
- Z. Quan, W. S. Loc, C. Lin, Z. Luo, K. Yang, Y. Wang, H. Wang, Z. Wang and J. Fang, Tilted face-centered-cubic supercrystals of PbS nanocubes, Nano Lett., 2012, 12, 4409–4413 CrossRef CAS PubMed.
- N. Nakazawa, Y. Zhang, F. Liu, C. Ding, K. Hori, T. Toyoda, Y. Yao, Y. Zhou, S. Hayase, R. Wang, Z. Zou and Q. Shen, The interparticle distance limit for multiple exciton dissociation in PbS quantum dot solid films, Nanoscale Horiz., 2019, 4, 445–451 RSC.
- L. Sandoval, H. M. Urbassek and P. Entel, The Bain versus Nishiyama–Wassermann path in the martensitic transformation of Fe, New J. Phys., 2009, 11, 103027 CrossRef.
- L. H. Zhang, M. J. Cheng, X. H. Shi, J. W. Shuai and Z. Z. Zhu, Bain and Nishiyama-Wassermann transition path separation in the martensitic transitions of Fe, RSC Adv., 2021, 11, 3043–3048 RSC.
- A. Wolcott, V. Doyeux, C. A. Nelson, R. Gearba, K. W. Lei, K. G. Yager, A. D. Dolocan, K. Williams, D. Nguyen and X.-Y. Zhu, Anomalously Large Polarization Effect Responsible for Excitonic Red Shifts in PbSe Quantum Dot Solids, J. Phys. Chem. Lett., 2011, 795–800 CrossRef CAS.
- W. Chen, J. Zhong, J. Li, N. Saxena, L. P. Kreuzer, H. Liu, L. Song, B. Su, D. Yang, K. Wang, J. Schlipf, V. Körstgens, T. He, K. Wang and P. Müller-Buschbaum, Structure and Charge Carrier Dynamics in Colloidal PbS Quantum Dot Solids, J. Phys. Chem. Lett., 2019, 10, 2058–2065 CrossRef CAS PubMed.
- W. Gong, P. Wang, D. Dai, Z. Liu, L. Zheng and Y. Zhang, Infrared colloidal quantum dots for photoelectric conversion devices, J. Mater. Chem. C, 2021, 9, 2994–3025 RSC.
- B. Chang, K. Schneider, I. Kuehnert and G. Heinrich, in Small Angle Scattering and Diffraction, ed. M. K. K. D. Franco and F. Yokaichiya, InTech, 2018, pp.51–67 Search PubMed.
- E. Euchler, A. K. Sambale, K. Schneider, K. Uhlig, R. Boldt, M. Stommel, A. Stribeck, M. Schwartzkopf, A. Rothkirch and S. V. Roth, Beamline-implemented stretching devices for in situ X-ray scattering experiments, J. Phys.: Conf. Ser., 2022, 2380, 012109 CrossRef.
- A. Buffet, A. Rothkirch, R. Döhrmann, V. Körstgens, M. M. Abul Kashem, J. Perlich, G. Herzog, M. Schwartzkopf, R. Gehrke, P. Müller-Buschbaum and S. V. Roth, P03, the microfocus and nanofocus X-ray scattering (MiNaXS) beamline of the PETRA III storage ring: the microfocus endstation, J. Synchrotron Radiat., 2012, 19, 647–653 CrossRef CAS PubMed.
- Z. Jiang, GIXSGUI: a MATLAB toolbox for grazing-incidence X-ray scattering data visualization and reduction, and indexing of buried three-dimensional periodic nanostructured films, J. Appl. Crystallogr., 2015, 48, 917–926 CrossRef CAS.
- G. Benecke, W. Wagermaier, C. Li, M. Schwartzkopf, G. Flucke, R. Hoerth, I. Zizak, M. Burghammer, E. Metwalli, P. Müller-Buschbaum, M. Trebbin, S. Förster, O. Paris, S. V. Roth and P. Fratzl, A customizable software for fast reduction and analysis of large X-ray scattering data sets: applications of the new DPDAK package to small-angle X-ray scattering and grazing-incidence small-angle X-ray scattering, J. Appl. Crystallogr., 2014, 47, 1797–1803 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nh00548d |
| This journal is © The Royal Society of Chemistry 2023 |