 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Heat flux concentrators based on nanoscale phononic metastructures†
Jian
Zhang
 ab,
Haochun
Zhang
*a,
Weifeng
Li
ab,
Haochun
Zhang
*a,
Weifeng
Li
 c and
Gang
Zhang
c and
Gang
Zhang
 *b
*b
aSchool of Energy Science and Engineering, Harbin Institute of Technology, Harbin 150001, China. E-mail: hczhang@hit.edu.cn
bInstitute of High Performance Computing, Agency for Science, Technology and Research (A*STAR), Singapore 138632, Singapore. E-mail: zhangg@ihpc.a-star.edu.sg
cSchool of Physics & State Key Laboratory of Crystal Materials, Shandong University, Jinan 250100, Shandong, China
First published on 11th September 2023
Abstract
In recent years, nanoscale heat flux regulation has been at the forefront of research. Nanoscale heat flux concentration is of potential importance in various applications, but no research has been conducted on local heat flux concentration. In this paper, we designed two heat flux concentrators using patterned amorphous and nanomesh structures, respectively. Using molecular dynamics simulation, we find that the heat flux in the central regions is much higher than that in the adjacent regions, with the concentration ratio arriving at 9-fold. Thus a heat flux concentrator is realized using these nanophononic metastructures. The phonon localization theory was used to explain the underlying mechanism. This work provides a direct design strategy for thermal concentrators using practical nanofabrication technologies.
1 Introduction
Manipulating thermal conduction at the nanoscale has attracted great interest1–3 due to its critical role in understanding the fundamental physics of phonons4 and developing controlling strategies in various areas of application, including nanoscale thermal management,5,6 thermoelectrics,7,8 and thermal protection.9 A countless number of theoretical and experimental studies have been conducted to explore the various effects on the thermal conductivity of nanoscale materials, including size, strain, defects, bonding strength, and geometry configuration.10–20 For example, the thermal conductivity of silicon nanowires is about two orders of magnitude lower than that of bulk silicon21 and increases with nanowire length.22 And thermal conductivity of multi-layer graphene depends significantly on the thickness, and interlayer phonon scattering plays a critical role in the in-plane thermal conductivity.23 Overall, most of these factors affect the thermal conductivity of materials via the material growth process.On the other side, after the materials are synthesized, their thermal conductivity can be further changed using the concept of phononic metamaterials (or metastructures).24–27 For example, the thermal conductivity of silicon nanoscale films can be reduced using periodic nanomesh of a holey structure, making it a promising candidate for thermoelectric applications.28,29 In periodic nanomesh, the periodicity of a hole array can induce the folding of the Brillouin zone, thus depressing phonon group velocity and reducing thermal conductivity. In experiments, the feature size of nanomesh is typical of about a few hundred nanometers, whose structure can be easily accessible with standard fabrication techniques, including electron beam lithography and reactive ion etching. Because of the development of the silicon-on-insulator technology, high-quality single-crystal silicon nanofilms with thicknesses down to a few nanometers30 are usually employed to fabricate two-dimensional phononic metastructures31 with tunable thermal conductivity.32 In addition to the electron beam, high-energy ion irradiation is also adopted to change the thermal conductivity of nanomaterials. This method can induce amorphization within the desired region, without causing significant voids, providing an ideal platform to explore phonon transport in nanoscale amorphous materials.33–35
These recent advancements in nanofabrication technologies have improved our ability to control thermal conductivity at the nanoscale, providing exciting opportunities to develop a large variety of thermal devices. The challenges in thermal management in nanoscale devices and renewable energy conversion have sparked great research interest in developing thermal/phononic devices,36 including thermal rectifiers,37–39 thermal transistors,40 thermal modulators,41 and ray phononics.42–45 Clearly, it is of both scientific significance and technological impact to realize novel thermal devices based on realizable nanofabrication technology.
In the present work, we designed a nanoscale heat flux concentrator by performing molecular dynamics simulations. We demonstrated the feasibility and functionality of this thermal concentrator, and we also identified the physical mechanism. Our results provide useful guidelines for the design of novel nanoscale thermal devices.
2 Calculation method
We show the atomistic models of the heat flux concentrator in Fig. 1. To achieve perfect surfaces, we cleave bulk Si supercells in the direction of [001], with the lattice constant of Si being 5.431 Å. A Si cubic unit cell (UC) is duplicated to create the nanofilm. The pristine nanofilm is made up of 60, 40, and 2 UC in the x, y, and z directions, respectively. As shown in Fig. 1, the grey section is the perfect silicon nanofilm, while the light blue parts are the functional sections. In this work, we consider two ways to construct the functional sections: the perforated concentrator (using patterned nanoholes); the amorphous concentrator (using amorphized silicon). For the perforated concentrator, the side width of the nanohole is 2 × 2 UC, with a spacing of 2 UC. For the amorphous concentrator, to generate the amorphous region, we start with the crystalline Si. We use the Nosé–Hoover thermostat46 to heat the crystalline Si from 300 K to 4000 K and equilibrate it at 4000 K (above the melting point) for 100 ps to achieve the amorphous state. Then it is quickly annealed to 300 K with a cooling rate of 185 K ps−1. This approach has been used to generate amorphous Si in previous studies.47–50 We refer to both nanoholes and amorphous regions as functional regions. For comparison, the pristine film is also considered.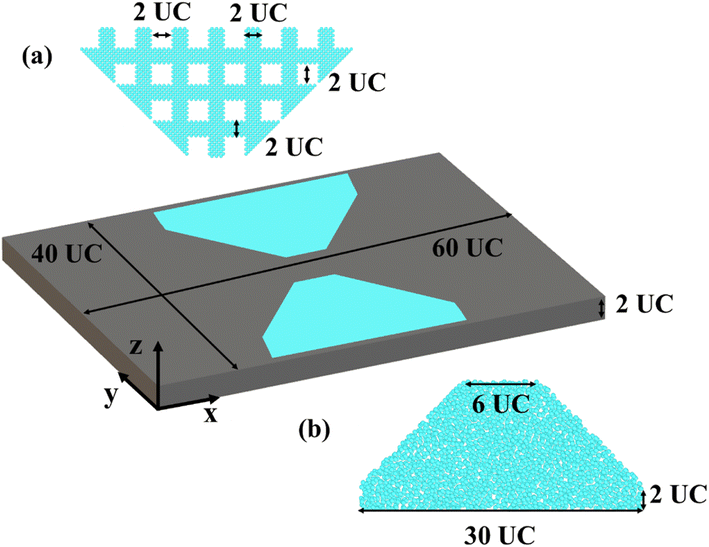 | ||
| Fig. 1 The atomistic models of the different heat flux concentrators. (a) The functional region of a perforated concentrator. (b) The functional region of an amorphous concentrator. | ||
We use the LAMMPS packages51 to conduct the non-equilibrium MD simulation to investigate the heat flux concentration of the different concentrators. The Stillinger–Weber potentials52 are used to describe the interactions between Si atoms in all MD simulations. At the start of the simulations, the system is first energy minimized, and then all atoms are set at 300 K with Gaussian distribution velocities. In the canonical ensemble (which keeps the number of atoms, volume, and temperature constant, also called NVT), the system is relaxed for 100 ps. Next, we fix the atoms in the region of 2 UC along the x-axis of both ends and use the Nosé–Hoover thermostat to establish a temperature gradient along the x-axis by placing the atoms in the thermostat region (including a hot bath and a cold bath, and their lengths are both 8 UC) at 320 K and 280 K, respectively. Finally, except for the thermostat and fixed regions, the system is placed in the micro-canonical ensemble (which keeps the number of atoms, volume, and energy constant, also called NVE) for MD simulations. It is conducted for 5 ns, after which the system reaches a nonequilibrium steady state within 2 ns.
3 Results and discussion
3.1 Heat current concentrator with a patterned amorphous section
During the simulations, we divide the system into 25 × 20 small blocks and calculate their heat flux and temperature. The heat flux profile of the amorphous concentrator is illustrated in Fig. 2(a) and other results are shown in Fig. S1 and S2.† The pristine film has a uniform temperature distribution from the hot to the cold bath, and the heat flux is distributed relatively uniformly along the x-axis, demonstrating that the system is in a nonequilibrium steady state. However, in the amorphous concentrator, the presence of a patterned amorphous section leads to a very different temperature distribution, with an increase in temperature along the x-direction near the amorphous region, creating a temperature gradient and driving the heat flux towards the central region. As a result, the local heat flux in the center is extremely high. Therefore, a heat flux concentrator is realized using this patterned nanophononic metastructure. In addition, we calculate the temperature gradient along the x-direction, as shown in Fig. S3.† The temperature gradient is uniformly distributed for the pristine film. However, the presence of the amorphous structure leads to a larger temperature gradient in the central region.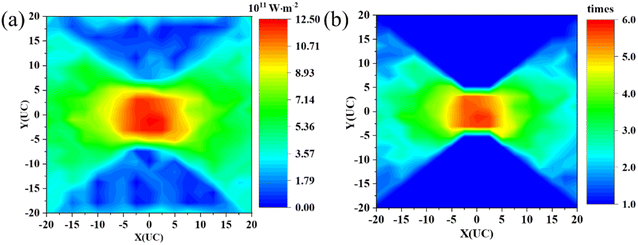 | ||
| Fig. 2 (a) The heat flux profile of the patterned amorphous concentrator. (b) The ratio of heat flux (RHF) of the patterned amorphous concentrator. | ||
To quantitatively evaluate the ability of heat flux concentration, we define the ratio of heat flux (RHF) as RHF = J/Jfunctional, where J is the local heat flux and Jfunctional is the average heat flux within the functional region as a reference. The RHF distribution of the amorphous concentrator is shown in Fig. 2(b). The RHF distribution profile is the same as the heat flux distribution, with the largest RHF in the central region, and the heat flux in the central region can reach 6 times that in the adjacent region.
Previously, temperature concentration was obtained by setting up core–shell53–55 or multilayer structures56,57 through transformation thermotics theory, effective medium theory,58 and topological optimization methods.59 However, the heat flux concentration ratio is not high. For example, Yu et al.53 designed a heat flux concentrator, in which the heat flux in the central region is about 2.6 times that of the background region. In the amorphous concentrator studied in the present work, remarkable heat flux concentration is realized due to the reduced thermal conductivity in the amorphous region.60–62
3.2 Heat flux concentrator based on a nanomesh structure
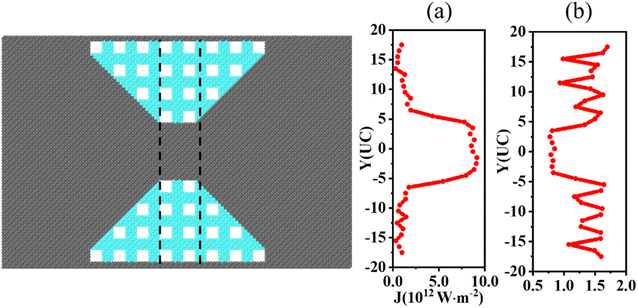
In recent years, nanomesh structures have shown promising potential for thermoelectric applications due to their low thermal conductivity and good electrical properties. In this section, we investigate the application of nanomesh structures to heat flux concentration. Again, we start by analyzing the heat flux and temperature profile of the perforated concentrator. As shown in Fig. 3(a), the perforated concentrator has a similar heat flux profile to the patterned amorphous sample. The local heat flux in the center is also extremely high. The main reason for this is the presence of nanomesh, which severely impedes the transfer of heat flux. This indicates that heat flux concentration can be achieved by arranging the nanomesh structure. Furthermore, we calculate the RHF of the nanomesh concentrator. Similarly, the average heat flux within the nanomesh region is set as a reference. We present the RHF distribution of the nanomesh concentrator in Fig. 3(b). The heat flux in the central region can be up to 9 times that in the adjacent region. Clearly, this is much higher than that in the amorphous concentrator, indicating that the arrangement of nanomesh is more effective in achieving heat flux concentration. The temperature gradient along the x-direction is shown in Fig. S3,† where the perforated nanomesh has an obvious non-uniform temperature gradient distribution.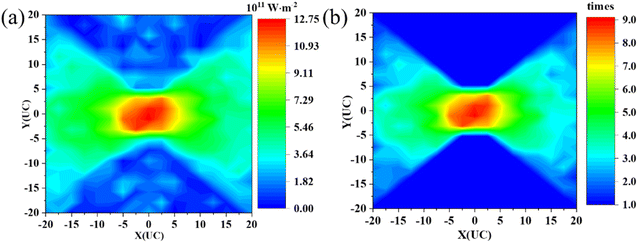 | ||
| Fig. 3 (a) The heat flux profile of the perforated concentrator. (b) The ratio of heat flux (RHF) of the perforated nanomesh concentrator. | ||
This is mainly because the nanomesh structure introduces a quadratic artificial periodicity, which may change the phonon dispersion relation and result in a reduction in the phonon bandgap, phonon density of states, and group velocity, which can suppress the thermal conductivity significantly.63,64
3.3 Phonon localization and heat flux regulation
In the aforementioned sections, we found that patterned amorphous and nanomesh structures can produce heat flux concentration and that nanomesh structures have higher heat flux concentration ability. In amorphous materials, a large number of heat carriers are spatially localized modes; thus, their contribution to heat conduction is significantly suppressed. Even delocalized diffusion, as they contribute to heat conduction in a diffusive manner, also results in low thermal conductivity.62 In a nanomesh structure, the artificial periodicity can modify the phonon dispersion relation, induce a decrease in phonon group velocity and thus suppress the local thermal conduction.63 Overall, the functional regions constructed by patterned amorphous or nanomesh structures reduce the local heat flux and eventually lead to a concentration of heat flux in the central region. Next, we use phonon localization theory to further explore the underlying physical insights.In the different structures, we choose the same region (except for the thermostat and fixed region) for calculating the velocity autocorrelation function, and the autocorrelation time is 30 ps. The phonon density of states (PDOS) can be calculated using the Fourier transform of the velocity autocorrelation,65
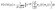 | (1) |
The mode participation rate (MPR) can provide detailed information on the effect of localization; it can be calculated based on the PDOS,66
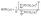 | (2) |
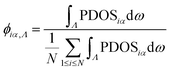 | (3) |
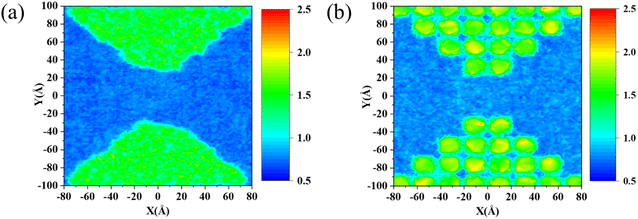 | ||
| Fig. 4 The intensity of localized phonon mode in different concentrators, (a) the amorphous concentrator and (b) the perforated concentrator. | ||
Finally, we select the same region along the x-axis in both concentrators and analyze the spatial distribution of heat fluxes and localized phonon modes within the region. The location-dependent heat flux and localized phonon mode distribution of the amorphous concentrator are shown in Fig. 5(a) and (b), respectively. The heat flux distribution in the same region of the pristine film is shown in Fig. S5.† For pristine films, the heat flux is uniformly distributed along the y-axis. As in Fig. 5(a), the central region of heat flux along the y-axis of the amorphous concentrator is much higher than the edge region. And, as shown in Fig. 5(b), the localized phonon modes along the y-axis are much lower in the central region than in the edge region. The more localized modes, the stronger the obstruction to heat flux, indicating that the localization of phonon modes in the functional region is the main reason for the heat flux concentration.
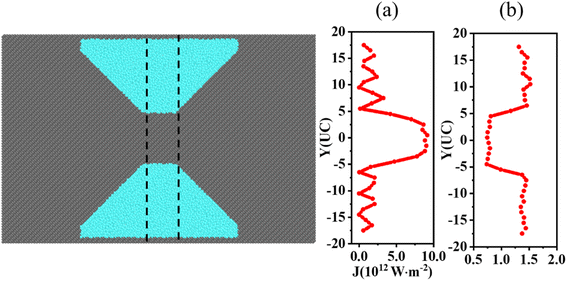 | ||
| Fig. 5 (a) The heat flux spatial distribution of the amorphous concentrator. (b) The distribution of intensity of localized phonon modes of the amorphous concentrator. | ||
In Fig. 6(a) and (b), we show the location-dependent heat flux and intensity of localized phonon modes of the perforated concentrator, respectively. The spatial distributions of the perforated and amorphous concentrators' heat fluxes are similar, with the central region being much higher than the edges. However, the strong Bragg scattering produced by the nanoholes results in non-uniform heat flux in the edge regions. At the same time, the spatial distribution of the localized modes also shows a non-uniform distribution at the edges and is smaller for larger heat fluxes. The Bragg scattering and strong phonon localization produced by the nanoholes ultimately lead to the heat flux concentration.
 | ||
| Fig. 6 (a) The heat flux spatial distribution of the perforated concentrator. (b) The localized phonon modes spatial distribution of the perforated concentrator. | ||
4 Conclusion
In summary, through molecular dynamics calculations, we design two heat flux concentrators using amorphous- and nanomesh-based nanophononic metastructures, respectively. We found that the heat fluxes in the central region of both concentrators are much higher than that in the adjacent regions. Furthermore, a more efficient concentration can be generated by the patterned nanoholes due to the stronger phonon localization. The underlying mechanisms are discussed based on phonon localization theory and the spatial distribution of localized modes. This work can reveal important applications in nanoscale heat flux regulation.Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. Zhang gratefully acknowledges the financial support from the China Scholarship Council (No. 202206120136).References
- D. G. Cahill, P. V. Braun, G. Chen, D. R. Clarke, S. H. Fan, K. E. Goodson, P. Keblinski, W. P. King, G. D. Mahan, A. Majumdar, H. J. Maris, S. R. Phillpot, E. Pop and L. Shi, Nanoscale thermal transport. II. 2003–2012, Appl. Phys. Rev., 2014, 1, 011305 Search PubMed.
- X. Qian, J. W. Zhou and G. Chen, Phonon-engineered extreme thermal conductivity materials, Nat. Mater., 2021, 20, 1188–1202 CrossRef CAS PubMed.
- A. A. Balandin, Phononics of Graphene and Related Materials, ACS Nano, 2020, 14, 5170–5178 CrossRef CAS PubMed.
- Z. W. Zhang, Y. L. Ouyang, Y. Cheng, J. Chen, N. B. Li and G. Zhang, Size-dependent phononic thermal transport in low-dimensional nanomaterials, Phys. Rep., 2020, 860, 1–26 CrossRef CAS.
- E. Pop, Energy dissipation and transport in nanoscale devices, Nano Res., 2010, 3, 147–169 CrossRef CAS.
- H. F. Song, J. M. Liu, B. L. Liu, J. Q. Wu, H. M. Cheng and F. Y. Kang, Two-Dimensional Materials for Thermal Management Applications, Joule, 2018, 2, 442–463 CrossRef CAS.
- R. K. Chen, J. Lee, W. Lee and D. Y. Li, Thermoelectrics of Nanowires, Chem. Rev., 2019, 119, 9260–9302 CrossRef CAS PubMed.
- Z. T. Tian, S. Lee and G. Chen, A Comprehensive Review of Heat Transfer in Thermoelectric Materials and Devices, Annu. Rev. Heat Transfer, 2014, 17, 425–483 CrossRef.
- S. Shin, Q. Y. Wang, J. Luo and R. K. Chen, Advanced Materials for High-Temperature Thermal Transport, Adv. Funct. Mater., 2019, 30, 1904815 CrossRef.
- G. Zhang and B. W. Li, Anomalous vibrational energy diffusion in carbon nanotubes, J. Chem. Phys., 2005, 123, 014705 CrossRef PubMed.
- A. C. Gadelha, D. A. A. Ohlberg, C. Rabelo, E. G. S. Neto, T. L. Vasconcelos, J. L. Campos, J. S. Lemos, V. Ornelas, D. Miranda, R. Nadas, F. C. Santana, K. Watanabe, T. Taniguchi, B. V. Troeye, M. Lamparski, V. Meunier, V. H. Nguyen, D. Paszko, J. C. Charlier, L. C. Campos, L. G. Cançado, G. M. Ribeiro and A. Jorio, Localization of lattice dynamics in low-angle twisted bilayer graphene, Nature, 2021, 590, 405–409 CrossRef CAS PubMed.
- Q. R. Cai, D. Scullion, W. Gan, A. Falin, P. Cizek, S. Liu, J. H. Edgar, R. Liu, B. C. C. Cowie, E. J. G. Santos and L. H. Li, Outstanding Thermal Conductivity of Single Atomic Layer Isotope-Modified Boron Nitride, Phys. Rev. Lett., 2020, 125, 085902 CrossRef CAS PubMed.
- W. J. Luo, A. D. Oyedele, Y. Y. Gu, T. S. Li, X. Z. Wang, A. V. Haglund, D. Mandrus, A. A. Puretzky, K. Xiao, L. B. Liang and X. Ling, Anisotropic Phonon Response of Few-Layer PdSe2 under Uniaxial Strain, Adv. Funct. Mater., 2020, 30, 2003215 CrossRef CAS.
- D. F. Li, J. He, G. Q. Ding, Q. Q. Tang, Y. Ying, J. J. He, C. Y. Zhong, Y. Liu, C. B. Feng, Q. L. Sun, H. B. Zhou, P. Zhou and G. Zhang, Stretch-driven increase in ultrahigh thermal conductance of hydrogenated borophene and dimensionality crossover in phonon transmission, Adv. Funct. Mater., 2018, 28, 1801685 CrossRef.
- H. D. Wang, S. Q. Hu, K. Takahashi, X. Zhang, H. Takamatsu and J. Chen, Experimental study of thermal rectification in suspended monolayer graphene, Nat. Commun., 2017, 8, 15843 CrossRef CAS PubMed.
- X. J. Liu, J. F. Gao, G. Zhang and Y. W. Zhang, MoS2-Graphene In-plane Contact for High Interfacial Thermal Conduction, Nano Res., 2017, 10, 2944–2953 CrossRef CAS.
- X. J. Liu, G. Zhang and Y. W. Zhang, Thermal Conduction across One-dimensional Interface between a MoS2 Monolayer and Metal Electrode, Nano Res., 2016, 9, 2372–2383 CrossRef CAS.
- J. Chen, J. H. Walther and P. Koumoutsakos, Covalently Bonded Graphene–Carbon Nanotube Hybrid for High-Performance Thermal Interfaces, Adv. Funct. Mater., 2015, 25, 7539–7545 CrossRef.
- X. K. Gu, Y. J. Wei, X. B. Yin, B. W. Li and R. G. Yang, Colloquium: Phononic thermal properties of two-dimensional materials, Rev. Mod. Phys., 2018, 90, 041002 CrossRef CAS.
- Y. Wang, H. X. Huang and X. L. Ruan, Decomposition of coherent and incoherent phonon conduction in superlattices and random multilayers, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 165406 CrossRef.
- A. Hochbaum, R. Chen and R. Delgado, et al., Enhanced thermoelectric performance of rough silicon nanowires, Nature, 2008, 451, 163–167 CrossRef CAS PubMed.
- N. Yang, G. Zhang and B. W. Li, Violation of Fourier's Law and Anomalous Heat Diffusion in Silicon Nanowires, Nano Today, 2010, 5, 85 CrossRef CAS.
- M. S. Mir, J. Insun and S. Li, Phonon-interface scattering in multilayer graphene on an amorphous support, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 16321–16326 CrossRef PubMed.
- S. Marianna, G. Bartlomiej, M. Jeremie, C. Emigdio, M. S. T. Clivia and A. Francesc, 2D Phononic Crystals: Progress and Prospects in Hypersound and Thermal Transport Engineering, Adv. Funct. Mater., 2019, 30, 1904434 Search PubMed.
- I. H. Mahmoud, T. Chia-Nien and H. Hossein, Thermal Conductivity Reduction in a Nanophononic Metamaterial versus a Nanophononic Crystal: A Review and Comparative Analysis, Adv. Funct. Mater., 2020, 30, 1906718 CrossRef.
- G. F. Xie, D. Ding and G. Zhang, Phonon Coherence and Its Effect on Thermal Conductivity of Nanostructures, Adv. Phys.: X, 2018, 3, 1480417 Search PubMed.
- G. L. Dai and J. P. Huang, Nonlinear Thermotics: Designing Thermal Metamaterials with temperature response, J. Nantong Univ., 2021, 20, 1–18 Search PubMed.
- J. Y. Tang, H. T. Wang, D. H. Lee, M. Fardy, Z. Y. Huo, T. P. Russell and P. D. Yang, Holey silicon as an efficient thermoelectric material, Nano Lett., 2010, 10, 4279 CrossRef CAS PubMed.
- G. F. Xie, Z. F. Ju, K. K. Zhou, X. L. Wei, Z. X. Guo, Y. Q. Cai and G. Zhang, Ultra-low thermal conductivity of two-dimensional phononic crystals in incoherent regime, npj Comput. Mater., 2018, 4, 21 CrossRef.
- A. M. Marconnet, M. Asheghi and K. E. Goodson, From the Casimir Limit to Phononic Crystals: Twenty Years of Phonon Transport Studies using Silicon-on-Insulator Technology, J. Heat Transfer, 2013, 135, 061601 CrossRef.
- A. Shchepetov, M. Prunnila, F. Alzina, L. Schneider, J. Cuffe, H. Jiang, E. I. Kauppinen, S. C. M. Torres and J. Ahopelto, Ultra-thin free-standing single crystalline silicon membranes with strain control, Appl. Phys. Lett., 2013, 102, 192108 CrossRef.
- B. Graczykowski, A. El Sachat, J. S. Reparaz, M. Sledzinska, M. R. Wagner, E. Chavez-Angel, Y. Wu, S. Volz, Y. Wu, F. Alzina and C. M. S. Torres, Thermal conductivity and air-mediated losses in periodic porous silicon membranes at high temperatures, Nat. Commun., 2017, 8, 415 CrossRef CAS PubMed.
- Y. Zhao, D. Liu, J. Chen, L. Zhu, A. Belianinov, O. S. Ovchinnikova, R. R. Unocic, M. J. Burch, S. Kim, H. Hao, D. S. Pickard, B. Li and J. T. L. Thong, Engineering the thermal conductivity along an individual silicon nanowire by selective helium ion irradiation, Nat. Commun., 2017, 8, 15919 CrossRef CAS PubMed.
- Y. S. Zhao, X. J. Liu, A. Rath, J. Wu, B. W. Li, W. X. Zhou, G. F. Xie, G. Zhang and J. T. L. Thong, Probing thermal transport across amorphous region embedded in a single crystalline silicon nanowire, Sci. Rep., 2020, 10, 821 CrossRef CAS PubMed.
- W. X. Zhou, Y. Cheng, K. Q. Chen, G. F. Xie, T. Wang and G. Zhang, Thermal Conductivity of Amorphous Materials, Adv. Funct. Mater., 2020, 30, 1903829 CrossRef CAS.
- N. Li, J. Ren, L. Wang, G. Zhang, P. Haenggi and B. Li, Colloquium: phononics: manipulating heat flow with electronic analogs and beyond, Rev. Mod. Phys., 2012, 84, 1045–1066 CrossRef.
- B. Li, L. Wang and G. Casati, Thermal diode: Rectification of heat flux, Phys. Rev. Lett., 2004, 93, 184301 CrossRef PubMed.
- C. W. Chang, D. Okawa, A. Majumdar and A. Zettl, Solid-state thermal rectifier, Science, 2006, 314, 1121–1124 CrossRef CAS PubMed.
- H. Tian, D. Xie, Y. Yang, T. L. Ren, G. Zhang, Y. F. Wang, C. J. Zhou, P. G. Peng, L. G. Wang and L. T. Liu, A novel solid-state thermal rectifier based on reduced graphene oxide, Sci. Rep., 2012, 2, 523 CrossRef PubMed.
- B. Li, L. Wang and G. Casati, Negative differential thermal resistance and thermal transistor, Appl. Phys. Lett., 2006, 88, 143501 CrossRef.
- X. J. Liu, G. Zhang and Y. W. Zhang, Graphene-based Thermal Modulator, Nano Res., 2015, 8, 2755–2762 CrossRef CAS.
- A. Roman, R. Aymeric, M. Jeremie and N. Masahiro, Heat guiding and focusing using ballistic phonon transport in phononic nanostructures, Nat. Commun., 2017, 8, 15505 CrossRef PubMed.
- A. Roman and N. Masahiro, Ray phononics: Thermal guides, emitters, filters, and shields powered by ballistic phonon transport, Mater. Today Phys., 2020, 15, 100272 CrossRef.
- J. C. Li, L. X. Weng and R. Aymeric, Design of thermal lens phononic nanostructure to generate tunable hotspots using quasi-ballistic phonon transport, J. Appl. Phys., 2022, 131, 195102 CrossRef CAS.
- Y. R. Song and G. Wehmeyer, Phonon ray tracing calculations of ballistic temperature and heat flux profiles in nanostructures, Mater. Today Phys., 2023, 33, 101040 CrossRef.
- H. J. C. Berendsen, J. P. M. Postma, W. F. v. Gunsteren, A. DiNola and J. R. Haak, Molecular dynamics with coupling to an external bath, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- L. N. Yang, B. Latour and A. J. Minnich, Phonon transmission at crystalline-amorphous interfaces studied using mode-resolved atomistic Green's functions, Phys. Rev. B, 2018, 97, 205306 CrossRef CAS.
- M. Ishimaru, S. Munetoh and T. Motooka, Generation of amorphous silicon structures by rapid quenching: A molecular-dynamics study, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 15133 CrossRef CAS.
- J. M. Larkin and A. J. H. McGaughey, Thermal conductivity accumulation in amorphous silica and amorphous silicon, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 144303 CrossRef.
- I. Stich, R. Car and M. Parrinello, Structural, bonding, dynamical, and electronic properties of liquid silicon: An ab initio molecular-dynamics study, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 11092 CrossRef CAS PubMed.
- S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- F. H. Stillinger and T. A. Weber, Computer simulation of local order in condensed phases of silicon, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 5262–5271 CrossRef CAS PubMed.
- G. X. Yu, Y. F. Lin, G. Q. Zhang, Z. Yu, L. L. Yu and J. Su, Design of square-shaped heat flux cloaks and concentrators using method of coordinate transformation, Front. Phys., 2011, 6, 70 CrossRef.
- R. Hu, S. Y. Huang, M. Wang, L. L. Zhou, X. Y. Peng and X. B. Luo, Phys. Rev. Appl., 2018, 10, 054032 CrossRef CAS.
- P. F. Zhuang, L. J. Xu, P. Tan, X. P. Ouyang and J. P. Huang, Breaking efficiency limit of thermal concentrators by conductivity couplings, Sci. China: Phys., Mech. Astron., 2022, 65, 117007 Search PubMed.
- S. Narayana and Y. Sato, Heat Flux Manipulation with Engineered Thermal Materials, Phys. Rev. Lett., 2012, 108, 214303 CrossRef PubMed.
- R. S. Kapadia and P. R. Bandaru, Heat flux concentration through polymeric thermal lenses, Appl. Phys. Lett., 2014, 105, 233903 CrossRef.
- X. Y. Shen, Y. Li, C. R. Jiang, Y. S. Ni and J. P. Huang, Thermal cloak-concentrator, Appl. Phys. Lett., 2016, 109, 031907 CrossRef.
- G. Fujii and Y. Akimoto, Topology-optimized thermal carpet cloak expressed by an immersed-boundary level-set method via a covariance matrix adaptation evolution strategy, Int. J. Heat Mass Transfer, 2019, 137, 1312–1322 CrossRef.
- A. Giri, B. F. Donovan and P. E. Hopkins, Localization of vibrational modes leads to reduced thermal conductivity of amorphous heterostructures, Phys. Rev. Mater., 2018, 2, 056002 CrossRef CAS.
- P. B. Allen and J. L. Feldman, Thermal conductivity of disordered harmonic solids, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 12581 CrossRef CAS PubMed.
- W. X. Zhou, Y. Cheng, K. Q. Chen, G. F. Xie, T. Wang and G. Zhang, Thermal Conductivity of Amorphous Materials, Adv. Funct. Mater., 2020, 30, 1903829 CrossRef CAS.
- G. F. Xie, D. Ding and G. Zhang, Phonon coherence and its effect on thermal conductivity of nanostructures, Adv. Phys.: X, 2018, 3(1), 719–754 Search PubMed.
- N. Zen, T. A. Puurtinen, T. J. Isotalo, S. Chaudhuri and I. J. Maasilta, Engineering thermal conductance using a two-dimensional phononic crystal, Nat. Commun., 2014, 5, 3435 CrossRef PubMed.
- A. Paskin and J. M. Dickey, Computer Simulation of the Lattice Dynamics of Solids, Phys. Rev., 1969, 188(3), 1407–1418 CrossRef.
- G. C. Loh, E. H. T. Teo and B. K. Tay, Phonon localization around vacancies in graphene nanoribbons, Diamond Relat. Mater., 2012, 23, 88–92 CrossRef CAS.
- Y. Wang, A. Vallabhaneni, J. N. Hu, B. Qiu, Y. P. Chen and X. L. Ruan, Phonon Lateral Confinement Enables Thermal Rectification in Asymmetric Single-Material Nanostructures, Nano Lett., 2014, 14, 592–596 CrossRef CAS PubMed.
- T. Liang, M. Zhou, P. Zhang, P. Yuan and D. G. Yang, Remarkably reduced thermal contact resistance of graphene/olefin block copolymer/paraffin form stable phase change thermal interface material, Int. J. Heat Mass Transfer, 2020, 151, 119395 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00494e |
| This journal is © The Royal Society of Chemistry 2023 |
