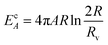Open Access Article
Open Access ArticleObservation of magnetic vortex configuration in non-stoichiometric Fe3O4 nanospheres†
Gopal
Niraula
 ab,
Denilson
Toneto
c,
Gerardo F.
Goya
ab,
Denilson
Toneto
c,
Gerardo F.
Goya
 d,
Giorgio
Zoppellaro
d,
Giorgio
Zoppellaro
 e,
Jose A. H.
Coaquira
e,
Jose A. H.
Coaquira
 b,
Diego
Muraca
b,
Diego
Muraca
 f,
Juliano C.
Denardin
*g,
Trevor P.
Almeida
f,
Juliano C.
Denardin
*g,
Trevor P.
Almeida
 h,
Marcelo
Knobel
f,
Ahmad I.
Ayesh
h,
Marcelo
Knobel
f,
Ahmad I.
Ayesh
 *i and
Surender K.
Sharma
*i and
Surender K.
Sharma
 *ja
*ja
aDepartment of Physics, Federal University of Maranhao, Sao Luis, 65080-805, Brazil. E-mail: surender76@gmail.com
bLaboratory of Magnetic Materials, NFA, Institute of Physics, University of Brasilia, Brasilia 70910-900, Brazil
cUniversidad Central de Chile, 8330601 Santiago, Chile
dInstituto de Nanociencia y Materiales de Aragón (INMA), Universidad de Zaragoza, 50018, Zaragoza, Spain
eRegional Centre of Advanced Technologies and Materials, Palacky University in Olomouc, Slechtitelu 27, 77900 Olomouc, Czech Republic
fInstitute of Physics “Gleb Wataghin” (IFGW), University of Campinas (Unicamp), Campinas, SP, Brazil
gUniversidad de Santiago de Chile (USACH), CEDENNA and Departamento de Física, Santiago 9170124, Chile. E-mail: juliano.denardin@usach.cl
hSUPA, School of Physics and Astronomy, University of Glasgow, Glasgow, G12 8QQ, UK
iPhysics Program, Department of Math., Stat. and Physics, College of Arts and Sciences, Qatar University, P. O. Box 2713, Doha, Qatar
jDepartment of Physics, Central University of Punjab, Bathinda, 151401, India
First published on 31st August 2023
Abstract
Theoretical and micromagnetic simulation studies of magnetic nanospheres with vortex configurations suggest that such nanostructured materials have technological advantages over conventional nanosystems for applications based on high-power-rate absorption and subsequent emission. However, full experimental evidence of magnetic vortex configurations in spheres of submicrometer size is still lacking. Here, we report the microwave irradiation fabrication of Fe3O4 nanospheres and establish their magnetic vortex configuration based on experimental results, theoretical analysis, and micromagnetic simulations. Detailed magnetic and electrical measurements, together with Mössbauer spectroscopy data, provide evidence of a loss of stoichiometry in vortex nanospheres owing to the presence of a surface oxide layer, defects, and a higher concentration of cation vacancies. The results indicate that the magnetic vortex spin configuration can be established in bulk spherical magnetite materials. This study provides crucial information that can aid the synthesis of magnetic nanospheres with magnetically tailored properties; consequently, they may be promising candidates for future technological applications based on three-dimensional magnetic vortex structures.
1. Introduction
The existence of a magnetic vortex state, consisting of non-collinear spin configuration and in-plane curling, enables negligible remanent magnetization at low fields with high magnetization at high fields in magnetic nanoparticles (MNPs). The intrinsic stability, topology-driven dynamics, and more interestingly the switching field-dependent electrical and magnetic properties (widely known as “on/off” switching property) offer a great opportunity to practice in industrial technology, from quantum computing to biomedical applications.1–11 Many studies have reported the dimension-based vortex nanostructures in magnetic-oxide MNPs with controlled shape and size, in a variety of morphologies such as ellipsoids,12 cubes,13,14 disks/dots,5,6,8,15,16 and rings.17,18 The three-dimensional (3D) vortex structure in MNPs with sizes of several hundred nanometers (i.e., above the single-domain size limit of most materials) allows manipulation of unusual non-collinear spin-textures, their electrical, magnetic, mechanical, and thermal properties comprising the crucial physical properties such as topology, geometry, vorticity and chirality. Interestingly, the 3D magnetic nano-/microstructure finds use in several areas from digital nanotechnology to cellular mechanobiology such as in sensing, giant data storage, magnetic random access memory technology, and actuation in the presence of magnetic field.5,19–29 Thus, an in-depth understanding of those physical properties is very important in the 3D structural arrangement at the sub-nanoscale level. Therefore, the 3D magnetic structure may serve as a great tool to respond/tackle the many unanswered questions and explore new research directions in an unprecedented way.Recently, theoretical and simulation studies were reported for 3D magnetic nanospheres where the vortex magnetic structure of the core exhibited a unique precession motion nearby the direction of an externally applied static field.30–32 This unique vortex-core reversal behavior and its dependence on the frequency of the applied AC magnetic field allowed large power absorption values,30–32 making them appealing for potential application in bio-diagnostics and magnetic hyperthermia,33 for example. While these studies have provided robust analytical and computational information on vortex nanospheres, there are not yet extensive reports on the successful production of iron-oxide vortex nanospheres, which is the obvious step to validate experimentally the theoretical models and hence the significant relevance of achieving the successful synthesis of such nanospheres with magnetic vortex configuration.
The magnetic vortex state in materials with diverse sizes and shapes studied so far appeared in stoichiometric magnetite (bulk).34–37 It is essential to obtain the materials properties in bulk to achieve effective performance in practical applications. Often, the nanoparticles exhibit a bulk property if they preserve their stoichiometry, which depends on several factors like shape, size, surface defects, charge ordering, cation vacancies, etc.6,38,39 Indeed, in magnetite, stoichiometry is strongly associated with a Verwey transition, which is essential for its potential applications in spintronics, sensors, energy conversion devices, and biomedical purposes.40 The Verwey transition (TV) near 120 K, also called the metal-to-insulator transition, arises as a result of the charge order–disorder of Fe2+ and Fe3+ that leads to sharp changes in the electric, magnetic, and structural properties.41,42 Particularly, the change in the unit cell structure from inverse-cubic-spinel to monoclinic, increase in resistance and sharp fall of magnetization below TV directly affect the efficacy of nanoparticles and limit prospective applications.40 The absence of the Verwey transition directly leads to the loss of stoichiometry influenced by several external factors, such as size, shape, growth during synthesis, defects, thermal treatment, etc.43,44 It is well known that the Verwey transition is size-/shape-dependent, usually appears in larger nanoparticles in the range of blocked single domain/ferromagnetic particles and gets suppressed in the superparamagnetic range (precisely for particles smaller than 20 nm) and completely disappears for particle sizes below 6 nm.39,40,45 Despite the great experimental effort, however, the existence of ionic-charge ordering below the Verwey transition, surface defects, cation vacancies, and contribution of size/shape to the loss of stoichiometry in large-scale sphere magnetite still remains mysterious and under debate.46,47
This paper reports for the first time the microwave-assisted hydrothermal (MAH) synthesis route for Fe3O4 nanospheres and examines their magnetic vortex-spin configuration by means of experiments, theoretical analysis, and micromagnetic simulation. Later, the role of surface defects and cation vacancies in the loss of stoichiometry (non-stoichiometric) in as-prepared magnetic vortex nanospheres is presented and discussed.
2. Materials/methods
2.1 Synthesis procedure
The α-Fe2O3 long ellipsoidal rods (LERs), short ellipsoidal rods (SERs) and nanospheres (NSs) were prepared by a microwave-assisted hydrothermal reaction of iron chloride (FeCl3) with the addition of sodium phosphate (NaH2PO4) and sodium sulfate (Na2SO4) as additives to control the shape and morphology. Briefly, 0.06 mol L−1(∼370 mg) of FeCl3 and 35 mL of distilled water were stirred for 15-20 minutes. The additives NaH2PO4 and Na2SO4 were mixed with 3 mL of distilled water separately and finally mixed with FeCl3 solution to make a mixture of a final volume of 38 mL; the concentrations of NaH2PO4 solution were 2.7 × 10−4 mol L−1, 5.4 × 10−4 mol L−1, mol L−1 and 4.32 × 10−3 mol L−1, and that of Na2SO4·10H2O solution was 1.65 × 10−3 mol L−1. After vigorous stirring for 10 minutes, the mixture was transferred into a reaction vessel in a Synth's microwave reactor, with an output power of 1000 W. The working cycle of the microwave reactor was set as (i) 20 °C minutes−1 rapid heating until 200 °C from room temperature, and (ii) 60 minutes at 220 °C. The system was then allowed to cool down to room temperature, and the final material was centrifuged and washed with excess distilled water and absolute ethanol and dried in a vacuum oven at 50 °C. In this way, we have obtained ∼300 mg of α-Fe2O3 nanoparticles. Fe3O4 nanoparticles were obtained via a reduction process from the prepared α-Fe2O3. The dried α-Fe2O3 powders were annealed in a tube furnace at 550 °C for 6 hours under a continuous hydrogen/argon gas flow [H2/(H2 + Ar)), 4/100]. The furnace was then cooled down to room temperature while kept under a continuous H2 gas flow. As compared with the starting materials of α-Fe2O3, the size, shape and morphology of Fe3O4 nanostructures were well preserved after the reduction process.The controlled conversion of α-Fe2O3 to Fe3O4 is not an easy task because it depends on several physio-chemical factors such as concentration of Fe3+, annealing temperatures, time, gas-flow rate, concentration of H2 gas, and amount of phosphate anions. Usually, thermal reductions are performed using a mixture of trioctylamine (TOA) and oleic acid (OA) in order to avoid the coalescence of bare NPs as reported elsewhere.8 However, in the present work, the size, phase and morphology without any addition of surfactants during the thermal reduction process.
2.2 Spectroscopic and magnetic characterization
2.2.7.1 Construction of the phase diagram. We started investigating the lower energy configurations in the case of NSs of diameter ‘D’. The system was relaxed to a local energy minimum and the final spin configuration and the lower energy states in NSs were studied. Thereafter, we compared the energy of each final configuration, and the one with a lower energy value was selected as the ground state. This process was repeated for several diameters and the phase diagrams as a function of energy ‘Etot’ and diameter ‘d’ were constructed. In this case, two idealized characteristic configurations have been evaluated: (i) a single domain state and (ii) a vortex state.
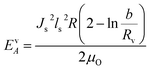 | (1) |
The anisotropy energy of the vortex area in the case of uniaxial anisotropy in the (x, y) plane
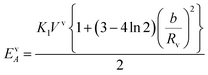 | (2) |
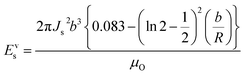 | (3) |
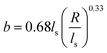 | (4) |
The energy of the curling region (volume Vcurl) is composed of exchange energy (EAc) and magnetocrystalline energy (EKc) and is given as
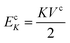 | (5) |
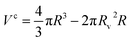 is the volume of the curling region.
is the volume of the curling region.
3. Results and discussion
Based on both recent reports and our own studies,17,53 we used phosphate anions for the shape-controlled synthesis of nanospheres (NSs). The complete synthesis process of defined α-Fe2O3 MNPs and their controlled conversion into Fe3O4 are provided above in Section 2.1 as well as in the ESI S1–S3.† The morphological changes of the as-prepared nanoparticles, from long ellipsoidal rods (LERs), short ellipsoidal rods (SERs) to nanospheres (NSs) with the decrease in the ratio of iron(III) to phosphate anions are shown schematically in Fig. 1a and their corresponding FESEM Fig. 1b–d. It is observed that when the ratio of iron(III) to phosphate anions is reduced by one half; LERs shortened their length, resulting in SERs which are further converted into NSs because of the reduced ratio of iron(III) to phosphate anions by 20 times. The size distribution of the obtained NSs (ESI S2†) could be fitted with a Gaussian distribution yielding an average diameter <d> = 700 ± 122 nm. The HRTEM images of the NSs (Fig. 1e) revealed lattice spacing of 0.251 nm and 0.210 nm, respectively, which corresponds to the lattice spacing of (311) and (400) planes of inverse spinel Fe3O4.54 The fast Fourier transform (FFT) pattern reflects the polycrystalline nature of NSs. Fig. 1f shows the XRD pattern of the Fe3O4 LERs, SERs, and NS reaction products along with their Rietveld analysis. It is found that both LERs and SERs contain the mixed phase of Fe3O4 and metallic iron (Fe0) whereas NSs are pure Fe3O4. All the diffraction peaks are indexed readily according to a cubic spinel phase (space group: Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m with JCPDS No. 19-0629, a = b = c= 8.37 Å) and the XRD Rietveld fitted data are given in the ESI (Table 1).†
m with JCPDS No. 19-0629, a = b = c= 8.37 Å) and the XRD Rietveld fitted data are given in the ESI (Table 1).†
The characteristic FTIR peaks between 600 cm−1 and 400 cm−1 observed in LERs, SERs and NS samples (ESI S3†) correspond to the α-Fe2O3 and Fe3O4 phases, with the absorption band at 545 cm−1 assigned to vibrational modes of Fe3O4. A second characteristic peak detected at 976 cm−1 is consistent with phosphate (PO43−) anions with typical wavenumbers within the 950–1200 cm−1 range.55 A very sharp peak emerges in the NS sample suggesting that a high concentration of phosphate groups are trapped on the nanoparticle surfaces.
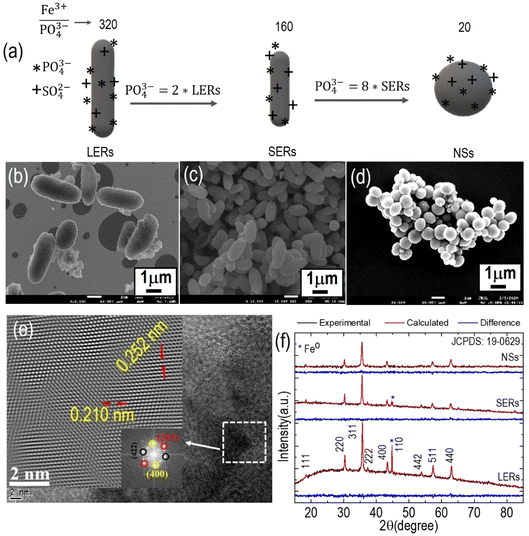
Fig. 2a shows a schematic of the vortex structure simulated for NSs with a cross-section drawing (Fig. 2c) showing the internal vortex orientation, as inferred from the simulations of the spin configurations as shown in Fig. 2b. The size of the NSs is ∼700 nm in diameter, which is above the single-domain region, i.e., one can predict that it belongs to a vortex region that avoids the singularity point of the exchange energy. Based on Fig. 2b and c, we assumed that the NSs consist of two-region curling-in-plane (x–y plane) and vortex-out-of-plane (z-axis). It is interesting to note in Fig. 2c, and its corresponding simulated spin-configuration highlighted by red and yellow colors, that the vortex region is formed in the shape of solid rods/cylindrical disks of radius Rv and height. Note that in the case of spheres, the simulations did not provide a vortex configuration in the whole particle volume, because of the aspect ratio (diameter/height) being close to 1. Rather, it creates a vortex-core region (Rv) within a limited cylindrical volume having the sphere diameter's height but a smaller internal cylinder radius and thus the vortex evolved as a cylindrical/rod shape (Fig. 2b and ESI S5†). This vortex region stabilizes the core of radius b, which exhibited the out-of-plane magnetization under the application of a magnetic field, i.e., magnetization has a non-zero component perpendicular to the plane of the vortex region (i.e., cylindrical disks). Within the vortex, core spins are aligned along the z-direction perpendicular to the in-plane circulating magnetizations (ESI S5†). Furthermore, in principle, the spin configuration within the vortex region should exhibit out-of-plane magnetization; from the simulated spin configuration (Fig. 2c); however, the region in between Rv and b can be considered as a transition domain from out-of-plane to in-plane.
This transition region is important in terms of change-in-energy (energy transition) from vortex to single-domain, which destroys the vortex state in NSs to the SD state. Overall, Fig. 2 indicates that the NS magnetic structure is described by a vortex-spin configuration with an unusual hysteresis loop, which needs to be investigated experimentally.
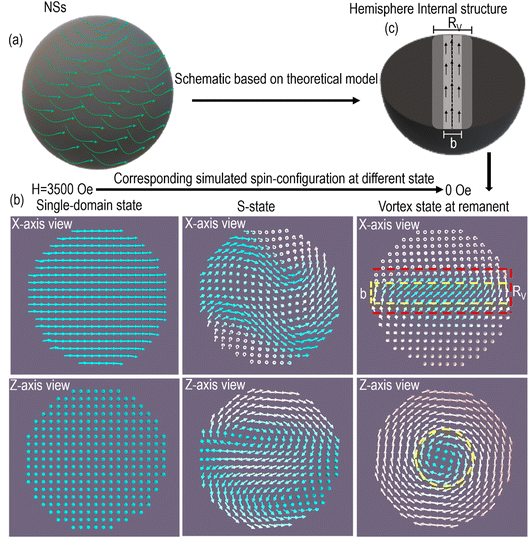
The vortex configuration in submicrometric ferromagnetic nanoparticles can be experimentally visualized by imaging techniques such as electron holography/tomography and magnetic force microscopy (MFM) techniques.13,56–61 Additionally, the transport of intensity equation (TIE)-based phase reconstruction through the Fresnel-contrast imaging technique in Lorentz transmission electron microscopy (LTEM) has been extensively used to examine the vortex behavior in magnetic NPs.62–64 We used the TIE phase reconstruction method to examine the vortex configuration in NSs, by considering its advantages compared to off-axis electron holography since it doesn't require the region of interest to be near vacuum. Moreover, such an approach preserves the original magnetic properties of the system under analysis and allows a larger field of view than typically found in off-axis electron holography.63,65,66 The experimental setup for studying magnetic vortex behavior requires an optimized sample preparation method to obtain well dispersed and homogeneous NP distribution to analyze a single, isolated particle. Observation of isolated NSs is required to avoid any influence of dipolar interactions among magnetic vortexes that could influence the spin arrangement.61 The Lorentz transmission electron microscopy results presented in Fig. 3 provide information on the size, morphology and magnetic properties of the NSs. The bright-field TEM images of Fig. 3a and d display NSs with ∼700 nm in diameter. The TIE was used to reconstruct phase images of each NS from a through-focus series (ESI S6†) of Fresnel contrast TEM images that were acquired in field-free Lorentz mode. The magnetic contributions to the phase shift (Fig. 3b and e) were isolated by physically flipping the sample 180° outside the TEM and image alignment/rotation was performed to calculate the differences in phase (ESI S6†).
The cosine of the phase was amplified to provide visualization of magnetic contours and the phase gradient provided directional information, using the color wheel shown in Fig. 3c and f, (inset). The result (Fig. 3c and f) clearly shows that both NSs are constituted by a spin vortex domain structure. The energy-diameter phase diagram obtained from micromagnetic simulations (Fig. 3g) shows the dependence of the final spin state on the diameter of the NSs. Specifically, the transition from a single-domain (SD) state to a vortex configuration occurs at the boundary line. This observation is fully consistent with both the theoretical model and micromagnetic simulation. It can be observed that the phase diagram is composed of three regions for increasing NS radius: a) single domain (in-plane); b) a transition (single-domain to a vortex) region; and c) a pure vortex region. The vortex state is the ground state for critical sizes above the single domain (≈90–95 nm for Fe3O4).67 The single-domain state is the most favorable configuration for particles below the critical size, and the full energies of the distinctive magnetization patterns decrease with increasing diameter D. It is likely that all size-/shape-dependent phase transitions (SPM to SD to vortex) are first-order temperature-dependent phase transitions from monoclinic to cubic, and in magnetite are associated with Verwey temperature, the so-called Verwey transition. The constructed energy-diameter phase diagram from the theoretical model agreed with the micromagnetic simulation. In any case, the small error at the boundary line is expected due to the impact of the cubic cell discretization within the micromagnetic recreation that contributes to the extra roughness energy and thus the full ground state energy of the framework that results in the discrepancy in overall theoretical and simulated energy profiles.9,51,68 The discreteness of the method and the utilization of a cubic mesh are the sources of systematic errors in nonrectangular systems, hence raising the imprecision of micromagnetic simulations reasoned by discretization.68 This is more applicable to NSs since the circular boundary is assessed by a staircase of straight-line segments. Such impacts are not observed in the theoretical phase diagram.
The vortex (flux-closure spin configuration) can occur in magnetic nanoparticles as a result of minimization of the total energy that includes magneto-crystalline anisotropy, exchange as well as magnetostatic energies. Although the formation of a vortex state is a consequence of energy competition between exchange and magnetostatic energy, the total energy of the curling-vortex state is mainly dominated by the exchange energy; thus, this interaction plays a key role in the formation of vortex states. The total energy, Etot, of NSs as a function of diameter (Fig. 3g) shows that Etot decreases with increasing diameter within the vortex region (Rv). The larger the particle diameter, the larger the vortex region which consequently increases the vortex core diameter, denoted by ‘b’ in Fig. 2c. This statement implies that NSs with larger diameter try to get relaxed/stabilized at lower energy state as their vortex/ground state. For diameter values above the single-to multi-domain limit (≈90–95 nm for Fe3O4), the NSs become the more energetically favorable state (lower energy state). Increasing the diameter of NSs, longer becomes the vortex core displacement of the vortex core, lowering the exchange energy and providing better stability of the vortex state by decreasing the remanent magnetization.69 While the total energy is the sum of several energies such as exchange, magneto-static (or demagnetizing energy), anisotropic energy etc. and magneto-static energy is dominated by the exchange interaction (ESI S8†), the single-domain state is dominated by the demagnetization energy at the surface.68,70 For large structures, the vortex state reduces the system energy by reducing stray fields and hence lowering the magnetostatic energy. The central vortex core in NSs contributes to the out-of-plane magnetization (i.e., mz ≠ 0) at the origin, which is stabilized by the exchange interactions and therefore the dynamic magnetization has noteworthy values outside of the vortex core, i.e., in-plane magnetization.71 Such out-of-plane magnetization leads to the observed magnetic remanence at H = 0, with the actual remanence values depending on the sizes of both NSs and the vortex core.
In addition to the imaging techniques, we further examined the vortex configuration in NSs through the magnetometry technique which allows us to visualize an unusual irreversible hysteresis loop in ferromagnetic vortex nanoparticles with negligible remanence and coercive field due to the switching behavior of the loop.17,18,72Fig. 3h shows the experimental and simulated hysteresis loops for NSs. The NSs are observed to exhibit a perfect irreversible magnetic behavior, as evidenced by the vortex configuration having magnetic remanence and coercive field of approximately 10 emu g−1 and 21 Oe, respectively. The small magnetic remanence (10 emu g−1) is expected from the vortex core of the NSs that induces an out-of-plane magnetization. Micromagnetic simulations consisting of moderate hysteresis loops with zero remanence and a coercive field of 21 Oe support these experimental results. The clear result of a vortex core in the center of NSs at H = 0 and its gyrotropic shift during the application of an external field, H > 0, evidences a vortex configuration in NSs. In such a domain structure of magnetic vortex, the hysteresis loop consists of a two-step magnetization reversal process which includes an S state in the present case to the vortex transition and vice versa.73,74 At a high external magnetic field H value, NSs fall into a saturation state or a single domain state because all spins are aligned parallel to the external field direction. To examine whether the simulated hysteresis fits the experimental data, we additionally calculated several hysteresis loops (ESI S4 and S5†) in two ways: (i) by varying the size; (ii) upon increasing the number of spheres with a diameter of 700 nm. We observed that the simulated hysteresis loops obtained by increasing the number of spheres tend to show results closer to the experimental ones. The simulated hysteresis loops evolve in a way more vertical, suggesting that the effect is gated by the number of spheres involved, and also periodic boundary conditions in the direction of the applied field (x-axis in the present case). The complete hysteresis loop phenomena (saturated/single-domain state, S-state and C-state in the hemisphere, and the vortex state) with respect to the magnetic field are presented in Fig. 3h and their magnetic state in Fig. 2b. Although the experimental coercive field values agree with simulated ones, the complete irreversible hysteresis loop appears quite different. The origin of such discrepancies is the different energy profiles as shown in the energy-diameter phase diagram (Fig. 3g) discussed above. In addition, the defect-/cation vacancy-free NPs require more accurate modeling data as compared to experimental ones.61 Overall, the simulated hysteresis loop for NSs is more convincing than previously reported data, which still shows a small loop with narrow nucleation and expulsion field (magnified inset in Fig. 3h); it is rare to find a clear nucleation and expulsion field (switching field) in 3D spherical particles because of their isotropic nature, and because their aspect ratio (h/d) is 1, unlike the switching field found in highly anisotropic particles such as 2D disk,6 rings,72 tubes and rods,12 which encode aspect ratio <1. Taking all together the theoretical analysis, experimental, and micromagnetic simulation, our findings confirm the existence of a vortex configuration in NSs.
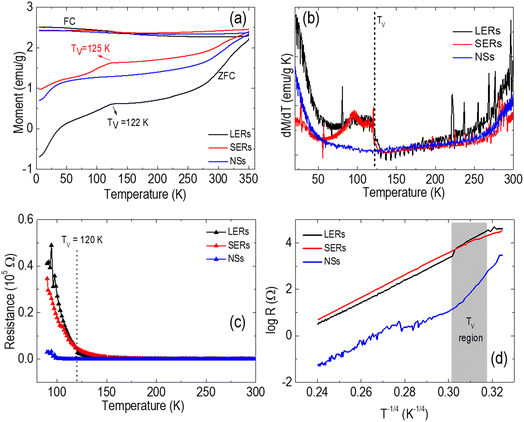
Fig. 4a and b show zero field cooling and field cooling (ZFC-FC) magnetization versus temperature in the absence or presence of an external magnetic field. The data clearly indicate a prominent Verwey transition (Tv) for the two samples i.e., LERs and SERs, which is typically met in stoichiometric Fe3O4, whereas no such transition is found in NSs. The Verwey transition for bulk Fe3O4 occurs at a temperature TV = 119 K, above which fast electron hopping among Fe2+ and Fe3+ ions occurs among the octahedral sites.40 For our samples, the Verwey transition was observed at TV ≈122 K and ≈125 K for LERs and SERs, respectively. As mentioned, no jump of magnetization at the TV was observed for NSs, suggesting the absence of this transition from the monoclinic to cubic phase structure.75,76 The MZFC/FCversus T curves in the whole temperature range suggest that the blocking temperature of all the samples (LERs, SERs and NSs) exceeds our experimental temperature limits of 5 ≤ T ≤ 350 K. We believe that LERs will exhibit the highest magnetic moment at the end of the process, likewise the highest magnetization obtained through the hysteresis curve (ESI S7†). In Fe3O4 MNPs, the sharp transition is related to the high crystallinity of nanoparticles and electron hopping between Fe2+ and Fe3+.77,78 The slightly sharper transition in LERs as compared to SERs is attributed to the higher percentage of stoichiometric Fe3O4 (i.e., 55% in LERs > 50% in SERs). This induces the comparatively effective ‘electron hopping’ between the Fe3+ and Fe2+ cations in the B-site of LERs at temperatures T > TV. In addition, the sharper transition in LERs is supported by eqn (2) and (3); significant cation vacancies were observed in SERs as compared to LERs and this fact should have hampered the regular Verwey transition. However, such a transition phenomenon does not appear in NSs, indicating that a long-range order for both Fe2+ and Fe3+ at the octahedral sites has been for T < TV.
Fig. 4c shows the temperature-dependent resistance that exhibits a metal-to-insulator transition, i.e., the Verwey transition, which increases exponentially with decreasing temperature below 120 K in LERs and SERs and is indicative of stoichiometric Fe3O4. Here, the temperature-dependent resistance curves are acquired as a function of increasing temperature, with the temperature stabilized for 20 minutes before a measurement is taken. This electrical transport measurement for all the samples was performed in a temperature range of 90–300 K. In the case of LERs and SERs, below 122 K and 125 K, a very sharp increase in resistance is observed, whereas no change in resistance is detected for NSs that almost remains constant until 100 K. Such an increase of resistance with decreasing temperature below 120 K in LERs and SERs is a signature of stoichiometric Fe3O4. Also, we have tested Mott's variable range hopping law.79Fig. 4d shows the logarithmic resistance as a function of T−1/4 in which LERs and SERs exhibit a small kink around 122 K (shaded region) which is clear evidence of the Verwey transition. However, no such kink is found in the case of NSs. Thus, both MZFC-FCversus temperature and electrical measurements provide clear evidence of surface defects and oxygen vacancies in NSs that suppress the Verwey transition, turning the material into non-stoichiometric Fe3O4.
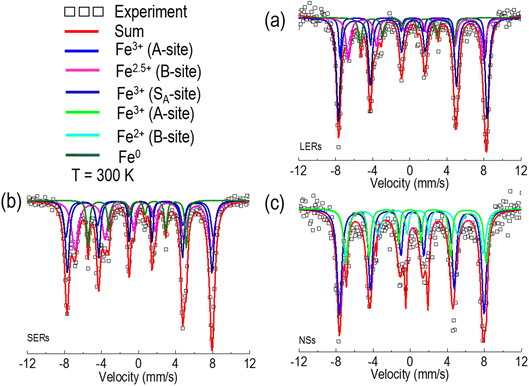
The Mössbauer spectroscopy can provide further insights upon disclosing the contributions of iron ions located either at A (tetrahedral) or B (octahedral) sites as well as surface defects and oxygen vacancy concentration. We have performed Mössbauer spectroscopy at 300 K as shown in Fig. 5a–c, as well as the hyperfine fitting parameters are shown in Table 3 of ESI.† The spectra of all samples were well fitted considering sextet patterns (magnetic sub-spectra). The spectrum for LERs and SERs (Fig. 5a and b) is well resolved by four sextets (three sextets for Fe3O4 and one for Fe0) and exhibits almost similar behavior in light of compositions of Fe cation distributions. The calculated values of hyperfine parameters for all the samples are consistent with the two crystallographic sites for iron ions in the cubic spinel (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) structure of Fe3O4.54 Nevertheless, the ratio of spectral area at A- and B-sites was found to be different as compared with bulk magnetite (i.e., 1
m) structure of Fe3O4.54 Nevertheless, the ratio of spectral area at A- and B-sites was found to be different as compared with bulk magnetite (i.e., 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 for free-defect crystals); such a ratio of composition indicates that the samples have not perfectly preserved their stoichiometry. We observed that much more Fe3+ cations are present in the A-site than in the bulk reference. Therefore, further deep analysis of Mössbauer fitting revealed that only ∼55% of Fe3O4 preserved its bulk behavior i.e., stoichiometry in LERs; 18.86% of Fe3+ in A-sites and 35.74% of Fe3+ in B-sites and ∼50% of Fe3O4 preserved its bulk behavior i.e., stoichiometry in SERs; 16.43% of Fe3+ in A-sites and 33.64% of Fe3+ in B-sites. The fitted sextet drawn in navy color represents A-sites (represented by SA) containing ∼26% and ∼41% of Fe3+ cations somewhere in the samples LERs and SERs, respectively.
2 for free-defect crystals); such a ratio of composition indicates that the samples have not perfectly preserved their stoichiometry. We observed that much more Fe3+ cations are present in the A-site than in the bulk reference. Therefore, further deep analysis of Mössbauer fitting revealed that only ∼55% of Fe3O4 preserved its bulk behavior i.e., stoichiometry in LERs; 18.86% of Fe3+ in A-sites and 35.74% of Fe3+ in B-sites and ∼50% of Fe3O4 preserved its bulk behavior i.e., stoichiometry in SERs; 16.43% of Fe3+ in A-sites and 33.64% of Fe3+ in B-sites. The fitted sextet drawn in navy color represents A-sites (represented by SA) containing ∼26% and ∼41% of Fe3+ cations somewhere in the samples LERs and SERs, respectively.
When electron hopping occurs in B-sites of LERs and SERs, the valences of Fe2+ and Fe3+ ions are averaged to Fe2.5+, and the distribution of charge for the stoichiometric magnetite can be estimated as
| (Fe3+)A [Fe22.5+]BO4 | (6) |
As previously mentioned above, the ratio-metric Fe cation population in A- and B-sites must be XB/XA = 2, where XB and XA are the area/population contained by Fe cations in each site, to claim the stoichiometric magnetite. However, according to the observed data shown in Table 3 (ESI†), the overall ratio XB/XA is about 0.78 and 0.59 for the samples LERs and SERs, respectively. This could be explained either by the presence of cation vacancies or/and by the surface effects. For the cation vacancy case (□) in B-sites, the LERs and SERs would correspond to the non-stoichiometric magnetite with the chemical formula for LERs
| (Fe3+)A[Fe0.782.5+□1.22]BO4 | (7) |
| (Fe3+)A[Fe0.592.5+□1.41]BO4 | (8) |
The cation vacancies are in increasing order which can be seen in eqn (2) and (3) as a result of a significant reduction of charge ordering between Fe3+ and Fe2+ at temperatures T < TV on the B-sites. In addition, one sextet of metallic iron (Fe0) is also observed in both samples and represented by olive color in Fig. 5a and b which is verified by analysis of the hyperfine parameters (as shown in ESI Table 3†) and agrees well with the results obtained from XRD data analysis (Table 1) of the ESI.†
For NSs, on the other hand, no evidence of stoichiometric Fe3O4 is found in terms of the available composition of Fe3+ and Fe2+. It is observed that three sextets containing one sextet of Fe cations in the A-site and two of Fe cations in the B-site (i.e., each of Fe3+ and Fe2+ cations) as shown in Fig. 5c. The presence of two sextets in the B-site, each from Fe3+ and Fe2+ cations, indicates absence of electron hopping (Fe2+ ⇄ Fe3+) at T > TV, probably due to surface effects. Thus, it is important to take an account of surface effects. For this, we have evaluated the cation charge distribution from data obtained from Mössbauer spectroscopy analysis. The fitting hyperfine parameters as given in Table 3 (ESI†) show that the distribution of Fe3+ and Fe2+ in A- and B-sites are far away from the bulk (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2). The overall non-stoichiometric cationic charge distribution in NSs caused by the defects/oxygen vacancies/surface effect is determined to be
2). The overall non-stoichiometric cationic charge distribution in NSs caused by the defects/oxygen vacancies/surface effect is determined to be
| (Fe3+)A[Fe0.6652+ ↔ Fe0.6653+]B[Fe0.673+]BO4 | (9) |
This result is further confirmed by ZFC and resistance measurements because no signal addressable to the Verwey phase transition is observed.
Let us recall the synthesis of the reaction products presented in this work; the LERs, SERs, and NSs were formed by simply increase of the concentration of phosphate anions in solution. Such an increase of concentration for phosphate anions, which consists particularly of O2, would then easily oxidize Fe2+ to Fe3+ ions to possess higher spin states. Consequently, the numbers of Fe3+ and Fe2+ ions on octahedral sites become incommensurate below TV, leading to the disappearance of charge ordering and loss of transition in NSs. The Mössbauer and magnetic data are easily explained by keeping in mind the synthetic process followed for the assembly of these systems. A higher percentage of oxidation state (Fe3+) is expected in fact to occur in NSs. The reduced population of Fe2+, increasing population of Fe3+ and raising cation vacancies are factors that are connected to each other. No transition was observed in NSs because of the absence and/or lacking electron hopping effects (Fe2+ ⇄ Fe3+), due to the availability of more cation vacancies/defects in the synthesized material. Thus, the loss of stoichiometry in NSs arises from the presence of a large number of Fe3+ cations, resulting from the increased concentration of phosphate anions employed during synthesis.
Overall, on one hand, we first prepared NSs and characterized their vortex configuration through several experimental and microscopic imaging techniques described above along with theoretical and simulation prediction. The theoretical and simulation predicted energy-diameter phase diagram of nanospheres (Fig. 3g) provides the evolution of energy with respect to the diameter. The phase diagram allows us to check whether the energy remains the same or varies in different regions (superparamagnetic, single-domain, and vortex regions). As expected, it seems that the energy continuously increases until the single-domain size of the sphere is reached and then it starts to decrease. Once the nanoparticle crosses its single-domain state, the magnetization/spin-configuration goes through several states such as C-state, flower state, onion state, S-state and finally the vortex state,30,32,36,37,80,81 which is the most stable state having the lowest energy profile, in order to become the stable (ground) state. From the theoretical/simulated energy-diameter phase diagram, the NSs with 700 nm in size clearly belong to the vortex region, which is further confirmed by the TIE experiment (Fig. 3a–f) together with magnetic measurement (hysteresis loss Fig. 3h). On the other hand, it is well established that the Verwey temperature (Tv) is associated with the stoichiometry of Fe3O4. The magnetization (ZFC-FC)-temperature experiment (Fig. 4a and b) together with electrical resistance measurement (Fig. 4c and d) were performed to examine the existence of Verwey temperature (Tv) as a signature of the stoichiometry of Fe3O4. These experiments along with Mössbauer spectroscopy confirmed that the NSs have lost their stoichiometry regardless of the existence of a magnetic vortex state.
4. Conclusion
We have synthesized Fe3O4 nanospheres close to the micrometer size by microwave irradiation, controlling the concentration of phosphate anions. A clear magnetic vortex spin configuration has been experimentally found, consistent with the proposed theoretical model and micromagnetic simulations performed to understand the microscopic origin of such structures. We found a loss of stoichiometry in the NSs, likely due to defects and cation vacancies at the surface layer, that hinders the electron hopping between Fe2+ and Fe3+ characteristic of bulk magnetite. The results demonstrate that the magnetic vortex spin configuration is successfully achieved in bulk spherical magnetite.Conflicts of interest
There are no conflicts to declare.Acknowledgements
GN is thankful to the Brazilian funding agency CAPES for providing a doctorate fellowship. SKS is very thankful to UGC-DAE Consortium for Scientific Research, India for providing financial support (CSR-IC-ISUM-54/CRS-337/2020-21/795). JAHC thanks CNPq (443652/2018-0) and FAPDF (00193-00000151/2019-20) for the financial support. GZ acknowledges the support from The Czech Science Foundation (22-26416S). GFG acknowledges partial financial support from the Spanish Ministerio de Ciencia, Innovación y Universidades (project PID2019-106947RB-C21). J. C. D. thanks CEDENNA (AFB220001) and Fondecyt 1200782 for financial support. MK and DM fully acknowledge the support from Fundação de Amparo à Pesquisa do Estado de São Paulo #21/04058-0, #17/10581-1 and CNPq, Brazilian agencies.References
- S. B. Choe, Y. Acremann, A. Scholl, A. Bauer, A. Doran, J. Stöhr and H. A. Padmore, Vortex Core-Driven Magnetization Dynamics, Science, 2004, 304(5669), 420–422, DOI:10.1126/SCIENCE.1095068.
- B. Van Waeyenberge, A. Puzic, H. Stoll, K. W. Chou, T. Tyliszczak, R. Hertel, M. Fähnle, H. Brückl, K. Rott, G. Reiss, I. Neudecker, D. Weiss, C. H. Back and G. Schütz, Magnetic Vortex Core Reversal by Excitation with Short Bursts of an Alternating Field, Nature, 2006, 444(7118), 461–464, DOI:10.1038/nature05240.
- R. Hertel, S. Gliga, M. Fähnle and C. M. Schneider, Ultrafast Nanomagnetic Toggle Switching of Vortex Cores, Phys. Rev. Lett., 2007, 98(11), 117201, DOI:10.1103/PhysRevLett.98.117201.
- B. Pigeau, G. de Loubens, O. Klein, A. Riegler, F. Lochner, G. Schmidt, L. W. Molenkamp, V. S. Tiberkevich and A. N. Slavin, A Frequency-Controlled Magnetic Vortex Memory, Appl. Phys. Lett., 2010, 96(13), 132506, DOI:10.1063/1.3373833.
- D.-H. Kim, E. A. Rozhkova, I. V. Ulasov, S. D. Bader, T. Rajh, M. S. Lesniak and V. Novosad, Biofunctionalized Magnetic-Vortex Microdiscs for Targeted Cancer-Cell Destruction, Nat. Mater., 2010, 9(2), 165–171, DOI:10.1038/nmat2591.
- G. Niraula, J. A. H. Coaquira, F. H. Aragon, A. F. Bakuzis, B. M. G. Villar, F. Garcia, D. Muraca, G. Zoppellaro, A. I. Ayesh and S. K. Sharma, Stoichiometry and Orientation- and Shape-Mediated Switching Field Enhancement of the Heating Properties of Fe3O4 Circular Nanodiscs, Phys. Rev. Appl., 2021, 15(1), 014056, DOI:10.1103/physrevapplied.15.014056.
- X. Liu, B. Yan, Y. Li, X. Ma, W. Jiao, K. Shi, T. Zhang, S. Chen, Y. He, X. J. Liang and H. Fan, Graphene Oxide-Grafted Magnetic Nanorings Mediated Magnetothermodynamic Therapy Favoring Reactive Oxygen Species-Related Immune Response for Enhanced Antitumor Efficacy, ACS Nano, 2020, 14(2), 1936–1950, DOI:10.1021/acsnano.9b08320.
- Y. Yang, X. Liu, Y. Lv, T. S. Herng, X. Xu, W. Xia, T. Zhang, J. Fang, W. Xiao and J. Ding, Orientation Mediated Enhancement on Magnetic Hyperthermia of Fe 3 O 4 Nanodisc, Adv. Funct. Mater., 2015, 25(5), 812–820, DOI:10.1002/adfm.201402764.
- G. Niraula, D. Toneto, E. Joshy, J. A. H. Coaquira, A. I. Ayesh, F. Garcia, D. Muraca, J. C. Denardin, G. F. Goya and S. K. Sharma, Energy Evolution, Stabilization, and Mechanotransducer Properties of Fe3O4 Vortex Nanorings and Nanodisks, Phys. Rev. Appl., 2021, 16(2), 024002, DOI:10.1103/PhysRevApplied.16.024002.
- D. Gregurec, A. W. Senko, A. Chuvilin, P. D. Reddy, A. Sankararaman, D. Rosenfeld, P. H. Chiang, F. Garcia, I. Tafel, G. Varnavides, E. Ciocan and P. Anikeeva, Magnetic Vortex Nanodiscs Enable Remote Magnetomechanical Neural Stimulation, ACS Nano, 2020, 14(7), 8036–8045, DOI:10.1021/acsnano.0c00562.
- M. S. Wolf, R. Badea and J. Berezovsky, Fast Nanoscale Addressability of Nitrogen-Vacancy Spins via Coupling to a Dynamic Ferromagnetic Vortex, Nat. Commun., 2016, 7(1), 1–7, DOI:10.1038/ncomms11584.
- H. Gao, T. Zhang, Y. Zhang, Y. Chen, B. Liu, J. Wu, X. Liu, Y. Li, M. Peng, Y. Zhang, G. Xie, F. Zhao and H. M. Fan, Ellipsoidal Magnetite Nanoparticles: A New Member of the Magnetic-Vortex Nanoparticles Family for Efficient Magnetic Hyperthermia, J. Mater. Chem. B, 2020, 8(3), 515–522, 10.1039/c9tb00998a.
- E. Pinilla-Cienfuegos, S. Mañas-Valero, A. Forment-Aliaga and E. Coronado, Switching the Magnetic Vortex Core in a Single Nanoparticle, ACS Nano, 2016, 10(2), 1764–1770, DOI:10.1021/acsnano.5b06776.
- L.-M. Lacroix, S. Lachaize, F. Hue, C. Gatel, T. Blon, R. P. Tan, J. Carrey, B. Warot-Fonrose and B. Chaudret, Stabilizing Vortices in Interacting Nano-Objects: A Chemical Approach, Nano Lett., 2012, 12(6), 3245–3250, DOI:10.1021/NL3012616.
- T. Shinjo, T. Okuno, R. Hassdorf, K. Shigeto and T. Ono, Magnetic Vortex Core Observation in Circular Dots of Permalloy, Science, 2000, 289(5481), 930–932, DOI:10.1126/science.289.5481.930.
- M. Goiriena-Goikoetxea, K. Y. Guslienko, M. Rouco, I. Orue, E. Berganza, M. Jaafar, A. Asenjo, M. L. Fernández-Gubieda, L. F. Barquín and A. García-Arribas, Magnetization Reversal in Circular Vortex Dots of Small Radius, Nanoscale, 2017, 9(31), 11269–11278, 10.1039/C7NR02389H.
- C.-J. Jia, L.-D. Sun, F. Luo, X.-D. Han, L. J. Heyderman, Z.-G. Yan, C.-H. Yan, K. Zheng, Z. Zhang, M. Takano, N. Hayashi, M. Eltschka, M. Kläui, U. Rüdiger, T. Kasama, L. Cervera-Gontard, R. E. Dunin-Borkowski, G. Tzvetkov and J. Raabe, Large-Scale Synthesis of Single-Crystalline Iron Oxide Magnetic Nanorings, J. Am. Chem. Soc., 2008, 130(50), 16968–16977, DOI:10.1021/ja805152t.
- Y. Yang, X. L. Liu, J. B. Yi, Y. Yang, H. M. Fan and J. Ding, Stable Vortex Magnetite Nanorings Colloid: Micromagnetic Simulation and Experimental Demonstration, J. Appl. Phys., 2012, 111(4), 044303, DOI:10.1063/1.3684963.
- A. Fernández-Pacheco, R. Streubel, O. Fruchart, R. Hertel, P. Fischer and R. P. Cowburn, Three-Dimensional Nanomagnetism, Nat. Commun., 2017, 8(1), 1–14, DOI:10.1038/ncomms15756.
- R. H. Blick, H. Qin, H. S. Kim and R. Marsland, A Nanomechanical Computer—Exploring New Avenues of Computing, New J. Phys., 2007, 9(7), 241, DOI:10.1088/1367-2630/9/7/241.
- P. Vavassori, M. Pancaldi, M. J. Perez-Roldan, A. Chuvilin, A. Berger, A. P. Vavassori, M. Pancaldi, M. J. Perez-Roldan, A. Chuvilin, A. Berger and P. Vavassori, Remote Magnetomechanical Nanoactuation, Small, 2016, 12(8), 1013–1023, DOI:10.1002/SMLL.201503351.
- L. Baraban, R. Streubel, D. Makarov, L. Han, D. Karnaushenko, O. G. Schmidt and G. Cuniberti, Fuel-Free Locomotion of Janus Motors: Magnetically Induced Thermophoresis, ACS Nano, 2013, 7(2), 1360–1367, DOI:10.1021/NN305726M/SUPPL_FILE/NN305726M_SI_009.AVI.
- A. V. Chumak, V. I. Vasyuchka, A. A. Serga and B. Hillebrands, Nat. Phys., 2015, 11(6), 453–461, DOI:10.1038/nphys3347.
- D. A. Allwood, G. Xiong, C. C. Faulkner, D. Atkinson, D. Petit and R. P. Cowburn, Magnetic Domain-Wall Logic, Science, 2005, 309(5741), 1688–1692, DOI:10.1126/SCIENCE.1108813/ASSET/4E1829EF-7E73-4727-995D-718FEF5B4EDD/ASSETS/GRAPHIC/309_1688_F3.
- S. Lequeux, J. Sampaio, V. Cros, K. Yakushiji, A. Fukushima, R. Matsumoto, H. Kubota, S. Yuasa and J. Grollier, A Magnetic Synapse: Multilevel Spin-Torque Memristor with Perpendicular Anisotropy, Sci. Rep., 2016, 6, 31510, DOI:10.1038/SREP31510.
- D. Kilinc, C. L. Dennis, G. U. Lee, D. Kilinc, G. U. Lee and C. L. Dennis, Bio-Nano-Magnetic Materials for Localized Mechanochemical Stimulation of Cell Growth and Death, Adv. Mater., 2016, 28(27), 5672–5680, DOI:10.1002/ADMA.201504845.
- M. A. Wheeler, C. J. Smith, M. Ottolini, B. S. Barker, A. M. Purohit, R. M. Grippo, R. P. Gaykema, A. J. Spano, M. P. Beenhakker, S. Kucenas, M. K. Patel, C. D. Deppmann and A. D. Güler, Genetically Targeted Magnetic Control of the Nervous System, Nat. Neurosci., 2016, 19(5), 756–761, DOI:10.1038/nn.4265.
- S. H. Cartmell, J. Dobson, S. B. Verschueren and A. J. El Haj, Development of Magnetic Particle Techniques for Long-Term Culture of Bone Cells with Intermittent Mechanical Activation, IEEE Trans. NanoBiosci., 2002, 1(2), 92–97, DOI:10.1109/TNB.2002.806945.
- N. Wang and D. E. Ingber, Probing Transmembrane Mechanical Coupling and Cytomechanics Using Magnetic Twisting Cytometry, Biochem. Cell Biol., 1995, 73(7–8), 327–335, DOI:10.1139/O95-041.
- S.-K. Kim, M.-W. Yoo, J. Lee, H.-Y. Lee, J.-H. Lee, Y. Gaididei, V. P. Kravchuk and D. D. Sheka, Resonantly Excited Precession Motion of Three-Dimensional Vortex Core in Magnetic Nanospheres, Sci. Rep., 2015, 5(1), 1–9, DOI:10.1038/srep11370.
- S.-K. Kim, M.-W. Yoo, J. Lee, J.-H. Lee and M.-K. Kim, Resonant Vortex-Core Reversal in Magnetic Nano-Spheres as Robust Mechanism of Efficient Energy Absorption and Emission, Sci. Rep., 6(1), 1–8, DOI:10.1038/srep31513.
- R. Ferrero, A. Manzin, G. Barrera, F. Celegato, M. Coïsson and P. Tiberto, Influence of Shape, Size and Magnetostatic Interactions on the Hyperthermia Properties of Permalloy Nanostructures, Sci. Rep., 2019, 9(1), 1–12, DOI:10.1038/s41598-019-43197-4.
- R. Ferrero, A. Manzin, G. Barrera, F. Celegato, M. Coïsson and P. Tiberto, Influence of Shape, Size and Magnetostatic Interactions on the Hyperthermia Properties of Permalloy Nanostructures, Sci. Rep., 2019, 9(1), 6591, DOI:10.1038/s41598-019-43197-4.
- C.-J. Jia, L.-D. Sun, F. Luo, X.-D. Han, L. J. Heyderman, Z.-G. Yan, C.-H. Yan, K. Zheng, Z. Zhang, M. Takano, N. Hayashi, M. Eltschka, M. Kläui, U. Rüdiger, T. Kasama, L. Cervera-Gontard, R. E. Dunin-Borkowski, G. Tzvetkov and J. Raabe, Large-Scale Synthesis of Single-Crystalline Iron Oxide Magnetic Nanorings, J. Am. Chem. Soc., 2008, 130(50), 16968–16977, DOI:10.1021/ja805152t.
- X. Li Liu, Y. Yang, C. Teng Ng, L. Yun Zhao, Y. Zhang, B. Huat Bay, H. Ming Fan, J. Ding, X. L. Liu, H. M. Fan, Y. Yang, J. Ding, C. T. Ng, B. H. Bay, L. Y. Zhao and Y. Zhang, Magnetic Vortex Nanorings: A New Class of Hyperthermia Agent for Highly Efficient In Vivo Regression of Tumors, Adv. Mater., 2015, 27(11), 1939–1944, DOI:10.1002/ADMA.201405036.
- Y. Yang, X. Liu, Y. Lv, T. S. Herng, X. Xu, W. Xia, T. Zhang, J. Fang, W. Xiao and J. Ding, Orientation Mediated Enhancement on Magnetic Hyperthermia of Fe3O4 Nanodisc, Adv. Funct. Mater., 2015, 25(5), 812–820, DOI:10.1002/ADFM.201402764.
- Y. Yang, X. L. Liu, J. B. Yi, Y. Yang, H. M. Fan and J. Ding, Stable Vortex Magnetite Nanorings Colloid: Micromagnetic Simulation and Experimental Demonstration, J. Appl. Phys., 2012, 111(4), 044303, DOI:10.1063/1.3684963.
- R. Das, J. Alonso, Z. Nemati Porshokouh, V. Kalappattil, D. Torres, M. H. Phan, E. Garaio, J. Á. García, J. L. Sanchez Llamazares and H. Srikanth, Tunable High Aspect Ratio Iron Oxide Nanorods for Enhanced Hyperthermia, J. Phys. Chem. C, 2016, 120(18), 10086–10093, DOI:10.1021/acs.jpcc.6b02006.
- A. Mitra, J. Mohapatra, S. S. Meena, C. V. Tomy and M. Aslam, Verwey Transition in Ultrasmall-Sized Octahedral Fe3O4 Nanoparticles, J. Phys. Chem. C, 2014, 118(33), 19356–19362, DOI:10.1021/JP501652E.
- M. Bohra, N. Agarwal and V. Singh, A Short Review on Verwey Transition in Nanostructured Fe3O4 Materials, J. Nanomater., 2019, 2019, 8457383, DOI:10.1155/2019/8457383.
- M. S. Senn, J. P. Wright and J. P. Attfield, Charge Order and Three-Site Distortions in the Verwey Structure of Magnetite, Nature, 2011, 481(7380), 173–176, DOI:10.1038/nature10704.
- E. J. W. VERWEY, Electronic Conduction of Magnetite (Fe3O4) and Its Transition Point at Low Temperatures, Nature, 1939, 144(3642), 327–328, DOI:10.1038/144327b0.
- F. Zhang, S.-W. Chan, J. E. Spanier, E. Apak, Q. Jin, R. D. Robinson and I. P. Herman, Cerium Oxide Nanoparticles: Size-Selective Formation and Structure Analysis, Appl. Phys. Lett., 2002, 80(1), 127, DOI:10.1063/1.1430502.
- T. Kim, S. Lim, J. Hong, S. G. Kwon, J. Okamoto, Z. Y. Chen, J. Jeong, S. Kang, J. C. Leiner, J. T. Lim, C. S. Kim, D. J. Huang, T. Hyeon, S. Lee and J. G. Park, Giant Thermal Hysteresis in Verwey Transition of Single Domain Fe3O4 Nanoparticles, Sci. Rep., 2018, 8(1), 5092, DOI:10.1038/s41598-018-23456-6.
- G. F. Goya, T. S. Berquó, F. C. Fonseca and M. P. Morales, Static and Dynamic Magnetic Properties of Spherical Magnetite Nanoparticles, 2003, DOI:10.1063/1.1599959.
- P. Piekarz, K. Parlinski and A. M. Oleś, Mechanism of the Verwey Transition in Magnetite, Phys. Rev. Lett., 2006, 97(15), 156402, DOI:10.1103/PhysRevLett.97.156402.
- L. R. Bickford, The Low Temperature Transformation in Ferrites, Rev. Mod. Phys., 1953, 25(1), 75, DOI:10.1103/RevModPhys.25.75.
- A. Vansteenkiste, J. Leliaert, M. Dvornik, M. Helsen, F. Garcia-Sanchez and B. Van Waeyenberge, The Design and Verification of MuMax3, AIP Adv., 2014, 4(10), 107133, DOI:10.1063/1.4899186.
- A. Vansteenkiste and B. Van de Wiele, MUMAX: A New High-Performance Micromagnetic Simulation Tool, J. Magn. Magn. Mater., 2011, 323(21), 2585–2591, DOI:10.1016/J.JMMM.2011.05.037.
- R. D. McMichael and B. B. Maranville, Edge Saturation Fields and Dynamic Edge Modes in Ideal and Nonideal Magnetic Film Edges, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74(2), 024424, DOI:10.1103/PhysRevB.74.024424.
- C. A. F. Vaz, C. Athanasiou, J. A. C. Bland and G. Rowlands, Energetics of Magnetic Ring and Disk Elements: Uniform versus Vortex State, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(5), 054411, DOI:10.1103/PhysRevB.73.054411.
- D. Goll, S. MacKe, A. E. Berkowitz and H. N. Bertram, Magnetic Ground States and the Role of Vortices in Ferromagnetic Hollow Nanospheres, Phys. B, 2006, 372(1–2), 282–285, DOI:10.1016/J.PHYSB.2005.10.067.
- G. Niraula, J. A. H. Coaquira, G. Zoppellaro, B. M. G. Villar, F. Garcia, A. F. Bakuzis, J. P. F. Longo, M. C. Rodrigues, D. Muraca, A. I. Ayesh, F. S. M. Sinfrônio, A. S. Menezes, G. F. Goya and S. K. Sharma, Engineering Shape Anisotropy of Fe3O4-γ-Fe2O3 Hollow Nanoparticles for Magnetic Hyperthermia, ACS Appl. Nano Mater., 2021, 4(3), 3148–3158, DOI:10.1021/ACSANM.1C00311.
- B. D. Cullity and C. D. G., Introduction to Magnetic Materials -Cap 6 FERRIMAGNETISM, IEEE press Wiely, 2009 Search PubMed.
- E. J. Elzinga and D. L. Sparks, Phosphate Adsorption onto Hematite: An in Situ ATR-FTIR Investigation of the Effects of PH and Loading Level on the Mode of Phosphate Surface Complexation, J. Colloid Interface Sci., 2007, 308(1), 53–70, DOI:10.1016/j.jcis.2006.12.061.
- X. Zhu, P. Grütter, V. Metlushko and B. Ilic, Magnetic Force Microscopy Study of Electron-Beam-Patterned Soft Permalloy Particles: Technique and Magnetization Behavior, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66(2), 024423, DOI:10.1103/PhysRevB.66.024423.
- X. Zhu, P. Grütter, V. Metlushko, Y. Hao, F. J. Castaño, C. A. Ross, B. Ilic and H. I. Smith, Construction of Hysteresis Loops of Single Domain Elements and Coupled Permalloy Ring Arrays by Magnetic Force Microscopy, J. Appl. Phys., 2003, 93(10), 8540, DOI:10.1063/1.1540129.
- J. E. Bonevich, K. Harada, T. Matsuda, H. Kasai, T. Yoshida, G. Pozzi and A. Tonomura, Electron Holography Observation of Vortex Lattices in a Superconductor, Phys. Rev. Lett., 1993, 70(19), 2952, DOI:10.1103/PhysRevLett.70.2952.
- S. Hasegawa, T. Matsuda, J. Endo, N. Osakabe, M. Igarashi, T. Kobayashi, M. Naito, A. Tonomura and R. Aoki, Magnetic-Flux Quanta in Superconducting Thin Films Observed by Electron Holography and Digital Phase Analysis, Phys. B, 1991, 43(10), 7631–7650, DOI:10.1103/PHYSREVB.43.7631.
- P. A. Midgley and R. E. Dunin-Borkowski, Electron Tomography and Holography in Materials Science, Nat. Mater., 2009, 8(4), 271–280, DOI:10.1038/nmat2406.
- C. Gatel, F. J. Bonilla, A. Meffre, E. Snoeck, B. Warot-Fonrose, B. Chaudret, L. M. Lacroix and T. Blon, Size-Specific Spin Configurations in Single Iron Nanomagnet: From Flower to Exotic Vortices, Nano Lett., 2015, 15(10), 6952–6957, DOI:10.1021/ACS.NANOLETT.5B02892.
- Z. Li, J. Su, S. Z. Lin, D. Liu, Y. Gao, S. Wang, H. Wei, T. Zhao, Y. Zhang, J. Cai and B. Shen, Field-Free Topological Behavior in the Magnetic Domain Wall of Ferrimagnetic GdFeCo, Nat. Commun., 2021, 12(1), 1–7, DOI:10.1038/s41467-021-25926-4.
- A. Kohn, A. Habibi and M. Mayo, Experimental Evaluation of the ‘Transport-of-Intensity’ Equation for Magnetic Phase Reconstruction in Lorentz Transmission Electron Microscopy, Ultramicroscopy, 2016, 160, 44–56, DOI:10.1016/J.ULTRAMIC.2015.09.011.
- C. Phatak, A. K. Petford-Long and M. De Graef, Three-Dimensional Study of the Vector Potential of Magnetic Structures, Phys. Rev. Lett., 2010, 104(25), 253901, DOI:10.1103/PHYSREVLETT.104.253901.
- A. Kohn, A. K. Petford-Long and T. C. Anthony, Magnetic Potential in Patterned Materials Determined Using Energy-Dependent Lorentz Phase Microscopy, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72(1), 014444, DOI:10.1103/PHYSREVB.72.014444.
- M. De Graef and Y. Zhu, Quantitative Noninterferometric Lorentz Microscopy, J. Appl. Phys., 2001, 89(11), 7177, DOI:10.1063/1.1355337.
- A. R. Muxworthy and W. Williams, Critical Single-Domain/Multidomain Grain Sizes in Noninteracting and Interacting Elongated Magnetite Particles: Implications for Magnetosomes, J. Geophys Res. Solid Earth, 2006, 111(B12), 12, DOI:10.1029/2006JB004588.
- P. O. Jubert and R. Allenspach, Analytical Approach to the Single-Domain-to-Vortex Transition in Small Magnetic Disks, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70(14), 144402, DOI:10.1103/PhysRevB.70.144402.
- K. Y. Guslienko, V. Novosad, Y. Otani, H. Shima and K. Fukamichi, Field Evolution of Magnetic Vortex State in Ferromagnetic Disks, Appl. Phys. Lett., 2001, 78(24), 3848–3850, DOI:10.1063/1.1377850.
- K. Y. Guslienko and K. L. Metlov, Evolution and Stability of a Magnetic Vortex in a Small Cylindrical Ferromagnetic Particle under Applied Field, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63(10), 4, DOI:10.1103/PhysRevB.63.100403.
- K. Y. Guslienko, W. Scholz, R. W. Chantrell and V. Novosad, Vortex-State Oscillations in Soft Magnetic Cylindrical Dots, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71(14), 144407, DOI:10.1103/PhysRevB.71.144407.
- X. L. Liu, Y. Yang, C. T. Ng, L. Y. Zhao, Y. Zhang, B. H. Bay, H. M. Fan and J. Ding, Magnetic Vortex Nanorings: A New Class of Hyperthermia Agent for Highly Efficient In Vivo Regression of Tumors, Adv. Mater., 2015, 27(11), 1939–1944, DOI:10.1002/adma.201405036.
- O. Kazakova, M. Hanson, A. M. Blixt and B. Hjörvarsson, Domain Structure of Circular and Ring Magnets, J. Magn. Magn. Mater., 2003, 258–259, 348–351, DOI:10.1016/S0304-8853(02)01057-0.
- A. Subramani, D. Geerpuram, A. Domanowski, V. Baskaran and V. Metlushko, Vortex State in Magnetic Rings, Phys. C: Supercond., 2004, 404(1–4), 241–245, DOI:10.1016/J.PHYSC.2003.11.044.
- J. P. Shepherd, J. W. Koenitzer, R. Aragn, J. Spalek and J. M. Honig, Heat Capacity and Entropy of Nonstoichiometric Magnetite Fe3(1-)O4: The Thermodynamic Nature of the Verwey Transition, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43(10), 8461–8471, DOI:10.1103/PhysRevB.43.8461.
- N. Guigue-Millot, N. Keller and P. Perriat, Evidence for the Verwey Transition in Highly Nonstoichiometric Nanometric Fe-Based Ferrites, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64(1), 124021–124024, DOI:10.1103/PhysRevB.64.012402.
- J. Santoyo Salazar, L. Perez, O. De Abril, L. Truong Phuoc, D. Ihiawakrim, M. Vazquez, J. M. Greneche, S. Begin-Colin and G. Pourroy, Magnetic Iron Oxide Nanoparticles in 10-40 Nm Range: Composition in Terms of Magnetite/Maghemite Ratio and Effect on the Magnetic Properties, Chem. Mater., 2011, 23(6), 1379–1386, DOI:10.1021/cm103188a.
- G. Muscas, G. Concas, C. Cannas, A. Musinu, A. Ardu, F. Orrù, D. Fiorani, S. Laureti, D. Rinaldi, G. Piccaluga and D. Peddis, Magnetic Properties of Small Magnetite Nanocrystals, J. Phys. Chem. C, 2013, 117(44), 23378–23384, DOI:10.1021/jp407863s.
- H. Qiu, L. Pan, L. Li, H. Zhu, X. Zhao, M. Xu, L. Qin and J. Q. Xiao, Microstructure and Magnetic Properties of Magnetite Thin Films Prepared by Reactive Sputtering, J. Appl. Phys., 2007, 102(11), 113913, DOI:10.1063/1.2817644.
- N. A. Usov, M. S. Nesmeyanov and V. P. Tarasov, Magnetic Vortices as Efficient Nano Heaters in Magnetic Nanoparticle Hyperthermia, Sci. Rep., 2018, 8(1), 1224, DOI:10.1038/s41598-017-18162-8.
- X. Liu, J. Zheng, W. Sun, X. Zhao, Y. Li, N. Gong, Y. Wang, X. Ma, T. Zhang, L. Y. Zhao, Y. Hou, Z. Wu, Y. Du, H. Fan, J. Tian and X. J. Liang, Ferrimagnetic Vortex Nanoring-Mediated Mild Magnetic Hyperthermia Imparts Potent Immunological Effect for Treating Cancer Metastasis, ACS Nano, 2019, 13(8), 8811–8825, DOI:10.1021/ACSNANO.9B01979.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00433c |
| This journal is © The Royal Society of Chemistry 2023 |