Novel two-dimensional Janus β-Ge₂XY (X/Y = S, Se, Te) structures: first-principles examinations

Abstract

Two-dimensional (2D) structures can stably exist in different allotropes. In this manuscript, we propose a new series of Janus structures based on the β-phase of germanium monochalcogenides, namely, β-Ge₂XY (X/Y = S, Se, and Te) monolayers. Our calculations indicate that Janus β-Ge₂XY monolayers have a stable crystal structure and possess anisotropic mechanical properties. At the ground state, β-Ge₂XY monolayers are semiconductors with a large bandgap and their electronic properties depend strongly on a biaxial strain. Strains not only change the bandgap but can also lead to a change in the bandgap characteristic, namely transitions from indirect to direct bandgap. Our findings not only introduce a new structure of germanium chalcogenide compounds but also show that they have superior physical properties suitable for applications in nanoelectronics.

---

1 Introduction

Two-dimensional (2D) nanomaterials have become a major issue of interest in the materials research community since the discovery of graphene.¹ With outstanding physical properties, graphene is expected to greatly contribute to the creation of a new generation of high-performance electronic and optoelectronic devices.^2,3 In parallel with the study of the mechanical and physical properties of graphene, the search for 2D graphene-like structures has been intensely promoted. As a result, the 2D family is constantly expanding with a series of new materials that have been successfully synthesized in recent times, namely silicene,⁴ transition metal dichalcogenides,⁵ and post-transition metal monochalcogenide compounds.⁶ Among them, group IV monochalcogenides are of particular interest due to their extraordinary physical features, environmental friendliness, and potential applications in new technologies.⁷

The physical features of 2D layered materials depend greatly on the number of atomic sublayers, stacking configuration, and especially their symmetric group. Along with the discovery of new materials, the search for different allotropes of existing materials is also of interest to scientists. Xu et al. have shown that group IV monochalcogenide compounds can stably exist in different structural phases, including α and β phases.⁸ Moreover, the γ-phase of group IV monochalcogenides (γ-GeSe) has been experimentally released recently.⁹ It has been indicated that, with different symmetry structures, the physical properties of phases of group IV monochalcogenides are significantly different.^8,10,11 Particularly, β-GeSe exhibits extremely high electron mobility, up to 2.93 × 10⁴ cm² V⁻¹ s⁻¹,⁸ which is suitable for nanoelectronic applications.

The Janus vertical asymmetric structures of 2D materials have been successfully synthesized experimentally.^12,13 The successful fabrication of Janus materials by atomic layer substitution has opened up great opportunities for creating many new materials with fascinating physical properties.^14,15 With the absence of mirror symmetry, Janus structures exhibit many new and outstanding physical properties that are not available to symmetric structures, such as the appearance of in-built electric fields¹⁶ or high out-of-plane piezoelectricity.¹⁷ With their outstanding physical properties, Janus asymmetrical structures have attracted special attention in recent times. Huang et al. indicated that Janus group-III monochalcogenide monolayers are perfect candidates for photocatalytic applications.¹⁸ In particular, Seixas showed that Janus structures created from the α-phase of group IV monochalcogenide materials have many physical properties that are superior to those of their original symmetric structures.¹⁹

Stimulated by the development trend of 2D Janus materials as above, in this study, we propose a series of Janus structures β-Ge₂XY (X/Y = S, Se, Te) and thoroughly investigate their crystal structures, stability, mechanical features, and electronic characteristics based on the density functional theory (DFT) method. We first focus on structural stabilities through the calculations for the phonon spectrum and other stability tests. The electronic properties and the effects of mechanical strains on the electronic characteristics have been investigated thoroughly and systematically in this paper.

2 Methodology

The DFT calculations in this paper were carried out using the Vienna ab initio simulation package,^20,21 using a plane-wave basis set with an energy cut-off of 500 eV to extend the Kohn–Sham orbitals. The projector augmented wave (PAW) approximation²² parameterized by Perdew, Burke, and Ernzerhof (PBE)²³ was selected to describe the exchange–correlation potential. Besides, the energy gaps of the studied structures were also corrected by using the Heyd–Scuseria–Ernzerhof (HSE06) functional.²⁴ We used the DFT-D3 method²⁵ to describe the van der Waals in the studied layered-structures. The first Brillouin zone (BZ) was sampled by a 15 × 15 × 1 k-point grid. The threshold for forces and energy in the structural relaxation is selected to be 1 × 10⁻³ eV Å⁻¹ and 1 × 10⁻⁶ eV, respectively. The phonon dispersions were carried out by using finite displacement approximation through the PHONOPY package.²⁶ We used ab initio molecular dynamics (AIMD) calculations with the canonical ensemble to test the thermodynamical stability of the studied structures.²⁷

3 Results and discussion

3.1 Crystal lattice and structural stabilities

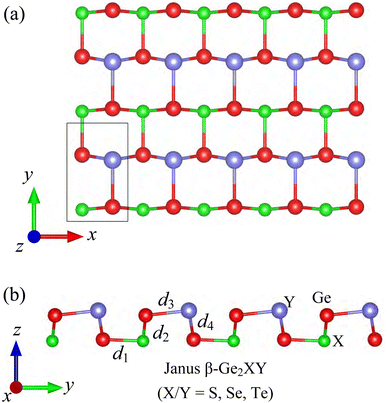
The crystal structures of Janus β-Ge₂XY (X/Y = S, Se, and Te) monolayers are shown in Fig. 1. The optimized lattice parameters of β-Ge₂XY are tabulated in Table 1. The shortest lattice constants a and b (along the x and y axes, respectively) are found for β-Ge₂SSe being 3.55 Å and 5.79 Å, respectively, while those of β-Ge₂STe and β-Ge₂SeTe are found to be higher. This results from the increase of ionic radii in the order of S, Se, and Te. The crystal structure of Janus β-Ge₂XY is highly anisotropic. However, the anisotropic ratio b/a for all three structures is almost the same despite the large difference between their lattice constants. It is calculated that the anisotropic ratio of β-Ge₂XY is about 1.6 as listed in Table 1. The anisotropic ratio of β-Ge₂XY is much higher than that of α-Ge₂XY.²⁸ The cation–cation bond lengths d are also scrutinized and listed in Table 1. The Ge–X bond length d₁ and Ge–Y bond length d₃ follow a similar trend of lattice constant when the atomic size of the chalcogen elements increases.

Fig. 1 (a) Top and (b) side views of crystal structures of β-Ge₂XY (X = S, Se, Te) monolayers.

Table 1 Lattice constants a and b (Å), cation–cation bond length d (Å), monolayer thickness Δh (Å), anisotropic ratio b/a cohesive energy E_coh (eV per atom), and elastic constants C_ij (N m⁻¹) of β-Ge₂XY monolayers

	a	b	d 1	d 2	d 3	d 4	Δh	b/a	E coh	C 11	C 12	C 22	C 66
β-Ge2SSe	3.55	5.79	2.42	2.54	2.53	2.69	1.79	1.63	−4.45	40.34	5.83	41.55	7.47
β-Ge2STe	3.71	6.03	2.44	2.52	2.73	2.91	1.95	1.63	−4.25	33.97	5.68	41.95	4.25
β-Ge2SeTe	3.77	6.08	2.69	2.56	2.92	2.72	2.04	1.61	−4.10	35.42	3.82	28.20	4.24

---

We next calculate the cohesive energy E_coh to evaluate the energetic stability and also the chemical bond strength in the studied monolayers. The cohesive energy can be written as

where E_tot indicates the total energy of the β-Ge₂XY monolayer; E_Ge, E_X, and E_Y are the energies of the single element Ge, X, and Y, respectively; N_Ge, N_X, N_Y, and E_Ge, E_X, E_Y refer respectively to the numbers of Ge, X, and Y atoms in the unitcell. The obtained values for E_coh of the β-Ge₂XY are also shown in Table 1. All three studied materials possess negative cohesive energies, demonstrating that they are energetically favorable. The high E_coh values indicate the strong intra-molecular bonds of β-Ge₂XY.

To check the structural stabilities, we first evaluate the phonon spectra of the investigated materials as presented in Fig. 2(a). The phonon spectra of β-Ge₂XY have 12 vibrational modes because their primitive cell contains four atoms as depicted in Fig. 1(a). The patterns of the phonon dispersion curves of all three structures are found to be similar. No negative frequencies exist throughout the Brillouin zone, implying that the studied materials are dynamically stable. In addition, we also carry out the AIMD simulations to evaluate the thermal stability. The AIMD calculations are performed within 8 ps (a time step of 1 fs) at 500 K. We present the total energy fluctuation to simulation time of the β-Ge₂XY at 500 K in Fig. 2(b). It is indicated that the total energies of β-Ge₂XY monolayers fluctuate slightly during the 8 ps AIMD simulation. No structural transitions nor breaking of chemical bonds in the studied materials after the test reveal that they have good thermal structural integrity at 500 K.

Fig. 2 Phonon spectra (a) and fluctuation of the total energies to simulation time at 500 K by AIMD calculations (b) of β-Ge₂XY monolayers.

We also evaluate the mechanical stability of the studied systems based on considering the elastic constants C_ij. Here, the standard Voigt notation for C_ij is utilized. For the 2D structure, C₁₁, C₁₂, C₂₂, and C₆₆ are four independent coefficients that should be calculated. The calculations for C_ij in the present study are based on the method suggested by Duerloo and co-workers.²⁹ The in-plane stiffness coefficients can be calculated by parabolic fitting the uniaxial strain-dependent elastic energies of the examined materials.²⁹ We here apply uniaxial strains from −2% to +2% in 0.5% increments along the two x- and y-directions. This method has been successfully used to evaluate the elastic constants of the similar 2D structures.^29–31

The obtained results for C_ij of β-Ge₂XY are also presented in Table 1. It is found that all four independent stiffness coefficients C_ij are positive and also satisfy the condition of C₁₁C₂₂ > C₁₂².^32,33 It implied that they meet Born–Huang's elastic stability conditions, demonstrating that the investigated materials are mechanically stable. From the obtained elastic constants C_ij, the directional dependent Young's modulus Y_2D and Poisson's ratio ν (indicated by angle α) can be given by:^34,35

where μ = sin α, ν = cos α, and Δ = (C₁₁C₂₂ − C₁₂²)/C₆₆. α denotes the angle formed by the armchair axis and the considered direction.

The calculated Y_2D(α) and P(α) of β-Ge₂XY are presented in Fig. 3. It is demonstrated that Y_2D(α) and P(α) of the examined materials are strongly directional anisotropic due to their lattice anisotropy. From Fig. 3(a), we can see that β-Ge₂SSe and β-Ge₂STe exhibit the highest Y_2D along the direction corresponding to α = 90°. Meanwhile, the maximum Young's modulus of β-Ge₂SeTe is found at α = 0°. This is due to the large difference in the chemical bond length between Ge–Te and Ge–S. The calculated values for the highest Young's modulus of β-Ge₂SSe and β-Ge₂STe are found to be 40.71 and 40.90 N m⁻¹, respectively. However, the difference between Y_2D(90°) and Y_2D(0°) for β-Ge₂SSe is very small. The obtained value for Y_2D(0°) of β-Ge₂SSe is 39.52 N m⁻¹. Young's modulus of β-Ge₂XY is minimum at α = 45° and α = 135°. The Y_2D of β-Ge₂XY is comparable with that of α group IV monochalcogenides³⁶ and their Janus structures.^37,38 The directional anisotropy of Poisson's ratio is also shown in Fig. 3(b).

Fig. 3 Polar diagrams of Young's modulus Y_2D(α) (a) and Poisson's ratio P(α) (b) for β-Ge₂XY monolayers.

3.2 Electronic properties

We here use the band structures and weighted bands to investigate the electronic features of the studied Janus materials. The calculated band diagrams of β-Ge₂XY monolayers are presented in Fig. 4, at both PBE and HSE06 levels. Our calculated results indicate that β-Ge₂XY monolayers exhibit semiconducting characteristics with an indirect bandgap. At the PBE level, the bandgaps of β-Ge₂SSe, β-Ge₂STe, and β-Ge₂SeTe are found to be 1.72, 1.04, and 1.15 eV, respectively. For comparison, the bandgap of β-Ge₂XY is wider than that of α-Ge₂XY, including α-Ge₂SSe (1.32 eV), α-Ge₂SSe (0.97 eV), and α-Ge₂SSe (0.88 eV).¹⁹ To correct the bandgaps of the studied materials, we also plot the band structures by using the HSE06 functional as also shown in Fig. 4. Our calculated results indicate that, near the Fermi level, the HSE06 band diagrams are similar profiles to the PBE band structures. However, there is an important difference that needs to be mentioned, which is that β-Ge₂STe is a direct semiconductor with both the CBM and VBM located at the S point at the HSE06 level as presented in Fig. 4(b). It should also be emphasized that, at the HSE06 level, the difference in energy between the CBM and minimum energy of the conduction band on the Y–Γ line of β-Ge₂STe is not very small. The obtained results demonstrate that, at the HSE06 level, meanwhile β-Ge₂STe exhibits direct semiconducting characteristics with a bandgap of 1.53 eV, β-Ge₂SSe and β-Ge₂SeTe monolayers are indirect semiconductors with bandgaps of 2.44 and 1.67 eV, respectively. The HSE06 band gap is much wider than those evaluated by the PBE approach.

Fig. 4 Band structures of β-Ge₂SSe (a), β-Ge₂Ste (b), and β-Ge₂SeTe (c) calculated using the PBE/HSE06 functional.

To get inside the nature of the formation of electronic structures, we studied the weighted band structures of β-Ge₂XY monolayers as shown in Fig. 5. The obtained results show that the weighted bands of the studied monolayers are quite similar. The conduction band minimum (CBM) is formed from the contribution mainly from the p-orbitals of Ge atoms while the p-orbitals of Y atoms make a major contribution to the valence band maximum (VBM). The contribution of the p-orbitals of the chalcogen atoms X and Y to the valence band is significant. Meanwhile, the contributions of the p-orbitals of Ge atoms to the conduction band are more prominent in comparison with other orbitals of all compound constituents.

Fig. 5 The PBE weighted bands of β-Ge₂Sse (a), β-Ge₂Ste (b), and β-Ge₂SeTe (c).

The physical features of nanostructured materials are susceptible to change under the influence of external conditions such as mechanical strains, pressure, or doping. Pereira and co-workers showed that mechanical strain changed the hopping energy and consequently changed the electronic characteristics of the material significantly.³⁹ The change in the crystal structure can give rise to many new physical features in 2D structures. Here, we evaluate the effects of biaxial strains ε_b on the band structure characteristics of the studied monolayers based on the DFT calculations. Quantitatively, we define the biaxial strain as ε_b = (δ – δ₀)/δ₀, where δ₀ and δ are the lengths of the computed cell before and after strain. In our calculations, the biaxial strain ranging from 0 to ±6% is applied to evaluate the effect of the biaxial strain on the energy band structure of the material. To confirm the stability of the crystal structures under strain, the crystal structures of strained β-Ge₂XY monolayers at ε_b = −6% and ε_b = +6% are studied by the AIMD simulations within 5 ps at 500 K as shown in Fig. 6. It is found that no structural transitions nor chemical bonds are breaking in the examined strained structures. In Fig. 7, we show the HSE06 band diagrams of β-Ge₂XY monolayers under various values of ε_b. It is shown that the band structures of β-Ge₂XY monolayers depend highly on the applied biaxial strain ε_b. While the strain does not change the indirect semiconductor characteristics of β-Ge₂Sse, the CBM of β-Ge₂Ste and β-Ge₂SeTe is shifted towards the Γ–X path when the compressive strain is introduced. As a result, the β-Ge₂STe monolayer becomes the direct bandgap semiconductor with both the CBM and VBM located at the S-point when the tensile strain (ε_b > 0) is applied as shown in Fig. 7(b). Meanwhile, the tensile strain is the cause of the indirect–direct bandgap transition in β-Ge₂SeTe as shown in Fig. 7(c). The strain not only drastically moves the CBM position, which leads to the indirect-to-direct bandgap transition, but also significantly changes the bandgap of all the examined materials. The dependence of the bandgap of β-Ge₂XY monolayers on ε_b is depicted in Fig. 8. It is found that the graph showing the strain-dependence of the bandgap of the examined structures is of the same form. While the bandgap of monolayers changes slightly in the presence of tensile strain, compressive strain rapidly reduces their bandgap as depicted in Fig. 8.

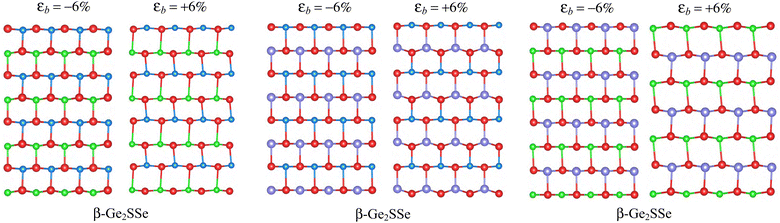Fig. 6 Crystal structures of strained β-Ge₂XY at ε_b = −6% and ε_b = +6% after 5 ps at 500 K by AIMD simulations.

Fig. 7 Band structures of (a) β-Ge₂SSe, (b) β-Ge₂STe, and (c) β-Ge₂SeTe monolayers at various values of ε_b.

Fig. 8 Dependence of bandgaps of β-Ge₂XY on biaxial strain ε_b. The filled and empty symbols indicate the indirect and direct bandgaps, respectively.

4 Conclusive remarks

We have constructed and examined the structural, mechanical, and electronic characteristics of a series of novel Janus structures β-Ge₂XY based on the DFT calculations. β-Ge₂XY materials have been predicted to be stable and they are promising to be experimentally synthesized. Our calculated results have indicated that β-Ge₂XY materials possess highly anisotropic mechanical characteristics due to their anisotropic crystal structures. All of these proposed 2D Janus structures are semiconductors with an indirect energy bandgap. The electronic characteristics of β-Ge₂XY monolayers can be easily modulated by mechanical strains and in particular phase transitions can be found at some suitable values of strain. The obtained results not only introduce novel Janus materials but also show that they have attractive physical properties with potential applications in nanoelectronics.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This research is funded by the Vietnam Ministry of Education and Training under Grant No. B2023.DNA.23.

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666.
2. K. S. Novoselov, D. Jiang, F. Schedin, T. J. Booth, V. V. Khotkevich, S. V. Morozov and A. K. Geim, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10451–10453.
3. N. A. Poklonski, S. A. Vyrko, A. I. Siahlo, O. N. Poklonskaya, S. V. Ratkevich, N. N. Hieu and A. A. Kocherzhenko, Mater. Res. Express, 2019, 6, 042002.
4. B. Lalmi, H. Oughaddou, H. Enriquez, A. Kara, S. Vizzini, B. Ealet and B. Aufray, Appl. Phys. Lett., 2010, 97, 223109.
5. J. N. Coleman, M. Lotya, A. O'Neill, S. D. Bergin, P. J. King, U. Khan, K. Young, A. Gaucher, S. De, R. J. Smith, I. V. Shvets, S. K. Arora, G. Stanton, H.-Y. Kim, K. Lee, G. T. Kim, G. S. Duesberg, T. Hallam, J. J. Boland, J. J. Wang, J. F. Donegan, J. C. Grunlan, G. Moriarty, A. Shmeliov, R. J. Nicholls, J. M. Perkins, E. M. Grieveson, K. Theuwissen, D. W. McComb, P. D. Nellist and V. Nicolosi, Science, 2011, 331, 568.
6. P. Hu, Z. Wen, L. Wang, P. Tan and K. Xiao, ACS Nano, 2012, 6, 5988.
7. C. Chowdhury, S. Karmakar and A. Datta, J. Phys. Chem. C, 2017, 121, 7615–7624.
8. Y. Xu, H. Zhang, H. Shao, G. Ni, J. Li, H. Lu, R. Zhang, B. Peng, Y. Zhu, H. Zhu and C. M. Soukoulis, Phys. Rev. B, 2017, 96, 245421.
9. S. Lee, J.-E. Jung, H. g. Kim, Y. Lee, J. M. Park, J. Jang, S. Yoon, A. Ghosh, M. Kim, J. Kim, W. Na, J. Kim, H. J. Choi, H. Cheong and K. Kim, Nano Lett., 2021, 21, 4305–4313.
10. L. Xu, M. Yang, S. J. Wang and Y. P. Feng, Phys. Rev. B, 2017, 95, 235434.
11. V. V. Tuan, A. A. Lavrentyev, O. Y. Khyzhun, N. T. T. Binh, N. V. Hieu, A. I. Kartamyshev and N. N. Hieu, Phys. Chem. Chem. Phys., 2022, 24, 29064–29073.
12. A.-Y. Lu, H. Zhu, J. Xiao, C.-P. Chuu, Y. Han, M.-H. Chiu, C.-C. Cheng, C.-W. Yang, K.-H. Wei, Y. Yang, Y. Wang, D. Sokaras, D. Nordlund, P. Yang, D. A. Muller, M.-Y. Chou, X. Zhang and L.-J. Li, Nat. Nanotechnol., 2017, 12, 744.
13. J. Zhang, S. Jia, I. Kholmanov, L. Dong, D. Er, W. Chen, H. Guo, Z. Jin, V. B. Shenoy, L. Shi and J. Lou, ACS Nano, 2017, 11, 8192–8198.
14. Z. Guan and S. Ni, Nanoscale, 2020, 12, 22735–22742.
15. Z. Guan, S. Ni and S. Hu, J. Phys. Chem. C, 2018, 122, 6209–6216.
16. C.-F. Fu, J. Sun, Q. Luo, X. Li, W. Hu and J. Yang, Nano Lett., 2018, 18, 6312–6317.
17. T. V. Vu, H. V. Phuc, A. I. Kartamyshev and N. N. Hieu, Appl. Phys. Lett., 2023, 122, 061601.
18. A. Huang, W. Shi and Z. Wang, J. Phys. Chem. C, 2019, 123, 11388.
19. L. Seixas, J. Appl. Phys., 2020, 128, 045115.
20. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
21. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
22. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
23. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
24. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207.
25. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
26. A. Togo, L. Chaput and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094306.
27. S. Nosé, J. Chem. Phys., 1984, 81, 511.
28. Y. Zhu, X. Wang and W. Mi, Phys. E, 2020, 117, 113802.
29. K.-A. N. Duerloo, M. T. Ong and E. J. Reed, J. Phys. Chem. Lett., 2012, 3, 2871–2876.
30. W.-Z. Xiao, G. Xiao and L.-L. Wang, J. Chem. Phys., 2016, 145, 174702.
31. Y. Guo, S. Zhou, Y. Bai and J. Zhao, Appl. Phys. Lett., 2017, 110, 163102.
32. F. Mouhat and F.-X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104.
33. Z. j. Wu, E. j. Zhao, H. p. Xiang, X. f. Hao, X. j. Liu and J. Meng, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054115.
34. N. T. Hung, A. R. T. Nugraha and R. Saito, J. Phys. D: Appl. Phys., 2018, 51, 075306.
35. P. Xiang, S. Sharma, Z. M. Wang, J. Wu and U. Schwingenschlögl, ACS Appl. Mater. Interfaces, 2020, 12, 30731.
36. L. C. Gomes, A. Carvalho and A. H. Castro Neto, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 214103.
37. K. Cheng, W. Hu, X. Guo, L. Wu, S. Guo and Y. Su, Phys. Chem. Chem. Phys., 2023, 25, 5663–5672.
38. K. D. Pham, RSC Adv., 2021, 11, 36682–36688.
39. V. M. Pereira, A. H. Castro Neto and N. M. R. Peres, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 045401.

---