Second-order Jahn–Teller effect induced high-temperature ferroelectricity in two-dimensional NbO₂X (X = I, Br)

Abstract

Based on the first-principles calculations, we investigated the ferroelectric properties of two-dimensional (2D) materials NbO₂X (X = I, Br). Our cleavage energy analysis shows that exfoliating one NbO₂I monolayer from its existing bulk counterpart is feasible. The phonon spectrum and molecular dynamics simulations confirm the dynamic and thermal stability of the monolayer structures for both NbO₂I and NbO₂Br. Total energy calculations show that the ferroelectric phase is the ground state for both materials, with the calculated in-plane ferroelectric polarizations being 384.5 pC m⁻¹ and 375.2 pC m⁻¹ for monolayers NbO₂I and NbO₂Br, respectively. Moreover, the intrinsic Curie temperature T_C of monolayer NbO₂I (NbO₂Br) is as high as 1700 K (1500 K) from Monte Carlo simulation. Furthermore, with the orbital selective external potential method, the origin of ferroelectricity in NbO₂X is revealed as the second-order Jahn–Teller effect. Our findings suggest that monolayers NbO₂I and NbO₂Br are promising candidate materials for practical ferroelectric applications.

---

Introduction

Ferroelectric (FE) materials, which exhibit spontaneous polarization that can be switched by an external electric field, have attracted tremendous research interest over the past decades due to their wide applications in capacitors, sensors, and non-volatile memories.^1–4 In the literature, many efforts have been made to develop perovskite-type oxides, such as BaTiO₃, PbTiO₃, PbZr_1-xTi_xO₃, and La_1/3NbO₃ in which the cations have an electron configuration of d⁰ (Ti⁴⁺, Zr⁴⁺, Nb⁵⁺).^5–8 Moreover, the spontaneous polarization of these compounds is usually induced by off-centering of cations which originates from the second-order Jahn–Teller (SOJT) effect.^9,10 SOJT-active cations have been shown to induce structural distortion, which would break the inversion symmetry, by anisotropic covalent bonding with ligands. Interestingly, the Curie temperature T_c of these compounds is far above room temperature (i.e., the T_c of BaTiO₃, PbTiO₃, PbZr_1−xTi_xO₃, and La_1/3NbO₃ is 393, 763, 659, and 473 K respectively).^11–14 This inspires us to search for high-temperature ferroelectric materials with SOJT-activated cations.

On the other hand, the urgent requirement for the miniaturization of electronic devices stimulates researchers to devote significant effort to reducing the thickness of thin-film ferroelectrics.^15,16 However, the depolarization field will destroy ferroelectricity at critical thicknesses for conventional ferroelectric compounds.¹⁷ Recently, the discovery of ferroelectricity in monolayer or few-layer van der Waals (vdW) materials provides new opportunities for reducing the size of ferroelectric devices to atomic thickness.^18–22 In addition, the weak interlayer interaction and the dangling bond-free surface of two-dimensional (2D) vdW materials make it easy to integrate them with other materials in applications.

Thanks to the development of high-throughput calculations and machine learning methods, plenty of calculations have been proposed to predict promising 2D ferroelectric materials. However, only a few dozens of them have been confirmed by experiments.^13,14 The most intuitive strategy for designing new 2D ferroelectric materials is to use the structure of existing 2D ferroelectric materials in the databases as a prototype and then test different combinations of chemical elements. To date, only tens of prototypes, like CuInP₂S₆ type,^15,16 SnTe type,^17,18 α-In₂Se₃ type,^19,20 1T′-MoTe₂ type,^21,22 sliding ferroelectrics and so on, are proposed theoretically and experimentally. Another strategy is to design new prototypes of 2D ferroelectric structures. Investigating the cation off-centring induced by the SOJT effect may provide insight into the design of new 2D ferroelectric structure prototypes.

In this work, we propose a new 2D ferroelectric structure prototype whose structural distortion is induced by the SOJT effect. Using first-principles calculations, we comprehensively investigate the ferroelectric properties of monolayer NbO₂I cleaved from its existing bulk counterpart. Total energy calculations show that the ferroelectric phase is the ground state with an in-plane ferroelectric polarization of 384.5 pC m⁻¹, and the intrinsic Curie temperature T_c as high as 1700 K. Moreover, with the orbital selective external potential (OSEP) method,²³ we reveal that the SOJT effect originates ferroelectricity in NbO₂I. The finite indirect band gap is about 0.95 eV, which indicates that monolayer NbO₂I is a semiconductor. The carrier mobilities of electrons and holes along the two directions are different due to the crystal anisotropy. We also systematically studied the electronic and ferroelectric properties of monolayer NbO₂Br, which has the same structure as NbO₂I with the replacement of I atoms by Br atoms. Our numerical results show that the properties of NbO₂Br are very similar to the ones of NbO₂I.

Calculation methods

All calculations in this work were based on density functional theory (DFT) implemented in the Vienna Ab initio simulation package (VASP).²⁴ The generalized gradient approximation (GGA) with the form proposed by Perdew, Burke, and Ernzerhof (PBE)²⁵ was chosen as the exchange–correlation functional. The Projector Augmented Wave (PAW) method²⁶ was used to describe electron–ion interactions. The vacuum distance was set larger than 30 Å in order to avoid spurious periodic interactions. The kinetic energy cutoff was set to 550 eV, and the first Brillouin zone was sampled with a grid of 17 × 15 × 1 k points according to the Monkhorst–Pack scheme.²⁷ The convergence criteria for electronic and ionic relaxations are 10⁻⁶ eV per atom and 10⁻³ eV Å⁻¹, respectively. van der Waals (vdW) correction was included using the D2 method.²⁸ The electronic contribution to polarization was calculated using the Berry phase method.^29,30. The nudged elastic band (NEB) approach^31,32 was used to simulate the minimum energy path (MEP) and associated energy barriers.

Results and discussion

The bulk NbO₂I material was successfully synthesized experimentally in 2007.³³ The crystal structure of NbO₂I possesses a centrosymmetric space group Pnma with a 7-coordinated Nb⁵⁺ cation and is shown as an example in Fig. 1. Interestingly, 7 ligands of Nb⁵⁺ form a pentagonal bipyramid that is connected via the apical O₁ atoms to chains and via three O₂ atoms to the double-layer structure (Fig. 1(b)). Between these double layers there are only weak van der Waals interactions of I atoms. Two I atoms and three O₂ atoms are on the pentagonal base plane. At the same time, the axial sites are occupied by the O₁ atom with very different Nb–O₁ distances of 1.78 and 2.20 Å, which indicate the shift of Nb⁵⁺ and form the structural distortion which could cause the polarization denoted in Fig. 1(c). However, the other Nb⁵⁺ ion in the double layer shifts to the opposite direction (Fig. 1(a)), and thus the bulk NbO₂I does not exhibit macroscopic polarization. As a comparison, the compound UO₂Br has a crystal structure very similar to NbO₂I except for equal U–O₁ distances and no displacement of the U atom (for details see Fig. S1†).³⁴ Thus, the space group of UO₂Br is Cmcm with inversion symmetry and has only the paraelectric (PE) phase without spontaneous polarization.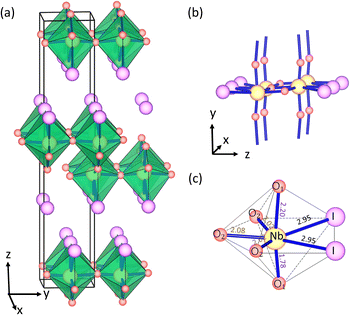

Fig. 1 (a) The layered bulk crystal structure of NbO₂I. (b) The connectivity of the polyhedral in NbO₂I. (c) Coordination polyhedron and bond length of Nb⁵⁺ in NbO₂I.

Because the bulk NbO₂I has a layered structure, it is of much interest to investigate the NbO₂I monolayer for promising ferroelectricity and other valuable properties. We first calculate the cleavage energy to check the accessibility of exfoliation and show the results in Fig. 2(a). The cleavage energy for NbO₂I and NbO₂Br is 0.28 and 0.21 J m⁻², respectively. They are smaller than the one of graphite.³⁵ The smaller cleavage energy means that the exfoliation of NbO₂I and NbO₂Br is feasible. Thus, one layer NbO₂I and NbO₂Br can be exfoliated from their bulk counterparts, as shown in the inset of Fig. 2.

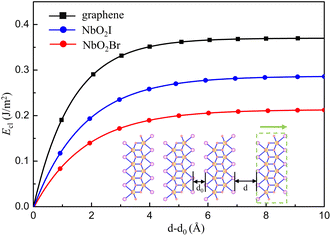Fig. 2 Cleavage energy E_clversus the separation distance d–d₀ in the process of exfoliating one NbO₂X (X = I, Br) layer from their bulk counterparts illustrated by the inset.

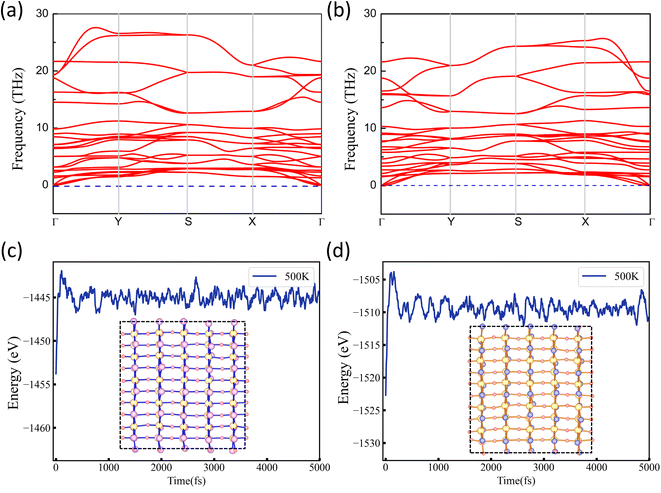
The crystal structure dynamics and thermal stability can be explored by calculating the phonon spectra and molecular dynamics (MD) simulations. The phonon spectra of NbO₂I and NbO₂Br along the high-symmetry lines are plotted in Fig. 4(a) and (b). It is observed that there is no imaginary phonon frequency in the entire Brillouin zone, confirming that NbO₂I and NbO₂Br are dynamically stable. Considering the probability of successful experimental fabrication, the MD simulation of a 5 × 5 supercell at 500 K with 5 ps time is carried out. The results are presented in Fig. 4(c) and (d) for NbO₂I and NbO₂Br, respectively. The MD simulation suggests the thermal stability of the two monolayers. For monolayer NbO₂Br, we systematically search all possible 2D structures with the Nb : O : Br composition equal to 1 : 2 : 1 using the particle swarm optimization (PSO)³⁶ structure search algorithm and first-principles calculations. After comprehensive calculation, we found that there are six most energetically stable structures, as listed in Fig. S2.† However, the most stable structure is still our NbO₂I prototype structure, which again confirms that our NbO₂I monolayer prototype is stable.

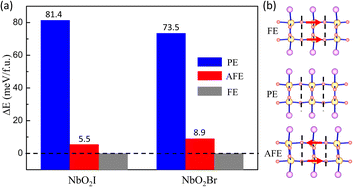
Now we start to explore the ferroelectric properties of monolayers NbO₂I and NbO₂Br. As we analyzed before, Nb⁵⁺ has a displacement from the centre of pentagonal bipyramids, causing the spontaneous polarization. To find the ground state, we set three configurations of Nb⁵⁺ in the monolayer, namely ferroelectric (FE), paraelectric (PE), and antiferroelectric (AFE), as shown by the schematics in Fig. 3(b). The total energies of the three configurations are illustrated in Fig. 3(a), in which we use the energy of FE as a reference energy and set it to zero. We can easily see that the FE state is the ground state, which is totally different from bulk NbO₂I with two Nb⁵⁺ ions in one layer shifting in opposite directions.

Fig. 3 (a) Relative energy per unit cell (in meV) of monolayer NbO₂X (X = I and Br) at different polarization directions and takes the energy of FE as reference. (b) Schematic diagram of different polarization directions, where the direction of the arrow indicates the displacement direction of the Nb atom.

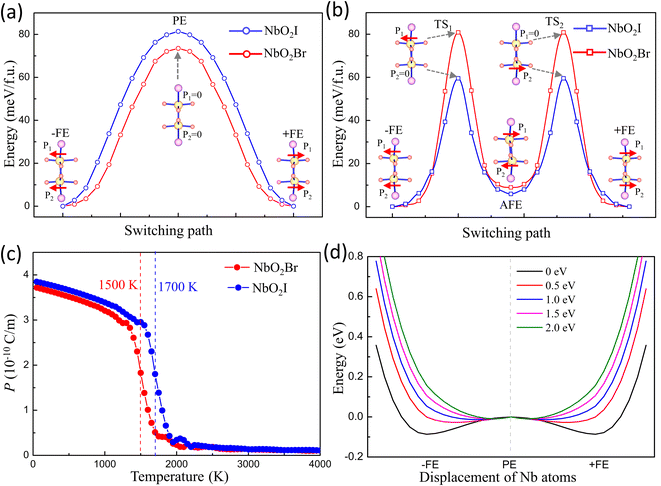
The fully relaxed monolayer structure reveals that the Nb⁵⁺ ion shifts from the centre of pentagonal bipyramids with an unequal bond length with two apical O₁ atoms. The polarization is therefore in the in-plane direction. By using the Berry phase method, the polarization Ps was estimated, with values equal to 384.5 and 375.2 pC m⁻¹ for NbO₂I and NbO₂Br, respectively. The reversal of polarization is realized through a phase transition between two symmetry-equivalent ferroelectric states with opposite Ps. We constructed two potential switching paths and computed the energy evolution using the NEB approach as shown in Fig. 5(a) and (b) in order to explore the polarization switching and the pertinent energy barrier of 2D NbO₂I and NbO₂Br. The PE phase is the intermediate state of the first path, and the AFE phase is the intermediate state of the second path. We discovered that the first path's energy barrier, which uses the PE phase as an intermediate state, is around 80 meV, whereas the second path's energy barrier is 60 meV. As a result, we came to the conclusion that the FE-AFE-FE transformation is possible during the NbO₂I monolayer's ferroelectric switching. However, in the case of the NbO₂Br monolayer, there is a slight difference (7 meV) of the energy barrier between the first and second paths. This indicates a potential transformation path of FE-PE-FE for the NbO₂Br monolayer that differs from the behaviour of the NbO₂I monolayer.

Fig. 4 (a) and (b) Phonon dispersions of the NbO₂X (X = I and Br) monolayer. (c) and (d) Evolution of total energy for the NbO₂I and NbO₂Br monolayers at 500 K from molecular dynamics simulation. Insets present the snapshots at the end of simulations.

Fig. 5 The energy evolution of two polarization switching paths of the FE NbO₂X monolayer in two cases: (a) the transition proceeds through an intermediate PE phase; (b) the intermediate phase during the switching path is the AFE configuration. The inset views display the structures of initial, transition (TS), and final states, where the direction of the red arrow indicates the displacement direction of the Nb atom. (c) Curie temperatures of NbO₂X monolayers using Monte Carlo (MC) simulations. (d) The double-well evolution as the external potential applied on Nb 4d_xy and 4d_xz orbitals.

Ferroelectricity is further emphasized by the Curie temperature above which the macroscopic spontaneous polarization disappears. The effective Hamiltonian of NbO₂I and NbO₂Br supercells is carried out by applying the Landau–Ginzburg phase transition theory (for more details see ESI†). After fitting the parameters of effective Hamiltonian we perform the Monte Carlo simulation to investigate the T_c of 2D NbO₂I and NbO₂Br. The numerical results are shown in Fig. 5(c), and the T_c of the NbO₂I (NbO₂Br) monolayer is as high as 1500 K (1700 K) that again proves that NbO₂X is a stable and robust 2D ferroelectric material.

It is well known that in the local coordinate of a pentagonal bipyramid, the d orbitals will be split into three groups by the crystal field. The d_xz and d_yz orbitals possess the lowest energy. When we transfer to the global coordinate of NbO₂I, the local d_xz and d_yz of Nb⁵⁺ in the pentagonal bipyramid will transfer to d_xy and d_xz. In the following parts, we will discuss the results in the global coordinate. The critical mechanism and feature of the SOJT effect are the hybridization between the empty cation's d orbitals (i.e., Ti⁴⁺, Nb⁵⁺) and occupied anion's p orbitals (i.e., O²⁻, I¹⁻).³⁷ Moreover, Wheeler and Hoffman et al.³⁸ and Kunz and Brown³⁹ pointed out that the magnitude of the distortion of the cation surrounded by its ligands (i.e., TiO₆²⁻, NbO₅I₂ pentagonal bipyramid in this work) attributable to the SOJT effect depends on the strength of hybridization between the empty cation's d orbitals and occupied anion's 2p orbitals.

The density of states of NbO₂I is plotted in Fig. 6(c). The partial density of states (PDOS) clearly shows that both apical O₁-2p and planar O₂-2p orbitals are mainly located between −8 and −1 eV, indicating that the 2p orbitals of apical O₁ and planar O₂ are fully occupied. The I-5p orbitals are mainly distributed from −5 eV to Fermi energy with a narrower bandwidth. The Nb-4d orbitals are located above the Fermi energy with the 4d⁰ configuration. However, there are finite states of 2p_y and 2p_z of apical O₁ distributing between 0.5 and 3 eV, where there are also major contributions from Nb 4d_xy and 4d_xz, which means that there are strong hybridizations between unoccupied Nb 4d_xy and 4d_xz orbitals and occupied apical O₁ 2p_y and 2p_z, indicating the SOJT effect in NbO₂I. The electronic structure of NbO₂Br shown in Fig. 6(d) is very similar to that of NbO₂I. As a result, we will not give a detailed discussion about NbO₂Br.

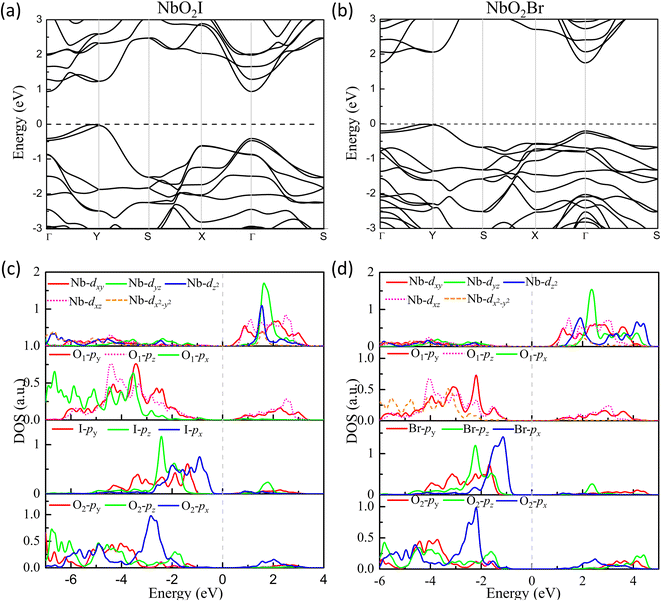Fig. 6 Energy band structures (a) and (b) for FE NbO₂X monolayers. Projected density of states (PDOS) for monolayers (c) NbO₂I and (d) NbO₂Br.

According to our discussion above, if we tune the strength of the hybridization, we can adjust the SOJT effect and further investigate the FE phase transition. Here, we apply the OSEP method by adding an external potential to raise the energy of Nb-4d_xy and 4d_xz orbitals by different values to increase the energy difference between them and O₁ 2p_y and 2p_z. The OSEP approach can introduce an exceptional external potential that only can be felled by certain appointed orbitals.²³ We take the 2 eV potential on Nb-4d_xy and 4d_xz as an example shown in Fig. S7.† The DOS of Nb-4d_xy and 4d_xz is indeed shifted-up by almost 2 eV, which indicates that the OSEP approach can effectively shift the energy of certain selective orbitals. More interestingly, due to a larger energy difference between Nb 4d_xy/4d_xz and O₁ 2p_y/2p_z, the strength of hybridization between them is decreased. One can expect that the SOJT effect induced distortion will disappear and result in a PE ground state instead of FE when hybridization between them vanishes.

Thus, we apply different external potentials on Nb-4d_xy and 4d_xz to study the FE phase transition in NbO₂I. Fig. 5(d) illustrates the results. When the external potential on Nb-4d_xy and 4d_xz rises, the characteristic double well of monolayer NbO₂I becomes shallower and eventually disappears, suggesting that the ground state becomes the PE phase. The same calculation is also carried out for NbO₂Br, and the same behaviour of double well evolution is obtained (shown in Fig. S6†). These results demonstrate that the SOJT effect is the reason for the ferroelectric phase transition.

Regarding the ferroelectricity, the band structure of NbO₂X monolayers is also calculated. Our numerical results demonstrate that both monolayers NbO₂I and NbO₂Br are Indirect bandgap semiconductors with E_g = 0.95 eV and 1.75 eV, respectively. As illustrated in Fig. 4, their valence band maximum (VBM) is near the Y point, while their conduction band minimum (CBM) is at the Γ point. The effective mass at the VBM for NbO₂I is 0.48 m0 along the x axis and 1.37 m₀ along the y axis, and the effective mass at the CBM is 0.44 m₀ along the x axis and 1.18 m₀ along the y axis, where m₀ is the electron mass (for more details see ESI†). Different effective mass values along the two axes show band structure anisotropy, which is caused by crystal structure anisotropy. Interestingly, the carrier mobility of holes is an order of magnitude greater than that of electrons, implying that NbO₂I is an excellent P-type semiconductor.

Conclusions

In summary, we explored the crystal structure, ferroelectric, and electronic properties of monolayers NbO₂I and NbO₂Br using first-principles calculation. We clarified that the FE phase is the energetically stable phase. The origin of polarization comes from the displacement of Nb⁵⁺ cations driven by the SOJT effect. The monolayers NbO₂I and NbO₂Br are indirect semiconductors with the calculated band gap of 0.95 eV and 1.75 eV respectively. In addition, the carrier mobility shows anisotropy along two directions. Our findings add a new member to the family of 2D ferroelectric prototypes, providing a microscopic mechanism of the FE phase transition that will help the discovery and design of new FE materials.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the Ministry of Science and Technology of the People's Republic of China (no. 2022YFA1402901), the National Science Fund for Distinguished Young Scholars (T2125004), the Nature Science Foundation of China (no. 12274228), and the Fundamental Research Funds for the Central Universities (no. 30922010805 and 30920041115).

References

1. C. Wang, Y. Lu, D. Cobden and J. Wang, Nat. Mater., 2023, 22, 542–552.
2. L. Qi, S. Ruan and Y.-J. Zeng, Adv. Mater., 2021, 33, 2005098.
3. X.-K. Wei, N. Domingo, Y. Sun, N. Balke, R. E. Dunin-Borkowski and J. Mayer, Adv. Energy Mater., 2022, 12, 2201199.
4. Z. Guan, H. Hu, X. Shen, P. Xiang, N. Zhong, J. Chu and C. Duan, Adv. Electron. Mater., 2020, 6, 1900818.
5. D. Kepaptsoglou, J. D. Baran, F. Azough, D. Ekren, D. Srivastava, M. Molinari, S. C. Parker, Q. M. Ramasse and R. Freer, Inorg. Chem., 2018, 57, 45–55.
6. V. F. Michel, T. Esswein and N. A. Spaldin, J. Mater. Chem. C, 2021, 9, 8640–8649.
7. J. Zhao, J. Gao, W. Li, Y. Qian, X. Shen, X. Wang, X. Shen, Z. Hu, C. Dong, Q. Huang, L. Cao, Z. Li, J. Zhang, C. Ren, L. Duan, Q. Liu, R. Yu, Y. Ren, S.-C. Weng, H.-J. Lin, C.-T. Chen, L.-H. Tjeng, Y. Long, Z. Deng, J. Zhu, X. Wang, H. Weng, R. Yu, M. Greenblatt and C. Jin, Nat. Commun., 2021, 12, 747.
8. R. Cervasio, Y. Peperstraete, T. Maroutian, R. Haumont, M. Verseils, J.-B. Brubach, R. Tétot, J. Creuze, P. Roy and E. Amzallag, J. Phys. Chem. C, 2022, 126, 12860–12869.
9. A. S. Ivanov, K. V. Bozhenko and A. I. Boldyrev, Inorg. Chem., 2012, 51, 8868–8872.
10. I. B. Bersuker, Chem. Rev., 2021, 121, 1463–1512.
11. L. Gigli, M. Veit, M. Kotiuga, G. Pizzi, N. Marzari and M. Ceriotti, npj Comput. Mater., 2022, 8, 209.
12. G. Sághi-Szabó, R. E. Cohen and H. Krakauer, Phys. Rev. Lett., 1998, 80, 4321–4324.
13. H. Brunckova, L. Medvecky, A. Kovalcikova, M. Fides, E. Mudra, J. Durisin, M. Sebek, M. Kanuchova and J. Skvarla, J. Rare Earths, 2017, 35, 1115–1125.
14. N. Zhang, H. Yokota, A. M. Glazer, Z. Ren, D. A. Keen, D. S. Keeble, P. A. Thomas and Z. G. Ye, Nat. Commun., 2014, 5, 5231.
15. G. R. Bhimanapati, Z. Lin, V. Meunier, Y. Jung, J. Cha, S. Das, D. Xiao, Y. Son, M. S. Strano, V. R. Cooper, L. Liang, S. G. Louie, E. Ringe, W. Zhou, S. S. Kim, R. R. Naik, B. G. Sumpter, H. Terrones, F. Xia, Y. Wang, J. Zhu, D. Akinwande, N. Alem, J. A. Schuller, R. E. Schaak, M. Terrones and J. A. Robinson, ACS Nano, 2015, 9, 11509–11539.
16. L. W. Martin and A. M. Rappe, Nat. Rev. Mater., 2016, 2, 16087.
17. J. Junquera and P. Ghosez, Nature, 2003, 422, 506–509.
18. R. Fei, W. Kang and L. Yang, Phys. Rev. Lett., 2016, 117, 097601.
19. C. Liu, R. Gao, X. Cheng, X. Yang, G. Qin, H. Gao, S. Picozzi and W. Ren, Phys. Rev. B, 2023, 107, L121402.
20. H. Ai, X. Song, S. Qi, W. Li and M. Zhao, Nanoscale, 2019, 11, 1103–1110.
21. C. Cui, F. Xue, W.-J. Hu and L.-J. Li, npj 2D Mater. Appl., 2018, 2, 18.
22. L. H. Jin, H. D. Wang, R. Cao, K. Khan, A. K. Tareen, S. Wageh, A. A. Al-Ghamdi, S. J. Li, D. B. Li, Y. Zhang and H. Zhang, APL Mater., 2022, 10, 060903.
23. (a) X. Wan, J. Zhou and J. Dong, Europhys. Lett., 2010, 92, 57007; (b) Y. Du, H.-C Ding, H.-C Sheng, S.Y. Savrasov, X. Wan, C.-G. Duan and J. Phys, Condens. Matter, 2013, 26, 025503.
24. (a) Y. Du, H.-C. Ding, L. Sheng, S. Y. Savrasov, X. Wan and C.-G. Duan, J. Phys.: Condens. Matter, 2013, 26, 025503; (b) G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
25. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
26. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
27. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
28. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
29. R. D. King-Smith and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 1651–1654.
30. R. Resta, Rev. Mod. Phys., 1994, 66, 899–915.
31. G. Henkelman, B. P. Uberuaga and H. Jonsson, J. Chem. Phys., 2000, 113, 9901–9904.
32. N. A. Zarkevich and D. D. Johnson, J. Chem. Phys., 2015, 142, 024106.
33. S. Hartwig and H. Hillebrecht, Z Naturforsch B, 2007, 62, 1543–1548.
34. M.-J. Crawford, A. Ellern, K. Karaghiosoff, P. Mayer, H. Nöth and M. Suter, Inorg. Chem., 2004, 43, 7120–7126.
35. R. Zacharia, H. Ulbricht and T. Hertel, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 155406.
36. H. Wang, Y. Wang, J. Lv, Q. Li, L. Zhang and Y. Ma, Comput. Mater. Sci., 2016, 112, 406–415.
37. Y. Inaguma, A. Aimi, Y. Shirako, D. Sakurai, D. Mori, H. Kojitani, M. Akaogi and M. Nakayama, J. Am. Chem. Soc., 2014, 136, 2748–2756.
38. R. A. Wheeler, M. H. Whangbo, T. Hughbanks, R. Hoffmann, J. K. Burdett and T. A. Albright, J. Am. Chem. Soc., 1986, 108, 2222.
39. M. Kunz and I. D. Brown, J. Solid State Chem., 1995, 115, 395.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00245d

---