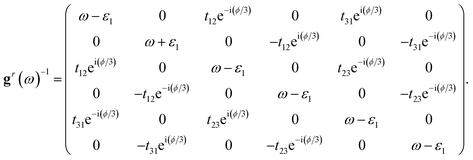DOI:
10.1039/D2NA00838F
(Paper)
Nanoscale Adv., 2023,
5, 1199-1211
Superior thermoelectric properties through triangular triple quantum dots (TTQD) attached to one metallic and one superconducting lead
Received
24th November 2022
, Accepted 18th January 2023
First published on 31st January 2023
Abstract
We theoretically investigate the thermoelectric transport properties of triangular triple quantum dots (TTQD) with the central quantum dot coupled to one metallic and one superconducting lead. The system shows significantly superior thermoelectric performance over parallel coupled triple quantum dots and those coupled to two conventional metallic leads. The thermoelectric coefficients strongly depend on the ratio of superconducting gap to interdot coupling, as well as asymmetry and interference effects. The thermopower exhibits single-platform and double-platform structures for different ratios of superconducting gap to interdot coupling. The thermopower and figure of merit achieve quite remarkable values near the superconducting gap edges where the single-particle tunnelling occurs. For symmetric coupling, the maximal figure of merit might reach the order of 102 when the superconducting gap is about half that of the interdot coupling. Moreover, the figure of merit can be further greatly enhanced by appropriately matching the electrode coupling asymmetry and interdot coupling asymmetry.
1 Introduction
The thermoelectric properties of nanoscale systems have been widely studied due to their expected application as highly efficient thermoelectric devices, converting thermal to electric energy or vice versa. The dimensionless thermoelectric figure of merit ZT = GS2T/κ, is generally used to measure the conversion efficiency. In principle, the effective methods to enhance thermoelectric efficiency include: increasing the electric conductance G and Seebeck coefficient (thermopower) S, and reducing the thermal conductance κ. However, these are rather difficult to realize because the three thermoelectric characters (G, S, κ) are closely related to each other, due to the Wiedemann–Franz law1 and Mott relation.2 In nanoscale systems, the thermal conductance κ can be significantly reduced by reducing the dimensions of the system. On the other hand, the Wiedemann–Franz law and Mott relation can be strongly violated due to the powerful quantum confinement effect and interference effect. All these are conducive to enhance the thermoelectric efficiency ZT in low-dimensional nanoscale systems.3–7
On account of this, the thermoelectric properties of low-dimensional nanoscale systems, especially quantum dot (QD) hybrid systems, have been widely investigated both experimentally and theoretically.8–17 A quantum dot is a zero-dimensional system with well-defined energy levels defined by a combination of size quantization and Coulomb-repulsion effects. It has wide application prospects in biomedicine, light emitting devices and single electron devices. There are many types of quantum dots, such as perovskite quantum dots, semiconductor quantum dots consisting of group II and VI elements, group III and V elements, alloys and heterostructures made of these semiconducting materials, and so on. However, quantum dots with excellent thermoelectric properties are mainly composed of telluride, selenide, their doping compounds and heterostructures. In recent years, increasing attention has been paid to multiple QD hybrid systems in different coupling regimes, due to their potential applications in highly efficient nano-electronic devices and fundamental physics research.18–29 The most common examples are double quantum dot (DQD) and triple quantum dot (TQD) systems, they not only have superior thermoelectric properties over the single quantum dot systems, but also have more means to regulate: it has been shown that the Dicke effect and level detuning play vital roles in improving the thermoelectric efficiency in parallel TQD and T-shaped DQD systems;20,25 it has also been demonstrated that the magnitude of ZT in a parallel DQD-AB ring system can be considerably enhanced by lead coupling asymmetry, quantum interference effects and magnetic flux.26–28 However, thermoelectric properties based on triangular triple quantum dot (TTQD) systems are not well explored.
On the other hand, although a lot of research has already been done on the transport properties of QDs coupled to superconducting leads,30–43 the research on the thermoelectric properties of such systems has only just started.15–17,44–47 Moreover, the Andreev transport regime was mainly investigated in three-terminal devices, where superconducting is just regarded as an additional property, and thermoelectric transport only appears between metallic–metallic lead.30,48–52 The few recent studies on two-terminal devices have confirmed that the thermoelectric properties of QD hybrid systems coupled to one conventional lead (metallic or ferromagnetic lead) and one superconducting lead, are remarkably better than those coupled to two conventional leads.16,28,29,45,47,53 It has been found that the thermoelectric efficiency of the former can even reach several times or even tens of times that of the latter, by comprehensively regulating the superconducting gap, interdot coupling and asymmetric parameters, which can also be additionally enhanced by the interference effect and interdot Coulomb interaction. This is mainly attributed to the unique tunnelling mechanism and high density of states distribution near superconducting gap edges. The Andreev tunnelling of Cooper pairs is only allowed inside the superconducting gap, while the tunnelling of single electrons is allowed outside the superconducting gap, both of them have significant impact on the thermoelectric properties. The very high density of states near superconducting gap edges changes rapidly with energy, which is mainly responsible for the high thermopower and low thermal conductivity near the superconducting gap edges. However, recent studies have mainly focused on single quantum dot,16,47 double quantum dot28,53 and parallel coupled triple quantum dot systems,29,45 the thermoelectric properties of TTQD coupling to one metallic–metallic and one superconducting lead have not been studied yet.
Therefore, in this paper we consider the thermoelectric properties of triangular triple quantum dots (TTQDs) attached to one metallic and one superconducting lead, as shown in Fig. 1. The basic thermoelectric characteristics (linear electric conductance G, thermal conductance κ, thermopower S and figure of merit ZT) are derived in the linear response regime using the nonequilibrium Green's function method. We first verified the excellent thermoelectric properties of the N-TTQD-S system compared with the N-TQD-S and N-TTQD-N systems. Due to the strong interference effect induced by the triangular configuration, the N-TTQD-S system shows remarkably higher thermoelectric efficiency than the traditional parallel coupled triple quantum dot system. In the case of symmetric coupling, there exists an optimal proportional relationship between the superconducting gap Δ and the interdot coupling t, i.e., Δ ∼ 0.5t, in such a case, the thermopower is enhanced while the thermal conductivity is suppressed, resulting in considerably high thermoelectric efficiency. Furthermore, when the central QD1 is weakly coupled to superconducting lead, the thermoelectric efficiency is greatly enhanced. In addition, the interference effects regulated by the interdot coupling asymmetry also has a significant impact on the thermoelectric properties.
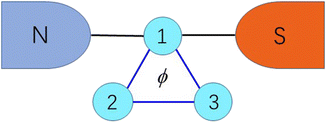 |
| | Fig. 1 Triangular triple quantum dots attached to one metallic and one superconducting lead. ϕ denotes the magnetic flux across TTQD. N = metallic lead, S = superconducting lead. | |
This paper is organized as follows. The model and basic analytical formulae are given in Section 2. The corresponding numerical results and discussion in the symmetric and asymmetric coupling cases are presented in Section 3. Finally, a summary and general conclusions are included in Section 4.
2 Model and formulae
The system under consideration consists of triangular triple quantum dots with the central QD1 attached to one metallic and one superconducting lead, as schematically shown in Fig. 1. The total Hamiltonian of the N-TTQD-S system is given by| | | H = HN + HS + HTTQD + HT. | (1) |
The metallic lead, noninteracting electrons with energy εkN and momentum k are described by
| | 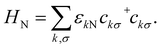 | (2) |
In the mean field approximation, the superconducting lead is described by the BCS Hamiltonian,
| | 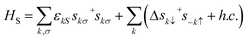 | (3) |
where
εkS and
Δ denote the relevant single-electron energy and superconducting gap. And
s+kσ (
skσ) represents the creation (annihilation) operator of an electron with energy
εkS and momentum
k, and the superconducting gap
Δ = |
Δ|e
iϕ0, in which the phase factor
ϕ0 can be neglected as there is only one superconducting lead.
54
The Hamiltonian of the triangular triple quantum dots is described as
| | 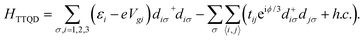 | (4) |
where the operators
d+iσ and
diσ are the creation and annihilation, respectively, of an electron with energy
εi and spin
σ in the
ith dot (
i = 1, 2, 3). Hopping between electrons in QD
i and QD
j,
tij, are with 〈
ij〉 = 〈12〉, 〈23〉, 〈31〉, and
ϕ is the magnetic flux across TTQD. The hopping between central QD1 to QD2 and QD3 are assumed to be equal,
i.e.,
t12 =
t31 =
t, while the hopping of QD2 to QD3,
t23, can be different from
t. Furthermore, scaling factor
η is introduced to described the asymmetry of
t23 to
t12 (
t31) with
η =
t23/
t. For simplicity, the electron Coulomb interactions were ignored for two reasons: one is that the behavior of the figure of merit is mainly attributed to the Seebeck coefficient and ratio between the electrical conductance and thermal conductance. Previous studies in similar systems have shown that the electron correlation effect will be cancelled due to the Seebeck coefficient and the ratio, in the absence of phonon thermal conductance;
55 the other reason is that at low temperature, the Coulomb interaction has almost no impact on the figure of merit. The last term
HT of the Hamiltonian accounts for the tunnelling between QD1 and the lead, and it takes the standard form
| | 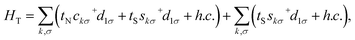 | (5) |
where
tN and
tS denote the relevant tunnelling matrix elements between QD1 and the N and S lead. The dot-lead coupling strengths of the QD1 to the left and right leads are given by
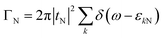
and
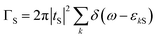
. Within the wide-band approximation, the coupling parameters
ΓN and
ΓS become independent of energy and can be considered as constants. In addition, we also introduce
γ =
ΓS/
ΓN to describe the asymmetry of the coupling of QD1 to the N and S lead.
On account of both single-particle tunnelling processes and Andreev tunnelling processes being allowed to occur when the right-hand lead is superconducting, the charge current I can be written as a sum of current IS due to single-particle tunnelling outside the superconducting gap and current IAR due to Andreev tunnelling inside the superconducting gap
with
| | 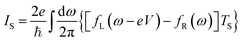 | (7) |
| | 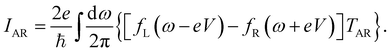 | (8) |
In a similar way, the heat current flowing out of the metallic lead can be written as
where
JS denotes the contribution from the single-particle tunnelling
| | 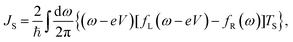 | (10) |
and
JAR denotes the contribution from Andreev tunnelling
| | 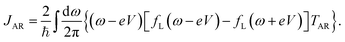 | (11) |
The transmission functions associated with single-particle tunnelling TS and Andreev tunnelling TAR, can be obtained by
| | | TS = (GrΓRGaΓL)ii (i = 1, 3, 5) | (12) |
| | | TAR = Grij(ΓLGaΓL)ji (i = 1, 3, 5; j = 2, 4, 6). | (13) |
Gr(
ω) and
Ga(
ω) are the system's retarded and advanced Green's functions in the matrix form, respectively, while
ΓL and
ΓR denote the coupling of QD1 to the lead. To be more specific,
Gr(
ω) can be solved by Dyson's equation
| | | Gr(ω)−1 = gr(ω)−1 − ∑r | (14) |
with
gr(
ω) and
∑r denoting the retarded Green's function of the isolated TTQD and the retarded self-energy, respectively. By deriving the relevant equation of motion in the Nambu space,
56gr(
ω) takes the following form
The retarded self-energy ∑r describes the interaction between QD1 and lead, it takes the form
| | 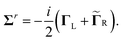 | (15) |
The first part is due to the coupling of QD1 to metallic lead
| | 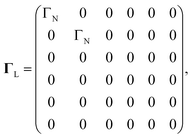 | (16) |
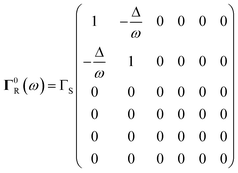
and the second part is due to the coupling of QD1 to superconducting lead
| | ![[capital Gamma, Greek, tilde]](https://www.rsc.org/images/entities/b_char_e1eb.gif) R = R = ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) S(ω)Γ0R S(ω)Γ0R | (17) |
with
| | 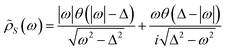 | (18) |
and
| |  | (19) |
whereas the coupling matrix
ΓR in
eqn (12) is quite different form that in
eqn (17), and takes the following forms:
with
| | 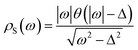 | (21) |
It is worth noting that ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) S(ω) and ρS(ω) denote different physical significance:
S(ω) and ρS(ω) denote different physical significance: ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) S(ω) represents the dimensionless modified BCS density of states, while ρS(ω) represents the ratio of the superconducting density of states to the metallic density of states.
S(ω) represents the dimensionless modified BCS density of states, while ρS(ω) represents the ratio of the superconducting density of states to the metallic density of states.
In the linear response regime, the electric current I and heat current J can be generally expressed as linear functions of temperature gradient ΔT and bias voltage drop ΔV applied between the two leads:
| | 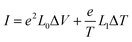 | (22) |
| | 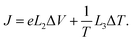 | (23) |
By expanding the Fermi distribution functions to the first order functions of ΔV and ΔT in eqn (6) and (9), the integrals Ln (n = 0, 1, 2, 3) take the following form:
| | 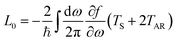 | (24) |
| | 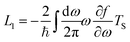 | (25) |
| | 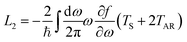 | (26) |
| | 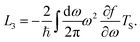 | (27) |
Based on the above, the charge conductance G can be expressed in terms of the integral L0
Similarly, the thermal conductance κ can be written as
| | 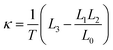 | (29) |
by defining the heat current in the absence of charge current. The thermopower (Seebeck coefficient)
S is defined as the ratio of the voltage drop Δ
V generated by the thermal gradients Δ
T in the absence of charge current (
I = 0). Thus, the Seebeck coefficient can be expressed as follows by taking account of
eqn (23) and
(24):
| | 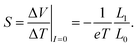 | (30) |
Finally, the system heat–electricity conversion efficiency is quantified by the dimensionless figure of merit ZT:
| | 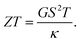 | (31) |
The thermal conductance here only includes the electron thermal conductance, ignoring the phonon thermal conductance, which leads to certain limitations of the model. Experimentally, the phonon thermal conductance can be effectively suppressed by some particular materials or designs in QD systems, for instance, adding a vacuum layer between the tunnelling junction for blocking the heat current delivered by phonon carriers, and embedding QDs into small diameter nanowires to significantly reduce the phonon thermal conductance. Therefore, it is crucially important to inhibit the phonon thermal conductivity as effectively as possible experimentally, which is also a key constraint to optimize the thermoelectric efficiency of our model.
3 Results and discussion
In such a N-TTQD-S system, three different tunnelling processes are allowed: conventional single-particle tunnelling, single-level Andreev reflection tunnelling and two-level Andreev reflection tunnelling processes. However, when the superconducting gap vanishes (Δ = 0), both the left and right leads become metallic-like, thus, the N-TTQD-S system degrades into an N-TTQD-N system, meanwhile only the conventional single-particle tunnelling process is allowed. In addition, the N-TTQD-N (or N-TTQD-S) system would further degrade into a N-TQD-N (or N-TQD-S) system when the coupling of QD2 to QD3 is absent (t ≠ 0, η = 0), corresponding to the parallel coupled triple quantum dots configuration. Even more, the N-TQD-N (or N-TQD-S) device would further degrade into a N-QD-N (or N-QD-S) device when t = 0, η = 0, corresponding to the single quantum dot structure.
We carry out the numerical calculations based on the above formulae and theory. For convenience, Γ0 is defined as the energy unit and all the system parameters are expressed in this unit. Before discussion, it is necessary to obtain the accurate eigenenergies of the triangular triple quantum dots. For simplicity, we assume that the levels of all three QDs are independent of electron spin and chosen as ε1 = ε2 = ε3 = ε. According to the strength of interdot coupling tij, the central triangular triple quantum dot configurations have symmetric coupling and asymmetric coupling as the two coupling modes. In the symmetric coupling case, the interdot coupling tij between the three quantum dots is the same, meanwhile, the coupling of QD1 to the left and right lead are the same, i.e., t12 = t23 = t31 = t (η = 1) and ΓS = ΓN (γ = 1). On the contrary, in the asymmetric coupling case, t23 = ηt12 = ηt31 = ηt (η ≠ 1) and (or) ΓS = γΓN (γ ≠ 1). For a single quantum dot configuration, the effective level is ε0 = ε. For parallel coupled triple quantum dot (TQD) configurations (η = 0), the effective levels re-metallicize to 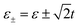 , moreover, for the triangular triple quantum dot (TTQD) configuration, the effective levels renormalize to
, moreover, for the triangular triple quantum dot (TTQD) configuration, the effective levels renormalize to 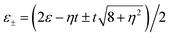 . In particular, in the symmetric coupling cases with η = 1, the effective levels degenerate to ε+ = ε + t and ε− = ε − 2t.
. In particular, in the symmetric coupling cases with η = 1, the effective levels degenerate to ε+ = ε + t and ε− = ε − 2t.
In this section, we first verify the superiority of the N-TTQD-S system compared with the N-TTQD-N and N-TQD-S systems, and then discuss the influence of the superconducting energy gap Δ and interdot coupling t in symmetric coupling cases (η = γ = 1) and the influence of asymmetry (γ ≠ 1 and η ≠ 1), successively.
3.1 The superiority of the N-TTQD-S system compared with the N-TTQD-N and N-TQD-S systems
The system we chose shows significant superiority in contrast to the N-TTQD-N (Δ = 0, η = 0) and N-TQD-S (Δ ≠ 0, η = 0) systems. In Fig. 2 and 3, we show the thermoelectric properties of the three different central quantum dot configurations respectively coupled to metallic and superconducting lead. The linear electric conductance G, electronic contribution to the thermal conductance κ, thermopower S and figure of merit ZT, are calculated as a function of the quantum dot's energy level ε/Γ0, for kBT = 0.1, ϕ = 2π and ΓN = ΓS = 0.1 (γ = 1). The figure of merit ZT, is generally used to describe the thermoelectric efficiency, the higher the figure of merit ZT, the higher the thermoelectric efficiency. As the blue line shows in Fig. 2(d), the thermoelectric efficiency of the N-TTQD-N system is obviously higher than that of N-QD-N and N-TQD-N systems. As defined in eqn (30), the thermoelectric efficiency is completely decided by the comprehensive behavior of the three basic thermoelectric characters G, κ and S. For the three different configurations, the variation of these thermoelectric coefficients (G, κ, S and ZT) are quite different as they are a function of the dot's level ε/Γ0, mainly owing to the different tunnelling channels of different configurations and the interference effect induced by them. To be specific, the different quantum dot configurations can lead to different effective levels, thus resulting in the different tunnelling channels. For the N-QD-N system, the central peaks at ε = 0 displayed in the spectrum of electric conductance G and thermal conductance κ, are associated with the conventional single-particle tunnelling process through the effective level ε0 = 0. However, for the N-TQD-N system, there exists two peaks in the vicinity of 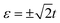 in the spectra of electric conductance G and thermal conductance κ, which is in association with the single-particle tunnelling processes through the two effective levels,
in the spectra of electric conductance G and thermal conductance κ, which is in association with the single-particle tunnelling processes through the two effective levels, 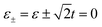 . By the same token, for the N-TTQD-N system in the symmetric coupling case with η = 1, the effective levels become ε+ = ε + t and ε− = ε − 2t, the resonance peaks appear in the vicinity of ε = −t and ε = 2t.
. By the same token, for the N-TTQD-N system in the symmetric coupling case with η = 1, the effective levels become ε+ = ε + t and ε− = ε − 2t, the resonance peaks appear in the vicinity of ε = −t and ε = 2t.
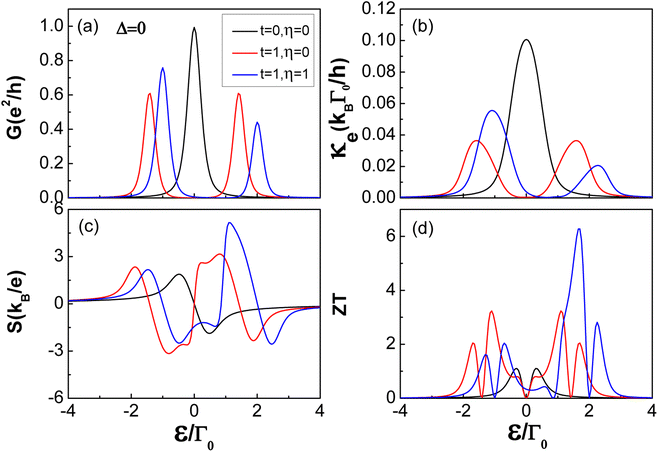 |
| | Fig. 2 Transport and thermoelectric coefficients: (a) electrical conductance G, (b) thermal conductance κ, (c) thermopower S, and (d) figure of merit ZT as a function of the quantum dot energy level ε/Γ0, in N-QD-N, N-TQD-N and N-TTQD-N – the three different systems for Δ = 0. The other parameters are set as T = 0.1, ΓS = ΓN = 0.1 (γ = 1). | |
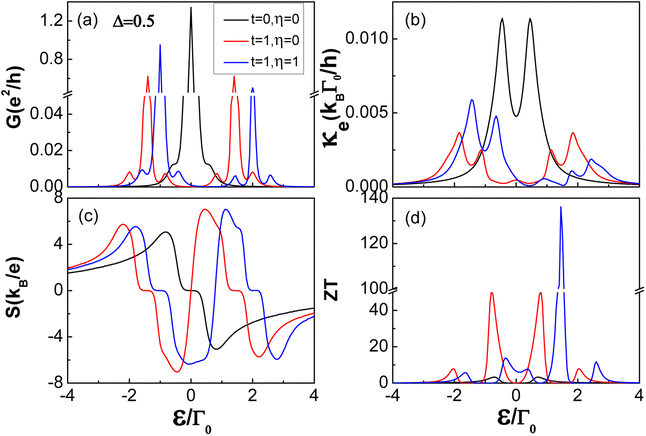 |
| | Fig. 3 Transport and thermoelectric coefficients: (a) electrical conductance G, (b) thermal conductance κ, (c) thermopower S, and (d) figure of merit ZT as a function of the quantum dot energy level ε/Γ0 in N-QD-S, N-TQD-S and N-TTQD-S – the three different systems for Δ = 0.5. The other parameters are set as in Fig. 2. | |
The sign change of thermopower S in Fig. 2(c) is associated with the type of main carrier; when the tunnelling is dominated by electrons (holes), the sign of thermopower is negative (positive). Taking together the behavior of the thermoelectric coefficients (G, κ and S and ZT), it is found that the higher figure of merit in the N-TTQD-N system results from a relatively smaller thermal conductance κ and larger thermopower S. The highest figure of merit for the N-TTQD-N system (ZT ∼7.7), is nearly twice that of the N-TQD-N system (ZT ∼3.4), and the highest figure of merit of the N-TQD-N system (ZT ∼3.4) is nearly triple that of the N-QD-N system (ZT ∼1.1). In conclusion, when the three different central quantum dot configurations are coupled to two metallic-like lead, the triangular triple quantum dot (TTQD) configuration exhibits excellent thermoelectric performance in comparison with the single quantum dot and parallel coupled triple quantum dots (TQD) configurations.
In Fig. 3 with Δ = 0.5, we again show the thermoelectric coefficients (G, κ, S and ZT) as a function of the dot energy level ε/Γ0 for the three different systems: N-QD-S, N-TQD-S and N-TTQD-S. Comparing the properties of the QD-metallic lead systems (seen in Fig. 2) and QD-superconducting lead systems (seen in Fig. 3), one can easily see three valuable points: first, the same central QD configuration coupled to one superconducting lead has higher thermoelectric efficiency than that coupled to two metallic leads, as shown by the same colour lines in Fig. 2(d) and 3(d). Second, due to there being more tunnelling processes involved when Δ ≠ 0, the thermoelectric coefficients display more resonance peaks. Third, there exists a platform of S = 0 in the thermopower spectrum when the central QD configurations are coupled to one superconducting lead.
For the N-QD-S system, as the black lines show in Fig. 3, the electric conductance G displays a narrow peak and two side peaks, the central peak at ε = 0 originates mainly from the single-level Andreev tunnelling inside the superconducting gap. While the two side peaks in the vicinity of ε = ±Δ are attributed to the single-particle tunnelling around the superconducting gap edges. As for the two-level Andreev tunnelling process, it can only occur for the case of ε+ and ε−(ε = −t/2) symmetrically distributing inside the superconducting gap. However, for Δ = 0.5 and t = 1, the two effective levels ε± = ±3t/2 are symmetrically distributed outside the superconducting gap, thus, the peak associated with the two-level Andreev tunnelling process does not appear in the electric conductance spectrum. In terms of the thermal conductance κ, it is worth the reminder that the Andreev tunnelling does not contribute to heat current in a thermally biased system. Thus, the thermal conductance κ just reveals two peaks associated with single-electron tunnelling to states outside the superconducting gap. As for thermopower S shown with the black line in Fig. 3(c), besides the particle-hole symmetry point, it also vanishes for an effective level ε inside the superconducting gap since the single-particle tunnelling processes are suppressed. Whereas the thermopower S gradually increases outside the edges of the superconducting gap, and rapidly reach maximum around the edges of the superconducting gap where density of the single-particle states reaches its maximum. As a result of the above behavior of thermoelectric coefficients (G, κ and ZT), the maximal figure of merit in the N-QD-S system (ZT ∼3.3) reaches triple that of the N-QD-N system (ZT ∼1.1).
As the red lines show in Fig. 3, for the N-TQD-S system, the electric conductance G displays two high peaks and four low sided peaks: the two high peaks at 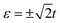 derive from the single-level Andreev tunnelling processes, while the four lower side peaks at
derive from the single-level Andreev tunnelling processes, while the four lower side peaks at 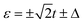 are induced by the conventional single-particle tunnelling through the superconducting gap edges. In addition, on account of that the electrons in the metallic lead are mainly concentrated around the Fermi level, the single-particle tunnelling through the superconducting gap edges is suppressed, thus, the two peaks associated with the single-level Andreev tunnelling are much higher than those associated with the conventional single-particle tunnelling. The Andreev tunnelling does not contribute to thermal conductance κ due to no electron states inside the superconducting gap. As a consequence, the thermal conductance exhibits only four peaks in the vicinity of
are induced by the conventional single-particle tunnelling through the superconducting gap edges. In addition, on account of that the electrons in the metallic lead are mainly concentrated around the Fermi level, the single-particle tunnelling through the superconducting gap edges is suppressed, thus, the two peaks associated with the single-level Andreev tunnelling are much higher than those associated with the conventional single-particle tunnelling. The Andreev tunnelling does not contribute to thermal conductance κ due to no electron states inside the superconducting gap. As a consequence, the thermal conductance exhibits only four peaks in the vicinity of 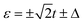 . For the N-TTQD-S system in the symmetric coupling case with η = 1, as the blue line in the spectrum of thermal conductance shows, due to the effective levels changing, the two high peaks resulting from single-level Andreev tunnelling move to ε = −t and ε = 2t, meanwhile, the four lower side peaks induced by the single-particle tunnelling move to ε = −t ±Δ and ε = 2t ±Δ. The resonance peaks in the spectrum of thermal conductance make corresponding movements.
. For the N-TTQD-S system in the symmetric coupling case with η = 1, as the blue line in the spectrum of thermal conductance shows, due to the effective levels changing, the two high peaks resulting from single-level Andreev tunnelling move to ε = −t and ε = 2t, meanwhile, the four lower side peaks induced by the single-particle tunnelling move to ε = −t ±Δ and ε = 2t ±Δ. The resonance peaks in the spectrum of thermal conductance make corresponding movements.
As the red and blue lines show in Fig. 3(c), different from the single quantum dot system, the thermopower displays the double-platform structure of S = 0 in both N-TQD-S and N-TTQD-S systems. It is noteworthy that the platform in the spectrum of thermopower for t > Δ is completely different from that for t = 0. As mentioned above, for t = 0, the thermopower vanishes for the case of the effective level ε0 being inside the superconducting gap, i.e., −Δ < ε0 < Δ. However, for the N-TQD-S and N-TTQD-S systems, the two effective levels ε± cannot simultaneously exist inside the superconducting gap when t > Δ, hence the thermopower vanishes only in special cases; to be specific, when one effective level ε+ (or ε−) locates inside the superconducting gap, the other level ε− (or ε+) must locate outside the superconducting gap at the same time, moreover, it must be far away from the Fermi-level. In such cases, a double-platform structure of S = 0 can form in the thermopower spectrum. Apart from this, whether inside or outside the superconducting gap, there exists resonance peaks in the spectrum of thermopower. In terms of the thermoelectric conversion efficiency, the N-TTQD-S system is obviously better than the N-QD-S and N-TQD-S systems, mainly attributed to the relatively small thermal conductance and large thermopower. Specifically, the highest figure of merit of the N-TTQD-S system (ZT ∼136.2) is nearly 2.5 times the N-TQD-N system (ZT ∼51.6), and the highest figure of merit of the N-TQD-N system (ZT ∼51.6) is 15 times that of the N-QD-N system (ZT ∼3.3). In addition, the maximum values of figure of merit are obtained in the vicinity of ε± ∼ ±Δ, meaning that conventional single-particle tunnelling processes at the edges of the superconducting gap play a significant role in improving thermoelectric conversion efficiency.
Comparing the behaviors of thermoelectric coefficients (G, κ and S and ZT) with the same central quantum configuration in Fig. 2 and 3, one can see that the same central quantum dot configurations coupled to superconducting lead have much better thermoelectric performance than those coupled to ordinary metallic lead. First, the induction of superconducting lead provides more channels for electron tunnelling. Second, the thermal conductance κ of superconducting-quantum-dot systems is only one-tenth that of metallic-quantum-dot systems, which greatly promotes the improvement of thermoelectric efficiency. Third, the amplitude of thermopower in superconducting-quantum-dot systems is nearly 1.5 times that the metallic-quantum-dot system, additionally contributing to the further improvement of thermoelectric efficiency. All these are the main attributes to the conventional single-particle tunnelling processes through the superconducting gap edges. After confirming the superiority of the N-TTQD-S system, we discuss the influence of other important system parameters (Δ, t and γ and η) on thermoelectric performance in the following.
3.2 Influence of superconducting gap Δ and interdot tunnelling coupling t for the case of symmetric coupling (η = γ = 1)
As described above, the type of electron tunnelling process is decided by the relative position of effective levels and superconducting gap edges, moreover, the effective levels of TTQD depend on the interdot coupling patterns and interdot coupling strength tij. Therefore, it can be inferred that the thermoelectric properties of the N-TTQD-S system may strongly dependent on the interdot coupling and superconducting gap. Let us now consider the influence of the superconducting gap and the interdot coupling on the thermoelectric properties for the case of symmetric coupling, i.e., t12 = t23 = t31 = t (η = 1) and ΓS = ΓN (γ = 1).
In Fig. 4, for fixed interdot coupling t = 0.5, we show the thermoelectric coefficients under different indicated values of the superconducting gaps Δ as a function of the dot's energy level ε/Γ0. The behavior of these thermoelectric coefficients is similar to that for the triangular triple quantum dot configuration with t ≠ 0, η ≠ 0 in Fig. 3. For the case of Δ ≠ 0, all three tunnelling processes are involved, both the electric conductance G and thermal conductance κ show a multi-peak distribution. The positions and origin of the different peaks are discussed above for Fig. 3. In addition, for the relatively larger superconducting gap Δ(Δ ≥ 3t/2), the two-level Andreev tunnelling process is allowed to occur. For example, for the QD level ε = t/2, the two effective levels symmetrically distribute inside the superconducting gap, i.e., ε+ = −ε− = −3t/2, thus resulting in a peak in the vicinity of ε = t/2 in the spectrum of electric conductance G. Apart from this, for Δ = 3t/2, the single-particle tunnelling processes through the effective levels ε+ = Δ and ε− = −Δ also occurs at ε = t/2. As a result, for Δ = 3t/2, the two-level Andreev tunnelling resonance peak is completely coincident with the two resonance peaks associated with the single-particle tunnelling processes. Consequently, as the inset of Fig. 4(a) shows, the seven resonance peaks originating from three different tunnelling processes degenerate into five resonance peaks. Meanwhile, the resonance peak at ε = t/2 is higher than the other two peaks induced by the single-particle tunnelling through the effective levels ε+ = −Δ and ε− = Δ.
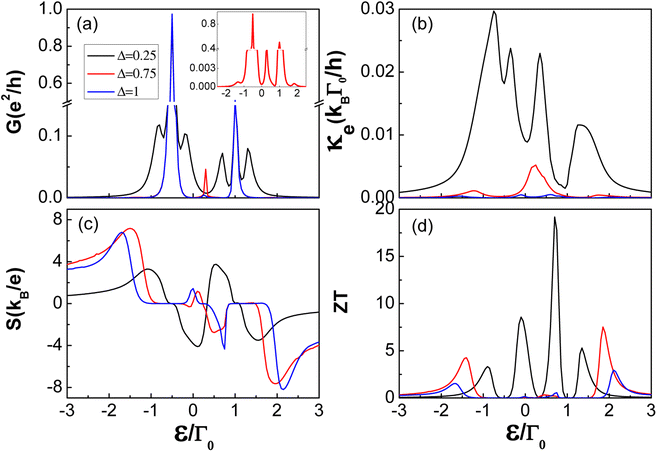 |
| | Fig. 4 Transport and thermoelectric coefficients: (a) electrical conductance G, (b) thermal conductance κ, (c) thermopower S, and (d) figure of merit ZT as a function of the dot energy level ε/Γ0, under indicated values of superconducting gap Δ for t = 0.5 and η = 1 in the N-TTQD-S system. Other parameters are the same as in Fig. 3. | |
In the spectra of electric conductance and thermal conductance with Δ ≠ 0, as the superconducting gap increases, the single-particle tunnelling resonance peaks in the vicinity of ε = −t ± Δ and ε = 2t ± Δ become lower and lower, this is mainly attributed to the suppression of conventional single-particle tunnelling around the edges of the superconducting gap with increasing Δ. More precisely, the bigger the superconducting gap Δ, and the farther the effective level ε± ∼ ±Δ is away from the Fermi level, the smaller the contribution of single-particle tunnelling around the superconducting gap edges. As is clearly seen in Fig. 4(c), the double-platform structure also appears in the spectrum of thermopower for the case of larger superconducting gaps. Due to the different causes of the single platform structure and double platform structure, the platform width depends on different system parameters. The width of S = 0 in the double-platform structure just depends on the superconducting gap and the energy level broadening, and it increases with increasing superconducting gap. However, the width of S = 0 in the single-platform structure is merely decided by the interdot coupling and the energy level broadening. The comprehensive variation of thermoelectric coefficients (G, κ and S) leads to the behavior of the figure of merit as shown in Fig. 4(d). Obviously, the highest thermoelectric efficiency is not obtained for the largest superconducting gap, it is mainly attributed to the increasing superconducting gap, which greatly suppresses the single-particle tunnelling process near the edges of the superconducting gap.
Next, we discuss the influence of interdot tunnelling for the case of symmetric coupling, the superconducting gap is taken as Δ = 0.5. The different interdot coupling types and coupling strength between quantum dots can not only provide different tunnelling channels for quantum interference, but also influence the interference effect through the effective coupling between effective levels and lead, thus affecting the thermoelectric properties of the system. The variation of the thermoelectric coefficients as a function of the dot's energy level ε/Γ0 for several values of the interdot coupling t, are shown in Fig. 5. The behavior of all the thermoelectric coefficients are consistent with those presented in Fig. 3 and 4 for t ≠ 0, η = 1. Because the effective levels vary linearly with the interdot coupling strength t, both the single-level Andreev tunnelling resonance peaks (ε± = 0) and the conventional single-particle tunnelling resonance peaks through the superconducting gap edges (ε± ∼ ±Δ), move accordingly with varying t, as seen in Fig. 5(a) and (b). On the other hand, for a fixed superconducting gap Δ, the contribution of both the single-level Andreev tunnelling and the conventional single-particle tunnelling would barely change, thus, the amplitude of these peaks changes very little. The position of the S = 0 double-platform in the spectrum of thermopower cause the corresponding movement of the varying interdot coupling t, but the platform width is completely independent of the interdot coupling t. This is in agreement with the corresponding results for the parallel coupled double quantum dot configuration. The relatively large thermopower and very small electron thermal conductance around the superconducting gap contribute to the large figure of merit for t = 1.
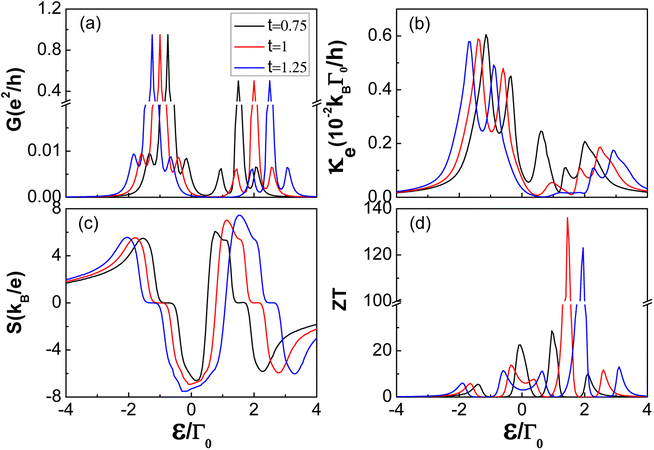 |
| | Fig. 5 Transport and thermoelectric coefficients: (a) electrical conductance G, (b) thermal conductance κ, (c) thermopower S, and (d) figure of merit ZT as a function of the dot energy level ε/Γ0, under the indicated values of interdot coupling t for Δ = 0.5 and η = 1 in the N-TTQD-S system. Other parameters are the same as in Fig. 3. | |
Considering the dependence of thermoelectric coefficients (G, κ, S and ZT) on the superconducting gap Δ and interdot coupling t, one can find that there exists an optimal constraint condition, which maximizes the figure of merit ZT. As Fig. 4(d) shows, the largest figure of merit most likely to be achieved is in the vicinity of Δ = 0.25 for t = 0.5. In a similar way, the figure of merit is maximized in the vicinity of t = 1 for Δ = 0.5. Thus it can be concluded that there probably exists optimum conditions between the superconducting gap Δ and the interdot coupling coefficient t, significantly enhancing the figure of merit in symmetric coupling cases. In the N-TTQD-S system we considered, Δ = t/2 is most likely to maximize the figure of merit in symmetric coupling cases. In Fig. 6, we present the dependence of the figure of merit on the interdot coupling t and ratio Δ/t, the QD level was set as ε = 2t − Δ(ε− ∼ −Δ), where the highest ZT may obtained. It is found that the figure of merit is always obtained in the vicinity of Δ/t = 0.5, strongly confirming the results in Fig. 3(d) and 4(d). In addition, the figure of merit can even reach an order of 102 over a wide range of parameters (t and Δ), as the red areas in Fig. 6 display.
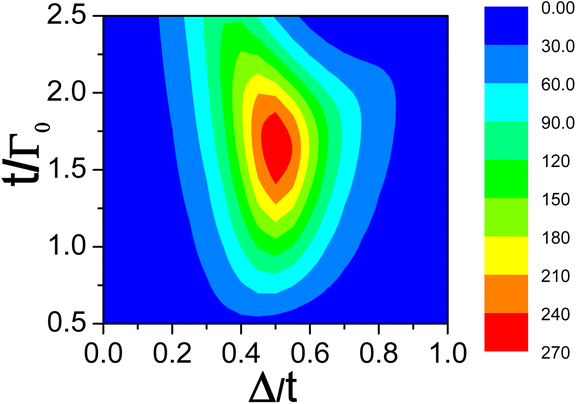 |
| | Fig. 6 Figure of merit ZT as a function of interdot coupling t, and ratio of superconducting gap Δ to interdot coupling t. Other parameters are the same as in Fig. 3. | |
3.3 Influence of the asymmetry (γ and η)
Consider now the case of asymmetric coupling, i.e., γ = ΓS/ΓN ≠ 1 and η = t23/t ≠ 1. In order to precisely investigate the impact of lead coupling asymmetry γ on thermoelectric properties, we set the interdot coupling asymmetry as η = 1. In Fig. 7, we show the thermoelectric coefficients as a function of the dot's energy level ε/Γ0, for different values of asymmetric coupling parameter γ. Along with the increase of lead coupling asymmetry parameter γ, the coupling between central QD1 and superconducting lead ΓS also increases, the tunnelling processes from the left lead to the right lead are enhanced at the same time. It is clear that the thermoelectric coefficients show significant dependence on the asymmetric coupling parameter γ: first, the increasing coupling coefficient ΓS contributes to the enhancement of electron tunnelling, as a result, the value of amplitude in the spectrum of electrical conductance and thermal conductance increases accordingly, as seen in Fig. 7(a) and (b); second, for a larger asymmetric coupling parameter γ, the platform width in the thermopower becomes wider due to the larger energy level broadening with increasing γ; third, with the decrease of asymmetry parameter γ, the maximal figure of merit around ε− = −Δ increases accordingly. In particular, when the asymmetry parameter γ is less than 1, the maximal figure of merit rises sharply with decreasing γ, this is mainly attributed to the relatively higher ratio of the electrical conductance to thermal conductance. It is found that the system may have higher thermoelectric conversion efficiency when the right superconducting lead is weakly coupled to the central QD configuration.
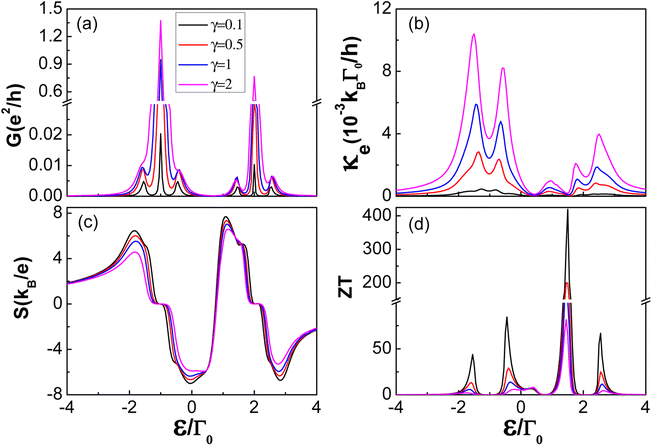 |
| | Fig. 7 Transport and thermoelectric coefficients: (a) electrical conductance G, (b) thermal conductance κ, (c) thermopower S, and (d) figure of merit ZT, as a function of the dot energy level ε/Γ0 under the indicated values of the asymmetry parameter γ(ΓS/ΓN) for Δ = 0.5, t = 1 and η = 1 in the TTQD device. Other parameters are the same as in Fig. 3. | |
The interference effects have a strong influence on the thermoelectric properties of multiple quantum dot systems. In the triangular triple quantum dot systems, the interference effects strongly depend on the coupling between different quantum dots. Following the case of γ = 0.1, the behavior of thermoelectric coefficients for different values of interdot coupling asymmetry η are shown in Fig. 8. As analysed before, the resonant peaks shift accordingly with the change of effective levels 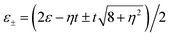 , as clearly seen in all spectra of thermoelectric coefficients in Fig. 8(a)–(d). In the weak coupling case with γ = 0.1, all the electron tunnelling processes are suppressed, thus, the amplitude in both electrical conductance and thermal conductance spectra, obviously decrease in comparison with the case of γ = 1. In addition, the lower single-particle tunnelling resonance peaks associated with the ε+ ∼ ±Δ increase with the increasing η, while those associated with the ε− ∼ ±Δ decrease with the increasing η, as clearly seen in Fig. 8(a) and (b). The different behaviors are mainly attributed to the influence of the interference effect on the different tunnelling transport channels. In contrast, the amplitude of thermopower S shows less dependence on the interdot coupling asymmetry η. The figure of merit completely depends on the above behaviors of thermoelectric coefficients (G, κ and S), it reaches a maximum value in the vicinity of ε± ∼ ±Δ, especially near ε− ∼ −Δ. Moreover, the figure of merit does not increase blindly with the increasing interdot coupling asymmetry η, too large an asymmetry parameter (η > 1) would also suppress the enhancement of thermoelectric efficiency. It is further strongly confirmed in the inset of Fig. 8(d), where the figure of merit ZT is plotted as a function of asymmetry parameter η with
, as clearly seen in all spectra of thermoelectric coefficients in Fig. 8(a)–(d). In the weak coupling case with γ = 0.1, all the electron tunnelling processes are suppressed, thus, the amplitude in both electrical conductance and thermal conductance spectra, obviously decrease in comparison with the case of γ = 1. In addition, the lower single-particle tunnelling resonance peaks associated with the ε+ ∼ ±Δ increase with the increasing η, while those associated with the ε− ∼ ±Δ decrease with the increasing η, as clearly seen in Fig. 8(a) and (b). The different behaviors are mainly attributed to the influence of the interference effect on the different tunnelling transport channels. In contrast, the amplitude of thermopower S shows less dependence on the interdot coupling asymmetry η. The figure of merit completely depends on the above behaviors of thermoelectric coefficients (G, κ and S), it reaches a maximum value in the vicinity of ε± ∼ ±Δ, especially near ε− ∼ −Δ. Moreover, the figure of merit does not increase blindly with the increasing interdot coupling asymmetry η, too large an asymmetry parameter (η > 1) would also suppress the enhancement of thermoelectric efficiency. It is further strongly confirmed in the inset of Fig. 8(d), where the figure of merit ZT is plotted as a function of asymmetry parameter η with 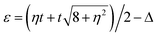 (corresponding to ε− = −Δ). The highest figure of merit can be obtained in the vicinity of η = 1, where the interference effect is most effective in improving thermoelectric performance.
(corresponding to ε− = −Δ). The highest figure of merit can be obtained in the vicinity of η = 1, where the interference effect is most effective in improving thermoelectric performance.
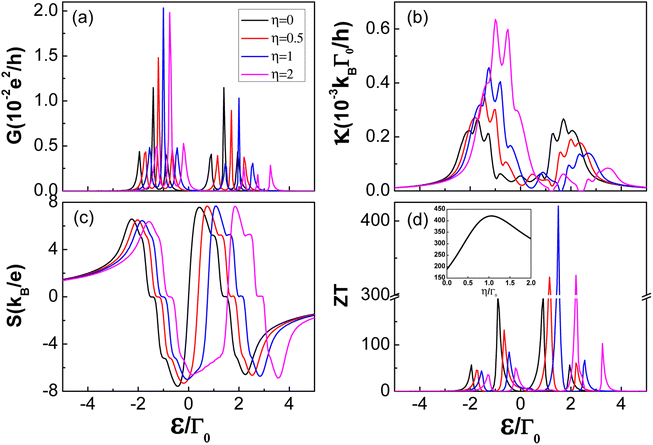 |
| | Fig. 8 (a) Electrical conductance G, (b) thermal conductance κ, (c) thermopower S, and (d) the figure of merit ZT as a function of asymmetry parameter η. Other parameters are the same as in Fig. 3. | |
As mentioned before, in all numerical calculations the phonon thermal conductance κph is ignored. However, this neglect of phonon thermal conductance is just valid in the situation κph/κe ≪ 1, and the condition of κph/κe > 1 may exist in practice. For the case of κph/κe > 1, we estimate the thermoelectric figure of merit ZT by adopting κph = 4k2Bπ2T/3h![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57 (an empirical expression for wires of size 200 nm) to model the phonon thermal conductance κph. It is found that the figure of merit will decrease to some extent, the optimization of thermoelectric efficiency in systems depends heavily on experimentally reducing the contribution of phonon thermal conductance κph as low as possible. The numerical results have shown that the N-TTQD-S device can achieve extremely high thermoelectric figure of merit ZT when the phonon conductance is ignored, and thus it could be used as a energy-conversion device that operates close to Carnot efficiency.58 For energy harvesting applications, both high figure of merit ZT and large power outputs are indispensable, however, there exists a trade off between them.59 In the system we considered, extremely large ZT values can be achieved within a wide range of adjustable parameters, which provides more possibilities for achieving large enough electrical power outputs.
57 (an empirical expression for wires of size 200 nm) to model the phonon thermal conductance κph. It is found that the figure of merit will decrease to some extent, the optimization of thermoelectric efficiency in systems depends heavily on experimentally reducing the contribution of phonon thermal conductance κph as low as possible. The numerical results have shown that the N-TTQD-S device can achieve extremely high thermoelectric figure of merit ZT when the phonon conductance is ignored, and thus it could be used as a energy-conversion device that operates close to Carnot efficiency.58 For energy harvesting applications, both high figure of merit ZT and large power outputs are indispensable, however, there exists a trade off between them.59 In the system we considered, extremely large ZT values can be achieved within a wide range of adjustable parameters, which provides more possibilities for achieving large enough electrical power outputs.
4 Conclusion
In summary, we have systematically analyzed the thermoelectric transport properties through a triangular triple quantum dot (TTQD) configuration with the central QD1 coupled to one metallic and one superconducting lead. Using the nonequilibrium Green's function method, we calculated the electrical conductance, thermal conductance, thermopower and figure of merit in the linear response regime. All these characteristics show clear dependence on the ratio of superconducting gap to interdot coupling Δ/t, lead coupling asymmetry and interference effect. Due to the interference effect and density distribution of single-particle states around the superconducting gap edges, the N-TTQD-S system shows outstanding thermoelectric performance over the N-TQD-S and N-TTQD-N systems. The single-platform and double-platform S = 0 structures in the spectrum of thermopower are attributed to different reasons: the former appears in the case of both the effective levels ε± inside the superconducting gap; while the latter appears when the effective level ε+ (or ε−) locates inside the superconducting gap, and the other level ε− (or ε+) must locate outside the superconducting gap at the same time, moreover, it must be far away from the Fermi-level. For the symmetric coupling cases, due to the large thermopower and remarkably small ratio of electrical conductance to thermal conductance in the vicinity of ε− = −Δ, the optimal figure of merit can even achieve an order of 102, by suitable regulation of the superconducting gap Δ and interdot coupling t. When the superconducting lead is weakly coupled to the QD1, the peak values of figure of merit near the superconducting gap edges increase as the asymmetric coupling parameter γ decreases. And the ZT value near the superconducting gap edges can increase several times in comparison to the symmetric coupling case, particularly when γ < 0.5. Moreover, it is also shown that the asymmetric interdot coupling parameter η has a significant impact on the thermoelectric coefficients. All these superior thermoelectric properties indicate that the N-TTQD-S device is a promising candidate for applications in energy harvesting, heat engines, power generators, thermal rectifiers and transistors.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the Shanxi Provincial applicable fundamental research Foundation (Grant No. 202103021223169), Shanxi Agricultural University Doctoral Research Start-up Grant (Grant No. 2021BQ104), Shanxi Province Doctor and Postdoctor Working Award Research Project (Grant No. SXBYKY2022002), Technological Innovation Programs of Higher Education Institutions in Shanxi (Grant No. 2020L0162), National Natural Science Foundation of China (Grant No. 12104321), Guangdong Basic and Applied Basic Research Foundation (Grant No. 2019A1515110210) and Shenzhen Science and Technology Program (Grant No. RCBS20200714114818341).
References
- R. Franz and G. Wiedemann, Ann. Phys. Chem., 1853, 165, 497 CrossRef.
- M. Cutler and N. F. Mott, Phys. Rev., 1969, 181, 1336 CrossRef CAS.
- M. Turek and K. A. Matveev, Phys. Rev. B: Condens. Matter, 2002, 65, 115332 CrossRef.
- J. Koch, F. von Oppen, Y. Oreg and E. Sela, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 195107 CrossRef.
- B. Kubala and J. Konig, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195316 CrossRef.
- X. Zianni, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 045344 CrossRef.
- X. M. Zhang, X. Chen and W. Lu, Phys. Lett. A, 2008, 372, 2816 CrossRef CAS.
- K. Schwab, E. A. Henriksen, J. M. Worlock and M. L. Roukes, Nature, 2000, 404, 974 CrossRef CAS PubMed.
- P. Reddy, S. Y. Jang, R. A. Segalman and A. Majumdar, Science, 2007, 315, 1568 CrossRef CAS PubMed.
- A. I. Hochbaum, R. Chen, R. D. Delgado, W. Liang, E. C. Garnett, M. Najarian, A. Majumdar and P. Yang, Nature, 2008, 451, 163 CrossRef CAS PubMed.
- A. I. Boukai, Y. Bunimovich, J. Tahir-Kheli, J. K. Yu, W. A. Goddard III and J. R. Heath, Nature, 2008, 451, 168 CrossRef CAS PubMed.
- K. Baheti, J. A. Malen, P. Doak, P. Reddy, S. Y. Jang, T. D. Tilley, A. Majumdar and R. A. Segalman, Nano Lett., 2008, 8, 715 CrossRef CAS PubMed.
- L. G. C. Rego and G. Kirczenow, Phys. Rev. Lett., 1998, 81, 232 CrossRef CAS.
- Y. Dubi and M. Di Ventra, Nano Lett., 2009, 9, 97 CrossRef CAS PubMed.
- R. Świrkowicz, M. Wierzbicki and J. Barnaś, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 195409 CrossRef.
- P. Trocha and J. Barnaś, Phys. Rev. B, 2017, 95, 165439 CrossRef.
- H. Yao, P. B. Niu, C. Zhang, W. P. Xu, Z. J. Li and Y. H. Nie, Eur. Phys. J. B, 2018, 91, 57 CrossRef.
- H. H. Fu and K. L. Yao, J. Appl. Phys., 2010, 108, 084510 CrossRef.
- Y. Han, W. J. Gong, H. M. Wang and A. Du, J. Appl. Phys., 2012, 112, 123701 CrossRef.
- Q. Wang, Q. H. Xie, Y. H. Nie and W. Ren, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 75102 CrossRef.
- L. Xiong and L. Yi, Phys. Lett. A, 2014, 378, 1392 CrossRef CAS.
- X. Yang, J. Zheng, C. L. Li and Y. Guo, J. Phys.: Condens. Matter, 2015, 27, 075302 CrossRef CAS PubMed.
- Z. L. He, J. Y. Bai, L. Cui, Q. Li, G. H. Han and B. L. Zhang, Phys. B, 2015, 477, 64 CrossRef CAS.
- S. C. Tian, Opt. Commun., 2016, 368, 129 CrossRef CAS.
- L. Xu, Z. J. Li, H. Y. Hou, P. B. Niu and Y. H. Nie, J. Phys. D: Appl. Phys., 2016, 49, 405305 CrossRef.
- M. Wierzbicki and R. Swirkowicz, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075410 CrossRef.
- P. Trocha and J. Barnaś, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 085408 CrossRef.
- H. Yao, C. Zhang, Z. J. Li, Y. H. Nie and P. B. Niu, J. Phys. D: Appl. Phys., 2018, 51, 175301 CrossRef.
- H. Yao, C. Zhang, P. B. Niu, Z. J. Li and Y. H. Nie, Phys. Lett. A, 2018, 382, 3220 CrossRef CAS.
- K. P. Wójcik and I. Weymann, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 165303 CrossRef.
- R. S. Deacon, Y. Tanaka, A. Oiwa, R. Sakano, K. Yoshida, K. Shibata, K. Hirakawa and S. Tarucha, Phys. Rev. Lett., 2010, 104, 076805 (
Phys. Rev. B: Condens. Matter Mater. Phys.
, 2010
, 81
, 121308
) CrossRef CAS PubMed.
- Q. F. Sun, J. Wang and T. H. Lin, Phys. Rev. B: Condens. Matter, 1999, 59, 3831 CrossRef CAS ; 1999, 59, 13126; 2001, 64, 134521..
- J. Wang, Y. Wei, H. Guo, Q. F. Sun and T. H. Lin, Phys. Rev. B: Condens. Matter, 2001, 64, 104508 CrossRef.
- T. Domański, A. Donabidowicz and K. I. Wysokiński, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 104514 CrossRef ; 2008, 78, 144515..
- T. Domański and A. Donabidowicz, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 073105 CrossRef.
- Y. P. Zhang, H. Yu, Y. F. Gao and J. Q. Liang, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 205310 CrossRef.
- R. López, M. S. Choi and R. Aguado, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 045132 CrossRef.
- F. Jiang, Y. H. Yan, S. K. Wang and Y. J. Yan, Phys. Lett. A, 2017, 381, 3831 CrossRef CAS.
- T. F. Fang, A. M. Guo and Q. F. Sun, Phys. Rev. B, 2018, 97, 235115 CrossRef CAS.
- X. Q. Wang, S. F. Zhang, Y. Han and W. J. Gong, Phys. Rev. B, 2019, 100, 115405 CrossRef CAS.
- Z. Scherübl, A. Pályi and S. Csonka, Beilstein J. Nanotechnol., 2019, 10, 363 CrossRef PubMed.
- J. V. Veen, D. D. Jong, L. Han, C. Prosko, P. Krogstrup, J. D. Watson, L. P. Kouwenhoven and W. Pfaff, Phys. Rev. B, 2019, 100, 174508 CrossRef.
- R. Taranko, K. Wrześniewski, B. Baran, I. Weymann and T. Domański, Phys. Rev. B, 2021, 103, 165430 CrossRef CAS.
- S. Y. Hwang, R. López and D. Sánchez, Phys. Rev. B, 2016, 94, 054506 CrossRef.
- W. P. Xu, Y. Y. Zhang, Q. Wang, Z. J. Li and Y. H. Nie, Phys. Lett. A, 2016, 380, 958 CrossRef CAS.
- L. Xu, Z. J. Li, Q. Wang and Y. H. Nie, AIP Adv., 2016, 6, 125012 CrossRef.
- P. Zhang, H. Wu, J. Chen, S. A. Khan, P. Krogstrup, D. Pekker and S. M. Frolov, Phys. Rev. Lett., 2022, 128, 046801 CrossRef CAS PubMed.
- K. I. Wysokiński, J. Phys.: Condens. Matter, 2012, 24, 335303 CrossRef PubMed.
- Z. Cao, T. F. Fang, L. Li and H. G. Luo, Appl. Phys. Lett., 2015, 107, 212601 CrossRef.
- G. Michałek, M. Urbaniak, B. R. Bulka, T. Domański and K. I. Wysokiński, Phys. Rev. B, 2016, 93, 235440 CrossRef.
- R. Hussein, M. Governale, S. Kohler, W. Belzig, F. Giazotto and A. Braggio, Phys. Rev. B, 2019, 99, 075429 CrossRef CAS.
- K. Wrześniewski and I. Weymann, Phys. Rev. B, 2020, 101, 155409 CrossRef.
- S. Verma and A. Singh, J. Phys.: Condens. Matter, 2022, 34, 155601 CrossRef CAS PubMed.
- S. Y. Hwang, D. Sánchez and R. López, New J. Phys., 2016, 18, 093024 CrossRef.
- D. M. T. Kuo and Y. C. Chang, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 205321 CrossRef.
- J. C. Cuevas, A. Martín-Rodero and Y. A. Levy, Phys. Rev. B: Condens. Matter, 1996, 54, 7366 CrossRef CAS PubMed.
- D. M. T. Kuo, C. C. Chen and Y. C. Chang, Phys. Rev. B, 2017, 95, 075432 CrossRef.
- D. M. T. Kuo and Y. C. Chang, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 205321 CrossRef.
- D. M. T. Kuo and Y. C. Chang, Nanomaterials, 2022, 12, 3357 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Cai-Ping
Cheng
,
Li-Li
Li
,
Rui
Guo
,
Yong
Guo
and
Chao
Zhang
,
Cai-Ping
Cheng
,
Li-Li
Li
,
Rui
Guo
,
Yong
Guo
and
Chao
Zhang
 *
*

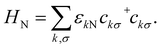
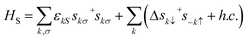
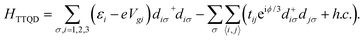
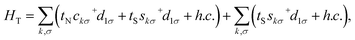
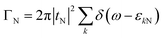 and
and 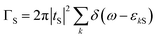 . Within the wide-band approximation, the coupling parameters ΓN and ΓS become independent of energy and can be considered as constants. In addition, we also introduce γ = ΓS/ΓN to describe the asymmetry of the coupling of QD1 to the N and S lead.
. Within the wide-band approximation, the coupling parameters ΓN and ΓS become independent of energy and can be considered as constants. In addition, we also introduce γ = ΓS/ΓN to describe the asymmetry of the coupling of QD1 to the N and S lead.
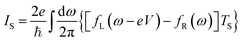
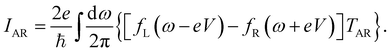
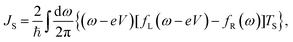
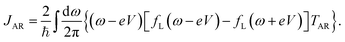
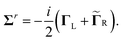

![[capital Gamma, Greek, tilde]](https://www.rsc.org/images/entities/b_char_e1eb.gif) R =
R = ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) S(ω)Γ0R
S(ω)Γ0R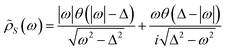

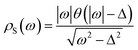
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) S(ω) and ρS(ω) denote different physical significance:
S(ω) and ρS(ω) denote different physical significance: ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) S(ω) represents the dimensionless modified BCS density of states, while ρS(ω) represents the ratio of the superconducting density of states to the metallic density of states.
S(ω) represents the dimensionless modified BCS density of states, while ρS(ω) represents the ratio of the superconducting density of states to the metallic density of states.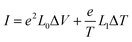
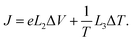
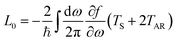
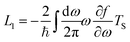
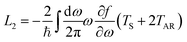
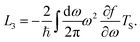
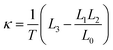
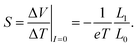
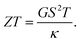
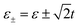 , moreover, for the triangular triple quantum dot (TTQD) configuration, the effective levels renormalize to
, moreover, for the triangular triple quantum dot (TTQD) configuration, the effective levels renormalize to 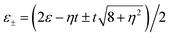 . In particular, in the symmetric coupling cases with η = 1, the effective levels degenerate to ε+ = ε + t and ε− = ε − 2t.
. In particular, in the symmetric coupling cases with η = 1, the effective levels degenerate to ε+ = ε + t and ε− = ε − 2t.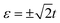 in the spectra of electric conductance G and thermal conductance κ, which is in association with the single-particle tunnelling processes through the two effective levels,
in the spectra of electric conductance G and thermal conductance κ, which is in association with the single-particle tunnelling processes through the two effective levels, 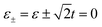 . By the same token, for the N-TTQD-N system in the symmetric coupling case with η = 1, the effective levels become ε+ = ε + t and ε− = ε − 2t, the resonance peaks appear in the vicinity of ε = −t and ε = 2t.
. By the same token, for the N-TTQD-N system in the symmetric coupling case with η = 1, the effective levels become ε+ = ε + t and ε− = ε − 2t, the resonance peaks appear in the vicinity of ε = −t and ε = 2t.

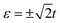 derive from the single-level Andreev tunnelling processes, while the four lower side peaks at
derive from the single-level Andreev tunnelling processes, while the four lower side peaks at 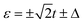 are induced by the conventional single-particle tunnelling through the superconducting gap edges. In addition, on account of that the electrons in the metallic lead are mainly concentrated around the Fermi level, the single-particle tunnelling through the superconducting gap edges is suppressed, thus, the two peaks associated with the single-level Andreev tunnelling are much higher than those associated with the conventional single-particle tunnelling. The Andreev tunnelling does not contribute to thermal conductance κ due to no electron states inside the superconducting gap. As a consequence, the thermal conductance exhibits only four peaks in the vicinity of
are induced by the conventional single-particle tunnelling through the superconducting gap edges. In addition, on account of that the electrons in the metallic lead are mainly concentrated around the Fermi level, the single-particle tunnelling through the superconducting gap edges is suppressed, thus, the two peaks associated with the single-level Andreev tunnelling are much higher than those associated with the conventional single-particle tunnelling. The Andreev tunnelling does not contribute to thermal conductance κ due to no electron states inside the superconducting gap. As a consequence, the thermal conductance exhibits only four peaks in the vicinity of 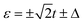 . For the N-TTQD-S system in the symmetric coupling case with η = 1, as the blue line in the spectrum of thermal conductance shows, due to the effective levels changing, the two high peaks resulting from single-level Andreev tunnelling move to ε = −t and ε = 2t, meanwhile, the four lower side peaks induced by the single-particle tunnelling move to ε = −t ±Δ and ε = 2t ±Δ. The resonance peaks in the spectrum of thermal conductance make corresponding movements.
. For the N-TTQD-S system in the symmetric coupling case with η = 1, as the blue line in the spectrum of thermal conductance shows, due to the effective levels changing, the two high peaks resulting from single-level Andreev tunnelling move to ε = −t and ε = 2t, meanwhile, the four lower side peaks induced by the single-particle tunnelling move to ε = −t ±Δ and ε = 2t ±Δ. The resonance peaks in the spectrum of thermal conductance make corresponding movements.



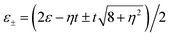 , as clearly seen in all spectra of thermoelectric coefficients in Fig. 8(a)–(d). In the weak coupling case with γ = 0.1, all the electron tunnelling processes are suppressed, thus, the amplitude in both electrical conductance and thermal conductance spectra, obviously decrease in comparison with the case of γ = 1. In addition, the lower single-particle tunnelling resonance peaks associated with the ε+ ∼ ±Δ increase with the increasing η, while those associated with the ε− ∼ ±Δ decrease with the increasing η, as clearly seen in Fig. 8(a) and (b). The different behaviors are mainly attributed to the influence of the interference effect on the different tunnelling transport channels. In contrast, the amplitude of thermopower S shows less dependence on the interdot coupling asymmetry η. The figure of merit completely depends on the above behaviors of thermoelectric coefficients (G, κ and S), it reaches a maximum value in the vicinity of ε± ∼ ±Δ, especially near ε− ∼ −Δ. Moreover, the figure of merit does not increase blindly with the increasing interdot coupling asymmetry η, too large an asymmetry parameter (η > 1) would also suppress the enhancement of thermoelectric efficiency. It is further strongly confirmed in the inset of Fig. 8(d), where the figure of merit ZT is plotted as a function of asymmetry parameter η with
, as clearly seen in all spectra of thermoelectric coefficients in Fig. 8(a)–(d). In the weak coupling case with γ = 0.1, all the electron tunnelling processes are suppressed, thus, the amplitude in both electrical conductance and thermal conductance spectra, obviously decrease in comparison with the case of γ = 1. In addition, the lower single-particle tunnelling resonance peaks associated with the ε+ ∼ ±Δ increase with the increasing η, while those associated with the ε− ∼ ±Δ decrease with the increasing η, as clearly seen in Fig. 8(a) and (b). The different behaviors are mainly attributed to the influence of the interference effect on the different tunnelling transport channels. In contrast, the amplitude of thermopower S shows less dependence on the interdot coupling asymmetry η. The figure of merit completely depends on the above behaviors of thermoelectric coefficients (G, κ and S), it reaches a maximum value in the vicinity of ε± ∼ ±Δ, especially near ε− ∼ −Δ. Moreover, the figure of merit does not increase blindly with the increasing interdot coupling asymmetry η, too large an asymmetry parameter (η > 1) would also suppress the enhancement of thermoelectric efficiency. It is further strongly confirmed in the inset of Fig. 8(d), where the figure of merit ZT is plotted as a function of asymmetry parameter η with 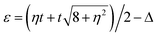 (corresponding to ε− = −Δ). The highest figure of merit can be obtained in the vicinity of η = 1, where the interference effect is most effective in improving thermoelectric performance.
(corresponding to ε− = −Δ). The highest figure of merit can be obtained in the vicinity of η = 1, where the interference effect is most effective in improving thermoelectric performance.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57 (an empirical expression for wires of size 200 nm) to model the phonon thermal conductance κph. It is found that the figure of merit will decrease to some extent, the optimization of thermoelectric efficiency in systems depends heavily on experimentally reducing the contribution of phonon thermal conductance κph as low as possible. The numerical results have shown that the N-TTQD-S device can achieve extremely high thermoelectric figure of merit ZT when the phonon conductance is ignored, and thus it could be used as a energy-conversion device that operates close to Carnot efficiency.58 For energy harvesting applications, both high figure of merit ZT and large power outputs are indispensable, however, there exists a trade off between them.59 In the system we considered, extremely large ZT values can be achieved within a wide range of adjustable parameters, which provides more possibilities for achieving large enough electrical power outputs.
57 (an empirical expression for wires of size 200 nm) to model the phonon thermal conductance κph. It is found that the figure of merit will decrease to some extent, the optimization of thermoelectric efficiency in systems depends heavily on experimentally reducing the contribution of phonon thermal conductance κph as low as possible. The numerical results have shown that the N-TTQD-S device can achieve extremely high thermoelectric figure of merit ZT when the phonon conductance is ignored, and thus it could be used as a energy-conversion device that operates close to Carnot efficiency.58 For energy harvesting applications, both high figure of merit ZT and large power outputs are indispensable, however, there exists a trade off between them.59 In the system we considered, extremely large ZT values can be achieved within a wide range of adjustable parameters, which provides more possibilities for achieving large enough electrical power outputs.