Open Access Article
Open Access ArticleFluorescence excitation enhancement by waveguiding nanowires†
Ivan N.
Unksov‡
 a,
Nicklas
Anttu‡
a,
Nicklas
Anttu‡
 b,
Damiano
Verardo
b,
Damiano
Verardo
 ac,
Fredrik
Höök
ac,
Fredrik
Höök
 d,
Christelle N.
Prinz
d,
Christelle N.
Prinz
 a and
Heiner
Linke
a and
Heiner
Linke
 *a
*a
aNanoLund and Solid State Physics, Lund University, Box 118, 22100 Lund, Sweden. E-mail: heiner.linke@ftf.lth.se
bPhysics, Faculty of Science and Engineering, Åbo Akademi University, FI-20500 Turku, Finland
cAlignedBio AB, Medicon Village, Scheeletorget 1, 223 63 Lund, Sweden
dDepartment of Physics, Chalmers University of Technology, 41296 Gothenburg, Sweden
First published on 20th February 2023
Abstract
The optical properties of vertical semiconductor nanowires can allow an enhancement of fluorescence from surface-bound fluorophores, a feature proven useful in biosensing. One of the contributing factors to the fluorescence enhancement is thought to be the local increase of the incident excitation light intensity in the vicinity of the nanowire surface, where fluorophores are located. However, this effect has not been experimentally studied in detail to date. Here, we quantify the excitation enhancement of fluorophores bound to a semiconductor nanowire surface by combining modelling with measurements of fluorescence photobleaching rate, indicative of the excitation light intensity, using epitaxially grown GaP nanowires. We study the excitation enhancement for nanowires with a diameter of 50–250 nm and show that excitation enhancement reaches a maximum for certain diameters, depending on the excitation wavelength. Furthermore, we find that the excitation enhancement decreases rapidly within tens of nanometers from the nanowire sidewall. The results can be used to design nanowire-based optical systems with exceptional sensitivities for bioanalytical applications.
1. Introduction
Semiconductor nanowires (NWs) can enhance fluorescence signals and are thus promising for optical biosensing, as demonstrated for a range of material systems, first for ZnO nanorods,1,2 and later for similar nanostructures of ZnO,3–6 GaP,7,8 Si,9,10 and InAs.11 The potential of such high-sensitivity fluorescence biosensing has been shown for several biomolecular systems.12 For example, ZnO nanorods have been used for detection of human α-fetoprotein,13 carcinoembryonic antigen,5,13 and unlabeled ATP14via fluorescence changes of DNA-templated silver nanoclusters in proximity of nanorods. Due to simultaneous readout from multiple NWs, these biosensors also have a potential for high throughput applications. For detection of proteins, a conventional method on planar substrates is the enzyme-linked immunosorbent assay (ELISA). Compared to this benchmark, ZnO nanorods15 have demonstrated higher or comparable sensitivity for detection of several biomarkers,15 and recently for detection16 of SARS-CoV-2 nucleocapsid proteins. GaP NWs have been used for single-molecule detection of proteins diffusing in supported lipid bilayers,17 of actin filaments propelled by myosin motors7 and for antibody-based detection of protein biomarkers at low concentration in human serum.8Quantitatively, the fluorescence signal from fluorophores bound to GaP NWs with wavelength-matching diameter is estimated to be enhanced 10–200-fold compared to fluorophores bound to a planar surface.8,18 Comparable fluorescence enhancement has also been shown on ZnO nanorods.5 Based on current understanding,19 three optical effects contribute to the enhanced signal from surface-bound fluorophores on NWs: (i) a waveguiding effect, by which light emitted from surface bound fluorophores is coupled into lightguiding modes in the NW,7,20,21 resulting in directional emission22–24 from the NW; (ii) the NW's influence on the radiative recombination rate, the so-called Purcell effect (this has been described for emission from InP NWs,22,25 and one can expect a corresponding effect on fluorophores bound to a NW); and (iii) the enhancement of excitation intensity at the location of the fluorophore.5,6,26,27 Contribution (iii) depends on excitation wavelength, thus investigating it separately from the other effects gives rise to results applicable to any fluorophore excited at a given wavelength.
Here, we address the contribution (iii), the enhancement of the excitation intensity, and quantitatively characterize the fluorescence excitation of fluorophores near the interface of GaP NWs by combining modelling and measurements of fluorescence photobleaching rate. Modelling-based studies of local field enhancement have previously been performed for ZnO5 and GaAs26,27 nanorods and nanowires. In ref. 27, the enhancement of excitation and emission was simulated, showing a decay within 50 nm from the NW interface, which was supported by intensity measurements; the modelling has also demonstrated waveguiding and an altered angular radiation pattern on the GaAs NWs. In these previous studies, however, the experimental quantification was based on absolute emission intensities which can be influenced by all three of the above contributions (i), (ii) and (iii). Here, for GaP nanowires, we use photobleaching rate to measure the excitation intensity enhancement specifically for a range of NW diameters.
We study vertical GaP NWs because they are expected to exhibit strong fluorescence enhancement due to their high refractive index (>3.1 for visible light). Additionally, the low absorption coefficient of GaP for wavelengths λ > 460 nm (ref. 28) limits the parasitic absorption of both excitation light and fluorescence signal. It should be noted that among the III–V semiconductor materials typically used for NW synthesis, GaAs, InAs and InP have refractive indexes even higher than that of GaP (Fig. S11†). However, these materials exhibit a non-negligible absorbance for visible light, which makes them less optimal than GaP NWs for fluorescence lightguiding. Moreover, due to their zinc blende structure, the GaP nanowires used in this study present an indirect band gap and therefore do not show prominent inherent photoluminescence, which otherwise could interfere with the signal from the fluorophores.
Here, Maxwell's equations were used to model19 light scattering by the NWs and the substrate by considering the numerical aperture (NA) of the illumination objective. This enables a prediction of the enhancement of the incident light intensity at the location of the fluorophores. We also probed the excitation enhancement experimentally by measuring the rate of photobleaching of fluorophores that were excited at the wavelength λ = 640 nm when bound to Al2O3-coated GaP NWs and reference planar Al2O3-coated GaP substrate. We obtained the photobleaching rate R from the time evolution of the signal in each sample, which provides a signal proportional to excitation enhancement29,30 without the calibrations otherwise required for measurements of absolute intensity. We additionally varied the thickness of the Al2O3 oxide layer on the GaP NWs, providing a quantitative determination of the decrease of local incident light intensity with increasing distance between fluorophore and NW surface at a length scale of tens of nm, in line with our modelling results.
2. Methods
2.1. Electromagnetic optics simulations
By modelling the electric field |E(rfluor)|2 induced by the incident light at the location rfluor (the vector that gives the position of the fluorophore in three dimensions (3D)), we obtained the excitation enhancement. We give below a summary of the modelling and refer to Sections 1 and 2 of the ESI† for full technical details.We modelled the diffraction of the incident light by solving the Maxwell equations with the finite-element method in Comsol Multiphysics, similarly as in ref. 22. The modelling was done for the excitation wavelength λ = 640 nm corresponding to the laser wavelength used in our experiments. The optical response of the materials is described by their refractive index n. At λ = 640 nm, we used n = 3.31 for GaP,28n = 1.77 for Al2O3,31 and n = 1.33 for the surrounding water.
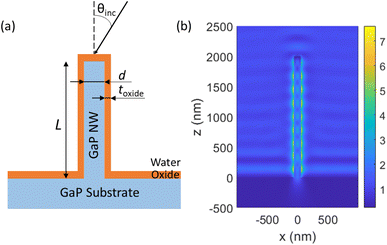
We modelled a single vertical GaP NW of diameter d and length L, standing on top of a semi-infinite GaP substrate, with a conformal Al2O3 oxide layer of thickness toxide coating the surface of both the NW and the substrate (see Fig. 1a). In the experiments, the NWs were functionalized with a thin (<10 nm (ref. 32 and 33)) layer of biomolecules, which is expected to have a negligible influence on the optical properties.
For illumination in a widefield microscope, we followed experimental conditions and assumed incoherent light from all angles θinc within the NA of the illumination objective (that is, we considered θinc < asin(NA/n) for the illumination). For NA = 1 and a surrounding media of n = 1.33, this corresponds to θinc < 49°. We modelled the electric field |E(rfluor)|2 that an incident plane wave gives rise to, separately for each incident angle and for each of the two orthogonal polarization states. For the overall enhancement, we integrated over the contributing angles and both polarization states. This procedure resulted in a modelled excitation enhancement ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) NW(rfluor) for a given fluorescence position. By averaging over the axial positions of the fluorophore on the nanowire sidewall, we obtained MNW, the average enhancement for surface bound fluorophores as compared to free fluorophores in water (without NWs, oxide layer or substrate present). As a reference, we modelled also Mplanar, the enhancement of incident light intensity for a fluorophore located on top of an Al2O3 layer of thickness toxide = 10 nm deposited on a GaP planar substrate, again as compared to free fluorophores in water.
NW(rfluor) for a given fluorescence position. By averaging over the axial positions of the fluorophore on the nanowire sidewall, we obtained MNW, the average enhancement for surface bound fluorophores as compared to free fluorophores in water (without NWs, oxide layer or substrate present). As a reference, we modelled also Mplanar, the enhancement of incident light intensity for a fluorophore located on top of an Al2O3 layer of thickness toxide = 10 nm deposited on a GaP planar substrate, again as compared to free fluorophores in water.
2.2. Photobleaching rate measurements
The fluorescence intensity of a fluorophore subject to photobleaching can be described by a mono-exponential model, I(t) ∝ e−Rt,34 where t is the time and R is the photobleaching rate. R is a useful measure for excitation intensity at sufficiently low light conditions when photobleaching is limited by the absorption of incident photons and, therefore, R increases linearly with excitation intensity.29 Note that this contrasts with the case of saturation of excitation at high excitation intensity, where de-excitation becomes the rate-limiting process, and R is then significantly affected by the radiative de-excitation rate krad and does not increase linearly with the light intensity. In our experiments, we checked that R increases linearly with increasing excitation power p (Fig. 2e and S5†), confirming that we are not in the saturation regime (see ESI Section 3 for full data†). In addition, we also find that the emission intensity increases linearly with p, again confirming that the measurements were carried out without the saturation (Fig. S6†). The excitation enhancement by NWs was obtained from measuring MNW/Mplanar, where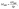
 RNW is the photobleaching rate of the fluorophores bound to the NW's Al2O3 coating, and Rplanar is the corresponding rate on a planar GaP reference sample with Al2O3 coating.
RNW is the photobleaching rate of the fluorophores bound to the NW's Al2O3 coating, and Rplanar is the corresponding rate on a planar GaP reference sample with Al2O3 coating.
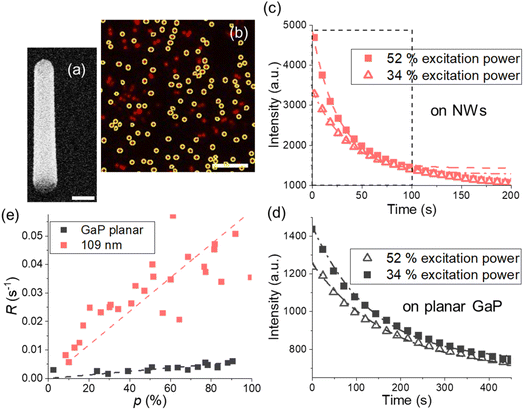 | ||
| Fig. 2 (a) GaP NW, SEM image under 30° tilt from top view, scale bar is 200 nm. (b) Fluorescence on the NWs with d = 109 ± 10 nm and toxide = 10 nm Al2O3, scale bar is 10 μm, average intensity from encircled areas is used for photobleaching curves. (c and d) Typical photobleaching curves fitted with a single exponent (dashed lines) for (c) the NW sample with d = 109 ± 10 nm and (d) GaP planar substrate with the same toxide = 10 nm. In (c), the first 100 s taken for the analysis are framed with a dashed black line. (e) Photobleaching rates for planar GaP and the NWs at varied excitation power p. Each data point corresponds to a photobleaching curve obtained from a different position on a sample. Photobleaching rates for other diameters are shown in Fig. S5.† | ||
2.3. Nanowire growth and surface functionalization
GaP NWs (Fig. 2a) were seeded by 50 nm Au nanoparticles and vertically grown using metalorganic vapour-phase epitaxy (MOVPE) (see ESI Section 4 for the details†). For experiments with NWs of a varied diameter, we used NWs with L = 1.7–2.8 μm, coated with toxide = 10 nm Al2O3 using ALD (Savannah S100, Cambridge NanoTech). When toxide was varied, NW samples from a single growth were used, with d = 109 ± 10 nm and L = 1.7 ± 0.2 μm (Fig. S8†). The diameters were measured at half-height of the NWs. When defined as (dbottom/dtop − 1), tapering of the NWs varied between samples in a range of 0.1–0.6. This tapering was not considered in the model. For an overview of the samples used in this study, see Table S1.†For functionalization with fluorophores, NW and planar Al2O3 coated substrates were glued into flow channels (sticky-Slide VI 0.4, ibidi GmbH) (ESI Section 5†) and washed with phosphate buffered saline (PBS, P4417, Sigma-Aldrich) pH 6, then incubated for 5 minutes with biotin-bovine serum albumin (BSA, Sigma-Aldrich), at 30 μM in PBS pH 7.0. Unbound BSA was washed away from the chamber using PBS pH 6, and the sample was incubated for 5 minutes with 50 μL of Alexa Fluor 647 streptavidin conjugate (S21374, ThermoFisher Scientific), at 30 μM in PBS pH 7.2, in the dark. After washing off the excess of unbound dyes with PBS at pH 6, the samples were kept in the dark until imaging, which was done in the flow channels filled with PBS, within a few hours from sample preparation. Both surface functionalization and imaging were carried out at room temperature.
2.4. Microscopy and image analysis
For imaging, we used a Nikon TE2000-U microscope with a Nikon Fluor 60X/1.00 DIC water immersion objective and 640 nm laser (see ESI Section 5 for setup details†). For image analysis, we used ImageJ35 and the Image Stabilizer plugin36 to correct for lateral drift. For more information on image analysis, see ESI Section 5.† Photobleaching curves were generated using the average intensities from the detected NWs (Fig. 2b) in a field of view and fitted with the model34I(t) = Ae−Rt + Ib, where Ib is an offset. The photobleaching rates R obtained at varied excitation power were fitted with a linear model (Fig. 2e and S5†).At times longer than 100 s, the fluorescence decay was observed to slightly slow down for NW samples (Fig. 2c). Therefore, we analyze only the data from the first 100 s of photobleaching when we compare the experimental results with modelling which assumes a time-independent MNW. However, for fluorophores on a planar GaP, where bleaching is the slowest, the intensity change in the first 100 s is in turn slightly deviating from mono-exponential decay (Fig. 2d), and exclusively for the planar samples we therefore chose a time window larger than 300 s.
3. Results
3.1. Modelling of excitation enhancement
We model the ratio that is, the excitation enhancement provided by NWs as compared to planar substrate. In Fig. 3, we show the modelled
that is, the excitation enhancement provided by NWs as compared to planar substrate. In Fig. 3, we show the modelled  for NWs with varying d at a fixed toxide = 10 nm and L = 2 μm. Here Mplanar = 0.57, i.e. the local intensity on the planar substrate is less than that in water (due to destructive interference between incident and reflected light). Thus ratios
for NWs with varying d at a fixed toxide = 10 nm and L = 2 μm. Here Mplanar = 0.57, i.e. the local intensity on the planar substrate is less than that in water (due to destructive interference between incident and reflected light). Thus ratios  mean an enhancement of excitation on the NW surface compared to a free fluorophore in water. For all considered d, the modelling predicts
mean an enhancement of excitation on the NW surface compared to a free fluorophore in water. For all considered d, the modelling predicts  with the smallest value of 3.5 at the smallest d = 50 nm, and a peak of 8.9 at d ≈ 110 nm (Fig. 3). There is a second peak of
with the smallest value of 3.5 at the smallest d = 50 nm, and a peak of 8.9 at d ≈ 110 nm (Fig. 3). There is a second peak of  at d = 220 nm. Furthermore, the peaks shift with varying excitation wavelength in a way that keeps the ratio dpeaknGaP(λ)/λ constant (Fig. S2†), which is useful to know if another wavelength is employed.
at d = 220 nm. Furthermore, the peaks shift with varying excitation wavelength in a way that keeps the ratio dpeaknGaP(λ)/λ constant (Fig. S2†), which is useful to know if another wavelength is employed.
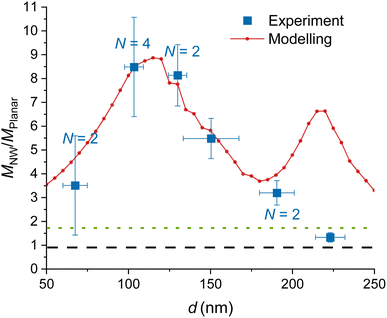 | ||
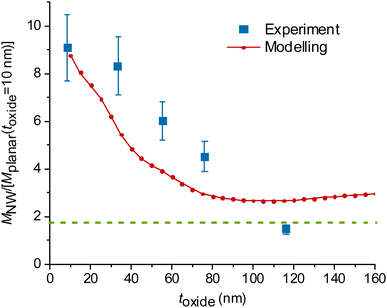
| Fig. 3 Experimental and modelled excitation enhancement MNW/Mplanar as a function of the GaP NW core diameter d for NA = 1, λ = 640 nm, toxide = 10 nm. MNW/Mplanar > 1.75 (dotted green line) corresponds to an enhancement on the NW surface compared to a free fluorophore in water. Numbers N > 1 indicate that multiple data points for samples with similar (±10 nm) diameter were averaged, and uncertainty was taken as standard deviation where it exceeds the measurement uncertainty. For the raw data, see Fig. S7.† | ||
At a fixed diameter d = 110 nm, close to the peak of  the model predicts a drop from
the model predicts a drop from  at toxide = 10 nm to
at toxide = 10 nm to  at toxide = 80 nm (Fig. 4). Such a rapid drop with increasing distance from the GaP sidewall of the NW core is expected based on the spatially resolved enhancement of the incident intensity in the vicinity of the NW (Fig. 1b and, for variation of toxide, Fig. S4†). From the spatially resolved enhancement, it is also expected that NW length has only a minor effect on the enhancement: for L = 2 μm, we find nine interference lobes in the axial direction, and hence a variation of the NW length is expected to average over multiple such lobes. Indeed, as shown in Fig. S1,† we found only a weak dependence of the enhancement on L for L ≥ 1 μm.
at toxide = 80 nm (Fig. 4). Such a rapid drop with increasing distance from the GaP sidewall of the NW core is expected based on the spatially resolved enhancement of the incident intensity in the vicinity of the NW (Fig. 1b and, for variation of toxide, Fig. S4†). From the spatially resolved enhancement, it is also expected that NW length has only a minor effect on the enhancement: for L = 2 μm, we find nine interference lobes in the axial direction, and hence a variation of the NW length is expected to average over multiple such lobes. Indeed, as shown in Fig. S1,† we found only a weak dependence of the enhancement on L for L ≥ 1 μm.
3.2. Experiments
We determine the photobleaching rate R experimentally for different excitation powers p (Fig. 2e and S5†). The slope of the plots is considered as and used for calculation of
and used for calculation of  The data obtained for multiple NW samples of similar d (±10 nm), with fixed toxide = 10 nm, are averaged together (raw data without averaging are shown in Fig. S7,† the samples are specified in Table S1†). The measurements in Fig. 3 show an enhancement
The data obtained for multiple NW samples of similar d (±10 nm), with fixed toxide = 10 nm, are averaged together (raw data without averaging are shown in Fig. S7,† the samples are specified in Table S1†). The measurements in Fig. 3 show an enhancement  for d = 100–150 nm, in agreement with the modelling, despite some heterogeneity of measurements between different samples, indicated by uncertainty bars.
for d = 100–150 nm, in agreement with the modelling, despite some heterogeneity of measurements between different samples, indicated by uncertainty bars.
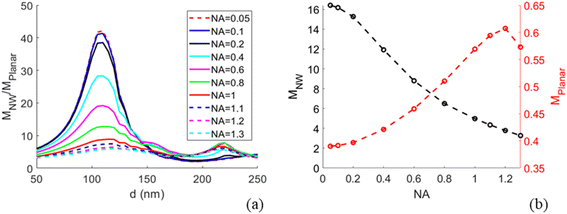
Modelling predicts a second, less-pronounced peak at d = 220 nm (Fig. 3), which we do not observe experimentally. The absence of this peak in experimental data may be due to several reasons. One possible reason is that tapering of the NWs, pronounced for larger diameters (see Methods) may alter the position and height of the second peak. Another reason can be a possibly smaller effective NA in experiments than the modelled NA, due to a narrow laser beam in our setup (for more detail, see ESI Section 5†). Modelling suggests that the second peak is flattened at NA < 0.6 (Fig. 5a).
We also find a rapid decay of the enhancement with the distance between fluorophores and the GaP interface of the NW, similar to the aforementioned trend seen in the modelled data (Fig. 4). For these experiments, we varied the distance by increasing toxide for the NW core diameter d = 109 ± 10 nm, at which we observed the largest enhancement (Fig. 3). As we study the effect of the distance between fluorophores and NWs, we used a single planar GaP reference, with a fixed toxide = 10 nm.
3.3. Modelling of auxiliary effects
With the modelling approach agreeing well with experiments, we extended the study by additional modelling investigations for future use in designing NW sensing platforms for readout with an optical microscope. In particular, near the peak of enhancement at d ≈ 110 nm we find that the modelled MNW/Mplanar increases strongly with decreasing NA (Fig. 5), a parameter of importance for low-cost imaging applications. By changing the NA to 0.05, we predict a 5-fold increase in excitation enhancement, with compared to
compared to  at NA = 1. This expected enhancement is partly due to the decrease in Mplanar from 0.57 to 0.39 but mostly due to an increase in MNW from 5.1 to 16.4. Thus, the NW interface and planar surface exhibit opposite tendencies with decreasing NA. The planar surface shows increased partial destructive interference between incident and reflected light, which reduces the electric field strength. This destructive interference is more prominent for normally incident light than for the light incident from a distribution of angles. In turn, for NWs with d ≈ 110 nm, the field enhancement according to our modelling is dominated by light incident from a narrow cone close to normal incidence (see Fig. S3b† for angle-resolved field enhancement).
at NA = 1. This expected enhancement is partly due to the decrease in Mplanar from 0.57 to 0.39 but mostly due to an increase in MNW from 5.1 to 16.4. Thus, the NW interface and planar surface exhibit opposite tendencies with decreasing NA. The planar surface shows increased partial destructive interference between incident and reflected light, which reduces the electric field strength. This destructive interference is more prominent for normally incident light than for the light incident from a distribution of angles. In turn, for NWs with d ≈ 110 nm, the field enhancement according to our modelling is dominated by light incident from a narrow cone close to normal incidence (see Fig. S3b† for angle-resolved field enhancement).
Lowering the NA to enhance the excitation around the NW may thus increase the contrast between the fluorescence from NW-bound molecules and background signal from fluorophores in solution (the contrast is enhanced through the increase in MNW) and fluorophores bound to the planar surface between the NWs (through the increase in MNW/Mplanar). This has potential for experiments in which there is a desire to probe the fluorescence of NW-bound molecules in the presence of fluorescent molecules in bulk and on surface between the NWs.
4. Conclusions
We studied the excitation enhancement for surface-bound fluorophores on Al2O3-coated GaP NWs of varied diameter and found that diameters of 90–140 nm and oxide thickness of 10 nm maximize the enhancement for widely used red excitation wavelengths. Measurements of the photobleaching rate are demonstrated to be useful when comparing excitation enhancement between different samples. Since the rate is obtained from the time evolution of the signal on a given sample, this approach eliminates the need of calibrations, while providing a result that is directly proportional to the enhancement of the excitation at the location of the fluorophore. This type of measurements also makes the quantification of the excitation enhancement independent of inherent bleaching characteristics of the fluorophores. The results are supported by finite element modelling of scattering of incident light for fluorophores bound to NWs and on a planar surface. We studied through simulations also the dependence of excitation enhancement on excitation wavelength, NW length, and NA of the objective. The modelling indicates that the main excitation enhancement maximum shifts in a predictable manner to smaller NW diameters for an excitation wavelength shorter than that used for the fluorophores in our experiments.Abbreviations
| ALD | Atomic layer deposition |
| NW | Nanowire |
| NA | Numerical aperture |
| SEM | Scanning electron microscopy |
Author contributions
I. N. U., H. L., C. N. P., and F. H. conceived the study. I. N. U. and D. V. grew the nanowires. I. N. U. performed the experiments and analyzed the data. N. A. performed the electromagnetic optics simulations. I. N. U. wrote the manuscript with input from all authors. All authors have given their approval to the final version of the manuscript.Conflicts of interest
H. L., N. A., C. N. P., D. V., and F. H. have financial interests in Aligned Bio AB.Acknowledgements
Swedish Research Council (project numbers 2019-02435, 2020-04226), NanoLund and Mats Paulsson Stiftelserna. NWs were grown and characterized in Lund Nano Lab (LNL). We are grateful to Peter Blomqvist and Sungyoun Ju for technical support and to Dr Gerda Rentschler for her help during photobleaching experiments. We also acknowledge Dr Sebastian Lehmann and Prof. Magnus Borgström, Jonas Tegenfeldt and Martin Magnusson for useful discussions and help.References
- A. Dorfman, N. Kumar and J. I. Hahm, Highly Sensitive Biomolecular Fluorescence Detection Using Nanoscale ZnO Platforms, Langmuir, 2006, 22(11), 4890–4895, DOI:10.1021/la053270+.
- A. Dorfman, N. Kumar and J. I. Hahm, Nanoscale ZnO-Enhanced Fluorescence Detection of Protein Interactions, Adv. Mater., 2006, 18(20), 2685–2690, DOI:10.1002/ADMA.200502616.
- W. Hu, Y. Liu, Z. Zhu, H. Yang and C. M. Li, Randomly Oriented ZnO Nanorods as Advanced Substrate for High-Performance Protein Microarrays, ACS Appl. Mater. Interfaces, 2010, 2(6), 1569–1572, DOI:10.1021/am100314w.
- W. Hu, Y. Liu, H. Yang, X. Zhou and C. M. Li, ZnO Nanorods-Enhanced Fluorescence for Sensitive Microarray Detection of Cancers in Serum without Additional Reporter-Amplification, Biosens. Bioelectron., 2011, 26(8), 3683–3687, DOI:10.1016/j.bios.2011.01.045.
- B. Du, C. Tang, D. Zhao, H. Zhang, D. Yu, M. Yu, K. C. Balram, H. Gersen, B. Yang, W. Cao, C. Gu, F. Besenbacher, J. Li and Y. Sun, Diameter-Optimized High-Order Waveguide Nanorods for Fluorescence Enhancement Applied in Ultrasensitive Bioassays, Nanoscale, 2019, 11(30), 14322–14329, 10.1039/c9nr02330e.
- T. Wang, A. Centeno, D. Darvill, J. S. Pang, M. P. Ryan and F. Xie, Tuneable Fluorescence Enhancement of Nanostructured ZnO Arrays with Controlled Morphology, Phys. Chem. Chem. Phys., 2018, 20(21), 14828–14834, 10.1039/C8CP01493K.
- L. Ten Siethoff, M. Lard, J. Generosi, H. S. Andersson, H. Linke and A. Månsson, Molecular Motor Propelled Filaments Reveal Light-Guiding in Nanowire Arrays for Enhanced Biosensing, Nano Lett., 2014, 14(2), 737–742, DOI:10.1021/nl404032k.
- D. Verardo, L. Liljedahl, C. Richter, B. Agnarsson, U. Axelsson, C. N. Prinz, F. Höök, C. A. K. Borrebaeck and H. Linke, Fluorescence Signal Enhancement in Antibody Microarrays Using Lightguiding Nanowires, Nanomaterials, 2021, 11(1), 227, DOI:10.3390/nano11010227.
- X. Zhao, M. H. Alizadeh and B. M. Reinhard, Harnessing Leaky Modes for Fluorescence Enhancement in Gold-Tipped Silicon Nanowires, J. Phys. Chem. C, 2016, 120(37), 20555–20562, DOI:10.1021/acs.jpcc.5b11702.
- M. Kandziolka, J. J. Charlton, I. I. Kravchenko, J. A. Bradshaw, I. A. Merkulov, M. J. Sepaniak and N. V. Lavrik, Silicon Nanopillars as a Platform for Enhanced Fluorescence Analysis, Anal. Chem., 2013, 85(19), 9031–9038, DOI:10.1021/ac401500y.
- R. S. Frederiksen, E. Alarcon-Llado, M. H. Madsen, K. R. Rostgaard, P. Krogstrup, T. Vosch, J. Nygå, A. F. I. Morral and K. L. Martinez, Modulation of Fluorescence Signals from Biomolecules along Nanowires Due to Interaction of Light with Oriented Nanostructures, Nano Lett., 2015, 15(1), 176–181, DOI:10.1021/nl503344y.
- M. Lard, H. Linke and C. N. Prinz, Biosensing Using Arrays of Vertical Semiconductor Nanowires: Mechanosensing and Biomarker Detection, Nanotechnology, 2019, 30, 214003, DOI:10.1088/1361-6528/ab0326.
- L. Guo, Y. Shi, X. Liu, Z. Han, Z. Zhao, Y. Chen, W. Xie and X. Li, Enhanced Fluorescence Detection of Proteins Using ZnO Nanowires Integrated inside Microfluidic Chips, Biosens. Bioelectron., 2018, 99, 368–374, DOI:10.1016/j.bios.2017.08.003.
- S. Shrivastava, N. M. Triet, Y. M. Son, W. I. Lee and N. E. Lee, Seesawed Fluorescence Nano-Aptasensor Based on Highly Vertical ZnO Nanorods and Three-Dimensional Quantitative Fluorescence Imaging for Enhanced Detection Accuracy of ATP, Biosens. Bioelectron., 2017, 90, 450–458, DOI:10.1016/j.bios.2016.09.089.
- M. Singh, A. Alabanza, L. E. Gonzalez, W. Wang, W. B. Reeves and J. Hahm, Ultratrace Level Determination and Quantitative Analysis of Kidney Injury Biomarkers in Patient Samples Attained by Zinc Oxide Nanorods, Nanoscale, 2016, 8(8), 4613–4622, 10.1039/C5NR08706F.
- J. Kim, S. K. Lee, J. H. Lee, H. Y. Kim, N. H. Kim, C. H. Lee, C. S. Lee and H. G. Kim, ZnO Nanowire-Based Early Detection of SARS-CoV-2 Antibody Responses in Asymptomatic Patients with COVID-19, Adv. Mater. Interfaces, 2022, 9(14), 2102046, DOI:10.1002/ADMI.202102046.
- D. Verardo, B. Agnarsson, V. P. Zhdanov, F. Höök and H. Linke, Single-Molecule Detection with Lightguiding Nanowires: Determination of Protein Concentration and Diffusivity in Supported Lipid Bilayers, Nano Lett., 2019, 19(9), 6182–6191, DOI:10.1021/acs.nanolett.9b02226.
- J. Valderas-Gutiérrez, R. Davtyan, S. Sivakumar, N. Anttu, Y. Li, P. Flatt, J. Y. Shin, C. N. Prinz, F. Höök, T. Fioretos, M. H. Magnusson and H. Linke, Enhanced Optical Biosensing by Aerotaxy Ga(As)P Nanowire Platforms Suitable for Scalable Production, ACS Appl. Nano Mater., 2022, 5(7), 9063–9071, DOI:10.1021/ACSANM.2C01372.
- N. Anttu, H. Mäntynen, A. Sorokina, J. Turunen, T. Sadi and H. Lipsanen, Applied Electromagnetic Optics Simulations for Nanophotonics, J. Appl. Phys., 2021, 129(13), 131102, DOI:10.1063/5.0041275.
- D. Verardo, F. W. Lindberg, N. Anttu, C. S. Niman, M. Lard, A. P. Dabkowska, T. Nylander, A. Månsson, C. N. Prinz and H. Linke, Nanowires for Biosensing: Lightguiding of Fluorescence as a Function of Diameter and Wavelength, Nano Lett., 2018, 18(8), 4796–4802, DOI:10.1021/acs.nanolett.8b01360.
- B. Chon, J. Truong, M. Hansen, J. I. Hahm and Y. J. Lee, Position- and Polarization-Specific Waveguiding of Multi-Emissions in Single ZnO Nanorods, ACS Photonics, 2019, 6(6), 1416–1424, DOI:10.1021/acsphotonics.8b01763.
- N. Anttu, H. Mäntynen, A. Sorokina, P. Kivisaari, T. Sadi and H. Lipsanen, Geometry Tailoring of Emission from Semiconductor Nanowires and Nanocones, Photonics, 2020, 7(2), 23, DOI:10.3390/PHOTONICS7020023.
- D. Van Dam, D. R. Abujetas, R. Paniagua-Domínguez, J. A. Sánchez-Gil, E. P. A. M. Bakkers, J. E. M. Haverkort and J. Gómez Rivas, Directional and Polarized Emission from Nanowire Arrays, Nano Lett., 2015, 15(7), 4557–4563, DOI:10.1021/acs.nanolett.5b01135.
- G. Grzela, R. Paniagua-Domínguez, T. Barten, Y. Fontana, J. A. Sánchez-Gil and J. Gómez Rivas, Nanowire Antenna Emission, Nano Lett., 2012, 12(11), 5481–5486, DOI:10.1021/nl301907f.
- N. Anttu, Modifying the Emission of Light from a Semiconductor Nanowire Array, J. Appl. Phys., 2016, 120(4), 043108, DOI:10.1063/1.4960017.
- R. Frederiksen, G. Tutuncuoglu, F. Matteini, K. L. Martinez, A. F. I. Morral and E. Alarcon-Llado, Visual Understanding of Light Absorption and Waveguiding in Standing Nanowires with 3D Fluorescence Confocal Microscopy, ACS Photonics, 2017, 4(9), 2235–2241, DOI:10.1021/acsphotonics.7b00434.
- R. S. Frederiksen, E. Alarcon-Llado, P. Krogstrup, L. Bojarskaite, N. Buch-Må, J. Bolinsson, J. Nygå, A. F. I. Morral and K. L. Martinez, Nanowire-Aperture Probe: Local Enhanced Fluorescence Detection for the Investigation of Live Cells at the Nanoscale, ACS Photonics, 2016, 3(7), 1208–1216, DOI:10.1021/acsphotonics.6b00126.
- D. E. Aspnes and A. A. Studna, Dielectric Functions and Optical Parameters of Si, Ge, GaP, GaAs, GaSb, InP, InAs, and InSb from 1.5 to 6.0 eV, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27(2), 985–1009, DOI:10.1103/PhysRevB.27.985.
- L. Song, E. J. Hennink, I. T. Young and H. J. Tanke, Photobleaching Kinetics of Fluorescein in Quantitative Fluorescence Microscopy, Biophys. J., 1995, 68(6), 2588–2600, DOI:10.1016/S0006-3495(95)80442-X.
- C. Eggeling, J. Widengren, R. Rigler and C. A. M. M. Seidel, Photobleaching of Fluorescent Dyes under Conditions Used for Single-Molecule Detection: Evidence of Two-Step Photolysis, Anal. Chem., 1998, 70(13), 2651–2659, DOI:10.1021/ac980027p.
- M. J. Dodge, Refractive Index, in Handbook of Laser Science and Technology, Volume IV, Optical Materials: Part 2, ed. M. J. Weber, CRC Press, Boca Raton, 1986, p. 30, DOI:10.1201/9781003067955.
- J. P. Dhandhukia, D. A. Brill, A. Kouhi, M. K. Pastuszka and J. A. MacKay, Elastin-like Polypeptide Switches: A Design Strategy to Detect Multimeric Proteins, Protein Sci., 2017, 26(9), 1785–1795, DOI:10.1002/pro.3215.
- B. Jachimska, M. Wasilewska and Z. Adamczyk, Characterization of Globular Protein Solutions by Dynamic Light Scattering, Electrophoretic Mobility, and Viscosity Measurements, Langmuir, 2008, 24(13), 6867–6872, DOI:10.1021/la800548p.
- D. M. Benson, J. Bryan, A. L. Plant, A. M. Gotto and L. C. Smith, Digital Imaging Fluorescence Microscopy: Spatial Heterogeneity of Photobleaching Rate Constants in Individual Cells, J. Cell Biol., 1985, 100(4), 1309–1323, DOI:10.1083/jcb.100.4.1309.
- J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J. Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Fiji: An Open-Source Platform for Biological-Image Analysis, Nat. Methods, 2012, 9(7), 676–682, DOI:10.1038/nmeth.2019.
- K. Li, The Image Stabilizer Plugin for ImageJ, https://www.cs.cmu.edu/%7Ekangli/code/Image_Stabilizer.html Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Further information on modelling, NW growth, sample preparation, setup, measurements and data analysis. See DOI: https://doi.org/10.1039/d2na00749e |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2023 |

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin