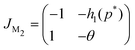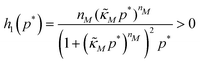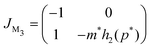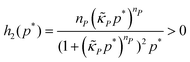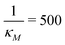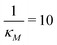Differential roles of transcriptional and translational negative autoregulations in protein dynamics
Christopher
Ryzowicz
and
Necmettin
Yildirim
 *
*
Division of Natural Sciences, New College of Florida, 5800 Bayshore Road, Sarasota, FL 34243, USA. E-mail: christopher.ryzowi18@ncf.edu; nyildirim@ncf.edu; Fax: +1-941-487-4396; Tel: +1-941-487-4214
First published on 11th November 2022
Abstract
Cells continuously respond to stimuli to function properly by employing a wide variety of regulatory mechanisms that often involve protein up or down regulations. This study focuses on dynamics of a protein with negative autoregulations in E. coli, and assumes that the input signal up-regulates the protein, and then the protein down-regulates its own production via 2 distinct types of mechanisms. The mathematical models describe the dynamics of mRNA and protein for 3 scenarios: (i) a simplistic model with no regulation, (ii) a model with transcriptional negative autoregulation, and (iii) a model with translational negative autoregulation. Our analysis shows that the negative autoregulation models produce faster responses and quicker return times to the input signals compared to the model with no regulation, while the transcriptional autoregulation model is the only model capable of producing oscillatory dynamics. The stochastic simulations predict that the transcriptional autoregulation model is the noisiest followed by the simplistic model, and the translational autoregulation model has the least noise. The noise level depends on the strength of inhibition. Furthermore, the transcriptional autoregulation model filters out the noise in the input signal for longer periods of time, and this time increases as the strength of the feedback gets stronger.
1 Introduction
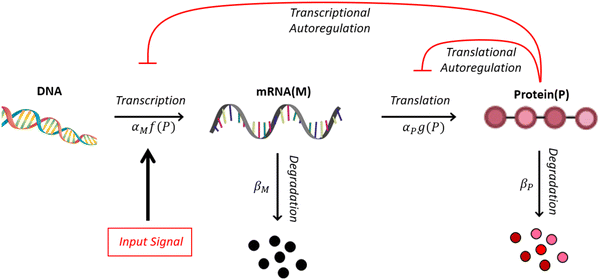
To maintain homeostasis, cells continuously respond to external signals via employing a variety of different internal regulatory mechanisms.1,2 Signals like changes in temperature, pressure, or adjacent cell activity can have drastic effects on a cell's ability to function properly.3 In response, cells often up-regulate or down-regulate the abundance of select proteins to carry out proper cellular functions such as cell proliferation, apoptosis and maintenance of cell structure.4 Failure to properly respond to such signals could cause detrimental diseases such as cancer, anemia, and low antibody counts. The process of protein synthesis provides a cell the chance for self-regulation of protein abundance, which involves two major steps, namely transcription and translation.In living organisms, deoxyribonucleic acid (DNA) is responsible for replicating and storing genetic instructions in the form of a long, double helix molecule. In order to regulate protein abundances and maintain cellular functions, instructions from DNA strands need to be encoded and transported for protein production. The first major step of protein synthesis requires messenger ribonucleic acid (mRNA), a single stranded molecule responsible for converting genetic information in DNA to a format compatible to synthesize proteins.5 The process in which DNA is transcribed into mRNA is called transcription. The process of transcription is initiated by RNA polymerase, which is an enzyme responsible for splitting the two strands of DNA from its double helix form and constructing an RNA strand with a complementary sequence of base pairs. With the newly constructed mRNA molecule, the final step of protein production, called translation, can begin. During translation, the mRNA strand carries the previously transcribed information to a small organelle in the cell called the ribosome, the site of protein synthesis.3 Finally, the genetic code from the mRNA is translated for production of a select protein(s). The process described is a simplistic overview of the process of protein synthesis, and does not take into account possible intracellular interactions that can affect the individual steps throughout the process.
At the genetic level, cells make use of a number of different types of regulatory mechanisms to produce proper cellular functions.6 One major form of regulation is achieved through a mechanism involving a gene's own end product, called autoregulation. Autoregulation is a common regulatory pattern recurring among different cell types. At gene expression level, autoregulation mechanisms can occur at the transcription or translation steps. When a protein regulates its own production by regulating the transcription of its gene, this is called transcriptional autoregulation. When the control takes place during the protein translation step, this is called translational autoregulation.
The translational control has received less attention in the literature, but there are a number of systems that includes translational autoregulation.7–9 One of the example systems in E. coli employing translational autoregulation is bacteriophage T4 infection. The expression of gene 32 during T4 infection of E. coli. was shown to be regulated by at least two intracellular components, namely single-stranded DNA and the gene 32 protein itself.10 Examples of systems involving transcriptional autoregulation include tryptophan operon, in which a repressor protein binds to an amino acid, called tryptophan, forming a repressor-tryptophan complex. Then, this complex binds to the operator region of the operon, which prevents the binding of RNA polymerase, inhibiting its own transcription rate.11,12 Transcriptional autoregulation is such a common regulatory mechanism, over 40% of known regulations in E. coli. are transcriptional.13
Both of these types of autoregulation can either be activatory (positive feedback mechanism) or inhibitory (negative feedback mechanism) in their effect on protein abundance, and they are labeled positive autoregulation and negative autoregulation, respectively.4,6,13 The focus of this study is negative autoregulation.14
There has been extensive research done in understanding regulatory mechanisms involving feed-forward loops, feedback loops, and autoregulatory mechanisms, to name a few.6 They have shown that these systems have the potential to generate complex dynamics such as oscillation, multiple steady states, and rapid or delayed responses.4,15,16 However, our understanding of how cells function and produce proper responses to input signals is far from complete, and is still an active research field. Here, we study differential roles of transcriptional and translational autoregulation mechanisms on dynamics of a protein, and used both deterministic and stochastic methods. Mathematical models describe dynamic evolution of mRNA and its protein.
2 Mathematical models
Protein synthesis is a dynamic process. To study how protein dynamics is controlled by transcriptional and translational negative autoregulations, a system of differential equations (ODEs) is set up based on the law of mass-action kinetics.4 The equations describing time evolution of mRNA (M) and protein (P) under negative autoregulation is a coupled system of differential equations of the form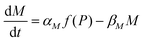 | (1) |
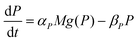 | (2) |
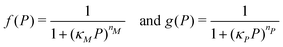 | (3) |
Eqn (1) describes the dynamic evolution of mRNA. The first term αMf(P) in this equation models the transcription of mRNA from DNA and the second term βMM models the degradation of mRNA. Here, the function f(P) mimics negative autoregulation of the mRNA transcription rate by the protein P. The positive parameters αM and βM are the proportionality constants for the production and degradation of mRNA, respectively. The function f is a strictly decreasing function of P starting from a maximum value of 1 and approaches 0 as P increases. The parameter κM is adjusting when the function f reaches half of its maximal value, which is 1/2. For example, if 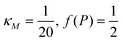 is attained when P = 20. As κM increases, the amount of protein required to reach half of the maximum value decreases, and vice versa. The parameter nM controls the steepness of the downward curve and approaches to a vertical line as nM increases, making f a switch-like inhibitory function, and completely turning off the transcription rate soon after
is attained when P = 20. As κM increases, the amount of protein required to reach half of the maximum value decreases, and vice versa. The parameter nM controls the steepness of the downward curve and approaches to a vertical line as nM increases, making f a switch-like inhibitory function, and completely turning off the transcription rate soon after 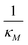 . For larger values of nM, a small increase in protein P around
. For larger values of nM, a small increase in protein P around 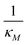 produces a larger inhibitory effect on the transcription rate.
produces a larger inhibitory effect on the transcription rate.
The dynamics of the protein is given by eqn (2). The first term αPg(P) in this equation models the translation of mRNA into protein and the second term, βPP, models the degradation of the protein P. Here, the function g(P) models negative autoregulation of protein translation rate by P. The positive parameters αP and βP are proportionality constants for the translation and degradation of the protein, respectively. The function g displays similar qualitative behavior as f, except the inhibition strength parameters are κP and nP.
2.1 A simple model with no autoregulation
A mechanism with no autoregulation is modeled by eqn (1) and (2) when κM = κP = 0, and the cartoon of this model is illustrated in Fig. 1 when you ignore the two red pathways. From now on, we will address this model as M1.2.2 A model with transcriptional autoregulation
A mechanism with transcriptional autoregulation is given by eqn (1) and (2) when κM, nM > 0 and κP = 0, which is illustrated in Fig. 1 with the red line labeled transcriptional autoregulation. From this point forward, we will address the transcriptional autoregulation model as M2.2.3 A model with translational autoregulation
A mechanism with translational autoregulation is modeled by eqn (1) and (2) when κM = 0 and κP, nP > 0, which is illustrated in Fig. 1 with the red line labeled translational autoregulation. From this point forward, we will address the translational autoregulation model as M3.2.4 Model parameters
The models introduced above include a number of unknown parameters describing the reaction rates. To make biologically realistic predictions in our numerical simulations, the values for these parameters must be fixed within physiologically reasonable ranges. The values used in our simulations are listed in Table 1 for the model organism E. coli, which is one of the most widely available choices for this type of study. The details of how these values are estimated or collected from the literature can be found in the Appendix section.| Parameters | Description | Value | Source |
|---|---|---|---|
| α P | Protein production rate | 7.70 min−1 | 17 |
| α M | mRNA production rate | 1.04 molec. per min | 18 |
| β P | Protein degradation rate | 0.02 min−1 | 19 and 20 |
| β M | mRNA degradation rate | 0.35 min−1 | 21 and 18 |
| n P | Hill coeff. for translational inhibition | 2 | Fixed |
| n M | Hill coeff. for transcriptional inhibition | 2 | Fixed |
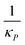
|
Inhibition strength for protein | [10, 500] molec. | Varied |
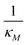
|
Inhibition strength for mRNA | [10, 500] molec. | Varied |
| S a | Input signal amplitude | [1, 4] | Varied |
3 Model analysis and numerical simulations
Nondimensionalization is a powerful method that allows to write the model equations in a dimensionless form by scaling dependent and independent variables. It reduces the complexity of the problem by decreasing the number of parameters without sacrificing dynamical properties of the models.By defining new variables for the dimensionless time (τ), mRNA (m) and protein (p) as τ = βMt, 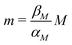 and
and 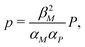 the model equations given in eqn (1) and (2) simplify to
the model equations given in eqn (1) and (2) simplify to
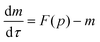 | (4) |
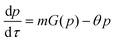 | (5) |
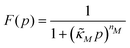 | (6) |
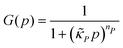 | (7) |
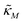 and
and 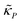 are all positive and given by
are all positive and given by 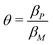 ,
, 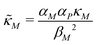 and
and 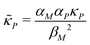 . Notice that both F and G are decreasing functions of p.
. Notice that both F and G are decreasing functions of p.
3.1 Steady state and stability analysis of the models
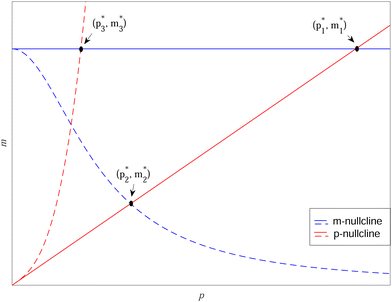
To study dependence of steady states to the model parameters, the steady state analysis is performed on each model. Fig. 2 summarizes the results.When both 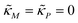 , the model simplifies to the model with no autoregulation, namely M1. This is a linear model with the nullclines of m = 1 and m = θp for m and p, respectively. In Fig. 2, the solid horizontal blue line represents the dimensionless mRNA nullcline, which is m = 1, and the solid red line represents the dimensionless protein nullcline, which is m = θp. Since the p-nullcline is an increasing function of p and m-nullcline is a constant function at 1, they can only intersect at a single point providing a unique steady state for this model at
, the model simplifies to the model with no autoregulation, namely M1. This is a linear model with the nullclines of m = 1 and m = θp for m and p, respectively. In Fig. 2, the solid horizontal blue line represents the dimensionless mRNA nullcline, which is m = 1, and the solid red line represents the dimensionless protein nullcline, which is m = θp. Since the p-nullcline is an increasing function of p and m-nullcline is a constant function at 1, they can only intersect at a single point providing a unique steady state for this model at 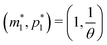 .
.
Model M1 is a linear system, which can be solved analytically for any given initial conditions, m(0) = m0 and p(0) = p0. The analytical solution of eqn (4) and (5) becomes
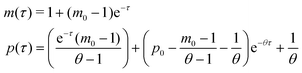 | (8) |
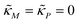 provided that θ ≠ 1. It is clear from eqn (8) that the time evolution of mRNA is driven by a single exponential function, namely e−τ, while the dynamics of protein is more complex and driven by two exponential functions, namely e−τ and e−θτ. Since both exponents are negative and real, we have
provided that θ ≠ 1. It is clear from eqn (8) that the time evolution of mRNA is driven by a single exponential function, namely e−τ, while the dynamics of protein is more complex and driven by two exponential functions, namely e−τ and e−θτ. Since both exponents are negative and real, we haveTherefore, the steady state of model M1 at
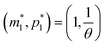 is always globally stable regardless of the selection of the parameters. Furthermore, the dynamics is determined only by θ, the ratio of degradation rates. For the case when θ = 1, the stability of the steady state stays unchanged, but the dynamics will depend on only one exponential function, namely e−τ, as there will be repeated eigenvalues at −1.
is always globally stable regardless of the selection of the parameters. Furthermore, the dynamics is determined only by θ, the ratio of degradation rates. For the case when θ = 1, the stability of the steady state stays unchanged, but the dynamics will depend on only one exponential function, namely e−τ, as there will be repeated eigenvalues at −1.
The steady state analyses for models M2 and M3 are more complex due to non-linearity introduced by the transcriptional and translational autoregulation terms. The phase plane analysis approach can be utilized to determine the number of steady states and their dependence on the parameters values. The nullcline for the dimensionless mRNA m becomes m = F(p), and the nullcline for the dimensionless protein p becomes 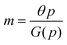 .
.
The intersection of these two nullclines give the steady states. Again, Fig. 2 shows a qualitative plot for the nullclines of all three models. For the model M2 (when 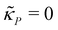 ), m-nullcline equation m = F(p) is a monotone decreasing function of p starting from 1 when p = 0 in the first quadrant regardless of parameter values (shown as dashed blue line), and p-nullcline m = θp is a straight line with positive slope starting from 0 when p = 0 in the first quadrant regardless of parameter selection (shown as solid red line). Therefore, it can be concluded that model M2 always attains a unique steady state at
), m-nullcline equation m = F(p) is a monotone decreasing function of p starting from 1 when p = 0 in the first quadrant regardless of parameter values (shown as dashed blue line), and p-nullcline m = θp is a straight line with positive slope starting from 0 when p = 0 in the first quadrant regardless of parameter selection (shown as solid red line). Therefore, it can be concluded that model M2 always attains a unique steady state at 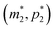 for any given parameter set as shown in Fig. 2. As seen in this qualitative illustration, the steady state of model M2 is smaller for both m and p compared to the steady state of model M1, which is not surprising as the autoregulation has inhibitory effect on mRNA transcription.
for any given parameter set as shown in Fig. 2. As seen in this qualitative illustration, the steady state of model M2 is smaller for both m and p compared to the steady state of model M1, which is not surprising as the autoregulation has inhibitory effect on mRNA transcription.
For the model M3 (when 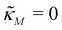 ), the m-nullcline equation m = 1 is a horizontal line in the first quadrant regardless of parameter selection (shown as solid blue line), and the p-nullcline equation
), the m-nullcline equation m = 1 is a horizontal line in the first quadrant regardless of parameter selection (shown as solid blue line), and the p-nullcline equation 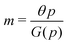 is an increasing function of p starting from 0 when p = 0 in the first quadrant regardless of parameter values (shown as dashed red curve). Therefore, we can conclude that model M3 also has a single steady state for any given parameter set, which is represented by
is an increasing function of p starting from 0 when p = 0 in the first quadrant regardless of parameter values (shown as dashed red curve). Therefore, we can conclude that model M3 also has a single steady state for any given parameter set, which is represented by 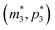 in Fig. 2. As seen in this qualitative graph, the steady state value of the protein p for model M3 is smaller than that of model M1 while the mRNA m steady state value is the same for both M1 and M3 models. Notice that the steady state value of the protein p becomes the same for both model M2 and model M3 when
in Fig. 2. As seen in this qualitative graph, the steady state value of the protein p for model M3 is smaller than that of model M1 while the mRNA m steady state value is the same for both M1 and M3 models. Notice that the steady state value of the protein p becomes the same for both model M2 and model M3 when 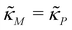 and nM = nP.
and nM = nP.
Due to the nonlinear nature of the autoregulation models M2 and M3, the local dynamics around steady state is studied, which can be determined by examining the eigenvalues of the respective Jacobian matrices. The Jacobian matrix of model M2 is given by
The eigenvalues of JM2 become
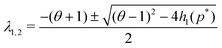 | (9) |
| |JM2| = θ + h1(p*) > 0 |
| Δ = (θ − 1)2 − 4h1(p*) < 0 |
| tr(JM2) = −(1 + θ) < 0 | (10) |
A similar stability analysis can be carried out for model M3. The Jacobian matrix JM3 of this model becomes
Notice, this matrix is a lower triangular matrix, and its eigenvalues are the entries of the main diagonal. Moreover, we can bypass the characteristic equation formulation and conclude the eigenvalues of JM3 are λ1 = −1 and λ2 = −m*h2(p*), which are both real and negative since the parameters are all positive, which also concludes that the steady state of M3 model is a stable node regardless of parameter selection.
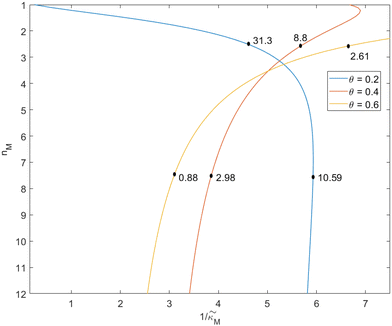
Since the transcriptional autoregulation model M2 is the only model that has the ability to display oscillations, this model is numerically solved, and a bifurcation diagram is produced in the 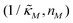 -plane. For this diagram, as nM is varied, the values of
-plane. For this diagram, as nM is varied, the values of 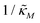 making the discriminant of the Jacobian matrix in eqn (9) zero is calculated, which gives the boundary between the oscillatory region and non-oscillatory region in the
making the discriminant of the Jacobian matrix in eqn (9) zero is calculated, which gives the boundary between the oscillatory region and non-oscillatory region in the 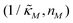 -plane. Our results for 3 different θ values are displayed in Fig. 3. The oscillatory regions for each θ value occurs to the left of each respective curve. For this plot, nM is varied between 1 and 12, and
-plane. Our results for 3 different θ values are displayed in Fig. 3. The oscillatory regions for each θ value occurs to the left of each respective curve. For this plot, nM is varied between 1 and 12, and 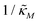 is changed between 0.15 and 7.5. The smaller value of this parameter mimics the stronger inhibition level. As seen in this figure, as θ values changes the size of the oscillatory region changes. The numbers on each curve represent the inhibition level on the boundary in the form of a percentage change of steady state in this model compared to model M1, which enable us to gauge how inhibition is affecting the steady state value along the curves. The inhibitions levels vary between 0.88% and 31.3% when θ = 0.2,0.4 and 0.6. As seen in this figure, for the oscillation to happen, inhibition level needs to be stronger for the larger θ.
is changed between 0.15 and 7.5. The smaller value of this parameter mimics the stronger inhibition level. As seen in this figure, as θ values changes the size of the oscillatory region changes. The numbers on each curve represent the inhibition level on the boundary in the form of a percentage change of steady state in this model compared to model M1, which enable us to gauge how inhibition is affecting the steady state value along the curves. The inhibitions levels vary between 0.88% and 31.3% when θ = 0.2,0.4 and 0.6. As seen in this figure, for the oscillation to happen, inhibition level needs to be stronger for the larger θ.
When θ = 0.6, our analysis shows that the model is capable of producing oscillatory dynamics in the presence of strong inhibition determined by the parameter 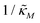 for all values of the hill coefficient nM between 1 and 12. The threshold value for the inhibition parameter estimated as
for all values of the hill coefficient nM between 1 and 12. The threshold value for the inhibition parameter estimated as 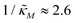 when θ = 0.6. Furthermore, as
when θ = 0.6. Furthermore, as 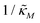 increases, mimicking weaker transcriptional inhibition, nM values required for the oscillatory dynamics decrease. For θ = 0.4, the area of the oscillatory region in the
increases, mimicking weaker transcriptional inhibition, nM values required for the oscillatory dynamics decrease. For θ = 0.4, the area of the oscillatory region in the 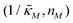 -plane shrinks for smaller nM values and expands for larger values of this parameter compare to when θ = 0.6. Our calculations predict that the threshold value for the inhibition parameter is
-plane shrinks for smaller nM values and expands for larger values of this parameter compare to when θ = 0.6. Our calculations predict that the threshold value for the inhibition parameter is 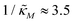 when θ = 0.4 for all values of the hill coefficient nM between 1 and 12. Moreover, when
when θ = 0.4 for all values of the hill coefficient nM between 1 and 12. Moreover, when 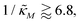 there is no nM value to make the model produce oscillatory dynamics. For θ = 0.2, the model can only oscillate when the inhibition is strong enough
there is no nM value to make the model produce oscillatory dynamics. For θ = 0.2, the model can only oscillate when the inhibition is strong enough 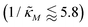 .
.
Fig. 4 depicts a representative time series plot showing how oscillation arises as the inhibition parameter 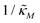 changes when θ = 0.6 in Fig. 3. The red curve is for when
changes when θ = 0.6 in Fig. 3. The red curve is for when 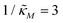 which falls in the right hand side of the boundary curve in Fig. 3 when nM = 10, and as seen in this plot, the time series simulation monotonically approaching to a steady state for this value of the parameter. On the other hand the blue curve corresponds to a value of
which falls in the right hand side of the boundary curve in Fig. 3 when nM = 10, and as seen in this plot, the time series simulation monotonically approaching to a steady state for this value of the parameter. On the other hand the blue curve corresponds to a value of 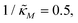 which is picked from the region on the left hand side of the same boundary curve when nM = 10, and the time series simulation corresponding to this value of the parameter shows a damped oscillatory dynamics as it approaches to a steady state. The oscillatory dynamics obtained in the M2 model can not be a sustained oscillation as the Jacobian matrix would always have a complex eigenvalue with a negative real part independent of the selection of the parameter values.
which is picked from the region on the left hand side of the same boundary curve when nM = 10, and the time series simulation corresponding to this value of the parameter shows a damped oscillatory dynamics as it approaches to a steady state. The oscillatory dynamics obtained in the M2 model can not be a sustained oscillation as the Jacobian matrix would always have a complex eigenvalue with a negative real part independent of the selection of the parameter values.
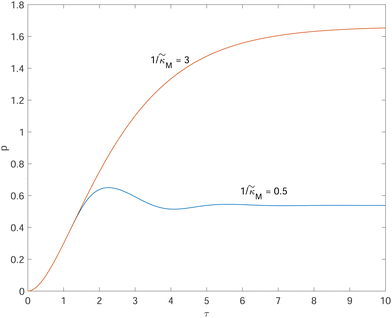 | ||
Fig. 4 Time series plot depicting oscillatory dynamics as 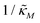 changes when θ = 0.6. The red curve is for changes when θ = 0.6. The red curve is for 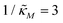 from the non-oscillatory region in Fig. 3, and the time series for p monotonically increases and approaches to a steady state for this value of the parameter. On the other hand the blue curve corresponds to a value of from the non-oscillatory region in Fig. 3, and the time series for p monotonically increases and approaches to a steady state for this value of the parameter. On the other hand the blue curve corresponds to a value of 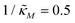 from the oscillatory region in Fig. 3, and the time series simulation for p corresponding to this value of the parameter displays a damped oscillatory trend to a steady state. from the oscillatory region in Fig. 3, and the time series simulation for p corresponding to this value of the parameter displays a damped oscillatory trend to a steady state. | ||
3.2 Comparison of protein dynamics
One way to compare the dynamics of the models is to look at how they dynamically respond to varying signal amplitudes. Here the dynamics produced by each dimensionless model Mk, (k = 1, 2, 3) to increasing signal amplitude are compared. Three metrics, each characterizing different aspects of the response curve, are used for the comparison purpose. The first metric is the half-maximal response (Ph), which is defined as half of the maximum protein level. This metric is scaled, dividing it by the value of the protein levels when Sa = 0 to make comparisons across models more realistic. The second metric is the response time (τh), which quantifies the time required to reach half of the maximum protein level. The third metric is the return time (τr), which measures the time required for the protein level to achieve a value within 5% of its steady state level.To introduce different signal amplitudes, we assumed that the input signal can increase the transcription rate, and modified the transcription rate in eqn (4) accordingly. The new mRNA transcription rate becomes 1 + Sa. Here 1 is our original dimensionless mRNA transcription rate, and Sa > 0 is the signal amplitude parameter. We assumed that the input signal can increase the transcription rate 2–5 fold for the full duration of time. To make the comparison, each dimensionless model Mk, (k = 1, 2, 3) is numerically solved in Matlab22 using the differential equation solver ode15s as the signal amplitude Sa changes within1,4 range, and the three metrics are calculated.
In our simulations, the signal is turned on at t = 0 by setting Sa equal to a value in the range,1,4 and kept constant for the entire time span of the simulations. The initial values for these simulations are calculated by solving the model equations when Sa = 0 with the parameters listed in Table 1 when 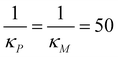 molecules and calculating the respective steady states. This parameter set mimics a strong negative feedback reducing protein steady state level by close to 90% in models M2 and M3. To calculate the response metrics as the signal amplitude increases, the model equations are solved numerically for 20 evenly spaced values of Sa changing within the interval.1,4 The simulation results are shown in Fig. 5.
molecules and calculating the respective steady states. This parameter set mimics a strong negative feedback reducing protein steady state level by close to 90% in models M2 and M3. To calculate the response metrics as the signal amplitude increases, the model equations are solved numerically for 20 evenly spaced values of Sa changing within the interval.1,4 The simulation results are shown in Fig. 5.
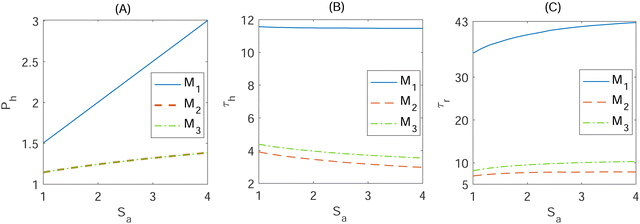 | ||
| Fig. 5 Dynamic responses from the dimensionless models Mk, (k = 1, 2, 3) in eqn (4) and (5) as the signal amplitude Sa increases. (A) Half of the protein abundance Ph, (B) response time τh and (C) return time τr. These metrics are calculated for 20 evenly spaced values of Sa between 1 and 4, mimicking 2 to 5 fold increase in the transcription rate due to the amplified signal. | ||
To begin, refer to the half-max protein abundance metric illustrated in Fig. 5A for the signal with varying amplitude between 1 and 4. As signal amplitude increases, all the models' half-maximum protein abundance increase linearly since a higher transcription rate results in higher mRNA abundance, which then leads to a higher protein abundance. However, model M1 half-max protein abundance increases at a faster rate compared to the models with negative autoregulation. Furthermore, the models' half-maximum protein abundance start at around Ph = 1.5 when Sa = 1 (one fold increase in transcription rate) for model M1 and Ph = 1.2 for models M2 and M3. Model M1 maintains the highest levels of half-max protein, starting at Ph = 1.5 and increasing to roughly about Ph = 3, which is higher compared to the models with autoregulations since there is no inhibitory loop regulating mRNA or protein production in this model. Model M2 and M3 share identical curves as Sa increases, starting at Ph = 1.2 and ending at about Ph = 1.4, because the equation for the protein steady state is the same for both autoregulation models. Therefore, the 1–4 fold increase in the transcription rate produces 50% to 200% increase in the protein level in M1, while this increase is between 20% and 40% in both M2 and M3.
For the same signal amplitudes, the half-maximum response time is illustrated as the signal amplitude increases in Fig. 5B. For model M1, the response time stayed nearly constant at about 12 as the signal amplitude increased, as there is no inhibition slowing down the production of mRNA or protein. However, model M2 and M3 reach half-max protein abundance faster as the signal amplitude increases compared to model M1. Both models share similar trajectories starting at τh ≈ 4 when Sa = 1 and ending at τh ≈ 3 when Sa = 4. This indicates that the negative autoregulations make the system respond to the input signal faster, which has been documented in the literature.13,23 Our simulation predicts that autoregulation models respond to the input signal roughly 3 fold faster than the model with no negative autoregulation. This value has been estimated as 5 fold using one dimensional equation with no cooperatively in ref. 13. We observed that the response time in M2 and M3 gets shorter compared to the response time in M1 as the hill coefficient increases. For example, the autoregulation models M2 and M3 responds to the input signal 2 times faster compared to M1 model when nM = nP = 1. This number is 5 when nM = nP = 4, and it becomes 8 faster when nM = nP = 8. M2 responds slower compared to M3. The difference in response time between M2 and M3 is relatively small (about 1.5 minutes) when nM = nP = 2.
The return time τr is graphed as the signal amplitude increases in Fig. 5(C). In model M1, we observe an increasing, saturating return time of about 36 to 42 as Sa increases and about a 4-fold longer time than the models with autoregulation. In contrast, models M2 and M3 require a shorter time, around τr ≈ 8, to achieve within 5% of the steady state level. In addition, they both have very similar trajectories as the signal amplitude increases to Sa = 4, illustrated by the close proximity of the dotted and dashed curves in Fig. 5C near the bottom of the graph. Longer return time in M1 model compared to models M2 and M3 is due to the fact that M1 model has no inhibitory regulation which allows for more protein to be produced by this mechanism as well as the negative nature of the autoregulations in models M2 and M3, making the system achieve the new steady state at a faster rate. It takes longer for M3 to reach the steady state after the signal. The difference between the return times for M3 and M2 models is roughly 6 minutes. Both τh and τr are larger in M3 compared to M2. This can be explained by the fact that in M3 model inhibition is at the translation step, which results in more mRNA being produced that causes larger values for these 2 metrics.
4 Stochastic simulations of the models
Deterministic models provide valuable regulatory information on the average dynamics of gene networks, and they rely on the fact that given a set of parameters and initial conditions, a model always yields the same output every time a simulation is executed. While deterministic models are a good baseline in studying dynamical systems, they do not take into account the molecular fluctuations among protein molecules. Stochasticity may have significant regulatory roles in the system's dynamics, particularly when the molecule numbers are small.24 To study regulatory roles of negative autoregulations on stochasticity and dynamics of the protein, all three models Mk, (k = 1, 2, 3) are stochastically simulated by using the Gillespie algorithm.25 The simulations are carried out using a Matlab package, which is a vectorized version of the Gillespie algorithm.26To compare the stochastic aspects of the models, the coefficient of variations (CV) is used, which is defined as the ratio of standard deviation (σ) to mean (μ), namely
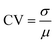 | (11) |
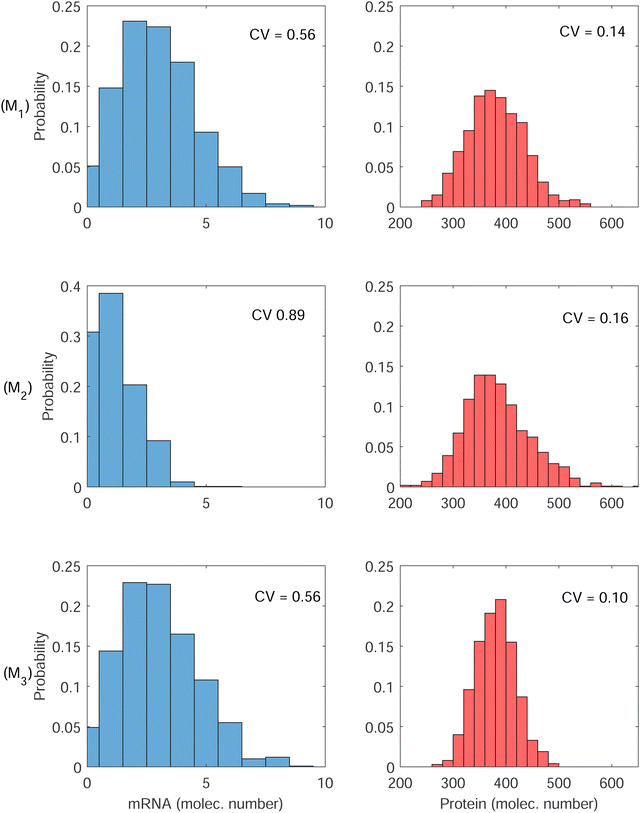
All three models were simulated 1000 times with the parameter values listed in Table 1 when 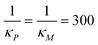 molecules. Then, the CV values are calculated for both mRNA (M) and protein (P) at the steady state. The initial values are selected as the steady states of the models calculated from the deterministic models for the same set of parameter values, except αP for M1. This parameter is set to αP = 2.94 per minute to get the same steady state protein level of 382 molecules with the inhibition models to make CV values comparable across all models. The stochastic simulations are run until time is 600 minutes, and the histograms for mRNA and protein for all three models are produced when t = 300 minutes, which are shown in Fig. 6. Similar histograms have been obtained at different time points (results are not shown).
molecules. Then, the CV values are calculated for both mRNA (M) and protein (P) at the steady state. The initial values are selected as the steady states of the models calculated from the deterministic models for the same set of parameter values, except αP for M1. This parameter is set to αP = 2.94 per minute to get the same steady state protein level of 382 molecules with the inhibition models to make CV values comparable across all models. The stochastic simulations are run until time is 600 minutes, and the histograms for mRNA and protein for all three models are produced when t = 300 minutes, which are shown in Fig. 6. Similar histograms have been obtained at different time points (results are not shown).
The first column has the histograms of mRNA for all three models, and the second column has the histograms for the protein for all three models. First row is for the model M1, second row is for M2 and finally third row is for M3. The CV values calculated from model M1 are 0.56 and 0.14 for M and P, respectively. These numbers are 0.89 and 0.16 for model M2, and 0.56 and 0.10 for model M3. Model M2 has the highest variability in both M and P molecule numbers. Since the negative autoregulation is acting on the transcription step in this model, the mRNA copy number is smaller, and low mRNA copy number leads to a higher variability in M, which also gets translated into protein counts producing higher variability in P.
While the variability calculated for M in model M1 and model M3 are roughly the same, model M3 has lower variability in P. Since the autoregulation is on the translational level in model M3, our simulations predict that while the variability in M stays unchanged, the variability in the protein counts reduces by 30% compared to the variability of protein counts in model M1. The roles of negative translational autoregulation in reducing noise have been reported in ref. 9 and 27. Our simulations also predict that the noise level depends on the strength of inhibition, it converges to ≈0.56 and ≈0.14 for mRNA and the protein respectively, as the inhibition strength gets weaker (Results are not shown).
We also tested the significance of the differences in CV values using t-test statistics. To this end, we run our code 10 times for each model. Each run included 100 simulations, and calculated CV values. For M1 and M2, the p-values calculated are 0.0007 and 0.3256 for M and P, respectively. This indicates that while the difference between the CV values for M are statistically meaningful (p < 0.05), the difference between the CV values for P are not (p > 0.05). Similar calculations were carried out for the models M1 and M3. We found that the p-values are 0.98 and 0.004 for M and P, respectively. This indicates that while the difference between the CV values for M are not statistically meaningful (p > 0.05), it is statistically different for P (p < 0.05). This is not a surprising observation as mRNA is not regulated by the feedback in M3. Finally we calculated p-values for M2 and M3. We found that the p-values are 0.0008 and 0.0002 for M and P, respectively. This indicates that the difference between the CV values for both M and P are statistically significant (p < 0.05).
4.1 Dynamic responses of the stochastic models to the noisy input signals
Dynamic responses of stochastic models to the noisy input signals have been compared. To introduce noise to the input signals, the mRNA transcription rate constant αM is adjusted to include random noise by adding white noise in this parameter. The new mRNA transcription rate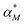 becomes
becomes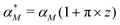 | (12) |
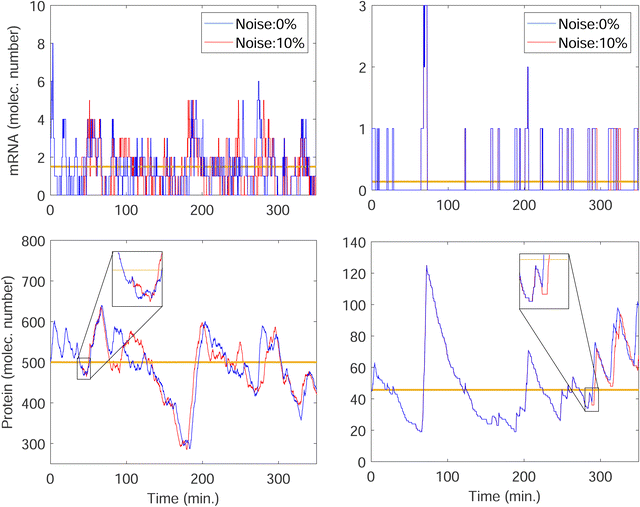
We stochastically simulated all three models with noisy input signals given in eqn (12), and looked at how they respond to noisy input under weak and strong negative autoregulations. Our simulations predict that model M2 filters out noise in the input signal for a longer period of time compared to both M1 and M3 models. The result from model M2 for a single cell simulation with no input noise and 10% input noise in the transcription rate are shown in Fig. 7. To produce this simulation we set π = 10%, and kept all the parameters fixed at their values in Table 1 while 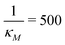 (left column) and
(left column) and 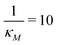 (right column). Fig. 7 shows mRNA and protein time series with both input noise levels superimposed on each other to compare the temporal dynamics and fluctuations. The random number generation seed is fixed for both noise levels in each simulation to mimic the same cell measurements. The horizontal yellow lines depict the steady state value of either mRNA (top) or protein (bottom) from the deterministic model. Notice that when
(right column). Fig. 7 shows mRNA and protein time series with both input noise levels superimposed on each other to compare the temporal dynamics and fluctuations. The random number generation seed is fixed for both noise levels in each simulation to mimic the same cell measurements. The horizontal yellow lines depict the steady state value of either mRNA (top) or protein (bottom) from the deterministic model. Notice that when 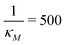 the two protein time series initially overlap, then diverge. This indicates that input noise is filtered out by this mechanism for a period of time (about 50 minutes) after the noisy input signal is introduced. For the stronger negative autoregulation, when
the two protein time series initially overlap, then diverge. This indicates that input noise is filtered out by this mechanism for a period of time (about 50 minutes) after the noisy input signal is introduced. For the stronger negative autoregulation, when 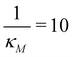 , the time of deviation gets longer (about 300 minutes), resulting in a 6-fold increase. A zoomed-in look at the graphs is provided where the first deviation from the shared curves takes place. Also, observe that the steady state of both mRNA and protein significantly decreases around 10-fold from the weaker inhibition to the stronger inhibition.
, the time of deviation gets longer (about 300 minutes), resulting in a 6-fold increase. A zoomed-in look at the graphs is provided where the first deviation from the shared curves takes place. Also, observe that the steady state of both mRNA and protein significantly decreases around 10-fold from the weaker inhibition to the stronger inhibition.
This leads to much smaller mRNA counts, resulting in a higher variability like we observed earlier in Fig. 6. The simulations predict that similar noise filtration does occur in the other two models.
To further investigate whether or not this observation holds at population levels, we ran our simulation 1000 times mimicking a population of 1000 cells and computed the noise filtration time for all three models for the same level of weak and strong negative autoregulation as before. The results of all our simulations are illustrated in Fig. 8 where 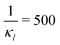 (left column) and
(left column) and 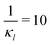 (right column) where l = {M,P}. Again, we have observed similar results indicating noise filtration is preserved at the population level in model M2. For both feedback strengths, model M2 clearly shows longer overall noise filtration times compared to models M1 and M3. The filtration time for model M2 is longer for stronger inhibition with a median time of roughly 30 minutes compared to weaker inhibition with a median time of roughly 10 minutes, a 3-fold change. For the other two models, M1 and M3, with weak negative autoregulation, the median filtration times are approximately the same and equal to roughly 5 minutes and 6 minutes, respectively. A similar behavior is observed with stronger inhibition.
(right column) where l = {M,P}. Again, we have observed similar results indicating noise filtration is preserved at the population level in model M2. For both feedback strengths, model M2 clearly shows longer overall noise filtration times compared to models M1 and M3. The filtration time for model M2 is longer for stronger inhibition with a median time of roughly 30 minutes compared to weaker inhibition with a median time of roughly 10 minutes, a 3-fold change. For the other two models, M1 and M3, with weak negative autoregulation, the median filtration times are approximately the same and equal to roughly 5 minutes and 6 minutes, respectively. A similar behavior is observed with stronger inhibition.
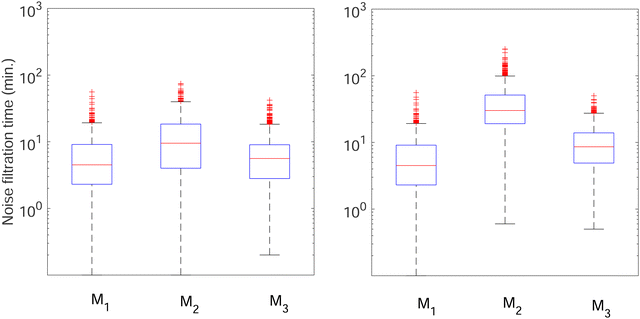 | ||
Fig. 8 Boxplots for all 3 models illustrating distributions of noise filtration times when changing from no noise to 10% input noise. Both sets of plots take parameters from Table 1, except 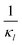 is set to 500 (left) and 10 (right) for the left and right graphs, respectively where l = {M,P}. is set to 500 (left) and 10 (right) for the left and right graphs, respectively where l = {M,P}. | ||
5 Conclusions
In this work, differential equation models were developed to study the effect of transcriptional and translational autoregulations on protein synthesis dynamics. The goal was to gain a better understanding of regulatory roles of the two negative autoregulation mechanisms, namely transcriptional and translational autoregulation. Our models are composed of two coupled ordinary differential equations (ODEs), which describe changes in mRNA and protein abundances over time. The model parameters were collected or estimated from the literature for E. coli. The steady state and stability analysis have been performed for each model, and we have shown that all three models are capable of producing only one steady independent of selections of the values for the parameters. Our analysis conclude that the models with no autoregulation and the model with translational autoregulation have only stable nodes regardless of parameter selection. Conversely, the model with transcriptional autoregulation is capable of producing both stable nodes and damped oscillatory dynamics around steady state for certain parameter sets.Numerical simulations of the deterministic models under different input signal profiles causing increase in the transcription rates show that the models with autoregulation respond to the input signals faster, and they also have shorter return time to the steady states. Furthermore, increase in the transcription rate by the input signal produces more protein in the model with no autoregulation, while this increase is smaller in the autoregulation models.
The analysis of the three models was further expanded by performing stochastic simulations using the Gillespie Algorithm in Matlab. First, stochastic simulations were performed to examine how the models differ with regards to noise levels at steady state. Our results show that the transcriptional autoregulation model is inherently the noisiest, while the translational autoregulation significantly reduces the noise in the protein counts compared to the model with no regulation. The role of translational negative feedback in reducing noise in protein counts is known.9 Our calculations shows that transcriptional negative autoregulation mechanism is 60 percent noisier than translational autoregulation mechanism for the parameter values we used. It has also been shown that post-transcriptional negative feedback attenuate noise more efficiently than classic transcriptional auto-repression.28 The biological systems make use of both regulatory mechanisms in decision making process. For example, it has been documented that post-transcriptional autoregulatory feedback is utilized to control noise in HIV protein expression and plays an important role in stabilizing viral fate.7 In this system, HIV strongly attenuates expression noise through a post-transcriptional negative feedback mechanism through a serial cascade of post-transcriptional splicing, whereby proteins generated from spliced mRNAs auto-deplete their own precursor unspliced mRNAs. This auto-depletion circuitry minimizes noise to stabilize HIV's commitment decision, and a noise-suppression molecule promotes stabilization.
The stochastic simulation results with noisy input signals predicts that the transcriptional autoregulation model filters out noise in the input signal for a period of time, but not as drastically in the other two models, and the noise filtration time is longer for stronger transcriptional autoregulations.
The deterministic and stochastic analysis of the models have shown that both types of negative autoregulations have distinctive regulatory roles in regulating the protein dynamics, and in silico experiments offer testable predictions for future experiments to better understand protein synthesis dynamics and its regulations.
Conflicts of interest
There are no conflicts to declare.Appendix: model parameters
In this section, we provide the details for the estimation of the unknown model parameters from the model organism E. coli. These values are listed in Table 1.
β
M
: the mRNA degradation parameter βM is estimated from experimentally measured half life of this molecule. mRNA is an unstable protein with a short half life between 2–5 minutes, on average.18,21 We took mRNA half life as 2 minutes in this study, and assume that the degradation is exponential, which gives us an estimate of 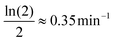 .
.
α
M
: the transcription rate parameter αM is dependent on the number of mRNA molecules per gene. The steady state mRNA molecule number per gene in E. coli are experimentally measured, and numbers vary between 2–3 molecules per gene.18 We took the steady state level of mRNA to be 3 molecules per cell. From eqn (1), the steady state of mRNA with no autoregulation is 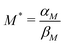 , which gives an estimate of
, which gives an estimate of 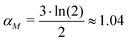 molecules per minute for this parameter.
molecules per minute for this parameter.
β
P
: protein half-life changes from protein to protein. The average protein half lives have been experimentally measured and found to be between 15 and 120 minutes for E. coli.19,20 In a more recent study, they studied the half-lives of 408 degradable E. coli proteins, and found out they form two distinct subpopulations of slow-degrading proteins and fast-degrading proteins. In this study, we employed a new method to estimate the protein half lives, and they found that the protein half lives as small as a few minutes to as long as over 1000 minutes.29 Here, we used a half-life of 30 minutes, resulting in an estimate of 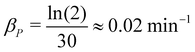 .
.
α
P
: the translation rate parameter αP is dependent on the number of protein molecules per gene. The average number of proteins per gene in E. coli varies between 150–1500 molecules.17 In our study, we assumed the average number to be 1000 molecules per gene. From eqn (2), the steady state protein level with no autoregulation becomes αPM* = βPP*, which leads to an estimate for the parameter as 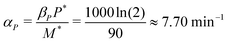 .
.
n M and nP: these represent hill coefficients which measure sharpness in the functions in eqn (3), and changes between 1 and 12 for biological systems.30 We took nM = nP = 2 in this study.
κ
M
and κP: these negative autoregulation parameters measure how much protein is needed to achieve half of the max response level. The lower κ values correspond to a higher number of protein molecules needed to achieve half of the maximum production rate. We used values from 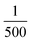 to
to 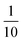 for this parameter to mimic weak or strong negative autoregulations.
for this parameter to mimic weak or strong negative autoregulations.
S a: the signal amplitude parameter Sa refers to the strength of input signal, which we changed from 1 to 4 to mimic up to a 5-fold change in the transcription rate αM of mRNA in our simulations, which is biologically reasonable.31
Acknowledgements
This work has been partially funded by the New College of Florida Faculty Development Fund.References
- A. Ay and N. Yildirim, Dynamics matter: differences and similarities between alternatively designed mechanisms, Mol. BioSyst., 2014, 10(7), 1948–1957 RSC.
- A. Ay, N. Wilner and N. Yildirim, Mathematical modeling deciphers the benefits of alternatively-designed conserved activatory and inhibitory gene circuits, Mol. BioSyst., 2015, 11(7), 2017–2030 RSC.
- Biochemistry, ed. C. K. Mathews, K. Van Holde and K. G. Ahern, Benjaminl-Cummings, San Francisco, 2000 Search PubMed.
- U. Alon, An introduction to systems biology: design principles of biological circuits, Chapman and Hall/CRC, 2006 Search PubMed.
- A. K. Mapp, A. Z. Ansari, M. Ptashne and P. B. Dervan, Activation of gene expression by small molecule transcription factors, Proc. Natl. Acad. Sci. U. S. A., 2000, 97(8), 3930–3935 CrossRef CAS PubMed.
- U. Alon, Network motifs: theory and experimental approaches, Nat. Rev. Genet., 2007, 8(6), 450–461 CrossRef CAS PubMed.
- M. M. K. Hansen, W. Y. Wen, E. Ingerman, B. S. Razooky, C. E. Thompson and R. D. Dar, et al., A Post-Transcriptional Feedback Mechanism for Noise Suppression and Fate Stabilization, Cell, 2018, 173(7), 1609–1621.e15 CrossRef CAS PubMed . Available from: https://www.sciencedirect.com/science/article/pii/S0092867418304586.
- B. Roy, D. Granas, F. Bragg, J. A. Cher, M. A. White and G. D. Stormo, Autoregulation of yeast ribosomal proteins discovered by efficient search for feedback regulation, Commun. Biol., 2020, 3(1), 1–9 CrossRef PubMed.
- P. S. Swain, Efficient attenuation of stochasticity in gene expression through posttranscriptional control, J. Mol. Biol., 2004, 344(4), 965–976 CrossRef CAS PubMed.
- G. Lemaire, L. Gold and M. Yarus, Autogenous translational repression of bacteriophage T4 gene 32 expression in vitro, J. Mol. Biol., 1978, 126(1), 73–90 CrossRef CAS PubMed.
- M. Santillán and M. C. Mackey, Dynamic regulation of the tryptophan operon: a modeling study and comparison with experimental data, Proc. Natl. Acad. Sci. U. S. A., 2001, 98(4), 1364–1369 CrossRef.
- M. C. Mackey, M. Santillán and N. Yildirim, Modeling operon dynamics: the tryptophan and lactose operons as paradigms, C. R. Biol., 2004, 327(3), 211–224 CrossRef CAS PubMed.
- N. Rosenfeld, M. B. Elowitz and U. Alon, Negative autoregulation speeds the response times of transcription networks, J. Mol. Biol., 2002, 323(5), 785–793 CrossRef CAS.
- T. Y. C. Tsai, Y. S. Choi, W. Ma, J. R. Pomerening, C. Tang and J. E. Ferrell Jr, Robust, tunable biological oscillations from interlinked positive and negative feedback loops, Science, 2008, 321(5885), 126–129 CrossRef CAS PubMed.
- N. Yildirim and M. C. Mackey, Feedback regulation in the lactose operon: a mathematical modeling study and comparison with experimental data, Biophys. J., 2003, 84(5), 2841–2851 CrossRef CAS.
- N. Yildirim, M. Santillan, D. Horike and M. C. Mackey, Dynamics and bistability in a reduced model of the lac operon. Chaos: An Interdisciplinary, J. Nonlinear Sci., 2004, 14(2), 279–292 CAS.
- Y. Ishihama, T. Schmidt, J. Rappsilber, M. Mann, F. U. Hartl and M. J. Kerner, et al., Protein abundance profiling of the Escherichia coli cytosol, BMC Genomics, 2008, 9(1), 1–17 CrossRef.
- M. A. Moran, B. Satinsky, S. M. Gifford, H. Luo, A. Rivers and L. K. Chan, et al., Sizing up metatranscriptomics, ISME J., 2013, 7(2), 237–243 CrossRef CAS PubMed.
- M. R. Maurizi, Proteases and protein degradation in Escherichia coli, Experientia, 1992, 48(2), 178–201 CrossRef CAS PubMed.
- P. Wong, S. Gladney and J. D. Keasling, Mathematical model of the lac operon: inducer exclusion, catabolite repression, and diauxic growth on glucose and lactose, Biotechnol. Prog., 1997, 13(2), 132–143 CrossRef CAS PubMed.
- S. Pedersen, S. Reeh and J. D. Friesen, Functional mRNA half lives in E. coli, Mol. Gen. Genet, 1978, 166(3), 329–336 CrossRef CAS PubMed.
- Mathworks, MATLAB, 2022. https://www.mathworks.com/products/matlab.html.
- V. Tyng and M. E. Kellman, Kinetic Model of Translational Autoregulation, J. Phys. Chem. B, 2018, 123(2), 369–378 CrossRef PubMed.
- M. Kaern, T. C. Elston, W. J. Blake and J. J. Collins, Stochasticity in gene expression: from theories to phenotypes, Nat. Rev. Genet., 2005, 6(6), 451–464 CrossRef CAS PubMed.
- D. T. Gillespie, Exact stochastic simulation of coupled chemical reactions, J. Phys. Chem., 1977, 81(25), 2340–2361 CrossRef CAS.
- J. Poleszczuk Gillespie algorithm for stochastic simulations of signaling pathways – vectorization in MATLAB. https://computecancer.wordpress.com/category/signaling-pathways/.
- M. M. Hansen and L. S. Weinberger, Post-Transcriptional Noise Control, BioEssays, 2019, 41(7), 1900044 CrossRef PubMed.
- M. M. Hansen and L. S. Weinberger, Post-transcriptional noise control, BioEssays, 2019, 41(7), 1900044 CrossRef PubMed.
- N. Nagar, N. Ecker, G. Loewenthal, O. Avram, D. Ben-Meir and D. Biran, et al., Harnessing Machine Learning To Unravel Protein Degradation in Escherichia coli, mSystems, 2021, 6(1), e01296-20 CrossRef.
- Q. Zhang, S. Bhattacharya and M. E. Andersen, Ultrasensitive response motifs: basic amplifiers in molecular signalling networks, Open Biol., 2013, 3(4), 130031 CrossRef.
- P. Sanchez-Vazquez, C. N. Dewey, N. Kitten, W. Ross and R. L. Gourse, Genome-wide effects on Escherichia coli transcription from ppGpp binding to its two sites on RNA polymerase, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(17), 8310–8319 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2023 |