Negative differential resistance based on phase transformation

Abstract

The negative differential resistance (NDR) device is attracting attention because of its broad potential application in neuromorphic computing and non-volatile memory. However, only a limited range of materials show NDR and, therefore, there is less choice in material selection for NDR devices. Considering this issue, we here demonstrate a novel current controlled NDR device based on phase transformation. To the best of our knowledge, this report is the first experimental demonstration that NDR can be induced by phase transformation. We believe that the impact of this demonstration is very large, as phase transformation is the most common phenomenon in materials and consequently most materials can be reconsidered as possible candidates for NDR devices. The prototype NDR device is constructed using hydrogen absorbing metal palladium (Pd) thin-wire and the phase transformation from metal-hydride to metal is employed for the demonstration. The observed NDR property shows a strong dependence on the current sweep speed. Also, it exhibits no current polarity dependence. Therefore, the NDR device based on phase transformation is significantly different from typical NDR devices such as tunnel diodes and memristors. The prototype NDR device has been found to be very useful for evaluating the hydrogen storage properties of metals. The advantage of this analysis method is that the storage properties can be acquired just by sweeping the applied current. This demonstration offers novel directions for both the development and utilization of NDR devices.

---

New concepts

We present a novel current controlled negative differential resistance (NDR) device based on phase transformation. To the best of our knowledge, this paper is the first experimental demonstration that phase transformation can induce the NDR phenomenon. We believe that the impact of this demonstration is very large, as phase transformation is the most common phenomenon in materials and consequently most materials can be reconsidered as possible candidates for NDR devices. The phase transformation-based NDR device exhibits several advantages such as its very simple working principle and potential for further development. The experimental demonstration focuses on the phase transformation from metal-hydride to metal and the observed NDR is very different from that observed in conventional devices such as tunnel diodes. Indeed, the proposed NDR device shows a strong dependence on the current sweep speed and it has been found to be very useful for evaluating hydrogen storage properties of metals. The advantage of this evaluation method is that the storage properties can be acquired just by sweeping the applied current. This research offers novel directions for both the development and utilization of NDR devices, and accelerates research in neuromorphic computing, non-volatile memory, and hydrogen storage metals.

Introduction

Negative differential resistance (NDR) refers to a negative differential slope in a current–voltage (I–V) characteristic curve of two-terminal devices.¹ This extraordinary property is applied to microwave oscillators and amplifiers which work at ultrahigh frequency such as tens of GHz. The historical NRD device is a pn-junction based tunnelling diode, which shows NDR originating from the quantum tunnelling effect at high bias voltage.^2,3 In recent decades, a similar NDR property based on electron tunnelling has also been observed in molecular films.^4–7 These kinds of bias voltage induced NDR are known as a voltage controlled NDR (VC-NDR). These days, intensive research can also be found on another type of NDR, namely, current controlled NDR (CC-NDR; V decreases with increasing applied I). The memristor-based CC-NDR device is currently attracting the most attention due to its potential application in neuromorphic computing and non-volatile memory.^8–10 The device typically consists of metal-oxide thin films such as titanium oxide (TiO₂) and niobium oxide (NbO₂) films, and the driving current is applied via metallic electrodes. Although the origin of CC-NDR observed on these devices is still under discussion, Joule heat plays an important role in the formation/destruction of the conductive filament in the metal-oxide film, the excitation of Mott metal-insulator transition in the film, and the Poole–Frenkel electron transport via defects in the metal-oxide lattice.^8–11 However, only a limited number of materials are known to show NDR properties and, therefore, there is less choice in material selection for NDR devices.

Considering this situation, we here report a novel CC-NDR device based on phase transformation. According to our literature survey, this is the first experimental demonstration that CC-NDR can be induced by phase transformation. As discussed later in the section “potential and advantages of phase transformation-based NDR devices,” this demonstration has a large impact on NDR studies. This is because phase transformation is one of the fundamental phenomena of materials and most of the materials can hence be reconsidered as candidates for NDR devices. Also, the phase transformation-based NDR device shows potential and several advantages. Therefore, we strongly believe that this study offers diversity and a novel direction for NDR studies in the future.

In this study, as an example demonstrating our idea, we designed an NDR device based on metal-hydride. The NDR device shows NDR as expected. However, unlike typical NDR devices, the observed NDR based on phase transformation from metal-hydride (high resistance) to metal (low resistance) shows a strong dependence on the sweep speed of I. Therefore, our NDR device is significantly different from typical NDR devices and it is expected to be very useful for analysing hydrogen storage properties, since important parameters such as phase transformation temperature from metal-hydride to metal can be measured just by sweeping the applied I. The cyclic hydrogen storage properties can also be evaluated from the NDR property during cyclic current sweeps.

Results and discussion

Proposal of the NDR device based on phase transformation

In this study, we employed “metal-hydride to metal” phase transformation as the first step of the demonstration, although the idea of the phase transformation-based NDR is not limited to the example described here. From the viewpoint of practical applications and performance, there may be a more suitable choice than the present metal-hydride (note: the present metal-hydride requires relatively high current/power to induce NDR switching, as its resistance is low). However, metal-hydride is adopted, because the phase transformation and resistance of metal-hydride systems have been investigated very deeply. Also, as the prototype device of metal-hydride can be constructed simply using the commercially-available bulk material (please refer to the section “Experimental method”) and it is hence possible to exclude complicated phenomena such as interfacial effects observed in thin-films, making it easier to demonstrate that the observed NDR purely originates from the phase transformation of metal-hydride.

Here, prior to proposing the NDR device based on phase transformation, it might be better to summarize the phase transformation of hydrogen storage metals briefly. In general, hydrogenation of metals consists of two steps.^12–16 The first step is the slight incorporation of hydrogen atoms into the metal lattice, resulting in a solid solution. Within this first step, the lattice maintains its original crystal structure and the physical properties remain almost unchanged from the initial metal state. Thus, in this paper, this phase is denoted as “metal,” although it may contain a small amount of interstitial solid solution hydrogen atoms. The second step occurring at higher hydrogen pressure involves the formation of a new phase consisting of metal and hydrogen. This new phase has a different crystal structure and contains a higher concentration of hydrogen atoms. Therefore, large differences can be found in physical properties. Accordingly, this phase is referred to as “metal-hydride” in this paper.

The resistance of hydrogen storage metals depends strongly on the amount of hydrogen atoms in the lattice.^17,18 This is because of the increased electron scattering by hydrogen atoms incorporated in the lattice. Therefore, from the viewpoint of relative resistance, “metal” represents a low resistance state (LRS) and “metal-hydride” represents a high resistance state (HRS).

Here, let us consider the electrical resistance change during the application of heat to the metal-hydride (Fig. 1). As shown in the figure, three mechanisms work together in response to temperature increase. The first mechanism is a resistance increase due to the increased phonon scattering (black-flow in Fig. 1). This increase is a well-known phenomenon in metals and is related to larger lattice vibration at higher temperatures. The impact of this first mechanism is small (in comparison to the third one), resulting in a gradual increase in resistance. The second mechanism is a resistance decrease originating from the slight hydrogen escape from the metal-hydride lattice in response to a temperature increase (red-flow in Fig. 1). This originates from the temperature dependence of hydrogen concentration in metal-hydride.¹³ It results in a resistance decrease and its impact is small and gradual (in comparison with the third one). However, its impact on resistance is comparable to that of the first mechanism. The third mechanism is a resistance decrease due to the phase transformation from metal-hydride to metal (metal-hydride → metal) (green-flow in Fig. 1). This mechanism is only active at the phase transformation temperature; however, it has a large and abrupt impact on resistance.¹⁹ This is because the phase transformation is a change in the crystal structure and is accompanied by large and abrupt decrease in hydrogen concentration in the lattice. Note that both second and third mechanisms originate principally from the escape of hydrogen; however, their impacts (small gradual ↔ large abrupt) and occurrence conditions (almost always in metal-hydride ↔ only at the phase transformation temperature) are completely different from each other. As discussed in the following section, the third mechanism, or the phase transformation, induces the NDR property.

Fig. 1 Flow diagram showing effects of temperature on the electrical resistance of metal-hydride. The flow shown in black is a typical response of metal and it results in small and gradual increase in resistance. The flows shown in red and green are only available in metal-hydride. In detail, the red-flow originates from the slight hydrogen escape in response to temperature increase and it has small and gradual impact on resistance. The green-flow is available only during the phase transformation and it leads to a large and abrupt decrease in resistance, as the phase transformation is the change in the crystal structure and it accompanies the large decrease in hydrogen concentration, or the huge amount of hydrogen escape from the lattice, at the phase transformation temperature. Because of red- and green-flows, smaller TCR and NDR can be observed in metal-hydride. Note that line thicknesses of arrows in the diagram are schematically weighted by their impacts.

The measured response against temperature is a sum of these three impacts, namely, a residue that remains after the cancellation of three mechanisms. Accordingly, a smaller temperature coefficient of resistance (TCR) may be observed, when the phonon scattering effect (black-flow) remains stronger than other mechanisms (red- and green-flows). The experimental observation of this situation is displayed later in the “Smaller TCR” section.

In contrast, when the supplied heat is enough to induce the phase transformation from metal-hydride to metal, the impact of the phase transformation (green-flow) may exceed the phonon scattering effect (black-flow). In such cases, a large and abrupt resistance decrease (from HRS to LRS) can be expected at the temperature of the phase transformation. This suggests that when the applied current is swept up to a sufficient level to induce the phase transformation, a decrease in R takes place. In other words, R decreases at a certain amount of current, namely, CC-NDR. This is the working principle of the proposed CC-NDR device based on the phase transformation and the NDR property can be observed at the current which induces phase transformation. Although the explanations here are focused on the NDR property originating from the HRS to the LRS during the current increasing sweep (sweep heated), the inverse phenomenon of NDR from the LRS to the HRS also takes place during the current decreasing sweep. The experimental demonstration of this CC-NDR is shown later in the “NDR property” section.

Design and fabrication of the NDR device

In the previous section, the possible NDR property of metal-hydride was discussed. To confirm this expectation, we designed an NDR device (Fig. 2). This device structure was inspired by our previous studies.^20–22Fig. 2(a) shows a schematic illustration of the device and measurement circuit. Fig. 2(b) shows a photo-image of the actual experimental setup. The device consists of a thin-wire of hydrogen storage metal and a metal nipple for ultrahigh vacuum equipment. As the thin-wire of hydrogen storage metal, palladium (Pd) thin-wire was employed. Note that Pd is known as the most famous hydrogen absorbing metal and the easiest metal to hydrogenate.^14–16 Therefore, as the first step in demonstrating our idea, Pd is the most suitable material. However, as the conductivity of Pd is very high, it requires a high current/power to induce NDR thermally. Therefore, from a practical aspect, considering factors such as power consumption of the device, materials having higher resistances, smaller heat capacity, etc. are suitable and, therefore, the next step of our study is the employment of such materials as the NDR element (please find our future report). The Pd thin-wire was placed in the nipple and hydrogenated using the process described in the Experimental section. Fig. 2(c) shows the change in electrical resistance (R) of Pd thin-wire during hydrogenation. The increase in R corresponds the amount of hydrogen atoms in the metal lattice.^17,18 It is clear from Fig. 2(c) that hydrogenation consists of two steps. The first step is the gradual increase region. In this region, hydrogen atoms slightly dissolve into the Pd lattice (crystal structure of Pd: face-centred cubic (fcc)). In the case of Pd, such a solid solution “metal” is usually denoted as the α-phase and shows similar characteristics to pure-Pd. According to the increase in the relative resistance (R/R₀, R₀ is the initial R before hydrogenation) at the transition point at t ≈ 40 s, the solubility limit in the α-phase is estimated to be 0.04 H/Pd (this number is calculated from the relation between R/R₀ and H/Pd in the literature¹⁷). This number is slightly larger than the literature value (0.02 H/Pd at 25 °C) measured on bulk material.¹³ However, we consider that it is still within the acceptable range, as the hydrogenation at this stage involves interstitial incorporation and it is very sensitive to defects, residual micro-strains, and grain boundaries in metal.¹⁶ The second step is the rapid increase region and it corresponds to the formation of a “metal-hydride” phase. The metal-hydride phase has a sodium chloride (NaCl) type crystal structure and is denotated as the β-phase. Once the wire completely transforms into the β-phase at t ≈ 110 s, no further large change in R can be observed even when the pressure is adjusted. Under the assumption that the progress of α → β phase transformation is 0% at t ≈ 40 s and 100% at t ≈ 110 s and the increase in R is proportional to the progress, the maximum transformation speed is estimated from the slope shown in Fig. 2(c) and it is around 2% s⁻¹. Also, the time constant of the phase transformation, or the time at 63.2% progress, is 33 s. This suggests that the transformation is slow and on the order of 10¹ s. After waiting for a long time, the relative resistance (R/R₀, R₀ is the initial R before hydrogenation) reaches to 1.77 (i.e., R is increased by 77%). According to the relation between resistance and hydrogen concentration,^17,18 this number indicates that the hydrogen concentration is 0.68 H/Pd (PdH_0.68). This H/Pd concentration is very reasonable from the viewpoint of the pressure–composition–isotherms (PCT) diagram in the literature (at hydrogen partial pressure p(H₂) = 10 kPa, thermodynamic equilibrium composition is PdH_0.67).¹³ Therefore, the Pd-thin-wire in the device was completely hydrogenated and we can conclude that the NDR device consisting of metal-hydride was fabricated successfully.

Fig. 2 Prepared NDR device. (a) Schematic illustration of the negative differential resistance (NDR) device and measurement circuit. The circuit consists of a programmable current source, digital voltmeter, and PC. (b) Photograph of the NDR device. The Pd thin-wire was placed in the nipple and annealed via electrical resistance heating in vacuum. Afterward, the N₂-10 vol% H₂ gas mixture was filled at 100 kPa (1 atm.). Therefore, the partial pressure of H₂ (p(H₂)) is 10 kPa. (c) Change in resistance (R) of the Pd thin-wire during hydrogenation. At time (t) is equal to 0 s, the N₂–H₂ gas mixture was introduced to the device and it was encapsulated at t ≈ 180 s and p(H₂) = 10 kPa. The axis on the right-hand-side shows a relative resistance (R₀ is an initial R at t = 0 s). It reaches 1.73 at t = 300 s and converges to 1.77 after waiting for a long time. The slope triangle in (c) indicates the maximum speed of the transformation.

Smaller TCR

First, the TCR of the NDR device was measured to confirm the impact of hydrogen on R (Fig. 3). To clarify the effect of H, the TCR measurement was performed in both N₂-10 vol%H₂ (p(H₂) = 10 kPa) and pure-N₂ (p(H₂) = 0 kPa) atmospheres. From Fig. 3, the TCR of the metal-hydride phase (β-PdH_0.68) was found to be 0.0009 K⁻¹. This number is very small (around one-fourth) compared to than the TCR of the metal phase (α-Pd) at p(H₂) = 0 kPa (0.0034 K⁻¹). From this result, there is no doubt that the red-flow shown in Fig. 1 really exists in the metal-hydride and the effect of red-flow (hydrogen escape) on the TCR is comparable to the typical effect of thermal vibration. Table 1 shows a summary of measured and literature TCRs. The measured TCR at p(H₂) = 0 kPa is equal to the literature TCR of pure-Pd,²³ while a relatively small TCR was observed in metal-hydride at p(H₂) = 10 kPa.

Fig. 3 Temperature dependence of resistance (R) of the Pd thin-wire. R is normalized using R at 23 °C (R_23 °C). TCR numbers shown in the figure were estimated from a slope around room temperature (range: 23–33 °C). TCR in α-Pd at p(H₂) = 0 kPa is in agreement with the number in literature, while much smaller TCR is observed in β-PdH_0.68 at p(H₂) = 10 kPa. Details are summarized in Table 1.

Table 1 Summary of measured TCRs of thin-wires. TCR numbers shown here are estimated from Fig. 3 and Fig. S1 (ESI). Note that all TCRs in this table are slightly different from typical TCR values, because the temperature range of TCRs shown in this table is 23–33 °C, while the typical range in the literature is 0–100 °C

p(H2) (kPa)	TCR of Pd thin-wire (K^−1)	TCR of Pt thin-wire (K^−1)
a Calculated from numbers at 20 °C and 27 °C in the literature.^23 b Calculated from the Callendar–Van Dusen equation for Pt (temperature range: 23–33 °C). The most typical constants are employed (A = 3.908 × 10^−3 °C^−1 and B = −5.775 × 10^−7 °C^−1).
0	0.0034 ± 0.0004	0.0036 ± 0.0004
10	0.0009 ± 0.0001	0.0038 ± 0.0004
Reference values in literature	0.0035^a	0.0036^b

---

The reference measurement on the Pt thin-wire is shown in Fig. S1 in the ESI.† The measured TCR of the Pt wire is 0.0036 K⁻¹ at p(H₂) = 0 kPa. This TCR number is slightly smaller than typical TCR values such as 0.00385 and 0.00392 K⁻¹.²⁴ However, this number is reasonable when one considers the temperature range (this study: 23–33 °C; typical: 0–100 °C) and the measurement accuracy (see Table 1). The measured TCR at p(H₂) = 10 kPa is 0.0038 K⁻¹ and it is almost equal to the number at p(H₂) = 0 kPa.

In short, a smaller TCR was observed for the metal-hydride. Therefore, the impact of hydrogen escape on resistance is significant. Accordingly, at the phase transformation temperature where the rapid escape of hydrogen atoms occurs, NDR could take place. In the next section, a very large current was applied to the devices for inducing the NDR property.

NDR property

Fig. 4(a) shows the I–V characteristic curve measured under the current sweep condition. The sweep sequence is 0 → +250 → 0 → −250 → 0 mA and the sweep speed is 0.4 mA s⁻¹. Therefore, one sweep loop takes 2500 s. At a glance, it is possible to observe the hysteresis CC-NDR properties at around I = ±150 mA. In detail, the NDR property was observed four times during the sweeps of 0 → +250, +250 → 0, 0 → −250, and −250 → 0 mA. The NDR observed during the current increasing sweeps (0 → +250 and 0 → −250 mA) corresponds to the β → α phase transformation [from metal-hydride (HRS) to metal (LRS)]. The NDR observed during the current decreasing sweeps (+250 → 0 and −250 → 0 mA) corresponds to the α → β phase transformation [from metal (LRS) to metal-hydride (HRS)]. The hysteresis is related to the splitting of the transformation temperature of hydrogenation/dehydrogenation, which is a typical characteristic of hydrogen storage metals.^12,15,16 The NDR property was further confirmed from the viewpoint of resistance (R) (Fig. 4(b)). The change in R from the HRS to a LRS was observed at a large applied current such as |I| ≳ 150 mA. The change in R reaches −32% at peak-to-peak. Note that a slight R increase can be found in the non-NDR regions of both LRS and HRS. This can be attributed to increased phonon scattering due to self-heating (temperature increase). Fig. 4(b) is symmetric about the vertical-axis, indicating no current polarity dependence. Considering the device structure and working principle of the device (the present NDR is induced thermally), the square of I associated with the input power is important rather than the polarity of I. For details, please find the explanations about Fig. 4(c); this result is reasonable. For further clarification, R is plotted against the input power (P; P = IV = RI²) (Fig. 4(c)). As the two curves of 0 → + 250 → 0 mA and 0 → −250 → 0 mA are overlapped completely, it is further confirmed that the NDR property is not dependent on the current polarity. From Fig. 4(c), it is also clear that the curve consists of two components: one is a large R decrease due to the phase transformation and another is a slight increase due to the self-heating. From the TCR number in Table 1, the extent of the temperature increase can be roughly estimated (right-hand-side axis of Fig. 4(c); note that this axis is valid only before the β → α phase transformation; after the transformation, it is impossible to estimate the temperature from R, as the influence of hydrogen escape becomes the dominating effect). The phase transformation from metal-hydride to metal takes place at an ≈80 °C increase. When R.T. is added to this number, the phase transformation temperature is estimated to be ≈100 °C. According to the PCT curve in the literature,¹³ the phase PdH_0.68 metal-hydride could transform to metal at 80 °C. Thus, the estimated temperature is slightly higher than the literature value. However, considering the hysteresis nature of hydrogen storage metals,^12,15,16 it can still be concluded that the estimated temperature is the phase transformation temperature from metal-hydride to metal and the NDR property observed here is related to the heat driven phase transformation (i.e., thermally induced phenomenon). Consequently, the direct effect of applied I is expected to have a minor impact on the phase transformation.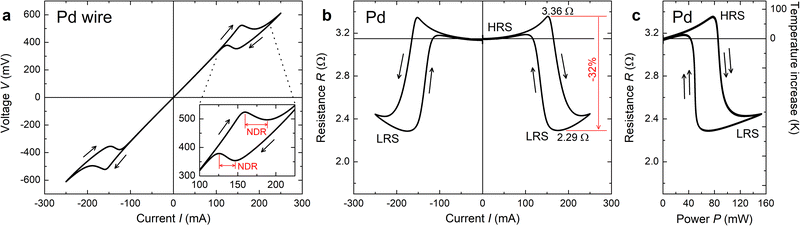

Fig. 4 NDR property based on phase transformation. (a) Current–voltage (I–V) curve of the NDR device consisting of Pd thin-wire. NDR can be found at I ≈ ±150 mA. The inset figure shows the close view around +150 mA and NDR regions are indicated using red arrows. Since the curve shows a symmetry, the same situation can be found at negative I (I ≈ −150 mA). (b) Current–resistance (I–R) curve estimated from (a). The symmetric decrease in R can be observed at larger I on both positive and negative polarities. As indicated by red lines, the decrease in R reaches 32% at peak-to-peak. (c) Input power–resistance (P–R) curve estimated from (a). Two curves corresponding to positive and negative I are completely overlapped, indicating no dependence on current polarity. The axis on the right-hand-side shows the increase in the wire temperature, which is estimated using the TCR in Table 1. Note that this temperature axis is valid only before β → α phase transformation.

In the case of Pt thin-wire, no hysteresis and no NDR can be observed (Fig. S2, ESI†), as Pt does not react with H₂. Instead, an increase in R is observed at a large applied I and corresponds to self-heating (as discussed below). In detail, from Fig. S2(a) (ESI;† in this figure, two curves are completely overlapped because of no hysteresis behaviour), it is found that the I–V relation is almost linear when I is small such as |I| < 50 mA. However, at |I| > 50 mA, a non-linear response can be observed. This non-linearity can be displayed as the quadratic curves of R against I (Fig. S2(b), ESI;† in this figure, two curves are completely overlapped because of no hysteresis behaviour). This quadratic response suggests that self-heating due to large current application is the origin of the observed non-linearity. Indeed, R shows an almost linear relation to P (= RI²) (Fig. S2(c), ESI†). The temperature increase was estimated from the TCR number shown in Table 1 and it is around 70 °C at |I| = 250 mA. Note that, in Fig. S2(c) (ESI†), two loops corresponding to positive and negative I applications are overlapped completely (i.e., four lines of 0 → +250, +250 → 0, 0 → −250, and −250 → 0 mA are overlapped completely, although they look like one line). This indicates that there is no current polarity dependence. These observations on the Pt wire are very reasonable, because no reaction should take place on the stable Pt wire under slight self-heating.

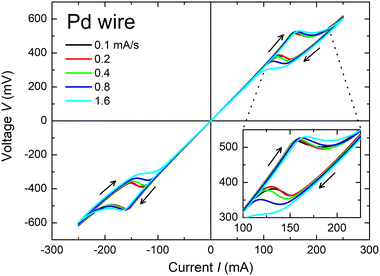
Sweep speed dependence

Fig. 5 shows the sweep speed dependence on the NDR property. Roughly speaking, there is less change during the current increasing sweeps of 0 → +250 and 0 → −250 mA (corresponding phase transformation: β → α). In contrast, a large difference can be found during the current decreasing sweeps of +250 → 0 and −250 → 0 mA (phase transformation: α → β). The higher sweep speed results in a larger hysteresis area. These observations indicate that α → β transformation is a slower reaction than β → α transformation. In other words, the hydrogen escape from metal-hydride is faster than the hydrogen incorporation into metal. This observation is consistent with the typical properties of hydrogen storage metals in the literature.^13,14 Therefore, from the sweep speed dependence of the NDR property, it is possible to measure the dynamic parameters of hydrogen storage properties such as the phase transformation speed and hydrogen diffusivity.

Fig. 5 Effect of the sweep speed on current–voltage (I–V) curves of the NDR device. At higher sweep speed such as 0.8 and 1.6 mA s⁻¹, larger hysteresis can be found in the I–V curve. This relates to the slow phase transformation between metal (α-phase) and metal-hydride (β-phase). From the comparison between increasing and decreasing current sweeps, β → α phase transformation is found to be faster than α → β phase transformation.

In the case of Pt thin-wire, no sweep speed dependence can be found (Fig. S3, ESI†). This result is reasonable, since nothing will happen except for self-heating.

Cyclic sweep

The cyclic sweep measurement has been conducted up to 10 cycles (Fig. 6). As one cycle consists of two metal-hydride ⇄ metal transformations, 10 cycles correspond to 20 sets of hydrogenation and dehydrogenation. At a glance, I–V curves show almost no cycle dependence. However, in detail, the decrease in measured V can be observed at a larger cycle number. This suggests that the amount of stored hydrogen was decreased and/or the wire morphology was changed. Note that the cyclic hydrogenation and dehydrogenation are well known to cause metal lattice degradation and result in the poor hydrogen storage capacity.^25,26

Fig. 6 Cycle characteristics of the NRD device measured at 0.4 mA s⁻¹ sweep speed. Roughly speaking, the current–voltage (I–V) curve shows a stable response to cycle. However, in a close view (inset figure), a slight decrease in V can be found.

In contrast, results from the Pt wire show no cyclic dependence (Fig. S4, ESI†). Note that, in Fig. S4 (ESI†), 10 loops (i.e., 20 lines) are overlapped completely. These observations indicate that nothing happens on the Pt wire at the slightly elevated temperature of 70 °C. From these cyclic measurements, we conclude that the cyclic hydrogen storage properties can be evaluated very easily using the current sweep and resulting NDR property (details of which are under investigation).

Long-term retention characteristics

The long-term retention characteristics of the NDR device were measured over 10⁵ s (Fig. 7). It is obvious that R at the HRS (applied I: 1 mA) is very stable. In the case of the LRS (applied I: 250 mA), R is almost stable. In detail, however, a slight gradual decrease in R during the initial period of time can be found at the LRS. This could be attributed to the slight escape of H from Pd thin-wire due to the continuous application of 250 mA, which induces an additional increase in the wire temperature. However, both HRS and LRS are stable enough to be distinguished from each other. These results also indicate that the amount of H₂ gas leakage is negligibly small from the viewpoint of the NDR property and, therefore, a H₂ gas atmosphere can be employed for electrical devices when H₂ gas is encapsulated properly.

Fig. 7 Long-term retention characteristics of the NDR device. Rs at the HRS and LRS are measured under continuous application of 1 and 250 mA, respectively.

Tailorability

Next, we demonstrate the tailorability of the NDR property. As the proposed NDR is based simply on self-heating, the input power P (= RI²) is of course an important parameter (and it determines the wire temperature). Accordingly, the NDR property may be tailored by adjusting R of the wire. To confirm this expectation, the NDR property of the thicker Pd thin-wire was also measured (Fig. 8). The diameter of the thicker wire was 0.1 mm (i.e., the diameter of the wire was doubled). For comparison, the result for 0.05 mm wire (originating from Fig. 5) is also shown. It is obvious that the employment of the thicker wire results in a large change in the NDR property. Indeed, the NDR region shifts to larger I. Roughly speaking, the required I for inducing NDR is almost doubled. This could be explained as follows: as R is proportional to the reciprocal of the square of the diameter, R of the thicker wire is one quarter of R of the thinner wire. Therefore, twice the I is required for injecting the same amount of P into the wire.

Fig. 8 Impact of the diameter of Pd thin-wire on the NDR property. I–V curves were measured at 0.2 mA s⁻¹. In the case of the thicker wire, larger I is required to induce NDR.

In addition to the required I, a large difference is also observed in the shape of the I–V curve. The larger hysteresis and smaller NDR observed on the thicker wire can be attributed to the slower hydrogen absorption/desorption due to its larger diameter. In short, the dimension of the wire has been found to have a large impact on the NDR property and, therefore, it can be used to tailor the NDR property.

Potential and advantages of phase transformation-based NDR devices

Finally, we summarize the potential and advantages of the proposed NDR device based on phase transformation. As described at the beginning of the section “proposal of the NDR device based on phase transformation,” the metal-hydride ⇄ metal phase transformation was employed only as an example. According to the measured results and discussion, it can be concluded that the condition for inducing CC-NDR consists only of the following three factors:

(1) HRS at low temperature

(2) LRS at high temperature

(3) Sufficient applied I to induce phase transformation resulting in HRS → LRS

When these criteria are satisfied, NDR can be simply observed during phase transformation. Therefore, we expect that, in future, a variety of novel NDR devices can be developed in accordance with these criteria and this report provides a starting point for them. Note that a H₂ gas atmosphere is required only for the present case of metal-hydride ⇄ metal phase transformation and the atmosphere is not a principal condition for inducing NDR.

The advantages of phase transformation-based NDR devices are yet to be identified; however, the following are at least some of the advantages and characteristics of the proposed devices.

(a) Very simple working mechanism. It employs phase transformation, which is one of the most typical phenomena of materials. Therefore, it has very broad applicability and almost any material can be reconsidered as a possible candidate for NDR elements. Also, this simple mechanism is expected to be more reliable compared to those based on metastable working mechanisms such as the formation of the conductive filaments,^9,10 because phase transformation is not a coincidental phenomenon but an inevitable phenomenon at the temperature of phase transformation.

(b) Large tailorability. As phase transformation can be controlled by employing materials science-based approaches²⁷ such as alloying, NDR based on phase transformation can be extensively tailored to meet the required specification. In addition, as shown in the previous section, material dimensions can also be employed in tailoring the NDR property.

Finally, we describe the suitable device structure for practical use. As the objective of this study is the demonstration of the novel mechanism for inducing NDR, we constructed the prototype device using bulk material, or commercially-available thin-wire, and the dehydrogenation reaction was employed. However, it results in very slow operation. Therefore, the next step toward practical use is to demonstrate NDR in a material which shows faster phase transformation. Another is to demonstrate NDR in thin-film devices, namely, miniaturized devices. The combination of these two is best, as they result in both higher operation speed and lower power consumption. In addition, the use of high resistance materials is desired for reducing the operation current. The material in which phase transformation is induced easily is of course preferred. As discussed in a), there are a huge number of candidate materials for these phase transformation-based devices and, therefore, contemporary approaches such as materials informatics²⁸ may be helpful in searching suitable materials.

Conclusions

Using the designed NDR device, it was demonstrated that the CC-NDR property can be realized through phase transformation. Therefore, a novel NDR device has been proposed and it is now available for further investigation. Because the device employs the most common phenomenon of materials, namely, phase transformation, as the origin of NDR, this proposal has relatively high applicability and most materials can be reconsidered as possible candidates for NDR devices. The criteria for inducing NDR are very simple and summarized in three lines. The potential, advantages, and future direction of the proposal are also discussed deeply and some of them remain to be studied. We believe that this demonstration increases the diversity of studies about NDR devices. Indeed, it widens the options for material selection for NDR devices and contributes to neuromorphic computing and non-volatile memory.

The demonstration of the proposed NDR mechanism was performed on the phase transformation between metal (LRS) and its hydride (HRS). The observed NDR property can be attributed not to the direct effect of the applied current but to the thermal effect, or Joule self-heating, on the phase transformation. Therefore, the device shows no current polarity dependence. Also, the observed properties of the NDR device are very different from those of conventional NDR devices and they can be explained by characteristics of the employed phase transformation from metal-hydride to metal. The proposed NDR device is found to be a very convenient analysis method to measure the hydrogen storage property of metals. Indeed, just by sweeping the applied current, important parameters such as the phase transformation temperature and hydrogenation/dehydrogenation speeds, of hydrogen storage metals can be acquired. We consider that this analysis method is suitable especially for the cyclic performance test, as it can be performed just by sweeping the applied current.

Regarding the TCR, a smaller TCR was found on metal-hydride and it originates from the gradual escape of hydrogen from the metal lattice. This observation indicates that the influence of hydrogen escape is comparable to the effect of the thermal vibration on resistance. Also, it suggests that the TCR of metals can be controlled by adjusting the hydrogen amount in the metal lattice.

Experimental

The NDR device was assembled using the ConFlat (CF) flanged stainless steel components for ultrahigh vacuum equipment. The Pd thin-wire (diameter: 0.05 mm, purity: 99.95%) was spot-welded to thick copper electrodes and connected electrically to the measurement circuit on the atmospheric side of the device. The hydrogenation of the Pd wire was performed through the following procedures. First, the Pd wire was annealed around 900 °C by applying large current (200 mA) in vacuum. Next, the nitrogen–hydrogen (N₂–H₂) gas mixture was slowly introduced into the NDR device. The H₂ concentration of the introduced gas mixture was 10 vol%. After the pressure reached to slightly higher than 100 kPa (1 atm.) at around 180 s, the pressure was adjusted to 100 kPa and the device was encapsulated at 100 kPa. Therefore, the partial pressure of H₂ gas (p(H₂)) was 10 kPa. The hydrogenation of the wire was confirmed by monitoring R of the wire. The applied current was only 1 mA and its effect on phase transformation was negligibly small (see the “NDR property” section). For comparison, a reference measurement on the Pt thin-wire (diameter: 0.05 mm, purity: 99.98%) was performed in the same manner. The results of the Pt reference measurement can be found mainly in ESI.†

The TCR of the prepared NDR device was confirmed using a low temperature oven and precision resistance meter. The applied I for the R measurement was 1 mA and this current is small enough to ignore any influences on the device (“NDR property” section). The current-reversal method was employed for removing electromotive force (EMF). As the temperature increase results in the elevation of p(H₂) and it may affect the TCR, the temperature range for the TCR measurement of this study is limited to the very narrow range of 23–33 °C. From a safety point of view, it is also preferable to restrict the temperature range of the TCR measurement to narrow limits near room temperature. Note that, at temperatures higher than room temperature, the device is at risk of explosion. This is because, at such temperatures, the inner pressure of the device exceeds the outer atmospheric pressure; however, such a situation is not assumed for the vacuum components employed for fabricating the prototype device.

The NDR property was measured using the circuit shown in Fig. 2(a). The measurement circuit consists of a programable current source and a digital voltmeter. They were connected to the device using the Kelvin four-wire connection method. The sweep sequence of I is 0 → +250 → 0 → −250 → 0 mA, or a triangular waveform having peak values of ±250 mA. The increase of the current sweep was 0.1 mA and the voltage was measured at each increment. Therefore, one sweep loop consists of ≈10 000 data points of (applied I, measured V). The sweep speed was 0.1–1.6 mA s⁻¹. R is simply calculated using Ohm's law (R = V/I).

The long-term retention characteristics of the NDR device were measured under the continuous application of constant I. As shown in Fig. 4, the applied I was chosen to be +1 mA for the HRS and +250 mA for the LRS. Note that, during the retention measurements, no temperature control was performed other than air-conditioned room temperature. Therefore, LRS is induced and retained simply by the application of a large I of 250 mA.

A thicker Pd thin-wire (diameter: 0.1 mm and purity: 99.9%) was also employed for demonstrating the tailorability of the proposed NDR. The wire was annealed by applying a large current (400 mA). The NDR property was measured under the sweep sequence of 0 → +500 → 0 → −500 → 0 mA. The sweep speed was 0.2 mA s⁻¹ (increase in sweep current: 0.2 mA and time period of each increase: 1 s). Other details are the same as those of the thinner wire.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the Grants-in-Aid for Scientific Research (KAKENHI) from the Japan Society for the Promotion of Science (JSPS) under grant no. 18K14137 and 21H05009.

References

1. P. R. Berger and A. Ramesh, in Comprehensive semiconductor science and technology, ed. P. Bhattacharya, R. Fornari and H. Kamimura, Elsevier, Amsterdam, 2011, ch 5.05, vol. 5, pp. 179–241.
2. L. Esaki, Phys. Rev., 1958, 109, 603–604.
3. H. Kim, M. A. Tanatar and R. Prozorov, Rev. Sci. Instrum., 2018, 89, 094704.
4. J. Chen, M. A. Reed, A. M. Rawlett and J. M. Tour, Science, 1999, 286, 1550–1552.
5. M. Grobis, A. Wachowiak, R. Yamachika and M. F. Crommie, Appl. Phys. Lett., 2005, 86, 204102.
6. X. W. Tu, G. Mikaelian and W. Ho, Phys. Rev. Lett., 2008, 100, 126807.
7. X. T. Li, D. Q. Zou, B. Bin, C. F. Fang, J. F. Zhao, D. M. Li and D. S. Liu, RSC Adv., 2017, 7, 25244–25252.
8. M. D. Pickett, J. Borghetti, J. J. Yang, G. Medeiros-Ribeiro and R. S. Williams, Adv. Mater., 2011, 23, 1730–1733.
9. S. Kumar, Z. W. Wang, N. Davila, N. Kumari, K. J. Norris, X. P. Huang, J. P. Strachan, D. Vine, A. L. D. Kilcoyne, Y. Nishi and R. S. Williams, Nat. Commun., 2017, 8, 658.
10. G. D. Zhou, S. K. Duan, P. Li, B. Sun, B. Wu, Y. Q. Yao, X. D. Yang, J. J. Han, J. G. Wu, G. Wang, L. P. Liao, C. Y. Lin, W. Hu, C. Y. Xu, D. B. Liu, T. Chen, L. J. Chen, A. K. Zhou and Q. L. Song, Adv. Electron. Mater., 2018, 4, 1700567.
11. G. A. Gibson, Adv. Funct. Mater., 2018, 28, 1704175.
12. T. B. Flanagan and W. A. Oates, Annu. Rev. Mater. Sci., 1991, 21, 269–304.
13. F. D. Manchester, A. San-Martin and J. M. Pitre, J. Phase Equilib., 1994, 15, 62–83.
14. A. Zuttel, Mater. Today, 2003, 6, 24–33.
15. Y. Fukai, The metal-hydrogen system: Basic bulk properties, Springer, Berlin-Heidelberg, 2005.
16. A. Pundt and R. Kirchheim, Annu. Rev. Mater. Sci., 2006, 36, 555–608.
17. Y. Sakamoto, K. Takai, I. Takashima and M. Imada, J. Phys.: Condens. Matter, 1996, 8, 3399–3411.
18. S. Wagner and A. Pundt, Acta Mater., 2010, 58, 1387–1394.
19. A. Pozio and S. Tosti, Materials, 2019, 12, 3551.
20. Y. Amagai, T. Shimazaki, K. Okawa, T. Kawae, H. Fujiki and N. H. Kaneko, Appl. Phys. Lett., 2020, 117, 063903.
21. H. Fujiki, Y. Amagai, K. Okawa, T. Harumoto and N. H. Kaneko, Measurement, 2021, 185, 110010.
22. T. Harumoto, H. Fujiki, J. Shi and Y. Nakamura, Int. J. Hydrogen Energy, 2022, 47, 34291–34298.
23. R. A. Matula, J. Phys. Chem. Ref. Data, 1979, 8, 1147–1298.
24. J. Fraden, Handbook of modern sensors: Physics, designs, and applications, Springer, New York, 5th edn, 2016.
25. H. X. Li, C. B. Wan, X. C. Li and X. Ju, Int. J. Hydrogen Energy, 2022, 47, 1723–1734.
26. J. T. Chen, Z. Y. Li, H. X. Huang, Y. J. Lv, B. G. Liu, Y. T. Li, Y. Wu, J. G. Yuan and Y. J. Wang, Scr. Mater., 2022, 212, 114548.
27. F. A. Lewis, K. Kandasamy, R.-A. McNicholl and X. Q. Tong, Int. J. Hydrogen Energy, 1995, 20, 369–372.
28. J. M. Rickman, T. Lookman and S. V. Kalinin, Acta Mater., 2019, 168, 473–510.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3mh00657c

---