A boost of thermoelectric generation performance for polycrystalline InTe by texture modulation

Abstract

The new rising binary InTe displays advantageously high electronic conductivity and low thermal conductivity along the [110] direction, providing a high potential of texture modulation for thermoelectric performance improvement. In this work, coarse crystalline InTe material with a high degree of texture along the [110] direction was realized by the oriented crystal hot-deformation method. The coarse grains with high texture not only maintain the preferred orientation of the zone-melting crystal as far as possible, but also greatly depress the grain boundary scattering, thus leading to the highest room temperature power factor of 8.7 μW cm⁻¹ K⁻¹ and a high average figure of merit of 0.71 in the range of 300–623 K. Furthermore, the polycrystalline characteristic with refined grains also promotes the mechanical properties. As a result, an 8-couple thermoelectric generator module consisting of p-type InTe and commercial n-type Bi₂Te_2.7Se_0.3 legs was successfully integrated and a high conversion efficiency of ∼5.0% under the temperature difference of 290 K was achieved, which is comparable to traditional Bi₂Te₃ based modules. This work not only demonstrates the potential of InTe as a power generator near room temperature, but also provides one more typical example of a texture modulation strategy beyond the traditional Bi₂Te₃ thermoelectrics.

---

New concepts

High thermoelectric (TE) performance of a material depends on high electrical conductivity (σ) and low thermal conductivity (κ). The new rising brittle InTe crystal possesses advantageous anisotropic transport of higher σ and lower κ along the [110] direction, being an ideal candidate to maximize the TE performance by improving the texture degree. However, how to improve the mechanical strength of the crystal represents a great challenge during practical manufacturing. Herein, the hot deformation method based on orientated single crystals of InTe can achieve the ideal texture degree of the material and improved bending strength, simultaneously, resulting in high TE performance and the successful fabrication of a thermoelectric module with a high conversion efficiency. This work provides a new texture modulation strategy to improve the feasibility of anisotropic TE materials in practical applications.

1. Introduction

Thermoelectric (TE) materials working in the low-mid temperature range can directly covert waste heat into electricity conversion and vice versa without any moving parts and noise, thus attracting intensive attention from the scientific and industrial community.^1–3 The heat-to-power conversion efficiency (η) is strongly related to the materials’ dimensionless figure of merit zT = S²σT/(κ_L + κ_e), where T, σ, S, κ_L and κ_e are absolute temperature, electrical conductivity, Seebeck coefficient, and lattice and electron thermal conductivity.⁴ Since S, σ, and κ_e are strongly coupled with each other through carrier concentration, it is extremely difficult to improve the electronic performance and final zT value, although band engineering of degeneracy,^5,6 curvature,⁷ and valley anisotropy have been intensely adopted.⁸ On the other hand, the independent modulation of κ_L can be utilized to increase the thermoelectric performance, thus promoting a rapid development of materials with intrinsically low κ_L governed by “phonon liquid electron crystal” (PLEC) and strong anharmonic chemical bonds, such as Cu₂Se,⁹ SnSe,¹⁰ Mg₃Sb₂,¹¹ AgSbTe₂,¹² InTe,^13,14etc.

The electrical and thermal transports of materials are largely determined by their chemical bonds, thus the intrinsic (quasi-) two dimensional (2D) and one dimensional (1D) crystals always possess anisotropic transport along different directions. It is effective to increase the zT value by modulating the texture orientation with high σ/κ value, as exemplified by the famous TE materials of Bi₂Te₃ and SnSe.^6,15 However, the high σ and high κ of the majority of these TE materials occur in the same direction, resulting in a relatively small degree of improvement in their TE performance through texture improvement. In contrast, the new binary material, InTe, has emerged as a rising star in the TE field due to its advantageous anisotropic transport along the [110] direction, where σ is higher and monotonically decreases, but κ is lower.^16,17 This property of InTe single crystals makes them an ideal candidate to maximize the TE performance by improving the texture degree.

InTe features a TlSe-type structure with one directional (1D) covalent chains of [In³⁺Te²⁻_4/2]⁻ along the c direction. These chains are weakly bridged by In⁺ cations with 5s² lone pair electrons (Fig. 1a),¹⁶ resulting in large anharmonic vibrations of In⁺ and strong anharmonic phono–phonon interactions. As a consequence, InTe exhibits extremely low κ_L along the [110] direction.^18,19 The unique transports and the low κ_L have been utilized to achieve high TE performance by doping Pb, Sb, Ga, Cd or Cu, and the deviations of In or Te from the stoichiometric ratio, as well as single crystal growth, promoting the peak zT up to 1.2 @648 K (summarized in Table S1, ESI†).^{13,14,20–26} However, the single crystal of InTe with the largest orientation is extremely brittle and easily cleaved along the (110) plane, which limits its application in thermoelectric generators.

Fig. 1 (a) Diagram of the anisotropic electron and phonon transports for InTe with a covalent chain of [In³⁺Te²⁻_4/2]⁻ along the c direction. (b) The PXRD patterns of a single crystal of InTe cleaved along the (110) plane. The upper right inset shows a photograph of the single crystal. (c) The PXRD patterns and (d) the bending strengths of <50-HP, 100-HP, Ingot-HP and ZM-HP samples.

In comparison, polycrystalline InTe samples show relatively high mechanical strengths and are free from the brittleness issues of single crystals, but they tend to exhibit weak textures. Recent work on varying the grain sizes of polycrystalline InTe indicates that the carrier scattering is predominated by the grain boundary (GB) for fine grains at low temperature, as observed in other thermoelectric materials, such as Mg₃Sb₂,^11,27 Te,²⁸ and NbCoSb, etc.²⁹ In detail, the electrical conductivity first rises and then descends around 500 K with a carrier concentration that remains nearly unchanged with increasing temperature.^19–25 This is in contrast to the monotonic decrease in σ above room temperature observed in InTe single crystal and leads to a significant deterioration in the overall TE performance.

Therefore, the ability to leverage both advantages of single- and poly-crystalline materials to achieve simultaneously high zT_avg and an improved mechanical strength is the most important issue for enhancing the comprehensive performance of InTe. In this work, we, firstly, systematically explored the impact of InTe grain size on the electrical conductivity, and discovered that grain boundary scattering (GBS) can be neglected when the average grain size is larger than 150 μm. Then, we used the hot deformation method based on the orientated single crystal (Fig. 1b) to achieve a high texture of the [110] direction, large grain size, and improved bending strength simultaneously. As a result, a high zT_avg of 0.71 between 300–623 K and a high peak zT of 0.95@623 K were achieved, demonstrating the promising application of InTe as a thermoelectric generator (TEG) material below 700 K based on the single crystal orientation and deformation.

2. Results and discussion

2.1. Characterization

To enhance the electrical conductivity of InTe at room temperature by reducing the grain boundary scattering, samples with different grain sizes were prepared and shown in Fig. 2 and Fig. S1 (ESI†). The grains are close to their initial sizes, increasing from ∼20 μm for <50-HP to ∼100 μm for 100-HP samples and then to >300 μm for the ZM-HP sample. EDS results confirmed the uniform distribution of In and Te elements of the crystal and deformed crystal, as shown in Fig. S2 (ESI†). The PXRD peaks of these samples were also well indexed with the InTe standard JCPDS card (PDF#81-1972), and no second phase was observed, being consistent with the EDS results. The slightly varied PXRD peak intensities of these samples reveal their different texture degrees (Fig. 1c), which can be calculated by the formula of , , , 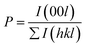where I(hkl) and I₀(hkl) are the peak integral intensities for the measured and randomly oriented samples, respectively.³⁰ It is clear that the increase of grain size is beneficial to elevating the texture degree of [110], and the ZM-HP achieves the highest texture of (110), which is 3 times that of the sieved coarse sample, favoring the improvement of electrical conductivity of InTe due to its unique anisotropic transport property. Moreover, decreasing the grain size significantly improved the mechanical bending strength because of the refined crystalline strengthening effect.³¹ Thus, the bending strength of the ZM-HP sample is improved by ∼23% based on the single crystal (Fig. 1d), which could promote the fabrication of TEG devices.

Fig. 2 Cross-section SEM images for (a) <50-HP, (b) 100-HP, (c) Ingot-HP and (d) ZM-HP. The insets are the grain size distributions of <50-HP and 100-HP, respectively.

2.2. Thermoelectric properties

We investigated the scattering mechanics based on the electrical transport of the samples with different grain sizes. Because the electrical conductivity trends of the <50-HP and 100-HP samples are quite similar to those of 100-HP and 150-HP, respectively (Fig. S3, ESI†), we analyzed the transport mechanism using <50-HP and 100-HP as representatives of fine and coarse sieved samples, respectively, despite their difference in carrier concentration and the Seebeck coefficient. The σ of the samples with different grain sizes within the range of 300–673 K is depicted in Fig. 3a, revealing that samples with an average size larger than 150 μm display electrical transport similar to that of the InTe crystal. In contrast, the <50-HP shows a considerably low σ of ∼32 S cm⁻¹ at 300 K, with a first increasing and then decreasing trend during 300–673 K, being consistent with the reported results of polycrystalline InTe.^20–23,26 The Hall carrier concentrations and mobilities μ_H are shown in Fig. 3b and c, respectively (the higher texture degree for ZM-HP would result in an underestimated n_H for the strongly anisotropic electrical transport of InTe based on the Kane band model,³² but it would have no effect on the investigation of the carrier scattering mechanism). The μ_H displays a positive temperature dependent relationship of μ∼T^1.79 for <50-HP, whereas samples with grain sizes of 100-HP, Ingot-HP, and ZM-HP show the negative relationships of μ∼T^−0.70, μ∼T^−1.29 and μ∼T^−1.4, respectively, within the temperature range of 300–550 K. Clearly, the acoustic phonon scattering (APS) (μ∼T^−1.5 relationship) is gradually strengthened, while the GBS is suppressed with increasing grain sizes.^28,29,33 This ultimately results in an increase of μ_H from 4.2 cm² V⁻¹ s⁻¹ for the <50-HP sample to 64.2 cm² V⁻¹ s⁻¹ for the ZM-HP sample, favoring the enhancement of the room temperature electrical conductivity.

Fig. 3 Temperature dependence of the electrical properties of InTe samples with different grain sizes. (a) Electrical conductivity, (b) Seebeck coefficient, (c) power factor, (d) Hall carrier concentration, and (e) Hall carrier mobility. (f) The Pisarenko plot of the Seebeck coefficient versus carrier concentration.

It is known that ionized impurity scattering (IIS), GBS, and bipolar diffusion (BD) would cause increased σ with the increase of the temperature. But compared with the monotonically decreased σ for the single crystal and the strengthened trend of APS for the InTe polycrystal with increasing grain sizes, it is reasonable to conclude that the GBS is the dominant scattering for the polycrystalline InTe with fine grains. Furthermore, in order to quantitatively evaluate the influence of the grain size on the GBS, we calculated the potential barrier (E_b) of GB based on the trapping state model.^29,34,35 Briefly, the trapping state can be considered as the result of abundant defects derived from the dangling bonds at the grain boundaries, which can be electrically charged after trapping the free carriers and then creates potential energy barriers to hinder the carrier transport. Thus, the ln(σT^1/2) − 1/k_BT plots were performed (Fig. S4, ESI†) to calculate the grain size dependent E_b.²⁹ The E_b values of <50-HP, 50-HP, InTe 100-HP and 150-HP were estimated to be 102.9 meV, 101.0 meV, 14.5 meV and 20.9 meV, respectively, which is consistent with the theoretical trend based on eqn (S2) (ESI†), i.e. the larger the grain size d, the smaller E_b. In addition, the increase of n_H gives rise to a smaller E_b,^29,35,36 and this is the reason for the slightly higher E_b of 150-HP than that of 100-HP.

In order to realistically describe the electron transport with GBS, the two-phase model proposed by Kuo et al. was adopted.³⁷ As shown in Fig. S5 (ESI†), the experimental data match well with the calculated curves when considering both the APS and GBS, suggesting that the GBS definitely plays a significant role in carrier transport near room temperature, while the APS contributes more at elevated temperatures. Furthermore, the temperature exponent r,³⁸ which can clearly show the transition of the carrier scattering mechanism when the temperature rises, was calculated by eqn (S4) and (S5) and shown in Fig. S3f (ESI†). For <50-HP and 50-HP, the r changes from positive to negation when the temperature increases, indicating the change of dominant scattering mechanism from GBS to APS. But for the 100-HP and 150-HP samples, the r is always negative, indicating the dominant APS in the whole temperature range.

The Seebeck coefficients as a function of temperature for all samples are presented in Fig. 3d, and their positive values indicate p-type transport. Obviously, the S increases with the enlargement of the grain size due to the decreased carrier concentration (Fig. 3b). Therefore, together with the weakened GBS, the power factor (PF) S²σ at room temperature was greatly improved, from 0.32 μW cm⁻¹ K⁻¹ for <50-HP to 8.68 μW cm⁻¹ K⁻¹ for ZM-HP sample (Fig. 3e), which is much higher than those of In_0.99Ga_0.01Te (4.94 μW cm⁻¹ K⁻¹) and InTe-single crystal along the [110] direction (3.24 μW cm⁻¹ K⁻¹).^13,17 Additionally, the repeat test of electrical properties demonstrated the high thermal stability of the ZM-HP sample (Fig. S6, ESI†).

For the sample with grain size larger than 100 μm, the scattering of charge carriers is dominated by APS. Thus, the single parabolic band (SPB) model can be used to study the σ–n_H relationship for the coarse samples, which can predict the optimal n_H to maximize the electrical performance. Fig. 3f shows that the S–n_H dependence fits well the SPB Pisarenko curves (i.e., S vs. n_H) with the density-of-states effective mass (m*_DOS) of 0.88 m_e during the temperature range of 300–600 K, which is close to those of coarse grain-In_0.99Ga_0.01Te,¹³ In_0.999Pb_0.001Te,²⁰ In_0.997Te ingot,¹⁴ and InTe-single crystal.¹⁷ Thus, the increase of the grain size not only suppresses the GBS to elevate the electrical conductivity but also has little effect on the m*_DOS. This means that the improvement of electrical conductivity by enlarging the grain size and the texture degree does not affect the S in this work, which is quite beneficial to the improvement of the electrical properties.

The thermal conductivity of the samples was analyzed using the <50-HP and 100-HP samples as representatives of fine and coarse sieved samples, respectively (Fig. S7, ESI†). The total thermal conductivity κ_total for all samples is presented in Fig. 4a. For the samples with coarse grains, the κ_total decreases continuously from 0.89 W m⁻¹ K⁻¹ for 100-HP to 0.73 W m⁻¹ K⁻¹ for the ZM-HP sample at room temperature. To analyze the effect of the grain size and texture on thermal transport, the κ_e (Fig. 4b) was evaluated by the Wiedemann–Franz law κ_e = LσT, where L is the Lorenz number estimated by L = 1.5 + exp(−|S|/116)⁴¹ as shown in Fig. S8 (ESI†), where S is the Seebeck coefficient. The κ_L was then estimated by subtracting the κ_e from the κ_total. However, the κ_L of Ingot-HP and ZM-HP calculated by this method is upturned at high temperatures, due to the bipolar thermal conductivity (κ_b) caused by the intrinsic excitation (Fig. 4c). It should be pointed out that the Umklapp scattering mechanism is dominant for phonon scattering above the Debye temperature and the relationship between κ_L and T can be expressed as κ_L = aT⁻¹ + b (where a and b are fitting parameters).^42,43 Therefore, the κ_L under intrinsic excitation was first estimated by subtracting the κ_e from the κ_total within 300–375 K, and then extrapolating the lattice thermal conductivity at the subsequent temperature. The κ_b was then calculated by the expression of κ_b = κ_total − κ_e − κ_L, which reveals the increased contribution of κ_b with the increase of the temperature and shown in Fig. 4d. Interestingly, InTe possesses lower κ_L along the [110] direction than along [001] due to the anisotropy thermal transport of InTe arising from the bonding asymmetry and lattice anharmonicity.^14,17 With the increase of the [110] texture, the room temperature κ_L decreases continuously from 0.75 W m⁻¹ K⁻¹ for 100-HP to 0.49 W m⁻¹ K⁻¹ for the ZM-HP sample. In particular, the ZM-HP sample has achieved a κ_L as low as 0.24 W m⁻¹ K⁻¹ (extrapolating value) at high temperature, which is lower than those of the sieved samples and the limit of κ_glass ∼ 0.32 W m⁻¹ K⁻¹, and even close to the limit of κ_diff ∼ 0.21 W m⁻¹ K⁻¹ (eqn (S7) and (S8), ESI†). In other words, the ZM-HP sample can fully utilize the anisotropic thermal and electrical transports of InTe to improve the TE performance.

Fig. 4 Temperature dependence of the thermal properties of InTe polycrystalline samples with different grain sizes. (a) Total thermal conductivity, (b) electron thermal conductivity, and (c) lattice and bipolar thermal conductivity. The dotted lines are the minimum thermal conductivity calculated by the Chaill model and diffusion model.^39,40 (d) Bipolar thermal conductivity of ZM-HP and Ingot-HP.

The figure of merits of all samples are presented in Fig. 5a. The ZM-HP sample exhibits the highest zT value of 0.36 at 300 K, owing to its optimal combination of grain size and [110] orientation factor, which represents the highest recorded room temperature zT value for polycrystalline InTe-based TE materials. In contrast, the sieved coarse samples exhibit close zT values of 0.56–0.74 at 700 K due to their similar texture degrees and reduced grain boundary scattering. Notably, the high texture of the ZM-HP sample results in a peak zT of 0.94 at 623 K, with a high average zT of 0.71 within 300–623 K (Fig. 5b). This is a remarkable 340% increase compared to the zT_avg value of 0.16 for <50-HP. Furthermore, the zT of ZM-HP is comparable to the traditional PbTe⁴⁴ and the CoSb₃.⁴⁵ In addition, the zT_avg of the ZM-HP sample is the second highest among all reported InTe-based TE materials and is the highest value among undoped InTe materials.

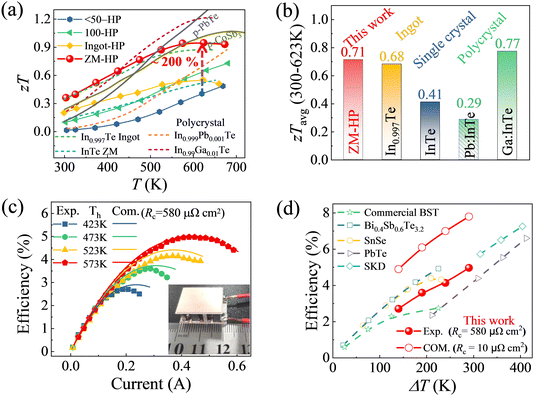Fig. 5 The performance of the samples with different particle sizes and the TEG module. (a) The comparison of the temperature dependent zT of InTe from our work and the reported InTe,^13,14,17,20 traditional PbTe⁴⁴ and CoSb₃.⁴⁵ (b) The average zT within 300–623 K for our InTe samples and other reported p-type InTe materials.^13,14,17,20 (c) Current dependence of the conversion efficiency for our InTe-Bi₂Te₃ modules, and the inset is the thermoelectric module. (d) The highest conversion efficiency under different temperatures for our module and the comparison with the reported results of SnSe-Bi₂Te_2.7Se_0.3,⁴⁶ Pb_0.96Na_0.02Mg_0.02Te-PbTe_0.987S_0.01I_0.003,⁴⁷ Ce_0.9Fe₃CoSb₁₂-Yb_0.3Co₄Sb₁₂/MWCNTs,⁴⁸ Bi_0.4Sb_1.6Te_3.2-Bi₂Te_2.7Se_0.3 and commercial BST.⁴⁹

2.3. Thermoelectric module

Due to the high zT_avg value of InTe, a TEG module, which consisted of p-type ZM-HP-InTe and commercial n-type Bi₂Te_2.7Se_0.3, was fabricated to realize a high experimental conversion efficiency. The TE performances of the commercial n-type Bi₂Te_2.7Se_0.3 are shown in Fig. S9 (ESI†). It is worth noting that the electrical and thermal conductivity of these two materials differ significantly. Therefore, the geometric factors of the module, such as the cross-sectional area ratios and the leg height, were first optimized theoretically by COMSOL and shown in Fig. S10 (ESI†). Clearly, the conversion efficiency rises monotonically in a small range with the increase of the leg length (Fig. S10a, ESI†), but the corresponding out power decreases. However, the conversion efficiency is greatly affected by the area of p-type InTe (A_p) and n-type Bi₂Te_2.7Se_0.3 (A_n). The cross-sectional area ratios were optimized to increase η from 6.1% to 7.7% when the leg length was set to be 6.8 mm with the hot side of 573 K and cold side of 283 K, respectively (Fig. S11, ESI†). Consequently, the dimensions of p-type InTe and n-type Bi₂Te_2.7Se_0.3 were cut to be 3.0 × 3.0 × 6.8 mm³ and 1.7 × 1.7 × 6.8 mm³, respectively. Here, Ni was used as the diffusion barrier on the two sides of the legs.² The simulated and experimental terminal voltage, output power and conversion efficiency, under the conditions of hot-side temperatures of 573 K, 523 K, 473 K and 423 K, and the cold-side of 283 K, were measured by changing the current (I) and are shown in Fig. S12 (ESI†) and Fig. 5c, respectively. The output power increases with the increase of the current and finally reaches a maximum value (P_max) when the external electrical load matched the module's internal resistance at a given temperature difference (ΔT). At ΔT = 290 K, the peak of the conversion efficiency is up to 5.0%, which is higher than those obtained by the SnSe based TEG device, and close to the traditional Bi₂Te₃ based devices under the same ΔT (Fig. 5d).^45,46,48,50 But because the contact resistance (R_c) and geometric factor have not been fully optimized, the output power and conversion efficiency are much lower than the theoretical values. By further optimizing the contact properties of InTe, including the introduction of a more proper metallic barrier and optimization of the bonding technology, the expected high output power and conversion efficiency can be achieved (Fig. S11, ESI†), indicating the promising application of InTe as a TEG material.

3. Conclusions

In this study, we aimed to improve the thermoelectric performance of InTe by optimizing the grain size and texture degree of the [110] direction, while simultaneously minimizing the grain boundary scattering. Finally, the hot-deformated single crystal with high texture degree achieved a high TE performance among the InTe-based TE materials, including the highest room temperature power factor, and low thermal conductivity, as well as a high zT_avg(300–623 K) of 0.71 with the peak zT of 0.95@623 K. Furthermore, the single TEG composed of p-type ZM-HP-InTe and commercial n-type B_i2Te_2.7Se_0.3 experimentally produced a high conversion efficiency of ∼ 5.0% when ΔT = 290 K, which could be further greatly increased by optimizing the geometric factors and the contact properties. Therefore, the new rising TE material of InTe has a promising application in thermoelectric power generators near room temperature.

4. Experiments

4.1. Sample preparation

In order to synthesize the pure phase of InTe, high-purity indium and tellurium particles were weighed in a stoichiometric ratio and then sealed in carbon-coated quartz tubes with a vacuum of ∼10⁻¹ Pa. The tubes containing In and Te were heated to 1123 K in 7 h, and then held at this temperature for 4 h before the furnaces were switched off. The obtained ingots were hand-ground and sieved with several grain size ranges of >150 μm, 100–150 μm, 50–100 μm, and <50 μm, respectively for hot pressing (marked as 150-HP, 100-HP, 50-HP and <50-HP, respectively). These powders were loaded into graphite dies with an inner diameter of 10 mm, which were placed in the hot-press sintering furnace. The sintering was performed under a uniaxial pressure of 50 MPa and a vacuum <5 Pa at 773 K for 30 min. The resulting pellets had high densities (>95% of the theoretical densities) and were cut into samples with dimensions of 10.0 × 2.0 × 2.0 mm³ and 6.0 × 6.0 × 1.5 mm³ for the measurement of the electrical and thermal properties.

4.2. Single crystal growth, orientation and deformation

In order to ensure the uniform distribution of the components, a low growth rate and small crystal size were adopted. The obtained ingots with a stoichiometric ratio of In and Te were sealed in carbon-coated quartz tubes with a vacuum of ∼ 10⁻¹ Pa. A V-shaped tube end was employed to minimize the number of seeded crystals at the beginning of the solidification. The sealed tube was then placed in a two-zone furnace for crystal growth, and kept under clockwise rotation at 2 revolutions per minute (rpm) during the growth. The heat zooms were heated to 1073 K in 2 h, and then held at this temperature for 2 h to ensure complete and homogeneous melting of the sample. They were subsequently cooled down to 983 K in 2 h with the tube's lactation at the center of the two zones. One zone was held at 983 K, while the other decreased to 943 K within 10 h to initiate crystallization. The crystal growth rate was set as 0.5 mm h⁻¹ with a thermal gradient of approximately 10 K cm⁻¹. After the crystal growth process was complete, both zones were cooled to 298 K in 10 h. The obtained crystal was ∼4 cm in length and is shown in Fig. 1b. The EDS results reveal the uniform distribution of the components (Fig S2, ESI†).

The top part of this single crystal and the ingot were loaded into graphite dies with an inner diameter of 20 mm, and the pressure direction was perpendicular to the (110) plane (marked as ZM-HP and Ingot-HP, respectively). The sintering was performed under a uniaxial pressure of 50 MPa with a vacuum <5 Pa at 783 K for 30 min. The obtained pellets with high densities (>95% of the theoretical densities) were cut for the measurements of the electrical and thermal properties.

4.3. Characterization

The phase purities of the samples were confirmed by powder X-ray diffraction (PXRD) using a Bruker AXSD8 Advance X diffractometer (Germany) with Cu K_α radiation of 1.5406 Å under 40 kV × 40 mA at room temperature within the 2θ range of 10–60°. A scanning electron microscope (Thermo Scientific Apreo 2 S HiVac, 5 kV) equipped with an energy-dispersive X-ray spectrometer (EDS) was employed to investigate the microstructures under 10 kV × 0.2 nA and chemical compositions under 16 kV × 1.6 nA. Mechanical strength measurement was performed by a bending strength testing machine (Shimadzu AGX-10KNVD) with the speed of 0.02 mm min⁻¹. The electrical conductivity and Seebeck coefficient were measured using a Ulvac ZEM-3 from 300 K to 773 K. The thermal diffusivity (D) was measured between 300 K and 773 K using the laser flash diffusivity technique on a LFA-467 instrument (Netzsch, Germany). The total thermal conductivity was calculated using the relation of κ = DC_pρ, where ρ is the density of the sample measured by the Archimedes method, and C_p is the specific heat capacity using the Dulong–Petit estimation. Hall coefficient (R_H) was measured by the van der Pauw technique with a self-made Hall electrical performance test system under a helium atmosphere. Hall carrier concentration (n_H) and Hall mobility (μ_H) were estimated by n_H = 1/eR_H and μ_H = σ/n_He, respectively.

4.4. Module fabrication and characterization

To assemble a single module, Bi₂Te_2.7Se_0.3 and InTe were used as n-type and p-type legs, respectively. The Ni layer with a thickness of approximately 10 μm, prepared by electroless plating, served as a diffusion barrier. The cut pieces were then connected to directly bonded alumina ceramics through welding, using Sn-Pb solder. Based on simulation results that considered the substrate size, the cross-sectional area of the p-type leg was three times that of the n-type leg. Therefore, the dimensions of the Bi₂Te_2.7Se_0.3 legs were 1.7 × 1.7 × 6.8 mm³, while the InTe legs were 3.0 × 3.0 × 6.8 mm³. For measuring the output power, internal resistance, heat flow, and energy conversion efficiency of the module, a homemade power generation efficiency characterization system was used. The hot-side temperatures were maintained between 423–573 K, while the temperature of the water cooler was kept at 283 K.

Author contributions

Jianghe Feng and Menghui Zhou designed this work and carried out material synthesis and material property tests, thermoelectric module simulation, fabrication and measurement, and wrote the draft of the manuscript. Juan Li, Guoying Dong and Shufang Gao carried out some electrical performance tests and calculations. Erbiao Min and Chuang Zhang carried out some thermoelectric module fabrication. Qiaqing He gave guidance and supervision. Rong Sun: gave supervision. Ruiheng, Liu designed this work and gave guidance and supervision, and performed article writing and revision.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Shenzhen Science and Technology Research Funding (No. JCYJ20210324115611030, JCYJ20220818102408017 and RCYX20200714114641193), and Guang Dong Basic and Applied Basic Research Foundation (No. 2022B1515020066). The authors also thank Shimadzu (China) Co., LTD. Guangzhou Branch for the mechanical strength measurement.

References

1. L. E. Bell, Science, 2008, 321, 1457–1461.
2. B. B. Jiang, W. Wang, S. X. Liu, Y. Wang, C. F. Wang, Y. N. Chen, L. Xie, M. Y. Huang and J. Q. He, Science, 2022, 377, 208–213.
3. M. Wu, H. H. Cui, S. T. Cai, S. Q. Hao, Y. Liu, T. P. Bailey, Y. Y. Zhang, Z. X. Chen, Y. B. Luo, C. Uher, C. Wolverton, V. P. Dravid, Y. Yu, Z. Z. Luo, Z. G. Zou, Q. Y. Yan and M. G. Kanatzidis, Adv. Energy Mater., 2023, 13, 2203325.
4. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114.
5. J. P. Heremans, V. Jovovic, E. S. Toberer, A. Saramat, K. Kurosaki, A. Charoenphakdee, S. Yamanaka and G. J. Snyder, Science, 2008, 321, 554–557.
6. Z. X. Chen, H. H. Cui, S. Q. Hao, Y. K. Liu, H. Liu, J. Zhou, Y. Yu, Q. Y. Yan, C. Wolverton, V. P. Dravid, Z. Z. Luo, Z. G. Zou and M. G. Kanatzidis, Energy Environ. Sci., 2023, 16, 1676–1684.
7. Y. Z. Pei, A. D. LaLonde, H. Wang and G. J. Snyder, Energy Environ. Sci., 2012, 5, 7963–7969.
8. H. J. Goldsmid, J. Appl. Phys., 1961, 32, 2198–2202.
9. H. L. Liu, X. Shi, F. F. Xu, L. L. Zhang, W. Q. Zhang, L. D. Chen, Q. Li, C. Uher, T. Day and G. J. Snyder, Nat. Mater., 2012, 11, 422–425.
10. L. D. Zhao, S. H. Lo, Y. S. Zhang, H. Sun, G. J. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373–376.
11. J. Mao, Y. X. Wu, S. W. Song, Q. Zhu, J. Shuai, Z. H. Liu, Y. Z. Pei and Z. F. Ren, ACS Energy Lett., 2017, 2, 2245–2250.
12. J. Ma, O. Delaire, A. F. May, C. E. Carlton, M. A. McGuire, L. H. VanBebber, D. L. Abernathy, T. H. G. Ehlers, A. Huq, W. Tian, V. M. Keppens, Y. Shao-Horn and B. C. Sales, Nat. Nanotechnol., 2013, 8, 445–451.
13. F. Li, X. Liu, N. Ma, L. Chen and L. M. Wu, Angew. Chem., Int. Ed., 2022, 61, e202208216.
14. M. K. Jana, K. Pal, U. V. Waghmare and K. Biswas, Angew. Chem., Int. Ed., 2016, 55, 7923–7927.
15. L. D. Zhao, G. J. Tan, S. Q. Hao, J. Q. He, Y. L. Pei, H. Chi, H. Wang, S. K. Gong, H. B. Xu, V. P. Dravid, C. Uher, G. J. Snyder, C. Wolverton and M. G. Kanatzidis, Science, 2016, 351, 141–144.
16. M. Parlak, C. Ercelebi, I. Gunal, H. Ozkan and N. M. Gasanly, Cryst. Res. Technol., 1996, 31, 673–678.
17. S. Misra, P. Levinský, A. Dauscher, G. Medjahdi, J. Hejtmánek, B. Malaman, G. J. Snyder, B. Lenoir and C. Candolfi, J. Mater. Chem. C, 2021, 9, 5250–5260.
18. J. W. Zhang, D. Ishikawa, M. M. Koza, E. Nishibori, L. R. Song, A. Q. R. Baron and B. B. Iversen, Angew. Chem., Int. Ed., 2023, 62, e202218458.
19. D. M. Rowe, CRC handbook of Thermoelectrics, Boca Raton, CRC edn, 1995.
20. S. Misra, A. Léon, P. Levinský, J. Hejtmánek, B. Lenoir and C. Candolfi, J. Mater. Chem. C, 2021, 9, 14490–14496.
21. H. X. Zhu, B. Zhang, G. W. Wang, K. L. Peng, Y. C. Yan, Q. Zhang, X. D. Han, G. Y. Wang, X. Lu and X. Y. Zhou, J. Mater. Chem. A, 2019, 7, 11690–11698.
22. S. S. Pan, H. Liu, Z. L. Li, L. You, S. N. Dai, J. Yang, K. Guo and J. Luo, J. Alloys Compd., 2020, 813, 152210–152216.
23. R. C. Huang, Y. Huang, B. Zhu, M. K. He, Z. H. Ge, L. W. Fu and J. Q. He, J. Appl. Phys., 2019, 126, 125108.
24. S. Y. Back, Y. K. Kim, H. Cho, M. K. Han, S. J. Kim and J. S. Rhyee, ACS Appl. Energy Mater., 2020, 3, 3628–3636.
25. S. Y. Back, H. Cho, Y. K. Kim, S. Byeon, H. Jin, K. Koumoto and J. S. Rhyee, AIP Adv., 2018, 8, 115227–115237.
26. H. X. Zhu, G. W. Wang, G. Y. Wang, X. Y. Zhou and X. Lu, J. Alloys Compd., 2021, 869, 159224–159229.
27. M. Wood, J. J. Kuo, K. Imasato and G. J. Snyder, Adv. Mater., 2019, 31, 1902337.
28. Y. H. Wu, F. Liu, Q. Zhang, T. J. Zhu, K. Y. Xia and X. B. Zhao, J. Mater. Chem. A, 2020, 8, 8455–8461.
29. C. L. Hu, K. Y. Xia, C. G. Fu, X. B. Zhao and T. J. Zhu, Energy Environ. Sci., 2022, 15, 1406–1422.
30. F. K. Lotgering, J. Inorg. Nucl. Chem., 1959, 9, 113–123.
31. M. Calcagnotto, D. Ponge and D. Raabe, Mat. Sci. Eng. A, 2010, 527, 7832–7840.
32. Y. Z. Pei, A. D. LaLonde, H. Wang and G. J. Snyder, Energy Environ. Sci., 2012, 5, 7963–7969.
33. K. Imasato, C. G. Fu, Y. Pan, M. Wood, J. J. Kuo, C. Felser and G. J. Snyder, Adv. Mater., 2020, 32, 1908218.
34. T. I. Kamins, J. Appl. Phys., 1971, 42, 4357–4365.
35. J. Y. W. Seto, J. Appl. Phys., 1975, 46, 5247–5254.
36. M. H. Zhou, J. Li, G. Y. Dong, S. F. Gao, J. H. Feng and R. H. Liu, Crystals, 2023, 13, 601.
37. J. J. Kuo, S. D. Kang, K. Imasato, H. Tamaki, S. Ohno, T. Kanno and G. J. Snyder, Energy Environ. Sci., 2018, 11, 429–434.
38. Q. Y. Qiu, Y. T. Liu, K. Y. Xia, T. Fang, J. J. Yu, X. B. Zhao and T. J. Zhu, Adv. Energy Mater., 2019, 9, 1803447.
39. D. G. Cahill, S. K. Watson and R. O. Pohl, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6131–6140.
40. M. T. Agne, R. Hanus and G. J. Snyder, Energy Environ. Sci., 2018, 11, 609–616.
41. H. S. Kim, Z. M. Gibbs, Y. L. Tang, H. Wang and G. J. Snyder, APL Mater., 2015, 3, 041506.
42. G. E. Shoemake, J. A. Rayne and R. W. Ure, Phys. Rev., 1969, 185, 1046–1056.
43. F. Hao, T. Xing, P. F. Qiu, P. Hu, T. Wei, D. R. Ren, X. Shi and L. D. Chen, ACS Appl. Mater. Interfaces, 2018, 10, 21372–21380.
44. K. Biswas, J. Q. He, I. Blum, C. Wu, T. Hogan, D. Seidman, V. Dravid and M. Kanatzidis, Nature, 2012, 489, 414–418.
45. P. A. Zong, R. Hanus, M. Dylla, Y. S. Tang, J. C. Liao, Q. H. Zhang, G. J. Snyder and L. D. Chen, Energy Environ. Sci., 2017, 10, 183–191.
46. B. C. Qin, D. Y. Wang, X. X. Liu, Y. X. Qin, J. F. Dong, J. F. Luo, J. W. Li, W. Liu, G. J. Tan, X. F. Tang, J. F. Li, J. Q. He and L. D. Zhao, Science, 2021, 373, 556–561.
47. B. H. Jia, Y. Huang, Y. Wang, Y. S. Y. Zhou, X. D. Zhao, S. T. Ning, X. Xu, P. J. Lin, Z. Q. Chen, B. B. Jiang and J. Q. He, Energy Environ. Sci., 2022, 15, 1920–1929.
48. Q. H. Zhang, Z. X. Zhou, M. Dylla, M. T. Agne, Y. Z. Pei, L. J. Wang, Y. S. Tang, J. C. Liao, J. Li, S. Q. Bai, W. Jiang, L. D. Chen and G. J. Snyder, Nano Energy, 2017, 41, 501–510.
49. H. L. Zhuang, J. Pei, B. Cai, J. Dong, H. Hu, F. H. Sun, Y. Pan, G. J. Snyder and J. F. Li, Adv. Funct. Mater., 2021, 31, 2009681.
50. Z. H. Liu, N. Sato, W. H. Gao, K. Yubuta, N. Kawamoto, M. Mitome, K. Kurashima, Y. Owada, K. Nagase, C. H. Lee, J. Yi, K. Tsuchiya and T. Mori, Joule, 2021, 5, 1196–1208.

---

Footnotes

† Electronic supplementary information (ESI) available: Modeling details of carrier grain boundary scattering, theoretical calculation of κ_L minimum and SPB model, COMSOL simulations, TE properties summary of InTe, and characterizations, including, grain sizes, component analysis, TE performances, and the stability analysis. See DOI: https://doi.org/10.1039/d3mh00292f

‡ These authors contributed equally to this work.

---