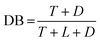PolySMart: a general coarse-grained molecular dynamics polymerization scheme

Abstract

The development of simulation methods to study the structure and dynamics of a macroscopically sized piece of polymer material is important as such methods can elucidate structure–property relationships. Several methods have been reported to construct initial structures for homo- and co-polymers; however, most of them are only useful for short linear polymers since one needs to pack and equilibrate the far-from-equilibrium initial structures, which is a tedious task for long or hyperbranched polymers and unfeasible for polymer networks. In this method article, we present PolySMart, i.e., an open-source python package, which can effectively produce fully equilibrated homo- and hetero-polymer melts and solutions with no limitation on the polymer topology and size, at a coarse-grained resolution and through a bottom-up approach. This python package is also capable of exploring the polymerization kinetics through its reactive scheme in realistic conditions so that it can model the multiple co-occurring polymerization reactions (with different reaction rates) as well as consecutive polymerizations under stoichiometric and non-stoichiometric conditions. Thus, the equilibrated polymer models are generated through correct polymerization kinetics. A benchmark and verification of the performance of the program for several realistic cases, i.e., for homo-polymers, co-polymers, and crosslinked networks, is given. We further discuss the capability of the program to contribute to the discovery and design of new polymer materials.

---

New concepts

Molecular dynamics (MD) simulation is a major asset in polymer modeling. Nevertheless, constructing close-to-equilibrium initial structures (i.e., a key to achieve realistic polymer models) is a great challenge. Due to the lack of a standard protocol to build up close-to-equilibrium initial structures, most existing MD methods can only model oligomers and very short polymer chains. Thus, current MD-made polymer models often lack important characteristics of real synthetic polymers: (i) very large molecular weights and (ii) wide molecular weight distributions. Bottom-up methods (which make polymers from monomers by mimicking the polymerization reactions through MD reactive schemes) are capable of constructing close-to-real size polymers; however, the existing methods are extremely case-dependent and able to handle only very limited polymer types. Here, we introduce a general bottom-up scheme (i.e., PolySMart: a free and open-sourced Python code package) by which one can construct any polymer architecture, i.e., linear, branched, dendritic, and 3D networks, based on a great variety of chemistries (e.g., polyurethanes, polyamidoamine, polyethers, and polyesters, as benchmarked in the paper), through reproducing/mimicking experimentally obtained polymerization kinetics. Thus, it enables MD modeling of an unlimited variety of polymers with realistic molecular weights and molecular weight distributions in the future.

1 Introduction

Macromolecules are an interesting class of materials with a large range of applications. Their characteristic feature is a large molecular size, which gives them the capability of inheriting various properties from the monomers. Thus, one can tune the final properties of macromolecules by incorporating different monomers and imposing a specific molecular topology by designing different chemical reaction routes. Experimental techniques with molecular-size resolutions have been great tools to establish structure–property relationships for synthesized macromolecules. However, using experimental trial and error methods is an expensive route in demand for cheaper, more functional, and sustainable technologies, while theoretical tools have been shown to be able to predict and model new materials.^1–3 Among them, molecular dynamics (MD) simulations proved to be able to provide valuable insights into existing and new macromolecules⁴ by calculating their structural and dynamic properties on a molecular scale.^5–7

Despite the success of atomistic MD simulations in predicting properties of molecular materials, the large length/time scale of conformational transitions in polymers has been a major challenge to model their behavior. Accordingly, several attempts have been made to overcome these limitations, such as the development of coarse-grained (CG) models to probe time and length scales associated with macromolecules.^8–10 CG models facilitate the simulation of large and complex polymers but generally fail in providing transferability for various macromolecules and thermodynamic conditions.¹¹ Nevertheless, the advancement in CG models during recent years promises a bright future for CG MD simulation of macromolecules,⁴ as exemplified in the development of Martini3,¹² which shows promising capabilities to provide a semi-quantitative level of accuracy. Another challenge in the modeling of macromolecules is generating reliable and close-to-equilibrium initial configurations (starting coordinates), which is of great concern for polymer modelers due to the large size and slow dynamics of this material class.¹³ Furthermore, it is also very hard to correctly capture the large degree of polydispersity in classical simulations, which (particularly) in the case of synthetic macromolecules, greatly influences their final properties.^14,15 Moreover, the rapid pace of materials development through advanced synthesis methods has enabled a remarkably diverse set of complex polymer architectures, e.g., hyperbranched¹⁶ and dendritic¹⁷ polymers, 3D polymer networks,¹⁸ and supramolecular polymers,¹⁹ so that generating their starting coordinates is not feasible without considering an automated bottom-up method, i.e., building up macromolecules by connecting monomers during a molecular relaxation process through an automated protocol. In general, two approaches have been used to prepare equilibrated polymer models through MD simulations. The first is building up macromolecules based on an input sequence of monomers in the exact input configuration and topology provided by the user combined with multiple energy minimization and relaxation steps,^13,20 while the second is polymerizing monomers/oligomers through a reactive MD scheme on all-atom²¹ or CG²² scales.

Due to the rather long polymerization time frame as compared to achievable atomistic MD simulation times (i.e., hundreds of nanoseconds), most of the all-atom time frames cannot achieve reasonable polymerization reaction conversions (>90%) to generate the real-size polymer models without imposing wrong kinetic/thermodynamic manipulations such as increasing the reaction cut-off to reach higher conversions. Also, most of the bottom-up methodologies are not sufficiently generic to be used for a large class of polymerization reactions and are mainly developed for specific chemical structures, i.e., epoxies with a focus on 3D crosslinked networks. For instance, Grest and Kremer generated a randomly crosslinked network starting from well-equilibrated melts of linear chains of polymers and investigated some network features.²³ The reactions were assumed to occur instantaneously, and the system was not relaxed, which causes large internal strains and high energy spots. Lin and Khare modified this single-step polymerization process using an annealing algorithm for finding reacting atoms and a final energy minimization to reduce the energy of the system.²⁴ This algorithm finds the optimal connectivity condition of new bonds in which the sum of the distances of these bonds is minimized. The first procedure for performing progressive polymerization/crosslinking reactions during a multi-step MD simulation was developed by Doherty et al.²⁵ Their method attempts to identify the atomic pairs that are spatially close and form the bond between them followed by energy minimization and relaxation steps. Repeating this procedure several times avoids the occurrence of local strains and results in the desired equilibrated structure. This general concept is the core of the most developed methods for generating polymeric structures and networks. Several researchers used similar methods with different details for constructing various topologies in several all-atom^26–29 or united-atom³⁰ forcefields. In order to avoid the drawback of the repeated discontinuities in the trajectories and energies of the system, which are caused by repetitive stopping, rewriting the topological information and continuing the dynamics, reactive force fields have been developed. These types of force fields (e.g., ReaxFF³¹), which use the concept of bond order to enable chemical reactions, are based on quantum mechanics (QM) calculations and allow an implicit QM consideration into the MD simulations. However, due to the computational cost of atomistic calculations, the system size and the simulation time frame that can be modeled by these systems are limited.

CG polymerization methods can reach reasonable reaction conversions due to the faster relaxation and longer achievable simulation times. Also, polymerization schemes on the CG level can be utilized for a large class of polymer chemistries (due to the lower level of complexities in bond formation/breakage) and may lead to more efficient high-throughput methods (due to the lack of force field related challenges). Note that in cases where atomistic detailed structures of polymers are needed, after reaching the desirable polymer sizes/polymerization conversions, a reverse mapping of the CG structure onto a fully atomistic representation can be done to proceed with all-atom MD simulations. According to this concept, Komarov et al. proposed a method for the polymerization of highly crosslinked epoxy networks in CG representation.³² The network formation and relaxation were performed by Monte Carlo simulation. Later, Gavrilov et al. updated this multiscale methodology by applying dissipative particle dynamics (DPD) and a probabilistic reaction scheme for the construction of epoxy networks and predicting topological properties.³³ Recently, some reactive models in the CG scale were also introduced that mimic the reactive events through a continuous potential with a balance between attractive and repulsive interactions. For instance, the titratable-MARTINI model models the pH-dependent simulations by describing the protonation/deprotonation equilibrium through individual CG beads representing acids/bases³⁴ instead of representing explicitly chemical bonding between CG beads. Also, sticky-MARTINI was developed to model silica polymerization by describing the siloxane bonds as a continuous Lennard-Jones interaction between virtual sites and sticky particles around a central silica particle.³⁵ This model is limited to a specific system, but the modeling concept has an outstanding potential to be generalized as a general force field for other reactions in different systems.

Previously, we developed a methodology for performing chemical reactions on the Martini CG mesoscale and validated the constructed structures for some linear and crosslinked polyurethane systems.^36,37 In the current work, we expand this route as a generalized method for performing any step-growth polymerization process, gathered in a scripting package (available at https://github.com/HMakkiMD/PolySMart), which we added to our reactive scheme for the GROMACS MD package.³⁸ Unlike most methods, the scheme is not designed for specific chemical structures and can be used for any addition polymerization to generate any polymer architecture (linear, branched, network, etc.) by introducing easy-to-prepare input files. A multi-step reaction process can also be considered, which offers a reactive scheme for observing the evolution of the system not only at the endpoint but during the whole process. The ability to define multiple parallel (or competitive) reactions and to simulate multifunctional groups with various reaction rates makes this method, contrary to simplified schemes, suitable for realistic step-growth (co)polymerizations. Also, this code package can reproduce the correct kinetics for competing polymerization reactions so that the final equilibrated polymer models can be generated through correct polymerization kinetics, a missing feature in most of the bottom-up polymerization methods.

In Section 2 the workflow methodology and algorithm are discussed and in Section 3 a set of robust validations against experimental results are presented to check the accuracy of our code package in constructing realistic polymer structures and topologies through several case study systems. Each system represents a special capability of this method: (3-1) a polydisperse mixture of polylactic acid in a simple melt homo-polymerization, (3-2) a realistic network structure of polyurethanes with dangling chains, (3-3) a multi-step synthesis of a complex dendritic structure with multifunctional groups, and (3-4) a hyperbranched polymer system with competitive parallel reactions.

2 Workflow methodology

The general idea behind this package is to perform polymerization reactions through MD simulations to (i) study the chemical and topological evolution of complex polymer structures during polymerization and (ii) obtain well-equilibrated real-size thermoplastic and thermoset polymers to further MD simulation studies. The algorithm utilized in PolySMart is based on exploring the functional groups for the species that can react (under user-defined conditions) and performing the reaction by modifying related topologies followed by energy minimization and further equilibrations. These steps are iterated until a specified condition, e.g., a reaction conversion, is satisfied.

Due to the discussed advantages of the CG representation on the atomistic scale, this package is basically designed using the Martini CG forcefield, which is shown to be among the most successful CG methods for macromolecules.^{10,12,36,39–44}

The scheme is developed in a generic way and can simulate any addition polymerization, performing multiple reactions with different natures at the same time, using non-stoichiometric reaction conditions, and performing multiple reactions in multiple steps on a certain functional group. A schematic of the workflow, which is divided into five major steps, is illustrated in Fig. 1.

Fig. 1 The workflow of PolySMart for performing a reaction process. As an example, a box containing three different molecules that can react with each other is illustrating the workflow.

Step 1: defining the inputs

All species must be defined on the CG scale by employing the Martini forcefield. To specify the input parameters an input file is introduced. This input file must provide (i) the topology file of all reagent molecules and their numbers in the system, (ii) the active beads and their maximum allowed number of reactions, (iii) the distance range that the reaction can take place within (reaction cut-offs), (iv) the probability of reactions for the reacting bead pairs, and (v) all kinds of possible new bonds, angles, and dihedrals (Martini), parameters which can be formed or changed during the reactions and the user wants to consider. Moreover, the number of iteration loops or conversion limit (termination conditions of the process) must be specified in this file. The simulation box containing all the species should be constructed before starting the reaction process. In the case of simulating solution polymerizations, solvents (or any other inactive molecules in the reaction process) should be inserted into the simulation box prior to the reaction and their information should be introduced in the input file accordingly.

Step 2: generating a single topology file based on the input topologies

The topology of the reacting species is evolving based on the reactions taking place. Thus, each reacting species stands a chance to connect to another one during a reaction cycle and the connectivity information should be updated accordingly. Therefore, the program merges the individual topology information of all the reagents (provided by the user as topology files) in this step by reading the input individual topology files, renumbering the beads, and editing the bonded parameters. Note that the non-reactive components (e.g., solvents) can be considered separately since their topological information does not change during the reaction. After obtaining a single topology for reacting species, the (user-defined) equilibration step is performed. However, this step is not necessary if the input structures have been well-equilibrated before.

Step 3: determining the reacting beads and forming neighboring lists

The specified reactions can take place when the reacting beads approach each other within a defined cut-off distance. This step function protocol avoids the formation of over/under-stretched bonds (that cause instabilities and high energy local points) and has proved to be effective for deciding whether the reaction is to be performed or not.⁴⁵ According to the input of the process, see step 1, for all the beads that can react at this stage their mutual distances are determined by a neighbor search. In the case where the distance of any reacting beads falls into the specified reaction cut-off (provided by the user in step 1), the probability of the reaction will be considered and the bead pairs that must be connected at this step are identified. The combination of reaction cut-off and assigned probability determine the speed of the reaction and final molecular structures. In the Martini3 forcefield, the beads are categorized into three sizes (i.e., regular, small, and tiny). Thus, we defined the reaction cut-off based on the Lennard Jones radii of the reacting beads (σ_ij parameters in the force field). In this way, the limitation of the geometrical effects for the approach of different bead pairs will be treated similarly for all possible reactions in the system. Now the probability can be determined by considering the relative reactivity of the bead pairs. Such a feature is of great importance for cases with two (or more) types of possible reactions on a bead type (e.g., for multiblock copolymers). For instance, consider that bead ‘A’ can react with both beads ‘B’ and ‘C’. If the relative reactivity of ‘B’ reacting with ‘A’ is twice as much as for ‘C’ reacting with ‘A’, the probability of the formation of ‘A–B’ and ‘A–C’ connections can be introduced as 1.0 and 0.5, respectively. The possibility of capturing more than one reaction on the same bead is another unique feature of PolySMart. Thus, if a reacting bead has two (or more) functional groups, the bead can react more than once. Accordingly, different conditions can be introduced for each of these reactions (in step 1), and the bead can react more than once, in cases where the conditions are satisfied. Note that, on each reaction cycle, only one reaction is allowed on each bead to avoid instabilities and high-energy local spots in the system.

Step 4: modifying topology and structure files

The core of the program lies in this step which modifies the topology information according to the reactions that took place. The modifications include changing the bead types and bead names and adding the newly formed bonded interactions in both the structure and topology files. The new bead types and names are read from the input file (step 1). The structure file and “atoms” and “constraints” sections of the topology file are modified accordingly. Adding new bonds to the “bonds” section of the topology file is straightforward. As a result of newly formed bonds, new angles, and dihedrals should be considered (in different cases, their numbers may be different according to the structure and complexity of the molecules). To this end, the program identifies new angles and dihedral angles that should be considered formed. The algorithm for finding these new bonded interactions is based on exploring the system for all the beads which are connected to the reacting beads (named second-order beads) and all the beads which are connected to the second-order beads (named third-order beads). After finding all the new bonds, angles, and dihedral angles in the system, the program matches them with the defined list of bonded interactions as specified by the user in the input file and determines the corresponding function types and constants. Eventually, the list of the new bonded interactions is added to the topology file if the parameters are provided by the user in the input file, otherwise will be ignored. The ignored bonded interactions will be gathered in a separate output file for the user's information.

Moreover, the reaction of beads may affect some other bonded parameters of the system in the vicinity of the reaction spots. This issue is especially important in the case of multifunctional beads and condensation reactions (due to the breakage of the bead to a smaller bead size). Multifunctional beads may undergo considerable changes in the previously existing angle and dihedral parameters after each reaction. Condensation reactions may also affect the bead type/size of the reactant bead (e.g., from polar to nonpolar or from R-type to T-type) which can have a considerable impact on the other existing bonds or angles. Therefore, PolySMart performs all necessary updates on the topology information of the system to maintain the topology of the polymer close to the equilibrated structure during the polymerization reaction.

The topology information for each cycle is accessible, making it possible to do post/during reaction data processing for analyses that need connectivity information of any species, e.g., the crosslinking density of complex networks and dispersity index.

Step 5: equilibration of the new structure

The addition of new bonded interactions is associated with instant structural instabilities due to the unrelaxed structures around the reaction spots. Hence, after each reaction cycle, an energy minimization step followed by a (user-specified) short equilibration step will be normally applied to eliminate these instabilities by putting the beads in the proper positions and correcting the orientations at these places. Then, the conversion of the reaction is calculated (based on the number of reacted and unreacted bead types specified in Step 1) and in cases where the termination condition is satisfied, the process stops. Otherwise, the iteration of the algorithm continues until the termination conditions are met.

It should be mentioned that the termination condition can be expressed as a conversion value limit for a specific reactive bead and the number of reaction cycles. The former is efficient in complex reactions where the user does not have an estimation about how the reactions will proceed and which species will be consumed sooner, while the latter can prevent the system from getting stuck in infinite loops in cases where the conversion of the reaction does not reach beyond the specified limit.

3 Test case results

3.1 Homo-polymerization of lactic acid

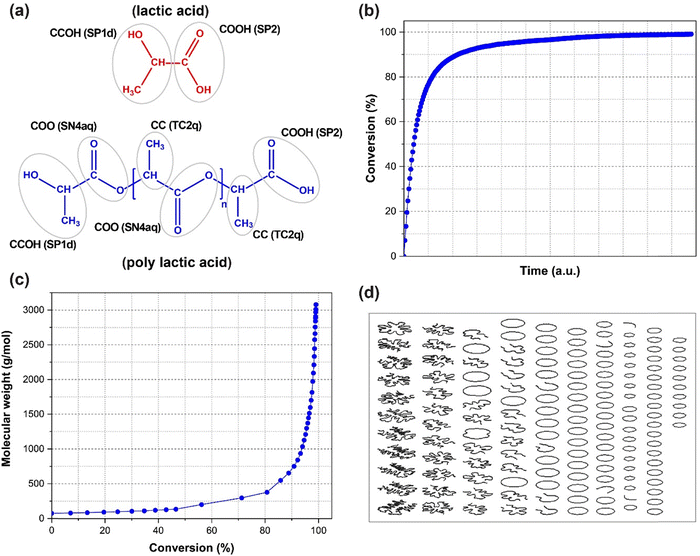
Building realistic initial structures is an important part of any computational simulation. This is challenging in simulations of polymers due to their long chains which need heavy computing power and longer times to ensure an equilibrated structure. This is particularly problematic for glassy polymers, for which annealing the structure above T_g and cooling down to room temperature generates unrealistic morphologies, due to the high heating/cooling rates in molecular simulations⁴⁶ not achievable experimentally. Furthermore, using a monodisperse structure for a polymeric system, which is widely used in MD simulations, is not necessarily a realistic assumption and might lead to serious misunderstanding of structure–property relationships.⁴⁷

Homo-polymerization of small monomers through step-growth polymerization is a simple but important example to evaluate the ability of PolySMart in producing reliable polymer structures with respect to (i) polymer chain size and distribution and (ii) well-equilibrated polymer morphology. To this end, we polymerize lactic acid (LA) to obtain polylactic acid (PLA), as a widely used polymer in biological applications^48,49 and analyze the performance of the process.

First, the interaction parameters and coordinate files of a box containing 25 000 monomers were generated by the Martini3 force field. The details of the force field generation and parameters are reported in ESI,† Section S2 and Table S1. Fig. 2(a) shows the CG structure of the monomer and polymer based on the Marini3 CG parameters. Next, the inputs related to the newly formed bonded interactions and the termination conditions (i.e., a conversion of 99%) were set. An initial 50 ns relaxation using NPT conditions was used. Thereafter the polymerization reactions were switched on. A reaction cut-off of about 5% larger than the van der Waals radius of the reacting beads was chosen. After each iteration loop, an energy minimization followed by a 1 ns relaxation under NPT conditions was done. Details of the MD simulation settings are reported in the ESI,† Section S3.

Fig. 2 Polymerization of the lactic acid test case. (a) Martini CG model and bead types for the monomer and polymer. (b) Evolution of the process conversion during the iteration loops of reactions. (c) Variation of the molecular weight of chains with the evolution of conversion. (d) A set of graphs representing the molecular structure of the chains at the final conversion. The chains are plotted only based on the connectivity information of the beads, and the positions of the beads and chains are changed to achieve a clear representation of all chains in the mixture.

Fig. 2(b) illustrates the conversion of the polymerization process as a function of reaction time. As shown, the conversion grows sharply at the beginning (due to the greater availability of monomers), considerably slows down after 90% conversion, and continues until it reaches 99% conversion at reaction cycle 291. In fact, this is a well-known characteristic of step-growth polymerizations.^50–52

Each individual chain length during the simulation was calculated. Knowing the bead's weight and length of each chain, the molecular weight and its distribution can be obtained. To evaluate the resulting polymer, the evolution of molecular weight at different stages of the reaction was calculated and shown in Fig. 2(c). Results show that the molecular weight grows very slowly at the beginning of the reaction and rapidly increases in the last steps of the polymerization, a typical kinetic for step-growth polymerizations.^50–52 Our results show that PolySMart can correctly mimic these trends. More accurate input values to PolySMart, such as quantum calculated cut-off distances for reacting beads, will result in more precise kinetic parameters, enabling PolySMart to better estimate the polymerization kinetics.

Table 1 compares the M_n, M_w, and dispersity index Đ values for the constructed polymer systems at three different conversion values above 95% with the experimental values for PLA synthesized without the presence of any catalyst obtained via GPC measurements.⁵³ Due to the relatively large variations in molecular weight at high conversions in step-growth polymerizations and also the challenges in measuring the exact conversion values in an experiment, a direct comparison between simulation and experimental results may not be straightforward. However, according to the results in Table 1, the structure obtained at 97.3% conversion seems to represent the structure of PLA closest as compared to the experiments.

Table 1 Molecular weights and dispersity index for our simulation and experimental data⁵³

	Experimental (GPC)	MD (PolySMart) at conversion
		95.2%	97.3%	98.1%
M n (g mol^−1)	1714	1210	1701	2093
M w (g mol^−1)	3600	2178	3359	4845
Đ	2.1	1.8	1.97	2.32

---

Fig. 2(d) depicts the structure of simulated chains at the final conversion. This graph is made based on the connectivity information of polymer chains only³⁶ without preserving the coordinates of each bead to have a clearer illustration of the chain distribution (a more detailed discussion about these graphs is given in the ESI,† Section S1). It is obvious that a variety of chain structures and sizes are obtained, a result that is far from simplified mono-size polymer chains often used in MD simulations. Also, the presence of loop chains and the wide distribution of chain sizes may cause specific interactions (e.g., physical entanglements), which must be considered for further structure–property relationships. More elaborate graphs for different conversion values given are depicted in Fig. S1 (ESI†) showing that up to conversion ≈70% almost no polymer chains are still formed and most of the components are in the form of unreacted monomers, dimers, trimers, and short oligomers. At conversion ≈90% still monomers and short oligomers are present and some chains are forming. With the evolution of the reaction, the chains rapidly grow in size and almost no monomers are present at conversion ≈99%. Thus, this case study signifies the importance of the possibility of reaching very high conversions in polymerization schemes, which is difficult in the case of pure all-atom MD approaches.

3.2 Crosslinked polyurethane networks

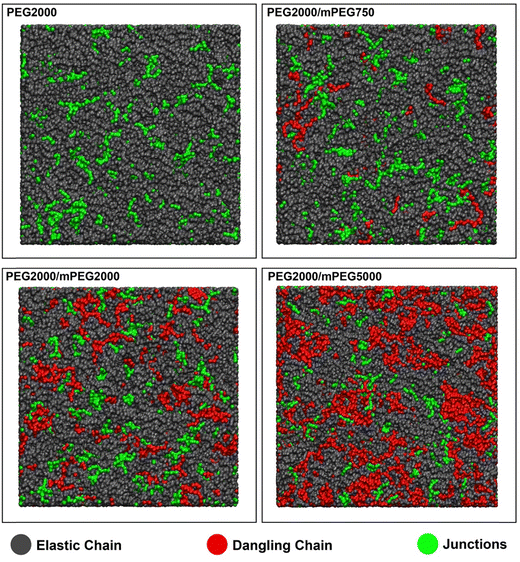
Crosslinked polymer networks are an important class of materials with a wide range of applications.^54–56 However, experimental characterization of the network structure to elucidate the relationship between the network topology and polymer properties is very challenging due to the insolubility of the polymer networks. Most of the earlier attempts to identify the properties of crosslinked polymer networks are based on statistical theories and models. Based on these models, the network is regarded as a uniform tree-like structure used to explain mechanical properties or solvent swelling.^57,58 However, defects in the polymer networks are unavoidable during crosslinking, and the inability to quantify defects impedes the prediction of polymer network properties.⁵⁹ Topological features of networks are divided into three length scales:⁶⁰ (i) 10–100 nm, which can be characterized using conventional scattering techniques, (ii) 1–10 nm, which can be characterized qualitatively (but not quantitatively) by using scattering and spectroscopic techniques, and (iii) <1 nm, which cannot be characterized using conventional experimental techniques.⁶⁰ MD simulations are capable of quantifying medium and smaller defects in polymer networks. Nevertheless, building up an equilibrated crosslinked polymer network in MD without a reactive scheme is unfeasible.²⁸ Thus, PolySMart can be used as an effective tool to generate reliable, complex, and experimentally relevant polymer networks for further analysis as well as to determine topological defects.

In this section, polyurethane networks based on polyethylene glycol (PEG), as elastic chains that connect to the network from two ends, and PEG monomethyl ether (mPEG), as dangling chains that connect to the network from one end, were prepared by PolySMart. For the evaluation of our model prediction and its analysis capacity compared to experimentally determined values, similar materials and reaction conditions were used as in the study by Albers et al.⁶¹ (i.e., elastic and dangling chain lengths, and crosslinker concentration). CG models of PEG with a molecular weight of 2000 g mol⁻¹, mPEG with molecular weights of 750, 2000, and 5000 g mol⁻¹, and a trimerized hexamethylene diisocyanate crosslinker, were created based on Martini3 (see Fig. S2 and Table S2, ESI† for bead typing and interactions). The termination condition of the reactions was set to a conversion of 98% for all models and Table 2 shows the calculated crosslinking density and M_c values. It should be noted that our calculated network properties, as shown in Table 2, were derived directly (and without approximation) from the network topology and based on bead connectivity information. Also, the Phantom network model⁶² is used to calculate the crosslinking density and M_c of networks based on experimental data (e.g., swelling properties), as taken from the study by Albers et al.⁶¹ and reported in Table 2. It should be noted that real polymer networks contain physical chain entanglements and topological defects (e.g., loops), which have complex influences on the polymer network properties^63,64 and have not been considered in the many polymer network models, including the Phantom model.

Table 2 M _c calculated from the simulation, and M_c calculated by using the standard phantom model based on experimental swelling data and crosslinking density⁶¹

	Simulation Mc (g mol^−1)	Experimental Mc (g mol^−1)	Crosslinking density (mol m^−3)
PEG2000	3650	3552 ± 562	345
PEG2000/mPEG750	3560	2127 ± 2	354
PEG2000/mPEG2000	4000	2710 ± 110	315
PEG2000/mPEG5000	4950	4422 ± 56	250

---

Fig. 3 displays simulation snapshots from the final polymerization of four cases presented in Table 2. As shown, a rather uniform distribution of crosslinking points (junctions) for all cases can be seen, which is expected due to the similar nature of elastic and dangling chains. Graph representations for all simulation results (similar to Fig. 2(d)) are shown in Fig. S5 (ESI†).

Fig. 3 MD snapshots of the final networks for crosslinked polyurethane.

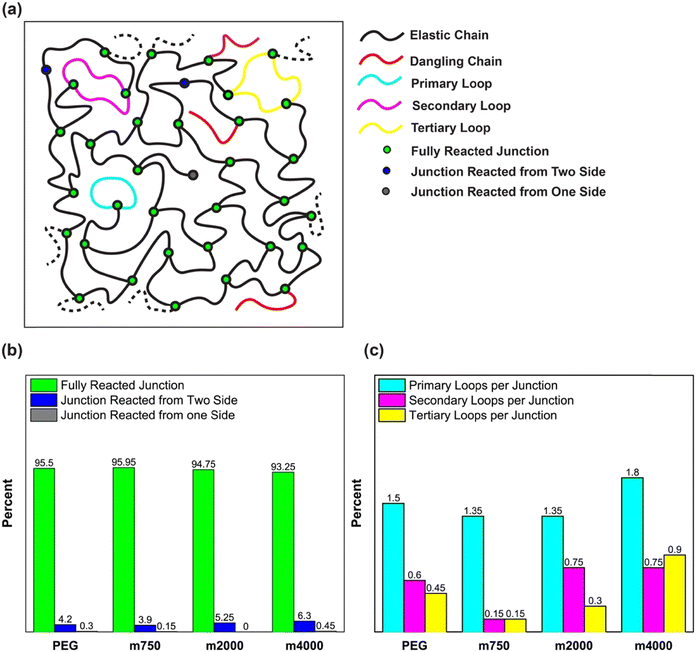
Based on the connectivity information of the modeled polymer network building blocks, we quantified the defects and network properties (see Fig. 4(a)), an infeasible analysis through direct experimental results. Fig. 4(b) shows the proportion of junctions in a network based on the number of reactions, a valuable property for synthetic polymer networks. Another network defect that causes the junction to be elastically disabled is the formation of different loops (see Fig. 4(a)). The formation of loops in various orders reduces the stiffness, extensibility, and toughness of the polymer network.⁶⁵ Considering that these loops are chemically and spectroscopically indistinguishable from completely reacted junctions, giving a quantitative measure for them is extremely challenging in experimental studies.^66–69 Here, we employed simple graph theory computations on the polymer networks generated by PolySMart to emphasize the capabilities of this tool in studying polymer network topologies (see Fig. 4(b) and (c)). Of course, it can be easily adapted for constructing more complex networks, e.g., interpenetrating polymer networks, to further study the structure–property relationships and formulate design principles for precisely tailored polymer networks.

Fig. 4 Crosslinked polyurethane test case: (a) schematic presentation of a typical polymer network and possible defects. (b) Junctions percentage based on the number of connectivity. (c) Loops percentage per junction.

3.3 Poly(amidoamine) dendrimers

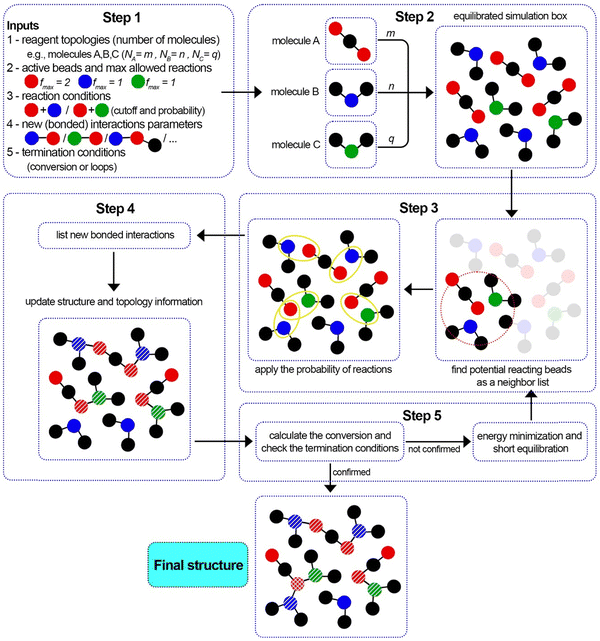
Dendrimers and dendritic polymers are another interesting class of polymers that find many applications including (but not limited to) biomedical (e.g., drug delivery) applications.^70–74 Dendrimers have a core segment with more than one functionality. Each functional group that grows as an arm also contains a terminal group with more than one functionality. This results in the formation of a star-shaped macromolecule which is growing exponentially with each generation.^75–78 These macromolecules can be produced with a large number of generations and can act as single-chain nanoparticles (up to tens of nanometers) for special species. Producing an equilibrated initial structure for these macromolecules is a challenging step in high-throughput MD simulations due to the complexity and the large size of the molecules. Here, we attempt to model the synthesis of a dendrimer utilizing PolySMart and try to validate the structural parameters. Note that the ability of PolySMart in performing multiple reactions on multi-functional bead types unlocks several polymerizations or crosslinking chemistries, e.g., amines, amides, etc., for modeling an unlimited library of dendrimer (or network) topologies.

We carried out our simulations according to the experimental procedure for the synthesis of NH₃-core polyamidoamine (PAMAM) dendrimer⁷⁶ until the 7th generation. Each generation is composed of two steps: (i) addition of the methyl acrylate to the amine-terminated molecule (from the previous generation or the core segment) as the alkylation step and (ii) condensation of the ester-terminated arm with ethylenediamine (EDA), see Fig. 5(a). The procedure was carried out on 10 core segments in methanol as a solvent. For the first step (the half generations), methyl acrylate molecules were added to a simulation box containing 10 solvated dendrimers in methanol. After a 50 ns relaxation, the reactions were switched on until the conversion of 99% (for detailed information on CG parameterization and MD simulations see ESI,† Sections S2 and S3). For the second step (the full generations), the unreacted methyl acrylate molecules were removed from the box and the EDA molecules were added, similar to the experimental process. Before switching on the reactions, a 50 ns relaxation step was performed on the simulation box. The reactions at this step continued up to full conversion. These two steps were repeated to produce 10 dendrimers of the 7th generation. A relaxed structure of a dendrimer molecule with the color-separated guide for beads of each generation is shown in Fig. 5(b). Three main arms are developed similarly and the terminal beads in each arm produced two similar branches in the next generation.

Fig. 5 PAMAM dendrimer test case: (a) the reactions of different steps in PAMAM dendrimer synthesis. (b) Schematic structure of a relaxed PAMAM molecule with the evolution of the generations. Beads belonging to each generation are specified with different colors. (c) The number of beads for each dendritic molecule during generations 3 to 7. (d) The radius of gyration R_g for dendrimers built with PolySMart in comparison with ideal structures calculated via atomistic MD simulations.⁷⁹

Fig. 5(c) shows the number of beads for 10 dendrimers in different generations. The monotonic growth of the particles is a characteristic feature of dendrimers, which is evident for the dendrimers generated by PolySMart (see Fig. 5(c)). All particles have the same size in every step of the generation development with a negligible deviation arising from the incomplete conversion of reactions in the half generations, as also expected in experimental synthesis. The radius of gyration R_g is another structural parameter that can be calculated for particles in each generation. The comparison of this parameter in the structure generated by PolySMart and other atomistic MD simulations⁷⁹ in Fig. 5(d) shows a good quantitative agreement. The larger deviations between our results and the reference values for higher generations are due to the incomplete conversion of reactions in our simulations as compared to the atomistic simulations assuming a complete and ideal structure for dendrimers (see Fig. 5(d)). PolySMart gives better control over the final dendritic structures due to the user-defined conversion limit of each generation step by using the reaction conversion values obtained from laboratory experiments. The results obtained in this case study verify the accuracy of the constructed structures by using PolySMart in cases where multi-functional bead types exist during the reaction.

3.4 Hyperbranched polymers

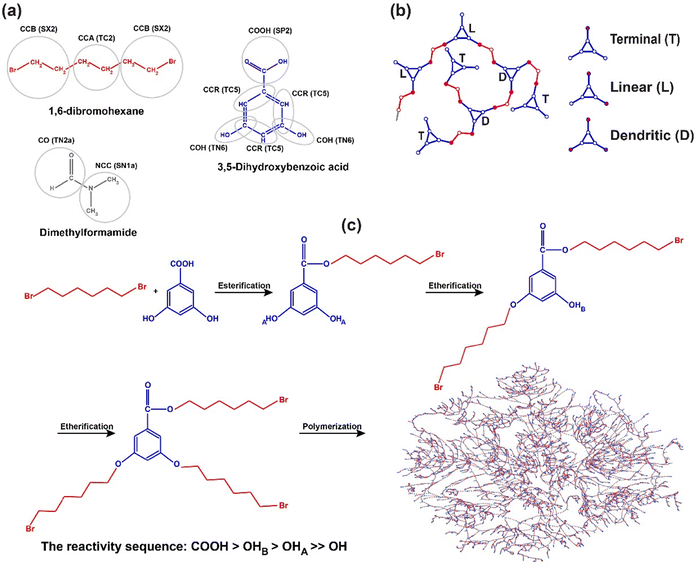
Hyperbranched (HB) polymers are a special sub-class of dendritic polymers that have attracted considerable interest due to their particular properties in comparison with linear and crosslinked polymers. For instance, HB polymers exhibit excellent solubility, low solution viscosity, modified melt rheology, irregular topology, and high functionality when compared with linear polymers.^16,80–83 These particular properties lead to the use of HB polymers in various applications ranging from functional coatings,⁸⁴ biomaterials,⁸⁵ nanocomposites,⁸⁶ opto-electric materials,⁸⁷ and additives.⁸⁸ Generally, HB polymers are easily prepared by the polymerization process of A₂ + B_n (where A₂ and B_n are monomers with two A and n B functional groups); however, the A₂ + B_n approach might result in HB structures with a high risk of gelation and unfavorable intramolecular cyclization. To overcome this problem, recently specific monomers with unequal reactivity, A₂ + CB_n were designed.⁸⁹ In this case study, we report the one-step polymerization process of HB polymers with 1,6-dibromohexane (A₂) and 3,5-dihydroxybenzoic acid (CB₂, C: carboxylic acid, B: hydroxyl) as monomers (see Fig. 6(a)), as also used in a recent experimental study.⁸⁹ The reaction between functional groups is based on nucleophilic substitution reactivity. The ¹H NMR spectra revealed the rate of reaction between Br and hydroxyl and carboxylic acid should be carboxylic acid (COOH) > second hydroxyl (OH_B) > first hydroxyl (OH_A) ≫ original hydroxyl (OH). It was also proven that the reactivity of the original B is negligible as compared to other reactants.⁸⁹ To find the reaction probability of different reactant species in simulations, we mimicked the reaction between monofunctional 1-bromohexane and 3,5-dihydroxybenzoic acid. We tuned the reaction probability ratio in PolySMart to achieve the same product ratio as reported in a reference paper.⁸⁹ More details are given in the ESI,† Section S3 while the comparison of the product ratio obtained by ¹H NMR analysis and MD simulation is listed in Table S10. The reaction probabilities that reproduced the product ratio closest as compared to experimental results were used for the polymerization process of the main case (1,6-dibromohexane + 3,5-dihydroxybenzoic acid). The original hydroxyl bead (COH) converts to the first hydroxyl bead (COH_A) after the reaction of carboxylic acid occurred, and the first hydroxyl bead (COH_A) converts to the second hydroxyl bead (COH_B) when the first hydroxyl bead was reacted (Fig. 6(c)). Different reaction rates can be simulated by incorporating these converting factors in PolySMart.

Fig. 6 Hyperbranched polymer test case: (a) CG mapping of monomers based on the Martini3 force field. Bead labeling is different from the Martini model. The corresponding Martini beads are mentioned in brackets. (b) Different unit types present in HB polymers. (c) The reactivity sequence of functional groups and final structure of the HB polymer.

For HB polymer synthesis by PolySMart, 2500 molecules of 1,6-dibromohexane, 2500 molecules of 3,5-dihydroxybenzoic acid, and 5000 molecules of dimethylformamide (DMF) were first inserted into the simulation box in accordance with the reference paper's molar ratio.⁸⁹ Following energy minimization, the system was equilibrated under NPT conditions. Thereafter the reaction between the hydroxyl or carboxylic acid and Br beads was done using PolySMart. This step was repeated until more than 99% of Br beads reacted.

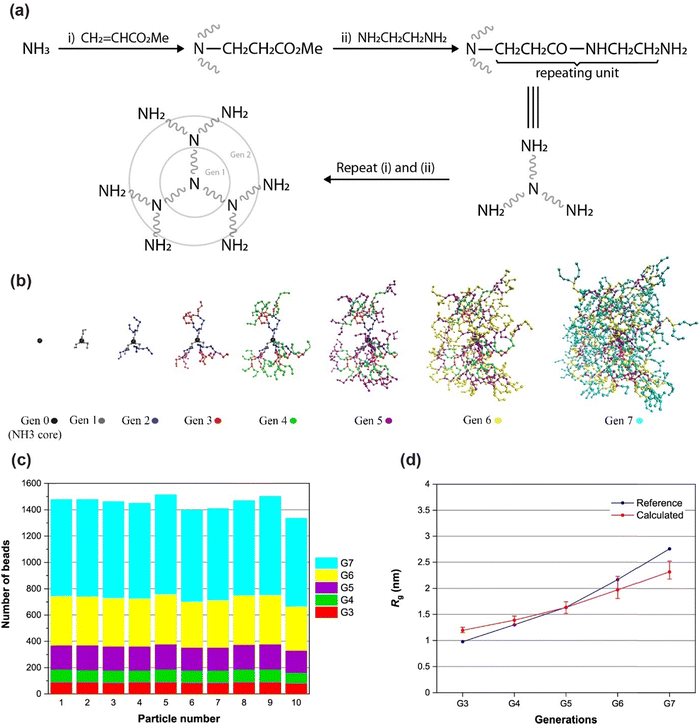
The degree of branching (DB) is one of the most important parameters for HB polymers affecting the physical and chemical properties of these polymer types. The DB was defined by Frechet et al.⁹⁰ using the following equation:

where T, L, and D are the number of terminal, linear, and dendritic units, respectively. Fig. 6(b) shows these types of units schematically.

The conversion of the reaction is plotted to examine different reaction rates for esterification and etherification (Fig. 7). The results obtained from the experimental ¹H NMR analysis show that the rate of esterification is much higher than that of etherification. As mentioned before, one of the abilities of PolySMart is considering diverse reaction probabilities for each reactant pair. The reaction probabilities of the CCB bead with COOH, COH_A, and COH_B beads were set to 1, 0.2, and 0.3, respectively. Our simulation results as shown in Fig. 7 show that these probabilities result in the esterification/etherification rate ratio, which mimics the experimentally obtained reaction kinetics, well. It should be mentioned that all MD simulations differ in time scale compared to real reactions. Therefore, mapping the dynamic events between them may require a scaling factor, a unique case-dependent parameter, that should be defined based on fitting simulation results to the experimental data. The models generated by PolySMart predict a DB of 0.57, close to the experimentally obtained value of 0.62 as determined by the ¹H NMR spectroscopy. This emphasizes the capability of PolySMart in predicting the evolution and final structure of HB during a rather complex set of reactions through correct polymerization kinetics and results in good agreement with the experimental ones. Of course, further experimentally-infeasible structural analysis (e.g., the average number of cyclic structures and cyclic index⁹¹) can be easily obtained by having the topological information of the simulated HB polymers.

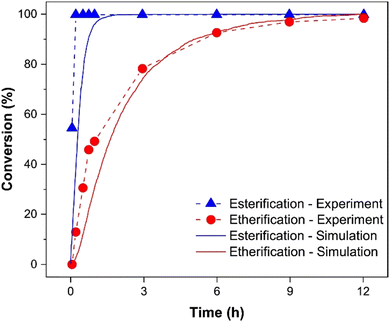Fig. 7 Comparison of conversion between results obtained by ¹H NMR and MD simulation for esterification and etherification reactions. Using the paper referenced, the results of conversion from ¹H NMR analysis were replotted.⁸⁹ In order to aid visual comparison, the experimental time and the simulation cycle at which the conversion reached 99% were mapped on each other and the rest of the plot was rescaled accordingly.

4. Conclusions

PolySMart, a general polymerization Python code package based on the Martini3 coarse-grained model, shows promising capabilities for constructing a comprehensive range of polymer architectures, e.g., linear, dendritic, hyperbranched, and 3D networks, from monomers or any reacting species (e.g., oligomers of prepolymers). PolySMart is not limited to specific chemistry and, in its current form, can model any addition polymerization. In this paper, we showed that the molecular weights and dispersity indices of model polymers generated by PolySMart are comparable to real polymers. It should be noted that having realistically polydispersed polymer models is of great importance in understanding structure–morphology relationships, an attribute that cannot be easily captured by many state-of-the-art polymer modeling packages. This code package is also capable of modeling multiple competing polymerization reactions through experimentally obtained reaction kinetics. In this paper, we showed that the structure and morphology of the polymers modeled are directly comparable with experimental and other simulation results. Furthermore, PolySMart can considerably expedite polymer model generation and effectively pave the way for polymer simulations and in this way contribute to the real process of materials development. The step-wise dynamic scheme of PolySMart facilitates the analysis of the evolution of the system during the reactions and the relaxation of the structures due to considering the instant update of bonded and nonbonded interactions in the system. This makes it a more realistic scheme as compared to random models or MC-based schemes. Care should be taken due to discontinuities of trajectories that may affect the total dynamics of the system as compared to reactive force fields. However, it should be noted that the level of discontinuity can be easily tuned by the reaction probabilities as set by the user in the input parameter file.

It should be noted that the current code of PolySMart cannot model the breakage of bonds between beads explicitly; thus, at present reversible reactions cannot be performed. Therefore, although the coarse-grained representation of the system allows for atomic reconstruction inside the beads, reactions in which bond breakage between beads is needed (e.g., long chain hydrolysis) cannot be modeled yet.

PolySMart can also be easily implemented in additional scripts in order to develop several tools to satisfy different external conditions during the polymerization process. Some examples are controlling solvent evaporation during the crosslinking, drop-wise monomer(s) addition during a (co)polymerization process and stepwise reactions, i.e., initiating a second reaction after the first reaction proceeds to a specific conversion.

It is worth noting that, in addition to the capability of the Martini3 model to produce semi-quantitative CG estimates for the properties of macromolecules, for cases where the presence of atomistic structures is essential, e.g., for conducting or ionic polymers, a complementary reverse-mapping algorithm/code can be applied to PolySMart results to generate a fully atomistic structure for the polymers considered. The development of a general reverse-mapping code for PolySMart is the topic of our current research.

Utilizing this method will bring new insights into polymeric materials by substantially facilitating modeling high-density packing in a more efficient way, leading to a closer-to-real architecture in which for example, multiple functionalities, time-dependent addition of components and evaporation or addition of solvent(s) are involved.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge Alborz Gharraee for helping in the revision of the Python scripting of the package. We are grateful to the group of Prof. Dr. Siewert-Jan Marrink (Groningen) for the useful discussion.

References

1. F. Soheilmoghaddam, M. Rumble and J. Cooper-White, High-Throughput Routes to Biomaterials Discovery, Chem. Rev., 2021, 121(18), 10792–10864,  DOI:10.1021/acs.chemrev.0c01026.
2. S. Axelrod, D. Schwalbe-Koda, S. Mohapatra, J. Damewood, K. P. Greenman and R. Gómez-Bombarelli, Learning Matter: Materials Design with Machine Learning and Atomistic Simulations, Acc. Mater. Res., 2022, 3(3), 343–357,  DOI:10.1021/accountsmr.1c00238.
3. O. Carrillo, C. A. Laughton and M. Orozco, Fast Atomistic Molecular Dynamics Simulations from Essential Dynamics Samplings, J. Chem. Theory Comput., 2012, 8(3), 792–799,  DOI:10.1021/ct2007296.
4. T. E. Gartner and A. Jayaraman, Modeling and Simulations of Polymers: A Roadmap, Macromolecules, 2019, 52(3), 755–786,  DOI:10.1021/acs.macromol.8b01836.
5. R. Rashmi, H. Hasheminejad, S. Herziger, A. Mirzaalipour, A. K. Singh, R. R. Netz, C. Böttcher, H. Makki, S. K. Sharma and R. Haag, Supramolecular Engineering of Alkylated, Fluorinated, and Mixed Amphiphiles, Macromol. Rapid Commun., 2022, 43(8), 2100914,  DOI:10.1002/marc.202100914.
6. M. Azimi, S. S. Mirjavadi, A. M. S. Hamouda and H. Makki, Heterogeneities in Polymer Structural and Dynamic Properties in Graphene and Graphene Oxide Nanocomposites: Molecular Dynamics Simulations, Macromol. Theory Simul., 2017, 26(2), 1600086,  DOI:10.1002/mats.201600086.
7. A. Fathizadeh, H. Schiessel and M. R. Ejtehadi, Molecular Dynamics Simulation of Supercoiled DNA Rings, Macromolecules, 2015, 48(1), 164–172,  DOI:10.1021/ma501660w.
8. N. Kawaguchi, K. Okubo and K. Aida, Molecular Cloning and Expression of Corticotropin-Releasing Hormone and Urotensin I in the Medaka, Oryzias Latipes, Fish. Sci., 2002, 68(sup2), 1281–1282,  DOI:10.2331/fishsci.68.sup2_1281.
9. J. T. Padding and W. J. Briels, Time and Length Scales of Polymer Melts Studied by Coarse-Grained Molecular Dynamics Simulations, J. Chem. Phys., 2002, 117(2), 925–943,  DOI:10.1063/1.1481859.
10. S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. De Vries, The MARTINI Force Field: Coarse Grained Model for Biomolecular Simulations, J. Phys. Chem. B, 2007, 111(27), 7812–7824,  DOI:10.1021/jp071097f.
11. P. Carbone, H. A. K. Varzaneh, X. Chen and F. Müller-Plathe, Transferability of Coarse-Grained Force Fields: The Polymer Case, J. Chem. Phys., 2008, 128(6), 064904,  DOI:10.1063/1.2829409.
12. P. C. T. Souza, R. Alessandri, J. Barnoud, S. Thallmair, I. Faustino, F. Grünewald, I. Patmanidis, H. Abdizadeh, B. M. H. Bruininks, T. A. Wassenaar, P. C. Kroon, J. Melcr, V. Nieto, V. Corradi, H. M. Khan, J. Domański, M. Javanainen, H. Martinez-Seara, N. Reuter, R. B. Best, I. Vattulainen, L. Monticelli, X. Periole, D. P. Tieleman, A. H. de Vries and S. J. Marrink, Martini 3: A General Purpose Force Field for Coarse-Grained Molecular Dynamics, Nat. Methods, 2021, 18(4), 382–388,  DOI:10.1038/s41592-021-01098-3.
13. F. Grünewald, R. Alessandri, P. C. Kroon, L. Monticelli, P. C. T. Souza and S. J. Marrink, Polyply; a Python Suite for Facilitating Simulations of Macromolecules and Nanomaterials, Nat. Commun., 2022, 13(1), 68,  DOI:10.1038/s41467-021-27627-4.
14. D. T. Gentekos, R. J. Sifri and B. P. Fors, Controlling Polymer Properties through the Shape of the Molecular-Weight Distribution, Nat. Rev. Mater., 2019, 4(12), 761–774,  DOI:10.1038/s41578-019-0138-8.
15. K. E. B. Doncom, L. D. Blackman, D. B. Wright, M. I. Gibson and R. K. O’Reilly, Dispersity Effects in Polymer Self-Assemblies: A Matter of Hierarchical Control, Chem. Soc. Rev., 2017, 46(14), 4119–4134,  10.1039/C6CS00818F.
16. Y. Zheng, S. Li, Z. Weng and C. Gao, Hyperbranched Polymers: Advances from Synthesis to Applications, Chem. Soc. Rev., 2015, 44(12), 4091–4130,  10.1039/C4CS00528G.
17. A. Carlmark, C. Hawker, A. Hult and M. Malkoch, New Methodologies in the Construction of Dendritic Materials, Chem. Soc. Rev., 2009, 38(2), 352–362,  10.1039/B711745K.
18. S. P. O. Danielsen, H. K. Beech, S. Wang, B. M. El-Zaatari, X. Wang, L. Sapir, T. Ouchi, Z. Wang, P. N. Johnson, Y. Hu, D. J. Lundberg, G. Stoychev, S. L. Craig, J. A. Johnson, J. A. Kalow, B. D. Olsen and M. Rubinstein, Molecular Characterization of Polymer Networks, Chem. Rev., 2021, 121(8), 5042–5092,  DOI:10.1021/acs.chemrev.0c01304.
19. T. F. A. de Greef and E. W. Meijer, Supramolecular Polymers, Nature, 2008, 453(7192), 171–173,  DOI:10.1038/453171a.
20. Y. K. Choi, S.-J. Park, S. Park, S. Kim, N. R. Kern, J. Lee and W. Im, CHARMM-GUI Polymer Builder for Modeling and Simulation of Synthetic Polymers, J. Chem. Theory Comput., 2021, 17(4), 2431–2443,  DOI:10.1021/acs.jctc.1c00169.
21. M. S. Radue, V. Varshney, J. W. Baur, A. K. Roy and G. M. Odegard, Molecular Modeling of Cross-Linked Polymers with Complex Cure Pathways: A Case Study of Bismaleimide Resins, Macromolecules, 2018, 51(5), 1830–1840,  DOI:10.1021/acs.macromol.7b01979.
22. J. Krajniak, Z. Zhang, S. Pandiyan, E. Nies and G. Samaey, Coarse-Grained Molecular Dynamics Simulations of Polymerization with Forward and Backward Reactions, J. Comput. Chem., 2018, 39(22), 1764–1778,  DOI:10.1002/jcc.25348.
23. G. S. Grest and K. Kremer, Statistical Properties of Random Cross-Linked Rubbers, Macromolecules, 1990, 23(23), 4994–5000,  DOI:10.1021/ma00225a020.
24. P.-H. Lin and R. Khare, Molecular Simulation of Cross-Linked Epoxy and Epoxy–POSS Nanocomposite, Macromolecules, 2009, 42(12), 4319–4327,  DOI:10.1021/ma9004007.
25. D. C. Doherty, B. N. Holmes, P. Leung and R. B. Ross, Polymerization Molecular Dynamics Simulations. I. Cross-Linked Atomistic Models for Poly(Methacrylate) Networks, Comput. Theor. Polym. Sci., 1998, 8(1–2), 169–178,  DOI:10.1016/S1089-3156(98)00030-0.
26. I. Yarovsky and E. Evans, Computer Simulation of Structure and Properties of Crosslinked Polymers: Application to Epoxy Resins, Polymer, 2001, 43(3), 963–969,  DOI:10.1016/S0032-3861(01)00634-6.
27. C. Wu and W. Xu, Atomistic Molecular Modelling of Crosslinked Epoxy Resin, Polymer, 2006, 47(16), 6004–6009,  DOI:10.1016/j.polymer.2006.06.025.
28. V. Varshney, S. S. Patnaik, A. K. Roy and B. L. Farmer, A Molecular Dynamics Study of Epoxy-Based Networks: Cross-Linking Procedure and Prediction of Molecular and Material Properties, Macromolecules, 2008, 41(18), 6837–6842,  DOI:10.1021/ma801153e.
29. C. Li and A. Strachan, Molecular Simulations of Crosslinking Process of Thermosetting Polymers, Polymer, 2010, 51(25), 6058–6070,  DOI:10.1016/j.polymer.2010.10.033.
30. D. R. Heine, G. S. Grest, C. D. Lorenz, M. Tsige and M. J. Stevens, Atomistic Simulations of End-Linked Poly(Dimethylsiloxane) Networks: Structure and Relaxation, Macromolecules, 2004, 37(10), 3857–3864,  DOI:10.1021/ma035760j.
31. T. P. Senftle, S. Hong, M. M. Islam, S. B. Kylasa, Y. Zheng, Y. K. Shin, C. Junkermeier, R. Engel-Herbert, M. J. Janik, H. M. Aktulga, T. Verstraelen, A. Grama and A. C. T. Van Duin, The ReaxFF Reactive Force-Field: Development, Applications and Future Directions, npj Comput. Mater., 2016, 2(1), 1–14,  DOI:10.1038/npjcompumats.2015.11.
32. P. V. Komarov, Y. T. Chiu, S. M. Chen, P. G. Khalatur and P. Reineker, Highly Cross-Linked Epoxy Resins: An Atomistic Molecular Dynamics Simulation Combined with a Mapping/Reverse Mapping Procedure, Macromolecules, 2007, 40(22), 8104–8113,  DOI:10.1021/ma070702.
33. A. A. Gavrilov, P. V. Komarov and P. G. Khalatur, Thermal Properties and Topology of Epoxy Networks: A Multiscale Simulation Methodology, Macromolecules, 2015, 48(1), 206–212,  DOI:10.1021/ma502220k.
34. F. Grünewald, P. C. T. Souza, H. Abdizadeh, J. Barnoud, A. H. de Vries and S. J. Marrink, Titratable Martini Model for Constant PH Simulations, J. Chem. Phys., 2020, 153(2), 024118,  DOI:10.1063/5.0014258.
35. A. P. Carvalho, S. M. Santos, G. Pérez-Sánchez, J. D. Gouveia, J. R. B. Gomes and M. Jorge, Sticky-MARTINI as a Reactive Coarse-Grained Model for Molecular Dynamics Simulations of Silica Polymerization, npj Comput. Mater., 2022, 8(1), 1–13,  DOI:10.1038/s41524-022-00722-w.
36. H. Ghermezcheshme, H. Makki, M. Mohseni, M. Ebrahimi and G. De With, MARTINI-Based Simulation Method for Step-Growth Polymerization and Its Analysis by Size Exclusion Characterization: A Case Study of Cross-Linked Polyurethane, Phys. Chem. Chem. Phys., 2019, 21(38), 21603–21614,  10.1039/c9cp03407b.
37. H. Vakili, M. Mohseni, H. Makki, H. Yahyaei, H. Ghanbari, A. González and L. Irusta, Self-Assembly of a Patterned Hydrophobic-Hydrophilic Surface by Soft Segment Microphase Separation in a Segmented Polyurethane: Combined Experimental Study and Molecular Dynamics Simulation, Polymer, 2020, 195, 122424,  DOI:10.1016/j.polymer.2020.122424.
38. D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, GROMACS: Fast, Flexible, and Free, J. Comput. Chem., 2005, 26(16), 1701–1718,  DOI:10.1002/jcc.20291.
39. G. Campos-Villalobos, F. R. Siperstein and A. Patti, Transferable Coarse-Grained MARTINI Model for Methacrylate-Based Copolymers, Mol. Syst. Des. Eng., 2019, 4(1), 186–198,  10.1039/c8me00064f.
40. E. Panizon, D. Bochicchio, L. Monticelli and G. Rossi, MARTINI Coarse-Grained Models of Polyethylene and Polypropylene, J. Phys. Chem. B, 2015, 119(25), 8209–8216,  DOI:10.1021/acs.jpcb.5b03611.
41. G. Rossi, L. Monticelli, S. R. Puisto, I. Vattulainen and T. Ala-Nissila, Coarse-Graining Polymers with the MARTINI Force-Field: Polystyrene as a Benchmark Case, Soft Matter, 2011, 7(2), 698–708,  10.1039/c0sm00481b.
42. G. Rossi, I. Giannakopoulos, L. Monticelli, N. K. J. Rostedt, S. R. Puisto, C. Lowe, A. C. Taylor, I. Vattulainen and T. Ala-Nissila, A MARTINI Coarse-Grained Model of a Thermoset Polyester Coating, Macromolecules, 2011, 44(15), 6198–6208,  DOI:10.1021/ma200788a.
43. F. Grunewald, G. Rossi, A. H. De Vries, S. J. Marrink and L. Monticelli, Transferable MARTINI Model of Poly(Ethylene Oxide), J. Phys. Chem. B, 2018, 122(29), 7436–7449,  DOI:10.1021/acs.jpcb.8b04760.
44. S. Nawaz and P. Carbone, Coarse-Graining Poly(Ethylene Oxide)–Poly(Propylene Oxide)–Poly(Ethylene Oxide) (PEO–PPO–PEO) Block Copolymers Using the MARTINI Force Field, J. Phys. Chem. B, 2014, 118(6), 1648–1659,  DOI:10.1021/jp4092249.
45. H. Makki, K. N. S. Adema, E. A. J. F. Peters, J. Laven, L. G. J. van der Ven, R. A. T. M. van Benthem and G. de With, A Simulation Approach to Study Photo-Degradation Processes of Polymeric Coatings, Polym. Degrad. Stab., 2014, 105, 68–79,  DOI:10.1016/j.polymdegradstab.2014.03.040.
46. L. J. Abbott, K. E. Hart and C. M. Colina, Polymatic: A Generalized Simulated Polymerization Algorithm for Amorphous Polymers, Theor. Chem. Acc., 2013, 132(3), 1–19,  DOI:10.1007/s00214-013-1334-z.
47. V. Triandafilidi, J. Rottler and S. G. Hatzikiriakos, Molecular Dynamics Simulations of Monodisperse/Bidisperse Polymer Melt Crystallization, J. Polym. Sci., Part B: Polym. Phys., 2016, 54(22), 2318–2326,  DOI:10.1002/polb.24142.
48. A. Basu, K. R. Kunduru, S. Doppalapudi, A. J. Domb and W. Khan, Poly(Lactic Acid) Based Hydrogels, Adv. Drug Delivery Rev., 2016, 107, 192–205,  DOI:10.1016/j.addr.2016.07.004.
49. J. Pretula, S. Slomkowski and S. Penczek, Polylactides—Methods of Synthesis and Characterization, Adv. Drug Delivery Rev., 2016, 107, 3–16,  DOI:10.1016/j.addr.2016.05.002.
50. G. Odian, Principles of Polymerization, John Wiley & Sons, 2004.
51. M. E. Rogers and T. E. Long, Synthetic Methods in Step-Growth Polymers, Wiley, Hoboken, NJ, 2003.
52. M. Zhang; S. M. June and T. E. Long, Principles of Step-Growth Polymerization (Polycondensation and Polyaddition), BT-Polymer Science, Elsevier, 2012, pp. 7–47 DOI:10.1016/B978-0-444-53349-4.00131-X.
53. K. Hiltunen, J. V. Seppälä and M. Härkönen, Effect of Catalyst and Polymerization Conditions on the Preparation of Low Molecular Weight Lactic Acid Polymers, Macromolecules, 1997, 30(3), 373–379,  DOI:10.1021/ma960919w.
54. D. A. Gyles, L. D. Castro, J. O. C. Silva and R. M. Ribeiro-Costa, A Review of the Designs and Prominent Biomedical Advances of Natural and Synthetic Hydrogel Formulations, Eur. Polym. J., 2017, 88, 373–392,  DOI:10.1016/J.EURPOLYMJ.2017.01.027.
55. H. Ghermezcheshme, M. Mohseni, M. Ebrahimi, H. Makki, E. Martinelli, E. Guazzelli, S. Braccini and G. Galli, Effect of Network Topology on the Protein Adsorption Behavior of Hydrophilic Polymeric Coatings, ACS Appl. Polym. Mater., 2022, 4(1), 129–140,  DOI:10.1021/acsapm.1c01071.
56. X. Chen, M. A. Dam, K. Ono, A. Mal, H. Shen, S. R. Nutt, K. Sheran and F. Wudl, A Thermally Re-Mendable Cross-Linked Polymeric Material, Science, 2002, 295(5560), 1698–1702,  DOI:10.1126/science.1065879.
57. P. J. Flory, Theory of Elasticity of Polymer Networks. The Effect of Local Constraints on Junctions, J. Chem. Phys., 1977, 66(12), 5720–5729,  DOI:10.1063/1.433846.
58. M. Gordon and R. M. Barrer, Good's Theory of Cascade Processes Applied to the Statistics of Polymer Distributions, Proc. R. Soc. London, Ser. A, 1962, 268(1333), 240–256,  DOI:10.1098/rspa.1962.0136.
59. R. Wang, A. Alexander-Katz, J. A. Johnson and B. D. Olsen, Universal Cyclic Topology in Polymer Networks, Phys. Rev. Lett., 2016, 116(18), 188302,  DOI:10.1103/PhysRevLett.116.188302.
60. Y. Gu, J. Zhao and J. A. Johnson, A (Macro)Molecular-Level Understanding of Polymer Network Topology, Trends Chem., 2019, 1(3), 318–334,  DOI:10.1016/j.trechm.2019.02.017.
61. P. T. M. Albers, L. G. J. Van Der Ven, R. A. T. M. Van Benthem, A. C. C. Esteves and G. De With, Water Swelling Behavior of Poly(Ethylene Glycol)-Based Polyurethane Networks, Macromolecules, 2020, 53(3), 862–874,  DOI:10.1021/acs.macromol.9b02275.
62. H. M. James and E. Guth, Theory of Rubber Elasticity for Development of Synthetic Rubbers, Ind. Eng. Chem., 1942, 34(11), 1365–1367,  DOI:10.1021/ie50395a025.
63. F. Campise, D. C. Agudelo, R. H. Acosta, M. A. Villar, E. M. Vallés, G. A. Monti and D. A. Vega, Contribution of Entanglements to Polymer Network Elasticity, Macromolecules, 2017, 50(7), 2964–2972,  DOI:10.1021/acs.macromol.6b02784.
64. W. Chassé, M. Lang, J.-U. Sommer and K. Saalwächter, Correction to Cross-Link Density Estimation of PDMS Networks with Precise Consideration of Networks Defects, Macromolecules, 2015, 48(4), 1267–1268,  DOI:10.1021/acs.macromol.5b00236.
65. R. Wang, M. K. Sing, R. K. Avery, B. S. Souza, M. Kim and B. D. Olsen, Classical Challenges in the Physical Chemistry of Polymer Networks and the Design of New Materials, Acc. Chem. Res., 2016, 49(12), 2786–2795,  DOI:10.1021/acs.accounts.6b00454.
66. K. Saalwächter, M. Gottlieb, R. Liu and W. Oppermann, Gelation as Studied by Proton Multiple-Quantum NMR, Macromolecules, 2007, 40(5), 1555–1561,  DOI:10.1021/ma062776b.
67. Y. Osada and J.-P. Gong, Soft and Wet Materials: Polymer Gels, Adv. Mater., 1998, 10(11), 827–837,  DOI:10.1002/(SICI)1521-4095(199808)10:11<827::AID-ADMA827>3.0.CO;2-L.
68. Y. Akagi, J. P. Gong, U. Chung and T. Sakai, Transition between Phantom and Affine Network Model Observed in Polymer Gels with Controlled Network Structure, Macromolecules, 2013, 46(3), 1035–1040,  DOI:10.1021/ma302270a.
69. E. R. Duering, K. Kremer and G. S. Grest, Structure and Relaxation of End-linked Polymer Networks, J. Chem. Phys., 1994, 101(9), 8169–8192,  DOI:10.1063/1.468202.
70. W. Cao and L. Zhu, Synthesis and Unimolecular Micelles of Amphiphilic Dendrimer-like Star Polymer with Various Functional Surface Groups, Macromolecules, 2011, 44(6), 1500–1512,  DOI:10.1021/ma1021242.
71. R. Kharwade, S. More, A. Warokar, P. Agrawal and N. Mahajan, Starburst Pamam Dendrimers: Synthetic Approaches, Surface Modifications, and Biomedical Applications, Arabian J. Chem., 2020, 13(7), 6009–6039,  DOI:10.1016/j.arabjc.2020.05.002.
72. R. K. Dey and A. R. Ray, Synthesis, Characterization, and Blood Compatibility of Polyamidoamines Copolymers, Biomaterials, 2003, 24(18), 2985–2993,  DOI:10.1016/S0142-9612(03)00122-4.
73. L. J. Fox, R. M. Richardson and W. H. Briscoe, PAMAM Dendrimer – Cell Membrane Interactions, Adv. Colloid Interface Sci., 2018, 257, 1–18,  DOI:10.1016/j.cis.2018.06.005.
74. N. T. Pourianazar, P. Mutlu and U. Gunduz, Bioapplications of Poly(Amidoamine) (PAMAM) Dendrimers in Nanomedicine, J. Nanoparticle Res., 2014, 16(4), 2342,  DOI:10.1007/s11051-014-2342-1.
75. D. A. Tomalia, H. Baker, J. Dewald, M. Hall, G. Kallos, S. Martin, J. Roeck, J. Ryder and P. Smith, A New Class of Polymers: Starburst-Dendritic Macromolecules, Polym. J., 1985, 17(1), 117–132,  DOI:10.1295/polymj.17.117.
76. D. A. Tomalia, H. Baker, J. Dewald, M. Hall, G. Kallos, S. Martin, J. Roeck, J. Ryder and P. Smith, Dendritic Macromolecules: Synthesis of Starburst Dendrimers, Macromolecules, 1986, 19(9), 2466–2468,  DOI:10.1021/ma00163a029.
77. D. A. Tomalia and J. M. J. Fréchet, Discovery of Dendrimers and Dendritic Polymers: A Brief Historical Perspective, J. Polym. Sci., Part A: Polym. Chem., 2002, 40(16), 2719–2728,  DOI:10.1002/pola.10301.
78. S. E. Seo and C. J. Hawker, The Beauty of Branching in Polymer Science, Macromolecules, 2020, 53(9), 3257–3261,  DOI:10.1021/acs.macromol.0c00286.
79. T. Çaǧin, G. Wang, R. Martin, N. Breen and W. A. Goddard, Molecular Modelling of Dendrimers for Nanoscale Applications, Nanotechnology, 2000, 11(2), 77–84,  DOI:10.1088/0957-4484/11/2/307.
80. C. R. Yates and W. Hayes, Synthesis and Applications of Hyperbranched Polymers, Eur. Polym. J., 2004, 40(7), 1257–1281,  DOI:10.1016/j.eurpolymj.2004.02.007.
81. Y. Segawa, T. Higashihara and M. Ueda, Synthesis of Hyperbranched Polymers with Controlled Structure, Polym. Chem., 2013, 4(6), 1746–1759,  10.1039/C2PY20877F.
82. W. Jiang, Y. Zhou and D. Yan, Hyperbranched Polymer Vesicles: From Self-Assembly, Characterization, Mechanisms, and Properties to Applications, Chem. Soc. Rev., 2015, 44(12), 3874–3889,  10.1039/C4CS00274A.
83. B. I. Voit and A. Lederer, Hyperbranched and Highly Branched Polymer Architectures—Synthetic Strategies and Major Characterization Aspects, Chem. Rev., 2009, 109(11), 5924–5973,  DOI:10.1021/cr900068q.
84. H. Yari, M. Mohseni and M. Messori, A Scratch Resistant yet Healable Automotive Clearcoat Containing Hyperbranched Polymer and POSS Nanostructures, RSC Adv., 2016, 6(79), 76028–76041,  10.1039/C6RA07824A.
85. Z. Li, Z. Zhang, K. L. Liu, X. Ni and J. Li, Biodegradable Hyperbranched Amphiphilic Polyurethane Multiblock Copolymers Consisting of Poly(Propylene Glycol), Poly(Ethylene Glycol), and Polycaprolactone as in Situ Thermogels, Biomacromolecules, 2012, 13(12), 3977–3989,  DOI:10.1021/bm3012506.
86. M. A. Hood, M. Mari and R. Muñoz-Espí, Synthetic Strategies in the Preparation of Polymer/Inorganic Hybrid Nanoparticles, Materials, 2014, 4057–4087,  DOI:10.3390/ma7054057.
87. A. Qin, C. K. W. Jim, W. Lu, J. W. Y. Lam, M. Häussler, Y. Dong, H. H. Y. Sung, I. D. Williams, G. K. L. Wong and B. Z. Tang, Click Polymerization:  Facile Synthesis of Functional Poly(Aroyltriazole)s by Metal-Free, Regioselective 1,3-Dipolar Polycycloaddition, Macromolecules, 2007, 40(7), 2308–2317,  DOI:10.1021/ma062859s.
88. M. T. Hunley, A. Harber, J. A. Orlicki, A. M. Rawlett and T. E. Long, Effect of Hyperbranched Surface-Migrating Additives on the Electrospinning Behavior of Poly(Methyl Methacrylate, Langmuir, 2008, 24(3), 654–657,  DOI:10.1021/la703119a.
89. X. Li, X. Liu, D. Shi, W. Wei, M. Chen and X. Liu, Facile Synthesis of Hyperbranched Polymers by Sequential Polycondensation, ACS Macro Lett., 2018, 7(7), 778–782,  DOI:10.1021/acsmacrolett.8b00443.
90. C. J. Hawker, R. Lee and J. M. J. Frechet, One-Step Synthesis of Hyperbranched Dendritic Polyesters, J. Am. Chem. Soc., 1991, 113(12), 4583–4588,  DOI:10.1021/ja00012a030.
91. H. Chen and J. Kong, Hyperbranched Polymers from A₂ + B₃ Strategy: Recent Advances in Description and Control of Fine Topology, Polym. Chem., 2016, 7(22), 3643–3663,  10.1039/C6PY00409A.

---

Footnote

† Electronic supplementary information (ESI) available: Connectivity graph for homo-polymerization of lactic acid, bonded interaction parameters, details of MD simulations, connectivity graph for cross-linked polyurethane networks, and details of hyperbranched polymer simulations. See DOI: https://doi.org/10.1039/d3mh00088e

---