Capsule self-oscillating gels showing cell-like nonthermal membrane/shape fluctuations

Abstract

A primary interest in cell membrane and shape fluctuations is establishing experimental models reflecting only nonthermal active contributions. Here we report a millimeter-scaled capsule self-oscillating gel model mirroring the active contribution effect on cell fluctuations. In the capsule self-oscillating gels, the propagating chemical signals during a Belousov–Zhabotinsky (BZ) reaction induce simultaneous local deformations in the various regions, showing cell-like shape fluctuations. The capsule self-oscillating gels do not fluctuate without the BZ reaction, implying that only the active chemical parameter induces the gel fluctuations. The period and amplitude depend on the gel layer thickness and the concentration of the chemical substrate for the BZ reaction. Our results allow for a solid experimental platform showing actively driven cell-like fluctuations, which can potentially contribute to investigating the active parameter effect on cell fluctuations.

---

New concepts

Here, we showcase a new concept of an experimental model for cell membrane fluctuations (CMFs) composed of millimeter-sized self-oscillating gels (SOGs). Cell membranes constantly fluctuate, affecting the essential functions of life. The current significant technological lacuna in the related discipline is to realize experimental models that can only reflect the active nonthermal contribution of CMFs. This study highlights a material-based new approach to realize experimental models for CMFs that can mirror only the influence of the nonthermal contribution: a millimeter-sized capsule SOG system showing cell-like membrane/shape fluctuations by Belousov–Zhabotinsky (BZ) reaction. The found mechanism of the gel fluctuations in this study shares a functional mechanism with cell fluctuations: the thickness fluctuations, only driven by the BZ reaction in the case of our study, induce shape fluctuations. Furthermore, the controllable gel fluctuations by manipulating the layer thickness give our system robustness as a model platform for realizing desirable cell-like fluctuations. The knowledge we found and demonstrated can open a new applicable field of soft materials to cover the unsolved issues in the biological field. Furthermore, since our study features an experimental base platform, various material-related technologies could be added to our system, promoting the birth of new advanced material-based systems.

Introduction

Cells show various dynamic behaviors. In a thermodynamic sense, cells constantly exchange both energy and matter with their exterior through cell membranes to maintain dynamic steady states.¹ Cell membrane fluctuations (CMFs) are necessary byproducts of the dynamic states. CMFs induce essential features for life, such as the diffusion of membrane proteins,² cell motility³ and vesicle trafficking.⁴ The driving forces of CMFs are derived from two components: (1) thermal fluctuations of phospholipids in the cell membrane⁵ and (2) nonthermal active components such as conformational changes of glycoproteins or ATP-induced cytoskeleton dissociation.^6,7 Until now, the thermal fluctuation component has been used to classically explain CMFs; however, the contribution of the active factors has attracted a lot of attention in recent years.^8–12

There has been growing interest in constructing experimental models for realizing CMFs driven by active contributions. For example, S. C. Takatori et al. reported a model encapsulating motile micron-sized Bacillus subtilis PY79 into giant unilamellar vesicles (GUVs).¹² In GUVs, the bacteria can travel and hit the membrane of the GUV. In other words, the bacteria-membrane collision drove the active force-induced shape fluctuation. H. R. Vutukuri et al. reported giant lipid vesicles containing self-propelling Janus colloidal particles as a microswimmer.¹³ The polystyrene particles half coated with Pt got propulsion by supplying hydrogen peroxide (H₂O₂) as a fuel. As a result, the propelling particles inside gave localized active internal forces when they touched the membrane, which can largely deform the lipid membranes. However, despite these efforts, developing experimental models exhibiting non-equilibrium CMFs by active factors is still challenging in the current field.

In this study, we report millimeter-scaled capsule self-oscillating gel (C-SOG)-based model systems exhibiting cell-like membrane/shape fluctuations reflecting the nonthermal contributions. Our approach has started from the viewpoint of materials; self-oscillating gels (SOGs) developed by our group. The SOGs feature autonomous and repetitive swelling/deswelling volume oscillations triggered by a Belousov–Zhabotinsky (BZ) reaction.¹⁴ The SOGs can be fabricated by introducing a tris(2,2′-bipyridine)ruthenium (Ru(bpy)₃²⁺, a catalyst for the BZ reaction) into a gel network.^14,15 During the BZ reaction, by adding chemical substances to an acidic external solution, Ru(bpy)₃²⁺ in the gel exhibits cyclic redox change between its reduced Ru(bpy)₃²⁺ and oxidized Ru(bpy)₃³⁺ states. The repetitive redox change leads to the redox state-dependent migration of water molecules, resulting in out-of-equilibrium volumetric oscillations during the BZ reaction.

We built our C-SOG model system showing cell-like surface fluctuation by harmonizing (1) an intrinsic functional property in the volume oscillation of the SOGs and (2) structural design. The volumetric self-oscillatory behavior during the BZ reaction depends on the gel size. Specifically, the SOGs exhibit isotropic volume oscillation if the gels are smaller than approximately 1 mm (i.e., the wavelength of the BZ reaction), and BZ chemical wave-dependent volume oscillation if larger than 1 mm.¹⁶ HBrO₂, which acts as an activator for the BZ reaction, could be periodically generated and randomly diffused through the matrix; a BZ chemical wave. Note that the diffused HBrO₂ can induce oxidation, followed by gel swelling. If the gel size is significantly large than the wavelength of the BZ reaction, HBrO₂ generated later could spread again before the previously propagated HBrO₂ is completely diffused throughout the matrix. From these backgrounds, we hypothesized that if we design the SOGs as a millimeter-sized capsule, the propagating BZ chemical wave along the gel surface could induce multiple and simultaneous local deformations in the various gel sites causing cell-like fluctuation behavior (Fig. 1(a)). As a platform design, C-SOGs were fabricated by synthesizing a poly(N-isopropylacrylamide-co-N-3-aminopropylmethacrylamide) (poly(NIPAAm-co-NAPMAm)) layer on spherical alginate–calcium (Alg/Ca) beads, followed by liquifying the Alg/Ca core part and sequentially conjugating bis(2,2′-bipyridine) (1-(4′-methyl-2,2′-bipyridine-4-carbonyloxy)-2,5-pyrrolidinedione) ruthenium(II) (Ru(bpy)₃–NHS) to the primary amine NAPMAm.

Fig. 1 (a) Schematic illustration of the capsule self-oscillating gels showing cell-like membrane and shape fluctuation during the BZ reaction and (b) their fabrication process.

Here we fabricated millimeter-scaled C-SOGs with various gel layer thicknesses. The bulk scale of this model could imply the definitive separation of thermal fluctuation.^17,18 We demonstrated that the randomly generated BZ chemical waves travel along the surface of the C-SOGs, inducing layer thickness and shape fluctuations. The gel fluctuations did not occur without BZ reactions, implying that gel fluctuations were only attributed to the nonthermal active volume oscillations caused by the BZ reaction. The shape fluctuations caused by the local thickness deformations of the C-SOGs by the BZ reaction can mirror the effect of nonthermal active contributions to CMFs. As previously described, the nonthermal active contribution to the CMFs includes ATP-dependent conformational changes of transmembrane proteins (ion pumps)^8,9,11 and ATP-dependent cytoskeletal dissociation.^7,19 The local deformation induced by the mechanical swelling/deswelling can randomly occur on the various sites in the cells by consuming ATP, resulting in cell membrane and shape fluctuations. Back to the C-SOGs, the quantitatively analyzed results indicated that the period and amplitude of the fluctuation behavior during the BZ reaction depended on the gel layer thickness. The thickened layer caused a more significant local deformation (i.e., micrometer-scaled amplitude) induced by the BZ reaction, inducing significant shape fluctuations. We also found that the gel fluctuations depended on the concentration of the chemical substrates of the BZ reaction. The influence of the chemical substrate concentration could correspond to the ATP dependency of the active contribution.⁷ Therefore, our results can be exploited as an experimental platform that only reflects active factors on CMFs, which can contribute to finding the specific effect of active factors on CMFs. Furthermore, we strongly believe that each developing process of our model system can give meaningful insight as a platform.

Results and discussion

Fabrication of the capsule self-oscillating gels

The C-SOGs were fabricated in four processes, as schematically shown in Fig. 1(b) (see Fig. S1 in ESI 2.1† for the detailed process). First, spherical Alg/Ca beads were fabricated from aqueous alginate solution and CaCl₂ aqueous solution using a syringe. The fabricated spherical Alg/Ca beads were immersed in the APS (initiator) solution to allow the APS molecules to be loaded into the Alg/Ca beads by diffusion, as described in a previous report.²⁰ Then, the APS-loaded Alg/Ca beads were transferred to a monomer solution containing NIPAAm, NAPMAm, N,N′-methylenebis(acrylamide) (BIS), and N,N,N′,N′-tetramethylethylenediamine (TEMED). During this immersion, the APS can be diffused from the Alg/Ca beads,²⁰ synthesizing the poly(NIPAAm-co-NAPMAm) layer on the Alg/Ca beads. After this, 0.1 M sodium citrate treatment for the capsule gels (CGs) was performed, resulting in liquifying of the core Alg/Ca beads. The Alg/Ca beads are physically crosslinked by ionic interaction between Ca²⁺ and carboxyl groups in the alginate structure, forming egg and box junctions.²¹ When the Alg/Ca beads are treated with solutions of chelators such as sodium citrate, an ionic exchange between Ca²⁺ and Na⁺ in the chelator solution occurs. Since Na⁺ cannot significantly play a role as a crosslinker to maintain the physical gelation, the Alg/Ca beads can be dissolved.²² To trace the liquified alginate after chelator treatment, we prepared CGs made of 5-aminofluorescein-labeled alginate (AF–Alg) (see Experimental Procedure 1.7. in the ESI†). We verified that the liquified AF–Alg remained in the capsular gel structure after chelator treatment (Fig. S2 in ESI 2.2†). The C-SOGs were fabricated by conjugating Ru(bpy)₃–NHS with a primary amine in NAPMAm in the poly(NIPAAm-co-NAPMAm) gel layer. The cross-sectional images in Fig. 2(a) reveal that each process was successfully conducted.

Fig. 2 (a) The images of the gels in each fabrication process, including the Alg/Ca beads, the capsule gels composed of the solidified and the liquified Alg/Ca beads, and the capsule self-oscillating gels. The scale bars are 1 mm. (b) The growth kinetics of the poly(NIPAAm-co-NAPMAm) layer thickness according to the various immersion conditions in APS solutions. The number following the character (APS) in the legends signifies the immersion times in the APS initiator solutions, while the x-axis indicates the immersion time in the monomer solutions.

Fig. 2(b) displays the growth kinetics of the poly(NIPAAm-co-NAPMAm) gel layer thickness controlled by the immersion times in the APS and monomer solutions. Each condition is referred to as “APS#” (the legend in Fig. 2(b)), where # represents the immersion time (min) of the Alg/Ca beads in the APS solutions. The immersion time in the monomer solutions is expressed as the x-axis. The respective graphs in Fig. 2(b) show similar trends, showing a rapid increase at the initial stage (∼5 min) followed by a steady state. The layer thicknesses after immersion for 30 min were as follows: 265 ± 44.0 μm for APS10, 341 ± 15.5 μm for APS20, and 400 ± 18.4 μm for APS60. Specifically, the varied immersion time in the APS solutions could lead to different amounts of APS molecules being diffused into the Alg/Ca beads.²⁰ The different immersion times in the monomer solution could indicate the different gelation times. Therefore, the immersion times can generate different gelation rates and layer thicknesses during the radical polymerization. These results offer a clear strategy for fabricating CGs and C-SOGs with the desired layer thickness.

Geometric changes of the gels in each redox state

Fig. 3 displays the temperature dependence of the geometries of the C-SOGs in each redox state. The evaluated geometries were the layer thickness (T)-to-whole size (diameter, S) ratio (T/S, eqn (1)) (Fig. 3(a)).

Fig. 3 (a) The schematic illustration describing the analyzed geometrical changes (T/S value) in each redox state. (b–d) The T/S values and the fitted curves as a function of the temperature in each redox state. The gels were classified according to the T/S values in the reduced state at 20 °C; (b) C-SOGs (0.043), (c) C-SOGs (0.027), and (d) C-SOGs (0.013). The gels were immersed in the BZ substrate solution containing [HNO₃] = 894 mM and [NaBrO₃] = 84 mM for the oxidized state, and [HNO₃] = 894 mM, [NaCl] = 84 mM, and [MA] = 64 mM for the reduced state. NaCl was added to maintain the ionic strength.

All volumetric changes depended on the temperature change in both the redox states (Fig. 3(b–d)). To classify the samples more clearly, we focused on the three samples according to the measured T/S values in the reduced state at 20 °C. The three C-SOGs are marked as follows: C-SOGs (0.043) (Fig. 3(b)), C-SOGs (0.027) (Fig. 3(c)), and C-SOGs (0.013) (Fig. 3(d)), where the numerical value in parentheses indicates the calculated T/S value in the reduced state at 20 °C. The layer thickness profiles as a function of temperature in each redox state are shown in Fig. S3 (ESI 2.3†). Considering the similar trend of each graph between Fig. 3 and Fig. S3 (ESI†), we verified that the ratio of the change in the whole size and layer thickness was similar. In other words, T/S can reflect the information on capsule layer thickness as a geometric indicator.

We mathematically fitted the measured data from the three groups to the Boltzmann sigmoidal equation (eqn. (S1), ESI†), which can model the phase transition of thermoresponsive gels.²³ The purpose was to calculate the difference in the numerical values of the geometries between the redox states by modeling. The mathematical modeling and the adjusted parameters are detailed in Tables S1 and S2 (ESI†). In all cases, the R² values were greater than 0.980, and the adjusted R² values were greater than 0.970. These results imply that the Boltzmann sigmoidal equation successfully fitted the experimental results. Fig. S4 (ESI†) shows the difference in the fitted values of T/S and the layer thickness between the redox states from 10 °C to 35 °C. The differences were maximized at around 20 °C, and the maximum values increased with the T/S values in the reduced state at 20 °C. For instance, the differences in T/S in each redox state at 20 °C were 2.16 × 10⁻² for C-SOGs (0.043), 1.06 × 10⁻² for C-SOGs (0.027), and 5.08 × 10⁻³ for C-SOGs (0.013). On the other hand, the differences in capsule layer thickness in each redox state at 20 °C were 30.9 μm for C-SOGs (0.043), 22.9 μm for C-SOGs (0.027), and 14.5 μm for C-SOGs (0.013). Considering all results, we set the observation temperature of volumetric self-oscillatory behavior during the BZ reaction to 20 °C.

The non-capsule solid spherical SOGs (referred to as “solid SOGs”) were fabricated as schematically illustrated in Fig. S5(a) (ESI 2.4.1†). The geometrical change of the solid SOGs in each redox state was characterized as an equilibrium swelling ratio (Fig. S6 in ESI 2.4.2†) by eqn. (S2) (ESI†). We also mathematically fitted the measured data of the solid SOGs by eqn. (S1) (ESI†). The fitting parameters are listed in Table S3 (ESI†). We determined the observation temperature for the BZ reaction to be 20 °C because the difference in equilibrium swelling ratio was the largest at 20 °C (0.331).

The SOGs are based on the thermo-responsive poly(NIPAAm) gel, which exhibits a volume phase transition temperature (VPTT).¹⁴ The poly(NIPAAm)-based gels swell below the VPTT and shrink above it because the degree of swelling changes drastically at the VPTT.²⁴ In the SOGs, when the conjugated Ru(bpy)₃ is oxidized (Ru(bpy)₃³⁺), the hydrophilicity and the VPTT of the gel network increase, leading to the water diffusing into the gel: swollen gels. On the contrary, in the reduced state (Ru(bpy)₃²⁺), the decreased hydrophilicity and VPTT of the gel network induce the outward diffusion of water from the gel network: shrunken gels. From this viewpoint, the volume transitions by the redox state changes can depend on the amount of Ru(bpy)₃ in the gel network because the amount of immobilized Ru(bpy)₃ could affect the volume of diffused water.^25–27 Since the current Ru(bpy)₃–NHS concentration (i.e., 70 mM) could lead all primary amine groups to saturatedly react with Ru(bpy)₃–NHS molecules,^25,27,28 the C-SOGs with a thicker layer can imply that more Ru(bpy)₃ might be conjugated than the C-SOGs with a thinner layer. Therefore, the equilibrated thickness difference between the redox states could depend on the gel layer thickness. From a geometrical perspective, the redox-state-dependent layer thickness transition could exert contractile pressure on the capsular gels. In this regard, we postulate that the whole gel size transition trend was dependent on layer thickness changes.

Note that the SOGs repetitively undergo swelling in the oxidized Ru(bpy)₃³⁺ and deswelling in the reduced Ru(bpy)₃²⁺ during the BZ reaction. Thus, the equilibrated volume difference (i.e., equilibrium swelling ratio) between the redox states can play a crucial role in inducing the actual volumetric self-oscillation behavior of the gel.¹⁴ Thus, it would be reasonable to express the equilibrated volume difference as a potential for the volumetric self-oscillations during the BZ reaction.

The BZ reaction can induce simultaneous gel layer thickness oscillation in various regions

We analyzed the volumetric oscillation behavior of the C-SOGs (0.043), C-SOGs (0.027), and C-SOGs (0.013) during the BZ reaction at 20 °C. Movies S1–S3 (ESI†) display the dynamic oscillation behaviors of the C-SOGs during the BZ reaction at 20 °C. As shown in Movie S1 (ESI†) for the C-SOGs (0.043)), the BZ chemical waves simultaneously spread along the surface of the C-SOGs, causing local gel layer deformation by oxidation. We visually checked that the local layer deformation change caused by the BZ reaction induced gel shape fluctuation, which was similar to the other movies (Movie S2 for C-SOGs (0.027) and Movie S3 for C-SOGs (0.013), ESI†). In detail, C-SOGs (0.043) and C-SOGs (0.027) display gel shape fluctuations during the BZ reaction exhibiting a relatively slow BZ chemical wave propagation. C-SOGs (0.013) exhibit gel shape flickering (i.e., faster oscillation) showing a relatively faster BZ chemical wave spreading. In contrast, the solid SOGs (Movie S4, ESI†) do not show volumetric and shape deformation during the BZ reaction.

We quantitatively characterized the gel layer deformation and shape fluctuations based on these results. We firstly evaluated the volumetric oscillation behaviors of the layer thickness with a time-lapse optical microscope. Considering the capsular structure of the gels, we regard that the gel layer deformation during the BZ reaction would correspond to the gel layer thickness fluctuation. Fig. 4(a1) visually shows the images of C-SOGs (0.043) taken at regular time intervals, while Fig. 4(a2) exhibits the gray-scale images (red channel) at the same time intervals as Fig. 4(a1). The regions pointed to with red arrows in Fig. 4(a2) indicate the local and simultaneous oxidation of the gel (dark; oxidized region, light; reduced region) during the BZ reaction in various areas. We named this phenomenon the multiple simultaneous layer thickness fluctuations (TFs).

Fig. 4 The thickness fluctuations (TFs) of the fabricated C-SOGs (0.043) during the BZ reaction at 20 °C. The concentrations of the BZ substrates were as follows: [HNO₃] = 894 mM, [NaBrO₃] = 84 mM, and [MA] = 64 mM. (a1) The images of the C-SOGs (0.043) taken at regular time intervals, and (a2) the gray-scale images (red channel) at the same time intervals. The red arrows indicated the oxidized point caused by the propagating BZ chemical wave. Analysis of TFs of (b) C-SOGs (0.043), (c) C-SOGs (0.027) and (d) C-SOGs (0.013). The representative image of (b1) C-SOGs (0.043), (c1) C-SOGs (0.027) and (d1) C-SOGs (0.013), which also exhibits the analyzed regions; Region 1 (black line), Region 2 (blue line), and Region 3 (red line). The overlapped oscillation profiles for (b2, c2, and d2) the thickness and (b2, c3, and d3) the gray value in all regions. The scale bars in (a, b1, c1 and d1) are 1 mm, while the scale bars in (b2 and b3), (c2 and b3) and (d2 and b3) are 500 s. (e) The calculated (e1) periods and (e2) amplitudes of the thickness oscillation in all regions. The periods and the amplitudes were calculated from the thickness profiles during the BZ reaction, i.e., from (b2, c2 and d2).

We quantitatively analyzed the TFs of the fabricated gels during the BZ reaction in three regions: Region 1 with a black line, Region 2 with a blue line, and Region 3 with a red line (Fig. 4(b1, c1 and d1) for C-SOGs (0.043), (0.027), and (0.013), respectively). As displayed in Fig. 4(b2, c2 and d2), the time profiles of the thickness change in each region were not synchronized. Likewise, each local color change caused by the spreading BZ chemical waves in the designated regions was not coupled (Fig. 4(b3, c3 and d3)). The color changes (high gray value; oxidized state) induced by the BZ reaction were expressed as the gray value (green channel).¹⁴ Then, we calculated the periods (Fig. 4(e1)) and the amplitudes (Fig. 4(e2)) of all prepared gels in each region during the TFs. The calculation methods are described in Fig. S7 (ESI 2.5†), where eqn. (S3) (ESI†) is for the period and eqn. (S4) (ESI†) is for the amplitude. The detailed profiles exhibiting thickness and gray value oscillation in each region are displayed in ESI 2.6†; C-SOGs (0.043) (Fig. S8, ESI†), C-SOGs (0.027) (Fig. S9, ESI†) and C-SOGs (0.013) (Fig. S10, ESI†). The profiles of the three regions confirmed that the mechanical responses, such as thickness changes, followed the gray value (green) change, which was consistent with the previous work.²⁹ As shown in Fig. 4(e1 and e2), the periods and the amplitudes were similar in the three regions in the C-SOGs with the same T/S values. Moreover, the higher T/S values resulted in a longer period and a larger amplitude. Note that the average periods and amplitudes of the TFs are sorted in Table 1.

Table 1 The calculated periods and amplitudes of the layer thickness fluctuations (TFs) and gel shape fluctuations (SFs) of the prepared C-SOGs during the BZ reaction at 20 °C

Fluctuation mode			C-SOGs (0.043)	C-SOGs (0.027)	C-SOGs (0.013)
Layer thickness fluctuation (TFs)	Region 1	Period (s)	217 ± 40.8	159 ± 37.5	120 ± 31.6
	Region 2		236 ± 24.4	145 ± 56.8	129 ± 42.6
	Region 3		233 ± 25.8	145 ± 27.0	119 ± 31.0
	Region 1	Amplitude (μm)	12.3 ± 3.62	8.21 ± 1.99	3.46 ± 1.04
	Region 2		11.3± 3.32	8.23 ± 2.65	3.83 ± 1.13
	Region 3		12.6 ± 1.79	8.05 ± 2.82	3.23 ± 1.58
Shape fluctuation (SFs)	Aspect ratio	Mean period (s)	280	163	112
		Mean amplitude (−)	0.70 × 10^−2	0.65 × 10^−2	0.25 × 10^−2
	Fluctuation deviation	Mean period (s)	300	165	103
		Mean amplitude (μm)	22.7	19.2	7.10

---

The BZ reaction can induce gel-shape fluctuations

We also evaluated the shape fluctuations (SFs) of the C-SOGs induced by the volumetric oscillation of the layer thickness during the BZ reaction at 20 °C. The SFs of the solid SOGs during the BZ reaction at 20 °C were also analyzed. We applied two shape descriptors to characterize the SFs quantitatively (Fig. 5(a)): (1) We analyzed the aspect ratio by dividing the maximum Feret diameter (D_max) by the minimum (D_min) (eqn. (2)). (2) We also analyzed the fluctuation deviation inspired by the variance equation. The fluctuation deviation was calculated by eqn. (3), where ΔD_t refers to the difference between D_max and D_min of each time point, and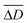 indicates the average of all ΔD_t values in the entire measurement time. The D_max and D_min were calculated by using Image J software (NIH, USA).

Fig. 5 (a) The schematic illustration for analyzing the shape fluctuations (SFs) during the BZ reaction at 20 °C. The definitions of the aspect ratio and the fluctuation deviation are also described. (b) The time profiles of the aspect ratio for C-SOGs (0.043) (b1) without and (b2) with the BZ reaction, (b3) C-SOGs (0.027), and (b4) C-SOGs (0.013). (c) The time profiles of fluctuation deviation for C-SOGs (0.043) (c1) without and (c2) with the BZ reaction, (c3) C-SOGs (0.027), and (c4) C-SOGs (0.013). Note that Fig. 5(b2–b4 and c2–c4) are the results with the BZ reaction. The external solution without the BZ reaction is [HNO₃] = 894 mM. The BZ substrate concentration was [HNO₃] = 894 mM, [NaBrO₃] = 84 mM, and [MA] = 64 mM. (d) The box and whisker plot displaying the (d1) periods and (d2) amplitudes of the aspect ratio of the prepared C-SOGs. The jittered dot plots in each plot were analyzed from the corresponding graphs in Fig. 5(b2–b4). (e) The box and whisker plot showing the (e1) periods and (e2) amplitudes of the fluctuation deviation of the prepared C-SOGs. The jittered dot plots in each plot were calculated from the respective graphs in Fig. 5(c2–c4). “n.s.” indicates not statistically significant (p > 0.05). (**, p < 0.005) The sample numbers are as follows; for the periods, C-SOGs (0.043) (n = 18), C-SOGs (0.027) (n = 29), and C-SOGs (0.027) (n = 44); for the amplitude, C-SOGs (0.043) (n = 16), C-SOGs (0.027) (n = 29), and C-SOGs (0.027) (n = 48).

The quantitatively analyzed results support that the structure and the layer thickness can affect the SFs. Fig. 5(b and c) display the time profiles of the aspect ratio and the fluctuation deviation of the prepared C-SOGs, respectively, at 20 °C. In particular, in C-SOGs (0.043), the time profiles of the shape descriptors did not show fluctuating behaviors when the BZ reaction did not occur (Fig. 5(b1 and c1)). In contrast, all fabricated C-SOGs showed fluctuating behaviors when the BZ reaction occurred (Fig. 5(b2–b4 and c2–c4)). This result signifies that the BZ reaction significantly contributed to the fluctuation of the capsular gels. Furthermore, the profiles of the C-SOGs showed large fluctuation as the layer thickness increased (Fig. 5(b3 and c3) for C-SOGs (0.027) and Fig. 5(b4 and c4) for C-SOGs (0.013)). In the solid SOGs, both shape descriptors do not exhibit volumetric changes (Fig. S11 in ESI 2.7†). Fig. 5(d and e) signify box-and-whisker plots with jitter plots, in which the data points correspond to the calculated periods or amplitudes from Fig. 5(b2–4 and c2–4). The median period and amplitude increased in both shape descriptors when the layer was thickened (Table 1). All detailed statistics from the diagrams are listed in Tables S4–S7 (ESI 2.8†). All periods between the three prepared C-SOGs are statistically significant in all analyses. All amplitudes are statistically significant except in only one case: between C-SOGs (0.043) and (0.027).

In this study, the size of all analyzed C-SOGs during the BZ reaction was approximately 2.5 mm. Therefore, as previously described, the BZ chemical wave propagated along the C-SOG surface and caused gel fluctuation during the BZ reaction, which can be regarded as functionally similar to the CMFs.

As shown in Fig. 4(d and e), the C-SOGs with a thicker layer exhibited a longer period and a larger amplitude. The increased amount of Ru(bpy)₃ in the gel network can induce a longer oscillation period and a larger volumetric amplitude during the BZ reaction.²⁵ In the C-SOGs, as previously mentioned, it could be considered that the thicker the layer, the more absolute amount of Ru(bpy)₃ the gel contains. The results from Fig. 3(b–d) supported the mentioned speculation, which indicated that the thicker layer brings about a more considerable layer thickness difference between the redox states. Therefore, we can control the TFs by varying the layer thickness.

We assert that the SFs originated from the volumetric deformation of the SOG layer (i.e., TFs) caused by the BZ reaction (Movies S1–S3, ESI†). Suppose a region of the C-SOGs layer swelled by the oxidation of Ru(bpy)₃ during the BZ reaction. Since the corresponding layer could be locally thickened following the swelling, the peripheral area (i.e., the non-swollen layer region) could be stretched, resulting in the local shape-deformation by the BZ reaction. Note that the C-SOGs in this study are millimeter-scaled; therefore, the BZ reaction waves are spreading out randomly. Therefore, the local shape-deformation can simultaneously appear in different locations, resulting in global shape-deformation (i.e., SFs) like a biological cell (e.g., red blood cells). Based on the results, we postulate that the thicker layer could induce large local shape-deformation affecting the global shape changes during the BZ reaction. Similarly, the specific and consistent trend of fluctuation behaviors on the layer thickness (Fig. 4 and 5) implies that layer thickness can determine the behaviors of TFs and SFs during the BZ reaction.

The capsular structure led to the whole system being capable of showing cell-like fluctuation behaviors even on the millimeter scale. For the volumetric swelling/deswelling, the water should be sufficiently diffused in or out of the SOGs to induce the volumetric oscillation following the redox change of Ru(bpy)₃ during the BZ reaction.^25–27 Note that the diffusion of water is relatively slower than the redox change of Ru(bpy)₃, which could cause insufficient diffusion of water throughout the gel network in the millimeter-scaled gels. From a similar perspective, we explain that solid SOGs in Fig. S11 and Movie S4 (ESI†) could not exhibit volumetric fluctuations and oscillations during the BZ reaction. On the other hand, in the C-SOGs, the regions for volumetric oscillation were relatively thinner (the micrometer-scale) than in the solid SOGs. Therefore, in the C-SOGs, the water molecules could move sufficiently before the change of Ru(bpy)₃ redox state and display volumetric oscillation despite the bulk scale of the whole system.

In this study, we have embodied the nonthermally-driven cell-like membrane and shape fluctuations in the C-SOGs induced by the propagating BZ chemical waves during the BZ reaction. Poly(NIPAAm-co-NAPMAm) layers with various thicknesses were synthesized on the millimeter-sized spherical Alg/Ca core bead, followed by dissolving the core part with sodium citrate. The fabricated C-SOGs, fabricated by Ru(bpy)₃–NHS conjugation, featured layer fluctuation behaviors like CMFs, driven by only the BZ reaction. In addition, the C-SOGs with thicker layer displayed more definite fluctuations with a longer period and a larger amplitude.

Here we discuss the developed C-SOG systems in this study to be an experimental model platform of CMFs. First, from a perspective of materials science, the chemomechanical volumetric oscillation of the SOGs is under a non-equilibrium state.¹⁵ The biological phenomena are also far from the equilibrium state: for instance, the cell membrane fluctuates by receiving energy or nutrients from the exterior. Similarly, the SOGs can volumetrically oscillate by receiving chemical substrates from the surrounding solution. From this viewpoint, we assert that the SOGs are promising materials for realizing non-equilibrium biological functions, including CMFs. In this study, we implemented the cell-like shape deformation phenomenon using the SOGs, which can reduce the gap between the soft materials and the biological cells. Furthermore, we believe that our unique approach with soft materials (particularly gels) gives a definite conceptual advance in the current field of CMF model systems. Specifically, our study features CMF-like fluctuations realized in the gel-based platform, which can be easily observed as well as controlled. Second, from a structural view, the capsule shape in this study offers a structural similarity to cells. The biological cells are enclosed by elastic membranes and filled with protoplasm. The C-SOGs were also composed of the elastic gel capsular layer and filled with liquified alginate.

Here, we debate the SOGs that compose the C-SOG system and induce gel fluctuations in more detail. We firstly consider the mechanism of the SOG system that the volumetrical swelling/deswelling behavior is subordinate to the nonlinear BZ reaction. That is, the nonlinearity of the BZ reaction and the responsiveness of SOGs to the BZ reaction will be major parameters that could ultimately determine the gel fluctuations in this study.³⁰ The former can mean how the BZ reaction changes according to the possible reaction conditions, including the BZ substrate concentration, temperature, and light intensity.³¹ The latter can indicate how the gel network can sensitively follow the BZ reaction kinetics, which can mainly be affected by the properties of the polymer structure.^27,32 We note that manipulating each parameter dominates the volumetric oscillatory behavior of the SOGs during the BZ reaction. Therefore, it will be reasonable that the introduced parameters can determine the gel fluctuation behavior of C-SOGs. We actually confirmed that the reduced BZ substrate concentration could slow the BZ chemical reaction, ultimately suppressing the gel fluctuation amplitude (Fig. S12 and Movies S5, S6) (see ESI 2.9† for detail). This phenomenon will be discussed later from a different perspective. Furthermore, we also emphasize that the degree of chemomechanical coupling between the parameters can significantly influence gel fluctuation in this study. This perspective can grant various insights to realize desirable fluctuation behavior in the current system toward a more practical experimental platform of CMFs.

From a functional view, we address additional important aspects of our experimental model in this study. Similar to the volumetric deformation noise of SFs (related to the widely distributed amplitude) (Fig. 5(b and c)), the fluctuation noise can be induced during ATP-dependent nonthermal CMFs.^4,33,34 We postulate that the degree of noise could affect the deformation mode during fluctuation in a cell as well as our gel system. Here we discuss the fluctuation noise in the C-SOG system from two perspectives; the possible origins and strategies for manipulating the noise. One possible reason is a non-homogeneity of the gel microstructure highly influenced by a gelation process. The current gelation would bring out microscopically nonhomogeneous structures such as dangling chains, loops, and trapped entanglement.^35,36 In the SOG system, the nonhomogeneous gel network can lead the BZ substrate to diffuse differently according to the gel regions. Therefore the rate of the BZ reaction could be varied with the gel regions, which could affect the volumetric oscillation behavior as well as the BZ chemical wave. Moreover, the structurally nonideal network can also induce a discriminated volume deformation ratio (i.e., amplitude). Another possible reason could be from the structural property (i.e., capsule design). As previously described, the regional layer deformation by the BZ chemical wave could affect the local deformation in another region. For example, a local swelling of a certain region might cause stress which could partially prevent the deformation of the adjacent layer because layer-swelling can pull the peripherical section. This could affect the fluctuation behavior of the gel shape, inducing noise in the profiles of the shape descriptors. We note that every mentioned parameter could ultimately contribute to the volumetric deformation noise during SFs. We assert that securing strategies for both increasing and decreasing the noise of SFs could benefit our study as an experimental model for CMFs. For that purpose, here we consider manipulating the homogeneity of the gel microstructure. This is because the cell membrane is naturally inhomogeneous, and that degree of inhomogeneity can affect CMFs.³⁷ One possible strategy is to realize a more homogeneous gel network, which could be achieved by decreasing the gelation temperature or adopting technologies for ideal polymer networks like tetra-polyethylene glycol (Tetra-Peg) prepolymers.³⁸ The other is to intentionally realize a relatively non-homogenous gel network, which might mimic the effect of cell membrane nonhomogeneity on CMFs. Upregulating the gelation temperature and downregulating the concentration of the crosslinker could help to control the homogeneity of the gel layer. The additional option is to locally control the amount of conjugated Ru(bpy)₃ in the C-SOGs, which can critically impact the propagating behavior of the BZ chemical wave.^28,31,39 In every case, we strongly believe that the C-SOG system in this study has definite potential as an experimental model for CMFs.

Our system design of the C-SOGs can reflect the separation of thermal and nonthermal active contributions to CMFs. Several studies have been proposed to understand the influence of the active contribution during CMFs.^{2,4,7–12,40,41} However, the superposition of those contributions during CMFs is still the primary difficulty in building active parameter-driven models, as the strength and effect of the thermal and active energies are similar on the small nanometer or micrometer-scales.^42,43 In this study, the thermal fluctuation can be neglected because of the enlarged millimeter-scale and increased amplitude, compared to CMFs as well as previous results from the references. Moreover, the C-SOGs without the BZ reaction did not exhibit gel fluctuations, implying that the effect of thermal contributions was not reflected in our model (Fig. 5(b1, b2 and c1, c2).

Our model also exhibited BZ reaction substrate-dependent fluctuations, which can mimic the feature of the nonthermal active contribution (Fig. S12, Movies S5 and S6) (see ESI 2.9† for the detailed description). The depletion of ATP leads to decreased CMFs.⁷ Similarly, the volumetric oscillation caused by the BZ reaction relies on the concentration of the substrates, including the oxidants (e.g., sodium bromate) or the reductants (e.g., MA).^44,45 In C-SOGs (0.027) as a representative sample, the diminished substrate amounts brought about relatively unapparent fluctuation behavior during the BZ reaction (Fig. S12 and Movies S5, S6, ESI†), compared to Movie S2 (ESI†). These features in our model system suggest an insightful guideline to build a model for understanding the influence of the nonthermal active contribution on membrane fluctuation more clearly.

Conclusions

In this study, we realized nonthermally operated gel layer and shape fluctuations in millimeter-sized capsule self-oscillating gels caused by the BZ reaction, which can be utilized as a model for cell membrane fluctuations. The millimeter-sized capsular structure with distinguished layer thickness was fabricated by synthesizing a gel layer on the spherical core Alg/Ca bead. Our study features the following two distinguishing factors compared to the previous models. (1) The millimeter scale of the gel system provided a definite division between the thermal and the nonthermal effects on the gel fluctuations. (2) The capsule self-oscillating gels without the BZ reaction did not exhibit the fluctuation behavior, indicating that the nonthermal active factor only drove the gel fluctuations. We also found that the capsule self-oscillating gels with thicker layer exhibit fluctuations with a longer period and a larger amplitude, indicating a strategy to control the fluctuation behavior. Furthermore, the concentration of the chemical substrates for the BZ reaction also affected the gel shape fluctuations, similar to the ATP effect on cell membrane fluctuations. As an experimental platform mimicking cell membrane fluctuations, our study can contribute to seeking the actual effect of the active parameters on cell membrane fluctuations.

The items below could be researched to create a practical cell-like fluctuating gel model close to life. One is to evaluate how the gel layer elasticity affects the fluctuations with an experimental approach as well as theoretical backgrounds. Since the bending and stretching elasticities of the biological membrane are important parameters for cell membrane fluctuations,^7,10 we postulate that layer elasticity can significantly affect the gel fluctuation. We anticipate that the amount of crosslinker is also a primary factor for the layer elastic properties. Our following study will report the relationship between elastic properties and gel fluctuations. Another is establishing the acid-free operating conditions for the volumetric self-oscillation behavior. From a biomimetic sense, realizing volumetric oscillation without externally adding acid would be a definite advancement from the current system. Finally, a third topic could be controlling the propagation of the BZ chemical wave, which could be realized by introducing a Ru(bpy)₃ concentration gradient to the C-SOGs. The propagating BZ chemical wave with a fixed direction might provide controlled layer/shape fluctuating behavior during the BZ reaction. The regulated layer/shape fluctuations could offer a more convenient platform to check the cause-and-effect relationship of the active contribution. Through the suggested efforts, we believe that a meaningful clue sharing the same principle with life may reveal its appearance from our model.

Author contributions

W. S. Lee contributed to designing the system, collecting the data, performing the analysis, and writing the paper. T. Enomoto, A. M. Akimoto, and R. Yoshida contributed to analyzing and organizing the data. All authors contributed to conceiving and designing the analysis.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported in part by the Grants-in-Aid for Science Research (No. 20H00388 to R.Y.) from the Ministry of Education, Culture, Sports, Science, and Technology of Japan. We would like to thank Ms Su-wen Lee for the English language editing.

References

1. A. Y. Chang and W. F. Marshall, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 21556–21562.
2. L. C. L. Lin and F. L. H. Brown, Biophys. J., 2004, 86, 764–780.
3. K. Keren, Eur. Biophys. J., 2011, 40, 1013–1027.
4. A. Biswas, A. Alex and B. Sinha, Biophys. J., 2017, 113, 1768–1781.
5. E. A. Evans and V. A. Parsegian, Proc. Natl. Acad. Sci. U. S. A., 1986, 83, 7132–7136.
6. Y. K. Park, C. A. Best, T. Auth, N. S. Gov, S. A. Safran, G. Popescu, S. Suresh and M. S. Feld, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 1289–1294.
7. H. Turlier, D. A. Fedosov, B. Audoly, T. Auth, N. S. Gov, C. Sykes, J. F. Joanny, G. Gompper and T. Betz, Nat. Phys., 2016, 12, 513–519.
8. N. Gov, Phys. Rev. Lett., 2004, 93, 268104.
9. P. Girard, J. Prost and P. Bassereau, Phys. Rev. Lett., 2005, 94, 088102.
10. L. C. L. Lin, N. Gov and F. L. H. Brown, J. Chem. Phys., 2006, 124, 074903.
11. V. G. Almendro-Vedia, P. Natale, M. Mell, S. Bonneau, F. Monroy, F. Joubert and I. López-Montero, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 11291–11296.
12. S. C. Takatori and A. Sahu, Phys. Rev. Lett., 2020, 124, 158102.
13. H. R. Vutukuri, M. Hoore, C. Abaurrea-Velasco, L. van Buren, A. Dutto, T. Auth, D. A. Fedosov, G. Gompper and J. Vermant, Nature, 2020, 586, 52–56.
14. R. Yoshida, T. Takahashi, T. Yamaguchi and H. Ichijo, J. Am. Chem. Soc., 1996, 118, 5134–5135.
15. R. Yoshida, Polym. J., 2022, 54, 827–849.
16. R. Yoshida, M. Tanaka, S. Onodera, T. Yamaguchi and E. Kokufuta, J. Phys. Chem. A, 2000, 104, 7549–7555.
17. F. Ritort, Adv. Chem. Phys., 2007, 31–123.
18. J. D. Norton, Am. J. Phys., 2017, 85, 135–145.
19. P. Bieling, T.-D. Li, J. Weichsel, R. McGorty, P. Jreij, B. Huang, D. A. Fletcher and R. D. Mullins, Cell, 2016, 164, 115–127.
20. C. Zarket and S. R. Raghavan, Nat. Commun., 2017, 8, 193.
21. S. H. Ching, N. Bansal and B. Bhandari, Crit. Rev. Food Sci. Nutr., 2017, 57, 1133–1152.
22. A. Kikuchi, M. Kawabuchi, A. Watanabe, M. Sugihara, Y. Sakurai and T. Okano, J. Controlled Release, 1999, 58, 21–28.
23. A. L. Navarro-Verdugo, F. M. Goycoolea, G. Romero-Meléndez, I. Higuera-Ciapara and W. Argüelles-Monal, Soft Matter, 2011, 7, 5847–5853.
24. Y. S. Kim, M. Liu, Y. Ishida, Y. Ebina, M. Osada, T. Sasaki, T. Hikima, M. Takata and T. Aida, Nat. Mater., 2015, 14, 1002–1007.
25. T. Masuda, A. Terasaki, A. M. Akimoto, K. Nagase, T. Okano and R. Yoshida, RSC Adv., 2015, 5, 5781–5787.
26. R. Mitsunaga, K. Okeyoshi and R. Yoshida, Chem. Commun., 2013, 49, 4935–4937.
27. W. S. Lee, T. Enomoto, A. M. Akimoto and R. Yoshida, NPG Asia Mater., 2022, 14, 12.
28. W. S. Lee, T. Enomoto, A. M. Akimoto and R. Yoshida, J. Mater. Chem. B, 2022, 10, 9887–9895.
29. I. Levin, R. Deegan and E. Sharon, Phys. Rev. Lett., 2020, 125, 178001.
30. V. V. Yashin and A. C. Balazs, Science, 2006, 314, 798–801.
31. L. Ren, L. Yuan, Q. Gao, R. Teng, J. Wang and I. R. Epstein, Sci. Adv., 2020, 6, eaaz9125.
32. J. Wang, L. Ren, Z. Yu, R. Teng, C. Pan, L. Yuan, I. R. Epstein and Q. Gao, J. Phys. Chem. B, 2022, 126, 1108–1114.
33. M. Guo, A. J. Ehrlicher, M. H. Jensen, M. Renz, J. R. Moore, R. D. Goldman, J. Lippincott-Schwartz, F. C. Mackintosh and D. A. Weitz, Cell, 2014, 158, 822–832.
34. N. Fakhri, A. D. Wessel, C. Willms, M. Pasquali, D. R. Klopfenstein, F. C. MacKintosh and C. F. Schmidt, Science, 2014, 344, 1031–1035.
35. X. Li, S. Nakagawa, Y. Tsuji, N. Watanabe and M. Shibayama, Sci. Adv., 2019, 5, eaax8647.
36. Y. Jochi, T. Seki, T. Soejima, K. Satoh, M. Kamigaito and Y. Takeoka, NPG Asia Mater., 2018, 10, 840–848.
37. C. Monzel and K. Sengupta, J. Phys. D: Appl. Phys., 2016, 49, 243002.
38. T. Sakai, T. Matsunaga, Y. Yamamoto, C. Ito, R. Yoshida, S. Suzuki, N. Sasaki, M. Shibayama and U.-i. Chung, Macromolecules, 2008, 41, 5379–5384.
39. L. Ren, M. Wang, C. Pan, Q. Gao, Y. Liu and I. R. Epstein, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 8704–8709.
40. E. Reister-Gottfried, S. M. Leitenberger and U. Seifert, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 031903.
41. F. Quemeneur, J. K. Sigurdsson, M. Renner, P. J. Atzberger, P. Bassereau and D. Lacoste, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 5083–5087.
42. S. Toyabe and M. Sano, J. Phys. Soc. Jpn., 2015, 84, 102001.
43. R. Phillips and S. R. Quake, Phys. Today, 2006, 59, 38–43.
44. D. Suzuki and R. Yoshida, J. Phys. Chem. B, 2008, 112, 12618–12624.
45. R. Yoshida, K. Takei and T. Yamaguchi, Macromolecules, 2003, 36, 1759–1761.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2mh01490d

---