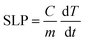The magnetopyroelectric effect: heat-mediated magnetoelectricity in magnetic nanoparticle-ferroelectric polymer composites

Abstract

Magnetoelectricity enables a solid-state material to generate electricity under magnetic fields. Most magnetoelectric composites are developed through a strain-mediated route by coupling piezoelectric and magnetostrictive phases. However, the limited availability of high-performance magnetostrictive components has become a constraint for the development of novel magnetoelectric materials. Here, we demonstrate that nanostructured composites of magnetic and pyroelectric materials can generate electrical output, a phenomenon we refer to as the magnetopyroelectric (MPE) effect, which is analogous to the magnetoelectric effect in strain-mediated composite multiferroics. Our composite consists of magnetic iron oxide nanoparticles (IONPs) dispersed in a ferroelectric (and also pyroelectric) poly(vinylidene fluoride–trifluoroethylene) (P(VDF–TrFE)) matrix. Under a high-frequency low-magnitude alternating magnetic field, the IONPs generate heat through hysteresis loss, which stimulates the depolarization process of the pyroelectric polymer. This magnetopyroelectric approach creates a new opportunity to develop magnetoelectric materials for a wide range of applications.

---

New concepts

This work demonstrates a heat-mediated magnetoelectric effect. Being different from the strain-mediated magnetoelectric effect, in which the deformation of the magnetostrictive material under a magnetic field strains the piezoelectric material, heat-mediated magnetoelectricity relies on the cross-talk between a material that is capable to generate heat under magnetic fields (e.g., magnetic hyperthermia effect) and a pyroelectric material. This approach expands the scope of the materials capable of transforming magnetic fields into electrical signals, which can open up new avenues to various non-conventional applications of magnetoelectric effects, especially in the biomedical fields.

Introduction

Recent years have seen increasing research efforts to develop magnetoelectric multiferroics. These materials combine two ferroic orderings – ferromagnetism (or antiferromagnetism) and ferroelectricity – which enables magnetoelectrics to generate electricity under magnetic fields.^1–6 This ability makes magnetoelectrics appealing for wide-ranging applications, including sensing, low energy consumption memory devices, wireless communications, energy harvesting, cell sorting, cell and tissue electrostimulation, drug delivery, and catalysis.^7–11 However, magnetoelectricity is a rare property in single-phase materials as ferromagnetism and ferroelectricity are usually exclusive to each other.¹² A primary challenge in developing single-phase magnetoelectric multiferroics is to discover new compounds and to develop synthetic strategies that can be used for their manufacturing. Additionally, magnetoelectricity is usually revealed at very low temperatures, with only a few exceptions at (or close to) room temperature such as BiFeO₃.^13,14 To overcome these limitations, magnetoelectrics can also be engineered by creating strain-mediated multiferroic composites in which a piezoelectric material is intimately coupled with a magnetostrictive material. In these composites, the deformation of the magnetostrictive material under a magnetic field strains the piezoelectric material, resulting in a change of its electrical polarization.¹⁵ This strategy benefits from many more options in terms of available materials and their compositions, enabling a plethora of architectures ranging from 2D layered superlattices and particulate composites to core–shell architectures. Although strain-mediated multiferroic composites have many potential applications, the availability of magnetostrictive materials with high strain and low toxicity is severely limited, which significantly restricts their potential applications, particularly in the field of biology.^16,17

Alternatively, the magnetoelectric effect could be attained via a heat-mediated mechanism by combining materials that can be magnetically heated and pyroelectric materials that change their electrical polarization when exposed to temperature changes. Pyroelectric materials are widely used in various fields, including commercial thermal imaging devices, thermal energy harvesting, and electrochemical processes such as disinfection and pollutant degradation.^18–20 Magnetocalorics are one type of material that can generate heat in the presence of a magnetic field under adiabatic conditions. However, triggering the magnetocaloric effect usually requires large magnetic fields – on the order of 1 to 5 T – and the library of magnetocaloric materials is mainly limited to Gd-based alloys, which are toxic in their non-chelated state.^21–23 In contrast, magnetic nanoparticles, when exposed to an alternating magnetic field, can generate heat through Néel and/or Brown relaxation, which involves the rapid reorientation of their magnetic moments in response to the magnetic field. One of the main advantages of using magnetic nanoparticles for heating is the vast availability of materials and shapes, along with the ability to use low-magnitude magnetic fields.^24,25 For example, FDA-approved iron oxide nanoparticles have been extensively used in magnetic hyperthermia to selectively kill cancerous cells, thermally trigger the release of a drug or as a contrast agent for magnetic resonance imaging.^26–29

The heat-mediated magnetoelectric approach opens up new possibilities for magnetoelectricity from magnetic nanoparticles and pyroelectric materials. This approach enables the combination of materials that could help overcome the limitations of strain-mediated magnetoelectricity and potentially unlock new bio-related applications that were previously not feasible due to the toxicity of strain-mediated magnetoelectric materials.²⁹

Here we show that pyroelectric polymer composites containing magnetic iron oxide nanoparticles (IONPs) can generate electrical currents under alternating magnetic fields (Fig. 1). We refer to this phenomenon as the magnetopyroelectric (MPE) effect, which is analogous to the magnetoelectric effect in composite multiferroics with a coupling mechanism based on heat instead of strain. We evaluate the impact of the alternating magnetic field pulse period on the MPE response, assess the effect of the concentration of IONPs in the film, and characterize the composite as a current source. A simulation is provided to corroborate the experimental results. The magnetopyroelectric effect opens new opportunities for the use of pyroelectrics in biomedicine, catalysis, and robotics, in which heat and electricity could play a synergistic role.

Fig. 1 The magnetopyroelectric effect is the combination of magnetic particle heating and pyroelectricity. An alternating magnetic field induces magnetic hysteresis and heats the magnetic nanoparticles causing a reversible depolarization of the pyroelectric material.

Results and discussion

The IONPs implemented in the composite films are fabricated via the thermal decomposition of iron oleate in eicosane. Transmission electron microscopy (TEM) images (Fig. 2a and Fig. S1, ESI†) show that the as-prepared particles are spherical with a diameter of 21.8 ± 1.8 nm (x̄ ± SD, n = 50) and high uniformity. X-ray powder diffraction of the IONPs (Fig. S5, ESI†) matches the peak pattern of magnetite and maghemite (PDF: 01-084-2782, 00-039-1346), and of hematite (PDF: 01-072-6229). Mössbauer spectra shows that 77 at% of Fe atoms are in a Fe³⁺ site, 22 at% are in a Fe^2.5+ site and 1 at% of Fe atoms in a wüstite-type site. The ratio between Fe³⁺ and Fe^2.5+ doesn’t match the typical occupancy of tetrahedral and octahedral iron sites in bulk magnetite [Fe³⁺]_tet[Fe²⁺,Fe³⁺]_octO₄. This implies a level of oxidation and confirms that describing the samples as Fe_3−xO₄ would be more appropriate, in accordance with the XRD results. The low uniformity in the shape of the hyperfine field distributions indicates the presence of structural defects (Fig. S2, ESI†). Vibrating sample magnetometry (Fig. 2b) shows that the IONPs have a saturation magnetization (M_s) of 52 emu g⁻¹ and a coercive field (μ₀H_c) of 1.5 mT. The observed saturation magnetization values, which are considerably lower than the bulk values of maghemite (∼70 emu g⁻¹) or magnetite (∼90 emu g⁻¹), are consistent with the presence of structural defects typically associated with particles synthesized via the thermal decomposition of iron oleate.^30–32 The heating power per unit of mass of IONPs, also denoted as specific loss power (SLP), is calculated from the heating rate of a dispersion of the IONPs in water (5 mg mL⁻¹) under an alternating magnetic field (500 kHz, 20 mT). The resulting temperature increase of the magnetic fluid is around 2.5 °C in 10 s, which corresponds to an SLP of 273 W g⁻¹ (Fig. 2c). Due to the high sensitivity of SLP to the size, shape, composition, and aggregation state of the particles,²⁴ commonly available IONPs tend to have smaller SLP values <100 W g⁻¹ for magnetic fields of similar frequency and intensity.^33–35 IONPs with much higher SLP values >1000 W g⁻¹ have been obtained by fine-tuning the aforementioned parameters, but their reproducibility is often complicated, because the synthesis methods are highly sensitive and their underlying mechanisms not well understood.^36,37

Fig. 2 Characterization of the composite films. (a) A TEM image (scale bar: 100 nm) of the iron oxide nanoparticles. (b) The magnetic hysteresis loop of the iron oxide nanoparticles. The inset shows the curve from −10 mT to 10 mT. (c) Magnetic heating of the iron oxide nanoparticles: the time-dependent temperature variation under an alternating magnetic field. (d) A typical composite film and (e) an SEM image of its cross section (scale bar: 1 μm). (f) X-ray diffraction patterns of P(VDF–TrFE) and composite films with different treatments. The dashed lines with pink and green color filling show the crystalline and amorphous deconvoluted peaks, correspondingly. (g) Pyroelectric coefficient as a function of temperature of films with different IONPs wt% and poling treatments, obtained by the Sharp-Garn method. For the poled samples, the dashed line represents the SE (n = 3). (h) Pyroelectric coefficient of the poled films with different IONPs wt% at the phase transition temperature. The error bars represent the SE (n = 3).

Composite films are prepared by mixing different amounts of IONPs in the poly(vinylidene fluoride–trifluoroethylene) (P(VDF–TrFE)) polymer, depending on the desired weight percentage (wt%). The obtained films are homogeneous in appearance, flexible, and brown colored (Fig. 2d and Fig. S3, ESI†). Scanning electron microscopy (SEM) was performed to image the cross-section of seven different films, showing that they have an average thickness of 83 ± 9 μm (x̄ ± SD, n = 7). No large IONP aggregates can be observed, indicating a good dispersion of the particles in the polymer mixture (Fig. 2e and Fig. S4, ESI†). X-ray diffraction in θ–2θ mode was used to assess the effect of annealing, poling, and the loading content of IONPs on the crystallinity order of the P(VDF–TrFE) (Fig. 2f and Fig. S5, ESI†). The peaks at 22.7° and 23.7° are background signals caused by the sample holder. The peak at 19.9° is assigned to the diffraction of (200) and (110) crystalline planes in the ferroelectric β-phase, and the shoulder at lower angles is associated with the amorphous phase.^38–42 For quantitative analysis, the crystalline and non-crystalline regions are deconvoluted using Voigt distribution functions. The degree of crystallinity, X_c, is calculated as the ratio of crystalline area to the sum of crystalline and non-crystalline areas under the fitted peaks. Annealing of a pure P(VDF–TrFE) film increases X_c from 0.27 to 0.64. The remaining samples, poled or with IONPs, have similar X_c (0.50–0.63) compared with the annealed P(VDF–TrFE). The peaks of the annealed samples show a slight shift towards lower angles related to an increase in interchain spacing, possibly caused by gauche defects introduced during the paraelectric to ferroelectric transition after cooling from annealing.⁴³ Conversely, the peaks of the poled samples show a slight shift towards higher angles, indicating that the strong electric field promotes tighter packing of the polymer chains within the crystals.⁴⁰

The pyroelectric coefficient quantifies the coupling between temperature and the spontaneous polarization of a certain material and is defined as 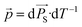. To characterize the pyroelectric coefficient of a material, the change in spontaneous polarization is usually measured indirectly through voltage or current signals. For example, in the Sharp-Garn method, the current generated by the sample is monitored while its temperature is oscillated according to T(t) = T_amp sin(ωt) + at + b, where T_amp, t, ω, a, and b are temperature amplitude, time, angular frequency of oscillation, slope, and offset.⁴⁴ The pyroelectric coefficient is then calculated as

where I_Amp, ϕ, A, and T_Amp are current amplitude, phase offset between current and temperature and electrode area. While the setup for this method is relatively simple, it allows for accurate and continuous characterization of the pyroelectric coefficients as a function of temperature, and it suppresses non-pyroelectric contributions caused by strain-activated piezoelectric and flexoelectric currents.^44–46

Using the Sharp-Garn method, the pyroelectric coefficient of nine films with different IONPs concentrations, including non-poled and de-poled pure P(VDF–TrFE) films, is measured between 25 °C and 125 °C (Fig. 2g). Poled films with 0, 0.3, 1.3, 2.6, 3.9, 5.1, and 11.9 wt% IONPs display pyroelectric coefficients that start at −20 μC K⁻¹ m⁻² for 25 °C and reach a minimum of −90 μC K⁻¹ m⁻² at 100 °C. Beyond this minimum, which indicates the approximate phase transition temperature of P(VDF–TrFE) from ferroelectric to paraelectric state,⁴³ the pyroelectric coefficient tends to zero as the films lose their spontaneous polarization, reaching 0 μC K⁻¹ m⁻² at 120 °C. Non-poled films and films that were subject to a complete temperature ramp (de-poled films) show negligible pyroelectric coefficients independent of the temperature, i.e., p(T) = 0. The difference between the pyroelectric coefficients of the poled films at the phase transition temperature is statistically insignificant (ANOVA, α = 0.001) regardless of the concentration of IONPs in the films (Fig. 2h).

To prove that the described composite films of IONPs and P(VDF–TrFE) display magnetopyroelectric coupling, the temperature changes induced by a pulsed alternating magnetic field are correlated to the induced pyroelectric current between the electrodes of the films (closed-circuit). Briefly, the experimental setup consists of a magnetic coil to generate the alternating magnetic field, a thermal camera to monitor the temperature of the films, and an electrometer to measure the generated currents. The films are framed by the edges and placed in the center of the coil with the electrodes parallel to the magnetic field to minimize eddy currents (Fig. S6, ESI†). Upon the application of the pulsed alternating magnetic field, the films should be heated by the hysteretic losses of the IONPs and cooled by natural convection of air, with their temperature saturating once thermal equilibrium is reached. Because of the pyroelectric property of the films, these temperature changes should then induce an electrical current proportional to the temperature change rate (Fig. 1).

Magnetopyroelectric coupling is demonstrated with three simple experiments in which the temperature and the current of a film is measured under a pulsed alternating magnetic field. In the first experiment, a non-poled (p = 0) composite film (11.9 wt% IONPs) is measured as a control. As expected, the temperature of the film increases sharply, accomplishing a maximum temperature increase (ΔT) of 45 °C in 50 s of alternating magnetic field. However, no pyroelectric current is detected (Fig. 3a). In the second control experiment, a poled (p ≠ 0) film of pure P(VDF–TrFE) is measured under the same conditions. In this case, the temperature of the film rises only by 10 °C, a small value caused by induction heating in the electrodes. The corresponding measured current is small but indicates a pyroelectric response from the poled P(VDF–TrFE) (Fig. 3b). In the last experiment, conducted under the same conditions, a poled (p ≠ 0) composite film (11.9 wt% IONPs) is measured. Here, the high temperature change rate provided by the IONPs, combined with the pyroelectricity given by the poled P(VDF–TrFE), results in significantly larger current peaks than those in the previous two control experiments (Fig. 3c). These results imply the presence of magnetopyroelectric coupling in the composite, i.e., the alternating magnetic field induces a pyroelectric current through magnetic heating of the IONPs. To ensure that the electrical signal originates from the film, the measurements were carried with both forward and flipped film orientations (Fig. 3c and d). After the film is flipped, the measured current is switched in sign, corroborating that the magnetopyroelectric signal originates in the film. The pyroelectric coefficient of the film (11.9 wt% IONPs, T = 100 s) is calculated from its magnetopyroelectric response according to

where I_p, A and dT/dt denote the pyroelectric current, the area of the measuring electrodes and the temperature change rate, which is obtained by fitting the heating or cooling temperature curves to a two-phase exponential (R² > 0.9995, SE < 0.16, Table S2, ESI†) and calculating the corresponding derivatives.

Fig. 3 Proof of magnetopyroelectric coupling. Upon the application of a pulsed alternating magnetic field (μ₀H = 20 mT, f = 500 kHz, T_pulse = 100 s), the temperature and the current are measured for (a) a non-poled P(VDF–TrFE) film with IONPs, (b) a poled P(VDF–TrFE) film and (c) a poled P(VDF–TrFE) film with IONPs in forward and (d) reversed orientation.

The obtained pyroelectric coefficients are in good agreement with the coefficients calculated using the Sharp-Garn method, further indicating that the measured currents are of pyroelectric origin (Fig. 4). The increasing error in the coefficients calculated from the heating step at high temperatures and from the cooling step at low temperatures originates from the small signal-to-noise ratio of the measured current as the films reach thermal equilibrium and from the presence of eddy currents during the heating step.

Fig. 4 Comparison of the pyroelectric coefficients from the MPE measurements and from Sharp-Garn measurements. Pyroelectric coefficients are calculated from the heating and cooling steps of the MPE data (Fig. 3c and d) according to eqn (2) and compared to pyroelectric coefficient obtained from the Sharp-Garn method. The dashed line indicates the SE.

The temperature and the current delivered by a magnetopyroelectric film (11.9 wt% IONPs) is measured and simulated for several pulse periods of the alternating magnetic field (Fig. 5a and Fig. S7, ESI†). The Supporting Information provides a detailed explanation of the model used for the simulation, which relies on basic heat transfer principles and pyroelectricity. Additionally, the model's parameters are also described, and its implementation is done using Python (Appendix S1, ESI†).

Fig. 5 Characterization of magnetopyroelectricity. (a) Magnetopyroelectric response of a composite film (11.9 wt% IONPs) measured for different pulse periods and the corresponding simulations (Appendix S1, ESI†). (b) Temperature and (c) current for composite films with different loading content of IONPs. (d) Maximum attained temperature change rate and current as a function of the loading content of IONPs in the film. The line is a guide to the eye. (e) Current and (f) voltage delivered by a film (11.9 wt% IONPs) connected to different resistor loads. (g) Positive quadrant of the I–V plot of a film (11.9 wt% IONPs). The dashed line is a guide to the eye.

Note that to obtain a good match between measured and simulated results, the simulated heating power of the IONPs in the films is set to 14% of that expected from the IONPs in water (SLP [W g⁻¹]·IONPs [g]).⁴⁷ This correction factor accounts for the decrease in heating power of the IONPs in the composite, possibly caused by their immobilized state and the corresponding suppression of Brownian relaxation. The remaining parameters of the model were either taken from the literature⁴⁸ or measured experimentally (Appendix S1, Fig. S9, ESI†). The measured and simulated results show that the minimum and maximum attained temperatures within each cycle become closer to the average temperature as the pulse period is shortened. This leads to smaller changes in the temperature dependent pyroelectric coefficient between heating and cooling steps and therefore more continuous and symmetric current peaks. A current offset, clearly visible for short pulse periods, is caused by the difference between the heating and cooling rates as the average temperature of the film approaches thermal equilibrium. At thermal equilibrium, this offset tends to zero and the current peaks become centered around 0 nA. Although the temperature variations within each cycle become undetectable for short pulse periods (<2.5 s), the simulations and the measured currents indicate that the heating and cooling rates remain undiminished for pulse periods down to 0.5 s.

The temperature and current of films with 0, 2.6, 5.1, and 11.9 wt% IONPs are measured under pulses of alternating magnetic field (T_pulse = 25 s) to characterize the effect of particle concentration on the magnetopyroelectric effect. Films with increased content of IONPs yield larger temperature change rates (Fig. 5b) and currents (Fig. 5c), both following a linear dependence with IONPs wt% (Fig. 3d). Again, the proportionality constant between maximum temperature change rate and current at room temperature is found to be 33.8 ± 5.2 μCK⁻¹m⁻² (n = 4), matching the previously reported pyroelectric coefficients of P(VDF–TrFE).^39,40,45,49

Pyroelectric materials act as current sources upon heating or cooling. The behavior of a magnetopyroelectric film (11.9 IONPs wt%) is assessed by measuring the current or voltage in a closed circuit consisting of the film and a resistor of 0.01, 0.1, 1, or 10 MOhm (Fig. S8, ESI†). In this range, the current delivered by the film is independent of the value of the resistor, peaking at −25 nA during heating and −50 nA during cooling. In accordance with Ohm's law V = IR, the voltage is proportional to the resistance, reaching 250 mV and −500 mV, correspondingly (Fig. 5e and f). In a more general approach, the current delivered by the film is plotted as a function of the voltage load given by a wide range of resistor values (0–300 MOhm). For the given experimental conditions, this MPE film can supply a maximum average power output of ∼ 120 nW, which corresponds to a current of 20 nA at a voltage load of 6 V (Fig. 5g). However, the maximum output power is expected to increase if the properties of the applied magnetic field (e.g., frequency, intensity or pulse period) and the fabrication procedure of the films (e.g., electrode quality, poling voltage) are optimized.

The coupling between magnetic heating of IONPs and pyroelectricity, which we call magnetopyroelectricity, has been demonstrated. First, the magnetic heating capability of IONPs fabricated via the thermal decomposition of iron oleate was quantified by performing SLP measurements, yielding a heating power of 273 W g⁻¹. Then, the pyroelectric performance of pure poled P(VDF–TrFE) was established to be − 20 μCK⁻¹m⁻² at room temperature via the Sharp-Garn method, matching values reported in literature.^{38,39,45,49,50} The functionality of each material was conserved after being integrated into a composite film. IONPs induced a temperature increase in the films of up to 45 °C in 50 s under an alternating magnetic field. The films remained pyroelectric, and their coefficient was unaltered by the concentration of IONPs. Both effects, magnetic heating and pyroelectricity, become coupled via heat in the composite films. As a result, we show that pyroelectric currents are triggered upon the application of alternating magnetic fields. The magnetopyroelectric coupling, here demonstrated with IONPs and P(VDF–TrFE), is cost-effective, up-scalable, and versatile since the polymer composite can be easily processed and shaped as desired. This magnetopyroelectric approach opens a new avenue to develop magnetoelectric materials for a wide range of applications.

Experimental

Synthesis of magnetic nanoparticles

Magnetic iron oxide nanoparticles were synthesized by thermal decomposition of iron oleate following an adapted protocol.^51,52 To produce the iron oleate, FeCl₃·6H₂O (Sigma-Aldrich CAS: 10025-77-1) (2.162 g, 8 mmol) and sodium oleate (abcr CAS: 143-19-1) (7.309 g, 24 mmol) were dissolved in a mixture of deionized water (12 mL), ethanol (Thommen-Furler AG CAS: 64-17-5) (16 mL) and hexane (Sigma-Aldrich CAS: 110-54-3) (28 mL) and were refluxed at 70 °C for 4 hours with stirring. The resulting iron oleate was thoroughly washed with water and aged for 6 days in an open glass bottle, under atmospheric conditions, with stirring at 700 rpm. Once aged, 7.43 mmol of iron oleate was mixed with sodium oleate, oleic acid (Sigma-Aldric 112-80-1) and eicosane (Sigma-Aldrich CAS: 112-95-8) in a 100 mL three-neck round-bottom flask maintaining a molar ratio of 1 : 0.5 : 0.825 : 17.7 (iron oleate : sodium oleate : oleic acid : eicosane). The flask openings were sealed, and the mixture was homogenized at 50 °C and 700 rpm overnight. Then, while stirring at 50 °C, N₂ atmosphere was introduced in the flask. After this, the thermal decomposition process was started: the mixture was heated from 50 °C to 345 °C at 3 °C min⁻¹, then it was kept at 345 °C for 30 min and finally it was removed from the heating mantle and allowed to cool to 25 °C. To improve the magnetic properties of the obtained particles, the resulting mixture was annealed in air at 150 °C for 2 hours (ramping time included) while stirring at 700 rpm. To remove the remaining organic substances, the particles were washed with 10 : 1 acetone:hexane and with 3 : 1 methanol:chloroform several times. The phase transfer from apolar (hexane, chlorophorm, etc.) to polar solvents (water, DMF) was carried by substituting the oleic acid on the surface of the particles for 3, 4-dihydroxyhydrocinnamic acid (DHCA) following a well-established ligand exchange protocol.⁵³ Briefly, hydrophobic particles (100 mg) were transferred into THF (Sigma-Aldrich CAS: 109-99-9) (5 mL) in a flask, and DHCA (Sigma-Aldrich CAS: 1078-61-1) (250 mg) was dissolved in THF (30 mL) in a different flask. Inert atmosphere (N₂) was introduced to both mixtures through several short cycles of vacuum and N₂. Then, the dispersion of particles was added dropwise to the solution of DHCA, previously heated to 50 °C. The mixture was left stirring thoroughly at 50 °C for 3–5 hours and then allowed to cool slowly. Particles from the resulting dispersion were precipitated with NaOH (Sigma-Aldrich CAS: 1310-73-2) (0.5–1 mL, 0.5 M) and subsequently washed with water until the pH was restored to 7. The particles were stored in water (typically no longer than two weeks).

Fabrication of pyroelectric films

Pyroelectric films were obtained by the annealing and poling of drop-casted P(VDF–TrFE). First, it was established that given the density (1.9 g cm⁻³) and size of the substrate (glass slide, 26 × 76 mm), 0.37 g of P(VDF–TrFE) were needed to obtain ∼ 100 μm films. Then, P(VDF–TrFE) (70/30) (Piezotech FC30) (0.37 g) was dissolved in dimethylformamide (DMF) (Sigma-Aldrich, CAS: 68-12-2) at a concentration of 10 wt%. The viscous mixture was poured on the substrate and dried in a ventilated oven at 60 °C for > 3 hours. The obtained films were annealed overnight at 120 °C. Then the films were peeled off from the glass substrate and cut into pieces (13 × 38 mm). An electrode (8 × 30 mm) was painted at the centre of each film with silver paint (PELCO Colloidal Silver 16034). Finally, the films were poled for 30 min at 120 °C under a corona electric field (13 kV, needle-film distance 2 cm), in which the painted electrode was grounded while the exposed side of the film was facing the biased needle. To ensure the film remained poled, the electric field was kept on as the films were cooled to room temperature. Pyroelectric films integrating magnetic nanoparticles were prepared following the same procedure, but the P(VDF–TrFE) powder was dissolved in a dispersion of DMF with the corresponding weight of magnetic nanoparticles. Note that the IONPs, which had been stored in water, were washed thoroughly with DMF before the P(VDF–TrFE) was added. The mixture was homogenized without magnetic stirring to avoid particle aggregation.

Transmission electron microscopy

The transmission electron microscopy (TEM) measurements were carried out on a FEI Talos F200X (Chem S/TEM) at 200 kV equipped with an X-FEG emitter and a CETA camera (16 M pixel CMOS Camera). The synthesized nanoparticles were diluted in hexane and dropped on a carbon-coated 400 mesh TEM grid. The grid was dried under air.

Scanning electron microscopy

The scanning electron microscopy (SEM) measurements were performed on a Zeiss ULTRA 55 at 5 kV equipped with a FEG emitter and an Inlens SE detector. The films were fractured in liquid nitrogen to avoid shear deformation on the edges, allowing us to image their true thickness.

X-ray diffraction

X-ray diffraction (XRD) measurements were performed on an Empyrean diffractometer with a copper X-ray source (λ = 1.5406 Å) and a PIXcel detector (Malvern Panalytical). The measured magnetic particles were phase transferred into water and freeze-dried. Films were measured without further treatment.

Vibrating sample magnetometry

Magnetic characteristics were evaluated using a vibrating sample magnetometer (VSM) (MicroSense). To prepare the sample, the powder of magnetic particles used for the X-ray diffraction measurement was weighed and then mixed in melted eicosane, which provided a solid pellet with the magnetic particles fixed in it at room temperature.

Transmission mössbauer spectroscopy

The Transmission Mössbauer Spectra (TMS) were obtained in transmission mode at room temperature and pressure using a conventional spectrometer with constant acceleration with a 25 mCi 57Co radioactive source in a Rh matrix. The spectra were recorded in a standard multichannel analyzer using a velocity range of ±12.2 mm s⁻¹, and were subsequently fitted with the NORMOS software. The samples were fitted using one or serveral distribution of hyperfine fields and one paramagnetic singlet. The fitted parameters are the isomer shift (δ), always expressed relative to the isomer shift of the bcc-Fe at room temperature, the quadrupole splitting (Δ) and the hyperfine magnetic field (BHF). In all cases the area expressed in % corresponds to the fraction of Fe atoms in a particular environment with respect the total amount of Fe atoms and the magnitudes inside parentheses are the standard deviation.

Specific loss power

In a typical specific loss power (SLP) measurement, a sample of IONPs dispersed in water (5 mg mL⁻¹) was placed in the center of an alternating magnetic field (f = 500 kHz, μ₀H = 20 mT) and its temperature was monitored with an optic temperature sensor (Osensa PRB-G40-01M-STM-MRI). The SLP was then calculated as
where C is the specific heat capacity of the dispersion per unit volume and m is the iron oxide concentration. The temperature change rate was only considered between t = 4 s and t = 10 s to avoid the initial non-linear regime. It is assumed that the system is adiabatic for the given time range and that C ≈ C_water = 4.184 J K⁻¹ mL⁻¹.⁵⁴

Pyroelectric coefficient

Pyroelectricity of the films was assessed using a custom-made setup based on the Sharp-Garn method. Samples consisted of films (13 × 38 mm) to which an electrode (8 × 30 mm) was painted on each side with silver paint. In a typical measurement, the sample was clamped on top of a thermoelectric plate and its electrodes were connected to a Keithley 6517A electrometer. The temperature of the sample, controlled by a PID feedback loop, was varied sinusoidally with an amplitude, frequency, and slope of 1 °C, 0.01 Hz and 7.2 °C h⁻¹, ensuring thermal equilibrium. The temperature and current readings were stored and processed in a Raspberry Pi. The pyroelectric coefficient as a function of the temperature could be calculated as stated in eqn (1).

Magnetopyroelectric characterization

Magnetopyroelectric currents were measured with a custom-made setup. The samples, prepared in the same way as for pyroelectric coefficient measurements, were framed using acryl holders, which left the electrode area exposed to air convection. The electrodes of the sample were contacted with two small pieces of copper foil that protruded from each acryl holder and which were connected to the Keithley 6517A electrometer. The sample was then placed in the center of the induction coil (magneTherm, NanoTherics) and pulses of alternating magnetic fields (f = 500 kHz, μ₀H = 20 mT, f_pulse = 0.01–2 Hz) were applied to the sample to induce heating and allow cooling. The generated pyroelectric current or voltage was measured with the electrometer and the temperature was monitored with an infrared camera (Fluke Ti Infrared Camera). Resistors, when used, were introduced far from the induction coil. Note that the copper foil and wires used to connect the sample to the electrometer were thin and fixed to a position parallel to the applied magnetic field, minimizing electrical noise and induction heating.

I–V plot

The current and voltage output of a film (11.9 wt% IONPs) was measured for load resistor values from 0 to 300 MOhm (smaller resistors were placed in series). The period of the pulsed alternating magnetic field was 2.5 s. For each resistor load, the average (n = 100–120) of the current and the voltage was calculated from the values ranging from 50 to 100 s.

Statistical information

The pyroelectric coefficients obtained via the Sharp-Garn method were measured in triplicate (different films, different days). The error-bars of the I–V plot correspond to the SD (n = 100–120).

Author contributions

JLL contributed to the design, data acquisition, data analysis, data interpretation and drafting of this work; JR contributed to the data acquisition and analysis; LH contributed to the development of the magnetic nanoparticles; AV contributed to the data acquisition; DVA contributed to the data interpretation; PB contributed to the acquisition and interpretation of TMS; XC contributed to the conception, data interpretation, funding acquisition, and supervision; SP contributed to the conception, funding acquisition, and supervision. All the authors contributed to the writing and revision of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

SP acknowledges funding from a Consolidator Grant from the European Research Council (ERC) under the European Union's Horizon 2020 Research and Innovation Programme (Grant Agreement No. 771565) and Swiss National Science Foundation (SNF) (No. 192012). X. C. is partially supported by SNF (No. CRSK-2_190451). JLL acknowledges his PhD grants in the framework of the project BeMAGIC funded by the European Union's Horizon 2020 Research and Innovation Programme under the Marie Skłodowska-Curie grant agreement No. 861145. PB acknowledges support from grant PID2020-112975GB-I00 funded by MCIN/AEI/10.13039/501100011033 and from grant AGAUR 2017-SGR-42 funded by Generalitat de Catalunya. M. V. acknowledges support from ARRS Grant N-0150. J. P.-L. acknowledges support from the European Research Council Starting Grant microCrysFact (ERC-2015-STG No. 677020), the Swiss National Science Foundation (project no. 200021_181988), and grant PID2020-116612RB-C33 funded by MCIN/AEI/10.13039/501100011033.

References

1. M. Fiebig, Revival of the magnetoelectric effect, J. Phys. D: Appl. Phys., 2005, 38, R123–R152.
2. N. A. Spaldin and M. Fiebig, The Renaissance of Magnetoelectric Multiferroics, Science, 2005, 309, 391–392.
3. P. Martins and S. Lanceros-Méndez, Polymer-Based Magnetoelectric Materials, Adv. Funct. Mater., 2013, 23, 3371–3385.
4. X.-Z. Chen, et al., Hybrid Magnetoelectric Nanowires for Nanorobotic Applications: Fabrication, Magnetoelectric Coupling, and Magnetically Assisted In Vitro Targeted Drug Delivery, Adv. Mater., 2017, 29, 1605458.
5. A. Nicolenco, et al., Strain gradient mediated magnetoelectricity in Fe-Ga/P(VDF-TrFE) multiferroic bilayers integrated on silicon, Appl. Mater. Today, 2020, 19, 100579.
6. X.-Z. Chen, et al., Magnetoelectric micromachines with wirelessly controlled navigation and functionality, Mater. Horiz., 2016, 3, 113–118.
7. N. A. Spaldin and R. Ramesh, Advances in magnetoelectric multiferroics, Nat. Mater., 2019, 18, 203–212.
8. M. Bibes and A. Barthélémy, Towards a magnetoelectric memory, Nat. Mater., 2008, 7, 425–426.
9. S. Kopyl, R. Surmenev, M. Surmeneva, Y. Fetisov and A. Kholkin, Magnetoelectric effect: principles and applications in biology and medicine– a review, Mater. Today Bio, 2021, 12, 100149.
10. M. Dong, et al., 3D-Printed Soft Magnetoelectric Microswimmers for Delivery and Differentiation of Neuron-Like Cells, Adv. Funct. Mater., 2020, 30, 1910323.
11. D. Kim, et al., Magnetoelectric Effect in Hydrogen Harvesting: Magnetic Field as a Trigger of Catalytic Reactions, Adv. Mater., 2022, 34, 2110612.
12. N. A. Hill, Why Are There so Few Magnetic Ferroelectrics?, J. Phys. Chem. B, 2000, 104, 6694–6709.
13. J. Wang, et al., Epitaxial BiFeO3 Multiferroic Thin Film Heterostructures, Science, 2003, 299, 1719–1722.
14. S. Picozzi and C. Ederer, First principles studies of multiferroic materials, J. Phys.: Condens. Matter, 2009, 21, 303201.
15. Y. Wang, J. Hu, Y. Lin and C.-W. Nan, Multiferroic magnetoelectric composite nanostructures, NPG Asia Mater., 2010, 2, 61–68.
16. J. Wang and W. Gao, Nano/Microscale Motors: Biomedical Opportunities and Challenges, ACS Nano, 2012, 6, 5745–5751.
17. F. Narita and M. Fox, A Review on Piezoelectric, Magnetostrictive, and Magnetoelectric Materials and Device Technologies for Energy Harvesting Applications, Adv. Eng. Mater., 2018, 20, 1700743.
18. D. Zhang, H. Wu, C. R. Bowen and Y. Yang, Recent Advances in Pyroelectric Materials and Applications, Small, 2021, 17, 2103960.
19. R. W. Whatmore, Pyroelectric devices and materials, Rep. Prog. Phys., 1986, 49, 1335–1386.
20. C. R. Bowen, et al., Pyroelectric materials and devices for energy harvesting applications, Energy Environ. Sci., 2014, 7, 3836–3856.
21. V. Franco, et al., Magnetocaloric effect: From materials research to refrigeration devices, Prog. Mater. Sci., 2018, 93, 112–232.
22. J. Ramalho, M. Ramalho, M. Jay, L. M. Burke and R. C. Semelka, Gadolinium toxicity and treatment, Magn. Reson. Imaging, 2016, 34, 1394–1398.
23. E. Akbas, F. Unal and D. Yuzbasioglu, Cellular toxicities of gadolinium-based contrast agents used in magnetic resonance imaging, J. Appl. Toxicol., 2022, 1–15.
24. J. Carrey, B. Mehdaoui and M. Respaud, Simple models for dynamic hysteresis loop calculations of magnetic single-domain nanoparticles: Application to magnetic hyperthermia optimization, J. Appl. Phys., 2011, 109, 083921.
25. R. Chen, M. G. Christiansen and P. Anikeeva, Maximizing Hysteretic Losses in Magnetic Ferrite Nanoparticles via Model-Driven Synthesis and Materials Optimization, ACS Nano, 2013, 7, 8990–9000.
26. S. Laurent, S. Dutz, U. O. Häfeli and M. Mahmoudi, Magnetic fluid hyperthermia: Focus on superparamagnetic iron oxide nanoparticles, Adv. Colloid Interface Sci., 2011, 166, 8–23.
27. C. A. Quinto, P. Mohindra, S. Tong and G. Bao, Multifunctional superparamagnetic iron oxide nanoparticles for combined chemotherapy and hyperthermia cancer treatment, Nanoscale, 2015, 7, 12728–12736.
28. I. Hilger and W. A. Kaiser, Iron oxide-based nanostructures for MRI and magnetic hyperthermia, Nanomedicine, 2012, 7, 1443–1459.
29. E. Hannachi and Y. Slimani, Advanced Progress in Magnetoelectric Multiferroic Composites: Fundamentals, Applications, and Toxicity, in Handbook of Magnetic Hybrid Nanoalloys and their Nanocomposites, ed. Thomas, S. and Rezazadeh Nochehdehi, A., Springer International Publishing, 2022, pp. 351–385 DOI:10.1007/978-3-030-90948-2_52.
30. D. Cabrera, et al., Unraveling viscosity effects on the hysteresis losses of magnetic nanocubes, Nanoscale, 2017, 9, 5094–5101.
31. A. Lak, S. Disch and P. Bender, Embracing Defects and Disorder in Magnetic Nanoparticles, Adv. Sci., 2021, 8, 2002682.
32. Z. Chen, Size and Shape Controllable Synthesis of Monodisperse Iron Oxide Nanoparticles by Thermal Decomposition of Iron Oleate Complex, Synth. React. Inorg., Met.-Org., Nano-Met. Chem., 2012, 42, 1040–1046.
33. S. Ota, et al., Quantitation method of loss powers using commercial magnetic nanoparticles based on superparamagnetic behavior influenced by anisotropy for hyperthermia, J. Magn. Magn. Mater., 2021, 538, 168313.
34. M. Kallumadil, et al., Suitability of commercial colloids for magnetic hyperthermia, J. Magn. Magn. Mater., 2009, 321, 1509–1513.
35. O. L. Lanier, et al., Evaluation of magnetic nanoparticles for magnetic fluid hyperthermia, Int. J. Hyperthermia, 2019, 36, 686–700.
36. J.-H. Lee, et al., Exchange-coupled magnetic nanoparticles for efficient heat induction, Nat. Nanotechnol., 2011, 6, 418–422.
37. J. Muro-Cruces, et al., Precise Size Control of the Growth of Fe3O4 Nanocubes over a Wide Size Range Using a Rationally Designed One-Pot Synthesis, ACS Nano, 2019, 13, 7716–7728.
38. J. F. Legrand, Structure and ferroelectric properties of P(VDF-TrFE) copolymers, Ferroelectrics, 1989, 91, 303–317.
39. A. Aliane, et al., Impact of crystallization on ferro-, piezo- and pyro-electric characteristics in thin film P(VDF–TrFE), Org. Electron., 2015, 25, 92–98.
40. C. Y. B. Ng, W. C. Gan, T. S. Velayutham, B. T. Goh and R. Hashim, Structural control of the dielectric, pyroelectric and ferroelectric properties of poly(vinylidene fluoride-co-trifluoroethylene) thin films, Phys. Chem. Chem. Phys., 2020, 22(4), 2414–2423.
41. Y. Li, et al., Investigation on in-situ sprayed, annealed and corona poled PVDF-TrFE coatings for guided wave-based structural health monitoring: From crystallization to piezoelectricity, Mater. Des., 2021, 199, 109415.
42. Y. Tajitsu, H. Ogura, A. Chiba and T. Furukawa, Investigation of Switching Characteristics of Vinylidene Fluoride/Trifluoroethylene Copolymers in Relation to Their Structures, Jpn. J. Appl. Phys., 1987, 26, 554–560.
43. R. Gregorio Jr. and M. M. Botta, Effect of crystallization temperature on the phase transitions of P(VDF/TrFE) copolymers, J. Polym. Sci., Part B: Polym. Phys., 1998, 36, 403–414.
44. L. E. Garn and E. J. Sharp, Use of low-frequency sinusoidal temperature waves to separate pyroelectric currents from nonpyroelectric currents. Part I. Theory, J. Appl. Phys., 1982, 53, 8974–8979.
45. S. Jachalke, et al., How to measure the pyroelectric coefficient?, Appl. Phys. Rev., 2017, 4, 021303.
46. I. Lubomirsky and O. Stafsudd, Invited Review Article: Practical guide for pyroelectric measurements, Rev. Sci. Instrum., 2012, 83, 051101.
47. M. Avolio, et al., In-gel study of the effect of magnetic nanoparticles immobilization on their heating efficiency for application in Magnetic Fluid Hyperthermia, J. Magn. Magn. Mater., 2019, 471, 504–512.
48. C. Y. Iguchi, W. N. dos Santos and R. Gregorio, Determination of thermal properties of pyroelectric polymers, copolymers and blends by the laser flash technique, Polym. Test., 2007, 26, 788–792.
49. T. Tansel, Effect of electric field assisted crystallisation of PVDF-TrFE and their functional properties, Sens. Actuators, A, 2021, 332, 113059.
50. Y. Wada and R. Hayakawa, A Model Theory of Piezo- and Pyro-electricity of Poly (vinylidene fluoride) Electret, Ferroelectrics, 1981, 32, 115–118.
51. E. Wetterskog, et al., Precise control over shape and size of iron oxide nanocrystals suitable for assembly into ordered particle arrays, Sci. Technol. Adv. Mater., 2014, 15, 055010.
52. J. Park, et al., Ultra-large-scale syntheses of monodisperse nanocrystals, Nat. Mater., 2004, 3, 891–895.
53. Y. Liu, et al., Facile Surface Functionalization of Hydrophobic Magnetic Nanoparticles, J. Am. Chem. Soc., 2014, 136, 12552–12555.
54. S.-Y. Wang, S. Huang and D.-A. Borca-Tasciuc, Potential Sources of Errors in Measuring and Evaluating the Specific Loss Power of Magnetic Nanoparticles in an Alternating Magnetic Field, IEEE Trans. Magn., 2013, 49, 255–262.

---

Footnote

† Electronic supplementary information (ESI) available: Additional TEM and Mössbauer characterization of IONPs, films with different loading of IONPs, additional SEM and SEM-EDX of the cross section of a film, XRD of films and IONPs, schematic of the measuring setup, effect of magnetic pulse period on MPE, schematic of the electrical circuit integration the MPE film, quadratic fit of the pyroelectric coefficient as a function of temperature, phase decay fitting of the temperature of a film, a simple model to simulate magnetopyroelectricity, calculated heat transfer coefficients. See DOI: https://doi.org/10.1039/d2mh01361d

---