(Si and B)-heterocyclic carbenes and theoretical design of new molecules

Abstract

Using density functional theory (DFT), we theoretically designed fifteen novel and stable (Si and B)-heterocyclic carbenes (SiBHCs). While these SiBHCs are structurally similar to the B-heterocyclic carbenes (BHCs), their carbene character originates from the charge-shift (CS) bond of the inverted C=C bond. To demonstrate the applicability of these novel carbenes, we showed that they can bind with silver complexes to form (SiBHC)AgC≡CH, which are thermodynamically and electronically stable and contain a planar tetracoordinate carbon (ptC). Notably, SiBHCs can go through Diels–Alder reactions with butadiene, and the Diels–Alder reactions are feasible both thermodynamically and kinetically. Based on SiBHCs as C₃ building blocks, we further designed three porous organic molecules (POMs) and one 2D covalent organic framework (COF). The three POMs (D1–D3) are situated at the minima on the potential energy surfaces and contain regular hexagonal channels. The POMs are extended into 2D structures with infinite lattices to produce a COF. The optimized lattice parameters of such a COF (COF-SiBHC-1) using an M06-2X functional under the periodic boundary condition (PBC) indicated that the COF is of hexagonal lattice. Thus, SiBHCs have potential applications in ptCs, organic chemistry and material design owing to their unusual geometrical and electronic structures.

---

Design, System, Application

Carbenes have been playing a significant role in organic chemistry, and considerable efforts have been made to develop new types of carbenes. Inspired by the recent experimental work reported by Li et al. (J. Am. Chem. Soc., 2021, 143, 8244–8248), we designed a family of novel carbenes, (Si and B)-heterocyclic carbenes (SiBHCs), and computationally demonstrated that they are stable and can bind with silver complexes to form stable (SiBHC)AgC≡CH, which contain a planar tetracoordinate carbon (ptC). They can also undergo Diels–Alder reactions with butadiene. Based on these novel carbenes, we further designed three porous organic molecules (POMs) and one 2D covalent organic framework (COF) whose structures and properties were studied computationally as well. We expect that this work is of general interest to the readership of MSDE.

Introduction

Carbene (CH₂) is a highly active intermediate and has played an important role in organic chemistry.^1–10 Recognizable ‘carbene’ research started with the attempts by Dumas et al. to isolate and characterize methylene in 1835.¹¹ Carbene can be divided into Fischer- and Schrock-type carbenes according to its electronic structure. Fischer- and Schrock-type carbenes were successfully synthesized in 1964 and 1974, respectively.^12,13 Remarkably, Arduengo et al. experimentally obtained a stable N-heterocyclic carbene (NHC) in 1991.¹⁴ Since then, NHCs have become a standing interest in experimental and theoretical domains due to their unique electronic structures and extensive applications in the fields of metal–organic chemistry^15–19 and catalysis.^20–24 Interestingly, carbenes can be produced by the isomerization of reactive intermediates C₅H₂ and C₇H₂ with a planar tetracoordinate carbon (ptC).^25,26

Recently, we theoretically designed a new type of carbene, i.e., B-heterocyclic carbene (BHC).²⁷ In contrast to the structures of Fischer- and Schrock-type carbenes, the carbene characteristic of BHCs arises from a charge-shift (CS) bond.^28–31 Moreover, we found that BHCs can act as ligands and Lewis bases to form complexes with ptC.^27,32–36 BHCs can also participate in the Diels–Alder reaction as dienophiles to generate novel [1.1.1]propellanes containing boron atoms.^37,38 Additionally, BHCs were recently used to design porous organic molecules (POMs)³⁹ and stabilize planar tetracoordinate silicon (ptSi).⁴⁰

Inspired by the recent work reported by Li et al., who found that SiH₂ can stabilize C=N bond to produce 1-aza-2,4-disilabicyclo[1,1,0]butanes,⁴¹ we anticipated obtaining a family of novel molecules X₂SiC₂BR given by the substitution of SiX₂ for the CX₂ unit in BHCs. As such, a type of novel carbene, (Si and B)-heterocyclic carbenes (SiBHCs), was anticipated. If the expected SiBHCs are stable, a new kind of molecule with a CS bond can be proposed as well. In addition, these SiBHCs may coordinate to transition metals as ligands, and the resulting complexes should contain ptCs. These new compounds with ptCs surely would enrich the ptC chemistry proposed by Hoffmann in 1970.⁴² The Diels–Alder reactions of SiBHCs with butadiene were also computationally explored. Finally, we rationally designed one kind of novel 2D covalent organic framework (COF) based on SiBHC building blocks. In contrast to COFs reported in the literature,^43–45 such COFs constructed with SiBHC building blocks can serve as ligands to form metal–organic frameworks (MOFs) with ptC compounds.³⁹

Computational methods

Previous studies of BHCs showed that the energies of BHCs are higher than those of their linear isomers, that is, the linear isomer of a BHC is more stable than the BHC itself.³⁵ Thus, in this work both the structures of SiBHCs and their linear isomers were studied using the density functional theory M06-2X functional⁴⁶ in combination with the 6-311G** basis set.⁴⁷ Vibrational frequencies of these molecules were calculated at the same level of theory to confirm the true minima on the potential energy surfaces. Geometry optimizations and frequency calculation of the complexes of SiBHCs coordinated to AgC≡CH were performed with the M06-2X functional and the SDD basis set⁴⁸ for Ag and the 6-311G** basis set for the rest atoms. Diels–Alder reactions of SiBHCs with butadiene were investigated at the same M06-2X/6-311G** level. To design a 2D COF based on SiBHC building blocks, we constructed three POMs. When these POM structures were extended into 2D structures with infinite lattices, a COF constructed from SiBHC building blocks was obtained. Both structural optimizations and frequency calculations of these POMs were performed. The COF was optimized under the periodic boundary conditions (PBCs). The Wiberg bond indices (WBIs) of the most stable SiBHCs and the products of the Diels–Alder reactions of SiBHCs with butadiene were derived via the natural bond orbital (NBO) analysis.⁴⁹ Nucleus-independent chemical shifts NICS(0) and NICS(1) at the centers of the three-membered rings formed from two C atoms and one B atom of SiBHCs were calculated using the gauge-independent atomic orbital (GIAO) method.⁵⁰ All the above calculations were performed with the Gaussian09 program.⁵¹ The AIM2000 program^52,53 was used to calculate electron density and Laplacian values of the chemical bonds of the most stable SiBHCs. Ab initio valence bond (VB) computations were carried out with XMVB.^54–56Ab initio molecular dynamical (AIMD) simulations with the example of B1 were carried out with the Vienna ab initio simulation package (VASP) program,^57,58 where the core and valence electrons were represented by using the projector augmented wave (PAW)⁵⁹ method and plane-wave basis functions with a kinetic energy cut-off of 400 eV. The generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE)⁶⁰ exchange–correlation functional was used in the AIMD calculations. The finite temperature simulations of the dynamic properties were performed at the temperatures 298 K and 673 K using the exact Hellmann–Feynman forces and applying the statistics of the canonical ensemble to the motion of atomic nuclei by means of a Nosé thermostat.⁶¹ Newton's equations of motion were integrated using the Verlet algorithm⁶² with a time step of 1 fs. B1 molecules were confined in a cubic box of 17 × 17 × 17 Å, and a vacuum distance of more than 10 Å was set to keep the interactions between the molecules in the adjacent boxes negligible. The Brillouin-zone sampling was restricted to the Γ-point. The optimization of atomic geometries was performed via a conjugate gradient algorithm until the residual forces acting on atoms were less than 0.1 eV Å⁻¹.

Results and discussion

On the basis of the structures of 1-aza-2,4-disilabicyclo[1,1,0]butanes⁴¹ and BHCs,²⁷ we designed (Si and B)-heterocyclic carbene (SiBHC), H₂SiC₂BH, as illustrated in Scheme 1a. H₂SiC₂BH (a) is the substituent of SiH₂ for the CH₂ unit in BHC (b). Scheme 1c illustrates the fifteen SiBHCs (X = H and R = H, Me, NH₂ and NO₂; X = F and R = H, Me, tBu, NH₂, CF₃ and NO₂; X = Me and R = H, Me, tBu, NO₂ and B(OH)₂). The linear isomers of SiBHCs are given in Scheme 1d. The linear isomers of SiBHCs are formed via two isomerization paths as displayed in Scheme 1S (in the ESI†). The optimized geometries and the relative energies of the possible structures of SiBHCs and their linear isomers are illustrated in Fig. 1S (in the ESI†). As shown from Fig. 1S,† the lowest energy structures of the fifteen SiBHCs were denoted as Ai (i = 1–15) and their expected isomers as Ai–j. For instance, A1 has only one linear isomer A1–1, but A2 has three isomers, which were labelled as A2–j (j = 1–3).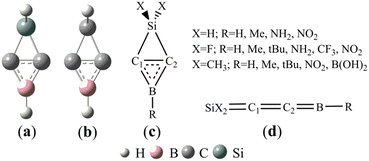

Scheme 1 (Si and B)-heterocyclic carbenes (SiBHCs) (a) and B-heterocyclic carbenes (BHCs) (b). Fifteen types of (Si and B)-heterocyclic carbenes (c) and the linear isomers (d).

Notably, all 15 SiBHCs (Ai) have significantly lower energy than their corresponding linear isomers (Ai–j). For example, the energies of A1 and A5 are lower than those of A1–1 and A5–1 by 30.2 and 49.0 kcal mol⁻¹, respectively. Thus, in contrast to BHCs,³⁵ SiBHCs are more stable compared with their linear isomers. In other words, the substitution of SiX₂ for the CX₂ unit in BHCs prefers to form SiBHCs. The energies of SiBHCs also depend upon the conformation of group R bonded to the boron atom in X₂SiC₂BR. Interestingly, A3–1 and A8–1 are much less stable than A3 and A8 by about 17.6 and 20.1 kcal mol⁻¹, respectively. The high stability of A3 and A8 can be attributed to the conjugated π bond between B and N. Vibrational frequency calculations confirmed that all Ai structures situate at the minima on the potential energy surfaces. Fig. 1 shows the optimized geometries of the Ai for the sake of clarity.

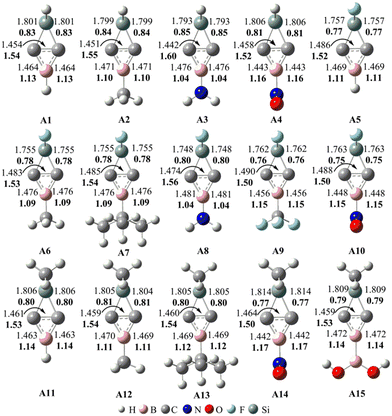Fig. 1 Optimized bond lengths (in plain) and calculated WBIs (in bold) in Ai (i = 1–15) at the M06-2X/6-311G** level. The bond lengths are given in Å.

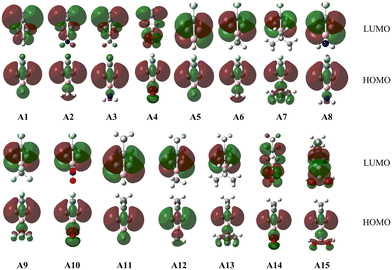
As seen from Fig. 1, the distances of the C–C, C–B and C–Si bonds in Ai (i = 1–15) are in the ranges of 1.442–1.490, 1.442–1.481 and 1.748–1.814 Å, respectively. The lengths of the C–C and C–B bonds in Ai are consistent with those of BHCs.^35,37 Thus, the substitution of SiX₂ for the CX₂ unit in BHCs does not impact the chemical bonds of the three-membered ring CCB in a noticeable way. We further calculated the WBIs of the C–C, C–B and C–Si bonds in Ai, which were incorporated into Fig. 1. The WBIs of the C–Si bonds in Ai are around 0.80, suggesting the single bond nature for the C–Si bonds. The WBIs of the C–C bonds in Ai are in the range of 1.50–1.60; thus, the C–C bonds are between single and double bonds. The WBIs of the C–B bonds in Ai are in the range of 1.04–1.17, indicating that C–B are not classical single bonds.

To better understand the bonding nature of the C–C and C–B bonds in Ai, we plotted the orbitals involved in the C–C and C–B bonds in Fig. 2 and Fig. 2S (in the ESI†). As shown in Fig. 2, the HOMOs of Ai are mainly the linear combination of the AOs of the two carbon atoms in the C–C bond, which is consistent with those of BHCs.^35,37 According to the π orbital and HOMO, it can be concluded that the C–C bond contains both π and CS bonds analogous to the inverted C–C bond in BHCs.³⁵ Fig. 2S shows an occupied π orbital extending over both carbon atoms and the boron atom, i.e. Π₃² with two π electrons moving over the three-membered ring (CCB). Thus, the shorter bond lengths and larger WBIs (>1.0) of the C–B bonds can be ascribed to the conjugate π orbital (aromaticity). Because the lengths, WBIs and the HOMOs are in good agreement with those of BHCs,^35,37 the Ai (i = 1–15) isomers were confirmed to have carbene characteristics that originate from the charge-shift (CS) bond. As such, Ai can be called SiBHCs. The calculated HOMO and LUMO energies and the HOMO–LUMO gaps of Ai are compiled in Table 1S (in the ESI†). The gaps between HOMO and LUMO of Ai are in the range of 8.23–9.20 eV, indicating the Ai isomers are electronically stable.

Fig. 2 HOMOs and LUMOs of Ai (i = 1–15).

Since the Ai (i = 1–15) isomers have similar structures, we employed the ab initio VB method BOVB/6-31G* to investigate the bonding of the inverted C–C bond in A1 and verify its CS nature. A1 can be described in terms of three resonance structures as shown in Scheme 2. Computations showed that ionic resonance structures make 34% contributions to the ground state of A1, suggesting that A1 favors a carbene structure by charge-shifting. Additionally, the calculated ratio of resonance energy to bond energy for the inverted C=C bond in A1 is 49% and meets the definition of a CS bond.

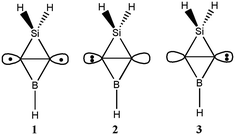Scheme 2 The covalent structure (1) and two ionic resonance structures (2 and 3) arising from charge-shift over the inverted C–C bond in A1.

Since Ai (i = 1–15) has a Π₃² delocalization π bond, the three-membered rings (CCB) are satisfied with the 4n + 2 rule and aromatic. Accordingly, both the NICS(0) and NICS(1) values in the centers of three-membered rings of Ai were calculated and are listed in Table 2S (in the ESI†). The NICS(0) and NICS(1) values are in the range from −38.4–−20.5 and −21.6–−11.1 ppm, respectively, indicating the strong aromaticity of these three-membered rings in Ai. The electron density and Laplacian values at the bond critical point (BCP) of Ai were calculated and are listed in Table 2S (in the ESI†). Table 2S† shows that the electron densities and Laplacian values of the inverted C=C bonds were close to 0.26 and −0.37, respectively.

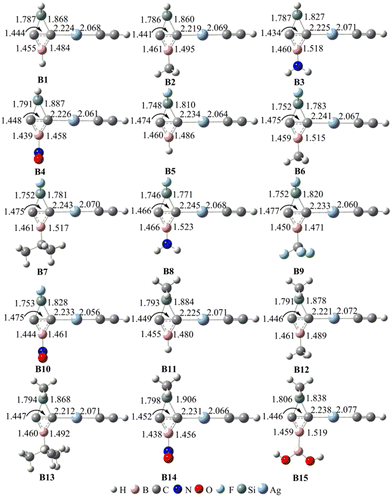
Similar to BHCs, the C–C bonds in Ai (i = 1–15) result in the carbene characteristics for these molecules. Accordingly, we optimized the silver complexes Bi (i = 1–15), which result from the coordination of Ai to AgC≡CH. The optimized geometries of these complexes are illustrated in Fig. 3. The binding energies between Ai and AgC≡CH and between L(=CO, NHC) and AgC≡CH in complexes LAgC≡CH, where CO or NHC coordinates to AgC≡CH, were calculated and are compiled in Table 3S (in the ESI†). The binding energies in the complexes LAgC≡CH (L=CO, NHC) were 18.4 and 45.2 kcal mol⁻¹, respectively. The binding energies in the complexes Bi formed from SiBHCs and AgC≡CH were in the range of 18.9–32.7 kcal mol⁻¹, suggesting that the formation of Bi is thermodynamically favorable and the coordination capability of SiBHCs ranges between CO and NHC. Frequency calculations also confirmed that Bi complexes are the minima on the potential energy surfaces, as they have no imaginary frequencies. The distances of ptC–Ag and Ag–C(≡CH) in complexes Bi (i = 1–15) are close to 2.231 and 2.068 Å, respectively. The lengths of the ptC–Ag bonds are consistent with those of BHCs,²⁷ indicating that the ptC–Ag bonds are coordination bonds. The short lengths of the Ag–C(≡CH) bonds in complexes Bi result from the ionic bond and coordination bond of the complexes AgC≡CH. The distances of the ptC–B, ptC–C and ptC–Si bonds in Bi are close to 1.489, 1.449 and 1.838 Å, respectively, which are consistent with those of BHCs.²⁷ Thus, the carbon atom (ptC) in complexes Bi forms four bonds. In addition, the sum of the four bond angles of Si–ptC–Ag, Ag–ptC–B, B–ptC–C and C–ptC–Si in Bi are close to 360°, showing that the five atoms Si, C, ptC, B and Ag atoms are located on one plane. Thus, all the complexes Bi (i = 1–15) contain ptCs.

Fig. 3 Optimized geometries of the complexes Bi (i = 1–15) at the M06-2X/6-311G** level. Bond lengths (in plain) and the smallest vibrational frequencies (in italic) are given in Å and cm⁻¹, respectively.

To confirm the thermodynamic stability of Bi, ab initio molecular dynamics (AIMD) simulations of B1 at T = 298 and 673 K were carried out and are illustrated in Fig. 2S (in the ESI†). As seen from Fig. 3S,† the structure of B1 has no significant changes at 298 K and 673 K for 8000 fs, in which the distances of Ag–C and Si–C are around 2.041 and 1.920 Å, respectively. Thus, B1 is thermodynamically stable.

Because the LUMOs of the SiBHCs Ai (i = 5–13) are similar to those of ethene and cyclopropene as shown in Fig. 2, these SiBHCs Ai (i = 5–13) can be dienophiles to undergo Diels–Alder reactions according to frontier molecular orbital theory. The Diels–Alder reactions of Ai (i = 5–13) with butadiene are shown in Scheme 3a. The transition states (TS_Ai-endo and TS_Ai-exo) and products (P_Ai) involved in the Diels–Alder reactions of Ai are illustrated in Scheme 3b, in which TS_Ai-endo and TS_Ai-exo were denoted in terms of the orientation of the SiX₂ unit in Ai toward butadiene.

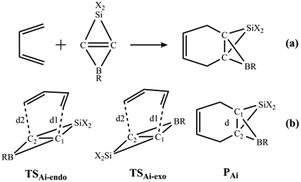Scheme 3 Diels–Alder reactions of SiBHCs with butadiene (a). Two transition states (TS_Ai-endo and TS_Ai-exo) and the products (P_Ai) (b).

The calculated reaction free energies and energy barriers of the Diels–Alder reactions of Ai (i = 5–13) with butadiene are given in Fig. 4. As seen from Fig. 4a, the reaction free energies of the Diels–Alder reactions are in the range of −33.6–−46.7 kcal mol⁻¹, indicating that these Diels–Alder reactions are thermodynamically feasible. Additionally, the electron withdrawing groups X and R can result in reduced reaction free energies. For instance, the reaction free energies of Ai (i = 5–10) are lower than those of Ai (i = 11–13), and the order of reaction free energies of Ai (i = 8–10) is A8 < A9 < A10. In particular, the reaction free energy of A10 is the lowest due to the strong withdrawing group NO₂.

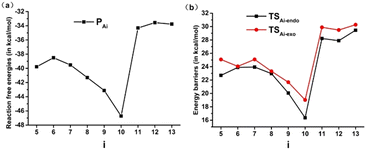Fig. 4 Reaction free energies (a) and energy barriers (b) of the Diels–Alder reactions of SiBHCs with butadiene.

Fig. 4b shows the energy profiles for the Diels–Alder reactions going through an endo and an exo pathways, and endo transition states (TS_Ai-endo) are of lower energies than exo transition states (TS_Ai-exo). This is consistent with the reactions of cyclopropenes and BHCs with butadiene.^37,38,63 The Diels–Alder reactions of Ai (i = 5–13) via transition state TS_Ai-endo to give P_Ai with energy barriers in the range of 16.4–29.5 kcal mol⁻¹, indicating that these Diels–Alder reactions are kinetically feasible. More interestingly, the sharpness of the energy barriers of the Diels–Alder reactions of Ai (i = 5–13) is completely similar to that of the reaction free energies. Thus, the electron withdrawing groups X and R substitution of SiBHCs can significantly reduce both the reaction free energies and energy barriers.

The optimized bond lengths of d1 and d2 (defined in Scheme 3) in the transition structures TS_Ai-endo and TS_Ai-exo of the Ai (i = 5–13) with butadiene are given in Table 4S (in the ESI†). As seen from Table 4S,† the distances of d1 and d2 in the endo and exo transition states are in the range of 2.260–2.378 Å,and in agreement with those of cyclopropene and BHCs with butadiene.^37,38,63 The optimized distances of the C₁–C₂ bonds in P_Ai (i = 5–13) are listed in Table 5S (in the ESI†). Table 5S† shows that the lengths and WBIs of the inverted C₁–C₂ bond in P_Ai are around 1.770 Å and 0.75, respectively, indicating the weak interaction between C₁ and C₂.

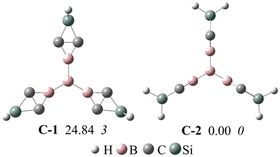
Previous studies showed that BHCs can be C₃ building blocks to obtain POMs.³⁹ In this work, we used three A1 isomers and a boron atom to obtain a C₃ building block with the formation of B–B bonds. The C₃ building blocks have two isomers owing to the conformation of A1, and these two isomers (C-1 and C-2) are illustrated in Fig. 5. C-1 is formed with three coplanar A1 monomers but in C-2, three A1 monomers are perpendicular to the plane formed from four boron atoms. The optimized geometries, relative energies, and the number of imaginary frequencies of C-1 and C-2 are presented in Fig. 5. C-2 is more stable than C-1 by 24.8 kcal mol⁻¹ and has no imaginary frequency. Based on C-2, we constructed three POMs by forming Si–Si bonds. The optimized geometries of the three POMs are displayed in Fig. 6. The lengths of the edges of the hexagonal channels in these POMs (D1–D3) are about 10.56 Å. Thus, the hexagonal channels in D1–D3 are regular hexagons, in which the apertures of the hexagonal channels are about 13.9 Å.

Fig. 5 The optimized structures, relative energy (in plain) and the number of imaginary frequency (in italic) of C-1 and C-2 at the M06-2X/6-311G** level. The relative energies are given in kcal mol⁻¹.

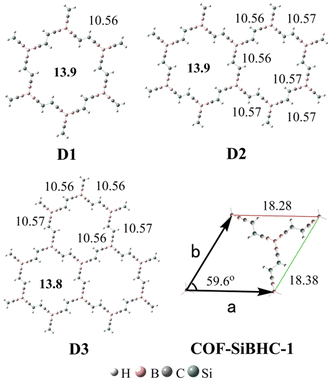Fig. 6 Optimized side lengths (in plain) and apertures (in bold) of D1–D3 and lattice parameters (in plain) of COF-SiBHC-1. The side lengths, apertures and lattice parameters are given in Å.

When the structures of D1–D3 were extended to 2D structures with infinite lattices, one kind of COF could be produced. The optimized lattice parameters of this COF (COF-SiBHC-1) using the M06-2X functional under the PBC are also illustrated in Fig. 6. The three lattice parameters (a, b and the angle between a and b) of COF-SiBHC-1 are 18.28 Å, 18.38 Å and 59.6°, respectively. Thus, such a 2D COF formed from SiBHCs is a hexagonal lattice. The apertures of the hexagonal channels of COF-SiBHC-1 are about 13.9 Å.

Conclusions

Based on the DFT computations, we rationally designed and theoretically predicted fifteen novel and stable SiBHCs derived from the substitution of SiX₂ for the CX₂ unit in B-heterocyclic carbenes (BHCs). SiBHCs at the singlet state were found to be lowest energy structures. The carbene characters of the SiBHCs result from the CS bond of the C–C bonds in SiBHCs, analogous to BHCs. The NICS(0) and NICS(1) values at the centers of the three-membered rings covering the CCB atoms of SiBHCs confirmed that SiBHCs are aromatic compounds. The binding energies of the complexes of SiBHCs with AgC≡CH indicated that the formation of (SiBHC)AgC≡CH would be thermodynamically favorable, in which the complexes of (SiBHC)AgC≡CH contain ptCs. These (SiBHC)AgC≡CH represent a new family of carbenes for designing complexes with ptCs. Computations also confirmed that the Diels–Alder reactions of the SiBHCs Ai (i = 5–13) with butadiene are feasible both thermodynamically and kinetically. These Diels–Alder reactions prefer endo transition states to give products. Finally, we designed three POMs and one kind of novel 2D COF based on SiBHC building blocks, in which the structures of D1–D3 are extended into 2D structures with infinite lattices to give 2D COF. The symmetry of 2D COF (COF-SiBHC-1) is approximately hexagonal, in which the apertures of the hexagonal channels of COF-SiBHC-1 are about 13.9 Å. We anticipate that these SiBHCs have potential applications in metal organic chemistry and material design due to their unusual structure and stability if they were isolated experimentally.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

The authors thank the National Natural Science Foundation of China for financial support (No. 21373133). This work was performed in part at the Joint School of Nanoscience and Nanoengineering, a member of the Southeastern Nanotechnology Infrastructure Corridor (SENIC) and the National Nanotechnology Coordinated Infrastructure (NNCI), which is supported by the National Science Foundation (Grant ECCS-2025462).

References

1. A. J. Arduengo, H. V. R. Dias, J. C. Calabrese and F. Davidson, Organometallics, 1993, 12, 3405–3409.
2. A. J. Arduengo, F. Davidson, H. V. R. Dias, J. R. Goerlich, D. Khasnis, W. J. Marshall and T. K. Prakasha, J. Am. Chem. Soc., 1997, 119, 12742–12749.
3. X.-Y. Yu, B. O. Patrick and B. R. James, Organometallics, 2006, 25, 2359–2363.
4. A. J. Arduengo and G. Bertrand, Chem. Rev., 2009, 109, 3209–3210.
5. J. A. Flores, N. Komine, K. Pal, B. Pinter, M. Pink, C.-H. Chen, K. G. Caulton and D. J. Mindiola, ACS Catal., 2012, 2, 2066–2078.
6. T. Sainsbury, M. Passarelli, M. Naftaly, S. Gnaniah, S. J. Spencer and A. J. Pollard, ACS Appl. Mater. Interfaces, 2016, 8, 4870–4877.
7. A. D. Dilman and V. V. Levin, Acc. Chem. Res., 2018, 51, 1272–1280.
8. R. Nakano, R. Jazzar and G. Bertrand, Nat. Chem., 2018, 10, 1196–1200.
9. G. K. Ramollo, I. Strydom, M. A. Fernandes, A. Lemmerer, S. O. Ojwach, J. L. van Wyk and D. I. Bezuidenhout, Inorg. Chem., 2020, 59, 4810–4815.
10. F. Vermersch, S. Yazdani, G. P. Junor, D. B. Grotjahn, R. Jazzar and G. Bertrand, Angew. Chem., Int. Ed., 2021, 60, 27253–27257.
11. J. B. Dumas and E. Peligot, Ann. Chim. Phys., 1835, 58, 5–74.
12. E. O. Fischer and A. Maasböl, Angew. Chem., Int. Ed. Engl., 1964, 3, 580–581.
13. R. R. Schrock, J. Am. Chem. Soc., 1974, 96, 6796–6797.
14. A. J. Arduengo, R. L. Harlow and M. Kline, J. Am. Chem. Soc., 1991, 113, 361–363.
15. L. J. Xu, W. P. Chen and J. L. Xiao, Organometallics, 2000, 19, 1123–1127.
16. N. Marion, O. Navarro, J. G. Mei, E. D. Stevens, N. M. Scott and S. P. Nolan, J. Am. Chem. Soc., 2006, 128, 4101–4111.
17. H. S. Yao, J. G. Zhang, Y. Zhang, H. M. Sun and Q. Shen, Organometallics, 2010, 29, 5841–5846.
18. S. P. Desai, M. Mondal and J. Choudhury, Organometallics, 2015, 34, 2731–2736.
19. H. Y. Zhang, R. Yuan, J. S. Song, X. Y. Li, Y. L. Zeng and Y. R. Mo, Organometallics, 2020, 39, 3240–3249.
20. M. G. Gardiner, W. A. Herrmann, C.-P. Reisinger, J. Schwarz and M. Spiegler, J. Organomet. Chem., 1999, 572, 239–247.
21. M. Poyatos, J. A. Mata and E. Peris, Chem. Rev., 2009, 109, 3677–3707.
22. A. Patra, S. Mukherjee, T. K. Das, S. Jain, R. G. Gonnade and A. T. Biju, Angew. Chem., Int. Ed., 2017, 56, 2730–2734.
23. C. Dutta, S. S. Rana and J. Choudhury, ACS Catal., 2019, 9, 10674–10679.
24. J. Jeong, J. Heo, D. Kim and S. Chang, ACS Catal., 2020, 10, 5023–5029.
25. A. Karton and V. S. Thimmakondu, J. Phys. Chem. A, 2022, 126, 2561–2568.
26. K. Thirumoorthy, A. Karton and V. S. Thimmakondu, J. Phys. Chem. A, 2018, 122, 9054–90641.
27. C. J. Zhang and F. F. Li, J. Phys. Chem. A, 2012, 116, 9123–9130.
28. S. Shaik, Z. H. Chen, W. Wu, A. Stanger, D. Danovich and P. C. Hiberty, ChemPhysChem, 2009, 10, 2658–2669.
29. W. Wu, J. J. Gu, J. S. Song, S. Shaik and P. C. Hiberty, Angew. Chem., Int. Ed., 2009, 48, 1407–1410.
30. S. Shaik, D. Danovich, W. Wu and P. C. Hiberty, Nat. Chem., 2009, 1, 443–449.
31. S. Shaik, D. Danovich, W. Wu, P. F. Su, H. S. Rzepa and P. C. Hiberty, Nat. Chem., 2012, 4, 195–200.
32. C. J. Zhang, H. Zhao and J. X. Li, Comput. Theor. Chem., 2015, 1054, 22–28.
33. S. N. Yang and C. J. Zhang, J. Phys. Chem. A, 2015, 119, 8950–8957.
34. X. F. Jia and C. J. Zhang, Comput. Theor. Chem., 2016, 1075, 47–53.
35. C. J. Zhang, D. X. Ma, S. N. Yang and J. X. Liang, ACS Omega, 2016, 1, 620–625.
36. C. J. Zhang, F. Fan, Z. M. Wang, J. S. Song, C. S. Li and Y. R. Mo, Chem. – Eur. J., 2018, 24, 10216–10223.
37. C. J. Zhang, Z. M. Wang, J. S. Song, C. S. Li and Y. R. Mo, Theor. Chem. Acc., 2019, 138, 106.
38. C. J. Zhang, H. Jiao and W. H. Jia, Comput. Theor. Chem., 2020, 1175, 112734.
39. C. J. Zhang, Z. Q. Tian, W. H. Jia and Y. R. Mo, Mol. Syst. Des. Eng., 2021, 6, 132–138.
40. C. J. Zhang, Z. Q. Tian and W. H. Jia, J. Phys. Chem. A, 2021, 125, 843–847.
41. J. C. Li, D. J. Goffitzer, M. Y. Xiang, Y. L. Chen, W. J. Jiang, M. Diefenbach, H. P. Zhu, M. C. Holthausen and H. W. Roesky, J. Am. Chem. Soc., 2021, 143, 8244–8248.
42. R. Hoffmann, R. W. Alder and C. F. Wilcox, J. Am. Chem. Soc., 1970, 92, 4992–4993.
43. A. P. Côté, A. I. Benin, N. W. Ockwig, M. O'Keeffe, A. J. Matzger and O. M. Yaghi, Science, 2005, 310, 1166–1170.
44. P. Kuhn, M. Antonietti and A. Thomas, Angew. Chem., Int. Ed., 2008, 47, 3450–3453.
45. F. J. Uribe-Romo, J. R. Hunt, H. Furukawa, C. Klöck, M. O'Keeffe and O. M. Yaghi, J. Am. Chem. Soc., 2009, 131, 4570–4571.
46. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
47. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
48. D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123–141.
49. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales and F. Weinhold, NBO Version 5.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2001.
50. P. v. R. Schleyer, C. Maerker, A. Dransfeld, H. J. Jiao and N. J. R. van Eikema Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318.
51. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013.
52. F. Biegler-König, J. Schönbohm and D. Bayles, J. Comput. Chem., 2001, 22, 545–559.
53. F. Biegler-König and J. Schönbohm, J. Comput. Chem., 2002, 23, 1489–1494.
54. L. Song, Z. Chen, F. Ying, J. Song, X. Chen, P. Su, Y. Mo, Q. Zhang and W. Wu, XMVB 2.1: an ab initio non-orthogonal valence bond program, Xiamen University, Xiamen, 2015.
55. L. Song, Y. Mo, Q. Zhang and W. Wu, J. Comput. Chem., 2005, 26, 514–521.
56. W. Wu, P. Su, S. Shaik and P. C. Hiberty, Chem. Rev., 2011, 111, 7557–7593.
57. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
58. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
59. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
60. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
61. S. Nosé, J. Chem. Phys., 1984, 81, 511–519.
62. L. Verlet, Phys. Rev., 1967, 159, 98–103.
63. B. J. Levandowski and K. N. Houk, J. Am. Chem. Soc., 2016, 138, 16731–16736.

---

Footnote

† Electronic supplementary information (ESI) available: Scheme 1S; Fig. 1S–3S; Tables 1S–5S; Cartesian coordinates, electronic energy (E) and the smallest vibrational frequency (v) of Ai (i = 1–15), Bi (i = 1–15), butadiene, P_Ai (i = 5–13), TS_Ai-endo (i = 5–13), TS_Ai-exo (i = 5–13), C-1, C-2 and D1–D3. Cartesian coordinates and electronic energy (E) of COF-SiBHC-1. See DOI: https://doi.org/10.1039/d2me00138a

---