Open Access Article
Open Access ArticleExperimental absence of the non-perovskite ground state phases of MaPbI3 explained by a Funnel Hopping Monte Carlo study based on a neural network potential†
Jonas A.
Finkler
 * and
Stefan
Goedecker
* and
Stefan
Goedecker
Department of Physics, University of Basel, Klingelbergstrasse 82, 4056 Basel, Switzerland. E-mail: jonas.finkler@unibas.ch; stefan.goedecker@unibas.ch
First published on 17th November 2022
Abstract
Methylammonium lead iodide is a material known for its exceptional opto-electronic properties that make it a promising candidate for many high performance applications, such as light emitting diodes or solar cells. A recent computational structure search revealed two previously unknown non-perovskite polymorphs, that are lower in energy than the experimentally observed perovskite phases. To investigate the elusiveness of the non-perovskite phases in experimental studies, we extended our Funnel Hopping Monte Carlo (FHMC) method to periodic systems and performed extensive MC simulations driven by a machine learned potential. FHMC simulations that also include these newly discovered non-perovskite phases show that above temperatures of 200 K the perovskite phases are thermodynamically preferred. A comparison with the quasi-harmonic approximation highlights the importance of anharmonic effects captured by FHMC.
1 Introduction
In recent years, perovskites have gathered a lot of attention due to their exceptional opto-electronic properties, which make them suitable for high performance devices, such as solar cells, lasers, photodetectors or light emitting diodes.1,2 The general structure of perovskites, given by the formula ABX3, consists of corner sharing BX6 octahedra arranged in a cubic lattice, that form cuboctahedral cavities, in which the A species are found. Due to many possible choices for the A B and X components, perovskites form a large design space that can be explored to optimize material properties.3,4Many perovskite materials undergo so-called tilting phase transitions, that are characterized by a cooperative tilting of the corner sharing octahedra that leaves the internal connectivity of the B and X atoms intact.5,6 Some materials, such as FaPbI3 and CsPbI3 can even undergo transitions to unwanted non-perovskite phases and there is ongoing research on stabilizing the perovskite phases.7,8
Due to the different properties of the phases, understanding and predicting the phase transition behaviour in perovskite materials is of great interest.
The presumably most widely used tools to study free energetic orderings in materials are the harmonic9 (HA) and quasi-harmonic10,11 (QHA) approximations. Unfortunately, the applicability of these methods to perovskites is limited since the tilting motion of the octahedral structure was found to be highly anharmonic.12–14
Many perovskites, such as CsSnI3,13 MaPbI3,15 or CsSnX3 and CsPbX316 can also be found in a high symmetry cubic phase, that is only stable at high temperatures. The geometries associated with these cubic phases can be constructed for small small unit cells but an analysis of their imaginary frequency phonon modes reveals, that they are dynamically unstable under collective rotations of the octahedral cages.12,17–19 The existence of these phases can therefore only be explained by entropic contributions to the free energy at higher temperatures. Carignano et al.14 found that the cubic symmetry of MaPbI3, is almost always broken locally and that the cubic symmetry found in experiments can be interpreted as averaging of distorted geometries. The HA and QHA are hence not directly applicable to these phases.
An alternative way to study phase transitions is a direct simulation of the atomistic dynamics through ab initio molecular dynamics (MD). Unfortunately, due to the high computational cost of ab initio methods, the affordable time-scales are limited. Classical force fields on the other hand would provide the required performance but their accuracy is limited by the simple functional form of the interaction potentials. Recently, his gap between performance and accuracy has been filled by machine learned potentials (MLPs). Once trained on high accuracy ab initio data, MLPs are able to predict energies and forces with almost ab initio accuracy at a fraction of the computational cost.20,21
In this paper, we developed a MLP to study phase transitions in methylammonium lead iodide (MaPbI3), where the B and X sites are formed by lead and iodine atoms and the A sites are occupied by the organic molecule methylammonium (MA) (CH3NH3).
Depending on the temperature, MaPbI3 can be found in three different phases in experiment. At low temperatures, MaPbI3 adapts an orthorhombic phase with Pnma symmetry. Upon heating above 160 K, MaPbI3 undergoes a first order phase transition to a tetragonal phase with I4/mcm symmetry. Under a further increase of the temperature above 330 K, the material was observed to undergo a second order phase transition to a cubic phase with Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry.22
m symmetry.22
A recent theoretical structure search,23 based on the minima hopping method,24,25 discovered two additional non-perovskite polymorphs of MaPbI3 that, according to DFT calculations based on the strongly constrained and appropriately normed26 (SCAN) density functional, appear to be significantly lower in energy than the experimentally observed phases. The energetically lowest polymorph is the double-delta structure, which has a unit cell containing 48 atoms and consists of edge-sharing octahedra forming pillars that are surrounded by Ma molecules. Results based on the random phase approximation (RPA) also support that the double-delta phase is lower in energy than the perovskite phases.27,28 The reported delta polymorph is higher in energy than the double delta phase but has a lower energy than the perovskite phases and consists of a unit cell containing 24 atoms, where face-sharing octahedra form pillars, arranged in a hexagonal pattern, that are uniformly surrounded my Ma molecules. The double-delta phase resembles the δ phase observed in CsPbI3,29 while the delta phase is similar to the δ phase of FaPbI3.7,30 The ground state geometries of the two delta and the three perovskite phases of MaPbI3 are shown in Fig. 1. A more detailed overview over the unit cells and geometries used for the simulations presented in this paper can be found in the ESI.†
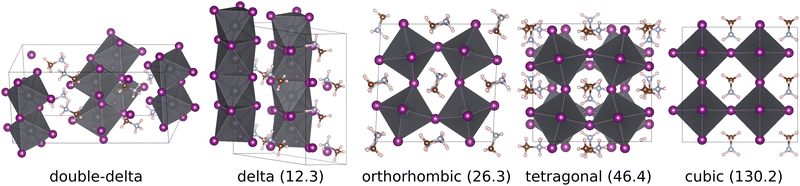 | ||
| Fig. 1 Ground state geometry of the two delta and the three perovskite phases of MaPbI3. The SCAN DFT ground state energy relative to the double-delta phase is given in parenthesis (meV f.u.−1). Note that the cubic geometry shown is only a local minimum in a smaller unit cell. The supercell shown here corresponds to a saddle point. Additional pictures can be found in the ESI.† | ||
The delta phase has also previously been investigated by Thind et al.31 In both CsPbI3 and FaPbI3, a transition to the non-perovskite δ phases can be observed. The stability of the perovskite phases of MaPbI3 is therefore rather surprising, given that the newly discovered non-perovskite phases should be energetically preferred. Understanding this unexpected behaviour using our MLP is unfortunately not straight forward. The large structural difference between the delta and the perovskite phases, suggests a complex reaction pathway, that would require unfeasibly long simulation times to explore through MD. Similarities can be found in the structurally similar phase transition between the hexagonal delta and cubic phases of FaPbI3. This transformations shows a complex reaction pathway with high barriers, that result in a large hysteresis of the transition with respect to temperature.32
To circumvent the problem of the high barriers, we extended our funnel hopping Monte Carlo (FHMC) method33 to periodic systems and applied it to MaPbI3 using our newly developed MLP. Similarly to a MD simulation, FHMC samples the Boltzmann distribution at a given temperature. However, it is not limited to a physical trajectory and carefully designed FHMC moves allow the Monte Carlo (MC) walker to jump between different phases, that are separated by high free energy barriers, without violating the detailed balance condition. Sampling of the true potential energy surface (PES) allows us to obtain phase transition temperatures without using any approximate expansion of the PES like in the HA and QHA. Additionally, the FHMC method is particularly well suited for applications with MLPs. Due to the global moves, the high energy transition states are not visited and do not need to be included in the training data.
2 The FHMC method
Many material properties emerge at finite temperatures due to the thermal motion of atoms. To compute these properties, an ensemble of geometries, distributed according to the Boltzmann distribution, has to be considered instead of a single ground state geometry. One possibility to generate such an ensemble are MD simulations coupled with thermostats,34 where Newtons equations of motion are solved to generate a trajectory. Another widely used approach are MC simulations that do not generate a trajectory but instead perform a random walk over the configuration space. In each step, a new configuration is proposed and then either accepted or rejected according to the Metropolis–Hastings criterion,35 which ensures, that the samples obtained during the random walk are distributed according to the Boltzmann distribution. The way new configurations are proposed is critical. In traditional MC simulations, local MC moves are used, where one or multiple atoms are displaced slightly. The magnitude of these displacements has to be chosen carefully. Large displacements are favourable, since they allow for a rapid exploration through the whole system. However, too large displacements lead to structures that are, in most cases, high in energy and will result in a low acceptance rate of the MC moves. Therefore a trade-off has to be made to determine the optimal magnitude of the displacements.A funnel is a feauture of the PES, where minima that are close in energy are arranged in a cascading manner towards the global minimum. Often, multiple funnels can be present, and the low lying minima from each funnel are separated by very high energy barriers. Due to the finite displacements, the MC walker is forced to take several steps across the barrier and accept some of the high energy transition states, even when the energy on the other side of the barrier is low. The high barriers in multi funnel systems can therefore slow down or even completely prevent complete sampling within feasible simulation times. This problem is known as broken ergodicity. Even though MC sampling of the Boltzmann distribution is, in theory, ergodic, meaning that every point on the PES will eventually be visited according to its Boltzmann probability, ergodicity can be broken in finite simulations of multi-funnel systems with high separating barriers. To overcome this problem, many algorithms, such as umbrella sampling,36 the stochastic self-consistent harmonic approximation,37 metadynamics,38 multicanoncial sampling,39 Wang–Landau sampling,40 nested sampling,41 the auxiliary harmonic superposition method,42 lattice switch MC43,44 or Boltzmann generators45 have been proposed in the past. Similarly, thermodynamic integration46 can be used to directly compute absolute free energies.
We recently developed a method called Funnel Hopping Monte Carlo33 (FHMC), that enables efficient MC simulations for multi funnel systems. The method introduces a global MC move, that enables the MC walker to jump directly from one low energy region to another, bypassing the high energy barriers entirely. Inspired by smart darting MC,47 FHMC takes advantage of the fact, that global optimization algorithms such as minima hopping24,25 are much more efficient than MC simulations in exploring the PES, since they do not have to generate a Boltzmann distribution. Therefore feedback mechanisms can be used that rapidly push the system out of funnels and across high barriers. The knowledge about the different minima can then be used during the MC simulation to introduce a new type of MC move, that directly targets the low energy region around other minima. These new moves have to be designed carefully, such that the detailed balance condition is not violated and the correct Boltzmann distribution is sampled by the MC walker. FHMC is therefore related to smart darting MC and lattice switch MC, which also use local minima to construct global MC moves. In these two methods, the atomic displacements from the nearest local minimum are directly added to the geometry of another local minimum to obtain the trial configuration. This will in most cases result in a high energy and hence low acceptance probability of the proposed move necessitating additional biasing in the case of lattice switch MC.43,44
The FHMC method therefore employs a different method to construct global MC moves. Gaussian mixtures (GMs) are used to approximate the Boltzmann distribution around the local minima. The GMs are fit, to samples obtained from MC simulations constrained to the region around the minima using the Expectation–Maximization algorithm.48 During the final MC simulation, global moves are proposed by sampling trial configurations from these GMs. A good fit of the GMs hence ensures that the proposed configurations are low in energy and have a high chance of being accepted.
The FHMC method was originally developed for systems with free boundary conditions, such as atomic clusters. The methods performance was demonstrated on the 38 atom Lennard-Jones (LJ) and 75 atom LJ clusters, which are known for their double funnel PES. The 75 atom LJ cluster is a particularly difficult system to treat with MC simulations, since not even parallel tempering49,50 simulations converge.51,52
In this work, we set out to extend the FHMC method to periodic systems and apply it to MaPbI3. This requires several adjustments of the FHMC algorithm that will be explained in the next sections. Some of the changes were required because the initial method was proposed for atomic clusters with free boundary conditions and hence the method needed to be adopted to periodic boundary conditions. Other changes were necessary because of the high rotational mobility of the Ma molecules present in MaPbI3.
2.1 Modification of the method for MaPbI3
In systems with periodic boundary conditions, only a finite number of symmetry operations, that preserve the periodic lattice of the unit cell, have to be considered. Since the maximum temperature of 400 K used in our FHMC simulations is below the melting temperature, permutations of atoms do not occur. We therefore only have to consider a fixed number of symmetry operation, that can be computed for the reference configurations obtained from minima hopping using spglib.53 For each operation that we have to consider, we first apply it to the current configuration of the MC walker. We then find the translation that minimizes the mass weighted RMSD by superimposing the centers of mass of the current configuration r and the reference R.
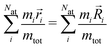 | (1) |
 | (2) |
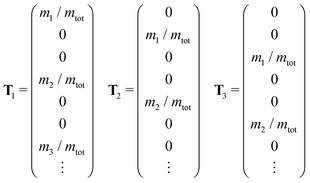
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) i weighted by factors ai, live in the space spanned by the basis vectors Bj. The total probability of the current configuration can then be evaluated as the mean over all Nsym applicable symmetry operations.
i weighted by factors ai, live in the space spanned by the basis vectors Bj. The total probability of the current configuration can then be evaluated as the mean over all Nsym applicable symmetry operations.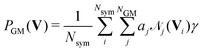 | (3) |
To propose a FHMC move, the process outlined above is reversed. First a random phase j is select and then a sample V′ is drawn from the respective GM. The sample is then transformed into an atomic displacement by applying the transformation from the coordinate system spanned by the basis vectors B to Cartesian coordinates. To obtain the new configuration, the displacement is added onto the reference configuration. The new configuration r′ is then accepted with the probability 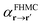 .
.
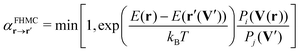 | (4) |
We therefore decided to couple the method with Hamiltonian replica exchange MC.54,55 We defined an artificial PES (APES) using the GMs, such that our FHMC moves are trivially accepted on the APES. The intermediate replicas will then allow for an exchange of configurations between the well sampled APES and the PES.
The GMs approximate the Boltzmann distribution PB as follows.
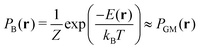 | (5) |
| EGM(r) = −ln(PGM(V(r)))kBT | (6) |
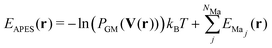 | (7) |
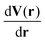 have to be included because the center of mass of the structures is fixed. This results in invariance of EAPES under translation.
have to be included because the center of mass of the structures is fixed. This results in invariance of EAPES under translation.
As we can see from eqn (4), FHMC moves will always be accepted on the APES, since the Boltzmann probability of EAPES is identical to the trial probability of the FHMC moves. The energy contributions EMaj(r) also cancel out in the FHMC moves, since the internal geometry of the Ma molecules is left unchanged by the FHMC moves and hence, the internal energy remains constant. Therefore, performing an FHMC simulation on the APES will converge extremely fast, since with every FHMC move, a new structure is generated which is, up to the internal geometry of the Ma molecules, completely uncorrelated to the previous geometry.
The MC simulation on the physical PES is then coupled to the APES using replica exchange MC. A series of intermediate PESs are defined using a parameter λ that varies from 0, at the physical PES, to 1 at the APES.
| Eλ(r) = (1 − λ)E(r) + λEAPES(r) | (8) |
Configurations between neighboring simulations are then exchanged at regular intervals according to the Metropolis–Hastings criterion. The acceptance probability αRX for replica exchange moves between two replicas a and b with configurations ra and rb and energy expressions Ea and Eb at temperatures Ta and Tb are given as follows.
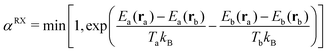 | (9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations after an equilibration period that lasted for 150
000 iterations after an equilibration period that lasted for 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iteration. We used unit cells containing 8 functional units for each phase as shown in Fig. 1. Additional details on the choice of unit cells can be found in the ESI.†
000 iteration. We used unit cells containing 8 functional units for each phase as shown in Fig. 1. Additional details on the choice of unit cells can be found in the ESI.†
3 Neural network potential
To obtain predictive power, a faithful representation of the PES is needed. It was previously shown, that density functional theory using the SCAN density functional is in good agreement with RPA results28 and experimental results.58 Unfortunately, performing FHMC simulations on a SCAN-DFT PES is not feasible due to the high computational cost and the large number of energy and force calculations that are required. We therefore decided to train a high dimensional neural network potential59 (HDNNP) using SCAN-DFT training data. We used the plane wave code VASP60–64 to perform DFT calculations. Details on the DFT settings are given in the ESI.† Unlike previously published machine learned potentials for MaPbI3,65,66 we also included the two non-perovskite phases in our training data. The HDNNP was trained by the RuNNer software67,68 using energies and forces. For the prediction of energies and forces, we employed our own code69 in the FHMC simulations and n2p270 in the MD simulations. Atom centered symmetry functions (ACSFs)71 were applied as atomic environment descriptors. A detailed list of the parameters of the ACSFs can be found in the ESI.† Neural networks consisting of two hidden layers with 10 nodes each were employed for each element, resulting in 3545 free parameters that were optimized during training. As activation function, the hyperbolic tangent and a linear function were used for the hidden and output layers respectively.To generate the training dataset, we took an active learning approach. We first trained a set of HDNNPs on a small set of structures that were sampled from a MC simulation driven by a classical force field72 and then recomputed with DFT. We then performed MC simulations for all 5 crystalline phases on the HDNNP-PES. The standard deviation between the energies predicted by the different HDNNPs, trained on the same data but with different initializations of the weights and biases, was applied to estimate the accuracy of the HDNNP's prediction for a given structure. The energies and forces of structures with the lowest accuracy were then recomputed with DFT and added to the dataset. This process was repeated until a satisfying accuracy was reached. The final dataset consists of 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 structures. We randomly selected 10% of the structures as a test set and used the remaining structures to train the HDNNPs. The resulting HDNNPs are highly accurate and can run stable MD simulations at up to 400 K. However, we found that in some rare cases, during our FHMC simulations, structures were generated by the FHMC moves, that would be extremely high in energy due to unphysically short bond lengths. As the training data for our HDNNPs was sampled from the Boltzmann distribution, such high energy structures are not present and the HDNNP prediction will be wrong. In some cases the HDNNPs would severely underestimate the energy which would lead to the acceptance of a highly unphysical configuration. To counteract this problem, we used the average over the predictions of five HDNNPs that were trained with a different weight initialization. A small positive energy bias was then added to configuration for which the prediction accuracy was low.
400 structures. We randomly selected 10% of the structures as a test set and used the remaining structures to train the HDNNPs. The resulting HDNNPs are highly accurate and can run stable MD simulations at up to 400 K. However, we found that in some rare cases, during our FHMC simulations, structures were generated by the FHMC moves, that would be extremely high in energy due to unphysically short bond lengths. As the training data for our HDNNPs was sampled from the Boltzmann distribution, such high energy structures are not present and the HDNNP prediction will be wrong. In some cases the HDNNPs would severely underestimate the energy which would lead to the acceptance of a highly unphysical configuration. To counteract this problem, we used the average over the predictions of five HDNNPs that were trained with a different weight initialization. A small positive energy bias was then added to configuration for which the prediction accuracy was low.
| E = Ē + ασ2 | (10) |
Table 1 shows the energy of the local minimum configuration for all phases considered in this paper. Energies per functional unit are given for DFT optimized geometries, the energy predicted by the NNP for the same geometry and the NNP energy after the lattice and atom positions were further relaxed on the NNP PES. The lattice parameters of the orthorhombic phase predicted by the NNP are in close agreement with the values obtained from DFT and experimental results22 at 10 K as can be seen in Table 2.
| Phase | SCAN | NNP | NNP relaxed |
|---|---|---|---|
| Double-delta | 0.0 | 1.5 | −2.2 |
| Delta | 12.3 | 20.6 | 11.1 |
| Orthorhombic | 26.3 | 28.7 | 26.1 |
| Tetragonal | 46.4 | 59.2 | 49.6 |
| Cubic | 130.2 | 138.3 | 124.7 |
| a | b | c | Volume | |
|---|---|---|---|---|
| SCAN | 8.99073 | 12.71980 | 8.62164 | 985.973 |
| NNP | 9.00764 | 12.69012 | 8.59005 | 981.912 |
| Experiment | 8.81155(6) | 12.58714(9) | 8.55975(6) | 949.38(1) |
The values for the cubic phase were obtained using a small unit cell containing only a single functional unit. When expanded to a 2 × 2 × 2 super cell, the cubic geometry is not a minimum anymore, but a saddle point.
We used a radial cutoff of 12 Bohr for our ACSFs. This distance is roughly equal to the distance between neighboring lead-iodine octahedra in the perovskite phases. It is important to note, that the HDNNP is able to describe interactions with a range of up to twice the maximum cutoff distance of the ACSFs, as atoms that are present in between the interacting atoms include both atoms inside their cutoff radius. To confirm, that the interaction between neighbouring Ma cations is adequately described by our HDNNPs, we placed two Ma molecules inside neighboring lead-iodine cages. The Pb and I atoms were placed at their high symmetry positions from the cubic phase. This way, the local environment of the Pb I cage, as seen by the Ma cation, is completely symmetric and invariant when a point symmetry operation is applied to the Ma cation through the cage center. We then compared the energies of the two cases, where both Ma cations were in parallel and anti-parallel configurations with DFT references. Due to the symmetry, the only difference in the environments of the Ma molecules is the Ma molecule in the neighboring cage. This allows us to test if the interaction between neighbouring Ma molecules is adequately described, by eliminating the interaction between the Ma molecules and the surrounding cage. The HDNNPs predict that on average, the parallel configuration is preferred by 61.3 meV which agrees well with the DFT result of 71.6 meV.
4 Results
4.1 FHMC study of the experimentally known phases
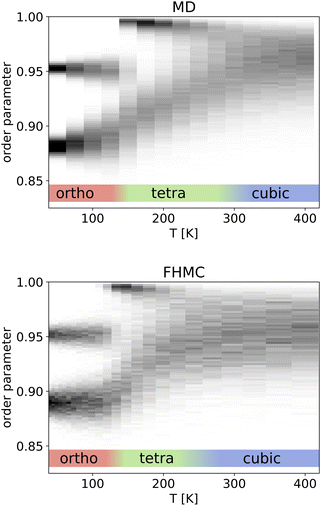
In a first step we ran FHMC simulation that only included the three experimentally known phases of MaPbI3. We also performed MD simulations using lammps74 and the HDNNP code n2p270 to validate our FHMC results. As we used variable cell shape MD, the determination of the phase from the lattice parameters is difficult. The variability of the lattice during the MD is close in magnitude to the variability between the different phases. This problem is not present in the FHMC simulations, since there the ratio between the lattice parameters is kept fixed to the value of the optimized unit cell and only the volume is allowed to change. However, an identification of a given phase using the lattice parameters is also not always possible. We observed, that sometimes geometries in one lattice are present, that show a tilting of the lead-iodine octahedra that is typical for another phase. This effect is especially pronounced for the tetragonal and cubic phases that have very similar lattice constants. We therefore used an order parameter, to determine the phase transition temperatures between the orthorhombic, tetragonal and cubic phases. This order parameter is given by the mean absolute value of the normalized dot product between vectors that span the three diagonals of neighboring lead-iodine octahedra pointing along the same axis. We hence obtain three order parameter values (one per diagonal of the octahedron) for each configuration, that indicate the tilting between neighboring lead-iodine octahedra. The mathematical details of the order parameter and an illustration of the vectors used to compute it can be found in the ESI.†In Fig. 2, histograms of the order parameter for different temperatures are shown. The MD simulations were performed at temperatures ranging from 25 K to 400 K with a spacing of 25 K. The order parameters were computed for a duration of 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ps after an equilibration period that lasted for the same duration. MD simulations that were initialized with a tetragonal or cubic geometry would only extremely rarely undergo a phase transition to the orthorhombic phase at temperatures close to the phase transition temperature, while the reverse transition was readily observed. We therefore initialized our simulation with the orthorhombic ground state geometry. Our FHMC simulations however, converge to the same relative probability of the different phases, independent of the phase that was used during initialization, since the FHMC moves allow for direct transitions between phases and are not hindered by energetic or dynamics barriers.
000 ps after an equilibration period that lasted for the same duration. MD simulations that were initialized with a tetragonal or cubic geometry would only extremely rarely undergo a phase transition to the orthorhombic phase at temperatures close to the phase transition temperature, while the reverse transition was readily observed. We therefore initialized our simulation with the orthorhombic ground state geometry. Our FHMC simulations however, converge to the same relative probability of the different phases, independent of the phase that was used during initialization, since the FHMC moves allow for direct transitions between phases and are not hindered by energetic or dynamics barriers.
The phase transition from the orthorhombic to the tetragonal phase can clearly be identified in both, the FHMC and the MD results, around 130 K by the disappearance of order parameter values around 0.95. The transition between the tetragonal and cubic phase is less clearly identifiable and occurs around 300 K in the MD simulation, where the two peaks in the order parameter histogram merge into a single peak. The FHMC results appear to show a slightly lower tetragonal cubic transition temperature. This is because of the high sensitivity of the transition to the lattice parameters.58 With increasing temperature, the ratio between the two lattice parameters of the tetragonal phase will get closer to one. Since this ratio is kept fixed to the ratio of the ground state geometry in our FHMC simulations, the tetragonal phase will necessarily be slightly strained at higher temperatures. Using the average lattice parameters of the tetragonal phase at 250 K obtained from variable cell shape MD in our FHMC simulations, we obtain a higher transition temperature that agrees extremely well with the MD results. The order parameter histogram of this simulation can be found in the ESI.† To keep our simulations consistent and to not introduce any bias by picking lattice parameters from different temperatures, we decided to use lattice parameters from ground state geometries.
4.2 FHMC study including the two delta phases
After confirming that FHMC is able to reproduce results obtained from MD simulations for the three experimental perovskite phases, we continue our investigation by performing FHMC simulations that include the two delta phases in addition to the three perovskite phases. Phase transitions involving the delta phases cannot be simulated using classical MD simulations. Both delta phases appear to be stable at our maximum simulation temperature of 400 K. We would therefore need to go to even higher temperatures or longer timescales to access the transition states, that connect the delta phases with the perovsite phases. Due to the large structural difference between the phases, complex transition states, that are not included in the training data of our HDNNPs are expected, rendering our HDNNPs inaccurate. Furthermore, we expect that the timescales needed for such transitions would be prohibitively large. This is supported by the fact, that even transitions between the structurally very similar orthorhombic and tetragonal phases are hard to observe in our MD simulations. Chen et al.32 experimentally investigated the structurally similar transition between the delta and cubic phases of FaPbI3 and found a large energetic barrier and reported complete kinetic trapping of the material in the higher energy cubic phase after cooling the material from 400 K to 200 K within 80 minutes. Clearly, such timescales are not accessible by any form of MD simulations. A large hysteresis of the transition between heating and cooling further supports the high free energy barrier and complex transition pathway.FHMC simulations can avoid this problem of high barriers and allow us to determine phase transition temperatures involving the delta phases without the need to also explore the large configuration space of transition states while still taking anharmonic effects into account without any approximation.
Unlike for the experimental phases, no transition from a delta phase to any other phase within the same lattice configuration was ever observed in our FHMC and MD simulations. We can therefore directly use the lattice configuration as an indicator of the non-perovskite phase.
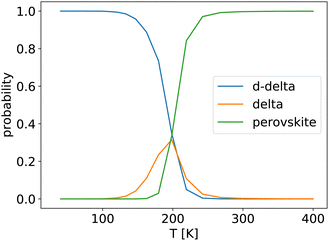
A plot showing the probability of finding the system in the double-delta, delta, or a perovskite phase versus temperature is shown in Fig. 3. At low temperatures, the double delta phase is dominant. The delta phase has only for a small temperature window a significantly non-zero probability. At higher temperatures above 200 K, the system is most likely to be found in the perovskite phases.
We also computed free energies using the HA and QHA for all phases, except the cubic phase using the phonopy code75 and our HDNNP. We excluded the cubic phase, since it does not relate to a minimum on the PES. Both, the HA and QHA, free energies are in qualitative agreement, indicating that effects of thermal expansion are not the main reason of the anharmonicity of the system. The relative free energies as well as plots of the phonon density of state for all phases are included in the ESI.†
We found, that even for the non-cubic phases, extremely tight settings, such as tight geometry optimization thresholds and small displacements for the calculation of the force constants through finite differences were necessary to avoid imaginary frequency modes. Similar finding were also reported by Marronnier et al.76 Compared to a DFT PES, where noise is present smaller displacements are not problematic on our HDNNP PES, since it is an analytical function, that can be evaluated with almost machine precision. Geometry optimizations were performed using the vc-SQNM algorithm.77
We then used the free energies computed within the QHA to calculate probabilities of finding the system in a given phase for the same unit cells that were used for the FHMC and MD simulations. The results are shown in Fig. 4.
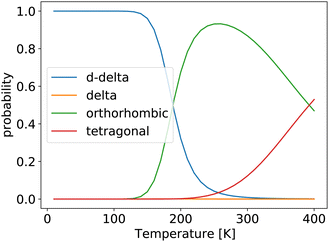 | ||
| Fig. 4 Probability of finding the system in a given phase, computed using the quasi-harmonic approximation. | ||
At low temperatures, the double-delta phase is most stable. Above 180 K the orthorhombic phase is predicted by the QHA to be thermodynamically more stable. This is surprisingly close to our FHMC results, that predict that the double-delta phase is only preferred up to a temperature of 200 K. However, the HA and QHA further predict, that the orthorhombic phase is preferred over the tetragonal phase up to a temperature of 380 K, which is inconsistent with experimental results as well es our FHMC and MD results. The correct prediction of the disappearing of the double delta phase above 200 K by the QHA, is therefore most likely an accidental result caused by error cancellation.
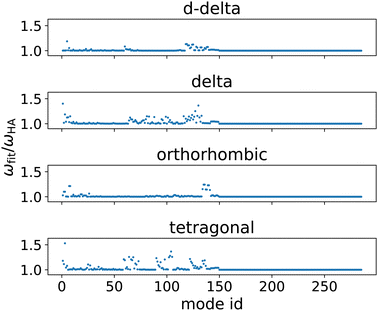
We also devised an additional test to further investigate the anharmonicity of the vibrational modes found by the HA. For this, we made an estimate ωfit of each vibrational frequency, that is not based on the second derivative of the potential energy at the local minimum but instead uses a quadratic fit of the potential energy through points placed further away from the minimum along the vibrational mode. These points were chosen such that they represent a realistic displacement from the local minimum as it could be observed during a finite temperature simulation. We first used the harmonic approximation to estimate the magnitude of the displacements, at which an energy of 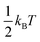 above the local minimum energy should be expected. This procedure was then repeated multiple times using the fitted curvature of the potential energy instead of the HA, such that a consistent fit was obtained. The converged fits were then used to estimate the vibrational frequencies ωfit. The ration between the ωfit calculated for a temperature of 300 K and the harmonic frequencies ωHA serves as a rough measure of the anharmonicity of each vibrational mode and are shown in Fig. 5. The results show the presence of anharmonic modes in all four phases. Interestingly, there seem to be fewer anharmonic modes in the double delta and the orthorhombic phase than in the delta and tetragonal phase. This might be an indication as to why the HA performs better for these two phases.
above the local minimum energy should be expected. This procedure was then repeated multiple times using the fitted curvature of the potential energy instead of the HA, such that a consistent fit was obtained. The converged fits were then used to estimate the vibrational frequencies ωfit. The ration between the ωfit calculated for a temperature of 300 K and the harmonic frequencies ωHA serves as a rough measure of the anharmonicity of each vibrational mode and are shown in Fig. 5. The results show the presence of anharmonic modes in all four phases. Interestingly, there seem to be fewer anharmonic modes in the double delta and the orthorhombic phase than in the delta and tetragonal phase. This might be an indication as to why the HA performs better for these two phases.
In general, however, it is not known, up to which temperatures the HA can be trusted and how strong the influence of the anharmonicity is in the final results. For example, Thind et al.31 also calculated free energies using the QHA for the delta and cubic phases and found a transition temperature of 750 K. This again is inconsistent with our FHMC results, which suggest a much lower transition temperature. Furthermore, it was also reported that the HA and QHA fail to assign the lowest free energy to the experimentally found tetragonal phase of the structurally similar system of CsSnI3.78
These results underline the high anharmonicity of the PES of perovskite materials and show, that methods beyond the HA and QHA are needed to obtain reliable phase transition temperatures.
5 Conclusions
We developed a highly accurate and reliable NNP for MaPbI3, that is trained on data including all three experimentally observed perovskite phases as well as the two theoretically predicted non-perovskite polymorphs. We studied phase transitions in MaPbI3 using MD, as well as FHMC, which we extended to periodic systems. The complicated nature of the PES required further modifications of the method, such as a special treatment of the Ma molecules and coupling FHMC with replica exchange MC. The final version of our FHMC method constructs an artificial PES (APES), based on Gaussian mixtures, on which all FHMC moves are accepted. These global MC moves, that directly jump from one phase to another, without violating detailed balance, allow for an extremely efficient sampling of the APES. We then couple a simulation on the proper machine learned PES to this APES through replica exchange. The efficiency of the method is further increased by including replica exchange moves between different temperatures. FHMC directly circumvents the high energy barriers, which makes it particularly well suited for applications based on machine learned potentials, since the complicated transition states do not need to be included in the training dataset.We validated the method by simulating the phase transitions between the three perovskite phases and comparing our results to long timescale MD simulations. An order parameter, that measures the tilting between neighboring lead iodine octahedra allows us to clearly identify the transition temperature between the orthorhombic and tetragonal phase at 130 K.
FHMC simulations including the delta and double delta phases, which have a lower potential energy than the perovskite phases, reveal, that above 200 K, the perovskite phases are thermodynamically favoured. This could explain the elusiveness of the delta phases in experiments. At room temperature MaPbI3 will readily form the perovskite phases and the low transition temperature combined with the high free energy barriers to the delta phases lead to kinetic trapping when the material is cooled down. A synthesis of the delta phases can therefore be expected to be very challenging and might only be possible under special conditions, such as high pressures as suggested by Flores et al.23 and very slow cooling rates.
A comparison with the QHA supports previous reports of the high anharmonicity of perovskite materials. While the QHA's prediction agrees with our FHMC results, in that the delta phase is only free energetically favoured at low temperatures, it fails to give a reasonable prediction for the orthorhombic to tetragonal phase transition temperature. This suggests, that the QHA's prediction of the delta to orthorhombic phase transition temperature is caused by accidental error cancellation. Furthermore, the QHA cannot directly be applied to the cubic phase, which does not correspond to a local minimum in the PES. Accurate predictions of transition temperatures, therefore require the use of methods beyond the harmonic approximation, such as our FHMC method.
Due to the rotational degrees of freedom of the Ma molecules, MaPbI3 turned out to be a particularly challenging system for the application of FHMC. This rare feature of MaPbI3 required an additional adaption of the FHMC method, which is a special treatment of the Ma molecules during FHMC moves. With this adaption the FHMC method should be similarly applicable to other perovskite materials with molecular cations, such as MaPbBr3 or FaPbX3. For many other perovskites, such as CsPbX3, as well as many other materials FHMC can be directly applied without this adaption. We therefore expect that the method is applicable to a large range of strongly anharmonic systems, such as other perovskite materials, silicates79 or superionic conductors.80
Author contributions
Both authors jointly contributed ideas for the methods and the content of this paper. JAF implemented the methods, performed the calculations and wrote the first draft of the manuscript. Both author jointly edited the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful for financial support from the Swiss National Science Foundation (SNF) (project number 182877) and a joint SNF/DFG project (SPP 2363, SNF project number: 206936). Calculations were performed at sciCORE (http://scicore.unibas.ch/) scientific computing center at University of Basel and the Swiss National Supercomputing Centre (CSCS) (project s963). We also want to thank Giuseppe Fisicaro and Ioannis Deretzis for fruitful discussions and Menno Bokdam and Georg Kresse for sharing their RPA results with us.References
-
J. M. Buriak, P. V. Kamat, K. S. Schanze, A. P. Alivisatos, C. J. Murphy, G. C. Schatz, G. D. Scholes, P. J. Stang and P. S. Weiss, Virtual Issue on Metal-Halide Perovskite Nanocrystals – A Bright Future for Optoelectronics, 2017 Search PubMed
.
- M. A. Green, A. Ho-Baillie and H. J. Snaith, Nat. Photonics, 2014, 8, 506–514 CrossRef CAS
.
- A. A. Emery and C. Wolverton, Sci. Data, 2017, 4, 1–10 Search PubMed
.
- A. Jain, O. Voznyy and E. H. Sargent, J. Phys. Chem. C, 2017, 121, 7183–7187 CrossRef CAS
.
- A. M. Glazer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384–3392 CrossRef CAS
.
- A. Glazer, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1975, 31, 756–762 CrossRef
.
- Z. Li, M. Yang, J.-S. Park, S.-H. Wei, J. J. Berry and K. Zhu, Chem. Mater., 2016, 28, 284–292 CrossRef CAS
.
- I. Deretzis, C. Bongiorno, G. Mannino, E. Smecca, S. Sanzaro, S. Valastro, G. Fisicaro, A. La Magna and A. Alberti, Nanomaterials, 2021, 11, 1282 CrossRef CAS
.
- K. Parlinski, Z. Li and Y. Kawazoe, Phys. Rev. Lett., 1997, 78, 4063 CrossRef CAS
.
- P. Pavone, K. Karch, O. Schütt, D. Strauch, W. Windl, P. Giannozzi and S. Baroni, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 3156 CrossRef CAS
.
- A. Togo, L. Chaput, I. Tanaka and G. Hug, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 174301 CrossRef
.
- F. Brivio, J. M. Frost, J. M. Skelton, A. J. Jackson, O. J. Weber, M. T. Weller, A. R. Goni, A. M. Leguy, P. R. Barnes and A. Walsh, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 144308 CrossRef
.
- C. E. Patrick, K. W. Jacobsen and K. S. Thygesen, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 201205 CrossRef
.
- M. A. Carignano, S. A. Aravindh, I. S. Roqan, J. Even and C. Katan, J. Phys. Chem. C, 2017, 121, 20729–20738 CrossRef CAS
.
- A. N. Beecher, O. E. Semonin, J. M. Skelton, J. M. Frost, M. W. Terban, H. Zhai, A. Alatas, J. S. Owen, A. Walsh and S. J. Billinge, ACS Energy Lett., 2016, 1, 880–887 CrossRef CAS
.
- R. X. Yang, J. M. Skelton, E. L. Da Silva, J. M. Frost and A. Walsh, J. Phys. Chem. Lett., 2017, 8, 4720–4726 CrossRef CAS PubMed
.
- C.-J. Yu, J. Phys.: Energy, 2019, 1, 022001 CAS
.
- N. A. Benedek and C. J. Fennie, J. Phys. Chem. C, 2013, 117, 13339–13349 CrossRef CAS
.
- L. D. Whalley, J. M. Skelton, J. M. Frost and A. Walsh, Phys. Rev. B, 2016, 94, 220301 CrossRef
.
- J. Behler, J. Chem. Phys., 2016, 145, 170901 CrossRef
.
- Y. Zuo, C. Chen, X. Li, Z. Deng, Y. Chen, J. Behler, G. Csányi, A. V. Shapeev, A. P. Thompson and M. A. Wood,
et al.
, J. Phys. Chem. A, 2020, 124, 731–745 CrossRef CAS PubMed
.
- P. Whitfield, N. Herron, W. Guise, K. Page, Y. Cheng, I. Milas and M. Crawford, Sci. Rep., 2016, 6, 1–16 CrossRef PubMed
.
- J. A. Flores-Livas, D. Tomerini, M. Amsler, A. Boziki, U. Rothlisberger and S. Goedecker, Phys. Rev. Mater., 2018, 2, 085201 CrossRef CAS
.
- M. Amsler and S. Goedecker, J. Chem. Phys., 2010, 133, 224104 CrossRef PubMed
.
- S. Goedecker, J. Chem. Phys., 2004, 120, 9911–9917 CrossRef CAS PubMed
.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402 CrossRef
.
- M. Bokdam and G. Kresse, 2022, personal communication.
- M. Bokdam, J. Lahnsteiner, B. Ramberger, T. Schäfer and G. Kresse, Phys. Rev. Lett., 2017, 119, 145501 CrossRef PubMed
.
- W. Ke, I. Spanopoulos, C. C. Stoumpos and M. G. Kanatzidis, Nat. Commun., 2018, 9, 1–9 CrossRef CAS PubMed
.
- L. Gu, D. Zhang, M. Kam, Q. Zhang, S. Poddar, Y. Fu, X. Mo and Z. Fan, Nanoscale, 2018, 10, 15164–15172 RSC
.
- A. S. Thind, X. Huang, J. Sun and R. Mishra, Chem. Mater., 2017, 29, 6003–6011 CrossRef CAS
.
- T. Chen, B. J. Foley, C. Park, C. M. Brown, L. W. Harriger, J. Lee, J. Ruff, M. Yoon, J. J. Choi and S.-H. Lee, Sci. Adv., 2016, 2, e1601650 CrossRef PubMed
.
- J. A. Finkler and S. Goedecker, J. Chem. Phys., 2020, 152, 164106 CrossRef CAS PubMed
.
- P. H. Hünenberger, Adv. Comput. Simul., 2005, 105–149 Search PubMed
.
- W. K. Hastings, Biometrika, 1970, 57, 97 CrossRef
.
- G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199 CrossRef
.
- L. Monacelli, R. Bianco, M. Cherubini, M. Calandra, I. Errea and F. Mauri, J. Phys.: Condens. Matter, 2021, 33, 363001 CrossRef CAS PubMed
.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef CAS PubMed
.
- B. A. Berg and T. Neuhaus, Phys. Lett. B, 1991, 267, 249–253 CrossRef
.
- F. Wang and D. P. Landau, Phys. Rev. Lett., 2001, 86, 2050 CrossRef CAS
.
- L. B. Pártay, G. Csányi and N. Bernstein, Eur. Phys. J. B, 2021, 94, 1–18 CrossRef
.
- V. A. Sharapov, D. Meluzzi and V. A. Mandelshtam, Phys. Rev. Lett., 2007, 98, 105701 CrossRef PubMed
.
- A. Bruce, N. Wilding and G. Ackland, Phys. Rev. Lett., 1997, 79, 3002 CrossRef CAS
.
- A. Jackson, A. Bruce and G. Ackland, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 036710 CrossRef CAS PubMed
.
- F. Noé, S. Olsson, J. Köhler and H. Wu, Science, 2019, 365, eaaw1147 CrossRef
.
- D. Frenkel and A. J. Ladd, J. Chem. Phys., 1984, 81, 3188–3193 CrossRef CAS
.
- I. Andricioaei, J. E. Straub and A. F. Voter, J. Chem. Phys., 2001, 114, 6994–7000 CrossRef CAS
.
- A. P. Dempster, N. M. Laird and D. B. Rubin, J. R. Stat. Soc.: Ser. B (Methodol.), 1977, 39, 1–22 Search PubMed
.
- R. H. Swendsen and J.-S. Wang, Phys. Rev. Lett., 1986, 57, 2607 CrossRef PubMed
.
- D. J. Earl and M. W. Deem, Phys. Chem. Chem. Phys., 2005, 7, 3910–3916 RSC
.
- V. A. Sharapov and V. A. Mandelshtam, J. Phys. Chem. A, 2007, 111, 10284–10291 CrossRef CAS PubMed
.
- P. Nigra, D. L. Freeman and J. Doll, J. Chem. Phys., 2005, 122, 114113 CrossRef PubMed
.
- A. Togo and I. Tanaka, 2018, arXiv:1808.01590 DOI:10.48550/arXiv.1808.01590.
- Y. Sugita, A. Kitao and Y. Okamoto, J. Chem. Phys., 2000, 113, 6042–6051 CrossRef CAS
.
- H. Fukunishi, O. Watanabe and S. Takada, J. Chem. Phys., 2002, 116, 9058–9067 CrossRef CAS
.
-
R. M. Neal
et al.
, Handbook of Markov Chain Monte Carlo, 2011, vol. 2, p. 2 Search PubMed
.
- S. Duane, A. D. Kennedy, B. J. Pendleton and D. Roweth, Phys. Lett. B, 1987, 195, 216–222 CrossRef CAS
.
- J. Lahnsteiner, G. Kresse, J. Heinen and M. Bokdam, Phys. Rev. Mater., 2018, 2, 073604 CrossRef CAS
.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS
.
- G. Kresse and J. Hafner, J. Phys.: Condens. Matter, 1994, 6, 8245 CrossRef CAS
.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS
.
- H.-A. Chen and C.-W. Pao, ACS Omega, 2019, 4, 10950–10959 CrossRef CAS PubMed
.
- R. Jinnouchi, J. Lahnsteiner, F. Karsai, G. Kresse and M. Bokdam, Phys. Rev. Lett., 2019, 122, 225701 CrossRef CAS PubMed
.
-
J. Behler, RuNNer–A program for constructing high-dimensional neural network potentials, Universität Göttingen, 2020 Search PubMed
.
- J. Behler, Int. J. Quantum Chem., 2015, 115, 1032–1050 CrossRef CAS
.
- J. A. Finkler, High-Dimensional-Neural-Network-Potential, 2022, https://github.com/Jonas-Finkler/High-Dimensional-Neural-Network-Potential.
- A. Singraber, J. Behler and C. Dellago, J. Chem. Theory Comput., 2019, 15, 1827–1840 CrossRef CAS PubMed
.
- J. Behler, J. Chem. Phys., 2011, 134, 074106 CrossRef PubMed
.
- C. Handley and C. Freeman, Phys. Chem. Chem. Phys., 2017, 19, 2313–2321 RSC
.
- J. A. Finkler, MaPbI3-HDNNP, 2022, https://github.com/Jonas-Finkler/MaPbI3-HDNNP.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in't Veld, A. Kohlmeyer, S. G. Moore and T. D. Nguyen,
et al.
, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS
.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS
.
- A. Marronnier, H. Lee, B. Geffroy, J. Even, Y. Bonnassieux and G. Roma, J. Phys. Chem. Lett., 2017, 8, 2659–2665 CrossRef CAS PubMed
.
- M. Gubler, M. Krummenacher, H. Huber and S. Goedecker, 2022, arXiv:2206.07339 DOI:10.48550/arXiv.2206.07339.
- E. L. Da Silva, J. M. Skelton, S. C. Parker and A. Walsh, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 144107 CrossRef
.
- S. Taraskin and S. Elliott, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 8572 CrossRef CAS
.
- M. K. Gupta, J. Ding, D. Bansal, D. L. Abernathy, G. Ehlers, N. C. Osti, W. G. Zeier and O. Delaire, Adv. Energy Mater., 2022, 2200596 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ma00958g |
| This journal is © The Royal Society of Chemistry 2023 |