Open Access Article
Open Access ArticleIn situ measurement of viscoelastic properties of cellular monolayers via graphene strain sensing of elastohydrodynamic phenomena†
Tianzheng
Guo
 a,
Xiaoyu
Zou
a,
Shalini
Sundar
b,
Xinqiao
Jia
a,
Xiaoyu
Zou
a,
Shalini
Sundar
b,
Xinqiao
Jia
 ab and
Charles
Dhong
ab and
Charles
Dhong
 *ab
*ab
aDepartment of Materials Science and Engineering, University of Delaware, Newark, Delaware 19716, USA. E-mail: cdhong@udel.edu
bDepartment of Biomedical Engineering, University of Delaware, Newark, Delaware 19716, USA
First published on 14th August 2023
Abstract
Recent advances recognize that the viscoelastic properties of epithelial structures play important roles in biology and disease modeling. However, accessing the viscoelastic properties of multicellular structures in mechanistic or drug-screening applications has challenges in repeatability, accuracy, and practical implementation. Here, we present a microfluidic platform that leverages elastohydrodynamic phenomena, sensed by strain sensors made from graphene decorated with palladium nanoislands, to measure the viscoelasticity of cellular monolayers in situ, without using chemical labels or specialized equipment. We demonstrate platform utility with two systems: cell dissociation following trypsinization, where viscoelastic properties change over minutes, and epithelial-to-mesenchymal transition, where changes occur over days. These cellular events could only be resolved with our platform's higher resolution: viscoelastic relaxation time constants of λ = 14.5 ± 0.4 s−1 for intact epithelial monolayers, compared to λ = 13.4 ± 15.0 s−1 in other platforms, which represents a 30-fold improvement. By rapidly assessing combined contributions from cell stiffness and intercellular interactions, we anticipate that the platform will hasten the translation of new mechanical biomarkers.
Introduction
Recent work in fundamental biology has increasingly developed connections between cell and tissue stiffness and function or state.1 While several techniques can assess single cell mechanical properties, there are few methods that can extract cell monolayer properties. Cell monolayers, in addition to individual cell stiffness, contain additional mechanical contributions from cell–cell and cell–protein interactions. Cells collectively interact with neighboring cells and surrounding proteins inside cell monolayers, and cell monolayers play a critical role in many physiological functions.2 In particular, the stiffness of cellular monolayers is both directly correlated to function, like in maintaining structural integrity, and indirectly, like in modulating mechanotransduction to downstream cellular pathways.3,4 Aberrant monolayer stiffness is known to indicate disease states,5 such as age-related macular degeneration in visual impairment (increased stiffness),6 degradation of epithelial layers in intestinal inflammatory diseases (decreased stiffness),7 and scarring in fibrosis (increased stiffness).8 These insights from biology position the stiffness of cellular monolayers as a versatile and novel biomarker for pathogenesis or pathophysiology, but a key limitation to translation has been the lack of simple platforms which can rapidly and accurately measure changes in the stiffness of cellular monolayers.Ideally, a platform for measuring monolayer stiffness should have the following features:9–11 it should give accurate and repeatable measurements, integrate into current cell culturing workflows, and measure stiffness in situ instead of only at endpoints. It should also avoid complicating experiments by introducing new labels or reagents, and not require capital-intensive or specialized equipment. Current techniques that assess the stiffness of cellular monolayers are limited by one or more of these burdens, which ultimately reduce the adoption and translation of mechanical stiffness as a biomarker.12–14 In one technique, a permeability assay measures the transport of fluorescently labeled microparticles across a barrier,15 but this technique introduces microparticle tracers into the cell culture, requires tuning of particle size, and is not a direct measurement of monolayer stiffness. Another technique is transepithelial/transendothelial electrical resistance (TEER),16 which provides quantitative measurements of tight junction dynamics in cell culture models of endothelial or epithelial monolayers by measuring how much of the electrical signal is blocked by the cell layer. TEER does not require labels or reagents but does require culturing cells near an electrode. These electrodes introduce new difficulties since the measured values depend on the position and shape of the electrodes and electrode insertion can disturb the integrity of the sample, especially when repeated over multiple days.17,18 In addition, the samples used in TEER might not be suitable for subsequent use in additional biological assays, which increases the number of samples needed and prevents the simultaneous measurement of cell stiffness alongside other chemical-based assays. Furthermore, traditional TEER measurements require a fully confluent cell layer to accurately measure barrier function. Measuring intermediate stages of cellular monolayers is more complex and faces reproducibility issues.16 Other optical techniques such as using optical tweezers19 or traction force microscopy20 require significant user knowledge to operate specialized equipment, develop appropriate controls, and perform analysis.
Through other indirect techniques which translate non-mechanical events to estimate mechanical parameters, Li et al.21 characterized the viscoelastic properties of fibroblast cell monolayers using thickness-shear-mode acoustic wave sensors. A cell layer was cultured onto a quartz resonator substrate to obtain an electrical admittance spectrum which would reflect acoustic impedance changes caused by cell monolayer adhesion. However, an interfacial layer between the cell monolayer and substrate with an unknown thickness would cause variations, and the calibration process is complex. Adamo et al.22 developed a microfluidic assay by measuring changes in cellular shape and transit times as cells pass through constrictions to obtain cell stiffness. Similarly, Guck et al.23 used a microfluidic optical stretcher to deform cells in order to find a link between cell function and elasticity. However, the refractive index of each sample needs to be determined before stretching which increases the operative difficulty. Both microfluidic approaches achieved a decreased measurement time, which improved throughput, but the techniques still require the assistance of capital-intensive optical-based characterization. Most importantly in monolayers or multicellular systems, these techniques only focus on the properties of a single cell and neglect the cell–cell and cell–protein interactions.
Here, to overcome existing limitations with current measurement techniques, we present a microfluidic-based platform which relies on the theory of elastohydrodynamic deformation (EHD)—the deformation of elastic walls under flow—as measured through piezoresistive graphene strain sensors.24 This platform is capable of non-invasive stiffness measurements in situ, under conventional cell culturing conditions, without the need for optical components or new reagents. By relying on relatively simple voltage measurements as opposed to microscopy techniques, the technique has better scaling for throughput or parallel experiments. We demonstrate platform utility through cellular monolayer dissociation via trypsinization, which occurs in minutes, and stiffness changes induced by a morphology change via epithelial-to-mesenchymal transition (EMT), which occurs over days. Our microfluidic-based platform provides a new facile route for investigating dynamic cellular mechanics at the multicellular level.
Materials and methods
Microfluidic platform design and fabrication
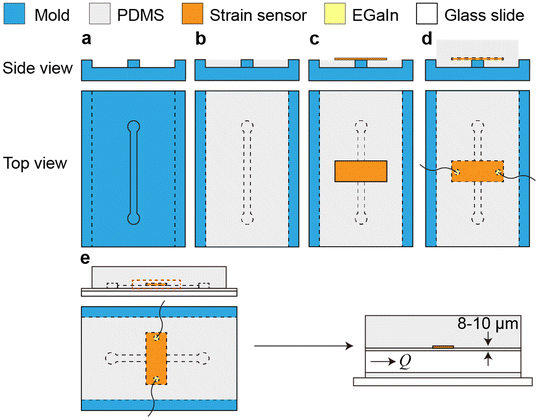
Standard soft lithographic techniques were used to fabricate microfluidic devices (Fig. 1). Polycarbonate stock (75 mm × 50 mm × 9 mm, TAP Plastics) was cut using a computer numerical control (CNC) endmill (MDX-50 Desktop Milling Machine, Roland Corp.) to form a negative mold of the device (Fig. 1a). The mold was spin coated with an 8% (w/w) poly(vinyl alcohol) (PVA, Mw = 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, Sigma-Aldrich Inc.) water solution at 300 rpm for 30 s after rinsing with ethanol and acetone and was dried on a hotplate. Then, PDMS (poly(dimethylsiloxane), Sylgard-184, Dow Corning Corp.) base and curing agent were mixed in a plastic cup, stirred thoroughly, and then degassed for 30 min. The PDMS mixture was then poured onto the mold, scraped with a doctor blade to achieve a thin layer above the channel, and cured at 65 °C for 15 min (Fig. 1b). After curing, a rectangular piece of metallic nanoisland graphene strain sensor (∼12 mm × 4 mm) with a copper backing layer was placed onto the negative channel spanning the short axis of the channel. After sensor placement, the copper backing was wet etched with a 15% w/w ammonium persulfate (APS) solution overnight at room temperature. After etching, the etchant was removed (Fig. 1c). A drop of eutectic gallium–indium (EGaIn) was placed on each side of the strain sensor to form electrical interconnects and then copper wires were placed into the EGaIn to form electrical leads. More PDMS was poured onto the cured PDMS (with the embedded graphene strain sensor) to a depth of 15 mm and was cured at 65 °C for 45 min (Fig. 1d). After curing, the device and mold were placed into warm water for 48 h in order to dissolve the PVA sacrificial release layer and release the PDMS block from the mold. After the PDMS block was separated from the mold and excess PDMS was trimmed from the device, fluid inlet and outlet holes were punched in the device using syringe needles, and PTFE tubes were inserted. A microscope slide (75 mm × 50 mm, Thermo Scientific) was spin coated with PDMS with the same monomer-to-curing agent ratio at 500 rpm for 30 s to form a layer of 50 μm and then cured at 65 °C for 7 min. The PDMS block was placed onto the glass slide coated with a partially cured layer of PDMS and was then cured for 30 min more at 65 °C to seal the channel (Fig. 1e). After curing, the device was ready for testing. The dimensions of the channel are 30 mm (L) × 1 mm (W) × 0.5 mm (H), and the sensor position ranges from 8 μm to 10 μm from the channel edge, as measured using a laser displacement sensor (KEYENCE LT-9010 M, resolution 0.01 μm).
000 g mol−1, Sigma-Aldrich Inc.) water solution at 300 rpm for 30 s after rinsing with ethanol and acetone and was dried on a hotplate. Then, PDMS (poly(dimethylsiloxane), Sylgard-184, Dow Corning Corp.) base and curing agent were mixed in a plastic cup, stirred thoroughly, and then degassed for 30 min. The PDMS mixture was then poured onto the mold, scraped with a doctor blade to achieve a thin layer above the channel, and cured at 65 °C for 15 min (Fig. 1b). After curing, a rectangular piece of metallic nanoisland graphene strain sensor (∼12 mm × 4 mm) with a copper backing layer was placed onto the negative channel spanning the short axis of the channel. After sensor placement, the copper backing was wet etched with a 15% w/w ammonium persulfate (APS) solution overnight at room temperature. After etching, the etchant was removed (Fig. 1c). A drop of eutectic gallium–indium (EGaIn) was placed on each side of the strain sensor to form electrical interconnects and then copper wires were placed into the EGaIn to form electrical leads. More PDMS was poured onto the cured PDMS (with the embedded graphene strain sensor) to a depth of 15 mm and was cured at 65 °C for 45 min (Fig. 1d). After curing, the device and mold were placed into warm water for 48 h in order to dissolve the PVA sacrificial release layer and release the PDMS block from the mold. After the PDMS block was separated from the mold and excess PDMS was trimmed from the device, fluid inlet and outlet holes were punched in the device using syringe needles, and PTFE tubes were inserted. A microscope slide (75 mm × 50 mm, Thermo Scientific) was spin coated with PDMS with the same monomer-to-curing agent ratio at 500 rpm for 30 s to form a layer of 50 μm and then cured at 65 °C for 7 min. The PDMS block was placed onto the glass slide coated with a partially cured layer of PDMS and was then cured for 30 min more at 65 °C to seal the channel (Fig. 1e). After curing, the device was ready for testing. The dimensions of the channel are 30 mm (L) × 1 mm (W) × 0.5 mm (H), and the sensor position ranges from 8 μm to 10 μm from the channel edge, as measured using a laser displacement sensor (KEYENCE LT-9010 M, resolution 0.01 μm).
Metallic nanoisland-on-graphene fabrication
Palladium was evaporated on a single layer of graphene at rate of 0.04 Å s−1. The strain sensor consists of a layer of copper foil, a layer of graphene and an 8 nm layer of palladium, which provides high sensitivity at low strains and is able to transduce deformation to electrical signals. The mechanism for this high sensitivity is postulated to be a combination of crack formation, improved sensor integrity, and quantum tunneling.24Madin–Darby canine kidney (MDCK) cell culture and characterization
Immediately following device fabrication, all devices were sterilized in 70% ethanol for 20 min, followed by a 15 min exposure to a bactericidal UV lamp with a 254 nm wavelength. Prior to cell culture, to promote cell attachment on PDMS, the PDMS channel wall was coated with collagen IV (collagen from human placenta, Sigma-Aldrich) (Fig. 2a). The device was incubated with 50 μg mL−1 collagen IV in 0.1% glacial acetic acid solution (in sterile PBS) at 37 °C in a humidified CO2 incubator for 4 h and then washed with sterile PBS. The device was placed upside down to help the collagen coating process on the top of the channel, which was where the graphene sensor was located. MDCK cells were sub-cultured on two 75 cm2 tissue culture-treated flasks. Cells were cultured and passaged according to the manufacturer's protocol in Eagle's minimum essential medium (EMEM, ATCC) supplemented with 10% fetal bovine serum (FBS) and 100 IU mL−1 penicillin–streptomycin in a humidified 37 °C incubator maintained at 5% CO2 and 95% air. The cell culture medium was changed every other day. Upon reaching confluency, cells were detached with 0.25% (w/v) trypsin-EDTA solution for 10 min and centrifuged at 450g for 5 min. Cell pellets were re-suspended in EMEM at a final concentration of 2 million cells per mL and the cell suspension was evenly pipetted into the channel. The cell culture medium was refreshed every day. The final cell seeding number is 1000 mm−2. Just as in the collagen coating process, the device was placed upside down to promote cell attachment to the top of the channel wall, near the sensor. | ||
| Fig. 2 Collagen IV coating on the PDMS and MDCK cell culture inside the microchannel. (a) PDMS wettability changes after collagen IV coating, which is shown by water contact angle measurement. The contact angle hysteresis shows that the contact angle of PDMS decreases from 99.1–120.7° ± 6.1° to 84.4–103.7° ± 5.4° after collagen IV coating. The immunostaining image of collagen IV (stained with monoclonal anti-collagen type IV antibodies produced in mouse, Sigma-Aldrich) inside the microchannel confirms that the wall is coated with collagen IV, and it was shown to be a patchy layer of discrete depositions of individual collagen proteins. (b) Bright-field and confocal images of MDCK cells inside the microchannel. On day 7, MDCK cells become confluent inside the microchannel. The thickness of the layer is ∼8 μm (ESI,† Fig. S5). Unlike that on the stiff surface, for example glass, it took longer for MDCK cells to be confluent on the softer surface, like PDMS, in our device. | ||
Contact angle measurement
Due to the size limitation of the channel structure, a separate substrate was coated with PDMS for the contact angle measurements. The PDMS solution with the same monomer-to-curing agent ratio was spin coated on a glass slide at 500 rpm for 30 seconds to form a PDMS film. The cured PDMS film was subjected to the same collagen IV modification described above. The contact angle hysteresis was measured at room temperature (Fig. 2a). A distilled water droplet was placed on the test substrates and the measured angles were averaged (3 samples of plain PDMS, 3 samples of collagen IV coated PDMS). Plain PDMS had a contact angle of 99.1–120.7° ± 6.1°, which decreased to 84.4–103.7° ± 5.4° after coating with collagen IV. The result shows that collagen IV coating was successful.Immunofluorescence
MDCK cells were fixed with 4% (w/v) paraformaldehyde (PFA, Sigma-Aldrich) in PBS for 15 min, followed by 3% BSA blocking incubation for nonspecific binding for 1 h at room temperature. Cells were then incubated with the primary antibodies vinculin (Sigma-Aldrich) and E-cadherin (BD Biosciences) diluted in 3% BSA (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400) at room temperature for 4 h. The primary antibody solution was then aspirated, and the cells were washed 3 times with PBST solution. Secondary antibodies Alexa Fluor 488 goat anti-mouse and Alexa Fluor 568 phalloidin (Thermo Fisher Scientific) were diluted in 3% BSA (1
400) at room temperature for 4 h. The primary antibody solution was then aspirated, and the cells were washed 3 times with PBST solution. Secondary antibodies Alexa Fluor 488 goat anti-mouse and Alexa Fluor 568 phalloidin (Thermo Fisher Scientific) were diluted in 3% BSA (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 and 1
400 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800, respectively) at room temperature for 4 h. After another triple wash with PBST solution, 4′,6-diamidino-2-phenylindole (DAPI, Thermo Fisher Scientific) was diluted in PBS solution (1
800, respectively) at room temperature for 4 h. After another triple wash with PBST solution, 4′,6-diamidino-2-phenylindole (DAPI, Thermo Fisher Scientific) was diluted in PBS solution (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000) at room temperature for 15 min. Fluorescence microscopy was performed using a Zeiss LSM 880 (Fig. 2b).
1000) at room temperature for 15 min. Fluorescence microscopy was performed using a Zeiss LSM 880 (Fig. 2b).
Electrical signal capture of wall deformation via droplet flow and analysis
Viscoelastic behavior was modeled with a Kelvin–Voigt model, which uses a combination of springs and dashpots connected in parallel. If constant stress is applied to a Kelvin–Voigt material and then released at time t1, the viscoelastic relaxation obeys the following equation: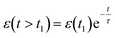 | (1) |
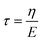 is the relaxation time.
is the relaxation time.
To monitor this viscoelastic relaxation behavior, brief stress is applied by flowing fluid droplets in the channel. As the sensor signal is proportional to the wall deformation, the voltage change can be described in terms of the viscoelastic relaxation as:
| V(t) = V0 − V(t1)e−λt | (2) |
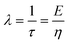 is the relaxation time constant. To fit the viscoelastic relaxation, the equation is linearized as:
is the relaxation time constant. To fit the viscoelastic relaxation, the equation is linearized as: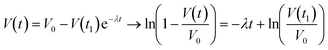 | (3) |
Results and discussion
Operational principle and device validation
Our platform is based on monitoring the flow-induced deformation of soft walls (elastohydrodynamic deformation, EHD) within a microfluidic channel.25–28 To extract the viscoelastic parameters of a sample, we monitored the viscoelastic relaxation of the wall to its baseline shape after perturbation by a droplet (schematic shown in Fig. 3a). For a pure fluid, Gervais et al.29 developed a model to describe the expected wall deformation as a function of parameters. Given the addition of a sample, i.e., a monolayer of cells, inside the fluid channel, the elastohydrodynamic deformation of the wall under flow will change in a manner that reflects the mechanical properties of the sample. At a constant flow rate, the relationships between the flow rate and the pressure and the channel deformation are given by:30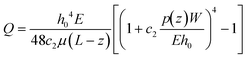 | (4) |
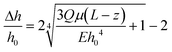 | (5) |
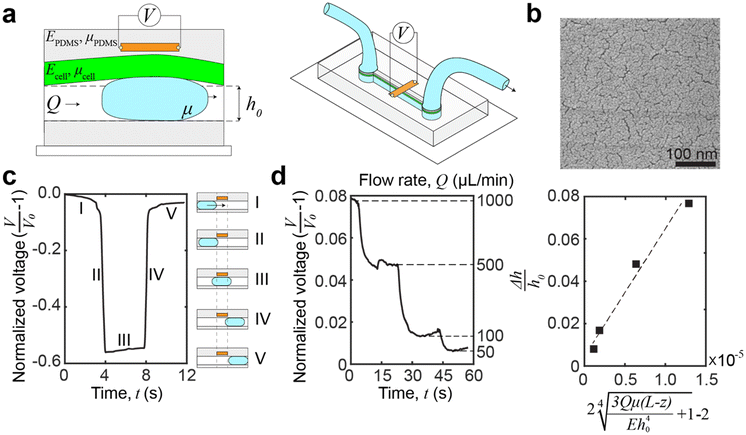 | ||
| Fig. 3 Microfluidic device and operation principle. (a) Schematic of the microfluidic device. A graphene strain sensor, embedded in the PDMS sidewalls, is placed in close proximity (∼8–10 μm) to the channel. The sensor measures the transient deformation caused by a passing droplet, and the deformation is a function of the properties of the channel sidewalls and any coatings, i.e., the cellular monolayer. (b) Scanning electron microscopy (SEM) images of palladium nanoislands on graphene. The thickness of the palladium only is 8 nm, and it is the nominal deposition thickness using a quartz crystal balance. (c) Voltage signal capture by introducing a water droplet in the channel. The voltage signal can be broken into distinctive regions which correspond to the location of the droplet relative to the channel and sensor. Region IV is used for relaxation analysis. (d) Demonstrating the sensing of elastohydrodynamic phenomena by monitoring the voltage change of the device at different flow rates. Experimental data fitted against theoretical prediction of deformation by eqn (5). The relationship between flow rate and elastohydrodynamic deformation is approximately linear at low pressures. The linearity is shown by R2 = 0.86. | ||
The expected deformation in most conventional microfluidic devices is low (<5 μm),36 and the relaxation times are fast (∼0.1 s).30 To measure this deformation, we embedded a graphene strain sensor within the device sidewalls (Fig. 3a), in close proximity (∼8–10 μm) to the channel.30 These piezoresistive strain sensors are made from graphene decorated with metallic nanoislands (Fig. 3b), which have sufficient sensitivity to measure elastohydrodynamic phenomena.24 The advantage of using piezoresistive strain sensors is that the electrical signal monitoring has an inherently high temporal resolution and a lower cost for scale up, especially when compared to optics-based lasers and cameras, or microscope-based platforms. Furthermore, by embedding the sensor within an elastic wall, the sensor reduces erroneous sources of contamination and does not introduce additional experimental complications, e.g., tracer particles or conjugated labels. These advantages enable widespread compatibility, scalability, and sufficient mechanical resolution for changes at the cellular level.
To induce transient deformation in the microfluidic channel, we flowed a water droplet into the channel. The voltage readings of the water droplet can be broken into five distinctive regions (Fig. 3c). In region I, we introduced a droplet into the channel, but as the droplet was far away from the sensor, the voltage showed a slight decrease which corresponds to the applied pressure driving the droplet, constricting the channel ahead of the droplet.37 In region II, the leading edge of the droplet crosses the boundary (dashed line on the left in Fig. 3c) of the sensor, leading to a reduction in voltage. Thus, we can calculate the droplet velocity by dividing the width of the strain sensor by the duration of region II. In region III, the main body of the droplet transits across the sensor strip, which results in a slight increase in the voltage due to the increasing area of the overlap between the droplet and the sensor. In region IV, the droplet has left the sensing area, and the voltage signal reflects the viscoelastic relaxation of the channel. Region IV is where the voltage data can be fitted to a viscoelastic model of the sample to extract viscoelastic parameters of the cellular monolayer (see eqn (3) in Materials and methods for the fitting procedure). Region V shows a second, slower relaxation of the channel back to the neutral height. This relaxation is a bulk phenomenon and is distinct from the interfacial viscoelastic relaxation in region IV. The bulk residual strain of the channel originates from the confined microfluidic geometry, as replicated in our simulations (see ESI,† Fig. S1).
A different drop size and flow velocity will induce a different force,37 but this variance has a negligible impact on viscoelastic measurements. This is because the timescale of the rise and fall of the voltage signal of the droplet (<0.1 seconds as seen in all figures) is much more rapid than the timescale of viscoelastic relaxation in the samples. Thus, the droplet can be modeled as a step-response. We also expect minimal variation in the rise and fall of the droplet within expected droplet velocities.37 Evidence of the consistency between droplets can be quantified by the low error of the viscoelastic measurement in the following sections. Thus, one of the advantages of our platform is that reliable viscoelastic properties can be obtained from hand-driven droplets. The velocity of the droplet can be extracted from the duration of section II and the sensor width. The bubble length can be calculated from the droplet velocity times the duration of section III.
To demonstrate that the sensor is measuring elastohydrodynamic phenomena, we verified that the sensor outputs match the theoretical relationship between the flow rate and channel deformation in eqn (5). The flow rate was varied for a continuous flow by using a PID-controlled microfluidic controller (Elveflow OB1 MK3+, 61 μbar resolution) while monitoring the voltage change. At lower pressures, the pressure drop is approximately linear with the imposed flow rate.29Fig. 3d shows that the relationship between the channel deformation and flow rates is as expected, demonstrating that the strain sensor is sensing elastohydrodynamic deformation and that the voltage readings are proportional to the channel deformation. An additional performance of the device in establishing elastohydrodynamic phenomena is provided in the ESI† (Fig. S2).
Transient viscoelastic properties of a monolayer under trypsinization
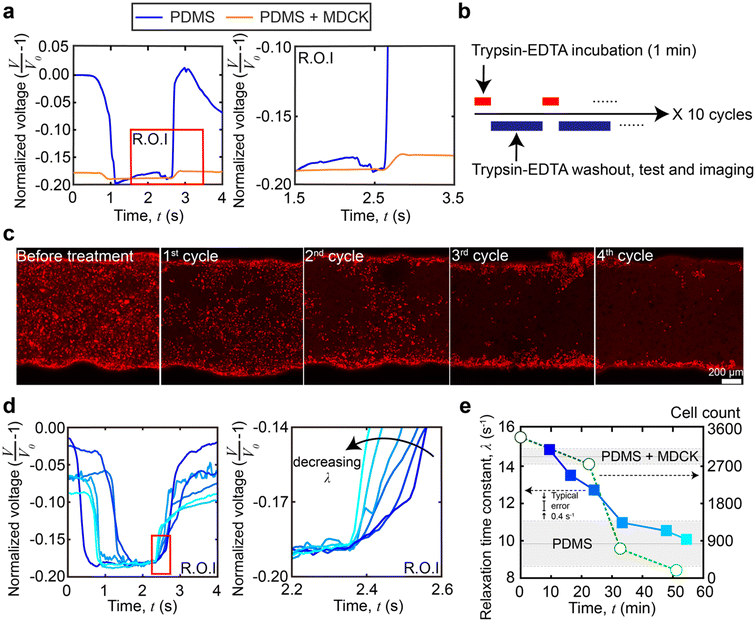
To demonstrate in situ measurements of dynamic stiffness changes in cellular monolayers, we dissociated a confluent Madin–Darby canine kidney (MDCK) epithelial cell monolayer with a standard 0.25% trypsin-EDTA (ethylenediaminetetraacetic acid) solution (see Materials and methods for channel coating, culture conditions, and determination of confluency). One droplet was placed inside the channel and was pushed through the channel. This process was repeated 10 times for each device. Prior to trypsinization, we obtained baseline viscoelastic relaxation time constants through the PDMS (λ = 9.9 ± 1.3 s−1, n = 30 from 3 different devices measured 10 times each, no significant difference with and without collagen IV coating on the channel wall) and a fully formed MDCK cell monolayer (λ = 14.5 ± 0.4 s−1, n = 30 from 3 different devices measured 10 times each). The higher λ value obtained in the channel with the MDCK monolayer indicates a higher overall stiffness within the channel. That is, although the MDCK cell monolayer (8 μm) is not necessarily stiffer than the PDMS (∼8–10 μm), the composite structure of PDMS with the MDCK cell monolayer is stiffer than the thinner PDMS structure alone. The mechanical contributions of the MDCK cell monolayer originate from a combination of the MDCK cell body, intercellular adhesion junctions, and extracellular matrix (ECM) proteins.38 The values are in agreement with those in a previous study39 being 13.4 ± 15.0 s−1 but have a much lower error. A standard deviation of 15.0 s−1 was obtained with n = 17 in total, and a standard deviation of 0.4 s−1 using our platform was obtained with n = 30 in total. An F-test was performed to show that our resolution is at least 24.7 times higher (F-test, F = 1406.25, 24.7–56.8, 95% CI). A higher resolution is important for resolving small mechanical changes during trypsinization. The trypsinization design is shown in Fig. 4b, which alternates between trypsin-EDTA incubation and measurement acquisition stages. Confocal microscopy images of the monolayers were taken (cells were labeled with CellTracker™ red, Life Technologies, Fig. 4c) concurrently with our viscoelastic measurements, which shows that the orthogonal nature of our stiffness measurements enables the standard use of fluorescence assays (n = 30 from 3 different devices measured 10 times each).The raw viscoelastic relaxation data at the different time points are shown in Fig. 4d. When plotted versus time, Fig. 4e shows the relaxation time constant changes over time as compared to the change in cell count during the trypsinization process (for clarity, the cell count and viscoelastic properties in a single experiment are shown in Fig. 4e, but additional replicates are shown in ESI,† Fig. S3). At the earliest timepoints (t = 0–10 minutes, cycles 1–2), the relaxation time constants (λ = 14.5 ± 0.4 s−1, n = 30 from 3 different devices measured 10 times each) matched the baseline of the confluent and intact MDCK cell monolayer inside the channel. At later timepoints, as expected, the trypsinization began to dissociate the MDCK monolayer,40 resulting in a decreased λ which was below 14.5 s−1 at around t = 10–20 minutes. However, when compared to the cell count, we observed that the layer softening occurred shortly after observable decreases in the cell count. Continued trypsin-EDTA solution exposure led to a further decrease of the relaxation time constant, until the value reached that of a bare PDMS channel (λ = 9.9 ± 1.3 s−1, n = 30 from 3 different devices measured 10 times each). Comparing the mechanical data with the cell count, the λ of the channel remains above the baseline of PDMS values between 30 and 40 minutes for a short time, even after the cell count drops to effectively zero (<500). This is likely due to residual basement membrane proteins, indicating that the platform can sense contributions from the cells and extracellular proteins to the overall mechanical stiffness of the monolayer.
In this trypsinization experiment, the loss of cells and the digestion of ECM proteins led to an expected decrease in stiffness. Critically, the higher resolution of our platform was able to resolve the small mechanical changes occurring during the trypsinization process. The concurrent stiffness and cell count measurements captured the different stages and the contributions of the cell body, cell–cell adhesion, basement membrane proteins secreted by MDCK cells, and ECM proteins to dissociation of the whole cell layer. At earlier time points, cell loss preceded the loss in stiffness, while at later time points, residual ECM and basement membrane proteins had a small, but detectable contribution to the channel stiffness where λ is ∼1.0 s−1 higher than the PDMS baseline, even after the cells were virtually absent after 30 minutes. Compared with the rate of decrease in the relaxation time constant (λ), the rate of cell count loss is higher. However, compared to the earlier decrease of relaxation time constant where λ decreased by ∼80% in 30 minutes—which is mostly due to cell count loss—the decrease of relaxation time constant in the last 20 minutes (λ reduced by an additional ∼20%) was more gradual when there were virtually no cells. This suggests that MDCK cell bodies contribute more to the monolayer stiffness than the ECM and basement membrane proteins. Our results are in agreement with those by Sorba et al.,41 who showed that in MDCK monolayers, the cell covered region had a higher relaxation time constant (10.09 ± 1.42 s−1) than the bare PDMS region (3.18 ± 1.47 s−1), via tensile testing, and that EDTA treated MDCK cells had a lower Young's modulus (6.86 ± 3.27 kPa) than untreated cells (23.3 ± 6.3 kPa).
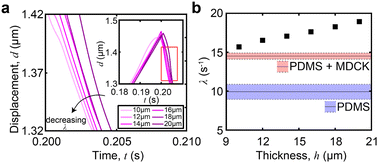
Thin-film correction factor for viscoelastic properties
In thin films, like the monolayer here, the apparent viscoelastic properties are a function of the cell thickness. We performed FEA simulations to determine the thin-film correction factor to isolate the true (thickness-independent) viscoelastic properties of the MDCK cell monolayer from contributions arising from thickness and the underlying PDMS (Fig. 5a). From our simulations, we obtained a simple correction factor to calculate the relaxation time constant relationship in a two-layer structure (Fig. 5b):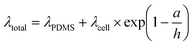 | (6) |
Transient viscoelastic properties during epithelial-to-mesenchymal transition
To demonstrate in situ stiffness changes derived solely from cellular processes like morphological changes—which do not result in cell loss—we added an EMT inducer, HGF, in the MDCK culture. EMT is a common disease marker, especially in fibrosis, which results in several biochemical, biophysical and mechanical changes.43,44 As this transition occurs slower than trypsinization, we maintained MDCK cells in an incubator at 37 °C and with 5% CO2 and 95% air. The only exception to the culturing conditions is when we briefly took cells into biosafety cabinets (room temperature, ambient conditions, ∼2 minutes) to obtain stiffness measurements.To investigate the stiffness change due to EMT, we simulated an in vitro EMT process in the microfluidic channel by introduction of hepatocyte growth factor (HGF, Invitrogen).45 We treated one group of MDCK cells with HGF while there was no HGF treatment for the control group on day 1. All other culture conditions were the same.46 On day 3, we removed the cell culture medium and flowed a droplet of PBS solution to acquire voltage signals. One droplet was placed inside the channel and was pushed through the channel. This process was repeated 10 times for each device.
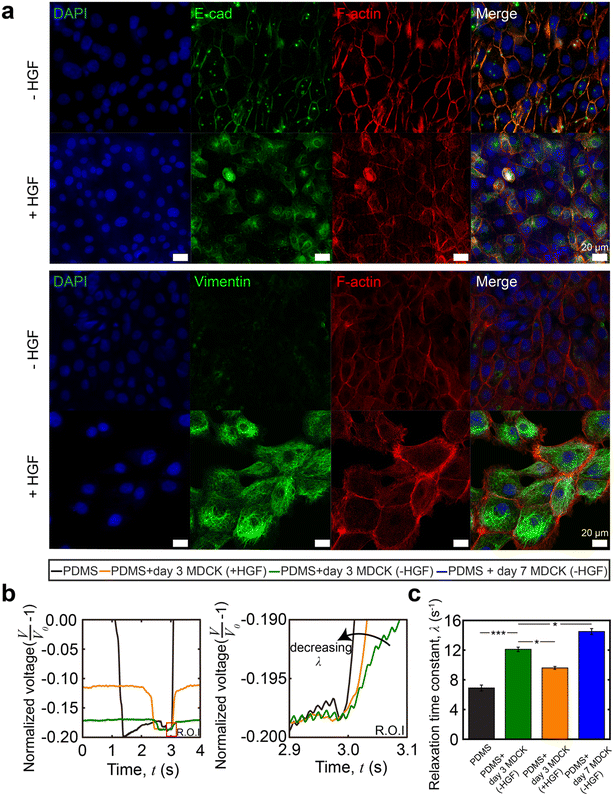
Immunostaining images confirmed typical morphological changes via EMT from HGF treatment (Fig. 6a). In agreement with prior reports,47,48 we observed the downregulation of E-cadherin and upregulation of vimentin expression. We also observed differences in cell packing and cell morphology: untreated MDCK cells displayed a cobblestone morphology as a closely packed cell monolayer with E-cadherin staining colocalizing at the areas of lateral cell–cell contacts. In contrast, in the presence of HGF, the MDCK cells adopted a spindle-shaped morphology and vimentin expression was significantly higher. HGF-treated MDCK cells have a lower value of the relaxation time constant (λ = 9.6 ± 0.9 s−1n = 30 from 3 different devices measured 10 times each) than the untreated group (λ = 12.2 ± 1.2 s−1, n = 30 from 3 different devices measured 10 times each, Fig. 6c). This indicates that the HGF treated MDCK cell layer is softer than the untreated cells. This is expected for the following reasons: in untreated MDCK cells, polarized cells interact with the basement membrane through integrins and are held together through adherent junctions.49,50 During EMT, the overall monolayer stiffness decreases due to weakened cell–cell adhesions and rearrangements in the cytoskeleton. Adherent junctions degrade and are replaced by proteins that provide greater junctional flexibility.51 This is shown by the diminished presence of E-cadherin localized to the periphery of the cells as punctuated dots because mesenchymal cells lack apico-basal polarity, which further shows morphological rearrangement upon EMT. Previous studies showed that the presence of vimentin networks reduced the effective cytoskeletal mesh size and decreased the viscoelastic relaxation time constant (λ) of the cytoskeleton, resulting in a softer cell layer.52
As part of our controls for this experiment, we also obtained the viscoelastic evolution of untreated MDCK cells during growth and monolayer formation. The relaxation time constant increases from the baseline of PDMS on day 1 to that of a confluent MDCK cell monolayer on day 7, as expected (Fig. 6c).
To confirm that the stiffness changes are due to differences in cell phenotype and not compromised cell metabolism, we performed a PrestoBlue assay (Fig. S4†). The result showed that there was no significant difference in metabolic activity between cells cultured with and without HGF, indicating that the relaxation time constant change was only due to phenotypic changes. Cell detachment also had negligible contributions to the relaxation time constant and stiffness. EMT has been linked to significant cytoskeleton remodeling that weakens cell–cell adhesions but strengthens cell–matrix adhesions.52 Unlike MDCK cells treated with the trypsin-EDTA solution, HGF treated MDCK cells are more resistant to the shear force from fluid flow and are unlikely to detach from the PDMS channel wall.
Conclusion
In this study, we developed a microfluidic system that leverages elastohydrodynamic phenomena to measure the viscoelasticity of cellular monolayers at both short (∼minutes) and long (∼days) time scales. The EHD phenomenon has a higher sensitivity compared to other techniques likely due to the Boussinesq-like dependence of substrate deformation on additional layers (here, represented by the cells). As the sensor is placed near the interface, at a distance of a similar length scale to the cellular monolayers, small changes in monolayer size or mechanical properties lead to large changes in the substrate and sensor response. By using EHD, we obtained a baseline on MDCK cells with a 30-fold reduction in the noise. This improved resolution made it possible to make direct mechanical measurements of monolayer integrity (trypsinization) and morphological changes (epithelial-to-mesenchymal transition). The short-term trypsinization experiments showed that both the cell body and extracellular matrix proteins contribute to the mechanical integrity of the monolayer, as expected. The long-term epithelial-to-mesenchymal transition experiments validated that epithelial monolayers become softer after EMT due to weakened intercellular adhesion. Throughout both experiments, the platform required minimal adjustments to cell culturing protocols and had significantly shorter acquisition times compared to AFM and other optics-based techniques. This minimal handling and data acquisition time made it easier to maintain cell culturing conditions, like sterility. In principle, this platform now enables simultaneous labeling and long-time monitoring of viscoelasticity in the field of drug screening and disease pathogenesis. Time resolved data could provide a method to investigate the kinetics of diseases which manifest as changes in stiffness. Similarly, the kinetics of drugs or exogenous transcription factors which impact stiffness could also be resolved. This platform would be especially useful in cell types and processes where the stiffness is expected to change, like in sepsis in vascular tissue or fibrotic processes in epithelial cells. Considering the ease of integration of the platform, which can be taken or removed from incubators as easily as any culture flask, the platform is well-suited to investigate temporal evolution with environmental effects like hypoxia. While we focused on monolayers here, we expect that the platform can be extended to thin films, including cells encapsulated in synthetic matrices. Given the wide use of cellular monolayers and importance of intercellular adhesions in diseases ranging from fibrosis and sepsis to cancer metastasis, among others, this platform will enable rapid monitoring of phenotypic changes in viscoelasticity for use in both basic biology and drug discovery.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We would like to thank Dr. Yong Zhao for the assistance with scanning electron microscopy. We acknowledge the W. M. Keck Center for the use of the scanning electron microscope and the Bio-imaging Center of the Delaware Biotechnology Institute for the use of the confocal microscope. This work was supported by the National Institutes of Health (R01DC014461, P20GM139760) and the University of Delaware Gore Graduate Fellowship.References
- S. Suresh, Biomechanics and Biophysics of Cancer Cells, Acta Mater., 2007, 55(12), 3989–4014 CrossRef CAS.
- D. A. Fletcher and R. D. Mullins, Cell Mechanics and the Cytoskeleton, Nature, 2010, 463(7280), 485–492 CrossRef CAS PubMed.
- C. Guillot and T. Lecuit, Mechanics of Epithelial Tissue Homeostasis and Morphogenesis, Science, 2013, 340(6137), 1185–1189 CrossRef CAS PubMed.
- J. M. Barnes, L. Przybyla and V. M. Weaver, Tissue Mechanics Regulate Brain Development, Homeostasis and Disease, J. Cell Sci., 2017, 130(1), 71–82 CrossRef CAS PubMed.
- Y. Nematbakhsh and C. T. Lim, Cell Biomechanics and Its Applications in Human Disease Diagnosis, Acta Mech. Sin., 2015, 31, 268–273 CrossRef CAS.
- J. S. Saini, B. Corneo, J. D. Miller, T. R. Kiehl, Q. Wang, N. C. Boles, T. A. Blenkinsop, J. H. Stern and S. Temple, Nicotinamide Ameliorates Disease Phenotypes in a Human IPSC Model of Age-Related Macular Degeneration, Cell Stem Cell, 2017, 20(5), 635–647 CrossRef CAS PubMed.
- M. Deiana, S. Calfapietra, A. Incani, A. Atzeri, D. Rossin, R. Loi, B. Sottero, N. Iaia, G. Poli and F. Biasi, Derangement of Intestinal Epithelial Cell Monolayer by Dietary Cholesterol Oxidation Products, Free Radical Biol. Med., 2017, 113, 539–550 CrossRef CAS PubMed.
- S. L. Friedman, D. Sheppard, J. S. Duffield and S. Violette, Therapy for Fibrotic Diseases: Nearing the Starting Line, Sci. Transl. Med., 2013, 5, 167sr1 Search PubMed.
- Y. M. Efremov, I. M. Zurina, V. S. Presniakova, N. V. Kosheleva, D. V. Butnaru, A. A. Svistunov, Y. A. Rochev and P. S. Timashev, Mechanical Properties of Cell Sheets and Spheroids: The Link between Single Cells and Complex Tissues, Biophys. Rev., 2021, 13, 541–561 CrossRef PubMed.
- L. Aoun, S. Larnier, P. Weiss, M. Cazales, A. Herbulot, B. Ducommun, C. Vieu and V. Lobjois, Measure and Characterization of the Forces Exerted by Growing Multicellular Spheroids Using Microdevice Arrays, PLoS One, 2019, 14(5), e0217227 CrossRef CAS PubMed.
- J. C. Villalobos Lizardi, J. Baranger, M. B. Nguyen, A. Asnacios, A. Malik, J. Lumens, L. Mertens, M. K. Friedberg, C. A. Simmons and M. Pernot, A Guide for Assessment of Myocardial Stiffness in Health and Disease, Nature Cardiovascular Research, 2022, 1(1), 8–22 CrossRef.
- A. Fuhrmann, J. R. Staunton, V. Nandakumar, N. Banyai, P. C. W. Davies and R. Ros, AFM Stiffness Nanotomography of Normal, Metaplastic and Dysplastic Human Esophageal Cells, Phys. Biol., 2011, 8(1), 15007 CrossRef CAS PubMed.
- M. Dao, C. T. Lim and S. Suresh, Mechanics of the Human Red Blood Cell Deformed by Optical Tweezers, J. Mech. Phys. Solids, 2003, 51(11–12), 2259–2280 CrossRef.
- F. K. Glenister, R. L. Coppel, A. F. Cowman, N. Mohandas and B. M. Cooke, Contribution of Parasite Proteins to Altered Mechanical Properties of Malaria-Infected Red Blood Cells, Blood, 2002, 99(3), 1060–1063 CrossRef CAS PubMed.
- L. Petit, M. Gibert, A. Gourch, M. Bens, A. Vandewalle and M. R. Popoff, Clostridium Perfringens Epsilon Toxin Rapidly Decreases Membrane Barrier Permeability of Polarized MDCK Cells, Cell. Microbiol., 2003, 5(3), 155–164 CrossRef CAS PubMed.
- B. Srinivasan, A. R. Kolli, M. B. Esch, H. E. Abaci, M. L. Shuler and J. J. Hickman, TEER Measurement Techniques for in Vitro Barrier Model Systems, J. Lab. Autom., 2015, 20(2), 107–126 CrossRef CAS PubMed.
- K. Benson, S. Cramer and H.-J. Galla, Impedance-Based Cell Monitoring: Barrier Properties and Beyond, Fluids Barriers CNS, 2013, 10(1), 1–11 CrossRef PubMed.
- B. Jovov, N. K. Wills and S. A. Lewis, A Spectroscopic Method for Assessing Confluence of Epithelial Cell Cultures, Am. J. Physiol., 1991, 261(6), C1196–C1203 CrossRef CAS PubMed.
- P. Polimeno, A. Magazzu, M. A. Iati, F. Patti, R. Saija, C. D. E. Boschi, M. G. Donato, P. G. Gucciardi, P. H. Jones and G. Volpe, Optical Tweezers and Their Applications, J. Quant. Spectrosc. Radiat. Transfer, 2018, 218, 131–150 CrossRef CAS.
- R. W. Style, R. Boltyanskiy, G. K. German, C. Hyland, C. W. MacMinn, A. F. Mertz, L. A. Wilen, Y. Xu and E. R. Dufresne, Traction Force Microscopy in Physics and Biology, Soft Matter, 2014, 10(23), 4047–4055 RSC.
- F. Li, J. H.-C. Wang and Q.-M. Wang, Thickness Shear Mode Acoustic Wave Sensors for Characterizing the Viscoelastic Properties of Cell Monolayer, Sens. Actuators, B, 2008, 128(2), 399–406 CrossRef CAS.
- A. Adamo, A. Sharei, L. Adamo, B. Lee, S. Mao and K. F. Jensen, Microfluidics-Based Assessment of Cell Deformability, Anal. Chem., 2012, 84(15), 6438–6443, DOI:10.1021/ac300264v.
- J. Guck, S. Schinkinger, B. Lincoln, F. Wottawah, S. Ebert, M. Romeyke, D. Lenz, H. M. Erickson, R. Ananthakrishnan and D. Mitchell, et al., Optical Deformability as an Inherent Cell Marker for Testing Malignant Transformation and Metastatic Competence, Biophys. J., 2005, 88(5), 3689–3698, DOI:10.1529/biophysj.104.045476.
- A. V. Zaretski, S. E. Root, A. Savchenko, E. Molokanova, A. D. Printz, L. Jibril, G. Arya, M. Mercola and D. J. Lipomi, Metallic Nanoislands on Graphene as Highly Sensitive Transducers of Mechanical, Biological, and Optical Signals, Nano Lett., 2016, 16(2), 1375–1380, DOI:10.1021/acs.nanolett.5b04821.
- X. Wang and I. C. Christov, Theory of the Flow-Induced Deformation of Shallow Compliant Microchannels with Thick Walls, Proc. R. Soc. A, 2019, 475(2231), 20190513 CrossRef PubMed.
- I. C. Christov, V. Cognet, T. C. Shidhore and H. A. Stone, Flow Rate-Pressure Drop Relation for Deformable Shallow Microfluidic Channels, J. Fluid Mech., 2018, 841, 267–286, DOI:10.1017/jfm.2018.30.
- E. Boyko, H. A. Stone and I. C. Christov, Flow Rate-Pressure Drop Relation for Deformable Channels via Fluidic and Elastic Reciprocal Theorems, Phys. Rev. Fluids, 2022, 7(9), L092201 CrossRef.
- G. Guyard, F. Restagno and J. D. Mcgraw, Elastohydrodynamic Relaxation of Soft and Deformable Microchannels, Phys. Rev. Lett., 2022, 129(20), 204501 CrossRef CAS PubMed.
- T. Gervais, J. El-Ali, A. Günther and K. F. Jensen, Flow-Induced Deformation of Shallow Microfluidic Channels, Lab Chip, 2006, 6(4), 500–507, 10.1039/b513524a.
- C. Dhong, S. J. Edmunds, J. Ramírez, L. V. Kayser, F. Chen, J. V. Jokerst and D. J. Lipomi, Optics-Free, Non-Contact Measurements of Fluids, Bubbles, and Particles in Microchannels Using Metallic Nano-Islands on Graphene, Nano Lett., 2018, 18(8), 5306–5311, DOI:10.1021/acs.nanolett.8b02292.
- A. Hemmasizadeh, M. Autieri and K. Darvish, Multilayer Material Properties of Aorta Determined from Nanoindentation Tests, J. Mech. Behav. Biomed. Mater., 2012, 15, 199–207 CrossRef PubMed.
- M. Malakouti, M. Ameri and P. Malekzadeh, Dynamic Viscoelastic Incremental-Layerwise Finite Element Method for Multilayered Structure Analysis Based on the Relaxation Approach, J. Mech., 2014, 30(6), 593–602 CrossRef.
- H. S. Gupta, J. Seto, S. Krauss, P. Boesecke and H. R. C. Screen, In Situ Multi-Level Analysis of Viscoelastic Deformation Mechanisms in Tendon Collagen, J. Struct. Biol., 2010, 169(2), 183–191 CrossRef CAS PubMed.
- N. Alam and N. T. Asnani, Vibration and Damping Analysis of Multilayered Rectangular Plates with Constrained Viscoelastic Layers, J. Sound Vib., 1984, 97(4), 597–614 CrossRef.
- S. R. Aglyamov, S. Wang, A. B. Karpiouk, J. Li, M. Twa, S. Y. Emelianov and K. V. Larin, The Dynamic Deformation of a Layered Viscoelastic Medium under Surface Excitation, Phys. Med. Biol., 2015, 60(11), 4295–4312, DOI:10.1088/0031-9155/60/11/4295.
- Y. Huang, K. Choi and C. H. Hidrovo, The Improved Resistance of PDMS to Pressure-Induced Deformation and Chemical Solvent Swelling for Microfluidic Devices, Microelectron. Eng., 2014, 124, 66–75 CrossRef.
- D. P. Gaver, D. Halpern, O. E. Jensen and J. B. Grotberg, The Steady Motion of a Semi-Infinite Bubble through a Flexible-Walled Channel, J. Fluid Mech., 1996, 319, 25–65 CrossRef.
- J. E. Wagenseil and R. P. Mecham, Vascular Extracellular Matrix and Arterial Mechanics, Physiol. Rev., 2009, 89(3), 957–989 CrossRef CAS PubMed.
- N. Khalilgharibi, J. Fouchard, N. Asadipour, R. Barrientos, M. Duda, A. Bonfanti, A. Yonis, A. Harris, P. Mosaffa and Y. Fujita, Stress Relaxation in Epithelial Monolayers Is Controlled by the Actomyosin Cortex, Nat. Phys., 2019, 15(8), 839–847 Search PubMed.
- B. L. Schumann, T. E. Cody, M. L. Miller and G. D. Leikauf, Isolation, Characterization, and Long-Term Culture of Fetal Bovine Tracheal Epithelial Cells, In Vitro Cell. Dev. Biol., 1988, 24(3), 211–216 CrossRef CAS PubMed.
- F. Sorba, A. Poulin, R. Ischer, H. Shea and C. Martin-Olmos, Integrated Elastomer-Based Device for Measuring the Mechanics of Adherent Cell Monolayers, Lab Chip, 2019, 19(12), 2138–2146 RSC.
- C. M. Flanigan and K. R. Shull, Adhesive and Elastic Properties of Thin Gel Layers, Langmuir, 1999, 15(15), 4966–4974 CrossRef CAS.
- R. Strippoli, R. Moreno-Vicente, C. Battistelli, C. Cicchini, V. Noce, L. Amicone, A. Marchetti, M. A. Del Pozo and M. Tripodi, Molecular Mechanisms Underlying Peritoneal EMT and Fibrosis, Stem Cells Int., 2016, 2016, 3543678 Search PubMed.
- R. Kalluri and R. A. Weinberg, The Basics of Epithelial-Mesenchymal Transition, J. Clin. Invest., 2009, 119(6), 1420–1428 CrossRef CAS PubMed.
- F. Liu, S. Song, Z. Yi, M. Zhang, J. Li, F. Yang, H. Yin, X. Yu, C. Guan and Y. Liu, HGF Induces EMT in Non-Small-Cell Lung Cancer through the HBVR Pathway, Eur. J. Pharmacol., 2017, 811, 180–190 CrossRef CAS PubMed.
- A. Ravikrishnan, T. Ozdemir, M. Bah, K. A. Baskerville, S. I. Shah, A. K. Rajasekaran and X. Jia, Regulation of Epithelial-to-Mesenchymal Transition Using Biomimetic Fibrous Scaffolds, ACS Appl. Mater. Interfaces, 2016, 8(28), 17915–17926 CrossRef CAS PubMed.
- M. K. Wendt, M. A. Taylor, B. J. Schiemann and W. P. Schiemann, Down-Regulation of Epithelial Cadherin Is Required to Initiate Metastatic Outgrowth of Breast Cancer, Mol. Biol. Cell, 2011, 22(14), 2423–2435 CrossRef CAS PubMed.
- S. Wu, Y. Du, J. Beckford and H. Alachkar, Upregulation of the EMT Marker Vimentin Is Associated with Poor Clinical Outcome in Acute Myeloid Leukemia, J. Transl. Med., 2018, 16(1), 1–9 CrossRef CAS PubMed.
- H. Oda, K. Tagawa and Y. Akiyama-Oda, Diversification of Epithelial Adherens Junctions with Independent Reductive Changes in Cadherin Form: Identification of Potential Molecular Synapomorphies among Bilaterians, Evol. Dev., 2005, 7(5), 376–389 CrossRef CAS PubMed.
- P. Hulpiau and F. Van Roy, Molecular Evolution of the Cadherin Superfamily, Int. J. Biochem. Cell Biol., 2009, 41(2), 349–369 CrossRef CAS PubMed.
- M. S. Balda and K. Matter, Tight Junctions at a Glance, J. Cell Sci., 2008, 121(22), 3677–3682 CrossRef CAS PubMed.
- S. E. Leggett, A. M. Hruska, M. Guo and I. Y. Wong, The Epithelial-Mesenchymal Transition and the Cytoskeleton in Bioengineered Systems, Cell Commun. Signaling, 2021, 19(1), 32 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3lc00457k |
| This journal is © The Royal Society of Chemistry 2023 |