Microfabricated acoustofluidic membrane acoustic waveguide actuator for highly localized in-droplet dynamic particle manipulation

Abstract

Precision manipulation techniques in microfluidics often rely on ultrasonic actuators to generate displacement and pressure fields in a liquid. However, strategies to enhance and confine the acoustofluidic forces often work against miniaturization and reproducibility in fabrication. This study presents microfabricated piezoelectric thin film membranes made via silicon diffusion for guided flexural wave generation as promising acoustofluidic actuators with low frequency, voltage, and power requirements. The guided wave propagation can be dynamically controlled to tune and confine the induced acoustofluidic radiation force and streaming. This provides for highly localized dynamic particle manipulation functionalities such as multidirectional transport, patterning, and trapping. The device combines the advantages of microfabrication and advanced acoustofluidic capabilities into a miniature “drop-and-actuate” chip that is mechanically robust and features a high degree of reproducibility for large-scale production. The membrane acoustic waveguide actuators offer a promising pathway for acoustofluidic applications such as biosensing, organoid production, and in situ analyte transport.

---

Introduction

Ultrasonic technologies have brought significant contributions to the field of microfluidics for precision manipulation techniques,^1–4 notably due to their relatively low power requirement and superior biocompatibility.^5,6 Ultrasonic actuators have demonstrated the ability to accomplish various microfluidic functions such as separation,^3,7–11 patterning,^12–17 trapping,^18–21 focusing,^22,23 concentrating,^24–26 and guiding^27–29 of particles and analytes, which are crucial functions for biomedical applications. To achieve such results, it is often required to enhance and confine the acoustic field near the analytes, which, at this scale, is a challenging endeavor. Ultrasonic actuators used in acoustofluidics generally fit into three categories: off-the-shelf commercial piezoelectric transducers glued onto the microfluidic substrate, interdigitated transducers (IDTs) on a bulk piezoelectric substrate, and transducers on a thin-film piezoelectric layer.

Commercial piezoelectric transducers attached to structures generate global acoustofluidic effects in microfluidic volumes. The acoustic energy is distributed into the whole device as bulk acoustic waves (BAWs) or Lamb waves, and its transmission is strongly affected by the attachment's position and mechanical properties. However, different methods can be leveraged to confine the acoustic fields. Carefully designed features to be bonded or etched onto the substrate like micropillars,^27,30 vibrating sharp edges embedded into microfluidic channels,^31–33 and micromachined holographic lenses^34,35 have successfully been used to enhance the intensity of the acoustofluidic effects. Likewise, finding the substrate's acoustic focal points, in relation to the position of the transducers,³⁶ and adding micromachined sound-trapping dimples onto the substrate can amplify converging flexural waves and their resulting acoustic fields.³⁷

IDTs on a bulk piezoelectric substrate can generate surface acoustic waves (SAWs) and Lamb waves and are utilized in various settings, from the generation of streaming inside a sessile droplet to particle separation inside a microfluidic channel. To accurately control the acoustic fields induced by the mechanical deformations originating from the IDTs, several approaches have been investigated, such as shaping the electrodes into focused IDTs,^38,39 slanted IDTs^40,41 and holographic IDTs,^42,43 and pairing IDTs with each other,^15,44–47 with microfluidic channels^23,48 or with other structural obstacles such as boundaries^24,49 and phononic crystals.^50,51

Piezoelectric thin film transducers can bring piezoelectric actuation to virtually any substrate, opening a wide array of possibilities for the development of acoustofluidic devices based on CMOS and MEMS processes, which allow for miniaturization of devices and wafer-level batch fabrication.^52–54 These processes can significantly benefit acoustofluidic lab-on-a-chip systems⁵⁵ due to their high degree of reproducibility, essential for consistent acoustic actuation, and low-cost batch fabrication. Thin-film transducers are compatible with most of the acoustophoretic methods deployed with their bulk piezoelectric counterparts, such as patterning,^56,57 sensing^44,58,59 and streaming generation.^44,60–62 However, the thin films can be deposited onto microfabricated features, enabling new actuation methods that were previously impossible. Microfabricated BAW cavity resonators featuring a piezoelectric thin film have been numerically⁶³ and experimentally⁵³ investigated. Microfabricated thin piezoelectric membranes have also been realized to locally enhance acoustofluidic phenomena for multimodal particle trapping on a Chladni microdisk by Vuillermet et al.⁶⁴ and particle transportation via flexural plate waves streaming by R. White's group.^65–70 However, as carried out by Vuillermet and White, microfabrication of membranes has relied on etching the back of the silicon wafer, which considerably weakens the structure of the device and complicates further microfluidic experiments and integration.

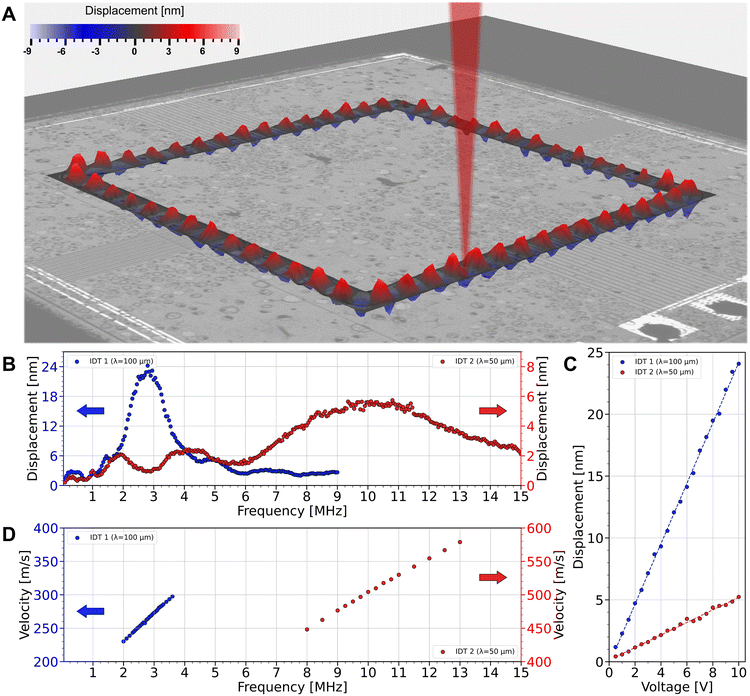
To advance the membrane approach pioneered by White and Vuillermet while preserving the batch fabrication and reproducibility qualities enabled by microfabrication, and improve the confinement of acoustofluidic effects, this study leverages a novel fabrication approach from piezoelectric over silicon-on-nothing (pSON).⁷¹ The acoustofluidic capabilities come from a microfabricated membrane acoustic waveguide actuator (MAWA) which drives flexural waves for in-droplet acoustophoretic manipulations. The MAWA is composed of a 2 μm-thick silicon (Si) membrane over a sealed and seamless cavity topped with a piezoelectric thin film (Fig. 1A). Leveraging this top-side fabrication technique allows for much more complex waveguide patterns than what is conventionally achievable through anisotropic/DRIE backside etching while avoiding weakening the mechanical structure. Such improvements leave the device completely flat and void of precarious backports, considerably facilitating the integration of membrane-based actuators to microfluidic systems and enabling versatile in-droplet localized acoustophoretic manipulation of particles (Fig. 1B).

Fig. 1 Functioning and novel acoustofluidic capabilities of the MAWA. (A) Schematic cross-section of the MAWA with aligned blue particles traveling in the wave propagation direction (white arrow). (B) Schematic of the MAWA device with a particle-laden sessile droplet on top with localized particles trapping on the membrane. (C) Schematic of the particle transport mechanism achieved experimentally under unidirectional traveling GFWs actuation from the MAWA. (D) Schematic of the cluster trapping mechanism achieved experimentally from counter-traveling GFWs by the MAWA. (E) Schematic of the rotating ring trapping mechanism achieved experimentally from counter-traveling GFWs by the MAWA. White chevron arrows are positioned to indicate the locations and directions from which the waves originate.

The MAWA consists of a piezoelectric thin film on a thin silicon layer and two pairs of IDTs which can together generate highly localized guided flexural waves (GFWs) as their propagation is circumscribed within the area of the sealed membrane. These waves travel at phase velocities smaller than the speed of sound in the fluid and produce strong localized evanescent streaming. Furthermore, several modes can easily be excited on the device's membrane using any of the 4 IDTs at various frequencies. Experiments show that acoustofluidic effects induced by traveling flexural waves can be leveraged to achieve complex particle manipulation functionalities: (1) GFWs can align and guide particles along the waveguide when a single IDT is actuated in acoustofluidic experiments (Fig. 1C). (2) Counter-traveling GFWs triggered by two opposed IDTs present the capability to trap particles in clusters and rings (Fig. 1D and E). (3) The distinct functions of the device are combined in a single experiment for in-droplet dynamic manipulation and in situ concentration of particles. The pSON-based MAWA emerges as a versatile toolset compatible with a wide variety of applications such as biosensing, organoid production, pulsation-free pumping, analytes separation, and acoustofluidic tweezing.

Device design and principles

Membrane acoustic waveguide actuator design

The device is a bulk Si chip featuring a 2 μm-thick Si membrane formed via the pSON process.⁷¹ The membrane has a width of 100 μm that is constant across the device and forms a rectangular closed-loop with rounded corners (Fig. 2A). A piezoelectric thin film of scandium-doped aluminum nitride (AlScN) is deposited on top of the flat surface bearing the membrane. The piezoelectric membrane device includes two different sets of IDTs (4 IDTs in total), which are used to generate GFWs traveling on the membrane. The IDTs are made of molybdenum (Mo) and are connected to the aluminum (Al) bond pads via Al routing. To prevent short-circuits between the two metal layers, an isolation layer of silicon dioxide (SiO₂) of 2 μm-thick is added, see Fig. 2B. The rectangular closed-loop shape of the membrane limits the reflection of the traveling waves and allows the IDTs to be positioned in pairs on opposite sides. The IDTs on opposite sides of the membrane waveguide share the same pitch and resonant properties, with IDTs 1 positioned at the top and bottom, and IDTs 2 positioned on the left and right segments, see Fig. 2A and insets. The IDTs 1 are designed for traveling waves with a wavelength of λ = 100 μm, while the IDTs 2 feature half the pitch at λ = 50 μm. The width of the interdigitated electrodes composing the IDTs is λ/4. The variation in the IDTs' design enables the excitation of two different sets of flexural waves and covers a broader frequency range, while the IDTs' configuration across the device segments allows for multiple combinations of IDTs to be simultaneously actuated. By actuating multiple IDTs and varying the actuation frequency, various resonance modes and traveling modes can be generated on the membrane waveguide. Both IDT designs have the anti-symmetric A0 mode as their primary flexural wave propagation mode on the membrane waveguide, which is in accordance with observations previously reported.⁶⁵

Fig. 2 Device's design and fabrication cross-section. (A) Top view of the acoustofluidic flexural wave device from an optical microscope. Dimensions of IDT 1 and IDT 2, pitch λ and finger width, are noted inside their respective inset bubble. The dashed line over the top IDT 1 represents the region where the schematic cross-section (B) is taken. (B) Schematic cross-section of the device with annotation of the layers' material and targeted thickness, the doped region, the buried cavity, and the membrane waveguide. The SiO₂ layer isolates the Mo electrodes of the IDTs from the Al layer of the bond pads and routing. (C) Photograph of a wire bonded device next to a Singaporean 0.10 SGD coin.

Electromechanical simulations of the MAWA were conducted using the finite element analysis (FEA) software COMSOL Multiphysics® (v6.0, Stockholm, Sweden) to characterize the frequency response (Fig. 3C) and the mode shape of the traveling flexural waves (Fig. 3A), see ESI† Movie S1. The simulated peak-to-peak displacement of the actuated membrane for a wide band of frequencies often utilized in acoustofluidics⁷² is shown in Fig. 3C and summarized in Table 1.

Fig. 3 Device's simulation results. (A) Tilted view of the linear simulation model's cross-section to show the deformation caused by the traveling GFWs. (B) Right-angled simulation model with GFWs traveling past a corner. All the simulation models have damping at the segments' end, hence the fast decay of the traveling waves. (C) Simulation results of the frequency response of both sets of IDTs from a 10 V_pk–pk sine signal with the MAWA immersed in water. Top inset shows the cross-section of the simulation model under deformation from sine actuation with traveling A0 GFWs propagating on both sides.

Table 1 Simulated and experimental results of the membrane displacement. Maximum peak-to-peak displacement amplitude and corresponding actuation frequency obtained from simulations and experiments for IDTs 1 and 2 immersed in water. The thickness of each material layer is also arranged on the right side for reference

	IDT	Water		Layer thickness (μm)
		Frequency (MHz)	Displacement (nm)	Si	AlScN	Mo
Simulations	1	2.88	24.19	1.8	0.4	0.15
	2	9.73	7.54
Experiments	1	2.82	24.21	2.0	0.3	0.2
	2	10.22	5.74

---

As a result of the waveguiding characteristics of the membrane, traveling flexural waves can change their direction of propagation and follow the complex shape of the membrane. As proof of concept, an alternative FEA model featuring an extra segment connected by a right-angled corner (Fig. 3B) was created. The simulation result shows that GFWs continue to propagate in the subsequent linear segment, past the corner, corroborating the experimental observations on changing the propagation direction, see ESI† Movie S2.

Actuation mechanism and mechanical characterization of GFWs

A signal generator generates a sinusoidal actuation signal of 10 V_pk–pk at a frequency ranging from 2–6 MHz for IDTs 1 and 7–16 MHz for IDTs 2. The actuation signal's electric field at the electrodes causes mechanical stress in the thin layer of piezoelectric AlScN via the inverse piezoelectric effect. The oscillating stress-induced deformations at the electrodes set the membrane in motion, forming traveling flexural waves. The generated waves traveling along the membrane were captured using a laser Doppler vibrometer (LDV), as illustrated in Fig. 4A. When a single IDT is continuously actuated, the flexural deformation of the membrane propagates on both adjacent segments and GFWs travel in both directions. The traveling waves dominate along the segments connected to the active IDT, while the segment opposite to the IDT is mainly populated by standing waves arising from the interference between the counter-traveling GFWs coming from both sides of the membrane waveguide,²⁸ see ESI† Movie S4.

Fig. 4 LDV characterization of the GFWs from the MAWA. (A) 3D visualization of the LDV measurement of the displacement of the water-loaded membrane under a continuous sine actuation signal of 10 V_pk–pk at 2.5 MHz from the bottom IDT 1 (λ = 100 μm). (B) LDV measurements of the frequency response of both sets of IDTs from a 10 V_pk–pk burst sine signal immersed in water. (C) Displacement amplitude of the membrane waveguide in immersion under water for different actuation voltages, ranging from 0.5 to 10 V, for IDT 1 at 2.8 MHz and IDT 2 at 10 MHz. (D) Phase velocity dispersion curve of the traveling flexural waves around the resonant frequency from both IDTs 1 and 2 immersed in water.

On the other hand, when two IDTs are continuously actuated at the same frequency, although they each behave independently, the counter-traveling flexural waves coming from each source IDT interfere with one another at the half-distance mark between the two actuated IDTs on the membrane waveguide. For the case of two opposite IDTs actuated simultaneously by a sine wave, traveling waves dominate on the segments adjacent to the IDTs, but the pattern quickly shifts on the subsequent linear segments where standing and rotating waves dominate, see ESI† Movie S5.

When IDTs are actuated in burst mode, see ESI† Movie S3, the LDV measurements reveal that the A0 traveling GFWs are confined onto the membrane waveguide. Furthermore, the group of waves can be seen preserving their momentum around a 90° corner and onto the next linear segment, as predicted by the simulation in Fig. 3B.

The amplitude of the GFWs on the piezoelectrically actuated membrane was measured using the LDV as a function of the actuation frequency, voltage amplitude, and loading medium. The experimental frequency response of the peak-to-peak membrane displacement induced by the two IDTs under immersion in water is shown in Fig. 4B and summarized in Table 1.

Following previous reports on flexural plate waves, the membrane displacement caused by the GFWs varies linearly with the actuation signal voltage⁶⁵ for a fixed frequency (Fig. 4C and D). Likewise, the phase velocity dispersion curves of the GFWs traveling on the membrane waveguide (Fig. 4E) are also linear. Flexural A0 waves are strongly dispersed in thin plates due to the mixing of shear and longitudinal waves, causing the phase and group velocities to vary with the frequency. When the plate is very thin, the phase velocity dispersion falls into a quasi-linear region at the very beginning of the dispersion spectrum,⁷³ which corroborates our experimental results.

Methods

Fabrication

The chip bearing the suspended membrane waveguide is a 3 mm × 3 mm microfabricated silicon chip from the piezoelectric over silicon-on-nothing process (pSON),⁷¹Fig. 2C. The chip can be further integrated with CMOS technology wafers by bonding. The pSON process starts with deep-etching arrays of micron-sized holes covering the exact shape corresponding to the desired membrane waveguide on the Si substrate. The etched wafer is then annealed at a high temperature to enable Si migration.^74–76 During this step, the silicon surrounding the etch holes diffuses and forms the sealed membrane, leaving a buried cavity underneath. The thickness of the membrane is around 2 μm, and the cavity is about 1 μm deep. Following the Si membrane formation, the relevant parts of the wafers are heavily doped by diffusion to form a conductive bottom electrode for the piezoelectric layer. The piezoelectric layer, here a 0.3 μm-thick layer of scandium-doped aluminum nitride (Al_0.85Sc_0.15N), is then deposited on the doped Si wafer to cover all the areas, including the membrane waveguide. Molybdenum (Mo), 0.2 μm-thick, is deposited and patterned into the interdigitated electrodes forming the IDTs, and a thin passivation layer of AlScN (50 nm) is added to prevent their oxidation. A patterned oxide layer is subsequently added to separate the final layer of aluminum (Al) (1 μm), forming the bond pads and electrical routing, from the Mo IDTs.

Flexural waves generation and characterization

The MAWA device is fixed on a PCB and wire bonded, Fig. 2C. A signal generator is connected to the PCB and generates the activation signal via SMA cables. To activate the device, a sinusoidal actuation signal of 10 V_pk–pk split into two outputs, and phase-shifted by 180° via a Balun device, is used at a frequency between 2 MHz and 15 MHz. To capture the GFWs' propagation in the time domain, the laser doppler vibrometer (LDV – Polytec MSA-500) and its internal function generator were used. To measure the voltage and frequency-dependent peak-to-peak membrane displacement, an external function generator (Keysight 33500B) was used to generate a 6-period-long sine burst actuation signal. A digital oscilloscope (Keysight DSOX4024A) is used to measure the output signal from the LDV. The measurements in the time domain were averaged 256 times for each frequency. The actuation signal at 10 V_pk–pk is swept from 0.05–9 MHz for IDT 1 and 0.05–15 MHz for IDT 2.

Finite element simulation

Simulations of the suspended flexural membrane waveguide were conducted using the finite element analysis (FEA) software COMSOL Multiphysics® (v6.0, Stockholm, Sweden). The FEA model in 3D consists of four pairs of interdigitated electrodes linearly arranged for each electrode to be uniformly spaced by λ/2. On both sides of the IDT, the segments guiding the flexural waves are subjected to a progressive Rayleigh damping to completely attenuate the deformation at the end of the segments and suppress any reflected standing wave. The solid mechanics, electrostatic and transient pressure acoustics physics, along with their multiphysics complements, piezoelectric effect and acoustic-structure boundary, were used for the model. The model is solved in the time domain, and the maximum membrane displacement on the waveguide after 6 periods is used as a data point. Akin to the LDV measurements, the actuation signal is 10 V_pk–pk and swept from 0.05–9 MHz for IDT 1 (λ = 100 μm) and 0.05–15 MHz for IDT 2 (λ = 50 μm).

Fluid sample preparation

For all the acoustofluidic experiments presented in this paper, a droplet of 5 to 10 μL of solution was added on top of the device. The liquid sample used for the experiments is a solution containing blue or red polystyrene particles (Magsphere, USA) with a diameter of 10 μm and 5 μm, respectively. Pluronic F127 at 0.5% m/m was added as a surfactant. The droplet was flattened to facilitate the microscope observations using a glass slide installed atop. The glass slide is supported by conformable sticky bumpers, positioning it 1 to 2 mm above the device, far greater than the 15 μm depth of the MAWA's evanescent acoustofluidic effects.

Experimental setup

Acoustofluidic experiments were conducted on the stage of a non-inverted reflection microscope (Olympus BX53M) with a video recording capable camera (Olympus DP27). A signal generator (Agilent 33220A) was connected to the PCB via SMA cables and provided the activation signal to the device. To activate the device, a continuous sinusoidal actuation signal of 10 V_pk–pk was generated at frequencies ranging from 2.5–3.15 MHz for IDT 1 and 9.8 MHz for IDT 2.

Results and discussion

Self-aligned particle transport

To characterize the acoustofluidic capabilities of the MAWA, a droplet of a solution containing polystyrene particles of 10 μm in diameter was added on top of the device such that the liquid covers the membrane and non-membrane areas. Under single-IDT actuation, where traveling GFWs are the most common waves populating the membrane waveguide, the particles on the membrane are attracted toward the maximum membrane displacement amplitude zone near the middle part of the membrane. Furthermore, the particles are pushed forward in the wave propagation direction until the traveling waves vanish while still staying in proximity to the membrane's surface. The combination of these two effects aligns the particles over a virtual ridge formed by the traveling GFWs and transports them following the traveling waves' path along the linear segments and around the corners of the membrane waveguide of the device. These experimental observations are depicted in the schematic of Fig. 5A and are valid for a short range of frequencies around the resonant frequency, usually ±1 MHz for the IDT 1. As soon as the continuous sine actuation is turned on, the particles are set in motion almost instantly (Fig. 5B) and stop all at once when the actuation is off. Fig. 5C shows the LDV measurement of the localized membrane displacement of GFWs at 2.5 MHz traveling around a corner, in the same device region as the one observed in Fig. 5B.

Fig. 5 Experimental results of particle alignment and transportation by the MAWA. (A) 3D schematic of the membrane waveguide under deformation from traveling GFWs. The aligned blue particles travel in the wave propagation direction (white arrow). The red ellipses illustrate the localized streaming in the bulk fluid causing the blue particles to align over the membrane. (B) Optical microscope images from before and during acoustofluidic actuation from the MAWA after 2 seconds, at which point the blue particles have been aligned and are traveling in the wave propagation direction (white arrow). White chevron arrows are positioned to indicate the locations and directions from which the waves originate. (C) LDV measurement of an underwater burst sine wave at 2.5 MHz,10 V_pk–pk, traveling clockwise (white arrow). Upward and downward membrane displacement is in the order of 4.5 nm. (D) Sequential time-stamped frames from optical microscope images showing 10 μm blue polystyrene particles moving upward under the IDT 1 actuation at 2.82 MHz, 10 V_pk–pk. (E) Particle velocities of traveling 10 μm polystyrene particles under actuation voltage amplitudes ranging from 4 to 10 V_pk–pk at 2.82 MHz. The error bars on the measurement points represent the standard deviation of the mean for the velocity of all the particles for each voltage amplitudes. Experiments recorded on video were processed using Trackpy to detect the particles and extract their velocity, see ESI.†

The first part of the particles' motion, regarding the membrane's attractive force and particles' self-alignment over the waveguide, is reminiscent of the phenomenon called inverse Chladni patterns⁶⁴ but limited to a very localized region. Literature reports that a strong acoustic streaming-induced drag force F_drag is usually the main driving force for such microscale patterns to arise inside a liquid.^37,77

In addition, the acoustic radiation force F_rad is also actively dragging particles downward, toward the vibrating substrate, and can even push microparticles to converge at an acoustic anti-node when the kinematic energy component of the radiation force dominates over the potential energy component.⁷⁷ In the present experiment, where the vibration comes from a directional traveling wave, the radiation force's contribution to the particle alignment on the membrane would still work in the same direction as the acoustic streaming for the in-plane force. Furthermore, the size of the particles, according to Dorrestijn et al.,⁷⁸ would also play a key role. At high frequencies, the thickness of the viscous boundary layer δ is significantly reduced following eqn (1),

where ν is the kinematic viscosity of the fluid, and ω the angular frequency of the acoustic perturbation. Around 2.88 MHz, the thickness of the viscous boundary layer, where the boundary streaming is confined, is only 314 nm, a fraction of the radius of the particles used in our experiments. As a result, the particles would predominantly be affected by the acoustic streaming-induced drag force F_drag in the bulk of the liquid pointing toward the flexural waves' anti-nodes. This force acting perpendicularly to the membrane is proportional to the time-averaged fluid velocity flowing toward the membrane, which is a second-order effect describing a steady flow emerging from the non-linear interaction of the sound waves in the fluid.

The second part of the particles' motion, a constant drift forward in the direction of the wave propagation when the particles are in the vicinity of the actuated membrane, is also attributable to acoustic streaming, according to Moroney et al.⁶⁵ The amplitude of the streaming is evanescent in the fluid in the direction normal to the membrane waveguide, varying as exp(−γz), with a depth of γ⁻¹, which is around 15 μm at 2.88 MHz in water.

where γ is the attenuation coefficient, k₀ is the wavenumber of the sound waves in the fluid, v_GFW is the phase velocity of the traveling waves, and c_f is the speed of sound in the fluid. This leads to the streaming-induced drag force being highly localized onto the membrane. Particles affected by the drag force are seen in motion in a composition of sequential movie frames from an optical microscope (Fig. 5D). Under the F_drag in the direction of the traveling waves, particles can reach velocities above 150 μm s⁻¹ (Fig. 5E), which has also been previously reported for flexural plate waves.^65,67 Furthermore, the particles' velocity profile from the data in Fig. 4D fits a parabolic curve, which reflects the second-order velocities' relation with the membrane displacement amplitude, v_2nd-order ∝ A²,⁶⁵ and confirms the involvement of a second-order streaming-induced force in the forward motion of the water-borne microparticles.

This one-of-a-kind transport mechanism differs considerably from the acoustofluidic transport mechanisms reported in the past, leveraging SAWs^24,45 and vibrating structures.^27,79 The latter often occupies a large footprint, presents limited degrees of freedom and, in some cases, cannot be fully realized through microfabrication processes. On the other hand, this novel type of piezoelectric thin film MAWA opens new avenues for highly localized streaming and particles transport as the pSON fabrication platform allows for customizable and scalable MAWA designs, further supported by a high degree of reproducibility, minimal footprint, and large-scale production.

Particle cluster trap

The acoustofluidic MAWA device consists of multiple IDTs which control localized flexural wave interference. The interference is categorized into two primary modes, namely, standing waves and rotating waves. To investigate the acoustofluidic capabilities of the two interference modes, the active surface of the device was loaded with a particle-laden droplet.

Fig. 6A shows a schematic featuring counter-traveling GFWs interfering on the membrane waveguide. The blue polystyrene particles are shown to be trapped in clusters at the nodes, where the membrane displacement is minimal. The experimental results represented by the schematic are seen in Fig. 6B, where 5 μm polystyrene particles are trapped and form several static clusters along a vertical segment of the membrane waveguide under continuous actuation from the opposed top and bottom IDTs 1. The LDV measurements corresponding to the membrane displacement during the experiment (Fig. 6C) show two frames separated by half a period and reveal that this type of trap arises when the flexural mode of the membrane waveguide segment features counter-propagating waves that interfere exactly to form constructive standing waves. By comparing the data of the two figures, one can see that the particles trapped by the standing waves are located precisely at the nodes between the alternating anti-nodes (red peaks and blue valleys).

Fig. 6 Experimental results of particle trapping from interfering GFWs. (A) 3D schematic of the membrane waveguide under deformation from counter-traveling GFWs. The blue particles are trapped at the flexural waves' nodes. The white arrows indicate the propagation direction of the waves. The red ellipses illustrate the localized streaming in the bulk fluid causing the blue particles to align over the membrane. The short red arrows illustrate the localized acoustic radiation force acting on the blue particles to trap them in clusters at the waves' displacement nodes over the membrane. (B) Optical microscope image from acoustofluidic trapping experiment showing 5 μm particles trapped on the membrane under dual IDT 1 actuation at 3.102 MHz, 10 V_pk–pk. White chevron arrows are positioned to indicate the location and directions from which the waves originate. (C) LDV measurement showing the two beats from a standing wave formed under continuous dual IDT actuation at 3.034 MHz, 10 V_pk–pk. The segments presented in (C) and (B) are from the same part of the device and aligned to show the relation between the position of the particle clusters and the location of the displacement nodes of the waves. (D) Arrangement of LDV measurement images covering half a period of a rotating wave, arising from continuous dual IDT actuation at 3.034 MHz, 10 V_pk–pk. The blue and red arrows indicate the movement of the anti-nodes toward the next frame. The dotted circle illustrates the rotational trajectory of the anti-node motion, while the × marks the node's position. (E) Optical image of particles trapped in a rotating ring at the same location as the LDV measurement of (D) has been conducted. The particles rotate clockwise, and the particles' orbit matches closely with the dotted circle used for the LDV measurement.

Particle trapping at pressure nodes is a common phenomenon in acoustofluidics. It is mainly attributed to the acoustic radiation force,^2,18,80–82 where a stationary acoustic field with a strong gradient acts on particles according to their physical properties and the ones from the liquid medium. By calculating the monopole scattering coefficient and the dipole scattering coefficient, one obtains the acoustic contrast factor.⁸³ In the present case, the acoustic contrast factor has a positive value (around 0.165), which indicates that the force pushes the particles to the acoustic pressure nodes. The nodes of the guided flexural standing waves and the acoustic pressure nodes being co-located, polystyrene particles should align with the flexural standing waves' nodes under a dominant acoustic radiation force, which agrees with our experimental observations.

Particle ring trap

Under dual IDTs actuation, other modes, such as rotating waves, arise by shifting the frequency away from a constructive standing mode. Being bound to a node, rotating waves⁸⁴ retain many of the acoustofluidic features present in standing GFWs. However, the rotating pattern of the anti-nodes around the node gives rise to a circularly traveling wave, which brings back the streaming-induced drag force F_drag and lateral F_rad responsible for the particle alignment along the trajectory of traveling waves. Rotating waves are defined as a wave field rotating around a fixed node. They may arise from the linear combination of two waves, as observed under the LDV (Fig. 6D). The circular trajectory of the anti-nodes is outlined by the dotted circle, while an × marks the central node. The colored arrows around the dotted circle depict the position and direction of the positive and negative anti-nodes.

The corresponding acoustofluidic experiment results (Fig. 6E) from the device loaded with a droplet of solution with 5 μm polystyrene particles are displayed along with the LDV results. The particles' orbit around the node in Fig. 6E coincides with the dotted circle representing the rotational trajectory of the anti-nodes in Fig. 6D.

The rotating wave here acts as a ring trap for the 5 μm particles, superposed on the virtual ridge formed by the anti-nodes motion. The traveling motion of the anti-nodes, akin to the traveling wave propagation with a single IDT, generates a highly localized F_drag which pushes the particles to orbit around the node. Other ring-like traps and features have been reported in acoustofluidic experiments before, based on mode-switching in a circular Chladni microplate,^64,77 asymmetric SAWs propagation,²⁴ bulk vibration of a substrate⁸⁵ and SAW microcentrifugation.⁸⁶ However, the ring trap mechanism presented here is highly localized, easily controllable, and scalable compared to the earlier works reported.

Highly localized dynamic particle control in a sessile droplet

The flexible and adaptable framework of the pSON fabrication platform allows for complex designs of membrane waveguides to be paired with multiple IDTs, all working together dynamically to transport and trap particles at different points on the device. The characteristics of the vibrational modes populating the membrane waveguide depend on the membrane geometry, the frequency, and the position of the IDTs. The working mechanism of the device is intuitive for the user, who can operate the system by adding a sessile droplet containing the desired sample on top of the device and activating the IDTs simultaneously or sequentially. The experiment illustrated in Fig. 7 demonstrates the capability of the MAWA device to dynamically control water-borne particles with precision and rapidity while switching from one actuation mode to another, all during the same experiment.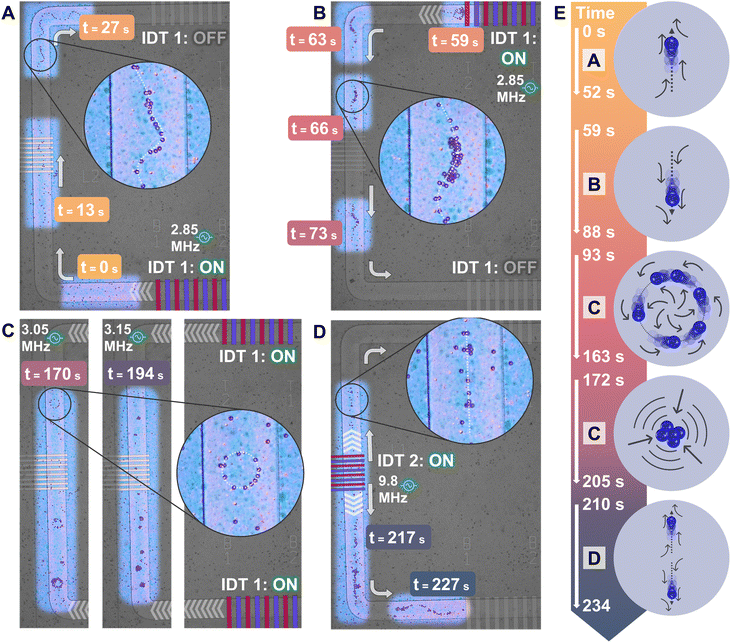

Fig. 7 Time evolution of dynamic control of particles in sessile droplet via MAWA. Parts (A) to (D) are arrangements of reframed snapshots extracted from ESI† Movie S6, acquired on an optical microscope. The time stamps associated with each snapshot are colored to follow the color gradient used in the timeline in part (E). Insets are added to magnify the phenomena observed under specific actuation modes. White arrows indicate the propagation direction of the waves and the particles. White chevron arrows are positioned to indicate the location and direction from which the waves originate. (A) Arrangement of 3 snapshots showing the particles' position at separate times to display the particles aligning on the membrane and the upward/clockwise particle transport caused by traveling GFWs originating from the bottom IDT 1 actuated at 2.85 MHz. (B) Arrangement of 4 snapshots showing the particles' position at separate times to display their downward/counterclockwise displacement from the top segment to the bottom one caused by traveling GFWs originating from the top IDT 1 actuated at 2.85 MHz. (C) Arrangement of 2 snapshots showing the particles' position and behavior at separate times. The left and middle snapshots are from the same segment, on the left side of the device, and are both obtained under dual IDT actuation (right) but at different frequencies. The rotating circle traps appear at 3.05 MHz, while the static cluster traps appear at 3.15 MHz. (D) Arrangement of 2 snapshots showing the particles' position at separate times to display the particle transport caused by traveling GFWs originating from the left IDT 2 actuated at 9.8 MHz. Particles previously trapped along the left segment move in two different directions, away from the actuated IDT 2. (E) Timeline for parts (A) to (D) presenting the linear time relation between each part and illustrating which acoustofluidic phenomena are observed.

Fig. 7 shows several individually time-stamped sequential frames of acoustofluidic experiments featuring 10 μm particles. The sequential displacement of the actuated particles over the membrane waveguide is illustrated in parts A to D of Fig. 7. To facilitate the understanding of the time dependence and evolution of the experiments, Fig. 7E presents a timeline featuring the dominant acoustofluidic phenomenon around different time stamps. The video of the dynamic control of particles is available as ESI† Movie S6. The experiment started with loading the particle-laden droplet onto the device. The particles slowly settled down and were initially scattered across the surface of the whole device at t = 0 s (Fig. 7A). At t = 8 s, the bottom IDT 1 was turned on, generating GFWs at 2.85 MHz, and the particles in the range of the membrane migrated toward the top of the device. Once the particles had reached the top segment of the device, the bottom IDT 1 was stopped, and the top IDT 1 was subsequently turned on. Particles were then driven back onto the left segment and traveled along the membrane downward (Fig. 7B). Shortly after t = 73 s, the top IDT 1 was stopped, and the particles halted. The sinuous shape of the particles' trajectory, see Fig. 7A and B and magnified insets, coincides with the ridgeline of the traveling GFWs in the currently active vibrational mode,²⁸ the latter of which depends on the actuation frequency. In preparation for the next step of the dynamic experiment, the actuation frequency was changed to 3.05 MHz, and both the bottom and the top IDTs 1 were simultaneously actuated. Under this dual actuation mode, rotating waves predominantly populated the left segment, which led to particles being redirected and trapped in rotating rings, see Fig. 7C and magnified inset. Soon after, the frequency was changed to 3.15 MHz, allowing standing waves to populate the segment. Hence, particles swiftly shifted from their ring formation into static clusters. Subsequently, after the 200 s mark, the actuation of IDTs 1 was stopped, and the left IDT 2 was turned on at 9.8 MHz. The traveling GFWs generated are seen dividing the clustered particles into two groups migrating toward the top and bottom parts of the device (Fig. 7D).

The MAWA generating GFWs is a powerful toolset with an intuitive working mechanism that can be leveraged for efficiently transporting, concentrating, and trapping particles throughout a single experiment and within the same device. The multiple actuation modes of the device offer an exceptional range of acoustofluidic functions and make membrane acoustic waveguides a versatile tool for acoustofluidics. Furthermore, the open and flat surface of the device makes it compatible with various manipulations and assays carried out inside sessile droplets.^37,87

Conclusions

In this study, we introduced, investigated, and operated a microfabricated acoustofluidic device based on a piezoelectric thin film membrane waveguide actuator for acoustophoretic manipulation. The MAWA generating membrane-borne GFWs producing a highly localized acoustofluidic response is utilized to dynamically transport, redistribute, concentrate, pattern, and trap microscale polystyrene particles inside a sessile droplet. We examined the mechanisms and capabilities of the GFW-generating MAWA through finite element simulations, LDV non-contact vibration measurements, and acoustofluidic experiments. Our investigation shows that the GFWs observed are anti-symmetric flexural waves with a relatively low phase velocity and high displacement amplitude due to the thinness of the lithographically defined membrane. Their travel path is bounded by the membrane waveguide, hence facilitating the waves' propagation along complex non-rectilinear trajectories under immersion in water. When the waveguide is immersed in water, the acoustic energy carried by the GFWs couples into the medium to generate highly localized linear and non-linear wave-fluid and wave-particle interactions giving rise to acoustofluidic phenomena, such as acoustic radiation forces on particles and acoustic streaming-induced drag forces. Using the piezoelectric thin film MAWA as a toolset to leverage the different GFWs modes and their corresponding acoustofluidic forces contribution, microscale particles can be dynamically manipulated via self-alignment over the waveguide, transportation along the waveguide, and trap formation near the guided flexural standing waves' nodes.

Specifically, GFWs traveling on the membrane waveguide affect particles in two ways: by drawing them toward the middle of the waveguide and pushing them in the direction of propagation of the flexural wave via the acoustic streaming-induced drag force. On the other hand, interfering flexural waves give rise to standing waves or rotating waves, which both have trapping capabilities. However, the balance between the acoustofluidics forces at play differs between the two types, which leads to different trapping modes. Standing waves form static particle clusters at the waves' nodes, while rotating waves form rotating ring clusters where the particles rotate around the nodes. The multidirectional transportation capability of the MAWA can be used for the local enrichment of particles anywhere along the membrane and the formation of several particle clusters for high-throughput biomedical applications.

The MAWA, realized by the pSON fabrication process, introduces a novel actuation method based on GFWs and their various modes, which can deliver a wide variety of highly localized acoustofluidic actuation functions. Actuation modes like traveling, standing and rotating guided flexural waves take advantage of the capability of the membrane waveguide to conform to complex planar geometries and synergistically operate with multiple pairs of IDTs. This versatility elevates the MAWA as a powerful toolset for performing and dynamically switching between advanced acoustofluidic actuation functions such as highly localized particle transportation, patterning, and trapping, all inside a sessile droplet. Moreover, the fabrication process of the device further drives the development of microfluidic devices by improving the miniaturization capabilities, ensuring reproducibility, and enhancing the device's structural integrity and compatibility with microfluidic systems. Compared to other acoustofluidic devices, the active acoustofluidic region and the transducers of the membrane waveguide devices occupy a very small footprint, can be fabricated at wafer-scale with unmatched precision, and do not necessitate backside etching. The intuitive and straightforward “drop-and-actuate” mode of operation of the device points to future generations of acoustofluidic MAWA to offer promising developments for high-throughput microfluidic biomedical applications targeted for lab-on-a-chip systems. Such compatible applications include pulsation-free pumping, analytes separation, cell spheroid and organoid production, local cell and particle enrichment and patterning, fluorescence and infrared-based detection amplification, and parallel lateral flow assay.

Author contributions

Conceptualization: PV, AL, JEYL, EJN. Fabrication: SM, JS, EJN, YK, PV. Methodology: PV, AL. Investigation: PV. Visualization: PV. Supervision: AL, JEYL, EJN, CL. Resources: JEYL, CL. Writing – original draft: PV. Writing – review & editing: PV, AL, JEYL, CL.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by A*STAR under the “Nanosystems at the Edge” programme (Grant No. A18A4b0055).

Notes and references

1. J. Rufo, F. Cai, J. Friend, M. Wiklund and T. J. Huang, Nat. Rev. Methods Primers, 2022, 2, 30.
2. M. Baudoin and J.-L. Thomas, Annu. Rev. Fluid Mech., 2020, 52, 205–234.
3. M. Wu, A. Ozcelik, J. Rufo, Z. Wang, R. Fang and T. Jun Huang, Microsyst. Nanoeng., 2019, 5, 32.
4. P. Zhang, H. Bachman, A. Ozcelik and T. J. Huang, Annu. Rev. Anal. Chem., 2020, 13, 17–43.
5. M. Wiklund, Lab Chip, 2012, 12, 2018.
6. M. A. Burguillos, C. Magnusson, M. Nordin, A. Lenshof, P. Augustsson, M. J. Hansson, E. Elmér, H. Lilja, P. Brundin, T. Laurell and T. Deierborg, PLoS One, 2013, 8, e64233.
7. T. Laurell, F. Petersson and A. Nilsson, Chem. Soc. Rev., 2007, 36, 492–506.
8. T. Franke, S. Braunmüller, L. Schmid, A. Wixforth and D. A. Weitz, Lab Chip, 2010, 10, 789.
9. P. Li, Z. Mao, Z. Peng, L. Zhou, Y. Chen, P.-H. Huang, C. I. Truica, J. J. Drabick, W. S. El-Deiry, M. Dao, S. Suresh and T. J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 4970–4975.
10. M. Afzal, J. Park, G. Destgeer, H. Ahmed, S. A. Iqrar, S. Kim, S. Kang, A. Alazzam, T.-S. Yoon and H. J. Sung, Zool. J. Linn. Soc., 2019, 188, 809–819.
11. H. Ahmed, G. Destgeer, J. Park, J. H. Jung, R. Ahmad, K. Park and H. J. Sung, Anal. Chem., 2017, 89, 13575–13581.
12. F. Guo, Z. Mao, Y. Chen, Z. Xie, J. P. Lata, P. Li, L. Ren, J. Liu, J. Yang, M. Dao, S. Suresh and T. J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 1522–1527.
13. J. P. K. Armstrong, J. L. Puetzer, A. Serio, A. G. Guex, M. Kapnisi, A. Breant, Y. Zong, V. Assal, S. C. Skaalure, O. King, T. Murty, C. Meinert, A. C. Franklin, P. G. Bassindale, M. K. Nichols, C. M. Terracciano, D. W. Hutmacher, B. W. Drinkwater, T. J. Klein, A. W. Perriman and M. M. Stevens, Adv. Mater., 2018, 30, 1802649.
14. B. Kang, J. Shin, H.-J. Park, C. Rhyou, D. Kang, S.-J. Lee, Y. Yoon, S.-W. Cho and H. Lee, Nat. Commun., 2018, 9, 5402.
15. D. J. Collins, B. Morahan, J. Garcia-Bustos, C. Doerig, M. Plebanski and A. Neild, Nat. Commun., 2015, 6, 8686.
16. B. Hammarström, N. R. Skov, K. Olofsson, H. Bruus and M. Wiklund, J. Acoust. Soc. Am., 2021, 149, 1445–1453.
17. G. T. Silva, J. H. Lopes, J. P. Leão-Neto, M. K. Nichols and B. W. Drinkwater, Phys. Rev. Appl., 2019, 11, 054044.
18. M. Evander and J. Nilsson, Lab Chip, 2012, 12, 4667.
19. B. Hammarström, M. Evander, H. Barbeau, M. Bruzelius, J. Larsson, T. Laurell and J. Nilsson, Lab Chip, 2010, 10, 2251.
20. M. Evander, L. Johansson, T. Lilliehorn, J. Piskur, M. Lindvall, S. Johansson, M. Almqvist, T. Laurell and J. Nilsson, Anal. Chem., 2007, 79, 2984–2991.
21. P. Favreau, A. Duchesne, F. Zoueshtiagh and M. Baudoin, Phys. Rev. Lett., 2020, 125, 194501.
22. Y. Chen, A. A. Nawaz, Y. Zhao, P.-H. Huang, J. P. McCoy, S. J. Levine, L. Wang and T. J. Huang, Lab Chip, 2014, 14, 916–923.
23. C. Devendran, K. Choi, J. Han, Y. Ai, A. Neild and D. J. Collins, Lab Chip, 2020, 20, 2674–2688.
24. Y. Liu, M. Ji, N. Yu, C. Zhao, G. Xue, W. Fu, X. Qiao, Y. Zhang, X. Chou and W. Geng, Biosensors, 2022, 12, 399.
25. A. Akther, E. P. Walsh, P. Reineck, B. C. Gibson, T. Ohshima, H. Abe, G. McColl, N. L. Jenkins, L. T. Hall, D. A. Simpson, A. R. Rezk and L. Y. Yeo, Anal. Chem., 2021, 93, 16133–16141.
26. J. Qian, H. Begum, Y. Song and J. E. Y. Lee, Sens. Actuators, A, 2021, 321, 112432.
27. Z. Ma, Y. Zhou, F. Cai, L. Meng, H. Zheng and Y. Ai, Lab Chip, 2020, 20, 2947–2953.
28. P. Vachon, S. Merugu, J. Sharma, A. Lal, E. J. Ng and C. Lee, in 2021 IEEE International Ultrasonics Symposium (IUS), IEEE, 2021, pp. 1–4.
29. P. Zhang, C. Chen, X. Su, J. Mai, Y. Gu, Z. Tian, H. Zhu, Z. Zhong, H. Fu, S. Yang, K. Chakrabarty and T. J. Huang, Sci. Adv., 2020, 6, eaba0606.
30. X. Lu, A. Martin, F. Soto, P. Angsantikul, J. Li, C. Chen, Y. Liang, J. Hu, L. Zhang and J. Wang, Adv. Mater. Technol., 2018, 4, 1800374.
31. N. Nama, P.-H. Huang, T. J. Huang and F. Costanzo, Lab Chip, 2014, 14, 2824–2836.
32. P.-H. Huang, N. Nama, Z. Mao, P. Li, J. Rufo, Y. Chen, Y. Xie, C.-H. Wei, L. Wang and T. J. Huang, Lab Chip, 2014, 14, 4319–4323.
33. Z. Wang, P.-H. Huang, C. Chen, H. Bachman, S. Zhao, S. Yang and T. J. Huang, Lab Chip, 2019, 19, 4021–4032.
34. Z. Ma, A. W. Holle, K. Melde, T. Qiu, K. Poeppel, V. M. Kadiri and P. Fischer, Adv. Mater., 2020, 32, 1904181.
35. Y. Gu, C. Chen, J. Rufo, C. Shen, Z. Wang, P.-H. Huang, H. Fu, P. Zhang, S. A. Cummer, Z. Tian and T. J. Huang, ACS Nano, 2020, 14, 14635–14645.
36. H. Bachman, Y. Gu, J. Rufo, S. Yang, Z. Tian, P.-H. Huang, L. Yu and T. J. Huang, Lab Chip, 2020, 20, 1281–1289.
37. P. Liu, Z. Tian, K. Yang, T. D. Naquin, N. Hao, H. Huang, J. Chen, Q. Ma, H. Bachman, P. Zhang, X. Xu, J. Hu and T. J. Huang, Sci. Adv., 2022, 8, 1–10.
38. D. J. Collins, Z. Ma and Y. Ai, Anal. Chem., 2016, 88, 5513–5522.
39. R. O'Rorke, A. Winkler, D. Collins and Y. Ai, RSC Adv., 2020, 10, 11582–11589.
40. J. Park, J. H. Jung, K. Park, G. Destgeer, H. Ahmed, R. Ahmad and H. J. Sung, Lab Chip, 2018, 18, 422–432.
41. J. Park, G. Destgeer, H. Kim, Y. Cho and H. J. Sung, Lab Chip, 2018, 18, 2936–2945.
42. M. Baudoin, J.-C. Gerbedoen, A. Riaud, O. B. Matar, N. Smagin and J.-L. Thomas, Sci. Adv., 2019, 5, eaav1967.
43. M. Baudoin, J.-L. Thomas, R. Al Sahely, J.-C. Gerbedoen, Z. Gong, A. Sivery, O. B. Matar, N. Smagin, P. Favreau and A. Vlandas, Nat. Commun., 2020, 11, 4244.
44. R. Tao, J. Reboud, H. Torun, G. McHale, L. E. Dodd, Q. Wu, K. Tao, X. Yang, J. T. Luo, S. Todryk and Y. Fu, Lab Chip, 2020, 20, 1002–1011.
45. T. D. Nguyen, Y. Fu, V.-T. Tran, A. Gautam, S. Pudasaini and H. Du, Sens. Actuators, B, 2020, 318, 128143.
46. J. Shi, S. Yazdi, S.-C. Steven Lin, X. Ding, I.-K. Chiang, K. Sharp and T. J. Huang, Lab Chip, 2011, 11, 2319.
47. M. Wu, Y. Ouyang, Z. Wang, R. Zhang, P.-H. Huang, C. Chen, H. Li, P. Li, D. Quinn, M. Dao, S. Suresh, Y. Sadovsky and T. J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10584–10589.
48. G. Destgeer, A. Hashmi, J. Park, H. Ahmed, M. Afzal and H. J. Sung, RSC Adv., 2019, 9, 7916–7921.
49. G. Destgeer, B. Ha, J. Park and H. J. Sung, Anal. Chem., 2016, 88, 3976–3981.
50. R. Wilson, J. Reboud, Y. Bourquin, S. L. Neale, Y. Zhang and J. M. Cooper, Lab Chip, 2011, 11, 323–328.
51. J. Reboud, Y. Bourquin, R. Wilson, G. S. Pall, M. Jiwaji, A. R. Pitt, A. Graham, A. P. Waters and J. M. Cooper, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15162–15167.
52. Y. Q. Fu, J. K. Luo, N. T. Nguyen, A. J. Walton, A. J. Flewitt, X. Zu, Y. Li, G. McHale, A. Matthews, E. Iborra, H. Du and W. I. Milne, Prog. Mater. Sci., 2017, 89, 31–91.
53. P. Reichert, D. Deshmukh, L. Lebovitz and J. Dual, Lab Chip, 2018, 18, 3655–3667.
54. L. Y. Yeo and J. R. Friend, Annu. Rev. Fluid Mech., 2014, 46, 379–406.
55. T. A. Franke and A. Wixforth, ChemPhysChem, 2008, 9, 2140–2156.
56. X. Tao, T. D. Nguyen, H. Jin, R. Tao, J. Luo, X. Yang, H. Torun, J. Zhou, S. Huang, L. Shi, D. Gibson, M. Cooke, H. Du, S. Dong, J. Luo and Y. Fu, Sens. Actuators, B, 2019, 299, 126991.
57. S. Maramizonouz, C. Jia, M. Rahmati, T. Zheng, Q. Liu, H. Torun, Q. Wu and Y. Fu, Int. J. Mech. Sci., 2022, 214, 106893.
58. A. H. Meng and R. M. White, in Micro- and Nanofabricated Electro-Optical Mechanical Systems for Biomedical and Environmental Applications, ed. P. L. Gourley, 1997, vol. 2978, pp. 227–233.
59. T. K. Eto, B. J. Costello, S. W. Wenzel, R. M. White and B. Rubinsky, J. Biomech. Eng., 1993, 115, 329–331.
60. W. B. Wang, Y. Q. Fu, J. J. Chen, W. P. Xuan, J. K. Chen, X. Z. Wang, P. Mayrhofer, P. F. Duan, A. Bittner, U. Schmid and J. K. Luo, J. Micromech. Microeng., 2016, 26, 075006.
61. Y. Wang, X. Tao, R. Tao, J. Zhou, Q. Zhang, D. Chen, H. Jin, S. Dong, J. Xie and Y. Q. Fu, Sens. Actuators, A, 2020, 306, 111967.
62. J. Zhou, H. F. Pang, L. Garcia-Gancedo, E. Iborra, M. Clement, M. De Miguel-Ramos, H. Jin, J. K. Luo, S. Smith, S. R. Dong, D. M. Wang and Y. Q. Fu, Microfluid. Nanofluid., 2015, 18, 537–548.
63. A. G. Steckel and H. Bruus, J. Acoust. Soc. Am., 2021, 150, 634–645.
64. G. Vuillermet, P.-Y. Gires, F. Casset and C. Poulain, Phys. Rev. Lett., 2016, 116, 184501.
65. R. M. Moroney, R. M. White and R. T. Howe, in IEEE Symposium on Ultrasonics, IEEE, 1990, pp. 355–358.
66. R. M. Moroney, R. M. White and R. T. Howe, Appl. Phys. Lett., 1991, 59, 774–776.
67. C. E. Bradley and R. M. White, in Proceedings of IEEE Ultrasonics Symposium ULTSYM-94, IEEE, 1994, vol. 1, pp. 593–597.
68. C. E. Bradley, J. M. Bustillo and R. M. White, in 1995 IEEE Ultrasonics Symposium. Proceedings. An International Symposium, IEEE, 1995, vol. 1, pp. 505–510.
69. N.-T. Nguyen and R. M. White, IEEE Trans. Ultrason. Ferroelectr. Freq. Control, 2000, 47, 1463–1471.
70. S. W. Wenzel and R. M. White, in IEEE Technical Digest on Solid-State Sensor and Actuator Workshop, IEEE, 1988, pp. 27–30.
71. J. Sharma, D. J. Goh, S. Merugu, Y. Koh, S. Ghosh, M. H. Khairy and E. J. Ng, in 2021 IEEE International Ultrasonics Symposium (IUS), IEEE, 2021, pp. 1–4.
72. P. Glynne-Jones, R. J. Boltryk and M. Hill, Lab Chip, 2012, 12, 1417–1426.
73. J. L. Rose, Ultrasonic Guided Waves in Solid Media, Cambridge University Press, 2014.
74. J. Su, X. Zhang, G. Zhou, C. Xia, W. Zhou and Q. Huang, J. Semicond., 2018, 39, 071005.
75. H. X. Wong and J. E.-Y. Lee, J. Microelectromech. Syst., 2022, 31, 943–950.
76. I. Mizushima, T. Sato, S. Taniguchi and Y. Tsunashima, Appl. Phys. Lett., 2000, 77, 3290–3292.
77. J. Lei, Microfluid. Nanofluid., 2017, 21, 50.
78. M. Dorrestijn, A. Bietsch, T. Açıkalın, A. Raman, M. Hegner, E. Meyer and C. Gerber, Phys. Rev. Lett., 2007, 98, 026102.
79. A. Aghakhani, H. Cetin, P. Erkoc, G. I. Tombak and M. Sitti, Lab Chip, 2021, 21, 582–596.
80. J. R. Friend and L. Y. Yeo, Rev. Mod. Phys., 2011, 83, 647–704.
81. W. Connacher, N. Zhang, A. Huang, J. Mei, S. Zhang, T. Gopesh and J. Friend, Lab Chip, 2018, 18, 1952–1996.
82. J. P. Black, R. M. White and J. W. Grate, in 2002 IEEE Ultrasonics Symposium, 2002. Proceedings, IEEE, Munich, Germany, 2002, vol. 1, pp. 475–479.
83. P. B. Muller, R. Barnkob, M. J. H. Jensen and H. Bruus, Lab Chip, 2012, 12, 4617.
84. P. H. Ceperley, Am. J. Phys., 1992, 60, 938–942.
85. W. Wang, L. A. Castro, M. Hoyos and T. E. Mallouk, ACS Nano, 2012, 6, 6122–6132.
86. A. Akther, S. Marqus, A. R. Rezk and L. Y. Yeo, Anal. Chem., 2020, 92, 10024–10032.
87. J. Nam, H. Choi, J. Y. Kim, W. Jang and C. S. Lim, Sens. Actuators, B, 2018, 263, 190–195.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2lc01192a

---