Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Short and long-range cyclic patterns in flows of DNA solutions in microfluidic obstacle arrays†
Oskar E.
Ström
 ,
Jason P.
Beech
,
Jason P.
Beech
 and
Jonas O.
Tegenfeldt
and
Jonas O.
Tegenfeldt
 *
*
Division of Solid State Physics, Department of Physics, Lund University, Lund, Sweden. E-mail: jonas.tegenfeldt@ftf.lth.se
First published on 6th February 2023
Abstract
We observe regular patterns emerging across multiple length scales with high-concentration DNA solutions in microfluidic pillar arrays at low Reynolds numbers and high Deborah numbers. Interacting vortices between pillars lead to long-range order in the form of large travelling waves consisting of DNA at high concentration and extension. Waves are formed in quadratic arrays of pillars, while randomizing the position of the pillar in each unit cell of a quadratic array leads to suppression of the long-range patterns. We find that concentrations exceeding the overlap concentration of the DNA enables the waves, and exploring the behavior of the waves as a function of flow rate, buffer composition, concentration and molecular length, we identify elastic effects as central to the origin of the waves. Our work may not only help increase the low throughput that often limits sample processing in microfluidics, it may also provide a platform for further studies of the underlying viscoelastic mechanisms.
Introduction
While the ability to analyze small samples using small reagent volumes is often considered a main advantage of microfluidics, low analyte throughput can also limit the types of studies that can be performed. If useful throughput is the amount of analyte per unit time, then it depends on both the volume throughput of the carrying fluid, and the concentration of the analyte. It can be increased by increasing either or both of these factors. However, different microfluidic phenomena occur at different ranges of flow velocities and concentrations, which places method-dependent constraints on the useful parts of the parameter space. As an example, we can consider deterministic lateral displacement (DLD).1Recently, high throughput DNA sorting was demonstrated using DLD.2 Throughputs reached 24 μL h−1 and 760 ng h−1 which corresponds to orders of magnitude improvement over existing microfluidic approaches. DLD has also been used for sorting of physiological concentrations of blood3 at high throughputs.4 Due to the nature of the sample both for blood and for DNA solutions, further increase in throughput is expected to be hampered by viscoelastic effects. While viscoelastic fluids have been shown to have a tunable effect in DLD,5 we showed both positive and negative contributions to the separation of long (>20 kbp) DNA molecules at high analyte concentrations. An observation we made during these separations at high DNA concentrations or high flow velocities was the emergence of fluctuations in concentration and in the local flow direction that led to decreases in the quality of the separation at concentrations of tens to hundreds of μg mL−1.2 Another example where high DNA concentrations are relevant is for sample preparation for nanopore sequencing (e.g. Oxford Nanopore: Ligation Sequencing Kit (XL SQK-LSK109-XL) and Rapid Sequencing Kit (SQK-RAD004)). The standard protocols require up to approximately 50 μg mL−1 which is within the range of concentrations for which we observe waves.
Here, we study the conditions under which these fluctuations emerge as striking patterns of macroscopic ordered waves in the rapid flow of high concentrations of DNA across our devices, which consist of quadratic arrays of micrometer sized pillars. Although fluctuations are common in these systems, refer to the recent review paper6 by Datta et al. for a thorough introduction to viscoelastic flow phenomena, our waves are strikingly regular and long range. The waves consist of DNA at higher concentration and extension, with two specific orientations and flow directions mirrored along the central axis of the device. We study their behavior as a function of flow rate, buffer composition, concentration and molecular length by direct observation of the DNA using both fluorescence and polarization techniques. In the flow of the DNA through our devices, we observe regions where the DNA appears to move in circular trajectories. We refer to these regions as vortices. We find that several phenomena occur at different spatial and temporal scales. At the single pillar scale (10−5 m), vortices form, grow, interact, and are shed into the flow. At the array scale (10−3 m), fluctuations in concentration are seen to form and to travel through the array. Based on the observed phenomena at multiple scales, we propose some possible mechanisms for the formation of the waves. We note that the formation of bands of DNA, depletion zones and vortices precede the emergence of waves. The synchronization of fluctuations and the shedding of vortices coincide with the passing wave fronts.
To describe the fundamental underlying mechanisms that lead to the formation of the macroscopic waves, we turn to various dimensionless numbers. Here, it is important to keep in mind that the dimensionless numbers and concentration ratios presented in this work are only useful for representing the state of the system at the onset of instability and wave behavior. Specifically, during states characterized by strong fluctuations, these numbers vary considerably with time and with location in the device.
We calculate the Reynolds number and find that Re = ρ·u·w/ηs < 0.1, where ρ and ηs is the density and viscosity of the solvent, u is the mean flow velocity and w is the gap between array rows, thereby excluding inertial effects in our systems. The Deborah number, De = (u/Lpp)τZ, where Lpp is center-to-center distance between array rows and τZ is the Zimm relaxation time, and the elasticity number, El = De/Re, are then used to quantify elastic effects. In control experiments we obtained a relaxation time for the highest concentration that was consistent with the estimate based on the Zimm relaxation time, see ESI,† section 4. As a simplification and as a conservative estimate, we define De, Re, and thus El as independent of concentration but remind the reader that polymer relaxation time has been shown to vary strongly with concentration,7–11 the type of flow,11 the shear rate12 and displays a high degree of molecular individualism, especially in the entangled regime.8,9 To illustrate the role of interactions between DNA molecules, we refer to C/C* which is the ratio between the concentration, C, of the DNA solution and the overlap concentration, C* = M/[(4π/3)Rg3NA].13 Here, M is the molecular weight of the DNA and NA is Avogadro's number. C* is the concentration above which DNA molecules no longer behave like isolated, individual molecules. We modify C* by changing Rg through changes in DNA molecular length and ionic strength. Intermolecular interactions range in magnitude from the semi-dilute unentangled regime at C* to the “entangled” at Ce ≈ 3C* (lowest reported limit9).
For detailed calculations and discussions about the dimensionless numbers, see ESI,† section 3.
In the following, we will refer to columns and rows of pillars. Rows are perpendicular to, and columns are parallel with, the flow direction.
Results
We note that the flow behavior differs at different length scales. In the following we therefore present our observations of fluorescently stained DNA flowing through a quadratic array first at the macroscopic scale where the waves are visible. We subsequently gradually increase the magnification to investigate the behavior of the flow around a few pillars and finally the flow around single pillars. We use both standard epifluorescence microscopy to visualize the motion of the DNA and fluorescence polarization microscopy to visualize the orientation and the extension of the DNA qualitatively.We investigate the criteria for wave formation, specifically the role of viscoelastic effects by varying the Deborah number, by varying the flow rates, and the role of intermolecular interactions by varying the ratio between the concentration and the overlap concentration. This is done by simply changing the concentration of the DNA or by manipulating the overlap concentration through varying the composition of the DNA solution.
Macroscopic view – waves
Above a threshold flow velocity, we observe long range waves as shown in Fig. 1(b), ESI† Movie S1. The transition from uniform flow to waves can be clearly seen when ramping the pressure up and down so that waves emerge and then disperse [Fig. 5(a), ESI† Movie S2]. Waves arise simultaneously across the array when high Δp is applied and disperse when Δp is decreased. The emergence of waves does not occur immediately at the start if the pillar array, but rather at about 10 pillar rows or 180 μm into the array [see Fig. 1(b)]. The waves are moving from top to bottom with the fluid flow direction, see ESI† Movie S1. The wave fronts alternate between two orientations (32.8° ± 4.2° and −34.5° ± 7.5° relative to the long-axis of the array) and persist for between hundreds of micrometers to several millimeters of travel along the device. When a large wave of a particular orientation passes or disperses, a large wave of the alternative orientation typically arises in its wake. The DNA waves represent long-range temporal and spatial synchronization of DNA concentrations and orientations across the pillar array. When observing entire wave systems at low magnification (2–4×), we typically observe the intensity to vary (relative to the mean intensity at low flow velocity) from as much as approximately double the mean intensity in the brightest peaks to as low as approximately one third in the darkest troughs. Note that the leading edge of the wave is steeper than the trailing edge. | ||
| Fig. 1 Waves emerge as DNA solutions flow above a threshold velocity in a quadratic micropillar-array (b) but not below the threshold (a) or at any flow velocity in a disordered array (c). (a–c) The micrographs are acquired with low magnification (2×) of λ DNA solutions at 400 μg mL−1. The pressure drop across each array is from top to bottom in the images. See ESI† Movie S1 for a video with the raw data. Scale bar is 300 μm. | ||
The occurrence of waves is strongly dependent on the regular geometry of the array. With a small randomization of pillar positions in the quadratic array, no waves are observed at any flow velocities, see Fig. 1(c) and 8 and ESI† Movie S1.
Microscopic view – vortices, depletion zones and flow direction switching
At greater magnification, see Fig. 2, we observe the DNA being depleted between the pillars within the rows as well as pairs of vortices being formed. The flow is seen to change direction, in this case moving from the right to the left as the vortex pair is shed into the flow. This process can be followed in a kymograph, Fig. 2(b), showing the fluorescence signal along the red dashed line in Fig. 2(a) over time. Note that the vortices become visible only when they contain DNA.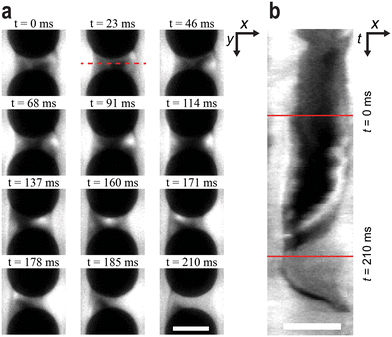 | ||
| Fig. 2 Vortex growth and shedding. (a) Time series of a vortex collecting DNA at the right side of the space in between the two pillars. Thereafter, it shifts position to the left side and is subsequently shed. (b) Kymograph over the series of events in a based on the red dashed line. λ DNA solution was used at C = 400 μg mL−1, u ≈ 3.2 mm s−1 and De ≈ 1300. See ESI† Movie S3 for a video representing the raw data. Scale bars are 10 μm. | ||
Intermediate scale – coupling macroscopic and microscopic behavior
At intermediate magnification it is possible to observe both the behavior of the DNA around single pillars and the coupling of the dynamic behavior across multiple pillars. Fig. 3 shows three regimes that occur, where different phenomena dominate, as the flow velocity is increased. We define the different regimes as follows: steady depletion (S) – a steady non-fluctuating zone of low DNA concentration is formed between the pillars. Cyclic (C) – the DNA concentration in the zone between the pillars varies in a cyclic manner with time. Waves (W) – while the microscopic picture appears chaotic, the term alludes to the fact that macroscopically, this is where we see the waves. | ||
| Fig. 3 Microscale observations of the three regimes: Steady depletion (S) cyclic (C) and waves (W). Micrograph snapshots of λ DNA solutions at C = 400 μg mL−1 and 7 × 4 pillars are shown in (a–c), whereas (d–f) show 4 s long kymographs between the rows (see red line in (a)). The first regime (S, at low u) is characterized by prominent depleted zones in between the pillars along the flow direction with minimal lateral flow fluctuations. The second regime (C) consists of large lateral undulating fluctuations and periodic growth and shedding of blobs in the depleted zones (red arrows). These blobs typically shift from one side of the depleted zone to the other as shown in (b, C regime). The third regime (W) is defined by oblique waves on-top of large lateral flow fluctuations in-between the waves. In a wave (blue arrows), the depleted zones have shifted to an angle perpendicular to the wave front as seen in (a, W regime). The same contrast and brightness settings have been applied for all images. To enhance visibility at high frame rates, an increased staining ratio of 1 fluorophore to 10 base pairs has been utilized. See ESI† Movie S3 for a video representing the raw data. Scale bars are 300 μm. | ||
At low applied pressure (u ≈ 120 μm s−1, De ≈ 51), Fig. 3(a and d), the DNA becomes depleted between the pillars along the columns. This results in bands of DNA that flow between the columns. At higher applied pressure (u ≈ 650 μm s−1, De ≈ 260), Fig. 3(b and e), the widths of these bands fluctuate and vortices are observed. The kymograph in Fig. 3(e) clearly shows both the periodic fluctuation of the widths of the bands of DNA and also how neighboring bands are coupled. As in Fig. 2, vortices can be seen. However, under these conditions they persist for longer and can be seen to move back and forth within the depleted zones with the same frequency as the band fluctuations before eventually shedding. At higher applied pressure (u ≈ 3.2 mm s−1, De ≈ 1300), Fig. 3(c and f), waves can be seen. At the wave fronts the flow is seen to switch direction, from moving solely along columns to moving with an additional considerable component along the rows. The orientation of the wave front is perpendicular to this flow direction. This is further corroborated by the polarization measurements that show extension of DNA molecules perpendicular to the wave fronts, see Fig. 4. Waves traveling in two directions with orientations approximately mirrored around the overall flow direction, see Fig. 1(b), form across the entirety of the device with the waves being coherent for most of their transit through the array.
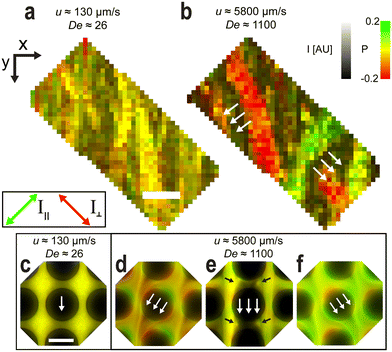 | ||
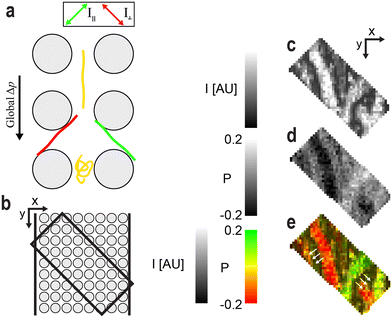
| Fig. 4 Polarization imaging showing the absence of polymer extension for low flow velocities and the significant extension along the wave fronts for high flow velocities. The signal appears green when the DNA molecules orient with one polarization channel and red with the other, perpendicular channel. (a and b) Snapshots of pillar arrays at low magnification (10×) and image-processed to remove the pillars. Sample is 400 μg mL−1 λ DNA. The images are colored where the fluorescence intensity, I, is represented by the pixel value and polarization emission ratio, P, is represented by the hue, saturation and value (HSV) color model. (c–f) Snapshots at high magnification (100×) for the same experimental run as (a and b). DNA strands are concentrated into diagonal streaks and there is a significant number of extended polymers that are pressed into the leading edges of the pillars, resulting in a contrasting polarization ratio. The black arrows in panel e point to the vortices. See ESI† Movies S6 and S7 for videos representing the raw data. Scale bar is 200 μm in (a) and 10 μm in (c). | ||
Orientation of DNA strands
Polarization measurements of the fluorescence allow us to monitor the local orientation of the DNA micro- as well as macroscopically, because the intercalating dye molecules (YOYO-1) adopt an orientation such that the transition dipole moment of the dye is approximately orthogonal to the backbone of the DNA.14,15 We excite using unpolarized light and by detecting the polarization of the emission we gain information about the local orientation and stretching of the backbone. Specifically, we image the DNA at two different perpendicular polarization orientations simultaneously, chosen to maximize their difference in intensity. To visualize the polarization on-top of the fluorescence intensity, images are colorized, with the pixel value denoting the fluorescence intensity and the hue denoting the emission polarization ratio, P = (I∥ − I⊥)/(I∥ + I⊥), see Fig. 4. See the Materials and methods for details on the image processing. At high magnification (100×) we observe two important phenomena. Firstly, the wave propagation orientation varies between the two wave angles and is rarely parallel to the side walls of the channel as would be expected for motion of fluids for Newtonian fluids or for viscoelastic fluids in the S regime. Secondly, the molecules are concentrated in streaks around the pillars [Fig. 4(d and f), ESI† Movie S6] and are stretched in the flow direction. At lower magnification (10×) we see that the polarization of DNA is the same throughout a wave and that the DNA is stretched perpendicularly to the orientation of the wave fronts, see Fig. 4(a and b) and ESI† Movie S7.Effect of flow velocity
To illustrate the influence of elastic effects we vary the velocity, thereby varying De, by changing the applied pressure. The progression S–C–W–C–S is clearly shown in Fig. 5(a) where Δp is ramped from zero to a value above which waves are seen and back.The kymographs in Fig. 5(c) show the waves with different time scales such that the total distance shown is similar for each flow velocity. It is clear from here that the lengths scales of the spatial pattern are the same independent of the flow velocity.
Effect of DNA concentration
To elucidate the effect of inter-molecular interactions we varied the concentration of DNA. We repeat experiments with λ DNA at concentrations between 25 μg mL−1 ≪ C* and 422 μg mL−1 ≫ C*. The lower limit was set at a concentration for which no significant instabilities were observed, and the upper limit was set by the concentration of the available DNA stock solution. See Table 1 for details on the preparation of the DNA samples. For solutions of λ DNA (48.5 kbp) with C/C* ≪ 1, a transition from S to C is observed for flow velocities of approximately 600 μm s−1 which corresponds to De ≈ 130, see Fig. 6(a). When C/C* ≈ 1, C appears earlier, 100 μm s−1 and De ≈ 25, and a further transition to W is observed at 7 mm s−1 and De ≈ 1 × 103. For the highest concentration tested, transitions from S to C and then to W are observed already for De < 103 and flow velocity of <3 mm s−1. When C/C* > 1, the relative magnitude of the elastic properties of the DNA solution dominates and relaxation times become much longer than the transit times across the curved streamlines around the pillars. See ESI† Movies S4a and S4b for a video comparison between low and high C at high De.| Figure No.a | C (μg mL−1) | L (μm) | Dye![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) bpb bpb |
Buffer | I (mM) | l p (nm) | w eff (nm) | R g (μm) | τ Z (s) | C/C* |
|---|---|---|---|---|---|---|---|---|---|---|
For all entries we have T = 22 °C.a The column “Figure No.” refers to the corresponding figure the sample appears in.b Dye![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) base pair staining ratio. base pair staining ratio. |
||||||||||
| 6a and b | 422 | 17 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
5× TE, 3% BME | 44 | 50.7 | 4.63 | 0.47 | 2.1 | 3.6 |
| 4, 5, 6a | 400 | 17 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
5× TE, 3% BME | 44 | 50.7 | 4.63 | 0.47 | 2.1 | 3.4 |
| 2, 3 | 400 | 19 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
5× TE | 31 | 51.0 | 5.79 | 0.54 | 2.6 | 5.1 |
| 1 | 400 | 17 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 50 |
1.8× TE | 11 | 52.9 | 11.2 | 0.62 | 2.7 | 7.4 |
| 6a | 200 | 17 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
5× TE, 3% BME | 44 | 50.7 | 4.63 | 0.47 | 2.1 | 1.7 |
| 6a | 100 | 17 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
5× TE, 3% BME | 44 | 50.7 | 4.63 | 0.47 | 2.1 | 0.86 |
| 6a and c | 50 | 17 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
5× TE, 3% BME | 44 | 50.7 | 4.63 | 0.47 | 2.1 | 0.43 |
| 6a | 25 | 17 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
5× TE, 3% BME | 44 | 50.7 | 4.63 | 0.47 | 2.1 | 0.21 |
| 6c | 50 | 17 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
0.20× TE | 1.2 | 76.6 | 43.3 | 0.88 | 4.2 | 2.7 |
| 6c | 50 | 17 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
0.13× TE | 0.79 | 91.0 | 56 | 0.80 | 3.4 | 2.1 |
| 6c | 50 | 17 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
0.10× TE | 0.61 | 103 | 65.4 | 0.93 | 5.0 | 3.2 |
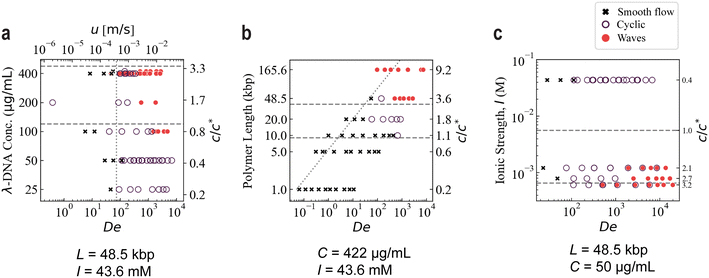 | ||
| Fig. 6 Phase diagrams of occurrence of waves in the quadratic array as a function of (a) polymer concentration of λ DNA, (b) polymer length at constant concentration (422 μg mL−1) and (c) ionic strength of the sample for λ DNA at 50 μg mL−1. The dashed horizontal lines indicate C* and the lower entanglement limit, Ce = 3C*.9 All three diagrams illustrate the requirements of high C/C* and high flow velocities for waves to arise. u represents the estimated mean flow velocity at the gaps of the array. To visualize the dependency of De on polymer length and ionic strength, respectively, the dotted non-horizontal lines in the three panels denote the lowest velocity where waves have been observed for a λ DNA sample, u = 250 μm s−1. The shape of these lines represents the dependency of De on polymer length and ionic strength, respectively. The number of independent data points is 226. In all three panels, the axes are scaled logarithmically except for the C/C* values indicated in the right-hand side axes which represent the individual values for the corresponding data sets and do not follow a simple scaling relationship. Note that some data points are labelled as exhibiting both a cyclic flow and waves. This represents data acquired in different devices. Note also that the data points denoted as smooth flow represent both entirely homogenous distribution of DNA as well as the steady depletion (S) as depicted in Fig. 3(a and d). | ||
Effect of polymer length
To further probe the influence of intermolecular interactions, we manipulate the overlap concentration by varying the contour length of the DNA. Note that this also affects the relaxation time. In experiments with DNA of different contour lengths we find that at the same concentration (C = 422 μg mL−1) only solutions of long molecules exhibit waves, see Fig. 6(b). See Table 2 for listing of the molecular lengths used and their physical parameters. The shortest samples, 1 kbp and 5 kbp, exhibit no flow fluctuations or waves (S regime) even at the highest velocities. Similarly to the results of varying the concentration, we start to observe the appearance of waves at C/C* ≈ O(1).| Figure No.a | Sample | N (kbp) | L (μm) | R g (μm) | τ Z (s) | C* (μg mL−1) | C/C* |
|---|---|---|---|---|---|---|---|
Values based on a buffer of 5× TE and 3% BME at T = 22 °C and with a dye to base pair ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 for the DNA. C = 422 μg mL−1. I = 44 mM and thus lp = 50.7 nm and weff = 4.63 nm.a The column “Figure No.” refers to the corresponding figure the sample appears in. 200 for the DNA. C = 422 μg mL−1. I = 44 mM and thus lp = 50.7 nm and weff = 4.63 nm.a The column “Figure No.” refers to the corresponding figure the sample appears in. |
|||||||
| 6b | 1 kbp | 1 | 0.30 | 0.05 | 2.2 × 10−3 | 2800 | 0.15 |
| 6b | 5 kbp | 5 | 1.7 | 0.13 | 37 × 10−3 | 670 | 0.65 |
| 6b | 10 kbp | 10 | 3.4 | 0.19 | 0.13 | 390 | 1.1 |
| 6b | 20 kbp | 20 | 6.9 | 0.28 | 0.43 | 230 | 1.9 |
| 6b | λ DNA | 48.5 | 17 | 0.47 | 2.1 | 120 | 3.6 |
| 6b | T4 DNA | 166 | 57 | 0.98 | 18 | 46.0 | 9.2 |
Effect of ionic strength
Another way to manipulate the overlap concentration is to vary the salt concentration and thereby the swelling of the polymer due to the change in electrostatic interactions. We find that, when below the threshold concentration of DNA for wave formation, lowering the ionic strength of the sample, I, causes waves to form. See Table 1 for a detailed list of the tested samples of varied I. DNA is a polyelectrolyte with phosphate groups on the backbone conferring a negative charge. Increasing the ionic strength screens this charge, decreases the inter-polymer interactions and decreases Rg, taking the solution further away from the overlap concentration. Our most prominent example of the effect can be seen in the figure for λ DNA at 50 μg mL−1 [Fig. 6(c)]. Waves are clearly seen at low ionic strengths but disappear completely at higher ionic strengths. It is interesting to note that the waves appearing under these conditions are slightly different than those at higher salt concentrations. Waves of different orientations occur only in separate parts of the array and do not cross, see ESI† Movie S5.Effect of solvent viscosity
To explore whether shear thinning plays an essential role in the formation of waves, we start with low concentration of DNA and add sucrose to adjust the viscosity to the values used above. The viscosity of the DNA solution is dependent on the DNA concentration and DNA solutions are also known to be highly shear thinning.16,17 The addition of sucrose increases the viscosity and is also known to reduce the shear thinning of DNA solutions giving us a Boger fluid (elastic fluid with constant viscosity).18 ESI† Fig. S1 shows that, for λ DNA at 50 μg mL−1 in 43% sucrose, clear waves form whereas at similar De with the DNA only dissolved in buffer, no waves appear. Even at De up to 1 × 104, no wave formation can be observed without added sucrose. Adding sucrose decreases the threshold concentration of DNA over which we observe waves at a given flow velocity. In other words, exceeding the overlap concentration is not a necessary condition for the initiation of the waves.Discussion
We demonstrate ordered macroscopic waves across device-scale distances which are the result of the synchronization of microscopic flow patterns around microscopic pillars.Fluctuations and elastic turbulence in viscoelastic flows
Several examples of elastic turbulence in micropillar arrays have previously been reported in the literature. One example occurring at high Weissenberg number, Wi (corresponding to the Deborah number used in our work) is the asymmetric transfer of fluid across single,19,20 pairs21 or an entire array of micro-pillars.22 For the case of single pillar or pair of pillars, the transfer of fluids is seen to be stable over time for certain ranges of Wi while for the array case, the “lane change” occurs transiently in aperiodic ways at random locations. This phenomena is similar to flow velocity waves that have been reported to propagate between the neighboring streams of pillar-pairs.23 Another phenomenon is the observation of coherent structures or streaks at flow velocities of similar magnitude. These have been shown to self-organize in straight channels in the wake following either 1D24 or 2D arrays25 of pillars. In the latter case, the streaks propagate perpendicularly to the flow in cycles, and eventually disintegrate at the end of each cycle. We believe these phenomena to be closely related to the large-scale waves presented here.Waves with somewhat similar appearance as those in our work have been observed recently26 in the flow of viscoelastic media in an array of pillars, so called canopy waves, but the geometry of the array, the molecules involved, the method of observation and the conclusions drawn about the nature of the waves differ from those presented here. Instead of fluorescently labelled DNA, the authors use hyaluronic acid combined with beads to trace the flow. Both flexible and rigid pillars are used with a slender geometry and, in contrast to our device, with a gap between the top of the pillar and the device cover so that the flow takes place not only between but also above the pillars. While our waves are characterized primarily by different concentrations and alignment of the DNA, the canopy waves are defined by distinct magnitudes and directions of the velocity vector field of the flow as well as motion of the pillars.
To our knowledge, DNA solutions have only been used as a sample to study elastic instabilities in microfluidics for contraction-flow devices.27–29 For single posts and post arrays, DNA has been demonstrated to be a good tracer that, in contrast to standard fluorescent microspheres, gives not only the trajectories but also information about the conformational state of the involved polymers in the flow of polyacrylamide solutions30 or polyethylene oxide solutions.31 Otherwise, a plethora of various solutions of other molecules have been used. These include solutions of aqueous wormlike micelles (WLM),19,21,32–35 high-weight polyacrylamide (pAAm),36,37 polyacrylamide in glycerol,38,39 hydrolyzed polyacrylamide (HPAM),22,40 hyaluronic acid,26 or polyethylene oxide (PEO) in water41–43 or in glycerol.44–46
Almost all of the published work on viscoelastic effects in porous materials has focused on either larger pillar or pillar gap dimensions. Arrays of pillars of the dimensions reported in these previous studies have little relevance for the separation of DNA molecules using microfluidics and specifically DLD. The combination of the small length-scales [R ≈ 7 μm, w (gap) ≈ 4 μm] together with the long relaxation times of long DNA strands puts our work in a regime of ultra-low Re and high De and thus ultra-high El. The smaller length-scale also results in smaller radius of curvature of the streamlines that has long been known to enhance elastic turbulence in a range of flow geometries.43,47,48
We estimate De in our experiments to cover a range between 10−1 and 104 across all studied samples and flow rates. Re ranges instead between 10−8 and 10−3 (the upper limit based on the viscosity of the solvent) and thus El reaches 105–109. Waves appear at De approximately 102–103 for concentrated λ DNA and T4 DNA and around De approximately 103–104 for the low salt (0.1× TE, 0.13× TE and 0.2× TE) and low-concentration (50 μg mL−1) λ DNA samples. Interestingly, El ≈ 108 for all occurrences of waves. The banding that we observe occurs for even the lowest flow velocities that we were able to observe but not at zero flow. This indicates the importance of elastic forces even at vanishingly low flow velocities in our system.
Our results are in agreement with studies showing an increased degree of elastic effects with reduced salt40,49 and polymer concentrations.28 Interestingly, Gulati et al. observed no vortex formation at 40 μg mL−1 λ DNA but increasing vortex formation with higher Wi (corresponding to the Deborah number used in our work) for 400 μg mL−1 λ DNA, similar to the lack of waves for our 50 μg mL−1 sample but waves occurring at C ≥ 100 μg mL−1. Note that the onset of elastic turbulence has been shown to be independent of the polymer concentration in large micropillar arrays50 and occurring at lower Wi for lower concentration for a polydisperse DNA solution in a micro-contraction geometry.27
Emergence of waves
We believe that waves form when a critical threshold of elastic stresses is exceeded. The threshold depends strongly on C/C* such that higher C/C* gives stronger intermolecular interactions which in turn increases the relaxation times. At higher flow velocities, shear rates are higher, leading to greater DNA extension and less time for the DNA molecules to relax as they flow across the curved streamlines. This in turn leads to higher rates of elastic stresses, resulting in temporal and spatial fluctuations in DNA concentration, local flow direction and in turn on the orientation, and extension of molecules. Others have shown similar effects in various microfluidic geometries where the degree of spatio-temporal flow velocity fluctuations has increased with increasing Wi.19,22,23,27–29,32,33,36–43,45,46,51 In our array, these instabilities present as bands with fluctuating widths and as vortex pairs that periodically grow and shed blobs of polymers. Similar processes have been observed previously for other polymer solutions40,46 although the synchronization of these fluctuations into large-scale wave patterns has not.Based on our imaging of DNA flow at multiple scales and on correlations between the observed phenomena we propose some possible mechanisms that might underlie the formation of waves.
Microscopic vortices, depletion zones and lift forces
On the microscopic scale of the individual pillar, depletion zones are formed between the pillars, which leads to bands of DNA between columns [Fig. 2 and 3(a and d)]. These might have their origins in interaction forces between the DNA and the pillars. Close to the channel wall, the number of possible conformations for a polymer is lower and entropic effects lead to migration away from the wall on the scale of the radius of gyration. This effect is not dependent on flow and might be considerable at very low flow rates leading to the depletion of DNA molecules from that part of the solvent that flows into the slow-moving regions between the pillars. During flow, the hydrodynamic wall lift force52 and/or the elastic lift force53 might push the DNA away from the pillar wall and contribute to depletion. The elastic lift force is predicted to increase with the polymer concentration and flow velocity.54 Further studies are required to ascertain which, if any, of these effects underlie the formation of depletion zones.At higher flow rates, and larger De, which depends on many factors such as the length of the DNA and the concentration as described above, the time required for the DNA to change its conformation is long compared to the interaction time with the pillars and elastic stresses build up. While we are unable currently to prove causation, we do see correlation between the formation of vortex pairs in the depletion zones and the oscillating widths of the DNA bands that form between the pillar columns, both of which become more pronounced as De increases. Once formed, vortices begin to pull in passing DNA and the concentration increases several-fold. When the vortex pair is “full” of DNA, it leaves the depletion zone and flows downstream (Fig. 2). Due to viscous coupling and large local changes in the flow field due to the vortex and emerging DNA “blob”, neighboring vortex pairs can be triggered to shed if they are critical in this sense. This could explain some of the concentration, and other threshold behavior of wave formation since it is only large systems of unstable vortex pairs that form simultaneously that can synchronize their shedding into waves. Subcritical systems form vortices but not at sufficient densities for waves to form. We believe that the nature of our periodic vortex pair growth and shedding is of similar nature to what has been previously reported in the literature.40,46 Note however, for the reported shedding reported in a 2D pillar array,40 there were large spacings between the pillars (porosity, ϕ = Vpore/Vtotal ≈ 0.7, compared to ϕ ≈ 0.52 in our array), and thus less blocking of their pillar gaps occur by the shed polymer blob. We speculate that the smaller spacings in our array could lead to a higher degree of coupling between neighboring vortices.
At sufficiently high De, the coupled fluctuations in the flow along the columns and the formation and shedding of vortices is unable to dissipate the buildup of elastic stress and large-scale changes in the flow direction are triggered as DNA flows between the columns. This flow direction switching occurs simultaneously with the shedding of DNA filled vortices over large numbers of pillars and is seen as a wave moving along the device. Because flow with a component towards one side of the channel will lead to a buildup of pressure, the local flow direction must switch, and so the next wave is oriented in the opposite direction.
Polarization measurements provide strong evidence for the relationship between the microscopic phenomena that emerge around the pillars and the formation of large-scale waves. At high magnification (100×) we see that vortex shedding takes place in either of two directions. As the DNA strands become stretched, the degree of polarization increases, which we illustrate as a clear red or green signal in Fig. 4. The fact that at low magnification (10×) entire waves are seen to contain DNA with the same orientation, and that this is the same orientation that is observed at the microscopic level indicates that it is the process of synchronized, directional vortex shedding that constitutes waves. The individual waves correspond not only to a higher concentration but also to a higher degree of stretching compared to the surrounding bulk DNA.
From ESI† Movie S5, acquired at low magnification (4×), it is clear that some of the waves radiate from specific sites in the array. This is consistent with the waves emerging from a system of inherently unstable vortices. When the conditions for wave emergence are reached, waves may be nucleated by random fluctuations, by the passing of a previous wave, or by a defect or clogging event in the array. Exactly why fixed nucleation points are more prevalent for some conditions is yet to be discerned.
Effect of solvent viscosity and shear thinning – Boger fluids
To elucidate the role of shear thinning we add sucrose to raise the solvent viscosity, leading to wave formation at lower C/C*. We note that because of reduced shear thinning due to the added sucrose, the viscosity and thus the relaxation time stays high even at high flow velocity. Elastic fluids with nearly constant viscosity are commonly known as ‘Boger fluids’55 and have been widely employed in the study of elastic turbulence in microfluidic systems.38,39,44–46 As a consequence of the added viscosity, the elastic stresses, represented by El, are increased by two orders of magnitude (from approximately 4.7 × 107 without sucrose to approximately 2.0 × 109 with sucrose). Our observations are in agreement with Hemminger et al. who also observed increased elastic instabilities when adding sucrose to a DNA solution. They flowed calf thymus DNA solution through a micro-contraction and observed an upstream vortex growth with 40% (w/w) sucrose but not without, at similar De.27 Similarly as when reducing the length scale, a significant increase in the relative magnitude in the elastic forces is achieved when increasing the solvent viscosity, which in turn could explain wave emergence with added sucrose.Relationship between length scales of array and polymers
The lengths of the DNA molecules may contribute in different ways to the formation of waves. Other than molecule–molecule interactions, as quantified using C/C*, the size of the molecules relative to the array geometry is posited to be a decisive factor. We find that it is only the long molecules that have a contour length on the same or greater length scale as the pitch of the array (∼18 μm) that can form waves. As these molecules may span between a flow constriction and a flow expansion site and can also become wrapped around pillars (see the work in ref. 56 and 57), they couple these together via both their interactions with the pillars, the fluid and with one another, amplifying the elastic nature of the fluid. We show this wrapping occurring in our devices in Fig. 4(d and f), where the polarization is perpendicular to the flow lines directly upstream of the pillars. This is consistent with the observation by Shi and coworkers of stronger viscoelastic fluctuations at similar De for pillars that were more tightly spaced in the flow direction in a 1D pillar array.44 In our case, the pillars are very tightly spaced which is likely to lead to a strong conformational hysteresis for the polymers when they flow across multiple pores.Conclusions & Outlook
We have observed the formation of device-scale waves in polymer solutions moving through a micropillar array. We identify the waves to consist of areas of stretched and oriented polymers, at higher concentrations than the bulk average, moving at two well-defined angles symmetrically around the mean flow direction. We have shown the link between the depletion of DNA between pillars, the generation and shedding of elastic vortex pairs, and the emergence of large-scale waves when fluctuations in these processes become synchronized. From the set of parameters commonly varied in microfluidic work with polymer solutions we have identified crucial factors involved in the formation of waves in micropillar arrays.The prospects to perform microfluidic operations on polymer solutions such as DNA that are relevant for a wide range of applications, at much higher concentrations than those presented in the literature, relies on an understanding of the onset of potentially disruptive phenomena such as those presented here. This may be particularly relevant for handling of complex biological samples consisting of high concentrations of macromolecules of different compositions exhibiting viscoelastic effects. From the perspective of separations in deterministic lateral displacement devices, this knowledge may allow throughputs to reach orders of magnitude larger per device cross-sectional area (1–200 μg h−1 in the present work) than previously shown. Conversely, mixing, which is another important microfluidic unit operation, is increased at the onset of flow instabilities.58 Understanding the phenomena presented here may facilitate the optimized mixing of analytes at high concentration.
In the interest of better understanding the fundamental mechanisms involved, in the future it might be of interest to carefully characterize the extension of the DNA in order to, for example, quantify the elastic energy flow in and out of the polymer contributing to the viscoelastic effects. From a more practical point of view, it would also be interesting to further explore the effects of array geometry as well as temporal and spatial fluctuations e.g., using multiple coloring schemes, particle image velocimetry (PIV) and frequency analysis. We showed how a randomization of the pillar array suppresses the waves. However, randomization can take place in many different ways that would be worth exploring. In our work we have not studied in detail the nucleation of the waves. An improved understanding of these types of mechanisms would be highly relevant for future device designs where waves are leveraged as a mechanism for improved mixing or the suppression of waves is used to ensure optimized sorting.
Materials and methods
Our experiments take place in standard microfluidics devices made using soft lithography. A schematic of a device is shown in Fig. 9. The pillar arrays are approximately 8 mm long and 800 μm wide and 10.9 ± 0.1 μm in depth. In the quadratic and disordered arrays, the pillars are 14 ± 0.3 μm in diameter. In the quadratic array, the gap is 4 ± 0.3 μm between rows and columns of the array whereas in the disordered array, the gap varies between 3 μm and 6 μm. The data is acquired using standard epi-fluorescence microscopy. The DNA strands are labelled with the bisintercalating fluorescent dye YOYO-1 using standard protocols. For the polarization microscopy, an Optosplit II is used to enable simultaneous acquisition of the two perpendicular polarization channels. Detailed descriptions are found in the ESI:† calculations of overlap concentrations and the ionic strengths, discussions and calculations of polymer radii, and calculations and reference measurements of relaxation times.Device design
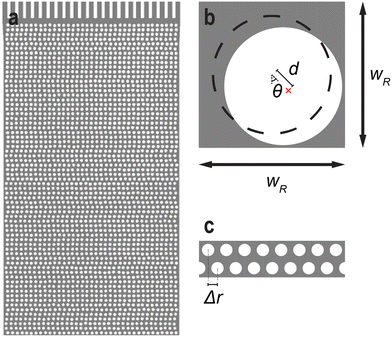
The microfluidic devices were designed with the layout editing software L-Edit 16.02 (Tanner Research, Monrovia, CA, USA). The unit cell of the quadratic array is shown in Fig. 7.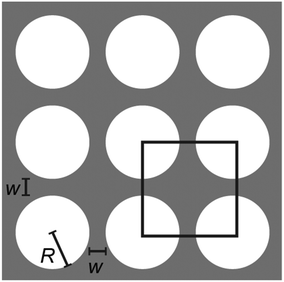 | ||
| Fig. 7 Array unit cell designs of the quadratic array. The lateral and vertical pillar–pillar gap, w = 4 ± 0.3 μm, and the pillar radius, R = 7 ± 0.15 μm where ± denotes the standard deviation. | ||
The disordered array was designed to have a random gap size ranging from 3 μm to 6 μm with a random row shift, see Fig. 8. The pillars have a radius of R = 7 ± 0.1 μm. Similarly to the quadratic array, the row-row pitch is set to 11 μm. Every row shifts laterally in a random magnitude between 0 μm and wR = 18.5 μm. Additionally, the position of the pillar inside each unit cell is randomly placed. The angle from the center of the unit cell, θ, as well as the displacement, d, is varied between −180° to 180° and 0 to 1.5 μm, respectively. This arrangement leads to a minimum pillar–pillar gap of 3 μm. This is close to the spatial resolution of the mask aligner with a slight margin.
Device fabrication
The device design was made using the layout editing software L-Edit 16.02 (Tanner Research, Monrovia, CA, USA). The devices were fabricated in polydimethylsiloxane (PDMS, Sylgard 184, Dow Corning, Midland, MI, USA) using standard replica molding.59 The master mold was made in SU-82015 (MicroChem, Newton, MA, USA) using UV-lithography (Karl Süss MJB4, Munich, Germany) with a photomask from Delta Mask (Delta Mask, Enschede, The Netherlands). Directly following the UV-lithography, the mold was coated with an anti-sticking layer of 1H,1H,2H,2H-perfluorooctyltrichlorosilane (ABCR GmbH & Co. KG, Karlsruhe, Germany). PDMS was poured on top of the master mold to a thickness of approximately 6 mm and cured for 1 h at 80 °C. The devices were cut out with a scalpel, holes, 1.5 mm in diameter, were punched for fluidics connection. The resulting PDMS cast was thoroughly rinsed with isopropanol, ultra-purified water (Milli-Q® water, Merck KGaA, Darmstadt, Germany) and blow-dried with nitrogen gas. To evaporate any liquid residue, PDMS casts were then placed on a hotplate (150 °C) for at least 5 min. The same washing procedure was performed with the coverslip glass slides (50 × 24 mm, No. 1.5H, Marienfeld, Lauda-Königshofen, Germany) used to seal the devices. Air plasma (Zepto, Diener electronic GmbH & Co. KG, Ebhausen, Germany) was used to activate PDMS and glass surfaces. Firstly, the glass coverslips were subject to plasma for 90 s. Then, the PDMS slabs were added to the plasma oven and both surfaces were subject to an additional 10 s of plasma. Prior to plasma treatment, the PDMS surfaces were cleaned using adhesive tape (Tesafilm® invisible tape, Tesa AB, Kungsbacka, Sweden). Immediately after plasma exposure, the two surfaces were bonded by pressing the PDMS on top of the glass slide. The device was then put in an oven at 120 °C for roughly a day to render the surface hydrophobic and stored in ambient conditions according to ref. 60 until use. A typical device mounted on the microscope can be seen in Fig. 9(b).Experimental setup
Flow in the devices was generated using nitrogen overpressure which was either controlled with a MFCS-4C pressure controller (Fluigent, Paris, France) or a custom-built manifold when applying pressures over 1 bar. The pressure in the custom-built setup was measured using a manometer (model 840081, Sper Scientific, Scottsdale, AZ, USA). The flow was measured by connecting the outlet to a flow sensor (Flow rate platform with flow unit S, Fluigent, Paris, France). See Fig. 10 for graphs of the flow rate dependence on the pressure difference. The devices were imaged using an Eclipse Ti microscope (Nikon Corporation, Tokyo, Japan) with acquisition software NIS-elements AR (v. 5.02.03) with a FITC filter cube, and illuminated with Solis-470C High-Power LED (Thorlabs, Newton, NJ, USA) or SOLA Light Engine (6-LCR-SB, Lumencor Inc, Beaverton, OR, USA). Objectives 2× (Nikon Plan UW, NA 0.06), 4× (Nikon Plan Fluor, NA 0.13), 10× (Nikon Plan Apo λ, NA 0.45, FoV of 819 μm), 20× (Nikon CFI Plan Apochromat λ, NA 0.75) and 100× (Nikon Plan Apo VC, Oil Immersion, NA 1.4) were used with an EMCCD camera (iXon Life 897, Andor Technology, Belfast, Northern Ireland) or a sCMOS Hamamatsu Orca Flash 4.0 (Hamamatsu, Shizuoka Pref., Japan). The videos were recorded with frame rates ranging from 10 to 116 s−1. For the polarization measurement, the emitted fluorescence light was passed through an emission light splitter (OptoSplit II, Cairn Research Ltd., Faversham, UK). Two perpendicular linear polarization channels were set up at a ±45° angle to the long axis of the array. The ambient temperature in the close proximity of the device was measured to 22 ± 1.4 °C (where ± denotes standard deviation). A schematic of the device and photo of a typical experimental setup can be seen in Fig. 9.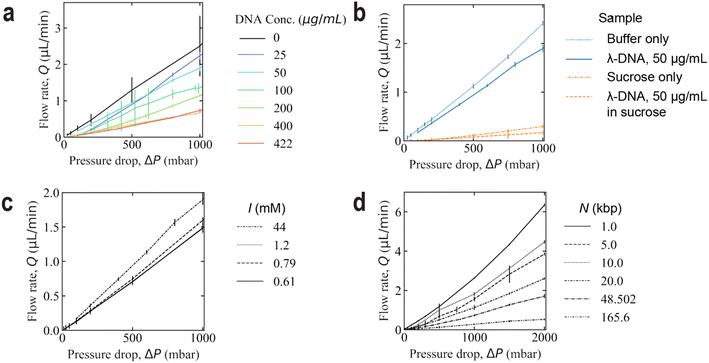 | ||
| Fig. 10 Volumetric flow rate dependence on the applied pressure drop across the device for varying DNA concentrations (a), fluid composition (b), ionic strength (c), and polymer length (d). In (a and c), λ DNA is used for all samples. In (d), the same concentration of 422 μg mL−1 is used for all lengths. 5× TE and 3% BME (I = 44 mM) is used as a buffer in (a, b and d). The buffers used in (c) can be read from Table 1. The error bars denote the standard deviation. The number of mean flow rate data points are 103, 32, 37, and 35, for each plot, respectively. The flow rate and pressure for each data point has been recorded during a duration of at least 20 s. | ||
Flow rate measurements and flow velocity calculation
The volumetric flow rate of the liquid, Q, was controlled by applying a pressure difference across the channel, Δp. The volumetric flow rate of the liquid, Q, follows from the Hagen–Poiseuille law, ΔP = RhQ, where Rh is the hydraulic resistance.The mean flow velocity inside the array, u, which is given in the figures is estimated based on u ≈ Q/A, where A is the cross-sectional area at an array row, A = h × w × N, where h is the depth of the device, w is the gap between the pillars and N is the number of gaps per row and Q is the measured volumetric flow rate.
We would like to note that the cross section of the deformable PDMS device expands as a function of the pressure difference between the interior and exterior, which leads to a small decrease in Rh, primarily at the high-pressure side of the device. This is seen via a non-linear dependence of Q on Δp. Fig. 10 shows this relationship with varying DNA concentration, solvent viscosity, ionic strength, and polymer length. It is also reasonable to expect the onset of any viscoelastic phenomena in the device to affect energy dissipation and that this will also affect the flow rate as a function of the applied pressure.61 These effects are not taken into account in the present work and are considered to be small.
Sample preparation
All DNA solutions, 1 kbp, 5 kbp, 10 kbp and 20 kbp (NoLimits, 500 μg mL−1, Thermo Fischer Scientific, Waltham, MA, USA); lambda phage DNA (λ DNA, 48.502 kbp, New England Bio-labs, Ipswich, MA, USA); and T4 DNA (T4GT7, 165.6 kbp, Nippon Gene, Tokyo, Japan) diluted to various concentrations (between 50 μg mL−1 and 422 μg mL−1) in filtered (200 nm pore) 5× Tris EDTA (50 mM Tris–Hcl and 5 mM EDTA, pH 8) and stained 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 bp
1 bp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dye with the bisintercalating dye YOYO-1 iodide (491ex/509em, Life Technologies, Carlsbad, CA, USA) for 2 h at 50 °C. Low-salt (0.1× TE, 0.13× TE, and 0.2× TE) samples were in 1× Tris EDTA. Both low salt samples and all samples measured at low magnification (2× and 4×) or higher magnification (20× and 100×) were stained at 10
dye with the bisintercalating dye YOYO-1 iodide (491ex/509em, Life Technologies, Carlsbad, CA, USA) for 2 h at 50 °C. Low-salt (0.1× TE, 0.13× TE, and 0.2× TE) samples were in 1× Tris EDTA. Both low salt samples and all samples measured at low magnification (2× and 4×) or higher magnification (20× and 100×) were stained at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 50
1 or 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 bp
1 bp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dye to increase the signal to noise ratio. 3% (v/v) β-mercaptoethanol (BME) was added to minimize photo-bleaching and 0.001% (w/w) Pluronic® F-127 (10 μg mL−1 and ∼12
dye to increase the signal to noise ratio. 3% (v/v) β-mercaptoethanol (BME) was added to minimize photo-bleaching and 0.001% (w/w) Pluronic® F-127 (10 μg mL−1 and ∼12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 Da per polymer) to prevent non-specific sticking of DNA or dye molecules to the channel walls (except when noted otherwise). For λ DNA samples, the solution was heated to 65 °C for 10 min and then rapidly cooled in an ice bath to remove concatemers. Caution! β-mercaptoethanol is fatal in contact with skin, toxic if inhaled or swallowed, may cause organ damage, causes serious eye damage, and is very toxic to aquatic life with long lasting effects. Avoid breathing in any form of the chemical. YOYO-1 causes mild skin irritation, eye irritation and may cause respiratory irritation. Both these substances must be handled with care and appropriate personal protective equipment.
500 Da per polymer) to prevent non-specific sticking of DNA or dye molecules to the channel walls (except when noted otherwise). For λ DNA samples, the solution was heated to 65 °C for 10 min and then rapidly cooled in an ice bath to remove concatemers. Caution! β-mercaptoethanol is fatal in contact with skin, toxic if inhaled or swallowed, may cause organ damage, causes serious eye damage, and is very toxic to aquatic life with long lasting effects. Avoid breathing in any form of the chemical. YOYO-1 causes mild skin irritation, eye irritation and may cause respiratory irritation. Both these substances must be handled with care and appropriate personal protective equipment.
Note that the relative concentration of Pluronic® F-127 is much lower for the concentrated DNA samples (approx. 40× for 400 μg mL−1 DNA). In addition, it is much less than C* for Pluronic® (the molecular weight of Pluronic® F-127 is approximately 2500× less than for λ DNA). Moreover, the molecules are believed to be bound to the surfaces to a large extent further decreasing the bulk concentration of the Pluronic®. See ESI† Tables S1 and S2 for a detailed comparison between λ DNA and Pluronic® polymers.
The sucrose samples were prepared by first adding powdered sucrose (molecular biology grade, Sigma-Aldrich, Saint Louis, MO, USA) to water and dissolving it under vigorous stirring at 50 °C. The sucrose solution was added to stained DNA solutions to reach a sucrose concentration of 43.4% (w/w).
Image processing of the pillar-free images
Image processing for the images and kymographs in the main section in which the pillars have been removed was only performed on magnifications using the 10× objective [see Fig. 11(a and b)]. The regions making up the pillar-free images were defined to cover the area between the pillars in the quadratic array, i.e. 3 × 2 pixels (4.8 μm × 3.2 μm), see Fig. 11(c). The mean intensity of these regions corresponds to each pixel value in the pillar-free images. The region center coordinates were automatically identified as half-way in-between the centers of the pillars. The pixels defining the pillars were themselves located by applying the Sobel edge detection algorithm followed by local Otsu thresholding.Two-channel polarization image processing
The emission light was split into two perpendicular polarizations and projected onto separate halves of the camera sensor using an Optosplit II. These halves were then overlaid using an enhanced correlation coefficient (ECC) image alignment algorithm from the OpenCV package in Python. The hue, saturation and value (HSV) color model was then employed to visualize the total fluorescence signal together with the polarization signal in the same image, see Fig. 12. The total fluorescence intensity of the two polarization halves is represented by the pixel value whereas the polarization emission ratio, P, represents the hue in the model. The limits of P are set to −0.2 and 0.2, translated to 0 (red) and 1/3 (green) in the HSV model. The saturation level is set to 1 for all pixels, not containing any information about the fluorescent micrographs.Data availability
The data presented in this study are openly available in Harvard Dataverse: Ström, O. E., Beech, J. P. & Tegenfeldt, J. O. Short and long-range cyclic patterns in flows of DNA solutions in microfluidic obstacle arrays. Harvard Dataverse (2022). https://doi.org/10.7910/DVN/OMCXZG.Author contributions
The author contribution statements have been written according to CRediT (Contributor Roles Taxonomy, see https://credit.niso.org for role descriptions): conceptualization, O. E. S., J. P. B., and J. O. T.; data curation, O. E. S.; formal analysis, O. E. S.; funding acquisition, J. O. T.; investigation, O. E. S., and J. P. B.; methodology, O. E. S., J. P. B., and J. O. T.; project administration, J. O. T.; resources, J. O. T.; software, O. E. S.; supervision, J. P. B., and J. O. T.; validation, O. E. S., J. P. B., and J. O. T.; visualization, O. E. S., J. P. B., and J. O. T.; writing – original draft, O. E. S., J. P. B., and J. O. T.; writing – reviewing & editing, O. E. S., J. P. B., and J. O. T.; O. E. S. discovered the waves.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was funded by the European Union within Horizon2020, grant number 634890 (project name BeyondSeq), EuroNanoMed (project name NanoDiaBac), by the Swedish Research council, grant number 2016-05739 and NanoLund, grant numbers p20-2019 and staff01-2020. All device processing was conducted within Lund Nano Lab.References
- L. R. Huang, E. C. Cox, R. H. Austin and J. C. Sturm, Continuous Particle Separation Through Deterministic Lateral Displacement, Science, 2004, 304, 987–990, DOI:10.1126/science.109456.
- O. E. Ström, J. P. Beech and J. O. Tegenfeldt, High-Throughput Separation of Long DNA in Deterministic Lateral Displacement Arrays, Micromachines, 2022, 13, 1754, DOI:10.3390/mi13101754.
- S. H. Holm, et al., Microfluidic Particle Sorting in Concentrated Erythrocyte Suspensions, Phys. Rev. Appl., 2019, 12, 014051, DOI:10.1103/PhysRevApplied.12.014051.
- N. M. Karabacak, et al., Microfluidic, marker-free isolation of circulating tumor cells from blood samples, Nat. Protoc., 2014, 9, 694–710, DOI:10.1038/nprot.2014.044.
- Y. Li, et al., Dynamic control of particle separation in deterministic lateral displacement separator with viscoelastic fluids, Sci. Rep., 2018, 8, 3618, DOI:10.1038/s41598-018-21827-7.
- S. S. Datta, et al., Perspectives on viscoelastic flow instabilities and elastic turbulence, Phys. Rev. Fluids, 2022, 7, 080701, DOI:10.1103/PhysRevFluids.7.080701.
- S. Pan, D. At Nguyen, T. Sridhar, P. Sunthar and J. Ravi Prakash, Universal solvent quality crossover of the zero shear rate viscosity of semidilute DNA solutions, J. Rheol., 2014, 58, 339–368, DOI:10.1122/1.4861072.
- R. E. Teixeira, A. K. Dambal, D. H. Richter, E. S. Shaqfeh and S. Chu, The individualistic dynamics of entangled DNA in solution, Macromolecules, 2007, 40, 2461–2476, DOI:10.1021/ma062932e.
- Y. Zhou and C. M. Schroeder, Dynamically heterogeneous relaxation of entangled polymer chains, Phys. Rev. Lett., 2018, 120, 267801, DOI:10.1103/PhysRevLett.120.267801.
- Z. Gong and J. R. van der Maarel, Translational and reorientational dynamics of entangled DNA, Macromolecules, 2014, 47, 7230–7237, DOI:10.1021/ma501618a.
- K.-W. Hsiao, C. Sasmal, J. Ravi Prakash and C. M. Schroeder, Direct observation of DNA dynamics in semidilute solutions in extensional flow, J. Rheol., 2017, 61, 151–167, DOI:10.1122/1.4972236.
- C.-C. Huang, G. Gompper and R. G. Winkler, Non-equilibrium relaxation and tumbling times of polymers in semidilute solution, J. Phys.: Condens. Matter, 2012, 24, 284131, DOI:10.1088/0953-8984/24/28/284131.
- M. Doi and S. F. Edwards, The theory of polymer dynamics, Oxford university press, vol. 73, 1988 Search PubMed.
- C. Carlsson, A. Larsson, M. Jonsson, B. Albinsson and B. Norden, Optical and photophysical properties of the oxazole yellow DNA probes YO and YOYO, J. Phys. Chem., 1994, 98, 10313–10321, DOI:10.1021/j100091a055.
- J. van Mameren, K. Vermeulen, G. J. L. Wuite and E. J. G. Peterman, A polarized view on DNA under tension, J. Chem. Phys., 2018, 148, 123306, DOI:10.1063/1.5004019.
- S. Pan, et al., Shear thinning in dilute and semidilute solutions of polystyrene and DNA, J. Rheol., 2018, 62, 845–867, DOI:10.1122/1.5010203.
- H. Dakhil, et al., Buffered λ-DNA solutions at high shear rates, J. Rheol., 2021, 65, 159–169, DOI:10.1122/8.0000136.
- S. Pan, D. A. Nguyen, P. Sunthar, T. Sridhar and J. R. Prakash, Uniaxial extensional viscosity of semidilute DNA solutions, Korea Aust. Rheol. J., 2019, 31, 255–266, DOI:10.1007/s13367-019-0026-1.
- S. J. Haward, N. Kitajima, K. Toda-Peters, T. Takahashi and A. Q. Shen, Flow of wormlike micellar solutions around microfluidic cylinders with high aspect ratio and low blockage ratio, Soft Matter, 2019, 15, 1927–1941, 10.1039/c8sm02099j.
- S. Varchanis, C. C. Hopkins, A. Q. Shen, J. Tsamopoulos and S. J. Haward, Asymmetric flows of complex fluids past confined cylinders: A comprehensive numerical study with experimental validation, Phys. Fluids, 2020, 32, 053103, DOI:10.1063/5.0008783.
- C. C. Hopkins, S. J. Haward and A. Q. Shen, Tristability in viscoelastic flow past side-by-side microcylinders, Phys. Rev. Lett., 2021, 126, 054501, DOI:10.1103/PhysRevLett.126.054501.
- S. De, et al., Lane change in flows through pillared microchannels, Phys. Fluids, 2017, 29, 113102, DOI:10.1063/1.4995371.
- A. Varshney and V. Steinberg, Elastic Alfven waves in elastic turbulence, Nat. Commun., 2019, 10, 652, DOI:10.1038/s41467-019-08551-0.
- B. Qin and P. E. Arratia, Characterizing elastic turbulence in channel flows at low Reynolds number, Phys. Rev. Fluids, 2017, 2, 083302, DOI:10.1103/PhysRevFluids.2.083302.
- N. K. Jha and V. Steinberg, Elastically driven Kelvin–Helmholtz-like instability in straight channel flow, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2105211118, DOI:10.1073/pnas.2105211118.
- C. de Blois, S. J. Haward and A. Q. Shen, Canopy elastic turbulence: spontaneous formation of waves in beds of slender microposts, arXiv e-prints, 2022, preprint, arXiv:2208.07651 [physics.flu-dyn], DOI:10.48550/arXiv.2208.07651.
- O. L. Hemminger, P. E. Boukany, S.-Q. Wang and L. Lee, Flow pattern and molecular visualization of DNA solutions through a 4: 1 planar micro-contraction, J. Non-Newtonian Fluid Mech., 2010, 165, 1613–1624, DOI:10.1016/j.jnnfm.2010.08.009.
- S. Gulati, S. J. Muller and D. Liepmann, Flow of DNA solutions in a microfluidic gradual contraction, Biomicrofluidics, 2015, 9, 054102, DOI:10.1063/1.4929927.
- S. Gulati, S. J. Muller and D. Liepmann, Direct measurements of viscoelastic flows of DNA in a 2: 1 abrupt planar micro-contraction, J. Non-Newtonian Fluid Mech., 2008, 155, 51–66, DOI:10.1016/j.jnnfm.2008.05.005.
- D. Kawale, et al., Polymer conformation during flow in porous media, Soft Matter, 2017, 13, 8745–8755, 10.1039/c7sm00817a.
- N. François, D. Lasne, Y. Amarouchene, B. Lounis and H. Kellay, Drag Enhancement with Polymers, Phys. Rev. Lett., 2008, 100, 018302, DOI:10.1103/PhysRevLett.100.018302.
- S. J. Haward, C. C. Hopkins and A. Q. Shen, Stagnation points control chaotic fluctuations in viscoelastic porous media flow, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2111651118, DOI:10.1073/pnas.2111651118.
- Y. Zhao, A. Q. Shen and S. J. Haward, Flow of wormlike micellar solutions around confined microfluidic cylinders, Soft Matter, 2016, 12, 8666–8681, 10.1039/c6sm01597b.
- S. J. Haward, C. C. Hopkins and A. Q. Shen, Asymmetric flow of polymer solutions around microfluidic cylinders: Interaction between shear-thinning and viscoelasticity, J. Non-Newtonian Fluid Mech., 2020, 278, 104250, DOI:10.1016/j.jnnfm.2020.104250.
- S. J. Haward, C. C. Hopkins, S. Varchanis and A. Q. Shen, Bifurcations in flows of complex fluids around microfluidic cylinders, Lab Chip, 2021, 21, 4041–4059, 10.1039/d1lc00128k.
- A. Varshney and V. Steinberg, Elastic wake instabilities in a creeping flow between two obstacles, Phys. Rev. Fluids, 2017, 2, 051301, DOI:10.1103/PhysRevFluids.2.051301.
- A. Lanzaro and X.-F. Yuan, Effects of contraction ratio on non-linear dynamics of semi-dilute, highly polydisperse PAAm solutions in microfluidics, J. Non-Newtonian Fluid Mech., 2011, 166, 1064–1075, DOI:10.1016/j.jnnfm.2011.06.004.
- B. Qin, P. F. Salipante, S. D. Hudson and P. E. Arratia, Upstream vortex and elastic wave in the viscoelastic flow around a confined cylinder, J. Fluid Mech., 2019, 864, R2, DOI:10.1017/jfm.2019.73.
- D. M. Walkama, N. Waisbord and J. S. Guasto, Disorder suppresses chaos in viscoelastic flows, Phys. Rev. Lett., 2020, 124, 164501, DOI:10.1103/PhysRevLett.124.164501.
- D. Kawale, et al., Elastic instabilities during the flow of hydrolyzed polyacrylamide solution in porous media: effect of pore-shape and salt, Soft Matter, 2017, 13, 765–775, 10.1039/c6sm02199a.
- Z. Li, X.-F. Yuan, S. J. Haward, J. A. Odell and S. Yeates, Non-linear dynamics of semi-dilute polydisperse polymer solutions in microfluidics: A study of a benchmark flow problem, J. Non-Newtonian Fluid Mech., 2011, 166, 951–963, DOI:10.1016/j.jnnfm.2011.04.010.
- L. E. Rodd, T. P. Scott, D. V. Boger, J. J. Cooper-White and G. H. McKinley, The inertio-elastic planar entry flow of low-viscosity elastic fluids in micro-fabricated geometries, J. Non-Newtonian Fluid Mech., 2005, 129, 1–22, DOI:10.1016/j.jnnfm.2005.04.006.
- L. Rodd, J. Cooper-White, D. Boger and G. H. McKinley, Role of the elasticity number in the entry flow of dilute polymer solutions in micro-fabricated contraction geometries, J. Non-Newtonian Fluid Mech., 2007, 143, 170–191, DOI:10.1016/j.jnnfm.2007.02.006.
- X. Shi and G. F. Christopher, Growth of viscoelastic instabilities around linear cylinder arrays, Phys. Fluids, 2016, 28, 124102, DOI:10.1063/1.4968221.
- X. Shi, S. Kenney, G. Chapagain and G. F. Christopher, Mechanisms of onset for moderate Mach number instabilities of viscoelastic flows around confined cylinders, Rheol. Acta, 2015, 54, 805–815, DOI:10.1007/s00397-015-0875-6.
- S. Kenney, K. Poper, G. Chapagain and G. F. Christopher, Large Deborah number flows around confined microfluidic cylinders, Rheol. Acta, 2013, 52, 485–497, DOI:10.1007/s00397-013-0712-8.
- P. Pakdel and G. H. McKinley, Elastic instability and curved streamlines, Phys. Rev. Lett., 1996, 77, 2459, DOI:10.1103/PhysRevLett.77.2459.
- G. H. McKinley, P. Pakdel and A. Öztekin, Rheological and geometric scaling of purely elastic flow instabilities, J. Non-Newtonian Fluid Mech., 1996, 67, 19–47, DOI:10.1016/S0377-0257(96)01453-X.
- G. Yao, J. Zhao, H. Yang, M. A. Haruna and D. Wen, Effects of salinity on the onset of elastic turbulence in swirling flow and curvilinear microchannels, Phys. Fluids, 2019, 31, 123106, DOI:10.1063/1.5120459.
- A. M. Howe, A. Clarke and D. Giernalczyk, Flow of concentrated viscoelastic polymer solutions in porous media: effect of MW and concentration on elastic turbulence onset in various geometries, Soft Matter, 2015, 11, 6419–6431, 10.1039/c5sm01042j.
- E. M. Ekanem, et al., Signature of elastic turbulence of viscoelastic fluid flow in a single pore throat, Phys. Rev. E, 2020, 101, 042605, DOI:10.1103/PhysRevE.101.042605.
- H. Ma and M. D. Graham, Theory of shear-induced migration in dilute polymer solutions near solid boundaries, Phys. Fluids, 2005, 17, 083103, DOI:10.1063/1.2011367.
- J. Y. Kim, S. W. Ahn, S. S. Lee and J. M. Kim, Lateral migration and focusing of colloidal particles and DNA molecules under viscoelastic flow, Lab Chip, 2012, 12, 2807–2814, 10.1039/C2LC40147A.
- K. Kang, S. S. Lee, K. Hyun, S. J. Lee and J. M. Kim, DNA-based highly tunable particle focuser, Nat. Commun., 2013, 4, 2567, DOI:10.1038/ncomms3567.
- D. F. James, Boger fluids, Annu. Rev. Fluid Mech., 2009, 41, 129–142, DOI:10.1146/annurev.fluid.010908.165125.
- N. P. Teclemariam, V. A. Beck, E. S. Shaqfeh and S. J. Muller, Dynamics of DNA polymers in post arrays: Comparison of single molecule experiments and simulations, Macromolecules, 2007, 40, 3848–3859, DOI:10.1021/ma062892e.
- G. C. Randall and P. S. Doyle, Collision of a DNA polymer with a small obstacle, Macromolecules, 2006, 39, 7734–7745, DOI:10.1021/ma061375t.
- A. Groisman and V. Steinberg, Efficient mixing at low Reynolds numbers using polymer additives, Nature, 2001, 410, 905–908, DOI:10.1038/35073524.
- Y. Xia and G. M. Whitesides, Soft lithography, Annu. Rev. Mater. Sci., 1998, 28, 153–184, DOI:10.1146/annurev.matsci.28.1.153.
- L.-H. Hung and A. P. Lee, Optimization of Droplet Generation by Controlling PDMS Surface Hydrophobicity, ASME 2004 International Mechanical Engineering Congress and Exposition, Nov. 13–19, 2004, pp. 47–48, DOI:10.1115/IMECE2004-61737.
- I. C. Christov, Soft hydraulics: from Newtonian to complex fluid flows through compliant conduits, J. Phys.: Condens. Matter, 2021, 34, 063001, DOI:10.1088/1361-648X/ac327d.
Footnote |
| † Electronic supplementary information (ESI) available: Additional relevant details as follows (PDF): wave results of adding sucrose to a low concentration sample, calculation of the overlap concentration and the ionic strength, calculations of various dimensionless numbers, comparison of polymer weight and concentration between Pluronic® and λ DNA, rheology measurements, detailed description of the supporting movies (Movies S1–S7). See DOI: https://doi.org/10.1039/d2lc01051h |
| This journal is © The Royal Society of Chemistry 2023 |