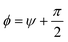A microfluidic method for passive trapping of sperms in microstructures

Abstract

Sperm motility is a prerequisite for male fertility. Enhancing the concentration of motile sperms in assisted reproductive technologies – for human and animal reproduction – is typically achieved through aggressive methods such as centrifugation. Here, we propose a passive technique for the amplification of motile sperm concentration, with no externally imposed forces or flows. The technique is based on the disparity between probability rates, for motile cells, of entering and escaping from complex structures. The effectiveness of the technique is demonstrated in microfluidic experiments with microstructured devices, comparing the trapping power in different geometries. In these micro-traps, we observe an enhancement of cells' concentration close to 10, with a contrast between motile and non-motile cells increased by a similar factor. Simulations of suitable interacting model sperms in realistic geometries reproduce quantitatively the experimental results, extend the range of observations and highlight the components that are key to the optimal trap design.

---

1 Introduction

It is estimated that the male factor is the origin of roughly half of the case of fertility problems.^1,2 Improving the selection of motile sperms, particularly when they are rare, would be beneficial for assisted reproduction technologies, for both zootechnics and human reproduction. These aspects emphasize the importance of scientific research on sperm motility, particularly for mammals, a field which is certainly blessed by the recent advancements in imaging techniques, molecular biology and computational analysis.^3–6

The most successful in vitro fertilisation techniques (e.g. Fertilisation in Vitro and Embryo Transfer (FIVET) and Intracytoplasmic Sperm Injection (ICSI)) are highly aggressive, particularly for the female partner, and very expensive so a part of the population cannot access them.⁷ Less expensive techniques, such as Intrauterine Insemination (IUI), are even more dependent on the selection of highly motile sperms, a problem which is typically solved by centrifugation, density gradients and swim-up techniques⁸ which can compromise the integrity of cells, mechanically or by exposition to DNA-disrupting chemical species.^9,10 Sperm selection is also important for sperm cryopreservation. Established selection techniques are moreover poorly effective in the most serious cases of oligospermia (<4 million cells per ml).¹¹ Microfluidics is certainly a promising road for the future of in vitro fertilization.^12–19 Microfluidic methods for sperm selection have been recently implemented,^20,21 demonstrating interesting capabilities and important reduction of damaging probabilities.^10,22–26 Many of these methods require the use of external pumping in the micro-flow through channels, which is a further source of possible mechanical stress on the cells as well as a technological complication affecting costs. Microfluidics-based techniques for sperm sorting without external flow pumping have also been investigated recently.^22,25,26 In these studies, the largest effort is devoted to the design of a ready-to-use chip for biomedical applications and to the evaluation of DNA fragmentation, while less attention is paid to the role of geometry and trap shapes, looking for possible physical effects that can enhance the sorting capacity.

The improvement of automatic techniques for separating motile cells from the non-motile ones can also impact diagnostic protocols. The evaluation of sperm concentration is typically operated by direct observation, under an optical microscope, in so-called Makler or Neubauer cameras, with noticeable approximation. The assessment of motility, not necessarily correlated with concentration, is another factor of subjectivity²⁷ so that the classical male fertility exam, the spermiogram, is considered to be of not really high statistical significance.²⁸ Less subjective approaches include expensive systems such as CASA (Computer Assisted Sperm Analysis) and flow cytometry.²⁹ Recent studies have evidenced how microfluidics is a promising technology for sperm diagnostics and point-of-care applications.³⁰

Our aim here is to demonstrate a new class of sperm sorting/concentration techniques which do not require external pumping in the micro-flows but still take advantage of low-cost and integrated microfluidic systems, obtained by soft-lithography microfabrication. This approach allows for the enhancement and modulation of the confinement effects experienced by cells in their dynamics even under a restricted diffusion condition, typical of flows at the microscale. In this case, a pumped active flow is not really necessary, because the cells are motile by themselves and a separation can occur spontaneously. Indeed, non-motile sperms behave as passive particles dispersed in the fluid, and therefore diffuse very slowly without preferences for particular regions of the channel. The motile cells, as other kinds of cells with self-propulsion (such as Escherichia coli, Bacillus subtilis and others), move very fast and display non-intuitive behavior in the presence of solid surfaces,^31–33 particularly adhesion,^34–38 swimming parallel to surfaces/obstacles^32,33,39,40 but also long-time trapping in partially closed geometries.^41,42 The consequence of this behavior for filtering purposes on general models and on real bacteria has been studied theoretically and experimentally.^43–46 From the point of view of statistical physics, the demixing (e.g. separation of motile and non-motile cells) originates from the contrast between opposite thermodynamic situations, i.e. equilibrium (non-motile cells) vs. non-equilibrium (motile cells). In the first case, one cannot expect spontaneous de-mixing, as dictated by the second principle of thermodynamics, whereas in the latter case, de-mixing is not forbidden, and the spontaneous ratchet effect due to asymmetric geometries is a way to realise it.^47–53

In our study, we investigate experimentally a wide range of microstructures within an integrated microfluidic device to determine the key components optimising the trapping/sorting power. A numerical simulation widens even more the range of accessible structures, confirming and deepening our understanding of the trapping mechanism. An important feature of sperm passive trapping, already emerged in previous research,⁴⁰ is the high trapping power of curved walls with a small curvature radius, such as corners.⁵⁴ Inspired by those previous studies, we take advantage of this effect to increase the sorting capability of a micro fluidic device. Thanks to this observation, the maximum relative concentration (the ratio between the density of motile cells inside and outside of the traps) achieved in our study is double that found using geometries with large curvatures. We expect that our study could be a starting point for the development of point-of-care applications for male fertility diagnostics and for automatization of sperm sorting procedures finalised to the less expensive in vitro fertilization techniques (e.g. IUI).

2 Results: experimental

Trapping experiments were carried out using quasi-2D hydrostatic microfluidic devices. Each integrated device consists of two networks of input/output microchannels connected to the microstructured chamber (Fig. 1) and filled, by capillarity, with bull sperm samples after standard thawing protocols. The microfluidic trapping devices are realized in polydimethylsiloxane (PDMS) by conventional soft-lithography and replica-molding techniques, starting from a patterned SU-8 master fabricated by photolithography.⁵⁵ The chamber is designed as a functional cell sorter, with a total surface area of approximately 80 mm² and an internal volume of about 1.2 μl, and is micro-structured inside (Fig. 1a). A network of rectangular microfluidic-channels is used to allow the injection of the sample by capillary imbibition⁵⁶ (see Methods for details). PDMS was chosen to ensure optical transparency for real-time microscopy imaging, compatibility with cells and biomolecules, flexibility and high conformability with the master structure (Fig. 1b).⁵⁷ The final sorting devices are produced by placing the microstructured polymeric replicas in conformal contact with glass substrates in order to obtain a perfect sealing of both the microchannels and chamber. A picture of the final device is shown in Fig. 1c. The dimensions and characteristics of both the microfluidic chamber and microstructures guarantee spontaneous imbibition and capillary displacement of the sample without any external pressure. In a microfluidic device with very low aspect ratio microstructures, the fluid displacement is in fact mainly driven by restricted diffusion and laminar flow.^56,58

Fig. 1 Design of microfluidic devices. a. Sketch of the quasi-2D hydrostatic microfluidic device showing the two networks of input/output capillaries connected to a cell sorter chamber including an array of microstructured trapping units. The chamber was filled, by capillarity, with bull sperm samples. The legend on the top shows the geometric characteristics of the 4 groups of differently shaped trapping units together with the corresponding acronyms used in the text. b. Picture of a patterned SU-8 master. c. Picture of the final microfluidic polydimethylsiloxane (PDMS) device for the passive trapping of sperms. Scale bars in b and c: 1 cm. (d–k): Microscope pictures with the design of the eight kinds of structures. The top row presents structures with big (B) gaps, L_gap ≈ 40 μm; the bottom row shows structures with small (S) gaps, L_gap ≈ 20 μm. The pictures were recorded in gray-scale from the microscope camera (see Methods) and coloured according to the following protocol. Red indicates motility, i.e. the red level of each pixel indicates the variance of that pixel along a sequence of 7 frames centred around a given frame. The original central frame is displayed in cyan (blue and green channels) to highlight fixed structures and non-motile sperm cells. Scale bars in d, f, h and j: 50 μm.

Details for microlithography and sample treatment procedures are given in the Methods section. The design of the functional chambers is based on an array with 4 groups of differently shaped trapping units, with each group containing several identical units separated by an average period of about 450 μm. Each trapping unit has a flower-like design made of n “petals” (with n = 4 or n = 5 and differently shaped petals) around a central region: the spaces between petals are the inlets allowing sperm cells to enter or leave a trapping unit; in the following we call them “gaps”, and their minimum distance is named L_gap and in the two chamber designs it has two values: 20 μm (“S” small) and 40 μm (“B” big). Each petal can have a “rounded” (⊂) or “cornered” () shape, as shown in Fig. 1a. A given structure is denoted by the combination of the three possible parameters L_gap × n × shape, e.g. B4⊂ stands for 4 rounded petals separated by big gaps, and this makes a total of 8 different kinds of traps, each repeated at least 9 times in order to collect a larger statistics in the results. Several experiments in re-printed channels with the same design (together with cumulated observations at different times) allowed us to increase even further the statistics. The average area of a trapping structure is ∼225 μm × 225 μm and the height of the channel is ∼15 μm, i.e. the trapping volume is – on average – 7 × 10⁻⁷ ml. At the typical observed sample concentration of 1.2–1.3 × 10⁷ motile cells per milliliter, one would find ∼8–9 cells in a structure. In contrast, the number of motile cells is found to be in the range of 20–80, corresponding to a density enhancement of a factor of 3–10, depending on the choice of n, L_gap and the shape of the petals, as detailed in the rest of the work.

One of the main results of our work is the role, in the sperm trapping mechanism, of petals, particularly of their shape. Histograms of petal occupation, shown in Fig. 2, show the results of the study of the whole structures (below). The average of each distribution is much larger than the average number of cells that is found in an equivalent area outside (and far from) the traps, marked by a black dashed vertical line in each graph. It is also evident that more cells are captured by -shaped petals rather than ⊂-shaped ones, and by smaller gaps (“S”) rather than large ones (“B”), while the number n of petals seems to have a less clear influence on cell trapping. Distributions are compatible with the Poissonian statistics (a p-value larger than 0.05) apart from two cases (B4 with p = 0.04 and S5 with p = 10⁻⁵). It is tempting to deduce that there is no correlation induced by interactions between the cells; however, direct observation suggests that the dynamics – particularly the movement from one petal to another – often occurs in groups of few coordinated cells (see Movies in the ESI†). Indeed, dynamical correlations are not incompatible with the Poissonian steady state statistics, but they are difficult to measure.

Fig. 2 Concentration in petals (experiments). Panels (a)–(h): Histograms of the observed numbers of motile cells in each petal. Each bin has a width of 2. Histograms in panels (a)–(d) are for the structures with -shaped petals; histograms in panels (e)–(h) are for the structures with ⊂-shaped petals. The first two columns (panels (a), (b), (e) and (f)) refer to big gap microstructures, L_gap = 40 μm, while the last two (panels (c), (d), (g) and (h)) are small gap microstructures, L_gap = 20 μm. The larger trapping power of petals with the -shape is evident. Poissonian distributions with the same average of the data are superimposed to the histograms in orange. Poissonian statistics is compatible with all data (p-value larger than 0.05) apart from the first and last cases of the top row (B4 with p = 0.04 and S5 with p = 10⁻⁵). The vertical dashed lines mark the number of motile cells that are found in the sperm liquid far from the structures, in an area equal to that of the petal.

In Fig. 3a, we show the results of the occupancy of the whole structure, which means counting the sum of motile cells in all the petals and in the central region of each structure. For the details about the way the statistics is collected, see the Methods section. The plot teaches us with fair accuracy that the number of motile cells per structure is affected positively by the shape of the petals (the ⊂-shape is surpassed by the -shape), and by the size of the gap (structures with big gaps are surpassed by structures with small gaps). These trends are quantified by statistical t-tests over a couple of distributions, using *s to mark how significant is the difference.‡ A higher significance is observed when the shape is changed. In Fig. 3b, we show the ratio between the average numbers of motile cells when one parameter is changed and the others are not, considering only changes in shape and in L_gap. It is seen that cornered structures, with respect to rounded ones, increase the number of trapped motile cells by a factor significantly larger than 1, up to a factor of 2 in the case of small gaps with 5 petals.

Fig. 3 Concentration in structures (experiments). The total number of motile cells in each structure (experiments). a. Box-plot representing the distributions over several structures of the same kind: each colored box contains a line representing the median, and its size covers the quartiles of the dataset, while the whiskers extend to show the rest of the distribution. On the top of the graph, we have included the results of statistical t-tests comparing pairs of distributions: each segment connects two significantly distinct distributions, with the p-value smaller than 0.05 (*), 0.005 (**) and 0.0005 (***). Pairs without a connecting segment are not significantly distinct. b. Ratios of the average numbers between the case of -shaped petals and ⊂-shaped petals, keeping L_gap and the number of petals fixed. c. Ratios of the average numbers between the case of small L_gap (“S”) and big L_gap (“B”), keeping the petal shape and the number of petals fixed. In plots b and c, the error bars represent the propagation of standard deviations.

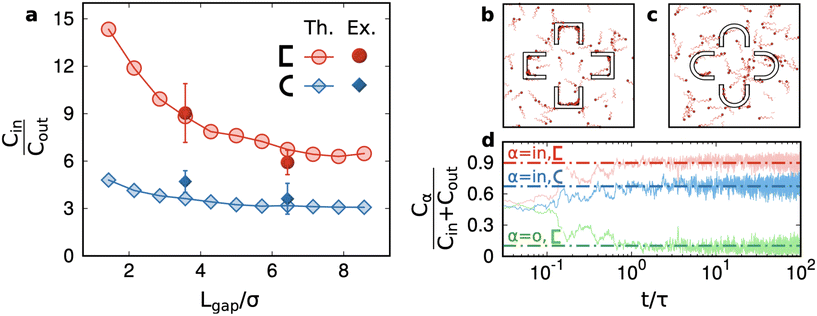
In Fig. 4a, we test our previous conclusions against the variability of the area of the structures as well as of the (motile) sperm cell concentration in the different samples and in the different regions of the same channel. We need to rule out that the results for the numbers of cells in the structure are not influenced by fluctuations of cells in the region and sample where we have performed the observation, which is known to display some (weak) variation. The plot in Fig. 4a illustrates the relative concentration of motile cells C_r = C_in/(C_in + C_out): where C_in is the average concentration (the number per unit area) of cells inside a structure, C_out is the average concentration outside of the structure, measured roughly in the mid distance between the structure and nearby structures (this ensures that surface effects are minimised). The relative concentration is defined to be constrained between 0 (no trapping) to 1 (infinite trapping), while the concentration ratio C_in/C_out = C_r/(1 − C_r) can grow to infinite. We remark that, with the cornered structures and small gaps, we get quite high values of this ratio: C_in/C_out ∼ 7–9. The use of a cornered structure is the key to get a concentration contrast much higher than the one achieved in previous studies.⁴⁰ The role of the curvature of walls is discussed in detail in section 3 and in the ESI† where our numerical results show that, at constant physical dimensions, smaller curvatures always enhance the trapping power of structures or membranes. The effect of the number of petals n going from 4 to 5 on the relative concentration is a reduction of roughly a factor ≈1.2 for all cases. This reduction is compatible, quantitatively, with the reduction, when going from n = 4 → n = 5, of the percentage of the area occupied by petals – which have the largest trapping power – with respect to the whole structure.

Fig. 4 Relative concentrations (experiments). a. Relative concentrations (averaged over 9 structures of the same kind) of motile cells between inside and outside of a structure. Error bars are standard deviations. b. Ratios (averaged over 9 structures of the same kind) between the motile cell concentration and non-motile cell concentration, always inside a structure. Error bars are standard deviations. For reference, the gray area represents the same ratio measured outside of the structures. The width of the gray area is the standard deviation. The dashed line marks equal concentrations (ratio 1).

The last observation we report is crucial for applications, as it concerns the ratio among motile and non-motile cells – details on their distinction are shown in the Methods section “Distinction between motile and non-motile cells”. The efficiency of a sperm sorting technique, in fact, is determined by the concentration of motile cells. The motile/non-motile ratio, if measured outside of the structures, in the free area not too close to the outer boundaries of the trapping structures, is quite unvaried in all the observed samples, and amounts to ∼0.7 ± 0.2, i.e. in the non-trapped regions, the sample hosts the majority of non-motile cells. In contrast, the ratio inside the trapping structures is clearly in favour of the motile cells, as shown in Fig. 4b, with values in the range of 4–15, depending on the structure type. The larger motile/non-motile ratios are measured for cornered structures with small gaps. The ratio between motile and non-motile cells has larger errors with respect to C_in/C_out. The percentage of motile cells is much higher than 1 for all the structures, and the largest values are reached in those with cornered petals. This measurement suggests that our mechanism acts as an efficient selector for the motility of sperms. This result is crucial in applications that usually require not only high concentrations but also cells with high motility.

3 Results: numerical

We have adopted a simplified model of the kind of “wagging” active Brownian particles, inspired by previous studies.^15,40 In the Methods section, we give the details of the model, where we describe it qualitatively in its essential aspects. Each cell is represented by its center of mass position and by the orientation of the self-propulsion direction (e.g. the tail average direction) in the plane. The orientation vector diffuses according to the rotational thermal Brownian motion with a very long persistence time (unperturbed sperm cells follow straight paths longer than any characteristic length in our experiment). The cells interact with each other through a soft potential. The walls exert a harmonic elastic repulsion together with a torque that tends to align the tail orientation to a direction forming a small angle with the wall (this is in accordance with “occupied cone” models that reproduce the effective excluded volume of the long tail^37,39). The “wagging” term consists of an oscillating force perpendicular to the cell orientation with a frequency comparable to that of sperm beating.^15,59 We have verified that all such components are necessary to obtain a behavior which is coherent with our experimental observations. In particular, the transversal oscillation is key to obtain the trapping power of corners which depends on their curvature.

The sizes of the structures, as well as the intrinsic properties of the sperms, such as speed, wagging frequency and persistence time, are fixed by experimental observations. The other parameters, such as the constants appearing in the repulsive potentials (for sperm–wall and sperm–sperm interactions) as well as constants in the aligning torque terms (see Methods), are fixed looking for reasonable comparison between numerical simulations and experiments for a single choice of L_gap and shape of the petals. After the initial calibration of the parameters, we ran simulations with different L_gap values and different petal shapes. Simulation results interpolate the experimental data very well, as shown in Fig. 5b and c (see also the videos in the ESI†).

Fig. 5 Results from simulations. a. Ratios between the average concentration of cells found inside and outside of a structure versus the width of the gap L_gap (normalised by the sperm head diameter σ, see Methods); b and c. Snapshots of simulations with different structure shapes; the snake-like lines following each sperm position are obtained by tracing its motion in a short period of the transversal force oscillation (see Methods). d. Relative occupancy as a function of time, confirming that the initial concentrations are equal and then change in time; the outside concentration is slightly depleted while the inside one increases to a plateau which depends on the petal shape.

The main result of our simulations is the trapping power for two kinds of pocket shapes (cornered and rounded) and a wide range of gap sizes (Fig. 5a). The figure demonstrates that cornered structures always have a higher trapping power than rounded ⊂ structures and that increasing the gap size reduces the trapping power. These two observations are in substantial agreement with the experiments. Remarkably, numerical simulations suggest that L_gap is certainly a less relevant parameter than the shape of the petals. Indeed, the red curve in Fig. 5a is always above the blue curve, that is with ⊂ structures – no matter how small is the gap size – one cannot achieve the relative concentration obtained with structures. We recall that decreasing the L_gap at a constant size of the petals implies a relative increase of the trapping surface: this is the qualitative explanation of the decreasing curves in Fig. 5a.

It is interesting to observe that in both cases, an asymptotic trapping power larger than 1 is found suggesting that even spare petals (not close in “flowers”) can be used to entrap sperms. Of course, increasing much more the L_gap would result in totally open structures and the measurement, in an experiment with a single structure surrounded by an infinite unconfined volume, would be dominated by bulk concentration; therefore, a decrease to 1 is expected, asymptotically: however, verifying this requires much larger simulation chambers to avoid finite-size effects. We remark that such finite-size effects are present also in our experiments. It would be interesting, in future experiments, to study if the relative position or orientation of the structures with respect to the entrance can influence the filling of each structure by capillary injection. We speculate that a more dense arrangement of traps (i.e. drastically reducing the distance between them) could lead to a reduction of the trapping performance, as the original sample, being loaded from the side of the chip, would find it more difficult to reach all the trapping units. Panel d in Fig. 5 is useful to evaluate the sorting time. The relative concentration, starting from the situation C_in = C_out, achieves an unbalanced plateau in a time t ∼ τ where τ is the persistence time of the model sperm cells (see Methods). In physical time, this corresponds to ∼100 seconds. This result also gives a hint about the fact that the experimental measurements, taken a few minutes after the chip filling, come from a steady regime.

Numerical simulations (not shown) with single sperm cells in a pocket with different curvature radii R confirm the origin, discussed already in ref. 40, that trapping is enhanced by radii smaller than the occupied size of the sperm cell, typically head diameter σ plus oscillation amplitude A, e.g. curvatures with R ≪ σ + A have a strong trapping power with respect to curvatures with R ≫ σ + A: this can be understood as a consequence of the fact that the interaction with a curved wall together with the transversal oscillation make it very unlikely for a sperm to follow the curvature without bouncing back. In contrast, a sperm model that has no wagging can align close to and follow any kind of curvature without coming back, emerging from the pocket and escaping from it. We refer to the movies in the ESI† for a rapid understanding of this scenario.

4 Conclusions

Motile cells, such as sperms or bacteria, display fascinating behavior which defies several basic aspects of the physics of mixtures realised with colloids, emulsions, suspensions, etc. Segregation of different parts of a standard mixture (one made of components which are not self-motile) is usually achieved by driving the mixture through externally imposed flows (such as centrifugation at the macroscale, or pumping a flow in microfluidic devices). The same happens, in standard sorting techniques, for sperm samples.^8,10 In this work, we have taken advantage of the intrinsic motility of sperms to obtain the segregation of motile cells in small confined regions. We have explored a family of microfluidic devices where three different parameters are tuned experimentally, in order to understand which strategy is optimal to enhance the concentration of motile sperms. We have also calibrated a simple but effective numerical model of sperm cells (including interactions between cells and between each cell and the boundaries) which reproduces the experimental results and opens a virtually infinite set of future explorations for improving the designs towards other needs and applications. We have given evidence – experimentally and theoretically – that the efficiency of our sorting method is mainly enhanced by the specific design of surfaces. Counterintuitively, their shape, in particular, small curvatures and cornered angles, plays a more important role than the size of the entrance (gap) of the trap: our device increases the concentration of motile sperms by an order of magnitude. This has been explained in terms of the increased self-trapping mechanism caused by the interplay between cornered angles and the peculiar swimming mechanism of sperms. The recent developments in microfluidic designing techniques offer a range of intriguing possibilities to further improve the efficiency of our trapping mechanism, for instance by manipulating the roughness of surfaces,⁶⁰ creating a plethora of additional angles with small curvatures.

Recent studies have already exploited microfluidics without flow-pumping for sperm sorting.^22,25,26 These studies are somehow complementary to ours, because they focus on the technology readiness of the chip and on the evaluation of DNA fragmentation, while our analysis explores the geometry of the device, looking for optimal shapes that can enhance physical effects for sorting. Moreover, the filtered sample obtained within our chip (that is the content of the trapping chambers) has a cell concentration which is higher than the original sample, that is, our chip is not only a filter/sorter but also a concentrator. Our device improves also the time-efficiency of the sorting process: in our study, the sorting time is of the order of a few tens of seconds, which is smaller than the typical times needed in previous studies.^22,25,26 The device proposed here is low-cost, disposable if needed, easy to fabricate and use, and suitable for later integration with more complex devices for clinical applications. Moreover, it is at quite a high level of technological readiness. In the future, such a trapping device may be implemented in a multiplexed system for the purpose of picking up highly motile cells. The motile sperm cells, trapped in the microstructures, can be taken away with subsequent rinsing or by providing apertures on the side of the chip and using a microscope-guided syringe to collect the concentrated sperm. For diagnostics purposes, one may imagine optical reading (through lighting levels) of the concentration in the confining region. A future development of our study concerns the correlation between sperm performance, e.g. speed or other parameters, and the features of the confining regions, which could help in designing more sophisticated chips for point-of-care diagnostic applications where a detailed spermiogram can be directly elaborated.

Our study suggests potential applications where oocytes are directly inserted into the trapping chambers of the chip of a microfluidic multilayered open device:⁶¹ the diameter of mature oocytes, including the zona pellucida, is smaller than 150–120 μm, comparable to the diameter of the central part of our chambers, which – however – can be easily redesigned with a slightly larger internal area, if necessary. This idea could be interesting for future research, and could also lead to a totally new in vitro fertilisation technique, which is in principle more effective than conventional IVF (thanks to the high concentration of motile, already selected, sperms around the oocyte) and where the final selection of the fertilising sperm is not due to the hand of the experimenter, as in ICSI, but to natural competition in oocyte penetration among several tens of sperms. A further advantage of such a conjectural technique is that semen needs neither preparation nor waiting in the dish/chip for the oocytes: as soon as the oocytes are ready (e.g. after incubation and other treatments which usually take hours), they are transferred in the chip trapping chambers and only then the raw sample, just after ejaculation or thawing, is injected by capillarity in the chip: at that point, in a few seconds, the chambers fill up with dense concentrations of ∼90% motile sperms, in close contact with their target.

5 Methods

5.1 Lithography of the structures

Microfluidic trapping devices are fabricated using conventional soft lithography and replica molding techniques using SU-8 (Microchem, YMC, Switzerland) masters. SU-8 masters are realized via standard optical lithography:^62,63 a thin layer of SU-8 negative photoresist is deposited onto a clean silicon substrate and the entire pattern of ad hoc designed photomasks (J.D. Phototools Ltd., Oldham, Lancashire, UK) is transferred on the photoresist film via UV exposure. The process has been optimized to obtain a height of (14.7 ± 0.5) μm for all the characteristic structures of the device. Each device consists of two networks of input/output microchannels connected to a microstructured chamber (Fig. 1a) in order to fill sperm samples by capillarity. Rectangular microfluidic channels have a dimension of 100 μm × 15 μm and a length of about 10 mm. The quasi-2D microstructured chamber has a total dimension of 10 mm × 8 mm × 15 μm and includes a 12 × 10 matrix with 4 groups of different trapping units: each group contains at least 30 identical trapping units separated by an average period of about 450 μm. As shown in Fig. 1a, the trapping area consists of a flower structure characterized by: i) a different number of “petals”, n = 4 or 5; ii) different shapes of petals, rounded (R) or cornered (C); iii) different opening spaces at the base of each petal, “gaps” L_gap, which are small (S, with L_gap = 20 μm) or big (B, with L_gap = 40 μm). The combination of these features creates a heterogeneous matrix for trapping analysis. The different units alternate every 3 rows of the matrix in order to ensure that they are all uniformly reached by the sperm cells via capillary motion and to collect a larger statistics in the results. Thereafter, the microfluidic trapping chips are obtained by replica molding, by casting a mixture of a PDMS pre-polymer and curing agent (10 : 1, Sylgard-184, Dow Corning – USA) onto one of the SU-8 masters. The PDMS is then polymerized at 140 °C for 15 min and then detached from the master. To promote the imbibition, the microchannels are opened with a razor blade and the replica is placed in conformal contact with a glass substrate to allow the closure of the device. To improve the sealing and displacement of the cell sample, both the replica and the glass are treated with oxygen plasma (Diener Pico, low pressure plasma system: 100 W, 240 cm³ min⁻¹ of O₂ flow; 0.5 mbar; 60 s).

5.2 Details about sperm solution preparation

Spermatozoa samples from bulls were obtained from “Agrilinea S.R.L” Rome, and preserved in a liquid nitrogen cylinder. The sperm samples were obtained in the form of sperms suspended in semen and packed in several vials. At the onset of the experiment, one vial of sperms was taken out of the nitrogen cylinder and immersed in a hot water bath at 37 °C for 10 minutes. After 10 minutes, the vial was taken out of the bath and immediately cut open using a pair of sterilized scissors and the entire content was poured out of the vial into an Eppendorf. Using a micropipette, 50 μl of the sperm suspension was sucked out from the Eppendorf and inserted into the microchannel, ensuring proper filling inside the structures. The ends of the channel were then sealed. The locomotion of the sperm cells was recorded by using a digital camera (Nikon, USA) connected to an inverted microscope. During the entire duration of the experiment, the microchannel placed on the stage of the microscope was subjected to a controlled temperature environment at 37 degrees centigrade using a heating unit and temperature sensors. In-house software developed using Python Programming language was used to capture and analyse the images. Naked-eye cell counting was performed on the image sequences (movies 20 seconds long with 50 frames per second acquisition), where each image has a 2048 × 2048 pixel resolution and captures (at a magnification of 10×) an area of ∼1330 × 1330 μm² (a matrix of 3 × 3 structures). Counting was repeated every 5 seconds to ensure the consistency of the numbers. The occupancy of each petal or structure is defined as the average between the count in the first 5 seconds and the count in the last 5 seconds. We waited ∼5–10 minutes, after the chip filling, to start image acquisition: this (according also to our numerical simulations, see Fig. 4d) guarantees a stationary state.

5.3 Distinction between motile and non-motile cells

In our experimental study, we have distinguished the class of motile and non-motile cells by means of a threshold on their velocity, at 1 μm s⁻¹. The choice of this value comes naturally from empirical evidence and is not particularly significant within a broad interval. Indeed, all our experimental observations come from 20 second-long recordings, and we have a resolution of slightly less than a micron per pixel. As a consequence, when we label a cell “non-motile”, we can conclude that it has moved less than 1 micron in 20 seconds, i.e. it has a speed lower than 0.05 μm s⁻¹. Cells with a velocity higher than this threshold have a non-negligible velocity that can be measured with a good resolution and that allows us to label a cell “motile”. However, we have rarely observed cells slower than 10 μm s⁻¹, so motile and non-motile cells are well-distinguished.

5.4 Model for the simulations

To reproduce our experimental findings, we model each sperm as a spherical active particle in the overdamped regime. The complex swimming mechanism of a single sperm is reproduced by effective time-dependent forces,⁴⁰ included in the dynamics of the center of mass position, x_i:where the constant γ is the drag coefficient and T is the solvent temperature. The term η_i is a white noise vector with zero average and unit variance accounting for the collisions between the solvent molecules and the active particles, such that 〈η_i(t)η_j(t′)〉 = δ(t − t′)δ_ij.

The particles interact through the force F_i = −∇_iU_tot, where 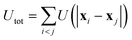is a pairwise potential. The shape U is chosen as a shifted and truncated Lennard-Jones potential:

for r ≤ 2^1/6σ and it is zero otherwise. The constants ε and σ determine the energy unit and the nominal particle diameter, respectively. The term F^w_i represents the repulsive force exerted by the obstacles, whose properties will be specified later.

The effects of the flagella are modeled by the active force, γv₀n_i, evolving according to the active Brownian particle (ABP) dynamics. In the ABP model, the active force acts locally on each particle, providing a constant swim velocity v₀ and a time-dependent orientation, n_i = (cos θ_i, sin θ_i). The orientation angle θ_i evolves stochastically via a Brownian motion:

where χ_i is a white noise with zero average and unit variance and D_r = 1/τ determines the persistence time of the active force. T^w_i is the torque exerted by the wall whose properties will be explained in detail later.

The last term in the right hand side of eqn (1) is a periodic time-dependent force which mimics the oscillations of the sperm head because the vector n^⊥ = (−sin θ, cos θ) points perpendicularly to the swimming direction n_i. The constants A and ω = 2πν_i determine the amplitude and the frequency of the oscillations, respectively.

5.4.1 Force and torque exerted by the walls. Each wall is described by a continuous closed line in the plane, representing its perimeter, which in some parts is external to the structure and in some other parts is internal. Locally (near the point of contact), it can always be written as y = w(x) and/or x = w(y). Let us consider one of the two cases (the first), while the other is obtained by simply exchanging x with y. In the first case, the force exerted by the wall reads:

F^w = − U′(w(x) − y)e, (4)

where is the unit vector orthogonal to the wall profile and U_w(r) is chosen as a harmonic repulsive potential truncated in its minimum:
where K determines the strength of the potential and Θ(r) is the Heaviside step-function.

The torque exerted by the walls, T^w_i, reads:

T^w_i(θ, r, ϕ) = −I(θ, ϕ)[small script l]₀|F_w| sin [2(θ − ϕ ± α)] (5)

where the angle ϕ defines the orientation of the wall and is defined as:
where ψ is the angle formed by the outward normal with respect to the x̂ axis. The function I selects the interval of θ which activates the torque, namely when the self-propulsion vector points inward with respect to the wall profile. The torque aligns the particle orientation to the orientation of the wall so that an angle ±α (the sign is determined by the orientation) is formed. This assumption is consistent with the experimental results since each sperm usually does not swim parallel to the wall but forms a relative angle of ≈10 degrees.^37,39,64 We remark that the torque is fundamental to avoid accumulation of particles (without sliding) close to the wall, as it is observed in simulations without torque.⁶⁵

5.4.2 Simulation parameters & geometrical setup. The typical size of the particle is chosen as σ = 6 μm, and accounts for the effective volume occupied by the head of each sperm, which is approximated as a disk. The persistence time is τ = 10² s, while the swim velocity is v₀ = 30 μm s⁻¹. The parameters of the thermal bath, γ and T, give rise to a diffusion coefficient D_t = 10² μm² s⁻¹ which is much smaller than the effective diffusivity due to the active force, D_a = ν₀²τ = 9 × 10⁴ μm² s⁻¹, as it usually happens for self-propelled particles.⁶⁶ Finally, the amplitude and frequency of the head oscillation read A = 3.5 μm and ν = 30/(2π) s⁻¹, respectively, in agreement with ref. 40. The energy scale of the interaction is chosen as ε = 1 μm² s⁻², while the parameters of force and torque of each wall are K = 10³ μm s⁻², [small script l]₀ = 6 μm² s⁻² and α = 10 degrees.

Simulations are performed using dimensionless units, rescaling the time and position through the time scale introduced by the active force and size of the sperm, namely t̄ = t/τ and x̄ = x/σ.

The numerical study is performed by simulating a system of N = 100 (not far from the average total number of particles in a similar area of the experiments) interacting particles in a box of size L₀ under periodic boundary conditions. In Fig. 6, we show the simulation setup with the symbols representing the fundamental lengths of the simulations. In units of the sperm head's diameter σ, we have used L₁ = 5, L₃ = 16, L₂ = L₃/2 + L₁ = 13, and , while the width of the walls is H = 2, and clearly, the radius of the half-circle representing the curved part of the petals is L₃/2.

Fig. 6 Setup of the simulations whose results are presented in Fig. 4. The sizes, given in units of σ (the particle diameter, ideally corresponding to the head of the sperm cell), are L₁ = 5, L₃ = 16, L₂ = L₃/2 + L₁ = 13, and 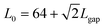, while the width of the walls is H = 2, and the radius of the half-circle representing the curved part of the petals is L₃/2. The value of L_gap is varied between 1 and 9 (again in units of σ), as shown in Fig. 5.

Author contributions

B. N., A. P., C. M., R. D. L. and I. V. conceived the idea and planned the experiments. I. V., A. Z. and V. A. designed and provided the microstructured devices. C. M., B. N. and I. V. performed the experiments. C. M., B. N. and A. P. carried out the experimental data analysis. L. C. performed the numerical simulations and their analysis. All the Authors contributed to the writing of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

BN and AP warmly acknowledge Valentina Casciani, Matteo Verdiglione, Marco Toschi and Daniela Galliano (all from IVI Roma Labs) for useful discussion and suggestions about sperm thawing and observation protocols. BN and AP also acknowledge the financial support from the Regione Lazio through the Grant “Progetti Gruppi di Ricerca” N. 85-2017-15257 and from the MIUR PRIN 2017 project 201798CZLJ. LC acknowledges support from the Alexander von Humboldt Foundation. I. V. acknowledge Dr. E. Quintiero for technical support and useful discussion. AZ and VA acknowledge the Project “GENESI” – Development of Innovative Radiopharmaceuticals and Biomarkers for the diagnosis of tumors of the male and female reproductive apparatus by the Italian Ministry of Economic Development.

Notes and references

1. C. L. Barratt, V. Kay and S. K. Oxenham, J. Biol., 2009, 8, 1.
2. K. A. Frey, Prim. Care, 2010, 37, 643.
3. B. M. Friedrich and F. Jülicher, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 13256.
4. B. M. Friedrich, I. H. Riedel-Kruse, J. Howard and F. Jülicher, J. Exp. Biol., 2010, 213, 1226.
5. E. A. Gaffney, H. Gadêlha, D. J. Smith, J. R. Blake and J. C. Kirkman-Brown, Annu. Rev. Fluid Mech., 2011, 43, 501.
6. J. S. Guasto, J. B. Estrada, F. Menolascina, L. J. Burton, M. Patel, C. Franck, A. Hosoi, R. K. Zimmer and R. Stocker, J. R. Soc., Interface, 2020, 17, 20200525.
7. W.-B. Schill, F. H. Comhaire, T. B. Hargreave, A. Lenzi and A. M. Isidori, Andrologia clinica, Springer, 2010.
8. C. M. Boomsma, M. J. Heineman, B. J. Cohlen and C. M. Farquhar, Cochrane Database Syst. Rev., 2004, CD004507.
9. A. Zini, A. Finelli, D. Phang and K. Jarvi, Urology, 2000, 56, 1081.
10. K. L. Rappa, H. F. Rodriguez, G. C. Hakkarainen, R. M. Anchan, G. L. Mutter and W. Asghar, Biotechnol. Adv., 2016, 34, 578.
11. G. D. Smith and S. Takayama, Mol. Hum. Reprod., 2017, 23, 257.
12. C. Han, Q. Zhang, R. Ma, L. Xie, T. Qiu, L. Wang, K. Mitchelson, J. Wang, G. Huang and J. Qiao, et al. , Lab Chip, 2010, 10, 2848.
13. K. Matsuura, T. Uozumi, T. Furuichi, I. Sugimoto, M. Kodama and H. Funahashi, Fertil. Steril., 2013, 99, 400.
14. C.-Y. Chen, T.-C. Chiang, C.-M. Lin, S.-S. Lin, D.-S. Jong, V. F.-S. Tsai, J.-T. Hsieh and A. M. Wo, Analyst, 2013, 138, 4967.
15. S. Tasoglu, H. Safaee, X. Zhang, J. L. Kingsley, P. N. Catalano, U. A. Gurkan, A. Nureddin, E. Kayaalp, R. M. Anchan and R. L. Maas, et al. , Small, 2013, 9, 3374.
16. H.-Y. Huang, H.-H. Shen, L.-Y. Chung, Y.-H. Chung, C.-C. Chen, C.-H. Hsu, S.-K. Fan and D.-J. Yao, IEEE Trans. Nanobioscience, 2015, 14, 857.
17. S. M. Knowlton, M. Sadasivam and S. Tasoglu, Trends Biotechnol., 2015, 33, 221.
18. Y. H. Hussain, J. S. Guasto, R. K. Zimmer, R. Stocker and J. A. Riffell, J. Exp. Biol., 2016, 219, 1458.
19. M. Zaferani, G. D. Palermo and A. Abbaspourrad, Sci. Adv., 2019, 5, eaav2111.
20. B. S. Cho, T. G. Schuster, X. Zhu, D. Chang, G. D. Smith and S. Takayama, Anal. Chem., 2003, 75, 1671.
21. T. G. Schuster, B. Cho, L. M. Keller, S. Takayama and G. D. Smith, Reprod. BioMed. Online, 2003, 7, 75.
22. R. Nosrati, M. Vollmer, L. Eamer, M. C. San Gabriel, K. Zeidan, A. Zini and D. Sinton, Lab Chip, 2014, 14, 1142.
23. W. Asghar, V. Velasco, J. L. Kingsley, M. S. Shoukat, H. Shafiee, R. M. Anchan, G. L. Mutter, E. Tüzel and U. Demirci, Adv. Healthcare Mater., 2014, 3, 1671.
24. K. Shirota, F. Yotsumoto, H. Itoh, H. Obama, N. Hidaka, K. Nakajima and S. Miyamoto, Fertil. Steril., 2016, 105, 315–321.
25. S. Xiao, J. Riordon, M. Simchi, A. Lagunov, T. Hannam, K. Jarvi, R. Nosrati and D. Sinton, Lab Chip, 2021, 21, 775–783.
26. M. Simchi, J. Riordon, J. B. You, Y. Wang, S. Xiao, A. Lagunov, T. Hannam, K. Jarvi, R. Nosrati and D. Sinton, Lab Chip, 2021, 21, 2464–2475.
27. A. Agarwal, A. Borges Jr and A. Setti, Non-invasive sperm selection for in vitro fertilization, Springer, 2016.
28. J.-C. Lu, Y.-F. Huang and N.-Q. Lü, Zhonghua Nankexue Zazhi, 2010, 16, 867.
29. J. K. Graham, Anim. Reprod. Sci., 2001, 68, 239.
30. G. Zheng, S. A. Lee, Y. Antebi, M. B. Elowitz and C. Yang, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 16889.
31. J. Elgeti, R. G. Winkler and G. Gompper, Rep. Prog. Phys., 2015, 78, 056601.
32. R. Nosrati, A. Driouchi, C. M. Yip and D. Sinton, Nat. Commun., 2015, 6, 8703.
33. S. Rode, J. Elgeti and G. Gompper, New J. Phys., 2019, 21, 013016.
34. N. C. J. Rothschild, Nature, 1963, 198, 1221.
35. G. Li, L.-K. Tam and J. X. Tang, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18355–18359.
36. D. Smith, E. Gaffney, J. Blake and J. Kirkman-Brown, J. Fluid Mech., 2009, 621, 289–320.
37. J. Elgeti, U. B. Kaupp and G. Gompper, Biophys. J., 2010, 99, 1018.
38. V. Magdanz, B. Koch, S. Sanchez and O. G. Schmidt, Small, 2015, 11, 781.
39. P. Denissenko, V. Kantsler, D. J. Smith and J. Kirkman-Brown, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 8007.
40. A. Guidobaldi, Y. Jeyaram, I. Berdakin, V. V. Moshchalkov, C. A. Condat, V. I. Marconi, L. Giojalas and A. V. Silhanek, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 032720.
41. M. Paoluzzi, L. Angelani and A. Puglisi, Phys. Rev. E, 2020, 102, 042617.
42. M. Yaghoobi, M. Azizi, A. Mokhtare and A. Abbaspourrad, Lab Chip, 2021, 21, 2791.
43. P. Galajda, J. Keymer, P. Chaikin and R. Austin, J. Bacteriol. Res., 2007, 189, 8704–8707.
44. L. Angelani, A. Costanzo and R. Di Leonardo, EPL, 2011, 96, 68002.
45. N. Koumakis, A. Lepore, C. Maggi and R. Di Leonardo, Nat. Commun., 2013, 4, 1.
46. N. Koumakis, C. Maggi and R. Di Leonardo, Soft Matter, 2014, 10, 5695.
47. H. A. Makse, S. Havlin, P. R. King and H. E. Stanley, Nature, 1997, 386, 379.
48. R. Di Leonardo, L. Angelani, D. Dell'Arciprete, G. Ruocco, V. Iebba, S. Schippa, M. P. Conte, F. Mecarini, F. De Angelis and E. Di Fabrizio, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 9541.
49. S. R. McCandlish, A. Baskaran and M. F. Hagan, Soft Matter, 2012, 8, 2527.
50. A. Gnoli, A. Petri, F. Dalton, G. Pontuale, G. Gradenigo, A. Sarracino and A. Puglisi, Phys. Rev. Lett., 2013, 110, 120601.
51. M. Medina-Sánchez, L. Schwarz, A. K. Meyer, F. Hebenstreit and O. G. Schmidt, Nano Lett., 2016, 16, 555.
52. C. Chen, X. Chang, P. Angsantikul, J. Li, B. Esteban-Fernández de Ávila, E. Karshalev, W. Liu, F. Mou, S. He and R. Castillo, et al. , Adv. Biosyst., 2018, 2, 1700160.
53. F. Striggow, M. Medina-Sánchez, G. K. Auernhammer, V. Magdanz, B. M. Friedrich and O. G. Schmidt, Small, 2020, 16, 2000213.
54. R. Nosrati, P. J. Graham, Q. Liu and D. Sinton, Sci. Rep., 2016, 6, 1.
55. Y. Xia and G. M. Whitesides, Annu. Rev. Mater. Sci., 1998, 28, 153.
56. I. Viola, D. Pisignano, R. Cingolani and G. Gigli, Anal. Chem., 2005, 77, 591.
57. A. Zizzari, M. Bianco, E. Perrone, M. Manera, S. Cellamare, S. Ferorelli, R. Purgatorio, A. Scilimati, A. Tolomeo and V. Dimiccoli, et al. , Chem. Eng. Process., 2019, 141, 107539.
58. A. Zizzari, M. Bianco, R. Miglietta, L. del Mercato, M. Carraro, A. Sorarù, M. Bonchio, G. Gigli, R. Rinaldi and I. Viola, et al. , Lab Chip, 2014, 14, 4391.
59. A. Gong, S. Rode, G. Gompper, U. B. Kaupp, J. Elgeti, B. Friedrich and L. Alvarez, Eur. Phys. J. E: Soft Matter Biol. Phys., 2021, 44, 1.
60. H. A. Guidobaldi, Y. Jeyaram, C. Condat, M. Oviedo, I. Berdakin, V. Moshchalkov, L. C. Giojalas, A. Silhanek and V. I. Marconi, Biomicrofluidics, 2015, 9, 024122.
61. S. Oh, H. Ryu, D. Tahk, J. Ko, Y. Chung, H. K. Lee, T. R. Lee and N. L. Jeon, Lab Chip, 2017, 17, 3405–3414.
62. A. Zizzari, V. Arima, A. Zacheo, G. Pascali, P. Salvadori, E. Perrone, D. Mangiullo and R. Rinaldi, Microelectron. Eng., 2011, 88, 1664.
63. M. S. Chiriacò, M. Bianco, F. Amato, E. Primiceri, F. Ferrara, V. Arima and G. Maruccio, Microelectron. Eng., 2016, 164, 30.
64. M. A. Bettera Marcat, M. N. Gallea, G. L. Miño, M. A. Cubilla, A. J. Banchio, L. C. Giojalas, V. I. Marconi and H. A. Guidobaldi, Biomicrofluidics, 2020, 14, 024108.
65. L. Caprini, F. Cecconi, C. Maggi and U. M. B. Marconi, Phys. Rev. Res., 2020, 2, 043359.
66. C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2lc00997h

‡ Our observations in Fig. 2 indicate a compatibility of cell count fluctuations with the Gaussian statistics, justifying the uses of t-test. We have also confirmed our results through a non-parametric Mann–Whitney test.

---