Reducing sample amount for forensic glass analysis using LA-ICP-TOFMS and multivariate statistics

Abstract

The forensic analysis of glass fragments is often limited by the size of objects found during investigation. Many of the glass fragments found on suspects are too small to be analysed with the established laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) method, and alternative methods like refractive index measurements show significantly higher error rates. This work builds on a previous method which used resolved laser pulses and a time of flight mass spectrometer (single pulse ICP-TOFMS) to analyse glass fragments pulse by pulse and get more information from one sample while requiring 25× less material. Resolved signals of individual laser pulses are achieved by using low dispersion ablation cells, of which two were compared: The parallel flow ablation cell (PFAC) designed for fast washouts using small spot sizes and a modified version (MPFAC) specifically made for using larger spot sizes. The signal durations of each laser pulse showed a narrow Gaussian distribution for the MPFAC compared to a wide bimodal distribution of the PFAC. Due to the significantly improved aerosol transport using the MPFAC, smaller and more reproducible relative standard deviations were observed. When applying standard interval matching procedures for forensic glass fragments, the PFAC achieved a success rate of up to 95%, while the MPFAC achieved 98%, which are comparable to the established LA-ICPMS method used by forensic institutes. Using multivariate statistics for matching requires significantly higher amounts of data points than dimensions, which previous methods did not allow. Using single pulse LA-ICP-TOFMS data, it was possible to use Hotelling's T²-test for matching. Direct application of the statistical tests resulted in unusable high amounts of error rates. However, closer investigation into the resulting F-values revealed a significant difference between the values of matching pairs and mismatching pairs. Increasing the F-value threshold for matching resulted in success rates around 99% for both ablation cell designs. This work validates the value of single pulse LA-ICP-TOFMS for the analysis of small samples which are commonly found in forensic applications. Furthermore, it showed the advantages of multivariate statistics and the necessary corrections that are required when used with real case samples.

---

Introduction

Broken float glass is a common piece of evidence in various crimes, and as such widely studied in a forensic context.^1,2 Upon breaking of a glass object, fragments thereof are spread in the vicinity and can be found in clothing and on the skin of anyone who was nearby at the time of breaking.³ The ability to match fragments found on a suspect to fragments found at a crime scene is an invaluable method to link suspects to the time and location of the crime.⁴ As part of the NITE-CRIME initiative in the early 2000s and further studies, reference materials and standard operating procedures for glass fragment analyses were established and have since been successfully used in forensics.^5,6 Most commonly, refractive index and trace element concentrations are used to match and mismatch samples, while element concentration matching by means of laser ablation inductively coupled plasma mass spectrometry (LA-ICPMS) has proven to be the most accurate method currently available.^7–10 The list of analysed elements marginally varies between forensic institutes as does the exact procedure of analysis.^4,11 However, a required sample volume of approx. 400 × 200 × 100 μm is required.⁶ While the low error rates make LA-ICPMS the most suitable method for the analysis of float glass fragments, the sample size requirements make it challenging to use for many of the case samples. Furthermore, the high dimensionality of the resulting data brings several complications for statistical treatment. Many statistical procedures were proposed for the matching of glass fragments from a known source (crime scene) to an unknown source (suspect).^4,11–15

Likelihood ratio approaches are commonly used in a variety of forensic disciplines, as they allow the weighing of different evidence against one another.¹⁶ There have been several approaches to implement likelihood ratios in float glass forensics.^12,13,17,18 However, their application requires large databases that are prone to systematic errors and a bias in the database can severely limit its applicability. Samples that were all gathered from the same manufacturing plant in a short time period can show very similar concentrations. As a result, real case samples can appear too diverse compared to the database and the results are meaningless for matching.¹⁴ Optimally, real case samples are used to form a database such as the BKA database of the German Federal Police.¹⁹ This database has shown to be an excellent diverse training set for these purposes. The exact number of samples required varies depending on the number of determined elements in the method and the statistical approach. However, an estimate can be made to require at least several hundreds of sources. Additionally, as there are regional differences in raw materials and glass manufacturing, the applicability of one database on a global scale is uncertain.¹⁷ Furthermore, the requirement of a large scale database for each forensic institute would be associated with a significant amount of labour and samples.

In contrast, a more straightforward method is interval-based matching. A permitted deviation is set for every element concentration in a sample. If another sample's element concentrations are all within the resulting interval, the samples are considered “a match”. This approach is the basis for the currently established and generally applied standard method,⁶ although deviations have been proposed and used based on empirical successes.^4,11 However, the method suffers from an all-or-nothing (“Fall off the cliff”) effect, where samples are either a match or a mismatch and no information on likelihood or similarity is given. Therefore, despite the low error rates and simplicity of the method, the need for alternative methods continues to exist.

Direct application of statistical tests has proven to be difficult. Pairwise comparison of individual elements result in the multiple comparisons problem,²⁰ while multivariate statistics require more observations than possible with the currently established method. As such in a previous study, a proof of concept was made for a method using single pulse LA-ICPMS with the goal of increasing the amount of observations. This method makes use of a low dispersion, two volume ablation cell to resolve individual laser pulses and analyse the samples pulse by pulse. This increased the amount of data points and information per sample. While using 25× less material, comparable results were achieved.²¹ However, higher standard deviations were observed which negatively affected the error rates of matching. Within this work, this method is revisited with a larger number of samples and data were acquired using improved instrumentation. Furthermore, the method was validated based on different statistical approaches to reduce the amount of samples that are currently too small for established methods.

Experimental

Instrumentation

All experiments in this work were carried out using an ArF excimer laser (193 nm, GeoLas C, Lambda Physik, Göttingen) equipped with either a parallel flow ablation cell (PFAC, as described by Neff et al.),²² or a modified PFAC (MPFAC) with the bottom opening widened from 1.5 mm to 3.5 mm (Fig. 1). These changes were made to improve the reproducibility of washout durations using larger spot sizes. The PFAC was designed for fastest washout using small spot sizes for imaging purposes and struggles with the direct aerosol transport for larger spot sizes. In contrast, the newly designed MPFAC results in longer washouts for small spot sizes, but shorter washouts for larger spot sizes as direct aerosol transport is still possible. These changes are discussed below in more detail. The ablation cell was operated with a mixture of helium (99.999%, PanGas AG, Dagmersellen, Switzerland) and argon (99.999%, PanGas AG, Dagmersellen, Switzerland). The ablation cell was equipped with a 3-D XYZ stage that can be controlled simultaneously with the laser trigger and data acquisition of the ICP-MS. This allowed for the acquisition of binned data that facilitated data treatment of single pulse laser ablation. A more detailed explanation of this system was described by Neff et al.²³ The ablation cell was coupled to an ICP-TOFMS instrument (icpTOF2R, TOFWERK AG, Thun, Switzerland) for quasi-simultaneous detection of the entire mass range.²⁴ The measurements were carried out in reaction cell mode, using a consistent flow of 2 mL min⁻¹ of hydrogen gas (99.9999%, PanGas AG, Dagmersellen, Switzerland). Operating conditions for laser and ICPMS are summarized in Table 1.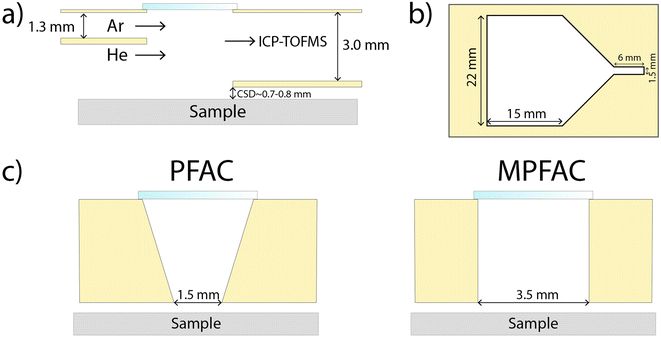

Fig. 1 Schematic description of the used low dispersion ablation cell, adapted from Neff et al.²² The samples are placed in a larger volume under He atmosphere. (a) Side view, (b) top view, (c) cross section at ablation region, view from ICP, showing the different opening widths for the PFAC and the MPFAC.

Table 1 Operating conditions for ICPMS

Laser ablation
Repetition rate	4 Hz
Laser fluence	13–17 J cm^−2
Spot size	90 μm
Carrier gas (Ar)	0.75–0.85 L min^−1
Carrer gas (He)	1.4–1.6 L min^−1
Number of pulses	110
Cell-to-sample distance	700–800 μm
ICPMS
RF power	1550 W
Auxiliary gas	0.8 L min^−1
Cooling gas	16 L min^−1
Reaction cell (H2)	2 mL min^−1
Sampling depth	5–5.5 mm
Time resolution	5 ms
Resolving power (m/z 56)	2000–2500
Notch filters	m/z 23.3–0.3 V
	m/z 28.1–0.2 V
	m/z 41.5–0.5 V
	m/z 56.0–0.1 V

---

Table 2 Error rates for both databases using different matching intervals

	PFAC (1.5 mm bottom opening)	MPFAC (3.5 mm bottom opening)	Standard method^a
a The standard method as proposed by Weis et al. is added for comparison.^4
5× Rel. SD
False neg. [%]	4.70	4.00	1.04
False pos. [%]	0.65	0.82	0.11
5× Rel. SD min
False neg. [%]	4.09	1.76
False pos. [%]	0.73	0.30

---

Samples

NIST SRM 612 was used as a tuning standard before every measurement.²⁵ The forensic float glass standards FGS 2 and FGS 1 were used as external calibration and quality control, respectively.² These reference materials were designed with the average float glass elemental composition in mind and function as matrix-matched standards. 60 larger float glass samples (diameter 3–10 cm) were provided by the Zurich Forensic Science Institute, Switzerland. The samples originate from different crime scenes in the greater Zurich area and consist of material taken from broken windows. Each sample represents one source and was broken into smaller (0.2–0.5 mm diameter) fragments using a pair of pliers. 10 of the smaller fragments for each source were then placed onto a microscope slide using double sided scotch tape. This resulted in a total of 600 glass fragments which were analysed and used for further statistical studies. Using the PFAC, the first 50 sources were analysed with the ablation cell as published, which serves as a second database. Due to the close geographical location of the samples and limited providers of float glass within Switzerland, similarities between the samples and therefore more false positive results were expected. However, the samples represent a realistic database for a national forensic science institute.

Analysis procedure

A sample holder was 3-D-printed with indentations to fit NIST SRM 612, FGS 1 and FGS 2 standards, as well as half of a microscope slide.²¹ This allowed for a generally flat continuous surface within the ablation cell, decreasing alterations of the gas flow. The microscope slide contained space for four different glass sources, resulting in a total of 40 glass fragments per slide. Tuning of the instrument was performed on NIST SRM 612 for high sensitivity in the mid-high mass range, ²³⁸U/²³²Th of 1.0–1.1, and a low oxide ratio (²³²Th¹⁶O/²³²Th < 0.5%). Each measurement consisted of 110 laser pulses, where the first 10 pulses were discarded due to crater formation effects and to avoid any surface contamination that could bias the analyses. A measurement series consisted of three measurements of FGS 2, followed by one measurement of five separate glass fragments from the same source, three measurements of FGS 1 for quality control, five more glass fragments from the same source, three more measurements of FGS 2 and finally a background measurement. These measurement series were repeated for 60 different glass sources using the MPFAC, and again for the first 50 glass sources using the published as-is PFAC.²²

Data processing

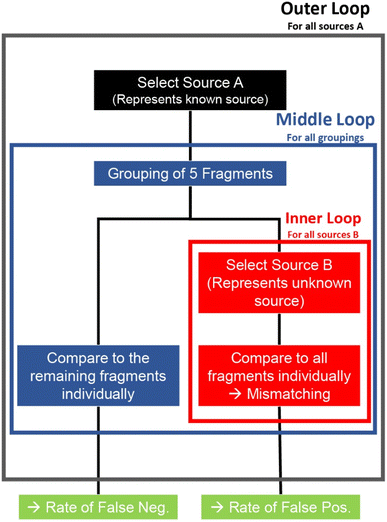
The measurement series allowed for an instrumental drift correction and quantification according to Longerich et al.,²⁶ counting each individual laser pulse as one measurement. The data of each pulse was indexed based on glass source i and number of fragments k within that source. This allowed the pooling of fragments with the same i to reduce error rates. This process represents the multiple measurements of a sample with a known source in a real case where there are no size limitations of samples. The pooling process was repeated for all possible combinations of same source fragments during the process of matching (Fig. 2). The list of elements used for matching consisted of Mg, Al, K, Ca, Ti, Mn, Fe, Rb, Sr, Zr, Ba, La, Ce, Nd and Pb. Here it needs to be mentioned, some commonly used elements in forensic glass analysis were excluded from this study. For example, Li could not be measured by the TOF instrument used due to its low mass and was excluded as such. Na and Si were too similar between samples due to being main elements and showed no effect on the method. Sn was excluded due to being a known heterogeneous element as a result of the manufacturing process.²⁷ Hf was excluded due to high correlation with Zr and adding no additional information.¹⁷

Fig. 2 Flowchart of the matching and mismatching procedure used in this study for all statistical treatment. Inner, middle and outer loop were repeated until all possible combinations of fragments were tested.

Two different matching procedures are presented here in this work. Interval matching consists of calculating the mean or median concentration of unknown samples and pooled known samples and comparing each concentration individually akin to the standard method. Different permitted intervals in this work were attempted based on the relative standard deviation (RSD) of the glass fragments. These deviations were then multiplied by five to compensate for sample inhomogeneities and measurement errors like in previous studies for best success rates.^4,11 The higher concentration is taken as the base, and the lower concentration is compared relative to it. The second procedure involved the use of Hotelling's T²-distribution,^28,29 making use of the “Hotelling” R-package. The pooled multidimensional data of known fragments was compared to individual fragments representing unknown samples. The resulting F-values²⁸ were then saved and analysed separately, which is discussed in the result section. Both matching procedures were repeated for all possible combinations of fragments for both databases. For both methods, pooling consisted of combining the data of five known samples for a total of 500 multidimensional data points each.

Results and discussion

Ablation cell dependence

The signal washout durations (FW 0.1 M) were determined for every single pulse on the external standard measurements of the two variations of the PFAC (Fig. 1). Signal duration is a direct consequence of the aerosol transport into the ICP.³⁰ Since gas dynamics determine the transport, turbulences caused by uneven samples like glass fragments can significantly alter the aerosol transport. Therefore, this section focuses on the washout of the ²³Na signal of the flat external calibration standard FGS 2, which should demonstrate more reproducible aerosol transport.

However, using kernel density estimates, it is visible that the narrower opening of the PFAC results in significantly less reproducible washout durations compared to the wider opening of the MPFAC. The narrow opening shows a lower minimum washout duration, but results in a bimodal, wide distribution. As ablation is a stochastic process for glass ablation using nanosecond lasers,³¹ this is assumed to be due to different and irregular expansions of the laser plume. A wider opening compensates for those effects by allowing a wider spatial distribution of aerosol to be transported densely into the plasma. Another difference between the two variations of ablation cells is also visible in the RSD of the quantification of the glass fragments and quality control standard (Fig. 3). Since matching processes are direct comparisons of two samples, the trueness of quantification is of less importance than the precision or reproducibility, which is represented by the RSD. Lower RSD are found in the low-to-mid mass range for the MPFAC, while maintaining comparable RSD for higher masses (Fig. 4). As a result, the MPFAC allows for more reproducible quantification and as shown in later sections, results in more successful matching. For future works, low dispersion ablation cells with comparatively larger openings should be chosen even at the cost of longer washout durations and marginally worse signal-to-noise.

Fig. 3 Kernel density estimates (KDE) of the aerosol washout durations (FW 0.1 M) for the two different ablation cell designs, varying in opening width between large and small volume. For the quality control standard FGS 1, a wider opening (blue) results in a more reproducible washout duration, shown as a narrow Gaussian shape. A potential bimodal distribution could be assumed, but is not resolved. A smaller opening (grey) results in a wide bimodal distribution with lower minima but also significantly higher maxima.

Fig. 4 RSD of all quantified elements for the glass fragment databases and the quality control standard FGS 1 with both ablation cell designs. A wider opening results in lower RSD for low-to-mid masses, and comparable RSD for high masses in the case of glass fragments. Increased RSD and standard deviation thereof of Zr and Pb are due to known inhomogeneities in glass fragments.

Interval matching

In a first attempt, the interval matching procedure of the currently established method was investigated. The RSDs were multiplied by five, as described in other studies for optimal results and to compensate for inhomogeneity.^4,11 The matching procedure was done as explained above. For both ablation cells, the resulting error rates were significantly higher than the established method ASTM E2927-16.⁶ A modification was applied to the permitted intervals, giving less room for deviations for lighter elements. This approach (Rel. SD_min) employed a minimum interval of 15% for all elements, and a maximum interval of 20% for light elements (Mg–K). The reasoning behind this decision were the noticeable amount of error rates as a result of deviations with these elements. This was an unexpected observation as most lighter elements are main elements of the float glass composition and should not differ significantly between glass sources. However, due to their high concentrations, these elements require the use of notch filters to reduce their signal due to the limited dynamic range of the microchannel plate detectors. The effects of notch filters are still poorly understood but we suspect an effect on signal stability.

Using this variation for the intervals, a significantly improved error rate is found for false positives and false negatives with the MPFAC, while the PFAC still shows little improvement, most likely due to worse aerosol transport for larger spot sizes. Therefore, the modified ablation cell design would be suggested for forensic applications. While a lower error rate than the established method was unlikely due to the 25-fold reduction in sample material, this approach manages to be a sufficient alternative for samples that are too small to be measured using the conventional method. At a success rate of approx. 98%, this method surpasses the alternative of refractive index measurements which show less than 95% success rates.³² However, considering the dependence of the accuracy of this method, a specific ablation cell taking the observations shown in this work into account will be required.

Hoteling's T²-test

Rather than comparing mean concentrations, the increased amount of data points which this method generates allow the use of multivariate testing. This work focused on the use of Hotelling's T²-test for the comparison of two multi-dimensional distributions. First, this method was applied using the data of the successful modified ablation cell with a wider opening (MPFAC). Pooling of the reference samples allowed a representation of the inherent variations of each element within samples from the same source. However, direct application of the test using a 1% α-threshold for a two-tailed test proved to be unsuccessful. The required threshold appeared to be too low for this application. Noticeable differences in the order of magnitude of the F-value were observed between samples from the same source and from different sources. Assuming different acceptable thresholds for the F-values (Fig. 5) revealed a significant reduction of error rates down to not only acceptable, but competitive levels when compared to the currently established standard method. The threshold can be varied based on the weighting of false negatives and false positives and the ethical discussion of which are preferable. For example, a minimum total error rate is observed at a threshold of approx. 100, while a more ethically preferential ratio of false negatives to false positives is found at approx. 75 in the case of the MPFAC. It is assumed, that the reason for this necessary higher threshold is a result of the inherently occurring inhomogeneity of the glass samples. As the statistical test uses the hypothesis of the two samples being indistinguishable, an assumption of equal concentrations is made. Since the test does not correct for inhomogeneity of elements, these deviations in concentrations are considered a reason for falsely distinguishing the samples. Since this is a multidimensional test, several small deviations for each element add up and result in significantly larger F-values. Other applications of the Hotelling's T²-test using X-ray fluorescence spectroscopy (XRF) analysis of glass fragments also showed larger rates of false negatives when directly applied with no false positives.⁷ It is possible that the origin of both is rooted in sample heterogeneity and a higher F-value threshold could show improved results.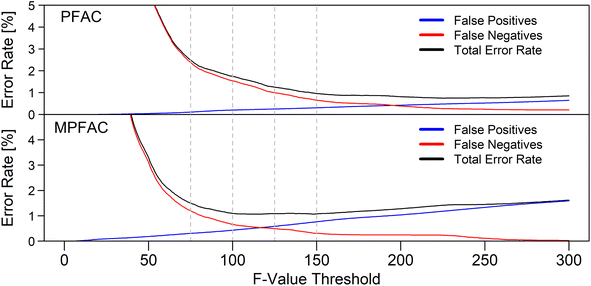

Fig. 5 Comparison of the effect of different F-value thresholds on the error rate of the statistical test for both ablation cells. Values for different thresholds can be found in Table 2 for the dashed lines.

Both ablation cells achieve low error rates comparable to the established method. However, the distributions for false negatives especially are shifted towards smaller thresholds when using the MPFAC. This is a result of the smaller RSDs, since the samples used were the same. For the use of different low dispersion ablation cells, this implies a necessity to repeat a study with known samples for the determination of their specific thresholds. However, after the determination of the characteristic threshold, different setups could be used with comparable results. In this study, it was observed that the PFAC shows similar error rates to the MPFAC but requires a threshold that is approx. 1.6–1.7 times higher. The mean RSD of the PFAC was also found to be 1.7× higher for the quality control standard compared to the MPFAC. While the two values are most likely the same due to coincidence, the statistical test is dependent on the standard deviations. It is possible that a RSD dependent correction could be made to determine the optimal thresholds. This does however require a larger sample size with different instrumentation (ablation cells, ICP instruments, laser wavelengths) with varying RSDs.

For the future of multivariate statistics for float glass analysis and other heterogeneous samples, a combination with interval statistics could show the optimal results with the lowest possible amount of errors. A test with empirically determined allowable deviations for each element could correct for the known inhomogeneities, while maintaining the advantages of multivariate statistics. However, no such statistical test currently exists. As an alternative, using a large inter-laboratory data base it would be possible to recalibrate the F-values in order to determine likelihood ratios.

Working with larger sample size

To validate the method with larger fragments, the data of three samples of the same source was pooled to represent a larger unknown fragment that could be analyzed multiple times. The statistical treatments discussed previously was then applied again to all possible combinations of same source matching, and a reduced amount of combinations for different source mismatching (Table 3). For each source, a random 24 out of 120 possible combinations were tested for same source combinations, and a random 50 out of 252 possible combinations for different source combinations. The reduction was made to reduce computational time with negligible effect on the statistical outcome. However, it has to be mentioned that this does not fully compare to actually measuring the same fragment multiple times. By using different fragments, the sample heterogeneity is compensated to a degree, reducing error rates with a stronger effect on false negatives.

Table 3 Error rates for different F-value thresholds calculated based on Hotelling's T² test for both ablation cells. The standard method has a rate of false negatives of 1.04% and a rate of false positives of 0.11%

	75	100	125	150
F-value threshold MPFAC
False neg. [%]	1.20	0.67	0.50	0.31
False pos. [%]	0.23	0.31	0.44	0.60
F-value threshold PFAC
False neg. [%]	2.38	1.54	1.00	0.65
False pos. [%]	0.11	0.20	0.27	0.33

---

For interval matching, the results compare to single fragment matching (Table 4). For the approach using minimum RSDs, slightly higher rates of false positives were observed. However, by adjusting the minimum thresholds it is possible to decrease the false positives while increasing false negatives until a favorable weighting of the two is achieved.

Table 4 Error rates for the statistical treatment of three pooled fragments representing an unknown source using interval matching

	PFAC (1.5 mm bottom opening)	MPFAC (3.5 mm bottom opening)
5× Rel. SD
False neg. [%]	4.79	4.01
False pos. [%]	0.39	0.19
5× Rel. SD min
False neg. [%]	0.99	0.60
False pos. [%]	0.52	0.38

---

For the multivariate approach, the necessary F-value threshold can be decreased significantly while achieving lower error rates (Table 5). The larger sample size allows for a better estimation of the population variance which improves the test's applicability. While the pooling of data in this work is not an exact replication of analyzing one fragment multiple times, this is a strong indicator that this method shows potential for the analysis of larger fragments as much as for smaller fragments. Surprisingly, the unmodified ablation cell shows negligible amounts of false positives. However, whether this is an effect of the data base or the cell itself is difficult to distinguish. Either way, multivariate statistics allow for a less instrumentation dependent analysis procedure than interval matching, making it the preferred matching method.

Table 5 Error rates for the statistical treatment of three pooled fragments representing an unknown source using multivariate matching based on Hotelling's T²-test

	50	60	70	80
F-value threshold PFAC
False neg. [%]	4.04	2.34	1.39	0.87
False pos. [%]	0.00	0.01	0.03	0.04
F-value threshold MPFAC
False neg. [%]	1.38	0.68	0.36	0.18
False pos. [%]	0.10	0.13	0.16	0.18

---

Furthermore, it is feasible to adapt the sampling procedure to the shape of the fragment. For example, 50 laser pulses can be drilled at a thinner area, and 100 at a thicker area of the fragment. This enables the analysis of irregular fragments with more data points than previously, improving the method's accuracy with every addition.

Conclusion

In this work, a single-pulse LA-ICP-TOFMS method for the analysis and matching of forensic float glass samples is presented. It demonstrates the effect of the low dispersion ablation cell design on the reproducibility of quantification. With improved aerosol transport by means of a wider opening for aerosol transport into the smaller volume, the RSDs for quality control and real case samples were reduced and appeared more reproducible. This decreased the error rates when using established interval matching procedures. For a 25× lower sample consumption, this method offers comparable error rates to the established standard method ASTM E2927-16.⁶ An optimized ablation cell design is proposed for low error rates, based on a modified version of the published PFAC. The direct application of Hotelling's T²-test for matching showed unusable amounts of errors (approx. 88–99% of false negatives). An investigation of the resulting F-values revealed significant differences between the F-values of matching fragments and mismatching fragments. Instead of using a two-tailed F-test, different thresholds were applied for matching and the resulting error rates were computed using samples of known origin. For both ablation cells, low error rates were achieved which are competitive with the established standard method. Adjustment of the threshold allows the changing of the ratio of false positives and negatives until an ethically preferred value is reached, with false positives (conviction of an innocent person) being less desirable. The two ablation cells used showed similar error rates at different F-value thresholds. This implies a need for calibration of the method for the setup used, but application of different instrumentation is possible. The need for significantly higher thresholds than a standard F-test would require is hypothesized to be caused by two connected effects. For one, float glass has inherent inhomogeneities, which means that two samples are similar but not equal in concentrations even if originating from the same source. As the test hypothesis assumes indistinguishable concentrations, this results in an increase of the F-value. Meanwhile, the sample shows micro-homogeneity, which results in a low variance in the measurement of a single fragment. Comparing the low variance of a single fragment to the significantly larger variance across multiple known reference samples further increases the resulting F-value. Nonetheless, this method offers new possibilities in analysing float glass fragments that have previously been too small to be analysed and statistically treated by means of element analysis. The increase in data points offers more information and provides the basis for multivariate statistics, even if corrections are necessary. Error rates were superior to alternative methods for fragments of this size, and are competitive or complementary to the method developed for larger fragments. This method shows the capabilities of single pulse analysis and the value of using a TOFMS instrument for simultaneous multi-elemental detection. For future studies the F-values could be recalibrated to determine likelihood ratios for (mis-)matching with a large inter-laboratory data base. Alternatively, a new statistical test could be developed allowing for empirically determined deviations for each element to compensate for homogeneity and allow direct application of a statistical test.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to gratefully acknowledge the financial support by ETH Zurich and assistance of the Zurich Forensic Science Institute for providing the samples and helpful discussions. We would like to thank the ETH Zurich D-CHAB machine shop and specifically Roland Mäder for the manufacturing of the ablation cells used in this study. Furthermore, we are thankful for the aid and review of Dr Peter Weis and Dr Gunnar Schwarz.

References

1. R. J. Watling, B. F. Lynch and D. Herring, J. Anal. At. Spectrom., 1997, 12, 195–203.
2. C. Latkoczy, D. Günther, G. J. Q. van der Peijl, J. Buscaglia, J. R. Watling, J. R. Almirall, J. A. Hoogewerff, M. Dücking, R. D. Koons, A. Dobney and Others, J. Forensic Sci., 2005, 50, 1–15.
3. J. Thornton, Interpretation of Physical Aspects of Glass Evidence, Taylor & Francis, 2001.
4. P. Weis, M. Dücking, P. Watzke, S. Menges and S. Becker, J. Anal. At. Spectrom., 2011, 26, 1273–1284.
5. J. Hoogewerff, D. Gunther, C. Latkoczy, R. J. Watling, J. Buscaglia, R. D. Koons, J. R. Ehleringer and S. Kelly, Forensic Sci. Int., 2003, 136, 1.
6. Standard Test Method for Determination of Trace Elements in Soda-Lime Glass Samples Using Laser Ablation Inductively Coupled Plasma Mass Spectrometry for Forensic Comparisons, ASTM International, 2022.
7. T. Trejos, R. Koons, P. Weis, S. Becker, T. Berman, C. Dalpe, M. Duecking, J. Buscaglia, T. Eckert-Lumsdon, T. Ernst, C. Hanlon, A. Heydon, K. Mooney, R. Nelson, K. Olsson, E. Schenk, C. Palenik, E. C. Pollock, D. Rudell, S. Ryland, A. Tarifa, M. Valadez, A. Van Es, V. Zdanowicz and J. Almirall, J. Anal. At. Spectrom., 2013, 28, 1270–1282.
8. T. Trejos, R. Koons, S. Becker, T. Berman, J. Buscaglia, M. Duecking, T. Eckert-Lumsdon, T. Ernst, C. Hanlon, A. Heydon, K. Mooney, R. Nelson, K. Olsson, C. Palenik, E. C. Pollock, D. Rudell, S. Ryland, A. Tarifa, M. Valadez, P. Weis and J. Almirall, Anal. Bioanal. Chem., 2013, 405, 5393–5409.
9. A. Funatsuki, M. Takaoka, K. Shiota, D. Kokubu and Y. Suzuki, Anal. Sci., 2016, 32, 207–213.
10. B. E. Naes, S. Umpierrez, S. Ryland, C. Barnett and J. R. Almirall, Spectrochim. Acta, Part B, 2008, 63, 1145–1150.
11. H. Dorn, D. E. Ruddell, A. Heydon and B. D. Burton, Can. Soc. Forensic Sci. J., 2015, 48, 85–96.
12. C. G. G. Aitken and D. Lucy, J. R. Stat. Soc., C: Appl. Stat., 2004, 53, 109–122.
13. R. Corzo, T. Hoffman, P. Weis, J. Franco-Pedroso, D. Ramos and J. Almirall, Talanta, 2018, 186, 655–661.
14. A. Akmeemana, P. Weis, R. Corzo, D. Ramos, P. Zoon, T. Trejos, T. Ernst, C. Pollock, E. Bakowska, C. Neumann and J. Almirall, J. Chemom., 2021, 35, 1–14.
15. A. van Es, W. Wiarda, M. Hordijk, I. Alberink and P. Vergeer, Sci. Justice, 2017, 57, 181–192.
16. G. S. Morrison, Sci. Justice, 2011, 51, 91–98.
17. D. Ramos, J. Maroñas and J. Almirall, Chemom. Intell. Lab. Syst., 2021, 217, 1–15.
18. A. Gupta, R. Corzo, A. Akmeemana, K. Lambert, K. Jimenez, J. M. Curran and J. R. Almirall, J. Chemom., 2020, 1–16.
19. A. Akmeemana, R. Corzo and J. Almirall, Forensic Chem, 2022, 27, 1–5.
20. R. G. Miller, Simultaneous Statistical Inference, Springer-Verlag, New York, 2nd edn, 1981.
21. P. Becker, C. Neff, S. Hess, P. Weis and D. Günther, J. Anal. At. Spectrom., 2020, 35, 2248–2254.
22. C. Neff, P. Becker and D. Gunther, J. Anal. At. Spectrom., 2022, 37, 677–683.
23. C. Neff, P. Keresztes Schmidt, P. S. Garofalo, G. Schwarz and D. Günther, J. Anal. At. Spectrom., 2020, 35, 2255–2266.
24. M. Burger, G. Schwarz, A. Gundlach-Graham, D. Käser, B. Hattendorf and D. Günther, J. Anal. At. Spectrom., 2017, 32, 1946–1959.
25. K. P. Jochum, U. Weis, B. Stoll, D. Kuzmin, Q. Yang, I. Raczek, D. E. Jacob, A. Stracke, K. Birbaum, D. A. Frick, D. Günther and J. Enzweiler, Geostand. Geoanalytical Res., 2011, 35, 397–429.
26. H. P. Longerich, S. E. Jackson and D. Günther, J. Anal. At. Spectrom., 1996, 11, 899–904.
27. H. Charnok, Phys. Bull., 1970, 21, 153.
28. H. Hotelling, Ann. Math. Stat., 1931, 2, 360–378.
29. C. Stein, Ann. Math. Stat., 1959, 27, 616–623.
30. P. Becker, J. Koch and D. Günther, J. Anal. At. Spectrom., 2022, 37, 1846–1854.
31. R. Hergenröder, O. Samek and V. Hommes, Mass Spectrom. Rev., 2006, 25, 551–572.
32. C. M. Bridge, J. Powell, K. L. Steele and M. E. Sigman, Spectrochim. Acta, Part B, 2007, 62, 1419–1425.

---