 Open Access Article
Open Access ArticleExperimental determination of ruthenium L-shell fluorescence yields and Coster–Kronig transition probabilities
Nils
Wauschkuhn
 *,
Katja
Frenzel
*,
Katja
Frenzel
 ,
Burkhard
Beckhoff
and
Philipp
Hönicke
,
Burkhard
Beckhoff
and
Philipp
Hönicke

Physikalisch-Technische Bundesanstalt, Abbestr, 2-12, 10587 Berlin, Germany. E-mail: nils.wauschkuhn@ptb.de
First published on 5th May 2023
Abstract
The L-shell fluorescence yields and the Coster–Kronig factors of ruthenium (and the corresponding uncertainty) were determined for the first time experimentally by applying radiometrically calibrated instrumentation of the Physikalisch-Technische Bundesanstalt. The resulting fluorescence yields (ωL3 = 0.0459(20), ωL2 = 0.0415(26), ωL1 = 0.0109(9)) and the Coster–Kronig factors (f23 = 0.177(32), f13 = 0.528(90), f12 = 0.173(73)) agree reasonable well with parts of the data from the literature.
1 Introduction
Ruthenium is a versatile and widely used chemical element playing a crucial role in important areas of science and technology. Several applications in the area of semiconductor fabrication or catalysis can be identified, where ruthenium is essential. For extreme ultraviolet lithography masks1,2 or as interconnect metal3–5 either ruthenium or ruthenium-containing materials are very relevant. In catalysis, ruthenium-based catalysts provide remarkable properties in several different applications.6 In addition to this, ruthenium is also of relevance for emerging applications for energy storage7,8 and medicine.9,10But, if X-ray fluorescence (XRF) based techniques are to be used for determining the ruthenium content in such materials, one quickly finds that the knowledge of the relevant atomic fundamental parameter (FP) data for ruthenium is very limited: for ruthenium, especially its L-shell FP data and namely the L-subshell fluorescence yields and Coster–Kronig factors (CK), no experimentally determined data seems to exist so far. Available data in the literature is either purely theoretically determined or perhaps even less favorable, only interpolated employing adjacent chemical elements. As these FPs quantitatively describe the process of X-ray fluorescence generation, they are very crucial for most quantification approaches in XRF. Thus, they have a direct influence on the accuracy of the XRF quantification results.
As this is a highly inadequate situation, we applied the PTB's reference-free X-ray spectrometry toolset in order to experimentally determine the fluorescence yields and the Coster–Kronig factors of the L-subshells of ruthenium for the first time. Based on transmission and fluorescence experiments on thin film samples, such FP data can be derived as already demonstrated for a wide range of chemical elements.11–15
2 Experimental procedure
For an experimental determination of L-shell fluorescence yields and Coster–Kronig transition probabilities, both fluorescence- and transmission experiments with a selective excitation of the three L-subshells on either a free standing thin foil or a thin coating on a carrier foil are required.11–13,15 In the present work, these experiments were conducted on the four-crystal monochromator (FCM) beamline16 of BESSY II using a vacuum chamber that is in-house developed.17 This chamber was endowed with a silicon drift detector (SDD) of which the detection efficiency is radiometrically calibrated and the response functions are determined experimentally.18 The employed sample was a highly homogeneous 150 nm ruthenium deposition on a 500 nm Si3N4 membrane. To be able to isolate the ruthenium contribution from the total sample transmission, also a blank membrane of nominally identical thickness was used. Any potential moderate variation in the Si3N4 membrane thickness is only a second-order contribution to the uncertainties. Both samples were positioned in the chamber's center by using an x–y-scanning stage. The angle between the incoming beam and the sample as well as the angle between sample surface and detector was set to 45°.The transmission measurements were conducted in an energy range around the Ru-L absorption edges between 2.1 keV and 4 keV. Furthermore, X-ray fluorescence measurements were performed in the incident-energy domain between 2.8 keV and 3.4 keV. The established methodology11,12,19,20 to derive the relevant L-shell FPs from this experimental dataset is described in the following.
According to the Sherman equation,21 the measured count rate of fluorescence photons of a one-elemental foil, which is irradiated under 45°, is the product of the fluorescence production cross section σLi of the considered shell, the incoming Φ0(E0) as well as the fluorescence photon flux Φid(E0), the detection efficiency of the SDD, the mass deposition of that element, the attenuation correction factor Mi,E0 and the solid angle Ω of detection of the SDD.
The self-attenuation correction factor takes into account the attenuation of the incident radiation and of the fluorescence radiation on its way through the sample. The corresponding sample-specific attenuation correction factor Mi,E0 is determined by transmission experiments taking advantage of the fact, that the knowledge of the ruthenium deposition thickness d and its density ρ is not needed since they appear only in a product with the mass absorption coefficient μS or with the subshell photoionization cross section τS. The product μSρd is derived from the transmittance data using the Lambert–Beer law.
For incident energies E0 between the L3 edge and the L2 edge, the fluorescence production factor for the L3-subshell is
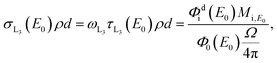 | (1) |
 | (2) |
Due to the so-called Coster–Kronig effect, the effective photoionization cross section τeff,Li(E0) for L3 and L2 is a linear combination with the higher bound shells since for photon energies above the excitation energy of the next subshell, created holes in L2 can decay into L3 by ejecting outer electrons. As a result, more than the directly created holes in L3 exist. The CK-factor f23 provides the probability for this to happen and similar transitions can occur between the L1 and the L2 and L3 shells. So for an incident photon energy above the L1 threshold, the fluorescence production factors are defined as:
| τeff,L3(E0) = τL3(E0) + f23τL2(E0) + [f13 + f12f23]τL1(E0) | (3) |
| τeff,L2(E0) = τL2(E0) + f12τL1(E0) | (4) |
| τeff,L1(E0) = τL1(E0) | (5) |
All relevant observables are accessible from the experimental data as μSρd are determined for the relevant energies by measuring the transmission of the ruthenium coating. Φid(E0) is determined by spectral deconvolution of the recorded SDD spectra considering the relevant fluorescence lines and relevant background contributions such as bremsstrahlung. Φ0(E0) and Ω are known because of PTB's calibrated instrumentation.22
Taking into account the theoretical ratio of scattering to ionization cross sections, which one can take from databases,23 the sample-specific total photoionization cross section τSρd can be derived. To isolate the subshell contributions of the different τLi, Ebel polynomials23 for each Li contribution as well as a total cross section for lower bound shells are scaled into the data (see Fig. 1). For this scaling process, only the datapoints slightly above each absorption edge are used to minimize the effect of the fine structure.
 | ||
| Fig. 1 τ S(E0)ρd determined for the ruthenium thin film: separation of the contributions of lower bound shells (yellow), L3 (green), L2 (red) and L1 (orange). | ||
With these determined τLiρd, the equations for the fluorescence production cross sections can be solved for ωLi. By replacing τLi by the effective photoionization cross section according to eqn (3)–(5), eqn (1) can be applied also for energies above the next subshell. Therefore, to determine f23, energies between EL3 and EL2 were considered, see Fig. 2: with the already determined ωL3, the modified version of eqn (1) can be solved for f23. f12 is determined in the same way but applied for the fluorescence of the L2 shell and for EL2 < E0 < EL1 with the already determined ωL2. With these determined f23 and f12, from the fluorescence of the L3 shell for energies above EL1, f13 can be determined.
3 Results
The determined fluorescence yields are ωL3 = 0.0459(20), ωL2 = 0.0415(26) and ωL1 = 0.0109(9). The resulting Coster–Kronig factors are f23 = 0.177(32), f13 = 0.528(91) and f12 = 0.173(73). These values are compared with values from the literature in Table 1 and Fig. 3 and 4. The respective uncertainties were calculated via error propagation. The main contributions to the total uncertainty budget of the fluorescence yields were arising from the spectral deconvolution (∼2%) and from the photoionization cross sections (∼2%). The uncertainty budget is calculated by applying the reference-free XRF approach for the FP determination, discussed in more detail in ref. 24.| Ru ωL3 | Ru ωL2 | Ru ωL1 | |
|---|---|---|---|
| This work (XRF) | 0.0459(20) | 0.0415(26) | 0.0109(9) |
| X-raylib25 (comp.) | 0.043 | 0.040 | 0.012 |
| Krause26 (comp.) | 0.043(9) | 0.040(10) | 0.012(4) |
| Perkins et al.29 (comp.) | 0.045231 | 0.043368 | 0.0084138 |
| McGuire28 (theory) | 0.0450 | 0.0418 | 0.00774 |
| Puri et al.27 (theory) | 0.045 | 0.043 | 0.0083 |
| Xu et al.30 (comp.) | 0.015 |
 | ||
| Fig. 3 Comparison of the experimentally determined Ru-L-subshell fluorescence yields with values from the literature. | ||
 | ||
| Fig. 4 Comparison of the experimentally determined Coster–Kronig factor f23 with values from the literature. | ||
The X-raylib25 and Krause26 values of ωL3 and ωL1 are slightly outside of the error domain of the values determined in this work. The agreement with respect to the theoretically calculated data of Puri27 and McGuire28 is better in the case of ωL3 but even worse for ωL1. The data of Perkins29 as well as the data by Xu30 behaves very similarly. For ωL2, all available data from the literature agrees well with the result obtained here. With respect to the Coster–Kronig factors, the tabulated data in X-raylib and the Krause compilation is in good agreement with our results. However, the results are on or slightly outside the boundary of our uncertainty budget for all three CK values. The data by McGuire and Puri is outside of our results considering their uncertainty budget.
4 Conclusion
The Coster–Kronig factors and the fluorescence yields of ruthenium are determined experimentally by applying PTB's radiometrically calibrated instrumentation. The values determined are in reasonably good agreement with the values from the literature, although some literature values are slightly outside the uncertainty ranges of this work. The magnitude of the determined uncertainties of this work is much lower than the estimated uncertainties of Krause26 in the case of the fluorescence yield values. With respect to the Coster–Kronig factors, similar uncertainties were achieved here. In summary, this uncertainty reduction will positively influence the total uncertainties of fundamental parameter-based quantitative X-ray fluorescence experiments.As stated already in previous works of our group,14,15,24,31 the X-raylib database is also in the case of the Ru-L shell fundamental parameters a reliable reference.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the ECSEL Joint Undertaking (JU) IT2 under grant agreement No 875999. The JU receives support from the European Union's Horizon 2020 research and innovation programme and the Netherlands, Belgium, Germany, France, Austria, Hungary, the United Kingdom, Romania and Israel.References
- M. Wu, J. F. de Marneffe, K. Opsomer, C. Detavernier, A. Delabie and P. Naujok, et al., Characterization of Ru4−xTax (x = 1,2,3) alloy as material candidate for EUV low-n mask, Micro Nano Eng., 2021, 12, 100089 CrossRef CAS . Available from: https://www.sciencedirect.com/science/article/pii/S2590007221000101.
- V. Philipsen, K. V. Luong, K. Opsomer, L. Souriau, J. Rip, C. Detavernier, et al., Mask absorber development to enable next-generation EUVL, in Photomask Japan 2019: XXVI Symposium on Photomask and Next-Generation Lithography Mask Technology, ed. A. Ando, International Society for Optics and Photonics. SPIE, 2019, vol. 11178, p. 111780F, DOI:10.1117/12.2537967.
- L. G. Wen, C. Adelmann, O. V. Pedreira, S. Dutta, M. Popovici, B. Briggs, et al., Ruthenium metallization for advanced interconnects, in IEEE International Interconnect Technology Conference/Advanced Metallization Conference, IITC/AMC, 2016, pp. 34–36 Search PubMed.
- K. Barmak, S. Ezzat, R. Gusley, A. Jog, S. Kerdsongpanya and A. Khaniya, et al., Epitaxial metals for interconnects beyond Cu, J. Vac. Sci. Technol. A, 2020, 38(3), 033406, DOI:10.1116/6.0000018.
- S. Kondati Natarajan, C. L. Nies and M. Nolan, The role of Ru passivation and doping on the barrier and seed layer properties of Ru-modified TaN for copper interconnects, J. Chem. Phys., 2020, 152(14), 144701, DOI:10.1063/5.0003852.
- R. Gramage-Doria and C. Bruneau, Ruthenium-catalyzed C–H bond functionalization in cascade and one-pot transformations, Coord. Chem. Rev., 2021, 428, 213602 CrossRef CAS . https://www.sciencedirect.com/science/article/pii/S0010854520305865.
- S. Hsu, S. Rommel, P. Eversfield, K. Muller, E. Klemm and W. Thiel, et al., A rechargeable hydrogen battery based on Ru catalysis, Angew. Chem., Int. Ed., 2014, 53(27), 7074–7078, DOI:10.1002/anie.201310972.
- T. Liu, Z. Liu, G. Kim, J. T. Frith, N. Garcia-Araez and C. P. Grey, Understanding LiOH chemistry in a ruthenium-catalyzed Li–O2 battery, Angew. Chem., Int. Ed., 2017, 56(50), 16057–16062, DOI:10.1002/anie.201709886.
- E. Antonarakis and A. Emadi, Ruthenium-based chemotherapeutics: are they ready for prime time?, Cancer Chemother. Pharmacol., 2010, 66, 1–9 CrossRef CAS PubMed.
- C. S. Allardyce and P. J. Dyson, Ruthenium in medicine: current clinical uses and future prospects, Platin. Met. Rev., 2001, 45, 62 CAS.
- M. Kolbe, P. Hönicke, M. Müller and B. Beckhoff, L-subshell fluorescence yields and Coster–Kronig transition probabilities with a reliable uncertainty budget for selected high- and medium-Z elements, Phys. Rev. A, 2012, 86, 042512 CrossRef.
- M. Kolbe and P. Hönicke, Reliable determination of fundamental parameters of Zr and Ti for a reliable quantitative X-ray fluorescence analysis, X-Ray Spectrom., 2015, 44(4), 217–220 CrossRef CAS.
- Y. Kayser, P. Hönicke, M. Wansleben, A. Wählisch and B. Beckhoff, Experimental determination of the gadolinium L subshells fluorescence yields and Coster–Kronig transition probabilities, X-Ray Spectrom., 2022,(1) DOI:10.1002/xrs.3313.
- P. Hönicke, R. Unterumsberger, N. Wauschkuhn, M. Krämer, B. Beckhoff and P. Indelicato, et al., Experimental and theoretical approaches for determining the K-shell fluorescence yield of carbon, Radiat. Phys. Chem., 2022, 110501 Search PubMed.
- N. Wauschkuhn, K. Frenzel, B. Beckhoff and P. Hönicke, Experimental determination of tantalum L-shell fluorescence yields and Coster–Kronig transition probabilities, J. Anal. At. Spectrom., 2023, 38, 197–203, 10.1039/D2JA00325B.
- M. Krumrey, Design of a four-crystal monochromator beamline for radiometry at BESSY II, J. Synchrotron Radiat., 1998, 5(1), 6–9 CrossRef CAS PubMed.
- M. Kolbe, B. Beckhoff, M. Krumrey and G. Ulm, Thickness determination for Cu and Ni nanolayers: comparison of reference-free fundamental-parameter based X-ray fluorescence analysis and X-ray reflectometry, Spectrochim. Acta B, 2005, 60, 505–510 CrossRef.
- F. Scholze and M. Procop, Modelling the response function of energy dispersive X-ray spectrometers with silicon detectors, X-Ray Spectrom., 2009, 38(4), 312–321 CrossRef CAS.
- P. Hönicke, M. Kolbe, M. Müller, M. Mantler, M. Krämer and B. Beckhoff, Experimental verification of the individual energy dependencies of the partial L-shell photoionization cross sections of Pd and Mo, Phys. Rev. Lett., 2014, 113(16), 163001 CrossRef PubMed.
- Y. Ménesguen, M. C. Lépy, J. M. Sampaio, J. P. Marques, F. Parente and M. Guerra, et al., A combined experimental and theoretical approach to determine X-ray atomic fundamental quantities of Tin, X-Ray Spectrom., 2018, 47(5), 341–351 CrossRef.
- J. Sherman, The theoretical derivation of fluorescent X-ray intensities from mixtures, Spectrochim. Acta, 1955, 7, 283–306 CrossRef CAS.
- B. Beckhoff, Reference-free X-ray spectrometry based on metrology using synchrotron radiation, J. Anal. At. Spectrom., 2008, 23, 845–853 RSC.
- H. Ebel, R. Svagera, M. F. Ebel, A. Shaltout and J. H. Hubbell, Numerical description of photoelectric absorption coefficients for fundamental parameter programs, X-Ray Spectrom., 2003, 32, 442–451 CrossRef CAS.
- R. Unterumsberger, P. Hönicke, J. Colaux, C. Jeynes, M. Wansleben and M. Müller, et al., Accurate experimental determination of gallium K- and L3-shell XRF fundamental parameters, J. Anal. At. Spectrom., 2018, 33(6), 1003–1013 RSC.
- T. Schoonjans, A. Brunetti, B. Golosio, M. S. del Rio, V. A. Solé and C. Ferrero, et al., The xraylib library for X-ray–matter interactions. Recent developments, Spectrochim. Acta B, 2011, 66, 776–784 CrossRef CAS.
- M. O. Krause, Atomic radiative and radiationless yields for K and L shells, J. Phys. Chem. Ref. Data, 1979, 8(2), 307–327 CrossRef CAS.
- S. Puri, D. Mehta, B. Chand, N. Singh and P. N. Trehan, L shell fluorescence yields and Coster–Kronig transition probabilities for the elements with 25 ≤ Z ≤ 96, X-Ray Spectrom., 1993, 22(5), 358–361 CrossRef CAS.
- E. McGuire, Atomic L-shell Coster–Kronig, Auger, and radiative rates and fluorescence yields for Na-Th, Phys. Rev. A, 1971, 3(2), 587 CrossRef.
- S. T. Perkins, D. E. Cullen, M. H. Chen, J. Rathkopf, J. Scofield, and J. H. Hubbell, Tables and graphs of atomic subshell and relaxation data derived from the LLNL evaluated atomic data library (EADL), Z = 1–100, UCRL-50400-Vol-30, 1991.
- J. Xu and E. Rosato, Relative intensities of diagram and satellite L-X-rays for elements Z = 37–56, J. Phys., 1987, 48(C-9), 661–664 Search PubMed.
- P. Hönicke, M. Kolbe, M. Krumrey, R. Unterumsberger and B. Beckhoff, Experimental determination of the oxygen K-shell fluorescence yield using thin SiO2 and Al2O3 foils, Spectrochim. Acta B, 2016, 124, 94–98 CrossRef.
| This journal is © The Royal Society of Chemistry 2023 |

