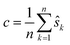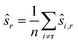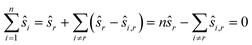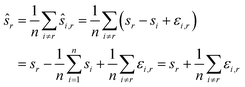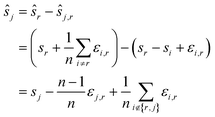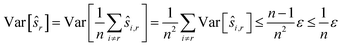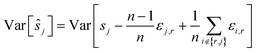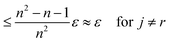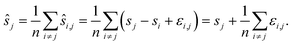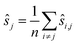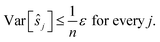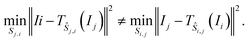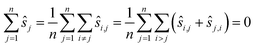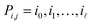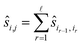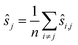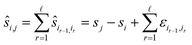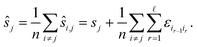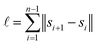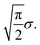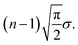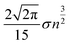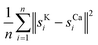Open Access Article
Open Access ArticleEfficient and robust image registration for two-dimensional micro-X-ray fluorescence measurements†
Felix
Bock
a,
Andreas
Gruber
b,
Kerstin
Leopold
 *b and
Henning
Bruhn
*b and
Henning
Bruhn
 *a
*a
aInstitute of Optimization and Operations Research, Ulm University, Ulm, Germany
bInstitute of Analytical and Bioanalytical Chemistry, Ulm University, Ulm, Germany
First published on 21st February 2023
Abstract
X-ray fluorescence spectrometry (XRF) is a technique that allows determining non-destructively the composition of elements within a sample. Focussing the excitation X-ray beam to a small spot that is moved in the x–y-direction relative to the sample adds lateral information. Such a two-dimensional micro-X-ray fluorescence (2D µ-XRF) spectrometer for desktop use is commercially available providing a resolution down to approximately 10 µm. With a µ-XRF spectrometer, it is inexpensive to take many scans of the same sample. With super-resolution methods, these can potentially be combined into a higher-resolution image. As a prerequisite, the misalignments of multiple scans (shifts and rotation) in the subpixel range have to be detected. We present a method for image registration of multiple images based on expander graphs that provides adjustable tradeoffs between registration quality and running time. We evaluate the algorithms on artificial and real µ-XRF data and we argue that our findings show that subpixel information is present in real µ-XRF data. This is a necessary condition for the applicability of multi-image super-resolution techniques to µ-XRF data in future work.
1 Introduction
The measurement of the local distribution of chemical elements, i.e. element mapping or imaging, is a highly topical research field in analytical chemistry. Many important conclusions can be drawn from the obtained information on chemical–physical and chemical–biological processes taking place at surfaces and interphases of technical materials, in the environment and in biological systems.1–3 Among the broad variety of analytical techniques available for element mapping, micro-X-ray fluorescence spectrometry (µ-XRF) in a laboratory set-up combines the advantages of non-destructive sample analysis with those of inexpensive routine measurement of large sample series.4,5 In commercially available 2D µ-XRF instrumentation poly capillary optics focus the X-ray radiation from an X-ray tube to an excitation spot of 5–25 µm in size. Fast scanning of the sample that is placed on an x–y-stage provides individual spectra for each measurement spot resulting finally in pixelated element images of the sample. The lateral resolution of these element images is mainly defined by the spot size and brilliance of the X-ray beam. In many fields of application, especially in biological and medical research, higher resolution is most desirable. Therefore, efforts to improve the resolution of laboratory µ-XRF set-ups have been made by several research groups in recent years.5 Approaches focus on providing higher brilliance of the X-ray spot by using either alternative sources, like a liquid metal jet X-ray source instead of an X-ray tube,6 and/or by enhanced focussing optics.7,8 Another approach is allowing pixels with overlapping spots, i.e. applying the so-called oversampling technique. Here, images at pixel sizes down to a few µm can be taken though at this level the resulting scans are already blurry and their effective resolution is worse. Yang et al.9 tackled this issue by measuring the X-ray spot more precisely, which in return allows using common image deblurring techniques to improve the effective resolution of images obtained by oversampling.As taking several scans with a µ-XRF spectrometer is still inexpensive, techniques of multi-image super-resolution appear attractive: multiple low-resolution images of the same object can be combined into a single high-resolution image.10 The low-resolution images will normally not be perfectly aligned but be shifted and rotated with respect to each other. These misalignments are the source of the subpixel information that is necessary to compute the high-resolution image. In order to make use of this, the image registration problem, the detection of the shifts and rotations between the images, has to be solved at a subpixel scale.
A large variety of image registration algorithms has been proposed.11–15 Typically, these algorithms are presented only for pairs of images. If there are more than two images, a common workaround is selecting one image as a reference.12,13 Then, the other images can be shifted onto this reference image.
The quality of the image registration is quite heavily dependent on the quality of the reference image. This may be noisy or suffer from artefacts as the image resolution in a super-resolution context is usually at the limit of the imaging device. To reduce the dependency on a single reference image, it has been proposed to determine all shifts simultaneously by minimising a global cost function.16–18 While this noticeably improves the quality of the registration, it comes with a significant computational burden. We present a method based on expander graphs that provides a trade-off between image registration quality and computation time. We demonstrate its advantages by comparing our method with the single reference method on µ-XRF data.
Besides photo images the image registration problem has already been considered for several medical diagnosis techniques such as mass spectrometry imaging (MSI),19 computed tomography (CT),20 and the combination of CT images and ultrasound images.21 Each type of image comes along with its own challenges.
This article is organised as follows: in Section 2, the parameters of the experiments are stated. In Section 3.1, the registration model is described and in Section 3.2 the algorithms are presented. Finally, in Section 4 the algorithms are evaluated on artificial data and on real µ-XRF measurements.
2 Experimental section
µ-XRF element images are obtained using a Bruker M4 Tornado (software version 1.5.2.48; Bruker Nano GmbH, Berlin, Germany). It is equipped with a rhodium X-ray tube operated at 50 kV and 600 µA. The polychromatic beam is focused via poly capillary lenses to a spot size of approximately 25 µm onto the sample at Mo Kα (17.480 keV). The detector, an XFlash 430, with an active area of 30 mm2 has a resolution of <145 eV at Mn Kα. To minimise interference with elements in the air, the analyses are carried out at a reduced pressure of 20 mbar. The selected area under investigation in this work is 1000 µm × 500 µm and comprises 250 × 125 pixels resulting in a nominal pixel size of 4 µm × 4 µm. The dwell time is set to 10 ms per pixel. An overall scan takes 10 min. Potassium (K) and calcium (Ca) in real samples are detected at K Kα1 (3.312 keV) and Ca Kα1 (3.691 keV). Spectra evaluation is performed using M4 Tornado evaluation software version 1.6.0.286.Cross sections of a Norway maple tree – Acer platanoides – with a thickness of 20 µm (GSL1 microtome, Schenkung Dapples, Zürich, Switzerland) are prepared to serve as a real sample. The dried microtome sections are fixed on a silicon wafer (Microchemicals GmbH, Ulm, Germany) in a class-100 laminar flow box (SuSi Super Silent, Spectec GmbH, Erding, Germany) in order to avoid any contamination. Sample carriers are then clamped to a house-made holder attached to the sample stage of the instrument.
3 Theoretical section
3.1 Registration model
In our method, we take several µ-XRF scans of the same sample. We model this mathematically: the data consist of n low-resolution images I1, I2, …, In (the scans) that arise from an unknown high-resolution image H (the sample) by a process that subjects the high-resolution image to the following transformations in this order:• Ti: first, an affine transformation that captures the rotation and translation of the ith image (i.e., in between measurements, the sample shifts or rotates a little bit);
• B: blurring due to the measurement optics;
• D: downsampling (i.e., the high-resolution image of the sample is transformed to the low resolution that is supported by the measurement device); and
• Ni: finally, addition of noise.
While Ti and Ni depend on the individual low-resolution image, B and D are the same for every image. In µ-XRF it turns out that the samples do not rotate in between measurements, so that the transformation Ti reduces to a translation by a 2-dimensional shift vector si = (si1, si2), where si1 expresses the shift in the x-direction, and si2 the shift in the y-direction. We will write Tsi for the translation with the shift vector si. (We note that, while we concentrate on translations, the presented methods can be generalised to allow rotations as well.)
Ultimately, an estimate of the high-resolution image H is desired. This requires an inversion of the transformations Ni, D, B and Ti. The inversion of the blurring and downsampling operators B and D are hard computational problems that, however, become easier if the translations Tsi are already known. We therefore concentrate here on image registration, the problem of recovering the shift vectors si.
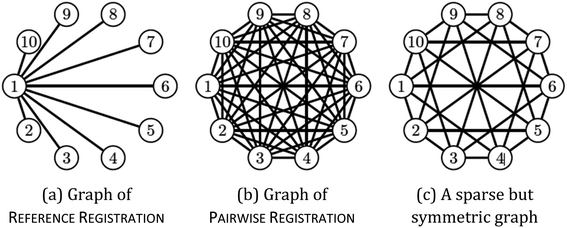
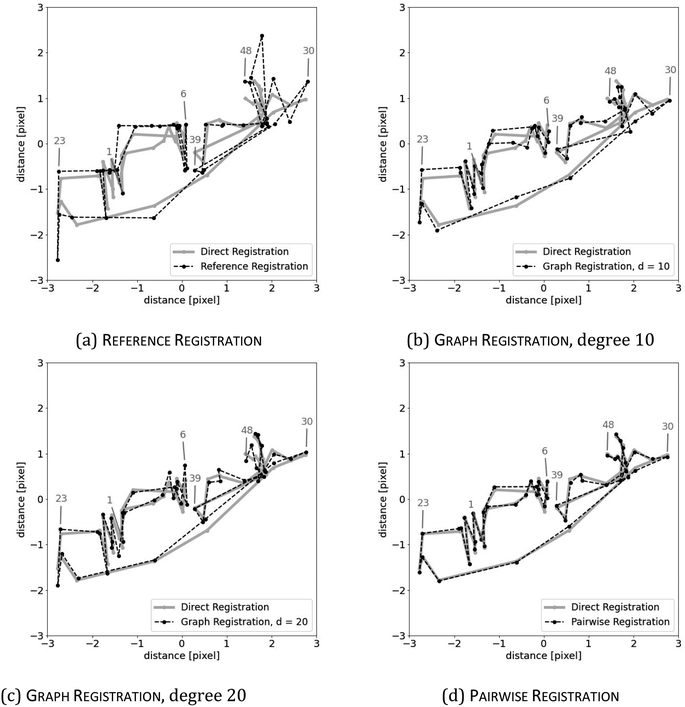
We may assume that the images are centered at the origin 0, i.e., that the sum of all shifts cancels out:
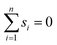 | (1) |
The translation Tsi commutes with B and also with D up to small errors due to interpolation. The shift vectors can thus be recovered by shifting the low-resolution images to the best possible fit.
A method often seen is as follows: pick a reference image Ir and then, for every other image, search for the shift that minimises the sum of squared differences to the reference image:12,13,22,23
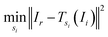 | (2) |
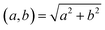 denotes the usual Euclidean norm in the plane.
denotes the usual Euclidean norm in the plane.
An alternative to the reference image method is to consider all pairs at once by using the sum of all sums of squared differences:
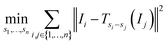 | (3) |
Note that this objective function is symmetric in the sense that all images are treated the same.
There is some fine print. The shifted images have to be evaluated at fractional pixel positions, which requires interpolation. In this article, we use one of the simplest interpolation methods, bilinear interpolation. Pixels at the border pose another problem. Due to the shifts, there are pixels in one image that are beyond the border of the other image. Since the shifts in our application are at most a few pixels, the cleanest way is to disregard pixels close to the border in the loss function.
3.2 Registration algorithms
Algorithms for image registration have two major competing goals: high accuracy and low running time. In this section, four algorithms are discussed with a different balance of these goals.The most straightforward way of minimising eqn (3) is to apply a standard solver, such as Nelder–Mead.24 Nelder–Mead is particularly suited as it does not require a differentiable objective function. Indeed, with bilinear interpolation, the optimisation goal eqn (3) is not differentiable. Instead of Nelder–Mead any other standard algorithm could be used. This would not (much) impact the following discussion. For easier comparability, direct registration (Algorithm 1, Table 1) centers the resulting shifts (line 3).
Minimising eqn (3) is a 2n-dimensional problem, i.e., the solution is a vector of 2n numbers (two for each of the n shifts). As a consequence, the running time will often be large.
Next, let us consider the reference image method eqn (2). If si is the true position during measurement i then the pairwise shift si,r of an image Ii to the reference image Ir satisfies the equation
| si,r = sr − si. |
Thus, the pairwise shifts can be used to compute estimates for the shifts as shown in reference registration (Algorithm 2, Table 2).
The choice of ŝr in line 2 ensures that the positions are centered as
We employ Nelder–Mead in line 1. While direct registration is a single 2n-dimensional minimisation problem, reference registration makes do with n − 1 2-dimensional minimisation problems. Reference registration is much faster as Nelder–Mead scales super-linearly with the dimension. Accuracy, in contrast, is reduced. Indeed, the algorithm depends heavily on the quality of the reference image: the noise and artefacts in it will have a great impact on computed shifts. In the hypothetical case, for example, that the reference image is pure noise, the resulting shifts will be completely random.
Let us formalise this insight. Noise makes the estimates ŝi,j for the pairwise shifts differ from the true shifts ŝi,j by an error term of 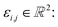
| ŝi,r = si,r + εi,r = sr − si + εi,r |
We compute for the estimate ŝr of the shift of the reference image:
We estimate the variance of the computed ŝi. The estimated shifts ŝi are 2-dimensional vectors and thus to compute the variance we need to treat each entry (in x- and in y-directions) separately. However, the computation is the same. As we do not want to encumber the notation with another subindex to distinguish between x- and y-entries, we write Var[ŝi] to denote the vector consisting of the variance of each entry. For simplicity, we assume that the errors εi,j are uncorrelated, and that the variance (of each entry) is bounded by a constant that does not depend on i, j or whether it is the x- or y-entry. We write ε for the 2-dimensional vector with both entries equal to that constant. We also assume that the mean error is 0, which seems reasonable given the symmetric roles of Ii and Ij.
We use only a basic property of variance: if X1, …, XN are uncorrelated random variables, and if a1, …, aN and b are constants then 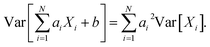 We get:
We get:
We see that for an increasing number of scans n, the variance Var[ŝr] of the reference image vanishes, while this is not the case for ŝi with i ≠ r. Vanishing variance25 means that, for increasing n, the estimate ŝr of the reference image is, with high probability, arbitrarily close to the true value sr. In other words, the more scans are taken, the more likely it is to recover the precise shift. Again, this cannot be guaranteed for other ŝi, i.e., for non-reference images.
In practice, the errors εi,r will be correlated. While this may dampen the overall error, it will still be quite noticeable.
To reduce the inaccuracies for non-reference images, pairwise registration (Algorithm 3, Table 3) computes estimates ŝi,j for every pair of images Ii,Ij. Using that the center is 0, i.e.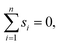 estimates for the positions are given by:
estimates for the positions are given by:
This can be interpreted as treating each image as the reference image for its own position. With the same assumptions as above, we obtain
In contrast to reference registration, here, the variance vanishes for all images, and thus, for an increasing number of scans, the estimation ŝj will be, with high probability, arbitrarily close to the true value sj.
Note that as a side effect of interpolation at a subpixel level, it may make a difference whether the image Ii is compared to Ij, or Ij to Ii. That is
As a consequence, the minimiser ŝi,j of the left-hand side does not need to coincide with the negative of the minimiser of the right-hand side. In practice, however, the difference turns out to be negligible even at a subpixel scale, which is the justification for line 3.
This choice saves on computation time and additionally ensures that the positions are centered:
The running time of pairwise registration is mostly determined by the number of pairwise shifts that are computed in line 2. As there are 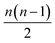 pairs i < j, the running time grows quadratically in n which results in large running times even for a moderate number n of scans.
pairs i < j, the running time grows quadratically in n which results in large running times even for a moderate number n of scans.
It would be desirable to construct an algorithm that uses an intermediate number of pairwise shifts to obtain results that are more precise than reference registration but not as time-consuming as pairwise registration.
This poses the question which pairwise shifts should be computed and how to use them to improve the accuracy.
Which pairwise shifts are computed in the two algorithms is illustrated in Fig. 1. We phrase these observations in the language of graphs.26 Each image is a vertex of this graph (the numbered circles in the figure), and whenever we directly compute the shift between two images then they are linked by an edge. Thus, for reference registration (Fig. 1a), every image is linked by an edge to the reference image (with index 1 in the figure) but there is no edge between any two non-reference images. The graph is very sparse, i.e. has few edges, which is indicative of a small running time. In contrast, the graph for pairwise registration (Fig. 1b) is very dense as every pair of images is compared, i.e. linked by an edge, resulting in a large running time. The asymmetry of the reference registration graph reflects the poor error asymptotics.
The aim now is to base image registration on a graph (Algorithm 4, Table 4) that is a compromise between the reference registration graph and the pairwise registration graph: sparse but very symmetric, a bit like the graph on the right in Fig. 1. We will discuss below how we choose the graph.
Given a graph for image registration, how do we compute the estimates ŝi,j? Whenever two vertices i, j are linked by an edge in such a graph, we directly compute ŝi,j. If they are not, then we proceed as in the reference image method: we take a sequence of distinct images 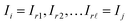 such that each of the two consecutive images is linked by an edge, and then compute the shift estimate ŝi,j as the sum of the directly computed shifts. For example, there is no edge between vertices 1 and 3 in the graph of Fig. 1c. But there is an edge from 1 to 2 and from 2 to 3, resulting in the estimate ŝ1,3 = ŝ1,2 + ŝ2,3.
such that each of the two consecutive images is linked by an edge, and then compute the shift estimate ŝi,j as the sum of the directly computed shifts. For example, there is no edge between vertices 1 and 3 in the graph of Fig. 1c. But there is an edge from 1 to 2 and from 2 to 3, resulting in the estimate ŝ1,3 = ŝ1,2 + ŝ2,3.
In the terminology of graph theory, such a sequence of distinct vertices, with each consecutive pair linked by an edge, is called a path. To reduce the error of the estimates ŝi,j, the path Pi,j from i to j should have few edges, and we will compute these to have the shortest number of edges possible.
The paths in line 6 can be computed easily with a standard algorithm, breadth-first search.27 Note that graph registration reduces to reference registration, or to pairwise registration, if the graph is chosen as the one on the left in Fig. 1 or as the one in the middle. The estimates ŝi,j decompose into:
This results in errors for the positions as follows:
To obtain small variances for ŝj the individual errors εr,t should only contribute to a few shortest paths Pi,j. This can be achieved by choosing a Moore graph28 as graph G. A Moore graph is highly symmetric. In particular, there is an integer d such that every vertex is linked to precisely d other vertices by an edge. We argue in the appendix (see ESI†) that the variance Var[ŝi,j] vanishes with increasing d which implies that, with high probability, ŝi,j converges to si,j with increasing d. The parameter d, on the other hand, also determines how many edges the graph contains, namely 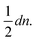 As the running time of graph registration depends mainly on the number of edges, we can use the parameter d to fine-tune the balance between precision and running time.
As the running time of graph registration depends mainly on the number of edges, we can use the parameter d to fine-tune the balance between precision and running time.
There are, unfortunately, only a few (non-trivial) Moore graphs. It turns out, however, that a random graph is highly likely to share many properties of a Moore graph. A random graph is one where, for a fixed number of vertices, we decide for each potential edge with probability p whether the edge is present or not. There are more sophisticated but not overly complex methods to choose a random graph such that each vertex is incident with precisely d edges.29
A key property of Moore graphs is a mathematical property called expansion.30 We generate a large number (in the hundreds) of random graphs and then test for good expansion. This can be done by inspecting the eigenvalues of the adjacency matrix.31 Generating many random graphs and then testing for good expansion can be performed very efficiently so that even for hundreds of such graphs, the procedure takes less than a second. Moreover, suitable graphs for typical pairs of n and d could be precomputed and stored in a database, so that the graph is only computed once.
The code for all methods is available on GitHub.32
4 Results and discussion
4.1 Data acquisition and pre-processing
We test the algorithms on artificial data and on real micro X-ray fluorescence (µ-XRF) data. For the artificial data, we take a high-resolution image and degrade it as described by the model in Section 3.1. The shifts are drawn independently from a 2-dimensional Gaussian distribution with mean µ = 0 and variance 16 in x- and in y-direction. After drawing all shifts, the shifts are centered at 0. Then the images are blurred with a Gaussian kernel of size 120 × 120 with standard deviations of 20 in the x-axis and 28 in the y-axis. From each side, 80 pixels are cut off to avoid artefacts at the border. Finally, the images are downsampled with a factor of 4 in both axes and Gaussian noise is added with mean 0 and a standard deviation of 10. Whenever this results in negative pixel values, the pixel value is set to 0. An example image is shown in Fig. 2. | ||
| Fig. 2 Artificial data with (a) showing the original image and (b) depicting a sample of a generated low-resolution and blurred image. | ||
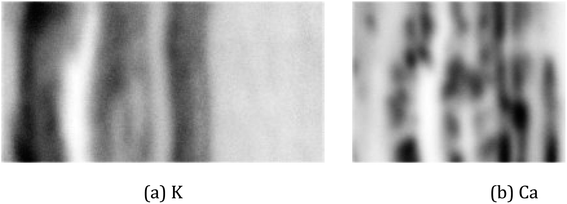
For the real µ-XRF images, cross sections of a twig of a Norway maple tree – Acer platanoides – are prepared and scans are taken with a nominal pixel size of 4 µm × 4 µm. Further experimental details are given in Section 2. The measurements are rather noisy as shown in Fig. 3 for the exemplary element maps of potassium (K) and calcium (Ca).
 | ||
| Fig. 3 Images of a cross-section of a twig. The pictures show a photo with the investigated area marked by the red rectangle (a) and µ-XRF scans for the elements potassium (b) and calcium (c). | ||
Typically, noise is assumed to be additive Gaussian noise. In µ-XRF images, however, noise appears to have more a complex behaviour. We found that preprocessing the measurements by blurring with a Gaussian kernel improves the quality of the image registration step. In our experiments, we used a Gaussian kernel of size 7 × 7 with standard deviations of 5 pixels in the x- and in the y-direction. The image registration results obtained with this pre-processing are described in Section 4.3.
4.2 Measures for evaluation
We compare the algorithms of Section 3.2 on the described artificial and real data. For the artificial data, we measure the• mean squared error to the (rescaled) ground truth (mse).
The ground truth has to be rescaled according to the factor of the downsampling. Real data make the evaluation much more challenging as there is no ground truth available. We evaluate the algorithms on three measures:
• fit quality (fit).
• path length (path).
• shift differences between the elements (diff).
The fit quality (fit) is the most direct measure: we simply determine the value of the objective function eqn (3) for the shifts found by each of the algorithms. This measure, fit, simply shows how well each algorithm manages to minimise the objective function eqn (3). It is not, however, the best measure of how close to the (unknown) true shifts the recovered shifts are since even the true shifts do not have a perfect fit score due to noise.
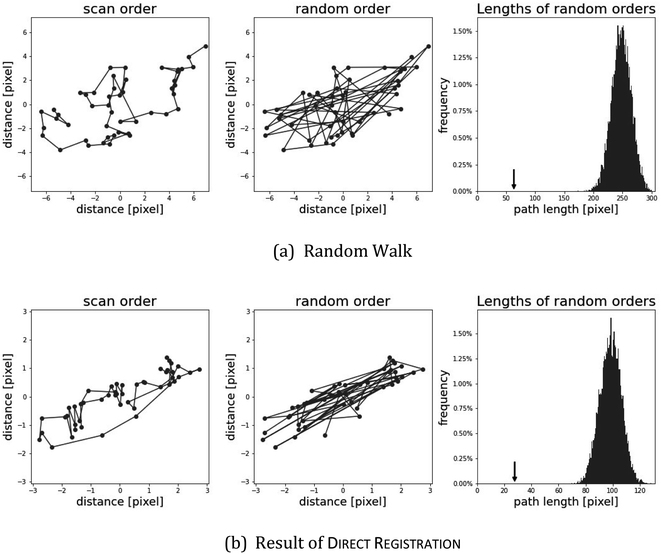
With the path length method, a variant of permutation tests,33 we aim to show that the recovered shifts are not random artifacts of the method. There are two extreme scenarios how the shifts s1, …, sn arise that each algorithm produces:
(a) The shifts are random artifacts of the algorithm, perhaps because there are no “true” shifts.
(b) The movement of the sample between measurements is reflected in the data, and the algorithm manages to detect the resulting shifts with reasonable accuracy.
Obviously, the truth will be between these two scenarios. With the measure path, we distinguish whether the truth is better represented by scenario (a) or by (b).
In scenario (a), the shifts s1, …, sn are the product of a random process that does not take the order of the shifts into account as the algorithms are invariant under permutation of the shifts (the order s1, …, sn is not used in any of the algorithms). As a result, the order s1, …, sn is not special, and the path s1–s2–…–sn in the plane is not special either. Therefore, we expect its length
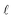 is contained in the q-quantile with very small q.
is contained in the q-quantile with very small q.
What happens if scenario (b) holds? Then, arguably, the shifts are best described by a random walk: between two scans, the sample moves a little, and this movement is added to the previous shift. For simplicity, let us assume that the movements si,i+1 between shifts si and si+1 in the random walk are distributed according to a 2-dimensional normal distribution with mean 0 and variance σ2 in each dimension. In this case the length of each movement si,i+1 is distributed according to a Rayleigh distribution with scale parameter σ.34 Hence, the expected length of each movement si,i+1 is
This results in an expected total length of the path s1–…–sn of
In contrast to scenario (a), if we subject the positions si to a random permutation τ we find that the expected length of the path of the permuted positions is roughly
The computation can be found in the appendix.
We see that the expected length of a permutation path grows with 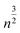 while the length of the random walk path only grows with n. This now allows us to distinguish between the two scenarios. If scenario (a) reflects the truth then the path length of the original scan order has a small probability to be among the 1% shortest paths, say. If, however, scenario (b) is closer to the truth, we expect the path length to be among the 1% shortest. To test this, we generated 10
while the length of the random walk path only grows with n. This now allows us to distinguish between the two scenarios. If scenario (a) reflects the truth then the path length of the original scan order has a small probability to be among the 1% shortest paths, say. If, however, scenario (b) is closer to the truth, we expect the path length to be among the 1% shortest. To test this, we generated 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 random permutations, computed the path length, and then determined the q-quantile of the path length of the actual scan order. This q-quantile can be seen in the column path of Tables 5 and 6.
000 random permutations, computed the path length, and then determined the q-quantile of the path length of the actual scan order. This q-quantile can be seen in the column path of Tables 5 and 6.
| Algorithm | Time [s] | fit | path | mse |
|---|---|---|---|---|
| No shift | — | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 923.2 923.2 |
— | 1.89770 |
| Reference registration | 170.1 | 9239.6 | 0.368 | 0.00353 |
| Graph registration, d = 4 | 325.4 | 9213.1 | 0.358 | 0.00200 |
| Graph registration, d = 10 | 826.7 | 9203.5 | 0.378 | 0.00138 |
| Graph registration, d = 20 | 1668.4 | 9203.5 | 0.388 | 0.00138 |
| Pairwise registration | 4183.3 | 9198.4 | 0.387 | 0.00100 |
| Direct registration | 113![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720.25 720.25 |
9198.3 | 0.374 | 0.00100 |
| Algorithm | Time [s] | fit | path | diff |
|---|---|---|---|---|
| No shift | — | 1431.7 | — | — |
| Reference registration | 112.2 | 492.0 | 0.000 | 0.238 |
| Graph registration, d = 4 | 228.4 | 483.5 | 0.000 | 0.131 |
| Graph registration, d = 10 | 575.9 | 482.4 | 0.000 | 0.103 |
| Graph registration, d = 20 | 1151.7 | 482.5 | 0.000 | 0.111 |
| Pairwise registration | 2440.8 | 481.9 | 0.000 | 0.087 |
| Direct registration | 116![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 813.0 813.0 |
481.8 | 0.000 | 0.094 |
As an illustration, we plot in Fig. 4 (top) an artificial example of scenario (b), the path length of a random walk compared to the path lengths of random permutations. The small arrow in the picture on the right side shows that the path length of the scan order is particularly short. Below, we show the same setting for the shifts of direct registration on twig µ-XRF data. While the path of direct registration appears to be the combination of random movement in conjunction with a possible systematic effect, we argue that they show similar phenomena.
When there is a usable signal in more than one element, we can do image registration for each element separately and compare the resulting shifts. If the algorithms work as intended then the corresponding shifts for the different elements should be close to each other.
Whether there are usable signals for more than one element highly depends on the sample. Sometimes, the signal may be too noisy for every element except one. In the twig data, we found that both potassium and calcium gave reasonable results. Consequently, we computed shifts sKi and sCai. We report the mean square difference of the shifts
4.3 Evaluation results
In addition to the evaluation measures, we tabulate the running times. The algorithms were run on an Intel Xeon Gold 6230 with 2.1 GHz and 12 GB memory. For every measure, averages over 10 runs are taken to obtain more reliable results. As a baseline, we also include a row “No shift” which corresponds to zero shifts for every image.The results of the artificial data created from the flower image in Fig. 2 are shown in Table 5. As predicted, the running times are increasing. Note that the running time for graph registration includes finding a suitable expander graph. This, however, amounts to well under a second. The fit value is improving but it never reaches zero. This is due to noise, which causes the ground truth itself to have a fit score of 9198.3. In the mse column, the improvements appear to be more significant and, indeed, the results get very close to the ground truth. In the column path, all values are about 0.37. That is about 37% of the random permutations result in a shorter path than the original ordering. This is as expected as the artificial shifts were not drawn from a random walk.
We carried out the same experiment for artificial data starting with other high-resolution images. We observed similar results, so we do not report them in detail. The fit values are also leveling off but at different values. This value depends on the size of the image, its brightness, and the noise level. Similarly, the path values are clustered at other values depending on the choice of the random shifts.
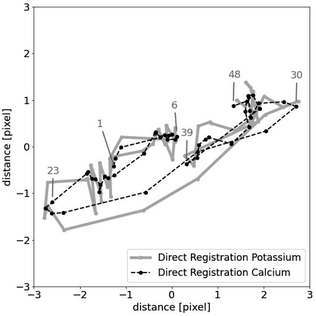
Table 6 shows the results for the µ-XRF data. Some representative results can be seen in Fig. 6. It shows similar characteristics as for the artificial data. Column diff appears to work as a reasonable stand-in for mse. A major difference is the column path: the value is always 0. This strongly indicates that the shifts in the µ-XRF data arise from a random walk. It also shows that every algorithm detects the shift and they only differ in their precision.
The first attempt of using the recovered shifts to compute a single image is shifting the multiple scans on top of each other and using their mean. The resulting higher resolution image of using the shifts of graph registration, with d = 20, is shown in Fig. 7. In comparison to the images in Fig. 3, this basic approach already visibly improves the quality of the element map.
 | ||
| Fig. 7 Shift corrected means of µ-XRF scans (with n = 48 scans) of the element potassium (a) and calcium (b); calculated by graph registration, with d = 20. | ||
The result, however, still looks blurry and there are no sharp edges. This is because the recovered shift is only used to reverse the transformations Ti (see the beginning of Section 3.1) but not the blurring transformation B. Finding the best possible way to reverse this transformation B is part of ongoing research.
Unfortunately, the quality of the resulting high-resolution image depends on the precision of reversing both transformations Ti and B simultaneously. Therefore, at least visibly, it is hard to see any differences between the shift-corrected means of the different methods proposed in Section 3.2. For a subsequent de-blurring, however, computing the shifts with sufficient precision seems essential.
Finally, computation time might further be decreased by restricting to a smaller area of interest. A first mapping of the complete sample could be followed by repeated scanning of the area of interest, to which then image registration is applied. A certain minimum size of the area of interest is necessary, though, as otherwise boundary effects will deteriorate the recovery quality.
5 Conclusion
We have succeeded for the first time in solving the image registration problem for real µ-XRF data of a biological sample. Our approach provides an adjustable tradeoff between computational time and image registration quality. All tested algorithms are able to recover consistently the shifts in artificial data, and they find shifts in real µ-XRF data that arguably reflect actual processes, the movement of the x–y-stage, during measurement. In particular, the comparison of the shifts with respect to different elements shows that the recovered shifts are reliable on a subpixel scale. Our findings, therefore, confirm the presence of subpixel information in a set of µ-XRF scans. As this is a necessary condition for the application of multi-image super-resolution techniques, our findings constitute a starting point for future improvements in the resolution of laboratory-based µ-XRF analysis. In addition, in future work, the new approach may be tested and adapted to other analytical imaging techniques based on scanning.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was funded by Vector-Stiftung in project P2019-0091. We are grateful to Lucian Kaack (Institute of Systematic Botany and Ecology, Ulm University) for the preparation of Acer platanoides cross sections.References
- C. M. Ackerman, S. Lee and C. J. Chang, Analytical Methods for Imaging Metals in Biology: From Transition Metal Metabolism to Transition Metal Signaling, Anal. Chem., 2017, 89(1), 22–41 CrossRef CAS PubMed.
- G. Guerriero, I. Stokes, N. Valle, J.-F. Hausman and C. Exley, Visualising Silicon in Plants: Histochemistry, Silica Sculptures and Elemental Imaging, Cells, 2020, 9(4), 1066 CrossRef CAS PubMed.
- D. Hartnell, W. Andrews, N. Smith, H. Jiang, E. McAllum, R. Rajan, F. Colbourne, M. Fitzgerald, V. Lam, R. Takechi and et al, A Review of Ex vivo Elemental Mapping Methods to Directly Image Changes in the Homeostasis of Diffusible Ions (Na+, K+, Mg2+, Ca2+, Cl−) Within Brain Tissue, Front. Neurosci., 2020, 13, 1415 CrossRef PubMed.
- V. K. Singh, N. Sharma and V. K. Singh, Application of x-ray fluorescence spectrometry in plant science: solutions, threats, and opportunities, X-Ray Spectrom., 2022, 51(3), 304–327 CrossRef CAS.
- C. Vanhoof, J. R. Bacon, U. E. Fittschen and L. Vincze, Atomic spectrometry update–a review of advances in x-ray fluorescence spectrometry and its special applications, J. Anal. At. Spectrom., 2021, 36(9), 1797–1812 RSC.
- L. Bauer, M. Lindqvist, F. Förste, U. Lundström, B. Hansson, M. Thiel, S. Bjeoumikhova, D. Grötzsch, W. Malzer, B. Kanngießer and I. Mantouvalou, Confocal micro-x-ray fluorescence spectroscopy with a liquid metal jet source, J. Anal. At. Spectrom., 2018, 33(9), 1552–1558 RSC.
- L. J. Bauer, R. Gnewkow, F. Förste, D. Grötzsch, S. Bjeoumikhova, B. Kanngießer and I. Mantouvalou, Increasing the sensitivity of micro x-ray fluorescence spectroscopy through an optimized adaptation of polycapillary lenses to a liquid metal jet source, J. Anal. At. Spectrom., 2021, 36(11), 2519–2527 RSC.
- K. Nakano, A. Matsuda, Y. Nodera and K. Tsuji, Improvement of spatial resolution of µ-XRF by using a thin metal filter, X-Ray Spectrom., 2008, 37(6), 642–645 CrossRef CAS.
- J. Yang, Z. Zhang and Q. Cheng, Resolution enhancement in micro-XRF using image restoration techniques, J. Anal. At. Spectrom., 2022, 37(4), 750–758 RSC.
- L. Yue, H. Shen, J. Li, Q. Yuan, H. Zhang and L. Zhang, Image superresolution: The techniques, applications, and future, Signal Process., 2016, 128, 389–408 CrossRef.
- D. I. Barnea and H. F. Silverman, A class of algorithms for fast digital image registration, IEEE Trans. Comput., 1972, 100(2), 179–186 Search PubMed.
- L. Chen and K.-H. Yap, An effective technique for subpixel image registration under noisy conditions, IEEE Trans. Syst. Man Cybern. A Syst. Hum., 2008, 38(4), 881–887 Search PubMed.
- M. Guizar-Sicairos, S. T. Thurman and J. R. Fienup, Efficient subpixel image registration algorithms, Opt. Lett., 2008, 33(2), 156–158 CrossRef PubMed.
- D. Keren, S. Peleg, and R. Brada. Image sequence enhancement using sub-pixel displacements, in CVPR, 1988, vol. 88, pp. 5–9 Search PubMed.
- B. D. Lucas and T. Kanade, An iterative image registration technique with an application to stereo vision, IJCAI, 1981, pp. 674–679 Search PubMed.
- W. Huizinga, D. H. Poot, J.-M. Guyader, R. Klaassen, B. F. Coolen, M. van Kranenburg, R. Van Geuns, A. Uitterdijk, M. Polfliet, J. Vandemeulebroucke and et al, PCA-based groupwise image registration for quantitative MRI, Med. Image Anal., 2016, 29, 65–78 CrossRef CAS PubMed.
- C. T. Metz, S. Klein, M. Schaap, T. van Walsum and W. J. Niessen, Nonrigid registration of dynamic medical imaging data using nd+ t b-splines and a groupwise optimization approach, Med. Image Anal., 2011, 15(2), 238–249 CrossRef CAS PubMed.
- C. Wachinger and N. Navab, Simultaneous registration of multiple images: similarity metrics and efficient optimization, IEEE Trans. Pattern Anal. Mach. Intell., 2012, 35(5), 1221–1233 Search PubMed.
- B. Balluff, R. M. Heeren and A. M. Race, An overview of image registration for aligning mass spectrometry imaging with clinically relevant imaging modalities, J. Mass Spectrom. Adv. Clin. Lab, 2022, 23, 26–38 CrossRef CAS PubMed.
- H. Dida, F. Charif and A. Benchabane, Image registration of computed tomography of lung infected with COVID-19 using an improved sine cosine algorithm, Med. Biol. Eng. Comput., 2022, 1–15 Search PubMed.
- N. Masoumi, C. J. Belasso, M. O. Ahmad, H. Benali, Y. Xiao and H. Rivaz, Multimodal 3D ultrasound and CT in image-guided spinal surgery: public database and new registration algorithms, Int. J. Comput. Assisted Radiol. Surg., 2021, 16(4), 555–565 CrossRef PubMed.
- S. Kim and W. Su, Subpixel accuracy image registration by spectrum cancellation, in 1993 IEEE International Conference on Acoustics, Speech, and Signal Processing, 1993, vol. 5, pp. 153–156 Search PubMed.
- R. Szeliski and et al, Image alignment and stitching: a tutorial, Found. Trends Comput. Graph. Vis., 2007, 2(1), 1–104 CrossRef.
- J. A. Nelder and R. Mead, A simplex method for function minimization, Comput. J., 1965, 7(4), 308–313 CrossRef.
- Z. Birnbaum, J. Raymond and H. Zuckerman, A Generalization of Tshebyshev's Inequality to Two Dimensions, Ann. Math. Stat., 1947, 18(1), 70–79 CrossRef.
- R. Diestel, Graph Theory, Springer-Verlag, 5th edn, 2017 Search PubMed.
- T. Cormen, C. Leiserson, R. Rivest and C. Stein, Introduction to Algorithms, The MIT Press, 2009 Search PubMed.
- A. J. Hoffman and R. R. Singleton, On Moore graphs with diameters 2 and 3, IBM J. Res. Dev., 1960, 4(5), 497–504 Search PubMed.
- A. Steger and N. C. Wormald, Generating random regular graphs quickly, Comb. Probab. Comput., 1999, 8(4), 377–396 CrossRef.
- M. Dinitz, M. Schapira and G. Shahaf, Approximate Moore graphs are good expanders, J. Comb. Theory. Ser. B, 2020, 141, 240–263 CrossRef.
- N. Alon, Eigenvalues and expanders, Combinatorica, 1986, 6(2), 83–96 CrossRef.
- H. Bruhn and F. Bock, Image Registration Code, https://github.com/henningbruhn/imgreg, 2023 Search PubMed.
- P. Good, Permutation Tests: A Practical Guide to Resampling Methods for Testing Hypotheses, Springer Science & Business Media, 2013 Search PubMed.
- A. Papoulis and S. U. Pillai, Probability, random variables, and stochastic processes, Tata McGraw-Hill Education, 2002 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ja00347c |
| This journal is © The Royal Society of Chemistry 2023 |