Quantitative prediction of the solvent fractionation of lignin

Abstract

Lignin is the most abundant and sustainable source of aromatics on earth. However, its heterogeneous structure and hard-to-predict physicochemical properties complicate its valorization potential in many applications. We present a combined experimental and theoretical approach to quantify and predict the fractionation of lignin in binary solvent blends. This serves as an important way to reduce feedstock heterogeneity, obtaining lignin fractions with better defined molecular features. Our model predicts how the yield, in terms of amount of dissolved lignin, varies with the solvent composition. To explain the experimental results, it is essential that we invoke the physical and chemical polydispersity of lignin in our model. We obtain quantitative agreement with experimental results on various molecular features of the dissolved lignin fractions, including the yield, molecular mass, and the number of functional hydroxyl groups. This work shows that the amount and nature of dissolved lignin can be tuned predictably using a combination of solvents, which paves the way for a broader applicability of lignin as a bio-based material.

---

Lignin is a naturally occurring complex polymeric material in lignocellulosic biomass. Despite the large annual production of over 50 megatons of lignin and the wide range of its potential applications,^1,2 almost all lignin is burned for energy recovery at this moment; only about 2% is used to produce specialty chemicals.^1,2 One of the main challenges holding back advanced applications lies in lignin's disperse chemical composition and molecular mass. This chemical and physical variation depends on the source and refinement approach, and even varies when the same source and refining approach are used.^1–3 A result of this variability is that unprocessed lignin has inconsistent material properties. Solvent fractionation can be used to selectively dissolve a subset of lignin, decreasing the molecular mass polydispersity and targeting its molecular features to a specific application.^4–6

As the interactions between lignin and solvent depend sensitively on the solvent at hand, changing the solvent results in the dissolution of fractions with different properties.⁷ Using a solvent blend, these solvent–lignin interactions can be tuned gradually by altering the solvent composition. Establishing a clear correlation between the properties of the solubilized lignin and the physio-chemical features of a given solvent is essential to deal with the natural variability of lignin as a biopolymer and select a subset with desired properties.

Various studies have focused on combining theory and experiments to characterize the solvolytical fractionation of lignin.^8–15 Yet, these studies do not account explicitly for the fractionation of lignin with a broad distribution in both physical and chemical features (i.e., molecular mass and functional groups) in solution, although these molecular features significantly affect solvent fractionation and final properties.^1,16,17 Here we present a theoretical framework, corroborated with experiments, to predict the fractionation of lignin from wheat straw in a methanol/ethyl acetate mixture, while accounting for both its physical and chemical polydispersity. The described method can be applied to lignin from other sources and in other solvent blends after accounting for the differences in molecular features due to the variable nature of lignin; in the appendix we apply our approach to literature data.

Fig. 1 shows experimental results (data points) on the yield η (solubilized fraction) of lignin in mixtures of methanol and ethyl acetate, showing a clear – and at first sight, perhaps surprising – non-monotonic dependence of the yield on composition. The continuous variation of the composition of the solvent also clearly makes the fractionation tunable.

Fig. 1 Measured yield of the solubilized lignin (data points) and the inverse RED from the Hansen solubility parameters (green curve) as a function of the volume fraction of ethyl acetate ϕ_EtOAc in the ethyl acetate–methanol solvent mixture. The error bars indicate the standard deviations of duplicate experiments.

Hansen solubility parameters¹⁸ provide a first step in the clarification of the non-monotonic dependence of yield on solvent composition. The amount of lignin that dissolves depends on the interaction between the lignin segments and the solvent mixture. When these interactions are described in terms of Hansen solubility parameters, the similarity between the parameters for the dispersion, polarity, and hydrogen-bonding energies of a polymer and a solvent determine the miscibility. In case the distance R_a between the polymer and the solvent in Hansen solubility parameter space is smaller than a critical distance R₀, the theory predicts that the polymer dissolves in that solvent. A so-called relative energy difference (RED) is defined as:¹⁸

For infinitely long, monodisperse polymers, Hansen solubility theory predicts that the polymer dissolves if RED < 1, while they are immiscible with the solvent if RED ≥ 1. Polydisperse, finite length polymers can also have limited solubility. In such a case, for example, only shorter polymers dissolve.

In this work we characterize the yield of solubilized lignin as a function of the RED in order to quantify it in terms of lignin–solvent interactions and, as we will show, convert the observed non-monotonic dependency of the yield on solvent composition into a monotonic one. Afterwards, we will use the distributions in molecular mass and functional groups to predict and explain this yield–RED dependency. Like Novo et al.,¹¹ the parameters are chosen in such a way that the yield of solubilized lignin is 70% at RED = 1. We also used the Hansen solubility parameters reported by Novo et al.¹¹ for lignin, being δ_dl = 21.42, δ_pl = 8.57, and δ_hl = 21.80 for the dispersion, polarity, and hydrogen-bonding interactions, and R₀ = 13.56.

Other sources report different solubility parameters of the same order of magnitude.^12,13 The difference in the used source or extraction method of lignin likely causes the difference between these interaction parameters. Due to this variation, not all lignin samples can be described by the same parameters. In comparisons of the results shown here and those from other lignin samples, the dependency of the RED on the used Hansen solubility parameters and normalization should be taken into account. Moreover, certain lignin/solvent combinations may exhibit chemical reactions or contain components leading to interactions that are not included here. In these cases, extensions or adaptations of the discussed method might be necessary. In the appendix we show that the Hansen solubility parameters differ somewhat when describing literature data by Yang et al.¹⁹ on lignin from a different source in different solvent mixture.

For methanol and ethyl acetate, the parameters δ_dm = 15.1, δ_pm = 12.3, δ_hm = 22.3, and δ_de = 15.8, δ_pe = 5.3, δ_he = 7.2 were used, respectively, to calculate the volume-weighted Hansen solubility parameters δ_ds, δ_ps, δ_hs for the solvent.¹⁸ The difference in the interactions of the pure solvents with lignin makes it possible to tune the fractionation by altering the solvent composition. The methanol/ethyl acetate solvent mixture has several advantages. Due to the large difference in δ_p and δ_h of these solvents, a wider range of RED values can be tested than for many other solvent mixtures. Also, the non-monotonicity of the RED/concentration dependency makes the comparison between the yield/concentration and yield/RED dependencies more insightful. Additionally, this solvent mixture is relatively easy to remove via evaporation, compared to, for example, a mixture containing glycerol. Depending on the application, other solvent mixtures can be more beneficial.

The interaction distance R_a for the combination of lignin and the solvent mixture is subsequently defined as:

R_a² = 4(δ_dl − δ_ds)² + (δ_pl – δ_ps)² + (δ_hl – δ_hs)². (2)

The equilibrium yield depends on the entropy gain from the increase in possible configurations and the enthalpy penalty from the effective repulsion between lignin and the solvent mixture. This repulsive interaction energy scales directly with the RED and indirectly with the solvent composition (see eqn (1) and (2)). For higher RED values, the repulsion is higher, and the equilibrium concentration lower. Surprisingly, a plot of the inverse RED as a function of the solvent composition (Fig. 1, green curve) is highly similar in shape to the plot of the solubilization yield. This signifies a surprisingly simple linear relationship between solubility and RED (see the data points in Fig. 2, discussed later in more detail). This linear behavior must result from the (distribution in) properties of lignin, as for simple monodisperse polymers a strongly non-linear dependency is expected based on, for instance, Flory–Huggins (FH) solution theory (see Fig. 2, solid grey curve).

Fig. 2 Dissolved amount of lignin as a function of the RED, from experiments (data points) and theory (curves, eqn (4)). The thick grey curve denotes standard Flory–Huggins (FH) theory for monodisperse polymers; the green dashed-dotted curve represents the extension towards polymers with a polydisperse molecular mass M distribution; the cyan dashed curve takes into account both polydispersity in molecular mass and in lignin–solvent interactions through the FH interaction parameter χ. The shaded area in between the theoretical predictions gives the range of possible η-values following from assuming minimal and maximal dissolution.

Hansen solubility parameters enable the determination of the dependency of the experimentally measured yield of solubilized lignin as a function of the RED, which is a measure for the interactions between solvent and solute. Solvency theories such as FH theory also enable one to predict this yield dependency from thermodynamics.^20,21 However, for lignin, applying FH theory is challenging, as the sheer number of (effective) components due to chemical and/or physical polydispersity renders direct numerical computations virtually impossible.²²

We will now briefly discuss the approximations that we made in order to simplify the calculations, allowing to address lignin solubility using FH theory. Firstly, for broad polydisperse distributions, the concentration of polymers of each individual length is small compared to the total concentration of polymers; as a result we assume that interactions between polymers of different lengths can be neglected up to some degree. Secondly, because of mass conservation, there is only a limited range of possible lignin concentrations if only small amounts of lignin are dissolved in an excess of solvent: the concentration of lignin in the solvent-rich phase S ranges from ϕ^S_l,min = 0 to ϕ^S_l,max = V₁/(V₁ + V_s), with V_l and V_s the total volume of lignin and solvent. Using these characteristics of the solvent fractionation of lignin, FH equations can be approximated in such a way that the ratio of the concentrations as a function of the RED can be calculated using a closed expression; for more information on these approximations we refer to our previous work.²³

The result of our approximate solutions to FH theory is a range of possible values for the concentration ratio φ^L_k/φ^S_k for each lignin “type” k between the lignin-rich phase and the solvent-rich phase, as a function of the RED: a minimum using the lower limit values and a maximum using the higher limits of the effective interactions, polymer lengths, and concentrations.

The theoretical description of the solvent fractionation of lignin with FH theory requires an assumption about the shape of the distribution of polymer sizes and chemical nature as input. Molecular mass distributions were therefore measured using GPC; the resulting experimental distributions are shown for different solubilized lignin fractions in Fig. 3 (black curves).

Fig. 3 Examples of log–normal fits of eqn (3) to the molecular mass distribution of solubilized lignin fractions obtained at various solvent compositions as measured using GPC. I/I_max is the normalized refractive index detector signal, which is proportional to the concentration (mass per unit volume).

Based on the molecular mass distributions from the experiments, we assume a log–normal distribution for the molecular mass of the lignin molecules. The relative number Θ_k of lignin molecules of type k = 1, 2,… is therefore approximated by

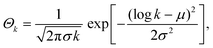where the molecular mass follows from M_k = ak. The constant a = 210 Da, which is an estimate of the effective mass of the FH monomers, converts the chain length to molecular mass, making k, σ, and μ dimensionless for simplicity. In this equation e^σ = 1.2 and e^μ = 2.7 × 10³ are the fitting constants for the molecular mass distribution.

We model to the variation in chemical nature by proposing an exponentially decreasing fraction of functional groups with increasing chain length. A correlation between the number of functional groups and the molecular size of lignin was already reported by Evastyanova et al.²⁴ The aliphatic, aromatic, and carboxylic hydroxyl content was measured using NMR. To reduce the number of parameters, only an effective interaction parameter χ that depends on the total hydroxyl content is used in the theory. Effectively, this means that only the ‘average’ interaction of a polymer chain is taken into account, neglecting some of the complexity of the system. The distribution in the fraction of functional groups is described by θ_k = b₁exp(−k/b₂) + b₃. The fitting constants b₁ = 0.0245, b₂ = 5 × 10³, and b₃ = 0.18 are determined using the distribution of the number of functional groups, which in this case is correlated with the molecular size. These fitting constants indirectly also depend on a, σ, and μ.

The mass distributions and functional group distributions for lignin from other sources can differ, affecting the resulting theoretical and experimental dependencies. Literature data or GPC and NMR measurements of the unfractionated sample can be used to determine these input parameters, after which the same procedure can theoretically predict the properties of the different fractions. In summary, in our model, Θ_k describes the relative number of lignin molecules of a certain type k, while θ_k describes the relative number of functional groups per monomer for lignin molecules of type k.

Fig. 3 compares the experimental molecular mass distribution to fits with eqn (3). Overall, the description is very good. In principle, it is possible to fit the experimental data in even more detail using multiple distribution functions, however, this would result in many fitting parameters. To simplify the interpretation of the results, we neglected the peak for monomers (around 210 Da) and smaller components and used only the data for molecular masses larger than 250 Da to fit the distribution used as input for the theoretical computations. Note that, for these fits, we take into account that eqn (3) describes the number distribution, while the measured GPC signal is sensitive to mass concentration instead.

The total solubilization yield now follows from the individual solubilized fractions of each lignin type k from FH theory:

The data from the measurements of the yield as a function of the volume fraction of ethyl acetate ϕ_EtOAc and the RED resulting from the Hansen solubility parameters (Fig. 3) are combined to find the experimental yield–RED dependency. Fig. 2 compares these experimental and theoretical dependencies. With a monodisperse FH calculation using the average length and number of functional groups, the dependency is as in the solid grey curve in Fig. 2; clearly this is an unsatisfactory description of the experiments as the dependence of yield on RED is much too steep. When only polydispersity in molecular mass is accounted for, this results in the green dashed-dotted curves. Although the predicted dependency is somewhat less steep, it is still far off from the experiments. With both polydispersity in the molecular mass and in the number of functional groups (here we use the total number of hydroxyl groups) included, the theory gives the cyan dashed curves as a result. This shows that it is essential to properly account for the polydispersity, both in terms of molecular mass and chemical composition, in order to understand and predict the experimentally measured dependency.

In the appendix we apply our framework to a second example, based on data published by Yang et al.,¹⁹ for lignin from a different source and in a different solvent mixture. They found a similar non-monotonic dependency of yield on solvent composition as us, which we show also becomes monotonic when plotted as a function of RED. Their data can be described satisfactorily with our framework, highlighting the broader applicability of our theoretical procedure.

With this model at hand, also other properties of the solubilized lignin can be predicted and compared to experimental results. The individual amounts of the different “types” of lignin can be used to calculate these properties, without introducing any new fitting parameters. For example, the weight-averaged molecular mass is given by and, therefore, can be predicted at each solvent composition.

〈M〉 = ∫Θ_kη_kM_kdk (5)

and number of hydroxyl groups of the dissolved lignin is given by

〈θ〉 = ∫Θ_kη_kθ_kdk. (6)

Using GPC and NMR, these molecular features of the dissolved lignin were separated and measured. Integration of the distributions resulting from the GPC curves gives the experimental weight-averaged molecular masses. Table 1 shows the measured aliphatic, aromatic, and carboxylic hydroxyl contents. The standard deviations given are based on the different dissolved lignin samples at each RED. The sum of these in volume fractions gives the average experimental fraction of functional groups. Fig. 4 shows a comparison between the calculated and the experimental dependencies. Overall, the agreement is excellent, even more so considering that lignin is a rather complicated biopolymer. These results show that not only the solubilization yield can be described accurately, but also the chemical features of these solubilized fractions can be predicted accurately by our model.

Fig. 4 Weight-averaged molecular mass (top) and the fraction of functional groups (bottom) of the solubilized lignin fractions as a function of RED. These properties were measured experimentally (points) and predicted theoretically using eqn (5) and (6) (curves).

Table 1 Aromatic, aliphatic, and carboxylic hydroxyl content, as measured using NMR. The concentrations are combined to calculate the average volume fraction of functional groups, as shown in Fig. 4

RED	Aromatic (mmol g^−1)	Aliphatic (mmol g^−1)	Carboxylic (mmol g^−1)
1.38	3.79 ± 0.07	0.57 ± 0.02	0.93 ± 0.06
1.29	3.66 ± 0.05	0.90 ± 0.02	0.62 ± 0.02
1.22	3.58 ± 0.08	1.02 ± 0.02	0.54 ± 0.01
1.14	3.48 ± 0.02	1.07 ± 0.02	0.48 ± 0.01
1.08	3.43 ± 0.06	1.09 ± 0.01	0.46 ± 0.01
1.02	3.30 ± 0.03	1.07 ± 0.00	0.46 ± 0.02
0.97	3.18 ± 0.07	1.12 ± 0.01	0.47 ± 0.00
0.95	3.45 ± 0.13	1.11 ± 0.02	0.33 ± 0.01

---

Concluding remarks

Lignin's molecular features are polydisperse and often considered to be unpredictable. Using solvent fractionation to obtain lignin with better-defined features makes it easier to use lignin in materials with reproducible properties. Our experiments show that a solvent blend comprising methanol and ethyl acetate can be used to selectively tune the properties of the solubilized lignin as a function of the solvent composition. We present a theoretical model, based on FH theory, that efficiently incorporates both the chemical and physical polydispersity that occur naturally in lignin. A comparison of the experiments and theory shows a quantitative agreement for the solubilized lignin yield, average molecular mass, and hydroxyl content. We show that, only when both chemical and physical polydispersity is included in our model, the molecular features of the solubilized lignin can be predicted accurately, aiding rational design of lignin-based materials with well-defined properties.

Experimental section

Experiments were performed using Protobind 1000 lignin extracted from wheat straw using soda pulping. The composition of the lignin was determined to be 94 wt% of Klason lignin, 4 wt% structural carbons and 2 wt% ash. For each experiment, a separate solvent mixture of 40 mL is prepared with varying volume fractions of methanol and ethyl acetate (Sigma Aldrich, HPLC grade). A new sample of 4 g of lignin is subsequently added to each solvent mixture. Fractionation was performed using a 100 mL Parr stirred batch reactor for 30 minutes at 473 K in an oxygen-free environment at 30 bar while stirring at 500 rpm. After fractionation, solid and liquid were separated using 4 DURAN® filter crucible with maximal pore sizes between 10 and 16 μm. After rotary evaporation at 333 K, lignin oligomers were dried at 353 K in a vacuum oven until a stable weight was obtained. The measured yield is corrected with a factor 0.94 to account for the purity of the sample.

Molecular mass distributions were measured using GPC system equipped with a Waters 2414 refractive index detector and three linear columns (Styragel HR1, Styragel HR4, Styragel HR5) at 303 K. The flowrate was 1 mL min⁻¹ and the eluent was tetrahydrofuran. Acetylation of the lignin oligomers was performed via the protocol described by Gosselink et al.²⁵ In the measurements 7 mg of lignin was dissolved in 1.5 ml of THF. The solution was filtered over 0.2 μm pore size PTFE syringe filters before use. Molecular masses were given relative to polystyrene standards with a calibration range of 500 Da to 2.52 MDa.

The aromatic and aliphatic hydroxyl groups as well as the carboxylic acids in lignin fractions were determined by ³¹P NMR spectroscopy after sample derivatization, according to the method described by Korntner et al.²⁶ 10 mg of lignin sample (dried in a vacuum oven at 80 °C, overnight) was dissolved in a 500 μL mixture of anhydrous pyridine and deuterated chloroform (1.6 : 1, v : v). Then, 100 μL of internal standard solution of 20.0 mg mL⁻¹ cholesterol (in an anhydrous pyridine and deuterated chloroform mixture, 1.6 : 1, v : v; 0.0051 mmol cholesterol), 50 μL of relaxation agent (chromium(III) acetylacetonate, 10 mg mL⁻¹ in anhydrous pyridine and deuterated chloroform, 1.6 : 1, v : v), and 50 μL of derivatizing agent (2-chloro-4,4,5,5-tetramethyl-1,3,2-dioxaphospholane) were added to the solution. The solution was stirred for 10 min, transferred into a dry 5 mm NMR tube and measured. The measurement was performed on a Bruker Avance III HD Nanobay 300 MHz apparatus (121.49 MHz for ³¹P NMR experiments) using the standard phosphorus pulse program, at ambient temperature, with 256 scans, relaxation delay 5 s, acquisition time 2 s, transmitter excitation frequency 140 ppm, and spectral width 396 ppm.

Author contributions

Stijn H. M. van Leuken: conceptualization, methodology, software, validation, formal analysis, investigation, writing – original draft, writing – review & editing, visualization. Dannie J. G. P. van Osch: conceptualization, methodology, validation, formal analysis, investigation, resources, writing – original draft. Panos D. Kouris: writing – review & editing Yawen Yao: data curation, formal analysis Monika A. Jedrzejczyk: data curation, formal analysis, investigation, writing – review & editing Geert J. W. Cremers: formal analysis, investigation, methodology Katrien V. Bernaerts: data curation, funding acquisition, writing – Review & editing Rolf A. T. M. van Benthem: validation, resources, writing – review & editing, supervision Remco Tuinier: validation, resources, writing – review & editing, supervision, project administration, funding acquisition. Michael D. Boot: resources, project administration, funding acquisition. Emiel J. M. Hensen: resources, writing – review & editing, project administration, funding acquisition. Mark Vis: conceptualization, methodology, validation, investigation, resources, writing – original draft, writing – review & editing, supervision.

Conflicts of interest

There are no conflicts to declare.

Appendix

The combined theoretical framework presented shows how the selective solubility and properties of solubilized lignin can be predicted using molecular features. The experiments and theory for the solubilized lignin yield, average molecular mass, and hydroxyl content extracted from wheat straw in ethyl acetate/methanol mixtures quantitatively agree. To illustrate the broader applicability of our technique, here we apply our method to published experimental results on industrial lignin in a methanol/dichloromethane mixture, as measured by Yang et al.¹⁹

The required input for the theory consists of the Hansen solubility parameters (parameters in eqn (2)), and the mass distribution and functional group distribution of the unfractionated lignin sample (parameters of eqn (3)). The Hansen solubility parameters for methanol and dichloromethane are δ_dm = 15.1, δ_pm = 12.3, δ_hm = 22.3, and δ_dd = 17.0, δ_pd = 7.3, δ_hd = 7.1.¹⁸ (The parameters for methanol are the same as in the ethyl acetate/methanol mixture.) The Hansen solubility parameters of lignin depend on their origin and extraction method. For the industrial lignin used by Yang et al.,¹⁹ we determined the Hansen solubility parameters to being δ_dl = 19.0, δ_pl = 14.4, and δ_hl = 13.7. Only the measurements where a yield of 100% is not reached (lignin concentrations of 300 g L⁻¹, 350 g L⁻¹, and 400 g L⁻¹) were used to set these parameters. These parameters are within the range of earlier published solubility parameters for lignin.^11–13

The reported weight-averaged molar mass of 5860 g mol⁻¹ and number-averaged molar mass of 4562 g mol⁻¹ from GPC measurements¹⁹ correspond to a log–normal distribution with e^σ = 1.6 and e^μ = 5.2 × 10³. For simplicity, we kept the hydroxyl content parameters equal to those used for the lignin extracted from wheat straw in the main text. Due to the larger average molar mass, this results in an average hydroxyl content decrease of 26% for the industrial lignin compared to lignin extracted from wheat straw. The NMR data and the lower polarity and hydrogen bonding solubility parameters confirm the lower hydroxyl content. However, it should be noted that the distribution of hydroxyl groups may differ for different types of lignin. Exact parameters can, nevertheless, not be set because the total hydroxyl content is not measured for the considered system.

Fig. 5 shows the experimentally measured yield and 1/RED as a function of the volume fraction of dichloromethane; the experimental data are taken from Fig. 1 in the paper of Yang et al.¹⁹ They also varied the concentration of lignin relative to the amount of solvent, resulting in different yields, as indicated with different colored symbols. Similar to our results for lignin from wheat straw, we see a non-monotonic trend for both the yield and 1/RED with a maximum for this industrial lignin. Combining the experimental measurements and the RED/concentration dependency gives the monotonic, experimental yield/RED dependencies in Fig. 6. The theoretical yield/RED dependency can be computed using the molecular mass and functional group distributions (eqn (3)) in eqn (4) as described in the main text. The variation in the added volume of lignin relative to the volume of solvent can be set by changing the V_p/V_s-ratio.

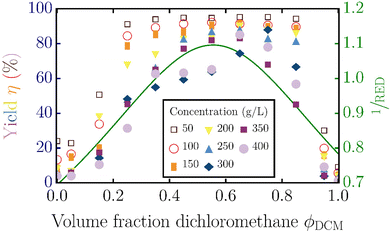Fig. 5 Measured yield of the solubilized lignin (data points) and the inverse RED from the Hansen solubility parameters (green curve) as a function of the volume fraction of dichloromethane ϕ_DCM in the dichloromethane–methanol solvent mixture. Experimental results in symbols reproduced from Yang et al.¹⁹ Symbols and colors correspond to the different concentrations of lignin added to the solvent mixture.

Fig. 6 Dissolved amount of lignin as a function of the RED, from experiments (data points) and theory (curves, eqn (4)). The different colors, symbols and dashing correspond to different concentrations of lignin (see legend) added to the solvent mixture. The area in between the theoretical predictions gives the range of possible η-values following from assuming minimal and maximal dissolution.

As shown in Fig. 6, like before, the physical and chemical polydispersity of lignin results in a less steep dependency of yield on RED. The yields for different lignin concentrations show an additional effect of the polydispersity, as explained next. For monodisperse samples, the yield/RED dependency at a low concentration is close to a rescaled version of the dependency at a higher concentration. For polydisperse samples, the effect of concentration is much weaker, because different polymer variations dissolve at different REDs, independent of the amount of lignin added. Together with the increasing range of possible concentrations, as predicted from our theoretical framework, with increasing added lignin concentration, this results in considerable overlap in the dependencies at various lignin concentrations.

The agreement of theory and already published experimental results in this section provide extra support for the general applicability of the approach described in the main text. Together with the results in the main text, these results show that molecular features of solubilized lignin can be predicted with reasonable accuracy by accounting for physical and chemical polydispersity.

Acknowledgements

This work was performed under the framework of Chemelot InSciTe and is supported by financial contributions from the European Interreg V Flanders, the European Regional Development Fund (ERDF) within the framework of OP-Zuid, the province of Brabant and Limburg and the Dutch Ministry of Economy. Furthermore, the authors thank the members of the Chemelot InSciTe, HiperBioPol and LOADED teams, Vertoro, and the members of the Laboratory of Physical Chemistry and Laboratory of Inorganic Materials & Catalysis at Eindhoven University of Technology for the fruitful collaboration, discussions, inspiration, and feedback.

References

1. M. Norgren and H. Edlund, Curr. Opin. Colloid Interface Sci., 2014, 19, 409.
2. D. Bajwa, G. Pourhashem, A. H. Ullah and S. Bajwa, Ind. Crops Prod., 2019, 139, 111526.
3. O. Yu and K. H. Kim, Appl. Sci., 2020, 10, 4626.
4. P. D. Kouris, D. J. G. P. van Osch, G. J. W. Cremers, M. D. Boot and E. J. M. Hensen, Sustainable Energy Fuels, 2020, 4, 6212–6226.
5. M. J. Cantow, Polymer fractionation, Elsevier, 2013.
6. F. Francuskiewicz, Polymer fractionation, Springer Science & Business Media, 2013.
7. T. Pang, G. Wang, H. Sun, W. Sui and C. Si, Ind. Crops Prod., 2021, 165, 113442.
8. C. Schuerch, J. Am. Chem. Soc., 1952, 74, 5061.
9. Q. Wang, K. Chen, J. Li, G. Yang, S. Liu and J. Xu, BioResources, 2011, 6, 3034.
10. A. Duval, F. Vilaplana, C. Crestini and M. Lawoko, Holzforschung, 2016, 70, 11.
11. L. P. Novo and A. A. Curvelo, Ind. Eng. Chem. Res., 2019, 58, 14520.
12. C. M. Hansen and A. Björkman, Holzforschung, 1998, 52, 445.
13. G. C. Vebber, P. Pranke and C. N. Pereira, J. Appl. Polym. Sci., 2014, 131.
14. V. Ponnuchamy, O. Gordobil, R. H. Diaz, A. Sandak and J. Sandak, Int. J. Biol. Macromol., 2021, 168, 792.
15. Q. Xia, Y. Liu, J. Meng, W. Cheng, W. Chen, S. Liu, Y. Liu, J. Li and H. Yu, Green Chem., 2018, 20, 2711.
16. W. Krigbaum and D. Geymer, J. Am. Chem. Soc., 1959, 81, 1859.
17. S. Enders, Polym. Thermodyn., 2010, 271–328.
18. C. M. Hansen, Hansen solubility parameters: a user's handbook, CRC press, 2007.
19. Y. Yang, J. Xu, Y. Kong, J. Zhou and X. Wang, Int. J. Biol. Macromol., 2023, 225, 219–226.
20. P. J. Flory, J. Phys. Chem., 1941, 10, 51.
21. M. L. Huggins, J. Phys. Chem., 1941, 9, 440.
22. R. A. Heidemann and M. L. Michelsen, Ind. Eng. Chem. Res., 1995, 34, 958.
23. S. H. M. van Leuken, R. A. T. M. van Benthem, R. Tuinier and M. Vis, Macromol. Theory Simul., 2023, 32, 2300001.
24. O. Sevastyanova, M. Helander, S. Chowdhury, H. Lange, H. Wedin, L. Zhang, M. Ek, J. F. Kadla, C. Crestini and M. E. Lindström, J. Appl. Polym. Sci., 2014, 131.
25. R. J. A. Gosselink, A. Abächerli, H. Semke, R. Malherbe, P. Käuper, A. Nadif and J. E. G. van Dam, Ind. Crops Prod., 2004, 19, 271–281.
26. P. Korntner, I. Sumerskii, M. Bacher, T. Rosenau and A. Potthast, Holzforschung, 2015, 69(6), 807–814.

---