Open Access Article
Open Access ArticleWhy copper catalyzes electrochemical reduction of nitrate to ammonia†
Mohammadreza
Karamad
*a,
Tiago J.
Goncalves
 c,
Santiago
Jimenez-Villegas
c,
Santiago
Jimenez-Villegas
 c,
Ian D.
Gates
*b and
Samira
Siahrostami
c,
Ian D.
Gates
*b and
Samira
Siahrostami
 *c
*c
aDepartment of Physics & Astronomy, University of Calgary, 2500 University Drive NW, Calgary, Alberta T2N 1N4, Canada. E-mail: Mohammadreza.karamad@ucalgary.ca
bDepartment of Chemical and Petroleum Engineering, University of Calgary, 2500 University Drive NW, Calgary, Alberta T2N 1N4, Canada. E-mail: idgates@ucalgary.ca
cDepartment of Chemistry, University of Calgary, 2500 University Drive NW, Calgary, Alberta T2N 1N4, Canada. E-mail: samira.siahrostami@ucalgary.ca
First published on 2nd December 2022
Abstract
Electrochemical reduction of nitrate (NO3RR) has drawn significant attention in the scientific community as an attractive route for ammonia synthesis as well as alleviating environmental concerns for nitrate pollution. To improve the efficiency of this process, the development of catalyst materials that exhibit high activity and selectivity is of paramount importance. Copper and copper-based catalysts have been widely investigated as potential catalyst materials for this reaction both computationally and experimentally. However, less attention has been paid to understanding the reasons behind such high activity and selectivity. Herein, we use Density Functional Theory (DFT) to identify reactivity descriptors guiding the identification of active catalysts for the NO3RR, establish trends in activity, and explain why copper is the most active and selective transition metal for the NO3RR to ammonia among ten different transition metals, namely Au, Ag, Cu, Pt, Pd, Ni, Ir, Rh, Ru, and Co. Furthermore, we assess NO3RR selectivity by taking into account the competition between the NO3RR and the hydrogen evolution reaction. Finally, we propose various approaches for developing highly active catalyst materials for the NO3RR.
Introduction
Ammonia is an important chemical in human life with a wide range of agricultural and pharmaceutical applications.1,2 It is mainly used as a fertilizer for large scale commercial food production. The mass production of ammonia has mainly relied on the Haber–Bosch process; that is, the reaction between atmospheric nitrogen and H2 at high temperature and pressure.3,4 Currently, heterogeneous iron-based catalysts are used in the Haber–Bosch process.5,6 This process is energy intensive with undesirable environmental impact: it currently accounts for 2–5% of the world’s energy demand and causes about 1% of total global energy-related CO2 emission.7 This urges the development of sustainable alternatives for ammonia synthesis that can alleviate these concerns.4,7–10Electrochemical reduction of nitrate (NO3RR) and nitric oxide (NORR) have emerged as attractive routes for ammonia synthesis.11–13 Due to its abundance in water resources and soil, nitrate (NO3) represents a promising source of nitrogen for ammonia synthesis.14 When coupled with renewable energy sources, the NO3RR can be used to produce a variety of products such as NH3, NO, N2O, and N2 at ambient conditions. The nitric oxides (NO and N2O) produced during the NO3RR can also be further reduced to ammonia. In addition, both the NO3RR and NORR, when coupled, can address one of the grand challenges of the 21st century, that is the high nitrate level in groundwater and soil with its deteriorating effect on the environment and human health. Despite its promise, one of the key challenges for developing large-scale implementation of NO3RR technology are efficient electrocatalysts that exhibit high activity and selectivity towards the desired product, i.e., ammonia.
In the search for efficient NO3RR electrocatalysts, transition metals such as Cu, Ag, Au, Ru, Rh, Ir, Pd, and Pt, as well as bimetallic alloys, have been frequently considered as potential candidates.2,15–31 Among transition metals, copper and copper-based catalysts have shown great promise for the selective and active NO3RR to ammonia. This has sparked immense interest in modulating the Cu active site through various strategies, such as metal doping, exposed facet manipulation, and nanostructuring of the catalyst.32–34 For example, Qin et al. investigated the reactivity of different exposed facets of Cu2O electrocatalysts.35 They found higher ammonia yields for the (100) facet when compared to the (111). Wang et al. reported nanowire arrays (NWAs) of CuO as an electrocatalyst for the reduction of nitrate.33 Interestingly, they unveiled a reconstruction of the NWAs during catalysis. This reconstruction was found to suppress the competing HER, producing a highly selective Cu/Cu2O NWA catalyst with a faradaic efficiency of 95.8% towards ammonia. More recently, Chen et al. demonstrated an extraordinarily active and selective catalyst for nitrate to ammonia.36 They reported reduction currents of 1 A cm−2 at low overpotentials (−0.13 V vs. RHE) with over 99% of nitrate being converted into ammonia using a Ru dispersed on Cu nanowire (Ru-CuNW) catalyst.
Fig. 1a summarizes the reported FEs for the NO3RR to ammonia on a number of Cu-based catalysts reported in the literature. As can be seen, almost all reported FEs are above 80% for Cu-based catalysts. The high FE can be attributed to lower activity towards the competing hydrogen evolution reaction (HER) at negative potentials.18,37,38Fig. 1b displays the measured current density, applied potential and FE at the same time. Other than high FE, the most successful copper-based catalysts would have a high current density at low applied potentials. This analysis shows that Ru-CuNW is the most active catalyst reported.
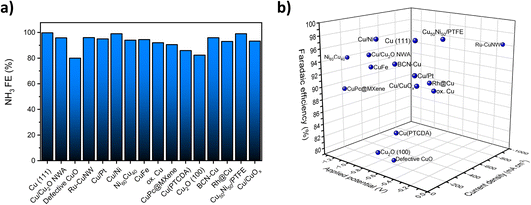 | ||
| Fig. 1 (a) Previously reported FEs for the NO3RR over selected Cu and Cu-based electrocatalysts. (b) Reported FEs and measured current densities at applied potentials for selected Cu and Cu-based electrocatalysts. Data extracted from ref. 20, 21, 32–36 and 39–47. | ||
To unravel the reasons behind such high activity and selectivity for the NO3RR to ammonia on Cu-based catalysts, we need to establish an understanding about the mechanism of the NO3RR to ammonia on transition metals. Several efforts have already been made in the literature to understand the NO3RR mechanism.18,33,48–53 Depending on the catalyst material, different reaction mechanisms have been proposed for the NO3RR to ammonia.14,19,54,55 Liu et al. studied the trends in NO3RR catalytic activity and selectivity by using DFT-based microkinetic modelling on transition metals through a direct electrocatalytic nitrate reduction mechanism at moderate nitrate concentrations and showed that the NO3RR proceeds through deoxygenation and hydrogenation steps at the catalyst surface.19 They proposed binding energies of oxygen and nitrogen atoms as descriptors for the catalytic activity and selectivity of nitrate reduction on transition metals and transition metal alloys. A similar mechanism has been used to study the NO3RR on Cu–Ni alloys and Ru surfaces.20 It has been widely accepted that nitrite (NO2) and NO are the key intermediates in the NO3RR.2 Therefore, a large body of research in the literature has focused on the NORR and NO2RR.2,15,49,56–59 In particular, the catalytic activity and selectivity of Pt for both the NORR and NO2RR to ammonia through sequential electrochemical steps where possible intermediates form only in proton and electron transfer reactions have been probed.49,60–62 The NO3RR, through sequential electrochemical steps, has also been suggested as the reaction mechanism and used to study the catalytic activity of transition metals and transition metal oxides.63 In this study, using Density Functional Theory (DFT) we investigate the trends in the catalytic activity of the NO3RR to ammonia through sequential electrochemical steps on different transition metal surfaces. We elucidate reaction paths for the NO3RR on different transition metals by performing a mechanistic study and developing activity descriptors for the NO3RR to ammonia using scaling relations between binding energies of NO3RR intermediates. This descriptor-based analysis leads to an understanding of the high activity and selectivity for copper among other transition metals and provides a guide to developing novel catalyst materials with enhanced activity for the NO3RR to ammonia.
Results and discussion
The overall electrochemical conversion of NO3− to NH3 involves the transfer of nine protons and eight electrons at a potential of 0.88 V versus the reversible hydrogen electrode (RHE):48| NO3− + 9H+ + 8e− → NH3 + 3H2O, E0 = 0.88 V | (R1) |
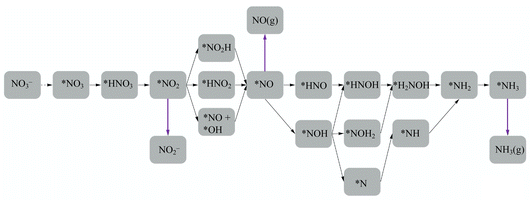
En route to the formation of NH3, the reduction of NO3− can follow multiple reaction pathways as outlined in Fig. 2, producing byproducts such as NO, N2O and N2.63 In one of the pathways that has been reported frequently in the literature, the NO3RR occurs in a sequence of deoxygenation and hydrogenation steps (pathway 1 in Fig. 3).20,50,64 In this pathway, the NO3RR proceeds through the *NO3 → *NO2 → *NO → *N deoxygenation steps followed by the *NH → *NH2 → *NH3 → NH3(g) hydrogenation steps. In the second pathway (pathway 2 in Fig. 3), the NO3RR proceeds through NO3− → *NO3 → *NO2 → *NO → *NOH → *NHOH → *NH2OH → *NH2 → *NH3 → NH3(g). These two pathways share similar deoxygenation steps until the formation of NO*. In pathway 1, NO* reduction proceeds through formation of N* through dehydrogenation of NO*, followed by formation of NH3(g) from N* via four subsequent hydrogenation steps. On the other hand, N* does not appear as an intermediate in pathway 2 and further reduction of NO* occurs through hydrogenation of NO* to form NOH* followed by five subsequent hydrogenation steps to the formation of NH3(g). Recently, by performing a systematic thermodynamic and kinetic analysis on the Cu(111) and Cu(100) surfaces, Hu et al. reported a high activation barrier for N* formation through the NO* dehydrogenation step, making pathway 2 more favorable in the NO3RR.50 They proposed a new pathway for the NO3RR that is a combination of pathways 1 and 2 (pathway 3 in Fig. 3). Their study, however, is limited to the Cu surface which is known as the most promising catalyst among transition metals for the NO3RR due to its high catalytic activity. It is desirable to understand the trends in NO3RR catalytic activity among other transition metals.54 Similar approaches have been used in the past for other electrochemical reactions where different descriptors have been developed to understand the trends in catalytic activities for these reactions by developing activity descriptors.65–68 These descriptors have been used to identify promising catalysts. In the present study, we aim to develop such descriptors to understand the trends for NO3RR catalytic activity among different transition metals.
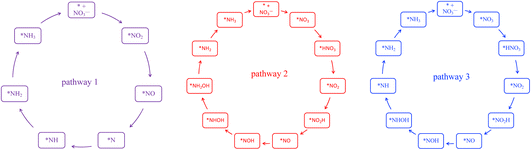 | ||
| Fig. 3 Three different reaction pathways for the NO3RR to ammonia on the Cu(111) surface reported by Hu et al.50 | ||
To model the NO3RR on transition metals Au, Ag, Cu, Pt, Pd, Ni, Ir, Rh, Ru and Co, we considered the pathways outlined in Fig. 2. The pathways considered herein include all those considered by Hu et al. for the NO3RR on Cu surfaces. As noted above, we limit our investigation to possible intermediates occurring only via electron–proton transfer reactions.63 These various electrochemical pathways are used to construct free energy diagrams for all eight metal surfaces (Fig. S1 in the ESI†). The free energy diagrams are obtained exclusively from calculations of the thermodynamic adsorption energies of the intermediates, excluding kinetic barriers. This method has been demonstrated to sufficiently capture activity and selectivity trends and has been employed in the modelling of various electrochemical processes such as the water oxidation reaction and the oxygen reduction reaction.68–71 Moreover, as will be discussed later, although we found that our NO3RR pathway for ammonia is slightly different from the one derived by Hu et al. using both thermodynamics and kinetics, both pathways resulted in similar catalytic activity prediction for the NO3RR to ammonia on Cu(111).
The initial step in the reaction mechanism, the adsorption of nitrate, is a solution mediated proton transfer and does not require an electron transfer. This step has been previously reported to be the rate limiting step in the NO3RR.20Fig. 4a presents the binding energies of *NO3 on the different transition metals. The horizontal dashed line shows the chemical potential of NO3−.72 It is found that all transition metals, with the exception of Au, bind *NO3. Therefore, it is expected that Au exhibits very low catalytic activity for the electrochemical reduction of NO3−, in agreement with a previous theoretical report by Wan et al., as well as experimental studies by Dima et al. that reported that NO3− electrochemical reduction on Au is hardly detectable.17,48
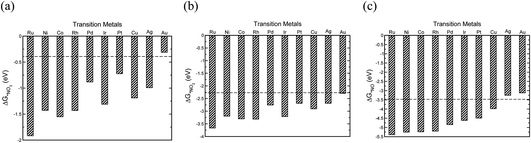 | ||
| Fig. 4 The binding energies of (a) *NO3, (b) *NO2, (c) *NO adsorbates on different transition metals (all calculated with reference to HNO3(g), H2(g) and H2O(g) species).72 | ||
Reduction of adsorbed nitrate creates adsorbed nitric acid (*HNO3), the first coupled electron–proton transfer. Following this, is the formation of adsorbed nitrite (*NO2) which has also been reported to be the rate-limiting step.17 If NO2− adsorption is sufficiently weak, relative to nitrite acid in the solution, desorption of *NO2 into solution will occur. The adsorption energy of *NO2 depends on the metal surface (Fig. 4b). Except Au, all metals bind NO2− and there is a high desorption barrier for NO2− formation. Therefore, except Au, further reduction of *NO2 on all metals is expected. The reduction of *NO2 results in the formation of *HNO2 or *NO2H. Our results show that *NO2H is unstable and dissociation of *NO2H to *NO and *OH occurs on the transition metal catalysts leading to the evolution of NO*, a key intermediate in the NO3RR.48–50,52 We also find that reduction of *NO2 to *NO is downhill in free energy over all the studied transition metals. After the formation of *NO, different pathways are possible for NH3 production, of which *HNO and *NOH paths are explored. Our calculations suggest that the NO3RR comes to a halt at the intersection of reaction pathways over Ag and Au (Fig. 4c). For transition metals other than Au and Ag, the formation of *NOH is more favourable over the *HNO intermediate. However, this mechanistic preference is less pronounced over Cu, Ir, Pd, and Pt, where the free energies of *HNO and *NOH are virtually the same (i.e., isoenergetic). Consequently, the reduction pathway over these metals is indistinguishable. Moreover, our results show that the formation of *NOH from *NO is the potential limiting step for nitrate reduction on Pt, Rh, Ni, Cu, and Pd. On the other hand, on Co, Ru, and Ir, reduction of *NO3 to *HNO3 is the potential limiting step.
Fig. 5 displays the free energy diagram for the lowest free energy path on the Cu(111) surface. Moreover, the free energy diagram containing the NO3RR intermediates reported by Hu et al. based on both thermodynamic and kinetic analysis is provided (in blue) for comparison. Fig. 5 shows that the NO3RR on Cu(111) follows a similar pathway to the one reported by Hu et al., that is NO3− → *NO3 → *NO2 → *NO → *NOH → *NHOH → *NH2OH → *NH2 → *NH3 → NH3(g). We, however, found that two intermediates involved in the NO3RR pathway to ammonia are different from the ones reported by Hu et al., as shown in the inset of Fig. 5. In particular, we found that the reduction of *NO2 results in the formation of *NO + *OH due to dissociation of *NO2H. In addition, while Hu et al. reported that the reduction of *NOH results in the formation of *NHOH, we found that the reduction of *NOH results in the formation of *N. Although Hu et al. have not reported the energetics as well as the kinetic barriers for the formation of *NO + *OH from *NO2H, the small differences that exist between the pathways presented in this work and reported by Hu et al. are presumably because of the slightly different settings used in our DFT calculations. We would like to emphasize that despite these slight differences, in both pathways the potential limiting step is the reduction of NO* to NOH*. The free energy diagrams for the most favorable pathways for the other transition metals considered in this study are provided in the ESI (see Fig. S2†).
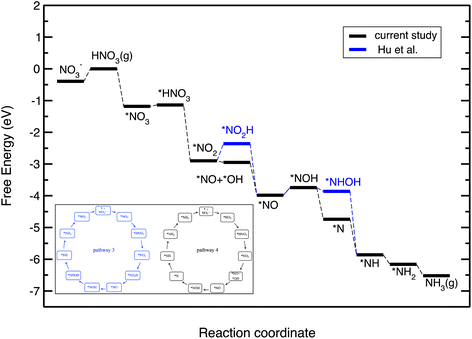 | ||
| Fig. 5 Free energy diagrams for the NO3RR on Cu(111). The black line denotes the constructed free energy diagram in the present study. The blue line shows the free energy diagram suggested by Hu et al.50 The inset shows the reaction pathway for the NO3RR to ammonia on Cu(111) reported by Hu et al. (pathway 3 in Fig. 3) as well as the one obtained in the present study (pathway 4). | ||
With the potential limiting step identified for all metals, the theoretical limiting potential for the electrochemical reaction to occur (i.e., the lowest potential, at which all the reaction steps are downhill in free energy) is obtained. The calculated limiting potentials range from −0.19 V to −0.72 V versus RHE, in order of Ir > Cu > Pt > Co > Ni > Rh > Ru > Pd, where Ag and Au are excluded since they are not expected to fully reduce nitrate to NH3 (Table 1). It is interesting to compare NO3RR catalytic activity over transition metals with previous experimental reports. Dima et al. describe a comparative study to determine the catalytic activity and selectivity of eight different polycrystalline electrodes, namely Pt, Pd, Rh, Ru, Ir, Cu, Ag, and Au for the NO3RR in acidic solution.17 They showed that the NO3RR catalytic activity decreases in the order Rh > Ru > Ir > Pd and Pt for the transition metals and in the order Cu > Ag > Au for the coinage metals. We note that the trends in catalytic activity shown in Table 1 are different from the ones reported by Dima et al. This is due to the fact that the catalytic activities reported by Dima et al. correspond to all NO3RR products including ammonia and hydroxylamine. In addition, our DFT calculations were performed on single facets, whereas Dima et al. used polycrystalline electrodes in their experiments.
| Metal | Potential limiting step | Limiting potential (V vs. RHE) |
|---|---|---|
| Cu | *NO → *NOH | −0.23 |
| Pt | *NO → *NOH | −0.33 |
| Ni | *NO → *NOH | −0.37 |
| Rh | *NO → *NOH | −0.39 |
| Pd | *NO → *NOH | −0.72 |
| Ir | *NO3 → *HNO3 | −0.19 |
| Co | *NO3 → *HNO3 | −0.34 |
| Ru | *NO3 → *HNO3 | −0.46 |
NO3RR activity volcanos
To investigate the NO3RR catalytic activity over transition metals, we employ the well-established volcano framework following the Sabatier principle. We first consider the linear scaling relations between different intermediates involved in the NO3RR to ammonia (Fig. 6). The NO3RR mechanism includes two sets of adsorbates. The first set are adsorbates that interact with the catalyst surface through the nitrogen atom and the second set interact via an oxygen atom. We use *NO and *OH as descriptors for the first and second sets of adsorbates due to the fact that the calculated adsorption energies of *N and *O intermediates over transition metals scale linearly with those of NO* and *OH, respectively.49,54,73Fig. 6a and b show the linear scaling relations for the first and second set of adsorbates, respectively. Fig. 6a shows that the binding energies of nitrogen bound species correlate to the binding energies of *NO (ΔG*NO). Similarly, the binding energies of oxygen bound species correlate to the binding energies of *OH (ΔG*OH). These correlations can be rationalized through the d-band model and the position of the d-band center.74 We would also like to emphasize that Au and Ag have been excluded when constructing the scaling relations. This is because Au and Ag do not bind several key intermediates such as *NO3, *NO2 and *NO. Therefore, the full NO3RR to ammonia does not occur on these metals.17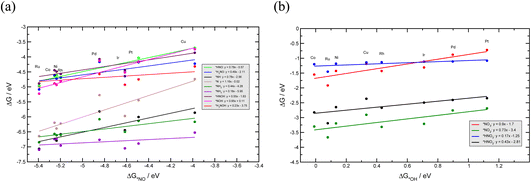 | ||
| Fig. 6 Linear scaling relations between NO3RR reaction intermediates that bind via (a) a nitrogen atom, and (b) via an oxygen atom. | ||
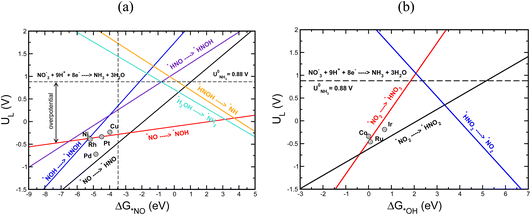
Using the scaling relation between the adsorbates that bind through nitrogen and oxygen, we construct a volcano-type relationship between the limiting potential and binding energies of NO*(ΔGNO*) and the binding energies of *OH (ΔG*OH), as shown in Fig. 7a and b. Each line in these volcano plots corresponds to an elementary reaction in the reaction network. Moreover, in constructing the volcano plots different reaction pathways were considered to take into account that the NO3RR may proceed through different reaction pathways on transition metals.
These volcano plots provide insights into the electrocatalytic activity of the transition metals. The potential limiting step (PLS) for the NO3RR corresponds to the elementary reaction with the most negative limiting potential, UL. The difference between the most negative limiting potential UL and the equilibrium potential (shown by horizontal dashed lines in Fig. 7a and b) defines the overpotential required to drive the NO3RR. This analysis shows that NO* → NOH* or NO* → HNO* are the PLS steps. For Cu, Pt, Ni, Rh, and Pd, the PLS is NO* → NOH*. Fig. 7a shows that the trends in catalytic activity obtained from the free energy diagrams agree well with the activity volcano analysis. The only outlier is Pd. This is because both the *NO → *NOH and *NO → *HNO lines in Fig. 7a are derived from linear scaling relations. More outliers are observed along the linear correlation for NOH* when constructed against HNO*. These outliers affect the accuracy of the linear fit. Nonetheless, both of those linear correlations are close to each other and are the lowest line with maximum distance from the equilibrium potential. Therefore, the formation of either NOH* or HNO* could well be the PLS, and both warrant consideration. The volcano plot in Fig. 7a shows that Cu is close to the cusp of the NO* → NOH* and NO* → HNO* lines, suggesting a superior catalytic activity over the rest of the studied transition metal surfaces. This explains why Cu has been repeatedly reported experimentally as an efficient catalyst for the NO3RR to ammonia. Note that Cu still has 1.11 V overpotential for the NO3RR to ammonia. Higher activities over Cu can be achieved by finding a catalyst material that has a weaker *NO binding energy. However, weaker *NO binding energies may result in the desorption of *NO in which case the full NO3RR to ammonia does not occur or NO(g) forms as the final NO3RR product. Ultimately, there is a ∼0.5 eV window for decreasing *NO binding energy and therefore increasing NO3RR catalytic activity. Another important feature in Fig. 7a is that the slope for the NO* → NOH* line is 0.05, indicating that the NO3RR catalytic activity is barely affected by changing the *NO binding energy. This mild slope originates from the fact that the *NOH and *NO binding energies scale linearly with a slope of 0.95 meaning that they are strongly coupled. This makes it almost impossible to change the binding energy of *NO without affecting the binding of *NOH. Interestingly, a similar feature has been observed as one of the limiting factors for catalyst development in the CO2 reduction reaction by Peterson et al. where the *CO → *CHO step was identified as the PLS with a slope of ∼0.15. They suggested several strategies for decoupling the binding energies of *CO and *CHO that could lead to catalysts with superior catalytic activity over Cu.66,75 The above results allude to two possible directions that should be considered in the design of improved NO3RR electrocatalyst systems with superior NO3RR catalytic activity over Cu:
(1) The catalyst material must break the scaling relations between *NO and *NOH/*HNO intermediates. This can be achieved by stabilization of NOH*/HNO* adsorbates relative to NO*. To this end, similar strategies that have been proposed for catalyst development for the CO2 reduction reaction can be applied for decoupling the binding energies of *NO and *NOH/*HNO, therefore leading to better performing catalyst materials (Fig. 7). We note that the above-mentioned limitations and the following suggested strategies to improve NO3RR catalytic activity are only applied to catalysts for which the NO3RR proceeds through the pathways where NO* → NOH*/*HNO is the PLS.
(2) Switching to new classes of materials that exhibit different scaling relations between *NO and *NOH/*HNO.
In the following we discuss possible strategies for breaking the scaling relations between *NO and *NOH/*HNO intermediates as depicted in Fig. 8.76
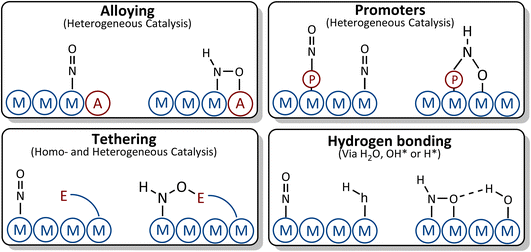 | ||
| Fig. 8 Suggested strategies for breaking the scaling relations between *NO and *NOH/*HNO adsorbates. | ||
(i) Alloying: by alloying with an element that has higher affinity towards oxygen, the *NOH and *HNO adsorbates with tilted adsorption structures may bind to the surface through both the nitrogen and oxygen atoms, causing the *NOH or *HNO adsorbates to bind more strongly to the surface than *NO. This strategy, however, should be taken with care. Although the element that has higher affinity towards oxygen does not influence the vertical adsorption structure of *NO, it may change the binding energy of *NO due to the change in adsorption site or modification of the electronic structure of the parent metal which could lead to stabilization of *NO, thus resulting in similar scaling relations to those of the parent metal. In addition, the presence of an element with higher affinity toward oxygen on the surfaces of the alloys facilitates water decomposition, which may give rise to *OH poisoning. If OH* binds too strongly to the surface, its reduction to water may become the potential limiting step rather than *NO reduction to *NOH/*HNO.
(ii) Tethering and ligand stabilization: ligands are tethered to the surface or designed in such a way that they can geometrically interact with *NO and *HNO. The oxygen tail of *HNO makes another bond with the ligand which could result in *HNO stabilization, while the binding energy of *NO is less influenced by the ligand due to its vertical adsorption structure.
(iii) Promoters: the presence of a promoter on the surface can change the binding energies of *NO, *NOH and *HNO by introducing new adsorption sites, modifying the electronic structure of adsorption sites, or a combination of both.
(iv) Hydrogen bonding: *NHO and *NOH are geometrically more suitable for interacting with H-containing ligands through hydrogen bonds. This leads to a stronger stabilization of *NOH/*HNO compared to *NO.
Fig. 7b shows a similar volcano plot to Fig. 7a constructed based on the linear scaling relationships for the intermediates bound through an oxygen atom. The two left legs of this volcano correspond to the *NO3 → *HNO3 and *NO2 → *HNO2 steps, and the right leg corresponds to the *HNO3 → *NO2 step. As discussed above, for Co, Ru and Ir the PLS was determined to be the formation of *HNO3 from adsorbed *NO3. Fig. 7b shows that the trends in catalytic activity obtained from the free energy analysis agree well with the volcano-type analysis. In addition, by comparing Fig. 7b with Fig. 7a, we can see that the slopes for the elementary reactions corresponding to the most negative limiting potentials, UL values, for the *NO3 → *HNO3 and *NO2 → *HNO2 steps are steeper than the one for the *NO → *NOH step. This indicates that high NO3RR catalytic activity can be achieved by tuning the oxygen affinities of transition metals for which *NO3 → *HNO3 is the PLS. This agrees with the recent theoretical–experimental study by Wang et al. on the NO3RR over ultrathin CoOx nanosheets where they showed that *NO3 → *HNO3 is the potential limiting step and suggested surface modification by surface oxygen atoms as an approach to tune the surface reactivity.77
In addition, we would like to note that the PLS for Ir, Co, and Ru is different from the ones for the Cu, Pt, Ni, Rh, and Pd transition metals. This is presumably because these two groups of materials have different affinities for nitrogen and oxygen, rendering different potential limiting steps. This may also be the rationale behind the fact that transition metal oxides exhibit different NO3RR catalytic activity than transition metals.43,78 For example, Wang et al. have reported a faradaic efficiency of 95.5% and selectivity of 81.2% for the NO3RR to ammonia over Cu/Cu2O.33 By comparing NO3RR catalytic activity and selectivity on Cu/Cu2O with that of Cu, they found that CuO facilitates the formation of the *NOH intermediate compared with Cu, resulting in enhanced NO3RR catalytic activity and selectivity. The latter might open new avenues for designing efficient catalysts for the NO3RR.
So far, we have only considered activity criteria for designing efficient catalysts. Catalytic selectivity is one of the key criteria in determining the overall performance of catalysts. At negative potentials, the hydrogen evolution reaction (HER) competes with the NO3RR. Therefore, in the following, further consideration will be given to the competing hydrogen evolution reaction.
Selectivity versus the HER
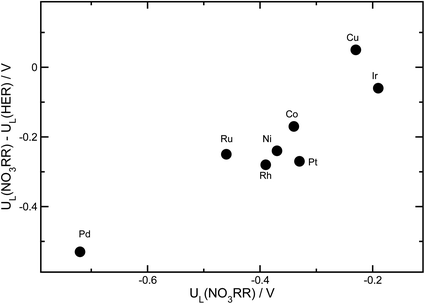
Beyond activity criteria, high selectivity towards the desired reaction products is a key factor in developing efficient catalysts for the NO3RR. At negative potentials, the hydrogen evolution reaction (HER) strongly competes with the NO3RR. The binding energy of *H has been shown to be a reasonable descriptor of hydrogen evolution activity for a wide variety of catalyst materials.79–81 To consider the trends in selectivity for the NO3RR for transition metals, we follow a similar approach that has been used for the electrochemical reduction of CO2.82–84 It has been shown that the difference between the limiting potentials for CO2 reduction and the HER captures the trends in selectivity. In Fig. 9, the difference between the limiting potentials for the NO3RR reduction and HER, i.e., UL(NO3RR) − UL(H2), is plotted against the limiting potential for the NO3RR, i.e., UL(NO3RR), for different transition metals. More positive UL(NO3RR) − UL(H2) corresponds to higher selectivity toward the NO3RR over the HER. This implies that the catalysts that are in the upper right region exhibit simultaneous high activity and selectivity towards the NO3RR. We would like to emphasize that this analysis does not evaluate the NO3RR selectivity towards NH3 or N2, rather it evaluates selectivity for the NO3RR over the HER. The results, displayed in Fig. 9, suggest that Cu is the most active and selective catalyst for the NO3RR. This agrees with previous experimental findings that reported Cu as one of the most promising catalysts for the NO3RR. Fig. 9 also shows that Ir stands out as the next most promising transition metal for the NO3RR. However, although Ir has higher catalytic activity than Cu, it exhibits lower selectivity towards NO3RR products, making H2 the dominant product under NO3RR conditions.Conclusions
Given the high emission intensities of conventional ammonia production from the Haber–Bosch reaction, methods such as the electrochemical reduction of nitrate (NO3RR) to ammonia appear attractive. Transition metals and transition metal oxides have been widely studied as potential catalyst materials for this reaction. However, the trends in the catalytic activity of the NO3RR for different transition metals have remained unclear. Herein, we investigate the underlying reaction mechanisms of the NO3RR to ammonia over different transition metal catalysts by calculating the binding energies of various reaction intermediates via Density Functional Theory (DFT). The binding energies of *NO and *OH adsorbates are identified as the reactivity descriptors using which we construct activity volcano plots and describe the trends in NO3RR catalytic activity across different transition metals. This analysis shows that the protonation of either *NO or *NO3 is the bottleneck step causing large overpotentials for the NO3RR to ammonia. In addition, we evaluated the selectivity toward NO3RR products by considering the competition between the NO3RR and HER. Our analysis explains why Cu is the most active and selective catalyst for the NO3RR to ammonia. Ultimately, we suggest possible approaches for designing catalyst materials with reduced overpotential by tuning the binding energies of *NO and *OH.Computational details
Density Functional Theory (DFT) calculations using the QUANTUM ESPRESSO package were conducted to determine the adsorption energies of various adsorbates.85 The Perdew–Burke–Ernzerhof (PBE) functional was used as the exchange correlation functional.86 The ion–electron interaction is described by ultrasoft pseudopotentials.87 For bulk metal nitrides, the Kohn–Sham wave functions were expanded in series of plane waves with a converged energy cut off of 550 eV and density cut off of 5500 eV. We investigate the NO3RR on 8 transition metal surfaces: namely, the close-packed facets of Au, Ag, Cu, Pt, Pd, Ni, Ir, and Co. The surfaces were modeled using a periodic 2 × 2 unit cell with four layers of metal atoms for each slab repeated in a supercell geometry with at least 17 Å of vacuum between successive slabs (see the ESI† for various convergence tests). For face-centered cubic metals, namely Au, Ag, Cu, Pt, Pd, Ni, and Ir, the (111) facet is used. For Co metal with a hexagonal-close-packed crystal structure, the (0001) surface is used. Adsorption was allowed on only one side of the slabs. In all calculations, the bottom two layers were fixed in their bulk structure whereas the top two layers and adsorbates on them were allowed to relax in all directions until the convergence criterion of an energy difference of 10−4 eV was met on the self-consistent field (SCF) cycle and forces on all atoms were converged to be lower than 0.025 eV Å−1. We use a Monkhorst–Pack grid with dimensions of 4 × 4 × 1 for sampling the first Brillouin zones.88 All adsorption sites were considered and only the most stable ones are reported here. The computational hydrogen electrode (CHE) method introduced by Nørskov et al.65 was used to calculate the free energy levels of all adsorbates. In this model, the free energy change of each electrochemical reaction step that involves an electron–proton transfer is calculated using the reversible hydrogen electrode (RHE), where the chemical potential of an electron–proton pair is equal to that of half of the hydrogen in the gas phase at standard conditions. The electrode potential is taken into account by shifting the electron energy by −eU where e and U are the elementary charge and the electrode potential, respectively. The limiting potential is defined as the negative of the maximum free energy difference between any two successive electrochemical steps. We applied a 1.12 eV correction to compensate for the DFT error of calculated formation energy of HNO3. The free energies of adsorption are calculated from ΔG = ΔEDFT + Δ(ZPE − TS), where ΔEDFT is the calculated electronic adsorption energy at zero Kelvin, ZPE is the zero-point energy, S is the entropy, and T is the temperature. Adsorption free energies are calculated by using HNO3 as a reference as suggested by Calle-Vallejo et al. taking into account zero-point energy and entropy corrections at T = 300 K.72 Zero-point energies and entropies were calculated using the finite difference scheme, within the rigid rotator/translator and harmonic oscillator approximation implemented in the Atomic Simulation Environment (ASE).89 As noted above, throughout this paper, we restrict our investigation to possible intermediates occurring in proton and electron transfer reactions. Moreover, all free energies are calculated relative to HNO3(g), H2O(g), and H2(g).Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the support from the University of Calgary′s Canada First Research Excellence Fund Program, the Global Research Initiative in Sustainable Low Carbon Unconventional Resources and the support provided by the Research Computing Service group at the University of Calgary.References
- J. W. Erisman, M. A. Sutton, J. Galloway, Z. Klimont and W. Winiwarter, Nat. Geosci., 2008, 1, 636–639 CrossRef CAS.
- V. Rosca, M. Duca, M. T. DeGroot and M. T. M. Koper, Chem. Rev., 2009, 109, 2209–2244 CrossRef CAS PubMed.
- C. Guo, J. Ran, A. Vasileff and S. Z. Qiao, Energy Environ. Sci., 2018, 11, 45–56 RSC.
- G. Soloveichik, Nat. Catal., 2019, 2, 377–380 CrossRef CAS.
- R. D. Milton, S. Abdellaoui, N. Khadka, D. R. Dean, D. Leech, L. C. Seefeldt and S. D. Minteer, Energy Environ. Sci., 2016, 9, 2550–2554 RSC.
- S. Z. Andersen, V. Čolić, S. Yang, J. A. Schwalbe, A. C. Nielander, J. M. McEnaney, K. Enemark-Rasmussen, J. G. Baker, A. R. Singh, B. A. Rohr, M. J. Statt, S. J. Blair, S. Mezzavilla, J. Kibsgaard, P. C. K. Vesborg, M. Cargnello, S. F. Bent, T. F. Jaramillo, I. E. L. Stephens, J. K. Nørskov and I. Chorkendorff, Nature, 2019, 570, 504–508 CrossRef CAS PubMed.
- M. Kitano, Y. Inoue, Y. Yamazaki, F. Hayashi, S. Kanbara, S. Matsuishi, T. Yokoyama, S. W. Kim, M. Hara and H. Hosono, Nat. Chem., 2012, 4, 934–940 CrossRef CAS PubMed.
- J. Kent, R. E. Green, J. Madden, a a Dadda, P. Cammarano, M. W. Pienkowski, J. D. Wilson, R. B. Bradbury, M. F. Heath, E. Signals, E. Assess-, E. Communities, J. a Mcneely, S. J. Scherr, J. G. Robinson, P. F. Donald, D. Southgate, K. Brown, P. E. Waggoner, D. T. Avery, E. B. Barbier, J. C. Burgess, A. Angelsen, D. Kaimowitz, A. Intensification, E. Development, C. B. Barrett, D. R. Lee, N. E. Borlaug, I. M. Goklany, M. W. Sprague and S. Development, Science, 2005, 4963, 2003–2006 Search PubMed.
- S. L. Foster, S. I. P. Bakovic, R. D. Duda, S. Maheshwari, R. D. Milton, S. D. Minteer, M. J. Janik, J. N. Renner and L. F. Greenlee, Nat. Catal., 2018, 1, 490–500 CrossRef.
- C. Tang and S. Z. Qiao, Chem. Soc. Rev., 2019, 48, 3166–3180 RSC.
- Y. Zeng, C. Priest, G. Wang and G. Wu, Small Methods, 2020, 4, 2000672 CrossRef CAS.
- J. G. Chen, R. M. Crooks, L. C. Seefeldt, K. L. Bren, R. Morris Bullock, M. Y. Darensbourg, P. L. Holland, B. Hoffman, M. J. Janik, A. K. Jones, M. G. Kanatzidis, P. King, K. M. Lancaster, S. V. Lymar, P. Pfromm, W. F. Schneider and R. R. Schrock, Science, 2018, 360(6391), eaar661 CrossRef PubMed.
- D. R. MacFarlane, P. V. Cherepanov, J. Choi, B. H. R. Suryanto, R. Y. Hodgetts, J. M. Bakker, F. M. Ferrero Vallana and A. N. Simonov, Joule, 2020, 4, 1186–1205 CrossRef CAS.
- J. Martínez, A. Ortiz and I. Ortiz, Appl. Catal., B, 2017, 207, 42–59 CrossRef.
- M. Duca, B. Van Der Klugt and M. T. M. Koper, Electrochim. Acta, 2012, 68, 32–43 CrossRef CAS.
- J. Li, G. Zhan, J. Yang, F. Quan, C. Mao, Y. Liu, B. Wang, F. Lei, L. Li, A. W. M. Chan, L. Xu, Y. Shi, Y. Du, W. Hao, P. K. Wong, J. Wang, S. X. Dou, L. Zhang and J. C. Yu, J. Am. Chem. Soc., 2020, 142, 7036–7046 CrossRef CAS PubMed.
- G. E. Dima, A. C. A. De Vooys and M. T. M. Koper, J. Electroanal. Chem., 2003, 554–555, 15–23 CrossRef CAS.
- E. Pérez-Gallent, M. C. Figueiredo, I. Katsounaros and M. T. M. Koper, Electrochim. Acta, 2017, 227, 77–84 CrossRef.
- J. X. Liu, D. Richards, N. Singh and B. R. Goldsmith, ACS Catal., 2019, 9, 7052–7064 CrossRef CAS.
- Y. Wang, A. Xu, Z. Wang, L. Huang, J. Li, F. Li, J. Wicks, M. Luo, D. H. Nam, C. S. Tan, Y. Ding, J. Wu, Y. Lum, C. T. Dinh, D. Sinton, G. Zheng and E. H. Sargent, J. Am. Chem. Soc., 2020, 142, 5702–5708 CrossRef CAS PubMed.
- C. Wang, Z. Liu, T. Hu, J. Li, L. Dong, F. Du, C. Li and C. Guo, ChemSusChem, 2021, 14, 1825–1829 CrossRef CAS PubMed.
- Z. Wang, S. D. Young, B. R. Goldsmith and N. Singh, J. Catal., 2021, 395, 143–154 CrossRef CAS.
- P. H. van Langevelde, I. Katsounaros and M. T. M. Koper, Joule, 2021, 5, 290–294 CrossRef.
- J. Wang, T. Feng, J. Chen, V. Ramalingam, Z. Li, D. M. Kabtamu, J. H. He and X. Fang, Nano Energy, 2021, 86, 106088 CrossRef CAS.
- Y. Yao, S. Zhu, H. Wang, H. Li and M. Shao, Angew. Chem., Int. Ed., 2020, 59, 10479–10483 CrossRef CAS PubMed.
- X. Deng, Y. Yang, L. Wang, X. Z. Fu and J. L. Luo, Adv. Sci., 2021, 8, 1–9 Search PubMed.
- X. Zhang, Y. Wang, C. Liu, Y. Yu, S. Lu and B. Zhang, Chem. Eng. J., 2021, 403, 126269 CrossRef CAS.
- J. Lim, C. Y. Liu, J. Park, Y. H. Liu, T. P. Senftle, S. W. Lee and M. C. Hatzell, ACS Catal., 2021, 11, 7568–7577 CrossRef CAS.
- M. Duca and M. T. M. Koper, Energy Environ. Sci., 2012, 5, 9726–9742 RSC.
- J. M. McEnaney, S. J. Blair, A. C. Nielander, J. A. Schwalbe, D. M. Koshy, M. Cargnello and T. F. Jaramillo, ACS SustainableChem. Eng., 2020, 8, 2672–2681 CrossRef CAS.
- B. H. Ko, B. Hasa, H. Shin, Y. Zhao and F. Jiao, J. Am. Chem. Soc., 2022, 144, 1258–1266 CrossRef CAS PubMed.
- X. Fu, X. Zhao, X. Hu, K. He, Y. Yu, T. Li, Q. Tu, X. Qian, Q. Yue, M. R. Wasielewski and Y. Kang, Appl. Mater. Today, 2020, 19, 100620 CrossRef.
- Y. Wang, W. Zhou, R. Jia, Y. Yu and B. Zhang, Angew. Chem., Int. Ed., 2020, 59, 5350–5354 CrossRef CAS PubMed.
- H. Liu, X. Lang, C. Zhu, J. Timoshenko, M. Rüscher, L. Bai, N. Guijarro, H. Yin, Y. Peng, J. Li, Z. Liu, W. Wang, B. R. Cuenya and J. Luo, Angew. Chem., Int. Ed., 2022, 61(23) DOI:10.1002/anie.202202556.
- J. Qin, L. Chen, K. Wu, X. Wang, Q. Zhao, L. Li, B. Liu and Z. Ye, ACS Appl. Energy Mater., 2022, 5, 71–76 CrossRef CAS.
- F. Y. Chen, Z. Y. Wu, S. Gupta, D. J. Rivera, S. V. Lambeets, S. Pecaut, J. Y. T. Kim, P. Zhu, Y. Z. Finfrock, D. M. Meira, G. King, G. Gao, W. Xu, D. A. Cullen, H. Zhou, Y. Han, D. E. Perea, C. L. Muhich and H. Wang, Nat. Nanotechnol., 2022, 17, 759–767 CrossRef CAS PubMed.
- T. Chen, H. Li, H. Ma and M. T. M. Koper, Langmuir, 2015, 31, 3277–3281 CrossRef CAS PubMed.
- Q. Hu, Y. Qin, X. Wang, Z. Wang, X. Huang, H. Zheng, K. Gao, H. Yang, P. Zhang, M. Shao and C. He, Energy Environ. Sci., 2021, 14, 4989–4997 RSC.
- R. Daiyan, T. Tran-Phu, P. Kumar, K. Iputera, Z. Tong, J. Leverett, M. H. A. Khan, A. Asghar Esmailpour, A. Jalili, M. Lim, A. Tricoli, R. S. Liu, X. Lu, E. Lovell and R. Amal, Energy Environ. Sci., 2021, 14, 3588–3598 RSC.
- C. Roy, J. Deschamps, M. H. Martin, E. Bertin, D. Reyter, S. Garbarino, L. Roué and D. Guay, Appl. Catal., B, 2016, 187, 399–407 CrossRef CAS.
- Y. J. Shih, Z. L. Wu, Y. H. Huang and C. P. Huang, Chem. Eng. J., 2020, 383, 123157 CrossRef CAS.
- L. Durivault, O. Brylev, D. Reyter, M. Sarrazin, D. Bélanger and L. Roué, J. Alloys Compd., 2007, 432, 323–332 CrossRef CAS.
- J. Yuan, Z. Xing, Y. Tang and C. Liu, ACS Appl. Mater. Interfaces, 2021, 13, 52469–52478 CrossRef CAS PubMed.
- L. X. Li, W. J. Sun, H. Y. Zhang, J. L. Wei, S. X. Wang, J. H. He, N. J. Li, Q. F. Xu, D. Y. Chen, H. Li and J. M. Lu, J. Mater. Chem. A, 2021, 9, 21771–21778 RSC.
- G. F. Chen, Y. Yuan, H. Jiang, S. Y. Ren, L. X. Ding, L. Ma, T. Wu, J. Lu and H. Wang, Nat. Energy, 2020, 5, 605–613 CrossRef CAS.
- X. Zhao, X. Jia, Y. He, H. Zhang, X. Zhou, H. Zhang, S. Zhang, Y. Dong, X. Hu, A. V. Kuklin, G. V. Baryshnikov, H. Ågren and G. Hu, Appl. Mater. Today, 2021, 25, 101206 CrossRef.
- W. He, J. Zhang, S. Dieckhöfer, S. Varhade, A. C. Brix, A. Lielpetere, S. Seisel, J. R. C. Junqueira and W. Schuhmann, Nat. Commun., 2022, 13, 1–13 CAS.
- H. Wan, A. Bagger and J. Rossmeisl, Angew. Chem., Int. Ed., 2021, 60, 21966–21972 CrossRef CAS PubMed.
- C. A. Casey-Stevens, H. Ásmundsson, E. Skúlason and A. L. Garden, Appl. Surf. Sci., 2021, 552, 149063 CrossRef CAS.
- T. Hu, C. Wang, M. Wang, C. M. Li and C. Guo, ACS Catal., 2021, 11, 14417–14427 CrossRef CAS.
- Z. Wang, J. Zhao, J. Wang, C. R. Cabrera and Z. Chen, J. Mater. Chem. A, 2018, 6, 7547–7556 RSC.
- Y. Wang, X. Qin and M. Shao, J. Catal., 2021, 400, 62–70 CrossRef CAS.
- T. Mou, Y. Wang, P. Deák, H. Li, J. Long, X. Fu, B. Zhang, T. Frauenheim and J. Xiao, J. Phys. Chem. Lett., 2022, 13, 9919–9927 CrossRef CAS PubMed.
- H. Niu, Z. Zhang, X. Wang, X. Wan, C. Shao and Y. Guo, Adv. Funct. Mater., 2020, 31(11), 2008533 CrossRef.
- H. Shin, S. Jung, S. Bae, W. Lee and H. Kim, Environ. Sci. Technol., 2014, 48, 12768–12774 CrossRef CAS PubMed.
- M. Duca, B. Van Der Klugt, M. A. Hasnat, M. MacHida and M. T. M. Koper, J. Catal., 2010, 275, 61–69 CrossRef CAS.
- M. Duca, V. Kavvadia, P. Rodriguez, S. C. S. Lai, T. Hoogenboom and M. T. M. Koper, J. Electroanal. Chem., 2010, 649, 59–68 CrossRef CAS.
- A. C. A. De Vooys, M. T. M. Koper, R. A. Van Santen and J. A. R. Van Veen, J. Catal., 2001, 202, 387–394 CrossRef CAS.
- J. Long, S. Chen, Y. Zhang, C. Guo, X. Fu, D. Deng and J. Xiao, Angew. Chem., Int. Ed., 2020, 59, 9711–9718 CrossRef CAS PubMed.
- A. Clayborne, H. J. Chun, R. B. Rankin and J. Greeley, Angew. Chem., Int. Ed., 2015, 54, 8255–8258 CrossRef CAS PubMed.
- A. Cuesta and M. Escudero, Phys. Chem. Chem. Phys., 2008, 10, 3628–3634 RSC.
- I. Katsounaros, M. C. Figueiredo, X. Chen, F. Calle-Vallejo and M. T. M. Koper, ACS Catal., 2017, 7, 4660–4667 CrossRef CAS.
- Y. Wang, C. Wang, M. Li, Y. Yu and B. Zhang, Chem. Soc. Rev., 2021, 50, 6720–6733 RSC.
- H. Liu, J. Park, Y. Chen, Y. Qiu, Y. Cheng, K. Srivastava, S. Gu, B. H. Shanks, L. T. Roling and W. Li, ACS Catal., 2021, 11, 8431–8442 CrossRef CAS.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- A. A. Peterson and J. K. Nørskov, J. Phys. Chem. Lett., 2012, 3, 251–258 CrossRef CAS.
- E. Skúlason, T. Bligaard, S. Gudmundsdóttir, F. Studt, J. Rossmeisl, F. Abild-Pedersen, T. Vegge, H. Jónsson and J. K. Nørskov, Phys. Chem. Chem. Phys., 2012, 14, 1235–1245 RSC.
- I. C. Man, H. Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS.
- V. Viswanathan, H. A. Hansen, J. Rossmeisl and J. K. Nørskov, ACS Catal., 2012, 2, 1654–1660 CrossRef CAS.
- J. H. Baek, T. M. Gill, H. Abroshan, S. Park, X. Shi, J. Nørskov, H. S. Jung, S. Siahrostami and X. Zheng, ACS Energy Lett., 2019, 4, 720–728 CrossRef CAS.
- S. Back, M. H. Hansen, J. A. Garrido Torres, Z. Zhao, J. K. Nørskov, S. Siahrostami and M. Bajdich, ACS Appl. Mater. Interfaces, 2019, 11, 2006–2013 CrossRef CAS PubMed.
- F. Calle-Vallejo, M. Huang, J. B. Henry, M. T. M. Koper and A. S. Bandarenka, Phys. Chem. Chem. Phys., 2013, 15, 3196–3202 RSC.
- F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. R. Munter, P. G. Moses, E. Skúlason, T. Bligaard and J. K. Nørskov, Phys. Rev. Lett., 2007, 99, 4–7 CrossRef PubMed.
- B. Hammer and J. K. Nørskov, Adv. Catal., 2000, 45, 71–129 CAS.
- X. Bai, L. Shi, Q. Li, C. Ling, Y. Ouyang, S. Wang and J. Wang, Energy Environ. Mater., 2021, 1–7 Search PubMed.
- A. Vojvodic and J. K. Nørskov, Natl. Sci. Rev., 2015, 2, 140–143 CrossRef CAS.
- J. Wang, C. Cai, Y. Wang, X. Yang, D. Wu, Y. Zhu, M. Li, M. Gu and M. Shao, ACS Catal., 2021, 11, 15135–15140 CrossRef CAS.
- R. Jia, Y. Wang, C. Wang, Y. Ling, Y. Yu and B. Zhang, ACS Catal., 2020, 10, 3533–3540 CrossRef CAS.
- T. F. Jaramillo, K. P. Jørgensen, J. Bonde, J. H. Nielsen, S. Horch and I. Chorkendorff, Science, 2007, 317, 100–102 CrossRef CAS PubMed.
- J. Greeley, T. F. Jaramillo, J. Bonde, I. Chorkendorff and J. K. Nørskov, Nat. Mater., 2006, 5, 909–913 CrossRef CAS PubMed.
- J. K. Nørskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23 CrossRef.
- C. Shi, H. A. Hansen, A. C. Lausche and J. K. Nørskov, Phys. Chem. Chem. Phys., 2014, 16, 4720–4727 RSC.
- D. Kim, C. Xie, N. Becknell, Y. Yu, M. Karamad, K. Chan, E. J. Crumlin, J. K. Nørskov and P. Yang, J. Am. Chem. Soc., 2017, 139, 8329–8336 CrossRef CAS PubMed.
- K. Chan, C. Tsai, H. A. Hansen and J. K. Nørskov, ChemCatChem, 2014, 6, 1899–1905 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. De Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- B. Hammer, L. Hansen and J. Nørskov, Phys. Rev. B, 1999, 59, 7413–7421 CrossRef.
- D. Vanderbilt, Phys. Rev. B, 1990, 41, 7892–7895 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188–5192 CrossRef.
- A. Hjorth Larsen, J. JØrgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. Bjerre Jensen, J. Kermode, J. R. Kitchin, E. Leonhard Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. Bergmann Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. SchiØtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2fd00145d |
| This journal is © The Royal Society of Chemistry 2023 |