Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The mechanochemical excitation of crystalline LiN3†
Adam A. L.
Michalchuk
 *
*
Federal Institute for Materials Research and Testing (BAM), Richard Wilstaetter Str 11, 12489, Berlin, Germany. E-mail: adam.michalchuk@bam.de
First published on 18th July 2022
Abstract
Mechanochemical reactions are driven by the direct absorption of mechanical energy by a solid (often crystalline) material. Understanding how this energy is absorbed and ultimately causes a chemical transformation is essential for understanding the elementary stages of mechanochemical transformations. Using as a model system the energetic material LiN3 we here consider how vibrational energy flows through the crystal structure. By considering the compression response of the crystalline material we identify the partitioning of energy into an initial vibrational excitation. Subsequent energy flow is based on concepts of phonon–phonon scattering, which we calculate within a quasi-equilibrium model facilitated by phonon scattering data obtained from Density Functional Theory (DFT). Using this model we demonstrate how the moments (picoseconds) immediately following mechanical impact lead to significant thermal excitation of crystalline LiN3, sufficient to drive marked changes in its electronic structure and hence chemical reactivity. This work paves the way towards an ab initio approach to studying elementary processes in mechanochemical reactions involving crystalline solids.
Introduction
Mechanochemical transformations describe the conversion of mechanical force into a chemical or physical transformation. The mechanisms that underpin such transformations have been subject to significant debate and remain an active area of research. To understand mechanochemical transformations, consideration must be given to cooperative phenomena spanning many orders of magnitude in both time and length. Moreover, the types of phenomena that need to be considered depend on the nature of the system being investigated.1 In fact, it is even not trivial to identify reactions that are directly driven by mechanical energy, as compared with those where mechanical action facilitates a thermal transformation.2 This immense complexity creates an exciting and vibrant field of research, ripe with both challenges and opportunities.As inherently out-of-equilibrium processes, mechanochemical transformations can be only understood by studying their evolution under dynamic conditions. Significant advances have been made towards studying the macroscopic dynamics of mechanochemical transformations, driven largely by the advent of time-resolved in situ (TRIS) analytical methods.3 TRIS X-ray powder diffraction has been widely used to follow the formation and consumption of crystalline phases as a function of milling time,4–7 and it has recently provided insights into the role of structural defects in activating mechanochemical transformations.8,9 By using TRIS X-ray absorption spectroscopy10 and optical fluorescence spectroscopy11 changes in the electronic structure of matter can be followed during mechanochemical transformations. Additionally, vibrational12–16 and NMR spectroscopies17 provide insight into the evolution of molecular structure during milling. Although powerful, these techniques only provide information at the macroscopic scale of length (down to ca. 10s of nanometers) and time (on the order of seconds). Correspondingly, events that occur more locally and transiently remain entirely unseen by available TRIS methods.
There is growing interest in studying with TRIS thermometry how temperature evolves over the course of a mechanochemical reaction. For example, TRIS thermometry has been used to identify the onset of phase transformations and reactions,16,18 or to better understand the thermodynamic conditions within the milling jar. By using TRIS thermometry, various authors have shown that over the course of a mechanochemical reaction, milling jars rarely exceed a few degrees.9,19 Such findings have questioned the role of temperature as an underlying driving force in mechanochemical transformations.
While the measurement of macroscopic phenomena has provided significant insight into mechanochemical transformations, they provide only an average, ‘slow’ view of how a dynamically stressed system evolves. To obtain a complete picture of a mechanochemical reaction, one needs to better understand the state achieved by the material in the moments directly following a dynamic mechanical strain. Ultrafast vibrational spectroscopy has long been used to characterise the response of solids to dynamic mechanical stress.20 Contrasting with macroscopic measurements, these ultrafast studies have provided strong evidence that extreme ‘thermal’ excitation occurs upon rapid mechanical loading.21,22,22 More recent studies using high speed thermometry have also confirmed that the shock-driven excitation of molecular solids drives exceptional local heating,23 for example reaching equivalents of over 4000 K in polymer-coated HMX.24 Importantly, these thermally excited states are highly transient (lasting only some pico- to micro-seconds), and hence do not represent conventional equilibrium temperatures. Rather, microscopic phenomena in mechanochemistry are associated with dynamical quasi-temperatures driven by high levels of vibrational excitation of the material.
Complementary to experimental studies of the microscopic dynamics of mechanochemistry, theoretical models have been developed.25–29 A subclass of these models have focused on describing how mechanical energy causes vibrational excitation of solids,25,30–33 and how this excess energy subsequently drives chemistry in the solid state.27,30 Based on an understanding of phonon–phonon collisions and the ensuing flow of vibrational energy in solids, atomistic models of the elementary stages of mechanochemical reactions provide unprecedented detail of mechanochemistry. To date, most elementary models of mechanochemistry have relied heavily on the use of experimental data, owing to the significant difficulties of the corresponding computations. This greatly limits their generality and predictive capabilities. Further developments of fully ab initio models of the elementary stages of mechanochemical reactions, based on state-of-the-art simulation techniques, are therefore required should a complete microscopic view of mechanochemistry be achieved.
Inspired by recent progress in the ab initio description of the elementary stages of mechanochemical reactions,27,31,34 these theoretical models are here adapted towards understanding the temporal evolution of vibrational quasi-temperatures in model systems exposed to hypothetical mechanical impulse. In this way we seek to obtain deeper insight into the conditions experienced by solids in the moments immediately following mechanical loading, i.e. within the region of space and time to which experiment remains largely blind. We first outline the theoretical background for the models developed and used in this work, followed by consideration of this framework on a model energetic material, crystalline LiN3.
Theory
When a mechanical impulse strikes a solid, an acoustic wave (e.g. compressive wave) is generated through the material. This acoustic wave interacts with the lowest frequency vibrations (external lattice modes) of the crystal. This interaction excites these external vibrational modes, increasing their vibrational quasi-temperature for some time. In their excited (or ‘hot’) states, these external modes can interact (or scatter) with each other via phonon–phonon collisions. In this way, energy can transfer from the ‘hot’ external modes towards higher frequency molecular vibrations. If sufficient energy reaches molecular vibrations, marked changes in the electronic behaviour of the molecules can occur, and hence chemistry can be driven forward for example by dynamic metallization.35To describe the transfer of energy from the external vibrational modes into the molecular vibrations, a conceptual Hamiltonian for the vibrations in a crystal can be written as
| Htot = Hvib + Hext + Hvib–ext | (1) |
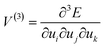 | (2) |
With knowledge of the strength of interactions between vibrations, it is possible to define the lifetime of a given vibrational band,
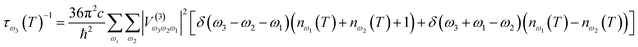 | (3) |
Using the average anharmonic approximation, our previous work has demonstrated that the mechanochemical reactivity of metal azides can be driven by transferring excess energy into the bending motion of the N3− anion.27,35,36 When this vibrational motion is excited, the crystalline azides achieve a transient metal-like state, wherein electronic excitations can be spontaneously achieved. Such excitations are sufficient to cause covalent bond rupture and the onset of chemistry.
It is worth noting a major caveat in the development of this theory. These models, as well as those developed in this work, are based entirely on harmonic vibrational frequencies, which are certainly a significant approximation at the high degrees of displacement under consideration. However, this approximation is expected to cause an underestimation of the achievable vibrational quasi-temperatures and phonon scattering rates. Moreover, our models consider only defect free crystals, again leading to an underestimation of phonon scattering rates. The inclusion of defects can be in principle added through explicit consideration of anharmonic scattering around defect sites, or through large scale molecular dynamics simulations. These issues will be further addressed in future publications.
Computational details
Simulations were performed within the framework of plane wave density functional theory, as implemented in QuantumESPRESSO v6.8.37 Input crystal geometries were taken from experimentally determined geometries, as available in the ICSD crystal data repository: LiN3 (#34675). The electronic structure was expanded in plane waves to a cut-off of 60 Ry for the kinetic energy and 480 Ry for the charge density. The core–valence interactions were approximated using projector-augmented wave pseudopotentials along with the exchange–correlation functional of Perdew–Burke–Ernzerhof (PBE)38 with the Grimme D3 dispersion correction (no damping).39 The experimental geometry was fully relaxed until residual atomic forces <5 × 10−5 Ry per atom, with electronic convergence of 1.0 × 10−12. Electronic structure was sampled on a Monkhorst–Pack40k-point grid of 3 × 3 × 3 (10 k-points in the irreducible Brillouin Zone). The optimized crystal structure is given in Table 1. The slight underestimation of the unit cell geometry as compared with experiment is expected, given experimental data are collected at room temperature, and simulations are inherently performed at 0 K. Electronic band gaps were calculated using the HSE06 screened hybrid functional,41 as implemented in the CRYSTAL17 suite,42,43 which is known to perform well for band gap simulations.31,44 For these calculations the unit cell geometry obtained from structural optimization in QuantumESPRESSO was used as input. Atom centred basis sets were selected for Li (Li_pob_TZVP_rev2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45) and N (N_pob_TZVP_rev2
45) and N (N_pob_TZVP_rev2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45) atoms. Five parameters control the tolerances for the two electron Coulomb and exchange contributions to the Fock matrix; here, the first four were set to 10−7, with the fifth set to 10−14. The electronic structure was integrated over a k-point net of 10 × 10 × 10 (SHRINK 10 10), leading to a total of >500 k-points.
45) atoms. Five parameters control the tolerances for the two electron Coulomb and exchange contributions to the Fock matrix; here, the first four were set to 10−7, with the fifth set to 10−14. The electronic structure was integrated over a k-point net of 10 × 10 × 10 (SHRINK 10 10), leading to a total of >500 k-points.
| a | b | c | α | β | γ | |
|---|---|---|---|---|---|---|
| P exp | 3.300 | 3.300 | 4.989 | 75.187 | 104.813 | 118.920 |
| P calc | 3.243 (−1.73) | 3.243 (−1.73) | 4.954 (−0.71) | 75.753 (−0.75) | 104.247 (−0.54) | 118.567 (−0.29) |
| V(PD2)exp | 45.417 | |||||
| V(PD2)calc | 43.833 (−3.488) |
Phonon frequencies were calculated using the finite differences method, as implemented in the Phonopy suite.46 Harmonic frequencies were generated using supercells of 3 × 3 × 3 (108 atoms) for LiN3. Subsequent anharmonic (third order) force constants were calculated using the Phono3py47 suite on supercells of 2 × 2 × 2 (32 atoms), for LiN3.
Ab initio molecular dynamics simulations were performed in QuantumESPRESSO using the unit cell geometry in Table 1, along with the same PBE-D3 level of theory and the same electronic structure criteria. Ion velocities were initiated at 450, 500, or 600 K, depending on the target temperature, and controlled using a Berendsen thermostat. The ion dynamics were modelled using the Verlet algorithm to integrate Newton's equations, with the equations of motion integrated using a time step of 1 fs.
Results and discussion
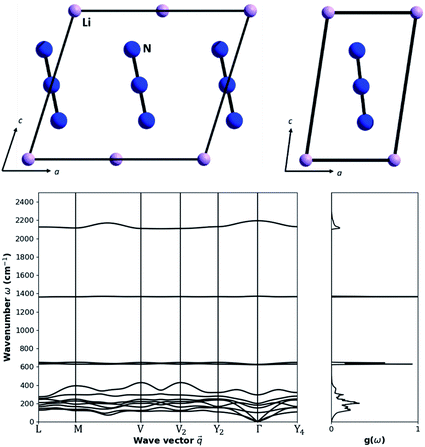
As a model system with which to explore the effects of mechanical impact on the vibrational heating we select crystalline LiN3, Fig. 1. This material is an energetic material (i.e. explosive), albeit with low sensitivity to mechanical impact, and hence its mechanochemical reactivity is of special interest. Importantly, LiN3 contains a small number of atoms in its unit cell, making it amenable to the computationally demanding simulations that are required.LiN3 crystallises in the monoclinic space group C2/m (point group C2h, 2/m), with the primitive cell containing a single N3− azido anion and one Li+ cation. Within this geometry, the N3− molecule (point group D∞h) sits on a crystallographic site with site symmetry C2h. This has the effect of splitting the molecular vibrational symmetry such that
| Πu → Au + Bu |
| Σg → Ag |
| Σu → Bu |
With four atoms in the primitive cell, there are a total of 12 vibrational frequencies at the Brillouin zone centre, Table 2. In addition to the four (internal) molecular vibrations, there are eight (external) lattice modes, of which three are acoustic modes (symmetry: Au + 2Bu) and the remaining five are optical modes (symmetry: Ag + Au + 2Bu + Bg). This gives the total 12 vibrations of symmetry 2Ag + 3Au + Bg + 6Bu. Modes with symmetry Ag + Bg are Raman active and can be therefore compared against literature experimental data for validation.
| ν/cm−1 | I.R. | Assignment | |
|---|---|---|---|
| M1 | 0 | Au | Acoustic |
| M2 | 0 | Bu | Acoustic |
| M3 | 0 | Bu | Acoustic |
| M4 | 106.55 | Bg | N3− rocking (a axis) |
| M5 | 154.25 | Ag | N3− rocking (b axis) |
| M6 | 184.42 | Au | Trans. Li + N3− (a axis) |
| M7 | 205.90 | Bu | Trans. Li + N3− (b axis) |
| M8 | 300.22 | Bu | Trans. Li + N3− (c axis) |
| M9 | 624.46 | Au | ν bend |
| M10 | 628.25 | Bu | ν bend |
| M11 | 1369.89 | Ag | ν str |
| M12 | 2191.48 | Bu | ν astr |
The highest frequency (2191.48 cm−1) normal mode corresponds to the asymmetric stretch (νastr) of the azido anion, with the symmetric stretch (νstr) appearing at 1369.89 cm−1. The symmetry broken bending modes (νbend) of the azido anion appear around 624 and 628 cm−1. These vibrational modes are of particular interest to the mechanochemistry of LiN3, as they can lead to dynamic metallization and hence spontaneous initiation of the explosive material.27,35 Our simulated vibrational frequencies are in good agreement with experimental Raman spectra of LiN3,49 for which νstr = 1372 cm−1 (simulation 1369.89 cm−1), νbend = 631 cm−1 (simulation 624, 628 cm−1), and νext = 125 cm−1 and 144 cm−1 (simulation 106.55 cm−1 and 154.25 cm−1). We note that the two external modes have significant temperature dependence, and some discrepancy between the experimental and simulated frequencies is therefore expected (experimental values at 141 K versus simulation at 0 K). The lattice vibrations all sit below 300 cm−1 at the Brillouin zone centre. The motion of the Li+ cation and N3− anion is generally well resolved for the lowest frequency optical modes (M4 and M5), which correspond to the rocking of the N3− anion over two orthogonal crystallographic axes. The three higher frequency optical modes include motion of both the Li+ cation and the N3− anion, comprising asymmetric translation of the ions approximately along the crystallographic axes.
Based on eqn (3), and restricted to the third-order anharmonic approximation of eqn (3), the transfer of vibrational energy requires that the total energy is conserved as two phonons are annihilated to create a single higher frequency vibration. Correspondingly, the transfer of energy into the lowest frequency molecular vibrations (M9 and M10, 624 and 628 cm−1) can be only approximately achieved via a single phonon scattering pathway: the scattering of two M8 modes (ν = 300 cm−1). Hence, the entire flow of energy into the azido anion is bottle necked by the rate of scattering into the M8 mode from the other external vibrations, and the subsequent self-scattering of M8. It is reassuring to find that energy transfer can be expected to occur much more readily once the full phonon dispersion relation is considered for LiN3, Fig. 1b. Away from k = 0, the acoustic branches rise in frequency to ca. 120 cm−1, joining the remaining optical branches to form a quasi-continuous band of phonon frequencies ranging from ca. 100 to 420 cm−1. Importantly, while the band dispersion in most optical branches is minimal, the highest frequency optical branch (M8) exhibits significant dispersion across k-space. This dispersion has the effect of generating phonon states up to ca. 420 cm−1, thereby making internal molecular vibrations significantly more accessible (e.g. by the additional scattering of M6 + M8 and M7 + M8). This is expected to prove essential for driving vibrational up-pumping in LiN3.
The increased number of scattering pathways across the dispersion curve becomes easily visible by considering the two-phonon density of states ρ(2), which can be calculated using the phonon density of states shown in Fig. 1. The curve for ρ(2), Fig. 2, is generated by solving δ(ω3 − ω2 − ω1) using as input the phonon density of states shown in Fig. 1. In the 1-D representation provided by Fig. 1, the degeneracy of phonon modes at a given frequency is taken as being equivalent to the integral of δ(ω − ωi), where the whole density of states has been normalized such that 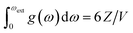 .30 The curve ρ(2) shows a significant amount of intensity at the νbend bands when the full phonon dispersion curve is accounted for, indicating that a large number of energy-conserving phonon–phonon scattering pathways exist to transfer vibrational energy from the external bands into the molecular vibrations. Importantly, we note that ρ(2) falls to zero around 1000 cm−1, thereby indicating that no third-order pathways exist to drive vibrational energy into higher lying molecular vibrations. For this reason, our semi-quantitative up-pumping models will consider only the contribution of νbend (see below).
.30 The curve ρ(2) shows a significant amount of intensity at the νbend bands when the full phonon dispersion curve is accounted for, indicating that a large number of energy-conserving phonon–phonon scattering pathways exist to transfer vibrational energy from the external bands into the molecular vibrations. Importantly, we note that ρ(2) falls to zero around 1000 cm−1, thereby indicating that no third-order pathways exist to drive vibrational energy into higher lying molecular vibrations. For this reason, our semi-quantitative up-pumping models will consider only the contribution of νbend (see below).
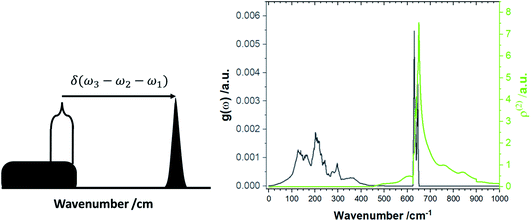 | ||
| Fig. 2 Two-phonon density of states, ρ(2). (Left) schematic representation for the formation of the two-phonon density of states, and (right) the ρ(2) for LiN3. | ||
Following the simulation of the harmonic frequencies, we calculated the explicit phonon–phonon scattering matrix elements (|V(3)|) that are necessary to simulate the energy transfer rates (lifetimes, τ) according to eqn (3). For this purpose, the third order force constants were calculated on a 2 × 2 × 2 supercell of LiN3 (total 32 atoms, 1224 perturbations) and projected onto the harmonic frequencies obtained using the 3 × 3 × 3 supercell (total 108 atoms) shown in Fig. 1. To ensure that accurate values of τ were obtained, the phonon–phonon collisions were calculated across a dense grid of points in the Brillouin zone. Convergence testing suggested this to be achieved on a grid of 14 × 14 × 14 grid points and a Gaussian smearing of 0.1 THz. Using this integration grid for the phonon scattering, the approximate phonon lifetimes were calculated at three temperatures, Table 3. For crystalline LiN3, the acoustic branches have the longest lifetimes of the external modes. The vibrational bands (M7 and M8) that are able to transfer energy into the molecular modes have remarkably short lifetimes of <1 ps at 20 K. The short lifetimes of the external modes reflect a significant degree of vibrational energy flow within the phonon region. The lifetimes of νbend are significantly longer than those of the external modes, presumably due to the limited number of pathways available for their scattering as discussed above. Within the context of building an up-pumping model, it follows that energy flow in and out of νbend should be much slower than the thermalization of the phonon bath. These relative lifetimes support the approximation that up-pumping models can begin from a thermalized phonon bath (i.e. where the quasi-temperatures of all external vibrational bands are assumed to be equal).31 We note that the significant lifetimes of the highest frequency modes are consistent with a lack of relaxation pathways of M11, whereas phonon dispersion gives rise to relaxation of M12 into M11 modes. Importantly, this suggests that we can neglect these modes from our conceptual models of vibrational energy flow during mechanical initiation in LiN3. As expected from eqn (3), the phonon lifetimes become significantly reduced as thermal scattering increases with temperature.
| Mode | Γ ν/cm−1 | τ/ps | ||
|---|---|---|---|---|
| 20 K | 100 K | 300 K | ||
| M1 | 0 | 0.25 | ||
| M2 | 0 | 4.16 | 1.24 | 0.36 |
| M3 | 0 | 2.63 | 0.94 | 0.30 |
| M4 | 106.55 | 1.87 | 0.71 | 0.23 |
| M5 | 154.25 | 1.44 | 0.61 | 0.20 |
| M6 | 184.42 | 1.03 | 0.52 | 0.18 |
| M7 | 205.90 | 0.45 | 0.26 | 0.10 |
| M8 | 300.22 | 0.19 | 0.14 | 0.07 |
| M9 | 624.46 | 9.17 | 5.14 | 2.09 |
| M10 | 628.25 | 9.11 | 5.14 | 2.09 |
| M11 | 1369.89 | 163.50 | 73.90 | 27.01 |
| M12 | 2191.48 | 34.37 | 16.28 | 6.09 |
High pressure behaviour and adiabatic heating
When a crystal with unit cell volume V0 at temperature T0 is adiabatically compressed to a final volume Vf, the partition of energy into work and heat is determined by50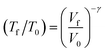 | (4) |
To this end we simulated the effects of compression on the molecular and crystallographic structures of LiN3 by systematically compressing the primitive LiN3 unit cell under hydrostatic loading to a maximum of 10 GPa. The use of hydrostatic loading is certainly a significant assumption given that mechanochemical transformations occur predominantly under uniaxial strains, which we consider in brief in ESI S5.† Interestingly, these simple anisotropic compression models do suggest that mechanochemical reactivity should depend markedly on the direction with which the mechanical stress is applied to the crystal, which will be the focus of dedicated follow-up investigations. Moreover, it is known that shear distortions can be also essential for driving mechanochemical phenomena, and the development of methodology to incorporate these distortions remains ongoing. However, without explicit knowledge of the direction of impact on a given crystal (which will indeed be averaged over many orientations in a powder sample), and to provide a proof-of-concept framework to explore mechanochemical transformations, hydrostatic compression serves as a convenient mechanical regime for the present contribution.
When exposed to hydrostatic pressures, the unit cell of LiN3 compresses in all three dimensions, Fig. 3. The principal strain axis (χ1) compresses by ca. 10% up to 10 GPa, while the third strain axis (χ3) compresses by only ca. 1%, Fig. 3a and ESI S1.† This yields an overall compression of the unit cell volume of ca. 17.9% at 10 GPa. With this magnitude of compression, a fit to the 3rd order Birch–Murnaghan equation of state yields a bulk modulus of 29.60 GPa. This is notably higher (i.e. the material is harder) than previously reported by experimental studies on the compressibility of LiN3, where a bulk modulus of ca. 20 GPa was reported for compression up to over 60 GPa.51 The larger value predicted from simulation is presumably due largely to the omission of thermal expansion in the DFT simulations, where the ambient pressure simulated unit cell is already ca. 3% smaller in volume than the ambient temperature geometry (see Table 1). Consistent with eqn (4), we can therefore expect that the calculated adiabatic heating will be lower than could be expected using experimental compressibility data.
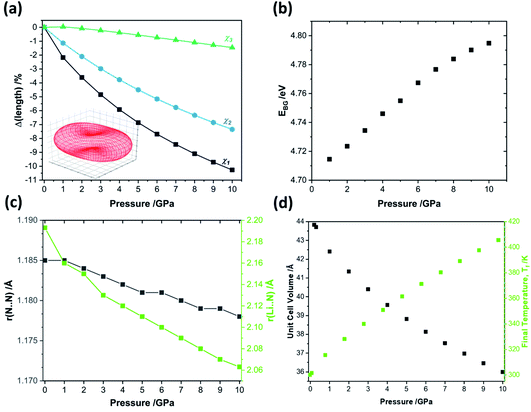 | ||
| Fig. 3 The effects of hydrostatic compression on the structure and properties of crystalline LiN3 from PBE-D2 simulations. (a) The response of the principal strain axes to hydrostatic compression alongside the (inset) compressibility indicatrix.52 Note χ1 = −0.5454a + 0.5268b + 0.6519c; χ2 = 0.7038a + 0.7104b + 0.0002c; χ3 = −0.5686a + 0.5573b − 0.6051c. (b) The effects of compression on the fundamental electronic band gap, as simulated at the HSE06 level of theory. (c) The response of the azido anion N–N bond lengths r(N⋯N) and the N⋯Li interaction length r(Li⋯N) to pressure. (d) The unit cell volume and corresponding final equilibrium temperature obtained from uniaxial compression, according to eqn (4). | ||
Additional calculations performed at the HSE06 level of theory suggest that compression of crystalline LiN3 to 10 GPa has negligible effect on the fundamental electronic band gap, which changes by <0.1 eV over the pressure range, Fig. 3b. Such a small response of the electronic structure is perhaps not surprising given that neither the N–N covalent bonds nor the Li⋯N interactions undergo any marked changes over the course of compression, Fig. 3c. It therefore follows that any mechanochemical reactivity of crystalline LiN3 is unlikely to be driven by a direct effect of the mechanical perturbation on the electronic structure. This opens the door to exploring more deeply a vibrationally driven mechanism for its mechanochemical behaviour.
The final parameter for eqn (4) – the mode average Grüneisen parameter, γ – depends on how mechanical perturbation (compression) alters the vibrational frequencies, ω of the crystalline phase,
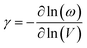 | (5) |
To approximate the value of γ for LiN3, we calculated the vibrational frequencies at each of the high-pressure unit cell geometries, ESI S2,† and calculated eqn (5) by considering only the frequencies at the Brillouin zone centre. As pressure increases, most of the zone centre vibrational bands harden (i.e. their frequencies increase). Due to its presumed essential role in facilitating energy flow from the external vibrations towards molecular vibrations, it is of particular note that M8 hardens from 300 cm−1 at ambient pressure to 360 cm−1 at 5 GPa, and up to 405 cm−1 by 10 GPa. At the same time, the azido anion bending modes (νbend, M9, M10), which are responsible for dynamical metallization in metal azides,35 soften with pressure (i.e. their frequencies decrease), decreasing from 624 cm−1 at ambient pressure to 613 cm−1 by 10 GPa. Together, the hardening of external lattice modes, coupled with softening of molecular vibrations, opens up a significant number of additional phonon–phonon scattering pathways capable of driving vibrational energy from the external modes into the internal molecular vibrations and hence driving chemistry. For example, while only three combinations (M8 + M8, M8 + M7, and M8 + M6) could drive chemistry at ambient pressure, many new pathways are available when the 10 GPa frequencies are considered. However, effectively all combinations of phonon–phonon scatterings involving M7 and M8 can lead to excitation of molecular vibrations when the full dispersion curves are considered at elevated pressures, see ESI S2.†
With consideration of the Brillouin zone centre vibrational frequencies, the mode averaged Grüneisen parameter was calculated to be 1.52, indicating only a minor degree of vibrational anharmonicity in LiN3. This has the effect of driving only a small degree of adiabatic heating during compression, with a maximum final equilibrium temperature, Tf in eqn (4), of ca. 405 K, Fig. 3d. We can contrast this with more highly anharmonic materials, such as a soft organic crystal like naphthalene, which display Grüneisen parameters on the order of 4.3,33 where a value of Tf on the order of 700–800 K could be expected.
To set the initial conditions for the adiabatically compressed solid, this excess energy must first be localised in the external lattice vibrations, which couple strongly to the mechanical stress. Following from the short lifetimes for the external states, we can assume that the excess energy is thermalized across all external vibrational bands in the first instance. Hence, with knowledge of the total available energy contained within the given crystal from being adiabatically compressed, it is next necessary to project this total energy onto the starting external vibrational states. This is achieved by considering (Fig. 4a) the relative energy–temperature relation (i.e. the heat capacity) of the total bulk crystal, Ctot and of the external modes, Cext,
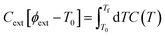 | (6) |
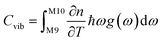 | (7a) |
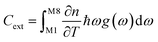 | (7b) |
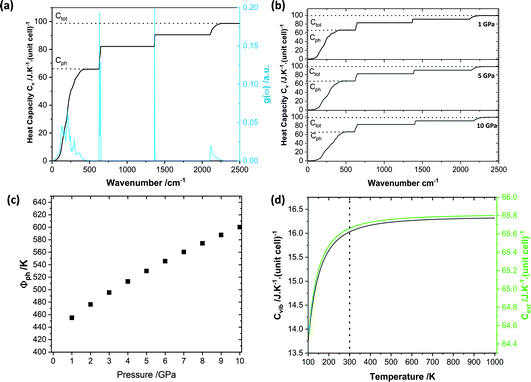 | ||
| Fig. 4 Vibrational thermodynamic behaviour of crystalline LiN3. (a) Vibrational heat capacity for LiN3, obtained from PBE-D2 simulations from integration over a 15 × 15 × 15 q-point mesh. The integrated heat capacity is given in black, alongside indications of the approximate phonon heat capacity (Cph) and total heat capacity (Ctot). (b) Heat capacity curves for each pressure are given in ESI S3.† (c) Effect of pressure on the initial phonon quasi temperature (φph). (d) Effect of temperature on the vibrational (black) and phonon (green) heat capacities. | ||
We define the cut-off between the external and internal vibrational regions based on visualisation of the eigenvectors, Table 2. Although this procedure is not always straightforward,30 the simplicity of LiN3 facilitates easy discrimination between the external and internal vibrational modes. Here we see that although the total energy input into the LiN3 lattice will increase with the degree of compression (Fig. 3d), the relative partitioning of the heat capacity remains unchanged, Fig. 4b. At low temperatures (or when the heat capacity is dominated by high frequency vibrations), one could expect the heat capacity in general to decrease with pressure (as high heat capacity favours lower vibrational frequencies). However, given the dominance of the low frequency bands in LiN3, the high temperature Dulong–Petit limit is reached even at ambient temperatures, such that the overall heat capacity of the system is conserved, Fig. 4b.
Following from eqn (6) the energy driven into the crystal by mechanical strain (see Fig. 3) can be used to define the initial phonon quasi-temperature for crystalline LiN3, Fig. 4c. At the lowest pressure studied here, the LiN3 external modes reach quasi-temperatures on the order of 420 K immediately following the mechanical impact (i.e. a temperature increase of ca. 120 K as compared with the thermalised solid temperature, 298 K). The initial quasi-temperature of the external vibrations increases approximately linearly with the magnitude of compression, reaching ca. 500 K for a 5 GPa impact, and up to ca. 600 K for a 10 GPa impact. We note that such impacts are unlikely to be reached in a conventional vibratory ball mill in the laboratory but this provides a picture for a potential mechanism that underpins the importance of carefully selecting impact energies when designing and interpreting mechanochemical experiments.
Energy flow under mechanical excitation
Inspired by developments of phonon energy flow in model organic aromatic compounds,26 we consider how mechanical impact on LiN3 can influence its mechanochemical reactivity. Using a quasi-equilibrium model, the system is segregated into two ‘thermal’ reservoirs: (1) the phonon bath which comprises the eight external mode branches, and (2) the molecular bath, which comprises the four molecular vibration bands. Following from eqn (3), the rate of vibrational energy transfer from the external lattice modes to the molecular vibrational bands depends on the anharmonic coupling term V(3), the number of pathways available for energy to flow through (i.e. the two phonon density of states ρ(2)), Fig. 2, and the difference in populations between the reservoirs, defined by their Bose–Einstein populations, n(T),| kup ∝ |V(3)|2ρ(2)[next(T) − nv(T)] | (8a) |
| kdown ∝ |V(3)|2ρ(2)[nv(T) − next(T)] | (8b) |
In the high temperature limit that is explored here, the population difference can be approximated by the difference in vibrational quasi-temperatures, such that [next(T) − nv(T)] → [ϕext − ϕv]. To bypass tedious computations, the product of |V(3)|2ρ(2) can be obtained from the low temperature phonon lifetime of the vibrational band into which vibrational energy is being transferred, here νbend, as calculated from simulations of phonon–phonon scattering, Table 2. This stems from the fact that at low temperatures the populations in eqn (8) tend towards zero. In crystalline LiN3, our simulated phonon lifetime for νbend at low temperatures is 9.1 ps.
We follow an early approximation to the vibrational rate equation33 by noting that the exchange of heat between the external and internal vibrational reservoirs must be conserved, such that the heat exchange per molecule depends on some energy transfer parameter λ according to 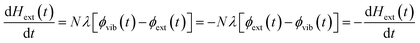 . By considering the molar heat capacities of the external and molecular vibrational regions, Fig. 4, the rate equations become
. By considering the molar heat capacities of the external and molecular vibrational regions, Fig. 4, the rate equations become
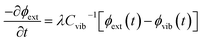 | (9a) |
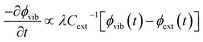 | (9b) |
Importantly, while one should account for the temperature dependence of the specific heat capacities in eqn (9), the high-temperature limit is achieved across all temperatures considered here, Fig. 4d. Correspondingly, a fixed specific heat capacity can be assumed in the case of LiN3 in the solution of eqn (9).
At the temperature where nvib − next = 1, the rate of up- and down-conversion from νbend is equivalent, and eqn (8) becomes equal to the low temperature limit, with the rate proportional to the low temperature phonon lifetime. This allows us to estimate a transfer rate constant (λ in eqn (9)) according to33
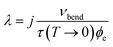 | (10) |
In crystalline LiN3, our simulated vibrational frequencies, Fig. 1 and Table 2, suggest that only a small number of phonon-scattering pathways dominate energy transfer into νbend, and the effect of j will be considered below. In the approximation of j = 1 for the first instance, we obtain a value of λ ≈ 2 × 1012 J K−1 mol−1 s−1, doubling or tripling for values of j = 2, 3, respectively. With initial simulations assuming a value of j = 1 and a mild mechanical impact of 1 GPa, ϕext quickly equilibrates with ϕvib, reaching equilibration at ca. 420 K within approximately 40 ps. We note that the final equilibrium temperature is somewhat lower than expected from Fig. 3d owing to the omission of the highest frequency (i.e. inaccessible) vibrational bands from the calculation. Following from the above discussion and Fig. 4c, the excitation of νbend increases with the magnitude of the impact, to ca. 485 K at a 5 GPa impact, and up to ca. 540 K for the highest (10 GPa) impact explored here. Importantly, as one considers an increasing number of vibrational scattering pathways (i.e. higher j) the equilibration period becomes faster, but does not affect the final equilibrium temperatures that are achieved. Thus, according to our semi-quantitative quasi-equilibrium simulations of phonon scattering, we expect significant heating of molecular vibrations in LiN3 to reach a maximum within ca. 40 ps within the framework of the present model. It is worth noting that, owing to various assumptions, including that our model begins with an equilibrated phonon bath, this timescale is likely to be somewhat underestimated, but provides an order of magnitude rate for processes involved in mechanochemical reactions.
To explore the effects of this elevated temperature on the chemical reactivity of LiN3 we performed a series of ab initio molecular dynamics simulations at elevated temperatures using the fixed, optimised geometry, Fig. 5. Our previous work on the dynamical metallization of NaN3 showed that sufficient excitation of νbend, to achieve ∠NNN of ca. 110° is sufficient to reach a metal-like state in metal azides, Fig. 5a.35 In this metal-like state, spontaneous electronic excitation can occur, and drive covalent bond rupture.27,36 In this light it is of particular interest to observe whether the temperatures achieved through the semi-quantitative up-pumping models can drive angle bending in a model metal azide. Starting at 450 K, our simulations suggest that the minimum value of ∠NNN that occurs is ca. 175°. While this is well below the bending angles required to drive spontaneous metallisation, it is worth noting that a degree of bending reduces the electronic band gap by ca. 0.2 eV in isostructural NaN3, with even this ‘mild’ shock temperature. As the temperature is increased to 500 K (i.e. consistent with a 5 GPa loading on LiN3), ∠NNN achieves a bending angle of ca. 162°, albeit only rarely. In isostructural NaN3 this degree of bending is associated with a decrease in the band gap of ca. 1 eV, Fig. 5b. Our ab initio molecular dynamics simulations suggest that over the course of its vibrational distortions at 500 K (coupling of νbend, νstr and νastr, see ESI S4†), the PBE band gap of LiN3 changes over a magnitude of up to 1.5 eV in LiN3 over the course of a few ps, Fig. 5c. Noting the underestimation of the compressibility (and hence underestimation of initial quasi-temperatures) we explored whether somewhat higher temperatures could drive LiN3 into dynamic metallization. Ab initio dynamics were correspondingly performed at 600 K. At this elevated temperature ∠NNN reaches a minimum value of ca. 157–160°, achieving these high bending angles regularly over the course of the vibrational distortions. These angles correspond to a band gap closing of ca. 1 eV in the isostructural NaN3 system (Fig. 5b) based on a pure bending motion. However, consistent with the 500 K trajectories, our ab initio simulations suggest that a reduction in the LiN3 band gap of >1.5 eV is possible at these quasi-temperatures owing to a combination of bending and stretching distortions of the azido anion. The perturbation of the band gap is similar at 500 and 600 K, thereby suggesting that relatively large differences in excitation pressure (e.g. 5 vs. 10 GPa) have only a minor influence on the maximum change of chemical reactivity. That said, the degree of excitation affects markedly the frequency of achieving extreme band gap alterations, and hence influencing the probability of altering chemical reactivity. Although our dynamics simulations, based on our semi-quantitative up-pumping model, suggest it is unlikely to be able to drive transient metallisation in crystalline LiN3, they clearly demonstrate how dynamic loading can have a marked impact on the electronic structure, and hence chemical reactivity, of materials.
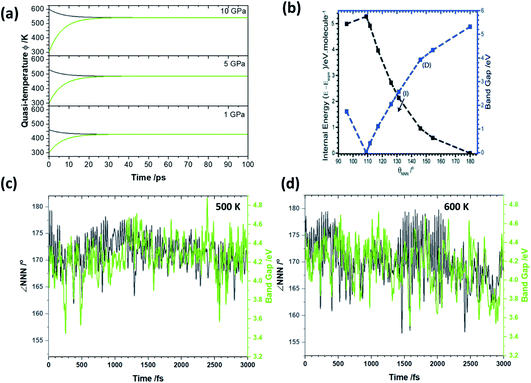 | ||
| Fig. 5 Effects of dynamic mechanical impact on the temperature and electronic behaviour of LiN3. (a) The temporal evolution of quasi-temperatures (black) ϕext and (green) ϕvib as a function of initial mechanical excitation at 10 GPa, 5 GPa and 1 GPa. (b) Effects of νbend on the electronic band gap of NaN3, isostructural to LiN3. Figure modified from ref. 35 with permission from the Royal Society of Chemistry. (c) The evolution of ∠NNN at 500 K, consistent with a 5 GPa shock loading, alongside the band gaps calculated at the PBE level of theory. (d) The evolution of ∠NNN at 600 K, consistent with a >10 GPa shock loading, alongside the band gaps calculated at the PBE level of theory. | ||
We can suggest that the relatively low compressibility of LiN3 (bulk modulus simulated as 29 GPa), coupled with its low degree of anharmonicity (γ, eqn (5)) and high Cext (Ctot/Cext = 1.5 in eqn (6)), is likely to be responsible for its low mechanochemical reactivity. In contrast, organic materials, such as the organic energetic material FOX-7 (bulk modulus ca. 11 GPa;53 and Ctot/Cext = 5 in eqn (6)), are expected to achieve significantly higher phonon quasi temperatures capable of driving a greater degree of chemistry as a result of dynamic mechanical impact. Even in their semi-quantitative form, numerical models of vibrational energy flow demonstrate the highly dynamic, out-of-equilibrium phenomena that must be considered when studying reactions driven by mechanochemical stimulation. With their continued development, such models are very promising towards exploring and understanding the elementary stages of mechanochemical reactions in crystalline materials.
Conclusions
Following a semi-quantitative quasi-equilibrium phonon up-pumping model, we explore the mechanical excitation of crystalline LiN3, a model energetic material. From previous work it is known that the excitation of the N3− bending mode of azide compounds can lead to dynamic metallisation and hence drive chemistry. Our ab initio phonon dispersion curves for LiN3 clearly show that vibrational energy can readily transfer to this bending mode via the highest frequency external lattice vibrations. Hence, LiN3 has a clear pathway to mechanical initiation. The high-pressure behaviour of LiN3 is used to identify the energies that are available to excite the LiN3 crystal lattice once exposed to mechanical stress. Based on ab initio phonon lifetimes, we subsequently demonstrate how this excess vibrational energy flows from the external lattice vibrations into the azido anion bending motion, achieving vibrational quasi-temperatures on the order of 500–600 K within 10s of ps, depending on the initial impact energy. We note that these rates are likely underestimates owing to the use of an equilibrated phonon bath as a starting model. Coupled with ab initio molecular dynamics simulations we show that such temperatures are insufficient to achieve dynamical metallisation in LiN3, but do drive significant (ca. 1–1.5 eV) changes in the material electronic structure and hence have marked impact on the material reactivity. We suspect that this low excitation – driven by low compressibility and low anharmonicity – is responsible for the poor explosive behaviour of LiN3 in response to mechanical impact. More highly compressible solids, such as conventional organic solids, will presumably achieve significantly higher degrees of vibrational excitation and hence a greater influence on their chemistry under dynamic mechanical loading. It is clear from models like that explored here that the processes that occur directly after a mechanical impulse is exerted on the material are significantly different – and more extreme – as compared with those measured at quasi-equilibrium (e.g. using bulk time-resolved in situ methods). The model presented here does include a series of significant approximations but stands as a proof of concept towards developing a computational perspective of the local conditions of solids exposed to dynamic mechanical impact. The continued improvement of these models, for example to include anisotropic distortions and defects, will certainly pave the way towards detailed atomistic views of mechanochemical reactions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
AM is grateful to CURTA54 (Free University Berlin) for access to computational resources.Notes and references
- E. Boldyreva, Chem. Soc. Rev., 2013, 42, 7719 RSC.
- A. A. L. Michalchuk, E. V. Boldyreva, A. M. Belenguer, F. Emmerling and V. V. Boldyrev, Front. Chem., 2021, 9, 29 Search PubMed.
- A. A. L. Michalchuk and F. Emmerling, Angew. Chem., Int. Ed., 2022, 61(21), e202117270 CrossRef CAS PubMed.
- F. Fischer, D. Lubjuhn, S. Greiser, K. Rademann and F. Emmerling, Cryst. Growth Des., 2016, 16, 5843–5851 CrossRef CAS.
- H. Kulla, S. Haferkamp, I. Akhmetova, M. Röllig, C. Maierhofer, K. Rademann and F. Emmerling, Angew. Chem., Int. Ed., 2018, 57, 5930–5933 CrossRef CAS.
- I. C. B. Martins, M. Carta, S. Haferkamp, T. Feiler, F. Delogu, E. Colacino and F. Emmerling, ACS Sustainable Chem. Eng., 2021, 9, 12591–12601 CrossRef CAS.
- J. Beamish-Cook, K. Shankland, C. A. Murray and P. Vaqueiro, Cryst. Growth Des., 2021, 21, 3047–3055 CrossRef CAS.
- G. I. Lampronti, A. A. L. Michalchuk, P. P. Mazzeo, A. M. Belenguer, J. K. M. Sanders, A. Bacchi and F. Emmerling, Nat. Commun., 2021, 12, 6134 CrossRef CAS PubMed.
- K. Linberg, P. Szymoniak, A. Schönhals, F. Emmerling and A. A. L. Michalchuk, ChemRxiv, 2022, 10 Search PubMed.
- P. F. M. de Oliveira, A. A. L. Michalchuk, A. G. Buzanich, R. Bienert, R. M. Torresi, P. H. C. Camargo and F. Emmerling, Chem. Commun., 2020, 56, 10329 RSC.
- P. A. Julien, M. Arhangelskis, L. S. Germann, M. Etter, R. E. Dinnebier, A. J. Morris and T. Friščić, ChemRxiv, 8(4), e1360 Search PubMed.
- S. Lukin, K. Užarević and I. Halasz, Nat. Protoc., 2021, 16, 3492–3521 CrossRef PubMed.
- L. Batzdorf, F. Fischer, M. Wilke, K.-J. Wenzel and F. Emmerling, Angew. Chem., Int. Ed., 2015, 54, 1799–1802 CrossRef PubMed.
- H. Kulla, A. A. L. Michalchuk and F. Emmerling, Chem. Commun., 2019, 55, 9793–9796 RSC.
- S. Haferkamp, A. Paul, A. A. L. Michalchuk and F. Emmerling, Beilstein J. Org. Chem., 2019, 15, 1141–1148 CrossRef.
- K. J. Ardila-Fierro, S. Lukin, M. Etter, K. Užarević, I. Halasz, C. Bolm and J. G. Hernández, Angew. Chem., Int. Ed., 2020, 59, 13458–13462 CrossRef PubMed.
- J. G. Schiffmann, F. Emmerling, I. C. B. Martins and L. Van Wüllen, Solid State Nucl. Magn. Reson., 2020, 109, 101687 CrossRef.
- H. Kulla, M. Wilke, F. Fischer, M. Röllig, C. Maierhofer and F. Emmerling, Chem. Commun., 2017, 53, 1664–1667 RSC.
- H. Kulla, C. Becker, A. A. L. Michalchuk, K. Linberg, B. Paulus and F. Emmerling, Cryst. Growth Des., 2019, 19, 7271–7279 CrossRef.
- D. D. Dlott, Annu. Rev. Phys. Chem., 1999, 50, 251–278 CrossRef PubMed.
- D. D. Dlott, in Advanced Series in Physical Chemistry, World Scientific, 2005, vol. 16, pp. 303–333 Search PubMed.
- D. S. Moore, S. C. Schmidt, M. S. Shaw and J. D. Johnson, J. Chem. Phys., 1989, 90, 1368–1376 CrossRef.
- S. You, M.-W. Chen, D. D. Dlott and K. S. Suslick, Nat. Commun., 2015, 6, 6581 CrossRef CAS.
- B. P. Johnson, X. Zhou, H. Ihara and D. D. Dlott, J. Phys. Chem. A, 2020, 124, 4646–4653 CrossRef.
- H. Kim and D. D. Dlott, J. Chem. Phys., 1990, 93, 1695–1709 CrossRef.
- J. R. Hill, E. L. Chronister, T. Chang, H. Kim, J. C. Postlewaite and D. D. Dlott, J. Chem. Phys., 1988, 88, 949–967 CrossRef.
- A. A. L. Michalchuk and C. A. Morrison, in Theoretical and Computational Chemistry, Elsevier, 2022, vol. 22, pp. 215–232 Search PubMed.
- S. V. Bondarchuk, J. Phys. Chem. A, 2018, 122, 5455–5463 CrossRef PubMed.
- S. V. Bondarchuk, New J. Chem., 2019, 43, 1459–1468 RSC.
- A. A. L. Michalchuk, J. Hemingway and C. A. Morrison, J. Chem. Phys., 2021, 154, 064105 CrossRef PubMed.
- A. A. L. Michalchuk, M. Trestman, S. Rudić, P. Portius, P. T. Fincham, C. R. Pulham and C. A. Morrison, J. Mater. Chem. A, 2019, 7, 19539–19553 RSC.
- J. Bernstein, J. Chem. Phys., 2018, 148, 084502 CrossRef.
- D. D. Dlott and M. D. Fayer, J. Chem. Phys., 1990, 92, 3798–3812 CrossRef CAS.
- A. A. L. Michalchuk, S. Rudić, C. R. Pulham and C. A. Morrison, Chem. Commun., 2021, 57, 11213–11216 RSC.
- A. A. L. Michalchuk, S. Rudić, C. R. Pulham and C. A. Morrison, Phys. Chem. Chem. Phys., 2018, 20, 29061–29069 RSC.
- A.A. L. Michalchuk, P. T. Fincham, P. Portius, C. R. Pulham and C. A. Morrison, J. Phys. Chem. C, 2018, 122, 19395–19408 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- J. Heyd, J. E. Peralta, G. E. Scuseria and R. L. Martin, J. Chem. Phys., 2005, 123, 174101 CrossRef PubMed.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2018, 8(4), e1360 Search PubMed.
- R. Dovesi, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. Bush, P. D'Arco, Y. Noël, M. Rérat, P. Carbonnière, M. Causà, S. Salustro, V. Lacivita, B. Kirtman, A. M. Ferrari, F. S. Gentile, J. Baima, M. Ferrero, R. Demichelis and M. De La Pierre, J. Chem. Phys., 2020, 152, 204111 CrossRef CAS.
- L. R. Warren, E. McGowan, M. Renton, C. A. Morrison and N. P. Funnell, Chem. Sci., 2021, 12, 12711–12718 RSC.
- D. Vilela Oliveira, J. Laun, M. F. Peintinger and T. Bredow, J. Comput. Chem., 2019, 40, 2364–2376 CrossRef CAS PubMed.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- A. Togo, L. Chaput and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094306 CrossRef.
- G. E. Pringle and D. E. Noakes, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1968, 24, 262–269 CrossRef CAS.
- Z. Iqbal, J. Chem. Phys., 1973, 59, 1769 CrossRef CAS.
- A. I. Kitaigorodsky, Molecular Crystals and Molecules, Academic Press, 1973, vol. 29 Search PubMed.
- S. A. Medvedev, I. A. Trojan, M. I. Eremets, T. Palasyuk, T. M. Klapötke and J. Evers, J. Phys.: Condens. Matter, 2009, 21, 195404 CrossRef CAS.
- M. J. Cliffe and A. L. Goodwin, J. Appl. Crystallogr., 2012, 45, 1321–1329 CrossRef CAS.
- S. Hunter, P. L. Coster, A. J. Davidson, D. I. A. Millar, S. F. Parker, W. G. Marshall, R. I. Smith, C. A. Morrison and C. R. Pulham, J. Phys. Chem. C, 2015, 119, 2322–2334 CrossRef CAS.
- L. Bennett, B. Melchers and B. Proppe, Curta: A General-Purpose High-Performance Computer at ZEDAT, Freie Universität Berlin, Berlin, Germany, 2020 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2fd00112h |
| This journal is © The Royal Society of Chemistry 2023 |