Adaptable sublattice stabilized high-entropy materials with superior thermoelectric performance

Abstract

High-entropy engineering is considered one of the most promising strategies in materials science, including the field of thermoelectrics. However, the presence of multiple elements with different atomic sizes and electronegativities in high-entropy materials often results in phase separation instead of the formation of a single phase. Herein, we propose that the adaptable sublattice can effectively stabilize single-phase high-entropy materials. Furthermore, the electrical and thermal transports can be efficiently tuned for much enhanced thermoelectric performance. Taking Mg_2−δ(Si, Ge, Sn, Bi) as a case study, the loosely bonded Mg sublattice is featured with large dynamic adaptability or flexibility, enabling it to release the large lattice strains caused by the large atomic size mismatch among Si, Ge, Sn and Bi. The resulting ultralow lattice thermal conductivity of 0.58 W m⁻¹ K⁻¹ at 800 K is not only approaching the amorphous limit but also lower than that of all known Mg₂X-based materials. Additionally, the interplay between the substitutional Bi_Sn defects and self-compensational Mg vacancies leads to an optimized carrier concentration and thereby high power factors. A maximum zT value of 1.3 is finally realized at 700 K in Mg_2−δSi_0.12Ge_0.13Sn_0.73Bi_0.02, which is among the top values of all Mg₂X-based materials. This study highlights the role of an adaptable sublattice in stabilizing high-entropy materials and offers a new pathway for exploring high-performance thermoelectric materials.

---

Broader context

Due to the countless combinations of compositions and processes, the world of high-entropy materials is brimming with opportunities, both in academic research and practical applications, including the field of thermoelectrics. However, previous studies have mainly focused on the preparation, properties, and applications of high-entropy materials, with little attention paid to their phase stability mechanisms. The presence of multiple elements with different atomic sizes and electronegativities in high-entropy materials often results in phase separation. In this study, using Mg_2−δ(Sn, Si, Ge, Bi) as a case study, we demonstrate that single-phase high-entropy materials can be effectively stabilized with the presence of an adaptable sublattice. The loosely bonded Mg sublattice in Mg_2−δ(Sn, Si, Ge, Bi) features large dynamic adaptability, which can effectively relieve the large stress caused by the large atomic size mismatch among Si, Ge, Sn and Bi. The distorted crystal lattice effectively blocks the heat-carrying phonons, resulting in an extremely low lattice thermal conductivity κ_L that approaches the glass limit. Meanwhile, the interplay between the substitutional Bi_Sn defects and self-compensational Mg vacancies leads to an optimized carrier concentration and thereby high power factors. A maximum zT value of 1.3 is finally realized at 700 K, which is among the highest values of all Mg₂X-based materials. This study offers a new avenue for exploring high-performance functional materials, including but not limited to high-entropy thermoelectrics, superalloys, structural ceramics, and thermal barrier coating.

Introduction

With the increasing severity of the energy crisis, the development of green, sustainable, and reproducible energy has become a common objective for humanity. Among the various options available, thermoelectric (TE) materials, which enables direct conversion of waste heat into electrical power, have garnered growing attention due to their emission free, reliable, and renewable nature. The energy conversion efficiency is valued by the materials’ dimensionless figure of merit zT, expressed as zT = S²σT/(κ_e + κ_L), where S, σ, κ_e, κ_L and T are the Seebeck coefficient, electrical conductivity, electronic thermal conductivity, lattice thermal conductivity and absolute temperature, respectively.^1–5 An ideal TE material should possess a high electrical conductivity for efficient electron transport, a large Seebeck coefficient for high output voltage, and a low thermal conductivity for large temperature differences. Over the past decades, numerous strategies have been proposed to optimize and decouple the electrical and thermal transports. Band engineering,^6–8 electron critical behaviour,^9,10 and disorder-induced electronic localization¹¹ have been used to improve the electrical transport, while the liquid-like or disordered ions,^12–15 hierarchical architecture,^16,17 and structural modularization¹⁸ have been introduced to suppress the lattice thermal conductivity.

Recently, entropy engineering has been recognized as a promising strategy to decouple the electrical and thermal transport properties of TE materials.¹⁹ In thermodynamics, entropy is usually associated with a state of disorder, randomness, or uncertainty.^20,21 High configuration entropy can be achieved by introducing different components by doping or alloying exotic elements, which enables the formation of a high-symmetry crystal structure, yielding a high band convergence and thereby a large Seebeck coefficient.^19,22 Besides, the presence of multiple solute components at the same lattice sites inevitably causes severe lattice distortion, which leads to strong scattering for heat-carrying phonons and results in low lattice thermal conductivity.^23–26 A lot of high-entropy TE materials, such as (Cu/Ag)₂(S/Se/Te),^27–29 (Pb/Sb/Sn)(S/Se/Te),^30–32 and (Ag/Mn/Ge/Sb)Te,^33,34 have been discovered and demonstrated superior TE performance. However, the application of entropy engineering in thermoelectrics is still in its infancy. The formation and stabilization mechanisms of high-entropy materials have not been thoroughly explored. One major obstacle in implementing an entropy engineering approach is the issue of phase separation. While the high configuration entropy is an essential driving force in stabilizing the structure, the increased number of elements with varying atomic sizes and electronegativities can often lead to a very large formation enthalpy that exceeds the impact of entropy.^35,36 Meanwhile, multiple combinations among various elements can lead to the generation of many possible phases with low formation enthalpy.³⁷ Previous studies have also shown that many high-entropy alloys do not actually possess a stable single-phase structure, but instead tend to form mixed phases through spinodal decomposition or the precipitation of second phases.^38–40 It is crucial to explore novel approaches to stabilize the high-entropy single-phase structure for high-performance thermoelectrics.

Recently, Zhao et al. demonstrated that the presence of highly diffusive cations can counterbalance the large atomic size and electronegativity mismatches of anions, which helps to escape phase separation and create a stable single phase.^11,18,41 In detail, the highly diffusive cations move quickly to the appropriate positions, which changes the coordination environment of the mismatched anions and thereby releases huge stress. Meanwhile, the crystalline but mismatched anions drive the cations into a disordered state, forming a unique meta-phase. Broadly, such a concept can be extended to the creation and stabilization of high-entropy materials. With the presence of an adaptable or flexible cationic sublattice, the distorted and disordered anionic sublattice with multiple solutes is expected to be stabilized.

In this work, we present a case study in Mg₂X (X = Si, Ge, Sn), a promising TE material characterized by its low mass density, environmental compatibility, and high TE performance.^42–46 The highly diffusive Mg ions in Mg₂X⁴⁷ make it a good material template to implement high-entropy engineering and study the pertinent effects on the TE properties. Through alloying Si, Ge, Sn, and Bi at the X lattice sites, along with the generation of Mg vacancies V_Mg (Fig. 1a), we obtained a series of single-phase high-entropy Mg_2−δSi_0.12Ge_0.13Sn_0.75−xBi_x materials. It is found that Mg exhibits a large atomic displacement, which effectively relieves the large stress caused by the mismatch of atoms. The distorted crystal lattice effectively blocks the heat-carrying phonons to reduce the lattice thermal conductivity κ_L. Meanwhile, the interplay between Bi doping and self-compensational Mg vacancies leads to an increase in the carrier concentration within the optimal range, yielding a high power factor exceeding 43 μW cm⁻¹ K⁻² at 600 K. Consequently, an exceptional maximum zT of 1.3 is realized at 700 K in the Mg_2−δSi_0.12Ge_0.13Sn_0.73Bi_0.02 sample, comparable to the other state-of-the-art Mg₂X based materials (Fig. 1b).

Fig. 1 (a) Structural diagram of Mg_2−δSi_0.12Ge_0.13Sn_0.75−xBi_x. (b) Temperature dependence of zT of samples Mg_2−δSi_0.12Ge_0.13Sn_0.75−xBi_x (x = 0, 0.02). The data from other studies are included for comparison.^49–51

Results and discussion

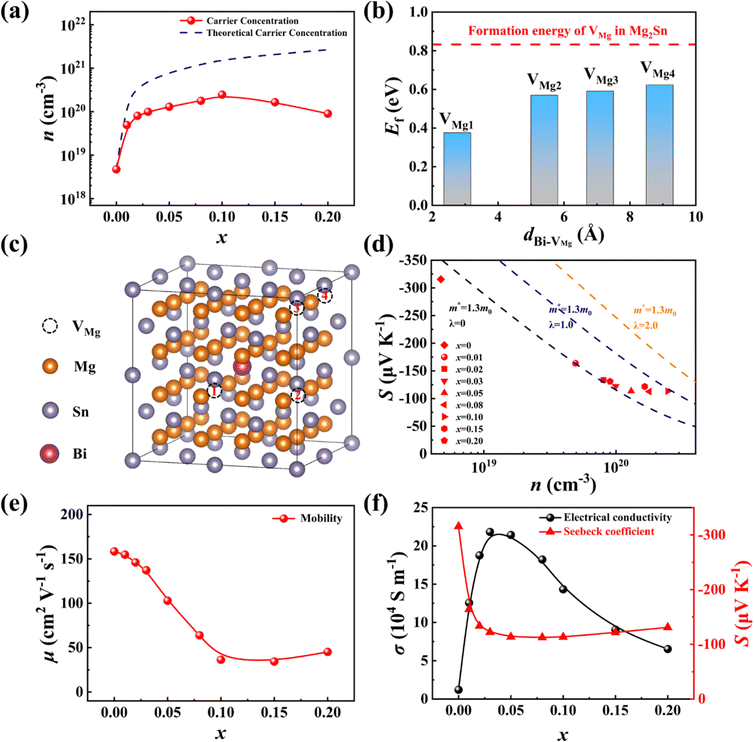
Considering the band convergence of Mg₂Ge_0.22Sn_0.78 and Mg₂Si_0.30Sn_0.70,^7,44,48 the composition between these two compounds is chosen as the matrix, and then Bi atoms and Mg vacancies are further introduced to tune the carrier concentration (see the quaternary phase diagram in Fig. S1, ESI†). The as-fabricated Mg_2−δSi_0.12Ge_0.13Sn_0.75−xBi_x samples exhibit a single-phase antifluorite structure in the XRD patterns as x < 0.15, and only a tiny amount of secondary phase Mg₃Bi₂ is observed in the x = 0.20 sample (Fig. 2a). All the elements are homogeneously distributed without obvious accumulation in the pellets (see Fig. S2, ESI†). Despite the significant differences in atomic radius and electronegativity, and even different valence states among Si, Ge, Sn, and Bi (see Table S1, ESI†), we obtain pure-phase high-entropy Mg_2−δSi_0.12Ge_0.13Sn_0.75−xBi_x materials. Rietveld refinement was conducted based on the XRD patterns and the corresponding results are listed in the ESI† (Fig. S3 and Tables S2, S3). The refined lattice parameter shows no clear trend with an increase in the Bi content (see Fig. S4, ESI†). Given the lattice expansion from the atomic radius difference between the Bi (1.547 Å) atom and Sn (1.450 Å) atom, the irregular variation of the lattice parameter should be attributed to lattice shrink caused by the self-compensation Mg vacancy. The semi-quantitative energy-dispersive X-ray spectroscopy (EDS) results also show that the relative Mg content is gradually decreased with the increase of the Bi content (Fig. 2b), confirming the formation of Mg vacancies. The value of δ is largely influenced by the change in the Bi content x. When two Sn are substituted by two Bi cations, the material becomes more deficient of roughly one Mg vacancy, i.e., δ ≈ 0.5x. Such a self-compensation effect has been also observed in other materials like skutterudites,⁵² Mg_2−δSn_1−xSb_x⁵³ and Cu_2−δTe_0.9−yI_0.1S_y.^18,22 The calculated configuration entropy ΔS for Mg_2−δSi_0.12Ge_0.13Sn_0.55Bi_0.20 is as large as 9.74 J mol⁻¹ K⁻¹, which is furtherly increased to 11.28 J mol⁻¹ K⁻¹ when considering the extra entropy introduced by the Mg vacancies.

Fig. 2 (a) Room temperature XRD patterns of Mg_2−δSi_0.12Ge_0.13Sn_0.75−xBi_x. (b) Relative Mg content measured by energy-dispersive X-ray spectroscopy (EDS). (c) Configuration entropy ΔS and (d) atomic displacement parameter U_iso as a function of the Bi content x. The dashed lines are a guide to the eye. (e) Fit of the crystallographic Fm3̄m model (red line) to 300 K PDF data (blue rings) of sample x = 0.10 and their difference (green line, offset for clarity). (f) Fit of the broken symmetry model (red line) to 300 K PDF data (blue symbols) of sample x = 0.10 and their difference (green line, offset for clarity). The corresponding crystal structure is included for reference.

The stabilization of single-phase high-entropy Mg_2−δSi_0.12Ge_0.13Sn_0.75−xBi_x is closely related to the adaptable and flexible nature of the Mg sublattice. Fig. 2d shows the atomic displacement parameter (ADP) of Mg and X (X = Si, Ge, Sn, Bi) refined from the XRD results. The errors of ADP are very small, which is indiscernible when added to the figures. Therefore, we list the ADP values along with the errors for Mg and X in Table S4, ESI.† Clearly, the ADP of Mg is more than two times larger than those of X atoms, suggesting a large dynamic adaptability of the Mg sublattice. Upon increasing the Bi alloying content, the ADPs of both Mg and X are further increased. Overall, the anions X with large atomic size mismatch form a disordered yet crystalline sublattice that defines irregular interstitial sites, in which the dynamic and mobile Mg migrate and bond with the nearby anions Si, Ge, Sn, or Bi to release the large stress.¹¹ We also try to investigate the local structure using synchrotron X-ray atomic pair distribution function (PDF) analysis. The PDF refinement details are listed in Table S5 (ESI†). The PDF data of the x = 0.10 sample can be well fitted by the perfect antifluorite structure (Fig. 2e), as well as the broken symmetry model with Mg atoms deviating from the center of the X tetrahedron (Fig. 2f). It seems the position of Mg has a weak impact on the PDF results because Mg is a weak scatter. The oscillation amplitude in the measured structure factor in the high Q region is quite low (see Fig. S5, ESI†), and the available Q_max (14 Å⁻¹) is not sufficiently high due to the use of a pinked beam with an energy of 40 keV. Consequently, resolving detailed structure information with the current data is difficult. In principle, it is possible to distinguish the contribution of different bonds down to a portion of around 5%, but it requires extremely high data quality and extensive subsequent modeling.

To further understand the formation and stabilization mechanism, we analyze the bonding character and formation enthalpy using ab initio calculations. A 2 × 2 × 2 supercell was constructed for Mg₆₄Sn₃₂ and Mg₆₄Si₄Ge₄Sn₂₀Bi₄, followed by the relaxation of the cell shape, cell volume and atomic positions. In pristine Mg₆₄Sn₃₂, all Mg–Sn bonds have a uniform bond length of 2.92 Å. However, for Mg₆₄Si₄Ge₄Sn₂₀Bi₄, the bond lengths change to 2.81 Å for Mg–Si, 2.83 Å for Mg–Ge, 2.93 Å for Mg–Sn, and 3.04 Å for Mg–Bi bonds. The significant variation in bond length suggests the severe lattice distortion in Mg₆₄Si₄Ge₄Sn₂₀Bi₄, which can be attributed to the distinct atomic and/or ionic radius of the anions (see Table S6, ESI†). Fig. 3b shows the projected crystal orbital Hamilton populations (pCOHP) for Mg–X (X = Si, Ge, Sn, Bi) bonds. The pCOHP patterns of Mg–X are distinct from each other. In particular, large antibonding (destabilizing) states below the Fermi level are observed for the Mg–Bi bond, in contrast to other three bonds. The bonding energy calculated from the integral pCOHP (IpCOHP) is only −0.51 eV for the Mg–Bi bond, which is increased to −0.65 eV for the Mg–Sn bond, −0.69 eV for the Mg–Ge bond, and −0.72 eV for the Mg–Si bond. The weaker bonding of Mg–Bi is partly attributed to its longer bond length. Besides, the energy difference between the s orbital of Mg and the p orbital of Bi is much larger than that between Mg and Si/Ge/Sn (see Table S6, ESI†), which also contributes to the weaker nature of the Mg–Bi bond compared to other bonds. Notably, the bonding energies of all Mg–X bonds are quite low, indicative of a weak covalent interaction. This is further supported by our deformation charge density results (see Fig. 3d). The low charge density between Mg and X points to weak covalent bonds, which, in turn, endows Mg with high adaptability and flexibility. Additionally, the charge density of Bi atoms surpasses that of Si, Ge and Sn, implying a higher electronegativity for Bi compared to Si, Ge, and Sn.

Fig. 3 (a) Average, maximum, and minimum bond length of Mg–X (X = Si, Ge, Sn, Bi) bonds in a 2 × 2 × 2 supercell of Mg₆₄Si₄Ge₄Sn₂₀Bi₄. (b) The projected crystal orbital Hamilton population (pCOHP) of Mg–X bonds. The Fermi level is represented by a horizontal dashed line. The bonding orbital has a negative pCOHP, while the antibonding orbital has a positive pCOHP. (c) Integrated pCOHP (IpCOHP) for the chemical bonds in Mg₆₄Si₄Ge₄Sn₂₀Bi₄. (d) Deformation charge density at the (101̄) plane.

Molecular dynamics (MD) simulations provide further details of the adaptability and flexibility of the Mg sublattice. As shown in Fig. 4, the results of MD calculations clearly show that the Mg atoms vibrate in a larger space relative to the X atoms at 300 K. With the temperature increasing from 300 K to 800 K, the trajectory of Mg tends to be more dispersive (see Fig. 4a and Fig. S6, ESI†), suggesting that the Mg atoms tend to be movable with an increase in temperature. In particular, the Mg atoms are delocalized to a level very fluid-like at high temperatures (e.g. 800 K), indicating that Mg atoms are loosely bonded to the neighboring X atoms, and display highly diffusive characteristics. This is also reflected in the atomic mean square displacement (MSD) of Mg derived from MD simulations. As shown in Fig. 4b, the MSD of Mg is obviously larger than those of Si, Ge, Sn and Bi in the whole temperature range, which is well consistent with the experimental ADP results. The large MSD and ADP of Mg are reminiscent of its high adaptability to the coordination environment. We examined three types of 2 × 2 × 2 supercells (termed S1, S2 and S3) and one 3 × 3 × 2 supercell (termed S4), as shown in Fig. S7 (ESI†). The change in total energy over simulation time exhibits relatively stable trends after just a few picoseconds, indicating that the four configurations quickly reach their equilibrium states in MD simulations (Fig. S8, ESI†). The calculated bond length (Fig. S9, ESI†), IpCOHP (Fig. S10, ESI†), and MSD (Fig. S11a, ESI†) of the 3 × 3 × 2 supercell are very close to those of 2 × 2 × 2 supercells. Therefore, we believe that 96 atoms in 2 × 2 × 2 supercells are sufficient to capture the correlated disorder type effects. The three different 2 × 2 × 2 supercells also exhibit similar trends and values, demonstrating that different configurations have little impact on the results.

Fig. 4 (a) Molecular dynamics simulations of the trajectory of Mg, Si, Ge, Sn, and Bi at 300 K, 500 K, and 800 K. (b) Calculated atomic mean square displacement (MSD) of Mg, Si, Ge, Sn, and Bi as a function of temperature. (c) Mixing enthalpy ΔH at 0 K and estimated free energy ΔG of Mg₆₄Si₄Ge₄Sn_24-nBi_n as a function of the Bi content n at 300 K. The blue squares denote the results after cell volume relaxation, while the green symbols denote the results after relaxing the cell shape, cell volume and atomic positions.

Further calculation of the mixing enthalpy is carried out to confirm the high adaptability of Mg for releasing the large stress. First, we relax the cell volume with all the atomic positions fixed within the cubic lattice. The resulting mixing enthalpy (ΔH) is very large, indicating such an atomic configuration is energetically unfavourable given the large atomic size mismatch among Si, Ge, Sn, and Bi. When we fully relax the cell shape, cell volume and atomic positions in the atomic structure, the mixing enthalpy dramatically drops down by nearly three times (see Fig. 4c and Fig. S11b, ESI†). Based on the calculated mixing enthalpy ΔH and configuration entropy ΔS, we calculate the free energy, ΔG = ΔH − TΔS, for Mg₆₄Si₄Ge₄Sn_24−nBi_n at 300 K. As shown in Fig. 4c, the calculated ΔG is close to zero when all the atomic positions are fixed, suggesting that high entropy alloys are metastable at this temperature. Moreover, it should be noted that the contribution of atomic vibration to the enthalpy is neglected here and the actual ΔG should be positive. After fully relaxing the cell volume, shape and atomic positions, the calculated ΔG of all compositions become far below zero, indicating that the structure has been stabilized. During the process of relaxation, the anionic sublattice practically retains its coherence despite a large atomic size mismatch; by contrast, Mg atoms undergo relocation depending on what specific X atom is nearby (see Fig. S12, ESI†). The Mg atomic relocation releases the otherwise large strain of the anionic sublattice.

The most thrilling effect of high-entropy engineering is its ability to suppress thermal transport. Fig. 5a shows the total thermal conductivity κ of Mg_2−δSi_0.12Ge_0.13Sn_0.75−xBi_x. The κ value for the Bi-free sample slightly decreases at low temperatures (<500 K) and starts to rise above 500 K, which is an indication of the bipolar effect. Upon increasing the alloying content of Bi, the bipolar effect is strongly suppressed, consistent with electrical transport results. The lattice thermal conductivity κ_L was extracted by subtracting the carrier contribution κ_e and bipolar contribution κ_bipolar from the total κ (see calculation details in the ESI†). As shown in Fig. 5b, the κ_L roughly follows a T⁻¹ dependency in the samples with a low Bi content (x < 0.03), suggesting that phonon–phonon scattering is the dominant scattering mechanism. However, the temperature dependence of κ_L clearly deviates from the T⁻¹ relationship upon further increasing the Bi alloying content, indicating strong phonon scattering from the point defects. Furthermore, with an increase in entropy induced by a random distribution of Si, Ge, Sn, and Bi in the anionic sites, as well as Mg and vacancies in the cationic sites, the κ_L value is gradually decreased (see Fig. 5c). The minimum κ_L value of the x = 0.15 phase-pure sample is merely 0.61 W m⁻¹ K⁻¹, which is close to the amorphous limit estimated by the Cahill's model and lower than that of all known Mg₂X based materials (see Fig. 5d). It is worth noting that the room temperature κ_L of Mg_2−δSi_0.12Ge_0.13Sn_0.55Bi_0.20 is slightly lower than the theoretical value predicted by the Callaway model (see Fig. S13, ESI†), suggesting that the secondary phase in this material can also suppress the thermal transport at low temperatures. Overall, the reduction in thermal conductivity contains the contributions from both high entropy engineering and secondary phases, but the former seems more obvious, attesting to the efficacy of entropy engineering.

Fig. 5 Temperature dependence of (a) total thermal conductivity κ and (b) lattice thermal conductivity κ_L. (c) Room temperature lattice thermal conductivity κ_L as a function of configuration entropy ΔS. The data from other studies are included for comparison^42–44,54 (the dashed line is a guide to the eye). (d) Temperature dependence of lattice thermal conductivity κ_L of x = 0.15 and 0.20 samples, in comparison with the data from other studies.^{7,44,48,50,53}

The interplay between the adaptable Mg sublattice and the distorted anion X sublattice also has a profound effect on the electrical transport properties. Fig. 6 presents the temperature dependent electrical properties of our Mg_2−δSi_0.12Ge_0.13Sn_0.75−xBi_x samples from 300 K to 800 K. The electrical conductivity σ of Bi-free Mg₂Si_0.12Ge_0.13Sn_0.75 remains almost unchanged before 500 K and then gradually increases with temperature due to intrinsic thermal excitation. After doping Bi in Mg₂Si_0.12Ge_0.13Sn_0.75, the σ value is significantly improved while thermal excitation is suppressed. For the samples with a low Bi content (x < 0.05), the temperature dependent σ follows a trend of T^−1.5, implying that electrical transport is dominated by acoustic phonon scattering. For the samples with a high Bi content (x > 0.08), the σ value remains nearly constant in the whole temperature range, indicating that ionized impurity scattering caused by Bi_Sn substitutional defects and Mg vacancies plays an important role in these samples. The Seebeck coefficient S of the Bi-free Mg₂Si_0.12Ge_0.13Sn_0.75 sample exhibits a peak value of −335 μV K⁻¹ at 450 K, pointing to the intrinsic excitation of carriers. The S values of all Bi-doped samples, regardless of the doping content, show the same temperature dependency, unlike the variation in σ.

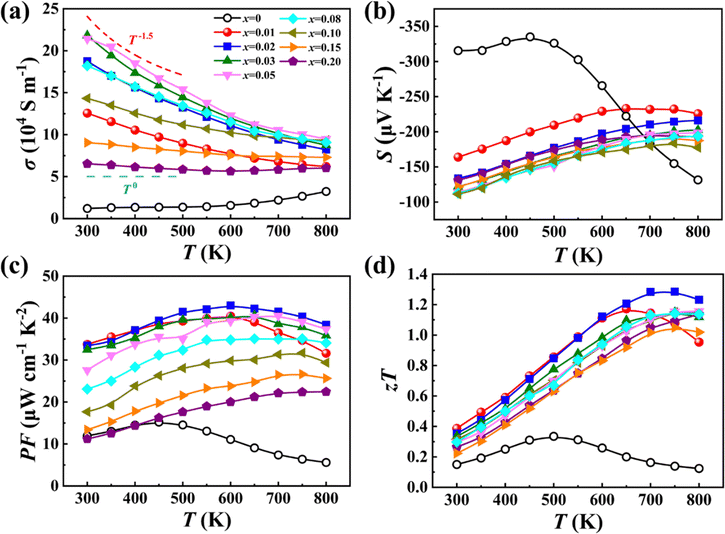Fig. 6 Temperature dependence of (a) electrical conductivity σ, (b) Seebeck coefficient S, (c) power factor PF and (d) zT of samples Mg_2−δSi_0.12Ge_0.13Sn_0.75−xBi_x.

Fig. 6c shows the temperature dependent power factor PF calculated from the measured σ and S. A maximum PF of 43 μW cm⁻¹ K⁻² is achieved at 600 K for the x = 0.02 sample, which is approximately triple that of the Bi-free sample. Thanks to the strongly suppressed κ_L and optimized electrical properties, a maximum zT of 1.3 is finally achieved at 700 K for the x = 0.02 sample, which corresponds to an improvement of 330% over that of the Bi-free sample (zT_max = 0.3). We have also studied the operational stability of our samples (x = 0.02, 0.20) by measuring the thermoelectric performance and elemental distribution after being subjected to extended times at elevated temperatures. As shown in Fig. S14–S17 (ESI†), the thermoelectric properties remain relatively unchanged after three thermoelectric measurement cycles (300–800 K) or after quenching from 800 K. Besides, all the elements are homogeneously distributed after heat treatments, and no obvious phase separation and spinodal decomposition are observed.

To further elucidate the effects of Bi alloying on the electrical transport properties of samples Mg_2−δSi_0.12Ge_0.13Sn_0.75−xBi_x, we carried out Hall measurements and defect calculations to investigate the carrier concentration (n) for all samples. For the Bi-free sample, the Hall concentration is very low, only 4 × 10¹⁸ cm⁻³, which is increased to 2 × 10²⁰ cm⁻³ for x = 0.10 owing to the donor effect of Bi doping. Upon further increasing x to 0.20, the change in the carrier concentration flattens out, which can be related to the segregation of the Mg₃Bi₂ impurity phase. The experimental value of n is lower than the predicted value assuming that all the Bi_Sn defects are fully ionized. This can be attributed to the self-compensation effect of V_Mg, which acts as an acceptor to offset part of the electrons. To examine this self-compensation effect, we performed first-principles calculations of the formation energy of V_Mg in both Mg₆₄Sn₃₁Bi and Mg₆₄Sn₃₂. For simplicity, the role of Si and Ge is not taken into account in calculations. Fig. 7b shows the formation energy of V_Mg as a function of the distance (d) between V_Mg and Bi atom. As the distance d changes from the 4th nearest neighbour (8.90 Å) to the 1st nearest neighbour (2.76 Å), the formation energy of V_Mg decreases from 0.62 eV to 0.38 eV. Moreover, the formation energy of V_Mg is much lower in Mg₆₄Sn₃₁Bi compared to that in Mg₆₄Sn₃₂. These results suggest that Bi is conducive to the formation of Mg vacancy due to its stronger ability to expand the lattice and disrupt the charge balance.^55,56 Based on the experimental carrier concentration n, we calculated the Mg content by assuming that each Bi_Sn introduces one electron and each V_Mg introduces two holes (refer to the calculation details in the ESI†). As shown in Fig. S18 (ESI†), the calculated Mg content is gradually decreased with an increase in the Bi content, which is in accordance with the experimental EDS results.

Fig. 7 (a) Experimental carrier concentration (red symbols) as a function of the Bi content x. The dashed blue line denotes the theoretical carrier concentration, assuming complete ionization of all Bi_Sn defects and the absence of any Mg vacancies. (b) Calculated formation energy of V_Mg at different sites for Mg₆₄Sn₃₁Bi. The formation energy of V_Mg in Mg₆₄Sn₃₂ is plotted for comparison (red dashed line). (c) Illustration of the different V_Mg sites in the Mg₆₄Sn₃₂ supercell. (d) Seebeck coefficient S as a function of the carrier concentration n. The Pisarenko lines (scattering parameter λ = 0, 1.0, 2.0) are plotted based on the single parabolic model (SPB). (e) Carrier mobility μ as a function of the Bi content x. (f) Electrical conductivity σ and Seebeck coefficient S as a function of the Bi content x.

The relationship between the Seebeck coefficient S and the carrier concentration n can be understood using the well-established Pisarenko plot by considering different carrier scattering mechanisms. Fig. 7d exhibits the experimental S and n data, in comparison with the theoretical Pisarenko plots with the same effective mass m* but different scatter factors λ. For the samples with a low Bi content (x < 0.03), the carrier transports are dominated by acoustic phonon scattering, and the experimental data align closely with the Pisarenko plot with an m* value of 1.3 m_e and a λ value of 0. As the Bi content increases, the strength of ionization scattering from V_Mg and Bi_Sn defects gradually increases, leading to an increase in the scattering factor λ. Consequently, the Seebeck coefficient due to ionization scattering is noticeably higher compared to acoustic phonon scattering.

Due to the transition from acoustic phonon scattering to mixed scattering, the carrier mobility μ gradually decreases with the increase of the Bi content x. The degraded μ is also a common consequence of high-entropy engineering. Specifically, the room temperature μ for x = 0 sample is around 155 cm² V⁻¹ s⁻¹, which is lowered to 45 cm² V⁻¹ s⁻¹ for sample x = 0.10. The sightly increase of μ for x = 0.20 sample is ascribed to the appearance of the Mg₃Bi₂ impurity phase. As both σ and S are governed by the carrier concentration and the carrier scattering mechanism, the Bi content dependent σ shows a downward ballistic curve, while S shows an upward ballistic curve (see Fig. 7f).

Conclusions

We successfully synthesized a series of phase pure high-entropy Mg_2−δ(Si, Ge, Sn, and Bi) materials, with the help of an adaptable Mg sublattice. The Mg sublattice, due to its loosely bonded nature, exhibits a large atomic displacement parameter, which endows it with high adaptability to release the large lattice stress. This is further confirmed by our dynamic simulations and formation enthalpy calculations. The severely distorted lattice provides strong scattering for heat-carrying phonons, giving rise to an extremely low κ value of 0.58 W m⁻¹ K⁻¹ at 800 K, which is lower than that of all known Mg₂X-based TE materials. Meanwhile, the self-compensational Mg vacancies counterbalance part of the electrons provided by the substitutional Bi_Sn defects, yielding an optimized carrier concentration and high power factors. As a collective consequence, a peak zT of 1.3 was obtained at 700 K for the x = 0.02 sample. We believe that the stabilization mechanism through the use of adaptable sublattices can also be applied to other material systems, such as Cu/Ag-based liquid-like materials, argyrodites, and the Mg₃Sb₂-like Zintl phase.

Experimental section

Sample preparation

A series of Mg_2−δSi_0.12Ge_0.13Sn_0.75−xBi_x (x = 0, 0.01, 0.02, 0.03, 0.05, 0.08, 0.10, 0.15, and 0.20) samples were successfully synthesized through the high-energy ball milling technique. High purity magnesium (99.5%, Aladdin), silicon (99.99%, Aladdin), germanium (99.99%, Aladdin), tin (99.99%, Aladdin), and bismuth (99.99%, Aladdin) powders were weighed out according to the stoichiometry of Mg_2−δSi_0.12Ge_0.13Sn_0.75−xBi_x. It is noted that 8 mol% excess magnesium powder was added to compensate for the loss of magnesium during the synthesis. The raw powders were loaded into stainless-steel ball milling jars in a glove box. Subsequently, the powders were mixed up for 30 min using an MSK-SFM-3-1 high energy ball milling machine with a rotational speed of 400 rpm, followed by ball-milling for 20–40 h in a MSK-SFM-3-1 high energy ball milling machine with a rotational speed of 1200 rpm. The obtained powders were then loaded into a graphite die with an inner diameter of 10 mm and pressed into bulk samples by spark plasma sintering (SPS) at 900 K for 15 min under a pressure of 80 MPa. The relative densities of the final pellet samples were larger than 98%.

Characterization

Room temperature X-ray diffraction (XRD) was conducted on an X-ray diffractometer (Malvern Panalytical) with Cu K_α radiation (λ = 1.5406 Å) which was operated at 40 kV and 40 mA. Rietveld refinements were carried out using the program jana2006. Pair distribution function (PDF) measurements were performed at the BL13HB beamline of the Shanghai Synchrotron Radiation Facility (SSRF). Finely grounded powder of Mg_2−δSi_0.12Ge_0.13Sn_0.65Bi_0.10 was sealed in 0.5 mm (outer diameter) quartz capillary. PDF measurements involved the use of a monochromatic X-ray beam with an energy of 40.00 keV (λ = 0.3066 Å). The chemical composition was analyzed using a field emission scanning electron microscope (FESEM, Tescan RISE-MAGNA, Czech Republic) equipped with an energy dispersive X-ray spectrometer (EDS, Oxford, UK). The electrical conductivity (σ) and the Seebeck coefficient (S) were measured using a ZEM-3 (ULVAC Co. Ltd) under a helium atmosphere. Thermal diffusivity (D) was measured under an argon atmosphere using the laser flash method (LFA 457, Netzsch Co Ltd). The density ρ was measured based on Archimedes’ principle and the heat capacity Cp was estimated using the Dulong–Petit law. The total thermal conductivity (κ) was calculated through the formula κ = ρC_pD. The carrier concentration (n) and mobility (μ) were calculated through the formulas n = 1/eR_H and μ = σR_H, respectively. The Hall coefficient was measured using the van der Pauw method (M91, Lake Shore Cryotronics Inc, USA) with a magnetic field of 790 mT at 300 K.

Pair distribution function data processing and analysis

The software Dioptas⁵⁷ was employed to integrate the raw data and convert it to intensity versus 2θ. Subsequently, the integrated data were passed to the program PDFgetX3, where standard corrections and background subtraction were performed to derive the PDF data. The Lorch function was used to eliminate the influence of Fourier effects. The refinement of the material structure was carried out using the PDFgui⁵⁸ program. Through iterative adjustments of various parameters, including lattice parameters, atomic positions, and displacement parameters, and by continuously comparing the theoretical PDF with the experimental PDF, satisfactory R_wp values can be achieved.

First-principles calculations

All first-principles calculations, based on density functional theory (DFT), were carried out with the Vienna ab initio Simulation Package (VASP) code by utilizing the projector augmented wave (PAW) method.^59,60 The Perdew–Burke–Ernzerhof (PBE) functional within Generalized Gradient Approximation (GGA) was employed for the electronic exchange and correlation potential.⁶¹ The plane wave energy cutoff was set to 400 eV for all DFT calculations. The primitive cell of cubic Mg₂Sn obtained from experimental data was fully relaxed until the total energy and force convergence criteria reached 10⁻⁶ eV and 0.01 eV Å⁻¹, respectively. A series of 2 × 2 × 2 supercells of Mg₆₄Si₄Ge₄Sn_24−nBi_n (n = 0, 1, 2, 4, 6) containing 96 atoms were randomly constructed by utilizing the VASPKIT code⁶² for the mixing enthalpy calculations. Two types of alloy systems were considered for mixing enthalpy calculations: one with fully relaxed supercells, and the other with only volume-optimized supercells. Additionally, to validate the reliability of the 2 × 2 × 2 supercell for bonding analysis and disorder properties, we examined three types of 2 × 2 × 2 supercells (termed S1, S2 and S3) and one 3 × 3 × 2 supercell (termed S4) for the Mg₆₄Si₄Ge₄Sn₂₀Bi₄ alloy. Considering the difficulty in relaxing the volume-optimized systems, only the total energy convergence criterion was selected for supercell relaxations. Bonding analyses, including the deformation charge density and the projected crystal orbital Hamilton population (pCOHP), were applied to the Mg₆₄Si₄Ge₄Sn₂₄Bi₄ alloy. The deformation charge density was obtained by subtracting the atomic charge density from the total charge density, and the pCOHP was calculated via the LOBSTER⁶³ code based on a ground state self-consistent DFT calculation. The Brillouin zone was sampled using a 5 × 5 × 5 k-mesh for structural relaxation of the primitive cell and a 2 × 2 × 2 Γ-centered k-mesh for supercells. Machine learning-accelerated ab initio molecular dynamics (AIMD) simulations were performed using the canonical (NVT) ensemble with the Nose–Hoover thermostat within a time step of 1.25 fs for a duration of 25 ps. The structures from the final 20 ps were analyzed to observe the dynamical effects on the Mg₆₄Si₄Ge₄Sn₂₀Bi₄ alloy through mean square displacement (MSD) analysis. Only one Γ point in the Brillouin zone was used for AIMD simulations. A range of temperatures from room temperature to 800 K with intervals of 100 K were used for AIMD simulations. To investigate the impact of Bi doping on the electrical properties of the Mg₂Sn host system, the formation energies of Mg vacancies with zero charge were calculated for both pristine Mg₆₄Sn₃₂ and the Mg₆₄Sn₃₁Bi alloy. All potential Mg vacancy sites at varying distances from the Bi atom were taken into account in the Mg₆₄Sn₃₁Bi alloy.

Author contributions

K. Z. and X. S. designed the study. H. G. prepared the samples and carried out the experiments. H. W. carried out the DFT and MD calculations. S. W. performed the XRD measurements. Z. Z. analyzed the crystal structures by Rietveld refinements. J. L. and H. G. analyzed the experimental data. H. L., L. F. and H. Z. analyzed the PDF data. H. C. performed the scanning electron microscopy experiments. H. G., H. W., K. Z., T. W. and X. S. analyzed the data and wrote and edited the manuscript. All authors discussed the results, read the paper and commented on the text.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Key Research and Development Program of China (2023YFB3809800), the National Natural Science Foundation of China (52372209, and 91963208), and the Shanghai Pilot Program for Basic Research-Chinese Academy of Sciences, Shanghai Branch (JCYJ-SHFY-2022-002). H. L. thanks the National Natural Science Foundation of China (grant number U1732120) for financial support. We acknowledge the PDF measurements support from the BL13HB beamline of Shanghai Synchrotron Radiation Facility (SSRF) and the computational support from the Center for High Performance Computing at Shanghai Jiao Tong University.

References

1. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114.
2. X. Shi, L. Chen and C. Uher, Int. Mater. Rev., 2016, 61, 379–415.
3. G. Tan, L.-D. Zhao and M. G. Kanatzidis, Chem. Rev., 2016, 116, 12123–12149.
4. X.-L. Shi, J. Zou and Z.-G. Chen, Chem. Rev., 2020, 120, 7399–7515.
5. J. Mao, Z. Liu, J. Zhou, H. Zhu, Q. Zhang, G. Chen and Z. Ren, Adv. Phys., 2018, 67, 69–147.
6. Y. Pei, X. Shi, A. LaLonde, H. Wang, L. Chen and G. J. Snyder, Nature, 2011, 473, 66–69.
7. W. Liu, X. Tan, K. Yin, H. Liu, X. Tang, J. Shi, Q. Zhang and C. Uher, Phys. Rev. Lett., 2012, 108, 166601.
8. G. Tan, F. Shi, S. Hao, H. Chi, L.-D. Zhao, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, J. Am. Chem. Soc., 2015, 137, 5100–5112.
9. H. Liu, X. Yuan, P. Lu, X. Shi, F. Xu, Y. He, Y. Tang, S. Bai, W. Zhang, L. Chen, Y. Lin, L. Shi, H. Lin, X. Gao, X. Zhang, H. Chi and C. Uher, Adv. Mater., 2013, 25, 6607–6612.
10. Z. Yue, K. Zhao, H. Chen, P. Qiu, L. Chen and X. Shi, Chin. Phys. Lett., 2021, 38, 117201.
11. K. Zhao, C. Zhu, W. Qiu, S. Yang, H. Su, P. Qiu, Y. He, M. Guan, T.-R. Wei, J. Ma, J. Liu, G. Zheng, F. Xu, X. Shi, J. He and L. Chen, Matter, 2022, 5, 605–615.
12. H. Liu, X. Shi, F. Xu, L. Zhang, W. Zhang, L. Chen, Q. Li, C. Uher, T. Day and G. J. Snyder, Nat. Mater., 2012, 11, 422–425.
13. W. D. Liu, L. Yang, Z. G. Chen and J. Zou, Adv. Mater., 2020, 32, 1905703.
14. K. Zhao, P. Qiu, X. Shi and L. Chen, Adv. Funct. Mater., 2020, 30, 1903867.
15. M. Li, H. Wuliji, Z. Zhou, P. Qiu, K. Zhao and X. Shi, J. Mater. Chem. A, 2023, 11, 10901–10911.
16. K. Biswas, J. He, I. D. Blum, C.-I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, Nature, 2012, 489, 414–418.
17. Y. Pei, G. Tan, D. Feng, L. Zheng, Q. Tan, X. Xie, S. Gong, Y. Chen, J.-F. Li, J. He, M. G. Kanatzidis and L.-D. Zhao, Adv. Energy Mater., 2017, 7, 1601450.
18. K. Zhao, C. Zhu, M. Zhu, H. Chen, J. Lei, Q. Ren, T.-R. Wei, P. Qiu, F. Xu, L. Chen, J. He and X. Shi, Adv. Mater., 2022, 34, 2108573.
19. R. Liu, H. Chen, K. Zhao, Y. Qin, B. Jiang, T. Zhang, G. Sha, X. Shi, C. Uher, W. Zhang and L. Chen, Adv. Mater., 2017, 29, 1702712.
20. E. Fermi, Thermodynamics, Courier Corporation, 2012.
21. B. Jiang, Y. Yu, J. Cui, X. Liu, L. Xie, J. Liao, Q. Zhang, Y. Huang, S. Ning, B. Jia, B. Zhu, S. Bai, L. Chen, S. J. Pennycook and J. He, Science, 2021, 371, 830–834.
22. Z. Zhang, K. Zhao, H. Chen, Q. Ren, Z. Yue, T.-R. Wei, P. Qiu, L. Chen and X. Shi, Acta Mater., 2022, 224, 117512.
23. Z. Zhang, H. Yao, Q. Wang, W. Xue, Y. Wang, L. Yin, X. Wang, X. Li, C. Chen, J. Sui, X. Lin, Y. Chen, X. Liu, J. Mao, G. Xie and Q. Zhang, Adv. Funct. Mater., 2022, 32, 2205215.
24. J. Xin, H. Wu, X. Liu, T. Zhu, G. Yu and X. Zhao, Nano Energy, 2017, 34, 428–436.
25. G. S. Nolas, D. Wang and X. Lin, Ren. Physiol. Biochem., 2007, 1, 223–225.
26. G. S. Nolas, D. Wang and M. Beekman, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 235204.
27. K. Zhao, K. Liu, Z. Yue, Y. Wang, Q. Song, J. Li, M. Guan, Q. Xu, P. Qiu, H. Zhu, L. Chen and X. Shi, Adv. Mater., 2019, 31, 1903480.
28. Z. Zhang, K. Zhao, T.-R. Wei, P. Qiu, L. Chen and X. Shi, Energy Environ. Sci., 2020, 13, 3307–3329.
29. M. Guan, K. Zhao, P. Qiu, D. Ren, X. Shi and L. Chen, ACS Appl. Mater. Interfaces, 2019, 11, 13433–13440.
30. T.-R. Wei, G. Tan, X. Zhang, C.-F. Wu, J.-F. Li, V. P. Dravid, G. J. Snyder and M. G. Kanatzidis, J. Am. Chem. Soc., 2016, 138, 8875–8882.
31. Z. Chen, Z. Jian, W. Li, Y. Chang, B. Ge, R. Hanus, J. Yang, Y. Chen, M. Huang, G. J. Snyder and Y. Pei, Adv. Mater., 2017, 29, 1606768.
32. T.-R. Wei, C.-F. Wu, X. Zhang, Q. Tan, L. Sun, Y. Pan and J.-F. Li, Phys. Chem. Chem. Phys., 2015, 17, 30102–30109.
33. Z. Ma, T. Xu, W. Li, Y. Cheng, J. Li, D. Zhang, Q. Jiang, Y. Luo and J. Yang, Adv. Funct. Mater., 2021, 31, 2103197.
34. B. Jiang, W. Wang, S. Liu, Y. Wang, C. Wang, Y. Chen, L. Xie, M. Huang and J. He, Science, 2022, 377, 208–213.
35. M. C. Troparevsky, J. R. Morris, M. Daene, Y. Wang, A. R. Lupini and G. M. Stocks, JOM, 2015, 67, 2350–2363.
36. Y. M. Zhang, S. Yang and J. R. G. Evans, Acta Mater., 2008, 56, 1094–1105.
37. H.-W. Luan, Y. Shao, J.-F. Li, W.-L. Mao, Z.-D. Han, C. Shao and K.-F. Yao, Scripta Mater., 2020, 179, 40–44.
38. H. Luan, L. Huang, J. Kang, B. Luo, X. Yang, J. Li, Z. Han, J. Si, Y. Shao, J. Lu and K.-F. Yao, Acta Mater., 2023, 248, 118775.
39. E. J. Pickering, R. Muñoz-Moreno, H. J. Stone and N. G. Jones, Scripta Mater., 2016, 113, 106–109.
40. Y.-J. Liang, L. Wang, Y. Wen, B. Cheng, Q. Wu, T. Cao, Q. Xiao, Y. Xue, G. Sha, Y. Wang, Y. Ren, X. Li, L. Wang, F. Wang and H. Cai, Nat. Commun., 2018, 9, 4063.
41. K. Zhao, E. Eikeland, D. He, W. Qiu, Z. Jin, Q. Song, T.-R. Wei, P. Qiu, J. Liu, J. He, B. B. Iversen, J. He, L. Chen and X. Shi, Joule, 2021, 5, 1183–1195.
42. M. B. A. Bashir, S. Mohd Said, M. F. M. Sabri, D. A. Shnawah and M. H. Elsheikh, Renewable Sustainable Energy Rev., 2014, 37, 569–584.
43. R. Santos, S. Aminorroaya Yamini and S. X. Dou, J. Mater. Chem. A, 2018, 6, 3328–3341.
44. W. Liu, H. S. Kim, S. Chen, Q. Jie, B. Lv, M. Yao, Z. Ren, C. P. Opeil, S. Wilson, C.-W. Chu and Z. Ren, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 3269–3274.
45. X. Cheng, N. Farahi and H. Kleinke, JOM, 2016, 68, 2680–2687.
46. J. de Boor, U. Saparamadu, J. Mao, K. Dahal, E. Müller and Z. Ren, Acta Mater., 2016, 120, 273–280.
47. N. Takagi, Y. Sato, T. Matsuyama, H. Tatsuoka, M. Tanaka, C. Fengmin and H. Kuwabara, Appl. Surf. Sci., 2005, 244, 330–333.
48. J. Mao, H. S. Kim, J. Shuai, Z. Liu, R. He, U. Saparamadu, F. Tian, W. Liu and Z. Ren, Acta Mater., 2016, 103, 633–642.
49. M. Ioannou, G. S. Polymeris, E. Hatzikraniotis, K. M. Paraskevopoulos and T. Kyratsi, J. Phys. Chem. Solids, 2014, 75, 984–991.
50. Y. Zhu, E. Dong, Z. Han, F. Jiang, J. Sui, W. Zhang and W. Liu, Acta Mater., 2021, 217, 117172.
51. R. Santos, M. Nancarrow, S. X. Dou and S. Aminorroaya Yamini, Sci. Rep., 2017, 7, 3988.
52. Y. Qiu, L. Xi, X. Shi, P. Qiu, W. Zhang, L. Chen, J. R. Salvador, J. Y. Cho, J. Yang, Y.-C. Chien, S.-W. Chen, Y. Tang and G. J. Snyder, Adv. Funct. Mater., 2013, 23, 3194–3203.
53. J. Xin, Y. Zhang, H. Wu, T. Zhu, T. Fu, J. Shen, S. J. Pennycook and X. Zhao, Small Methods, 2019, 3, 1900412.
54. L. Chen, G. Jiang, Y. Chen, Z. Du, X. Zhao, T. Zhu, J. He and T. M. Tritt, J. Mater. Res., 2011, 26, 3038–3043.
55. J. Lei, H. Wuliji, K. Zhao, T.-R. Wei, Q. Xu, P. Li, P. Qiu and X. Shi, J. Mater. Chem. A, 2021, 9, 25944–25953.
56. H. Wuliji, K. Zhao, X. Cai, H. Jing, Y. Wang, H. Huang, T.-R. Wei, H. Zhu and X. Shi, Mater. Today Phys., 2023, 35, 101129.
57. C. Prescher and V. B. Prakapenka, High Press. Res., 2015, 35, 223–230.
58. C. Farrow, P. Juhás, J. Liu, D. Bryndin, E. Bozin, J. Bloch, T. Proffen and S. Billinge, J. Phys.: Condens. Matter, 2007, 19, 335219.
59. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
60. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
61. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
62. V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033.
63. R. Nelson, C. Ertural, J. George, V. L. Deringer, G. Hautier and R. Dronskowski, J. Comput. Chem., 2020, 41, 1931–1940.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ee02788k

---