Open Access Article
Open Access ArticleCollecting the space-distributed Maxwell's displacement current for ultrahigh electrical density of TENG through a 3D fractal structure design†
Li Ang
Zhang‡
ab,
Shuhai
Liu‡
b,
Juan
Wen
 b,
Xiaoqing
Huo
a,
Bolang
Cheng
b,
Zhiyi
Wu
a,
Longfei
Wang
*a,
Yong
Qin
b,
Xiaoqing
Huo
a,
Bolang
Cheng
b,
Zhiyi
Wu
a,
Longfei
Wang
*a,
Yong
Qin
 *b and
Zhong Lin
Wang
*b and
Zhong Lin
Wang
 *acd
*acd
aCAS Center for Excellence in Nanoscience Beijing Key Laboratory of Micro-Nano Energy and Sensor, Beijing Institute of Nanoenergy and Nanosystems, Chinese Academy of Sciences, Beijing 101400, China. E-mail: lfwang12@binn.cas.cn; zhong.wang@mse.gatech.edu
bInstitute of Nanoscience and Nanotechnology, School of Materials and Energy, Lanzhou University, Gansu 730000, China. E-mail: qinyong@lzu.edu.cn
cGeorgia Institute of Technology, Atlanta, Georgia 30332, USA
dYonsei Frontier Lab, Yonsei University, Seoul 03722, Republic of Korea
First published on 11th July 2023
Abstract
Triboelectric nanogenerator is an emerging technology that can convert low-frequency and irregular mechanical energy into electricity and has broad applications in the fields of distributed energy harvesting, self-powered sensing, and the Internet of Things. However, it is still a challenge to achieve high electrical energy density owing to the limited surface tribocharge density. Herein, we report a three-dimensional fractal structured nanogenerator (FSNG), which can efficiently collect the triboelectrification induced space-distributed Maxwell's displacement current, and hence largely improve the electrical energy density. The output charge density, power density, and energy density of FSNG break the record and reach up to 8 mC m−2, 2.18 MW m−2, and 0.39 J m−2 cycle−1, respectively, and can be further improved by optimizing the fractal unit. In addition, the equivalent fractal circuit models for FSNG with the same functionality are developed for a deep understanding of the FSNG. This study not only creates a new record of high electrical output of nanogenerators but also paves a more efficient way for mechanical energy scavenging toward practical applications.
Broader contextTriboelectric nanogenerator (TENG) is an emerging technology that can convert low-frequency and irregular mechanical energy into electricity and has broad applications in the fields of distributed energy harvesting, self-powered sensing, Internet of Things, etc. However, the electrical energy density of TENG is severely limited by the key problem of the limited surface tribocharge density owing to the high-voltage breakdown. In this work, we develop a three-dimensional fractal structured nanogenerator (FSNG), which can efficiently collect the space-distributed Maxwell's displacement current and significantly improve the electrical energy density of TENG. The output charge density, power density, and energy density of FSNG break the record and reach up to 8 mC m−2, 2.18 MW m−2, and 0.39 J m−2 cycle−1, respectively, and can be further improved by optimizing the fractal unit. Compared with classical TENG with high open-circuit voltage (∼kV) and low current (from nA to μA), the FSNG exhibits a substantially different characteristic with high current (from mA to A) and low open-circuit voltage (100–200 V), which is much more suitable for powering broad practical electrical appliances. This work paves the way for efficient mechanical energy harvesting toward practical applications. |
Introduction
With the development of human society, large numbers of distributed, mobile, and wireless electronics have become a part of our life.1–3 It is critical to develop suitable green power sources to supply a huge number of electronics in the field of Internet of Things (IoT).4–6 Mechanical energy such as biological motion and vibration in the environment are abundant and ubiquitous and one of the most important sources of green energy. Nevertheless, most of the mechanical energy is low-frequency and irregular in amplitude, which cannot be easily utilized by the current electromagnetic generator or turbine technology.7,8 As a new and feasible technology by coupling the triboelectric effect and the electrostatic effect, triboelectric nanogenerator (TENG) with the capacity of converting distributed and irregular mechanical energy from the environment and human body into applicable electrical power draws great attention,9 which exhibit the merits of high efficiency, light weight, wide material choice, etc.10 Important progresses of TENG have been made in high-entropy energy harvesting, self-powered sensing, and implantable medical devices, which make it a competitive power source for distributed and mobile electronics.11,12 However, TENG has an output characteristic of high open-circuit voltage but low current. The high voltage could cause air or dielectric breakdown, while the output current highly depends on the limited surface charge density, which severely hinders their practical applications.To increase the output charge density, a series of novel technologies has been proposed, such as triboelectric material options,13 vacuum control,14,15 surface physical and chemical modification,16–19 tribolayer modification,20–22 ion injection,23 charge pumping,24,25 self-polarization,26 multiple electrodes,27,28 and air-breakdown effect.29 Based on the above methods, the output charge density has been substantially boosted to 5.4 mC m−2. It seems that these efforts are mainly focused on improving the triboelectric effect, in other words, increasing the generation of surface triboelectric charges when two materials come into contact but not effectively utilized. Nevertheless, further improvement in the electrical energy density of TENG is still severely limited by the key problem of high-voltage breakdown. To make a breakthrough, we reexamine the fundamental of TENG. In essence, the nanogenerator uses the Maxwell's displacement current as the driving force for effectively converting mechanical energy into electric power. According to the expanded Maxwell's equations for moving the charged media system,30–32 the displacement current is JD = ε∂E/∂t + (∂Ps)/∂t, where the term ε∂E/∂t represents the displacement current due to the time variation of electric field caused by free charge. On the other hand, the triboelectric materials or other media that do periodic relative movement could create the electrostatic surface charges, which induces an additional Wang term of ∂Ps/∂t, resulting in a space-distributed Maxwell's displacement current. However, for classical TENGs with a pair of electrode plate, they can only collect the planar Maxwell's displacement current (Fig. 1(b) and (c)). Thus, electrostatic surface charges cannot be fully utilized, resulting in relatively low electrical density with high voltage and low current.
In this work, we developed a three-dimensional (3D) fractal structured nanogenerator (FSNG), which can collect the space-distributed Maxwell's displacement current more efficiently and achieve a record-breaking output performance with the highest charge density (8 mC m−2), power density (2.18 MW m−2), and energy density (0.39 J m−2 cycle−1) without any power management. Compared with classical TENG, the FSNG exhibits a characteristic of independent output with high charge density and low open-circuit voltage. The performance of FSNG can be further improved by increasing the numbers of fractal units, as predicted by the discharging formulas. Moreover, the equivalent circuit models based on the same fractal theory are developed for understanding the insight of the FSNG. Our results provide a promising strategy for achieving high performance TENGs toward practical applications.
Results and discussion
Prototype and working principle of the FSNG
To demonstrate our idea, we proposed the FSNG by coupling the fractal theory,33 triboelectrification effect, and 3D electrostatic induction effect. With increasing fractal dimension, the structure becomes more complex and finer, as shown in Fig. S1a (ESI†). As we all know, when a metal plate is placed in a uniform electric field, the internal field density is zero, and the upper and lower surface have opposite charge. Meanwhile, the induced charge density would be equal to the electrostatic charge, as shown in Fig. S1b (ESI†). Actually, two laminated metal plates, which are close (enough to ignore the edge effect) and electrically connected, could be regard as a Faraday cage by ignoring the edge effect. If we flip and shift the lower half structure, a classical freestanding triboelectric-layer mode TENG is obtained. Actually, more similar Faraday cages could be deployed in the electric field for more finely collecting the Maxwell's displacement current, which likes fractal structure. After induction, each metal plate has a negative or positive charge whose density nearly equals the electrostatic charge density. Gathering all the induced charge in metal plates, the output charge density could be increased manifold. In other words, the fractal structure divides the high potential difference that easily causes breakdown into several lower parts, which means higher energy conversion efficiency.Inspired by the above theory, the FSNG is constructed. Fig. 1(a) illustrates the structure of the FSNG, which consists of triboelectric part and 3D fractal electrostatic induction part. The polyurethane (PU) foam and polytetrafluoroethylene (PTFE) film form the triboelectric part, which can easily transfer and keep triboelectric charges during the electrification process. Below them, a stack of polyethylene terephthalate (PET) layers (10 μm) sandwiched by two electrode (Ag) films forms a series of plane capacitors consisting of a PET dielectric and a pair of electrodes, acting as units of the fractal structure. The bottom electrode of one unit is connected to the top electrode of the unit below the diode. Overall, the upper and lower electrodes of each unit are gathered through motion switch, respectively. The distributions of electric field and potential of classical TENG and FSNG have been calculated by the finite element simulation (Fig. 1(b) and (d), Fig. S2 and Note S1, ESI†). The periodic relative motion of triboelectric charges could cause the variation of dipole moment, which stimulates the space-distributed Maxwell's displacement current.34 For classical TENG with two electrode structure, it can only collect the planar Maxwell's displacement current roughly. As shown in Fig. 1(b), there is still a strong electric field distributed in the outer space of the TENG, whereas it is not utilized and converted at all. In such a case, the electrostatically induced charge density on the electrode is recorded as σind. The potential difference between both of the electrodes is recorded as Utribo (Fig. 1(c)). For the FSNG, a 3D fractal structure is constructed, and a uniform electric field is created in each fractal unit (Fig. 1(d)). The distribution of electric field is mainly concentrated on the space between each fractal unit, which can be fully utilized and converted. In this case, each electrode could induce a charge density of nearly σind, and the electrical potential between the upper and lower electrode of each unit is kept as Uind, which is dependent on the potential of two electrodes (Utribo) and the number (n) of fractal units (Fig. 1(e)). Gathering the charges of n units, the output charge density of FSNG could be up to ∼nσind, which is about n folds higher than that of classical TENG. Hence, the electrical energy density can be largely improved while the high-voltage breakdown can be suppressed. In contrast to classical TENG, the FSNG could show a characteristic of low-voltage and high current. It should be noted that the above is the simulation result under the ideal situation, in which the induced charge density of each electrode may decrease with the increase in the number of fractal unit in practice. These results indicate that the 3D fractal design of the FSNG can more effectively collect the space-distributed Maxwell's displacement current and converting it to capacitive conduction current.
We realize an independent output instead of separate outputs by applying diodes between each fractal units and mechanical switches, even though the FSNG include several fractal units. The motion switches as a whole divide the working process into two parts: induction process and output process. To make sure that all fractal units are connected in series in the induction process while connected in parallel in the output process, the diodes are arranged clockwise. Fig. 1(f) illustrates the detailed process of charge transfer of FSNG. The PU foam and PTFE film will be charged because of triboelectrification effect when the two materials slide back and forth. In the original state (Fig. 1(f-I)), all motion switches and diodes except for the one between the top two electrodes are turned off. There is no charge induced in electrodes except for the two electrodes in the top layer because of isolation, although there is potential difference between them. Then, during the PU foam sliding to right (Fig. 1(f-II), induction process), all diodes except for the one between two electrodes in top layer are forward connected (refer to the direction of the electrostatic field induced by triboelectric charges in the triboelectric part) to achieve the electrostatic separation of charges between two electrodes of all units. When the PU foam slides to the right-hand side (Fig. 1(f-III)), the charges of each electrode reach the maximum Q. At the same time, all the switches are turned on (Fig. 1(f-IV), output process) so that all positively charged electrodes are connected in parallel with the total charge of +nQ, and all negatively charged electrodes are also connected in parallel with the total charge of −nQ. As a result, an independent output with high electric energy density is achieved without any additional power management. After the above output process, there is no charge or potential difference in all electrodes except the two electrodes in the top layer for the electrostatic equilibrium. When the PU foam moves in the reverse direction, the motion switches and diodes except for the one between the top layer electrodes are turned off because of the inversion of the electric field. Thus, there is no charge flowing between all the electrodes except the top layer electrodes when the PU foam moves in the reverse direction. Meanwhile, the diode between the top layer electrodes is on and the charge in the top right electrode flows to the top left electrode with the PU foam moving backward until it returns to the original state (Fig. 1(f-I)). With such unique 3D fractal design, the FSNG can harvest mechanical energy more efficiently.
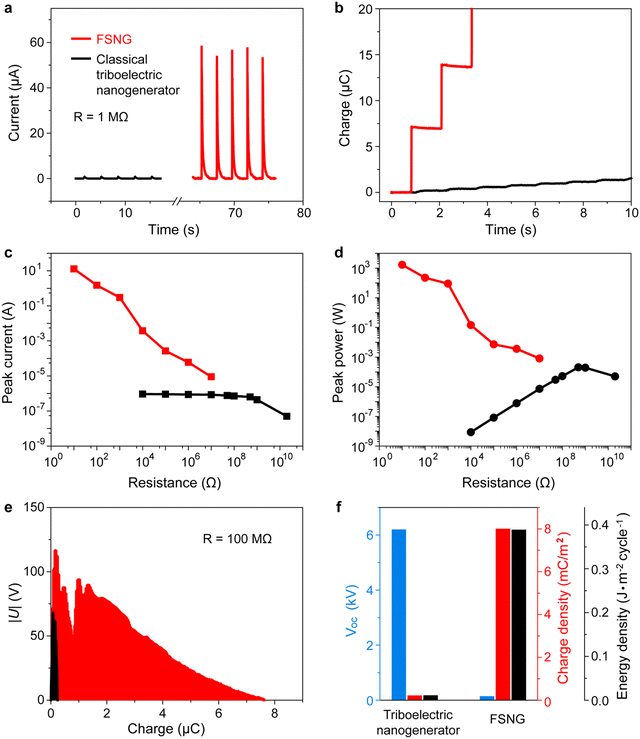
The output characteristic of the FSNG
Compared with classical TENG, the FSNG exhibits a substantially different characteristic of high output current and low open-circuit voltage, which is more suitable for powering broad practical electrical appliances. Fig. 2, Fig. S3 and S7 (ESI†) show the detailed comparison of the FSNG with 40 fractal units and a classical TENG with the same triboelectric part, and all measurements are tested in the same conditions (temperature of 20 °C, relative humidity of 35%, and the same driving curve of the linear motor). The output charge of FSNG can reach up to 7.2 μC, corresponding to 8 mC m−2 (Fig. S7d and Movie S1, ESI†), which is nearly 40 times as much as that of the classical TENG (Fig. S3d, ESI†). Meanwhile, the open-circuit voltage of FSNG is about ∼140 V (Fig. S7b, ESI†), which is appropriate for the needs of daily electronics, while the voltage of the TENG with the same triboelectric materials is up to 6 kV (Fig. S3b, ESI†), which is too high and can easily cause the breakdown of mobile electronics.The output current, power, and energy density of FSNG are highly related to the output charges. Fig. 2a shows that the typical output current of FSNG (load resistance R of 1 MΩ) reaches 60 μA, whose curve fits the exponential function of capacitor discharge. As a contrast, the same diode is connected between the two electrodes of classical TENG so that the classical TENG achieves only positive current. Fig. 2(b) shows the high output charges compared with the classical TENG. In addition, the output current of FSNG increases with decreased resistance load and can reach an ultrahigh current of 14 A when the resistance load is 10 Ω, which is about 107 times higher than that of the classical TENG (Fig. 2(c)). As a result, high instantaneous power (Note S2, ESI†) of FSNG can be achieved with a maximum value of 1.96 kW (corresponding to 2.18 MW m−2) with a 10 Ω resistance load, which is more than 1010 times larger than that of the classical TENG (Fig. 2(d)). The output energy density, another important performance index of a nanogenerator, was characterized. Fig. 2(e) shows the curve of U–Q (voltage versus charge) at a load resistance of 100 MΩ during one cycle operation of the FSNG and the classical TENG. Based on the formula35 of  , the output energy density of FSNG is obtained and can be high as 0.39 J m−2 cycle−1, which is about 40 times higher than that of the classical TENG. In addition, to get rid of the effect of the motion switch structure, a classical TENG with the same motion switch structure has been fabricated, whose output performance presents the same characteristics as that of classical TENG (output voltage, charge, and energy) except for the peak value of current, as shown in Fig. S4 (ESI†). Also, compared with the FSNG, the control group shows much higher output voltage and lower output current, charge, power, and energy density. The control group further demonstrates that the excellent output performance of FSNG is not only attributed to the motion switch structure but also to the unique 3D fractal design for efficiently collecting space-distributed Maxwell's displacement current. The output characteristics are summarized in Fig. 2(f), which indicate that the FSNG can more effectively utilize the surface triboelectric charges to induce more movable charges, with great potential to solve the problem of high-voltage breakdown and low current of TENG and achieve high electrical energy density.
, the output energy density of FSNG is obtained and can be high as 0.39 J m−2 cycle−1, which is about 40 times higher than that of the classical TENG. In addition, to get rid of the effect of the motion switch structure, a classical TENG with the same motion switch structure has been fabricated, whose output performance presents the same characteristics as that of classical TENG (output voltage, charge, and energy) except for the peak value of current, as shown in Fig. S4 (ESI†). Also, compared with the FSNG, the control group shows much higher output voltage and lower output current, charge, power, and energy density. The control group further demonstrates that the excellent output performance of FSNG is not only attributed to the motion switch structure but also to the unique 3D fractal design for efficiently collecting space-distributed Maxwell's displacement current. The output characteristics are summarized in Fig. 2(f), which indicate that the FSNG can more effectively utilize the surface triboelectric charges to induce more movable charges, with great potential to solve the problem of high-voltage breakdown and low current of TENG and achieve high electrical energy density.
Critical factor for the output performance of the FSNG
Each unit can be regarded as a capacitor made of PET dielectric layer sandwiched by an upper electrode and a lower electrode. The number of fractal units, area of electrode plate, and gap between two electrode plates are critical factors for the output performance of FSNG. Actually, the effect of the electrode plate area and the gap of two electrode plates is correlated, whose ratio is directly proportion to the capacitance of the fractal unit. In the process of researching the effect of the number of fractal units, for reducing the edge effect, the ratio of the area of electrode plate to the gap of two electrode plate, which is in direct proportion to the capacitance, should be large enough. The threshold value will be discussed later. Its output characteristic could be described by the discharging process of the capacitor. The theoretical and experimental performance of FSNGs with various fractal units are investigated systematically. In the ‘OFF’ state of motion switches (Fig. 1(e)), the charge in the tribolayers is ±σtribo, which could cause a potential different of Utribo between the upper and lower electrodes. If the number of units is n, the capacitance of each unit can be written as C, and the potential difference should be Uind = σind/C. It should be noted that the boundary condition eqn (1) must be satisfied, which means that the induced charge (σind) in each electrode could be equal to the charge (σtribo) generated by triboelectrification if n is less than Utribo/Uind. In our device, the Utribo and σtribo are approximately equal to 6 kV and 0.2 μC by measuring the output voltage and charge between the two electrodes of the top layer below the tribolayer, and the capacitance of each unit approximately equals to 3 nF. On putting these experimental parameters into theoretical simulations, we could calculate that the charge σind in each electrode equals to the charge σtribo generated by triboelectrification (0.2 μC) when the number of units (n) is less than 100. Nevertheless, if the n is larger than 100 (Eqn 2), the Uind would decrease on further increasing the n, and the induced charge σind will decrease, which is a negative for the output performance of the FSNG. | (1) |
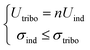 | (2) |
In the ‘ON’ state of motion switches, n fractal units get together in parallel to drive charge for the load resistance. The open-circuit voltage Voc, output charge Qoutput, load current Ioutput, and output energy per cycle Eoutput could be calculated by eqn 3–6. The simulated relationship between the output performance of FSNG and the number of fractal units is shown by dotted lines in Fig. 3(a)–(d). When n is less than 100, the Voc remains constant (dotted line, Fig. 3(a)), while the Qoutput linearly increases with increasing number of fractal units (dotted line, Fig. 3(b)). It can be also found that the output peak current remains constant, but the discharging time of the current increases with increasing n (dotted line, Fig. 3(c)). More importantly, the output energy per cycle Eoutput substantially increases with increasing n (dotted line, Fig. 3(d)), which indicates that the FSNG could convert mechanical energy and drive electronics more efficiently. When the n is larger than 100, the Voc, I, and Eoutput gradually decrease with the increase in n but the output charge still remains constant. All the above analysis is under ideal conditions. In fact, considering the leakage electric field caused by the edge effect, the increasing slope would be smaller with increasing n.
| Voc = σind/C | (3) |
| Qoutput = nσind | (4) |
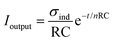 | (5) |
 | (6) |
To verify the above theoretical analysis, we experimentally fabricated FSNGs with 4, 14, and 40 fractal units, respectively. The corresponding experimental results of open-circuit voltages, output charges, currents, and energies per cycle are exhibited by solid lines or bars in Fig. 3(a)–(d). More details about their output performances are shown in Fig. S5–S7 (ESI†). It can be found that the experimental data of output charge, load current, and energy per cycle of FSNG with different number of fractal units are consistent with the simulation results, which further demonstrate that the largely enhanced output performance of the FSNG is attributed to the unique 3D fractal design. The open-circuit voltage remains about 140 V, which is higher than the simulation. The difference may be due to the charge accumulation from previous working cycles before measuring. The output charge and energy density of FSNG with 40 units could reach up to 8 mC m−2 and 0.39 J m−2 cycle−1, which not only break the record but are also much higher than that of various types of triboelectric nanogenerators14,15,23,24,26,29,33,36–40 (Fig. 3(e) and (f)). In addition, the stability tests of the FSNG are carried out, as illustrated in Fig. S7 (ESI†), from which we can clearly see the quite stable state after more than 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles of operation. Three points should be emphasized here. First, the FSNG is a new kind of nanogenerator with independent output of high-current and low voltage, which can more efficiently collect space-distributed Maxwell's displacement current, but not simple multilayers superimposed in series or parallel. Second, no additional power management is used within the FSNG. Third, according to the theoretical simulation, the output performance of the FSNG could be further greatly improved by increasing the fractal units.
000 cycles of operation. Three points should be emphasized here. First, the FSNG is a new kind of nanogenerator with independent output of high-current and low voltage, which can more efficiently collect space-distributed Maxwell's displacement current, but not simple multilayers superimposed in series or parallel. Second, no additional power management is used within the FSNG. Third, according to the theoretical simulation, the output performance of the FSNG could be further greatly improved by increasing the fractal units.
The equivalent fractal circuit for the FSNG
The fractal units of FSNG can effectively utilize the electric field generated by surface triboelectric charges and possess the function of charge induction, which can be replaced by commercial capacitors in theory. To deeply understand the working mechanism of FSNG and the effect of capacitance of the fractal unit, a classical TENG with equivalent fractal circuit (EFC) has been developed with capacitors, motion switches, and diodes (Fig. 4(a)). In the induction process, the motion switches are all turned off, and hence capacitors are charged in series by the TENG (red route in Fig. 4(a-I)). On the other hand, in the output process, all the motion switches are turned on, leading all the charged capacitors being in parallel and outputting the electric signal (red route in Fig. 4(a-II)). Next, the influence of capacitors (n = 40) with different capacitance on the output characteristic of TENG is investigated, whose photograph is exhibited in Fig. S8a (ESI†). The output performance of the TENG without EFC is also characterized as a control group (Fig. S8b and c, ESI†). It can be found that the output charge of the TENG with EFC would nearly reach the saturation value of 46 μC (dotted line, Fig. 4(b)) if the capacitance (each capacitor) is greater than 10 nF, which is about 40 times higher than that without EFC. The threshold value of capacitance is not fixed and changed with the output voltage of the TENG part and the number of capacitors. The open-circuit voltage (Fig. 4(c)) and the peak value (Fig. 4(d)) of load current of the TENG with EFC exhibit a decreasing trend with increasing capacitance, while the discharging time of the load current increases with increasing capacitance. As for the capacitor with 100 nF, the discharge process could even last a few seconds.Considering the characteristic of Voc, output charge, and discharging time shown above, capacitors (n = 40) with a capacitance of 22 nF are selected to construct the EFC for fabricating high performance FSNG. The output curves of open-circuit voltage, load current, and output charge of the TENG with EFC are presented in Fig. S9 (ESI†). Fig. 4(e) shows the peak current and instantaneous power with different load resistance, which both increase with decreasing load resistance. Owing to the EFC, the performance of TENG is substantially improved with a maximum current of 22 A and a power of 4.8 kW (at the resistance of 10 Ω). According to the plot of load voltage versus transfer charge (U–Q), a high output energy of 2.1 mJ during one cycle of operation is obtained (Fig. 4(f)). The FSNG can be used to charge a 10 μF capacitor to 10 V in 3 s and a 100 μF capacitor to 10 V in 30 s, respectively, which is much faster than that of the TENG without EFC and further demonstrates the high output charge and energy of the TENG with EFC (Fig. 4(g)). In addition, the influence of capacitor numbers (n = 10, 20, 30, 40) of EFC is also investigated, as shown in Fig. S10 (ESI†). It can be found that using EFC instead the fractal unit of FSNG not only significantly improves the output performance of the TENG and achieve the same functionality with FSNG but also help to deeply understand the working principle of FSNG. Moreover, the EFC could be used for various types of TENGs with all kinds of tribomaterials and structure size, which show the advantages of low cost, simple process, and universality (Fig. S11, ESI†).
Demonstrations of the FSNG
To demonstrate the high-output performance presented above, a FSNG with an effective area of 8 × 9 cm2 is used to drive various electronic devices at low frequency (1–1.5 Hz). The LED strips with rated power of 120 W are successfully lighted by the FSNG in light and dark environment owing to its high output charge (Fig. 5(a) and (b) and Movie S2, ESI†), which shows the advantages of the high instantaneous power of FSNG. A digital vernier caliper and a temperature hygrometer are continuously driven by the FSNG through an energy-storage capacitor at low operating frequency of 1 Hz and 1.5 Hz, respectively (Fig. 5(c) and (d) and Movie S3, S4, ESI†), which demonstrate the high output electric energy as well as a high average power of FSNG. The discharging time is much longer than the classical TENG due to the large equivalent capacitance, which means we can save the buffer circuits in some application scenarios. Furthermore, a dozen LEDs with 10 mm diameter could be lighted for more than 10 s during one cycle of operation without any energy management circuit, as shown in Fig. 5(e) and (f) and Movie S5 (ESI†), which display its characteristic of slow-release of electrical energy. Although we only display the power supply to small appliances with the small-sized FSNG, we could further generate a large output energy by optimizing the fractal design, increasing the area of the triboelectric part, or the integration of FSNG.Conclusion
In summary, we have proposed and developed a new kind of FSNG for more efficiently collecting the space-distributed Maxwell's displacement current. Compared with classical TENG, the FSNG exhibits the characteristic of independent output with high current density and low open-circuit voltage. The output charge density, peak power density, and energy density of the FSNG break the record and reach up to 8 mC m−2, 2.18 MW m−2, and 0.39 J m−2 cycle−1, which can be further improved by optimizing the fractal unit of the FSNG. Furthermore, the equivalent fractal circuits for FSNG with the same functionality are developed, giving us an in-depth understanding of the principle of FSNG. This work not only provides a promising strategy for efficiently collecting the space-distributed Maxwell's displacement current for high-performance TENGs but also paves the way for efficient mechanical energy harvesting toward practical applications.Author contributions
L. F. W. and Y. Q. conceived the project. L. F. W., Y. Q. and L. A. Z. designed the experiments. L. A. Z., and S. H. L. performed the experiments. L. F. W., Y. Q., L. A. Z., S. H. L, J. W. and Z. L. W. analyzed the results. All authors contributed to discussions and writing of the manuscript.Data availability
The data are available from the corresponding authors on reasonable request.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
This research was supported by the National Key R&D Project from Minister of Science and Technology (2021YFA1201601), and the National Natural Science Foundation of China (Grant No. U21A20175).References
- A. He, S. Srikanteswara, K. K. Bae, J. H. Reed and W. H. Tranter, Energy consumption minimization for mobile and wireless devices-a cognitive approach, IEEE Trans. Broadcast Telev. Receivers, 2010, 56, 1814–1821 Search PubMed.
- D. Dai and J. Liu, Human powered wireless charger for low-power mobile electronic devices, IEEE Trans. Broadcast Telev. Receivers, 2012, 58, 767–774 Search PubMed.
- J. Yick, B. Mukherjee and D. Ghosal, Wireless sensor network survey, Comput. Networks, 2008, 52, 2292–2330 CrossRef.
- A. Al-Fuqaha, M. Guizani, M. Mohammadi, M. Aledhari and M. Ayyash, Internet of Things: A survey on enabling technologies, protocols, and applications, IEEE Commun. Surv. Tutorials, 2015, 17, 2347–2376 Search PubMed.
- K. A. Cook-Chennault, N. Thambi and A. M. Sastry, Powering MEMS portable devices—a review of non-regenerative and regenerative power supply systems with special emphasis on piezoelectric energy harvesting systems, Smart Mater. Struct., 2008, 17, 043001 CrossRef.
- R. Haight, W. Haensch and D. Friedman, Engineering. Solar-powering the Internet of Things, Science, 2016, 353, 124–125 CrossRef CAS PubMed.
- W. C. Chye, Z. Dahari, O. Sidek and M. A. Miskam Electromagnetic micro power generator-A comprehensive survey. IEEE Symposium on Industrial Electronics and Applications (ISIEA), 2010, pp. 376–382.
- I. Sari, T. Balkan and H. Kulah, An electromagnetic micro power generator for wideband environmental vibrations, Sens. Actuators, A, 2008, 145, 405–413 CrossRef.
- J. Tian, X. Chen and Z. L. Wang, Environmental energy harvesting based on triboelectric nanogenerators, Nanotechnology, 2020, 31, 242001 CrossRef CAS PubMed.
- H. Qin, et al., A universal and passive power management circuit with high efficiency for pulsed triboelectric nanogenerator, Nano Energy, 2020, 68, 104372 CrossRef CAS.
- W. Xu, et al., A droplet-based electricity generator with high instantaneous power density, Nature, 2020, 578, 392–396 CrossRef CAS PubMed.
- R. Hinchet, et al., Transcutaneous ultrasound energy harvesting using capacitive triboelectric technology, Science, 2019, 365, 491–494 CrossRef CAS PubMed.
- H. Zou, et al., Quantifying the triboelectric series, Nat. Commun., 2019, 10, 1427 CrossRef PubMed.
- J. Wang, et al., Achieving ultrahigh triboelectric charge density for efficient energy harvesting, Nat. Commun., 2017, 8, 88 CrossRef PubMed.
- Y. Liu, et al., Quantifying contact status and the air-breakdown model of charge-excitation triboelectric nanogenerators to maximize charge density, Nat. Commun., 2020, 11, 1599 CrossRef CAS PubMed.
- A. Ahmed, et al., Toward high-performance triboelectric nanogenerators by engineering interfaces at the nanoscale: Looking into the future research roadmap, Adv. Mater. Technol., 2020, 5, 2000520 CrossRef CAS.
- Z. B. Li, et al., Small-sized, lightweight, and flexible triboelectric nanogenerator enhanced by PTFE/PDMS nanocomposite electret, ACS Appl. Mater. Interfaces, 2019, 11, 20370–20377 CrossRef CAS PubMed.
- S. Gong, et al., Monocharged electret generator for wearable energy harvesting applications, Adv. Sustainable Syst., 2018, 2, 1700178 CrossRef.
- F. R. Fan, et al., Transparent triboelectric nanogenerators and self-powered pressure sensors based on micropatterned plastic films, Nano Lett., 2012, 12, 3109–3114 CrossRef CAS PubMed.
- X. Kang, C. Pan, Y. Chen and X. Pu, Boosting performances of triboelectric nanogenerators by optimizing dielectric properties and thickness of electrification layer, RSC Adv., 2020, 10, 17752–17759 RSC.
- B. Chai, et al., Conductive interlayer modulated ferroelectric nanocomposites for high performance triboelectric nanogenerator, Nano Energy, 2022, 91, 106668 CrossRef CAS.
- S. Cui, et al., Improving performance of triboelectric nanogenerators by dielectric enhancement effect, Matter, 2022, 5, 180–193 CrossRef CAS.
- S. Wang, et al., Maximum surface charge density for triboelectric nanogenerators achieved by ionized-air injection: methodology and theoretical understanding, Adv. Mater., 2014, 26, 6720–6728 CrossRef CAS PubMed.
- W. Liu, et al., Integrated charge excitation triboelectric nanogenerator, Nat. Commun., 2019, 10, 1426 CrossRef PubMed.
- L. Xu, T. Z. Bu, X. D. Yang, C. Zhang and Z. L. Wang, Ultrahigh charge density realized by charge pumping at ambient conditions for triboelectric nanogenerators, Nano Energy, 2018, 49, 625–633 CrossRef CAS.
- H. Wu, et al., Achieving remarkable charge density via self-polarization of polar high-k material in a charge-excitation triboelectric nanogenerator, Adv. Mater., 2022, 34, 2109918 CrossRef CAS PubMed.
- R. Zhang, et al., Multichannel driving triboelectric nanogenerator for enhancing the output charge density, Nano Energy, 2022, 98, 107272 CrossRef CAS.
- G. Cheng, et al., Multilayered-electrode-based triboelectric nanogenerators with managed output voltage and multifold enhanced charge transport, Adv. Energy Mater., 2015, 5, 1401452 CrossRef.
- Z. Zhao, et al., Rationally patterned electrode of direct-current triboelectric nanogenerators for ultrahigh effective surface charge density, Nat. Commun., 2020, 11, 6186 CrossRef CAS PubMed.
- Z. Wang, On the expanded Maxwell's equations for moving charged media system - General theory, mathematical solutions and applications in TENG, Mater. Today, 2022, 52, 348–363 CrossRef.
- Z. Wang, The expanded Maxwell's equations for a mechano-driven media system that moves with acceleration, Int. J. Mod. Phys. B, 2022, 0, 2350159 Search PubMed.
- Z. Wang, Maxwell's equations for a mechano-driven, shape-deformable, charged-media system, slowly moving at an arbitrary velocity field v(r,t), J. Phys. Commun., 2022, 6, 085013 CrossRef.
- W. Liu, et al., Switched-capacitor-convertors based on fractal design for output power management of triboelectric nanogenerator, Nat. Commun., 2020, 11, 1883 CrossRef CAS PubMed.
- Z. Wang, On the first principle theory of nanogenerators from Maxwell's equations, Nano Energy, 2020, 68, 104272 CrossRef CAS.
- H. Wu, S. Wang, Z. Wang and Y. Zi, Achieving ultrahigh instantaneous power density of 10 MW/m(2) by leveraging the opposite-charge-enhanced transistor-like triboelectric nanogenerator (OCT-TENG), Nat. Commun., 2021, 12, 5470 CrossRef CAS PubMed.
- F. Xi, et al., Universal power management strategy for triboelectric nanogenerator, Nano Energy, 2017, 37, 168–176 CrossRef CAS.
- X. Cheng, et al., High efficiency power management and charge boosting strategy for a triboelectric nanogenerator, Nano Energy, 2017, 38, 438–446 CrossRef CAS.
- X. Xia, H. Wang, P. Basset, Y. Zhu and Y. Zi, Inductor-free output multiplier for power promotion and management of triboelectric nanogenerators toward self-powered systems, ACS Appl. Mater. Interfaces, 2020, 12, 5892–5900 CrossRef CAS PubMed.
- Z. Wang, et al., Ultrahigh electricity generation from low-frequency mechanical energy by efficient energy management, Joule, 2021, 5, 441–455 CrossRef.
- Z. Cao, et al., A compact triboelectric nanogenerator with ultrahigh output energy density of 177.8 J m−3 via retarding air breakdown, Nano Energy, 2022, 93, 106891 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Materials and methods, supplementary notes S1 to S2, Fig. S1–S13 and Movies S1–S5. See DOI: https://doi.org/10.1039/d3ee01248d |
| ‡ These authors contribute equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |