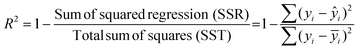Direct measurements of size-independent lithium diffusion and reaction times in individual polycrystalline battery particles

Abstract

Polycrystalline Li(Ni,Mn,Co)O₂ (NMC) secondary particles are the most common cathode materials for Li-ion batteries. During electrochemical (dis)charge, lithium is believed to diffuse through the bulk and enter (leave) the secondary particle at the surface. Based on this model, smaller particles would cycle faster due to shorter diffusion lengths and larger surface-area-to-volume ratios. In this work, we evaluate this widespread assumption by developing a new high-throughput single-particle electrochemistry platform using the multi-electrode array from neuroscience. By measuring the reaction and diffusion times for 21 individual particles in liquid electrolytes, we find no correlation between the particle size and either the reaction or diffusion times, which is in stark contrast to the prevailing lithium transport model. We propose that electrochemical reactions occur inside secondary particles, likely due to electrolyte penetration into cracks. Our high-throughput, single-particle electrochemical platform further opens new frontiers for robust, statistical quantification of individual particles in electrochemical systems.

---

Broader context

Li-ion batteries contain an ensemble of micron-sized particles as building blocks. It has long been assumed that lithium enters the particle at the surface and diffuses into the bulk. As a result, smaller particles would charge faster than larger ones. In this work, we evaluate this foundational precept for polycrystalline NMC, the most common battery cathode material. We designed a new platform to charge and discharge individual battery particles based on the multi-electrode array, which was developed to measure electrical potentials from mammalian neurons. By cycling many individual particles, we show that smaller particles are no faster than larger ones. As a result, our result shows that electrochemical reactions not only occur at the surface, as widely believed but also within the bulk, likely a result of cracking. Our work not only presents a substantial leap in precise, microscopic characterization of electrochemical systems, but also enables the improved design of more effective energy storage materials, as well as more accurate modeling and predictions of battery operations for the end user.

Introduction

Electrochemical ion insertion of guest species into host structures is widely used in various applications,¹ including neuromorphic computing,² electrochromic windows,³ and, most prominently, energy storage.⁴ The ion insertion rate is a critical determinant for important performance parameters including switching speed, charging rate, and power density. The ion insertion rate strongly depends on two size-independent intensive properties: the solid ion diffusion rate in the bulk, and the reaction rate at the electrode/electrolyte interface.⁵ Therefore, an accurate understanding of the diffusion and reaction rate is critically important for designing ion insertion devices.

Layered Li(Ni,Mn,Co)O₂ (NMC) and Li(Ni,Co,Al)O₂ (NCA) are the most widely used cathodes for Li-ion batteries. NMC and NCA secondary particles (∼10 µm) consist of a sintered polycrystalline agglomerate of many primary particles, each 100–500 nm. The lithium insertion and removal rates are critical factors for power density^6–8 and battery modeling. The standard model for ion insertion states that lithium reacts at the surface of the secondary particle,^6–17 and then diffuses into the particle through the bulk and possibly the grain boundaries.^18,19 Under this model, smaller particles would charge and discharge faster than larger particles due to shorter diffusion lengths and higher surface-area-to-volume ratios.^6–17

In this work, we evaluate the accuracy of this intuitive and widespread assumption that smaller particles charge and discharge faster. Inspired by the field of neuroscience,²⁰ we designed and developed a multi-electrode array that enables high-throughput electrochemical cycling of many individual battery particles. In contrast to previous works using microneedle contacts^6,7,10,21,22 or scanning micropipettes^23–25 which analyzed a limited number of particles, we conduct full electrochemical cycling and analysis on over 20 individual particles under identical conditions. We generate a statistically significant dataset on reaction and diffusion times for many particles.

To our surprise, neither the diffusion nor the reaction times depend on the diameter (size) of the secondary particle, in stark contraction to the standard particle model of lithium transport within a particle.^6–17 Instead, our single-particle electrochemistry data shows that the characteristic diffusion length is essentially independent of the secondary particle size.^26,27 We propose that our results likely arise from intergranular cracking, which causes the electrolyte to penetrate into the secondary particle,^28,29 thereby facilitating lithium transport by making the diffusion length independent of and much shorter than the secondary particle diameter. Our work shows that the standard description of intraparticle lithium transport, whereby lithium enters the secondary particle surface and diffuses into the bulk, is not accurate for this material. As a result, the widely-used Doyle–Fuller–Newman electrochemical model⁹ should be revised for polycrystalline NMC particles. This work has substantial implications the design of cathode materials. It further shows the potential of high-throughput, single-particle measurements to unveil the kinetics of electrochemical systems and other energy materials at the micro- to nano-scale.

Results

Multi-electrode array design

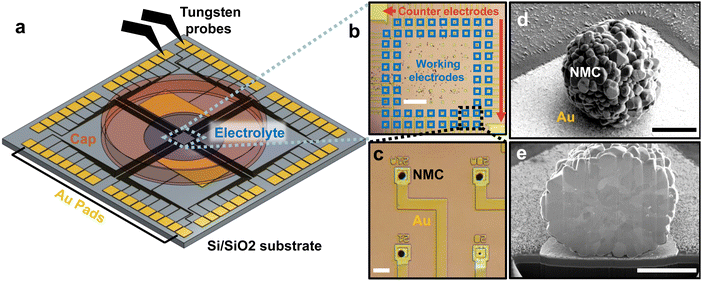
We designed and fabricated a multi-electrode array consisting of lithographically-patterned Au microelectrodes (100 nm thick) on a 2 cm Si substrate with 500 nm of insulating SiO₂ thermal oxide (Fig. 1a). This design was inspired by the multi-electrode arrays commonly used in neuroscience to measure extracellular field potentials from mammalian neurons.²⁰ Our multi-electrode array consists of 62 square microelectrodes, each 20 × 20 µm and separated by 150 µm. Each microelectrode is connected to a large ∼1 mm² contact “pad” on the edge of the chip with patterned 20 µm-wide Au “wires.” A 50-nm-thick silicon nitride layer is deposited and patterned to passivate the Au wires; this ensures that only a 20 × 20 µm area on each microelectrode is exposed to the liquid electrolyte to minimize parasitic resistance and capacitance. The lithography design file is given in the Data Archive.

Fig. 1 Design and fabrication of multi-electrode arrays (a) Schematic illustration of high-throughput multi-electrode array. Au microelectrodes are patterned on a silicon substrate with 500 nm thermal oxide. Au contact pads, about 1 mm each, are patterned on the boundary of the array and electrically connected to the microelectrodes in the center. (b) An optical image of the electrodes. The chip contains 2 large counter/reference electrodes and 62 smaller working microelectrodes. (c) Magnified image of four working microelectrodes with assembled NMC particles. Each Au microelectrode is 20 × 20 µm; the Au wires are passivated with 50 nm of silicon nitride. (d) SEM image of a particle on a working microelectrode. (e) Cross-section SEM of a particle obtained using plasma focused ion beam milling. The scale bars in each image equal 300 µm (b), 30 µm (c), 3 µm (d), 3 µm (e) respectively.

After fabricating the multi-electrode array, we construct the working electrodes. Each working electrode contains a single polycrystalline Li(Ni_0.5Mn_0.3Co_0.2)O₂ (NMC532, BASF TODA) particle on a microelectrode (Fig. 1b–d; SEM images and particle size distribution in Fig. S1 and 2, ESI†). We scatter a small amount of NMC532 particles in the middle of the array, then use an xyz micromanipulator with a tungsten needle with a 1 µm-wide tip to manually place the particle on each working electrode (Fig. S3, ESI†). The unused particles remain disconnected on the chip. We anneal the chip at 400 °C for 1 h to improve the electrical and physical contact between the particle and the microelectrode. As we shall show later, the electronic contact resistance is essentially negligible.

We next construct the counter/reference electrode. In addition to the 62 microelectrodes, our design also includes two larger electrodes, 5 × 3 mm each. The counter/reference electrode consists of a slurry of partially delithiated Li_0.6FePO₄ mixed with PVDF and carbon, previously shown to have a reliable reference voltage ∼3.4 V vs. Li/Li⁺.³⁰ We use this reference to report all future voltages. With a mass >0.1 mg, the mass and capacity of the macroscopic Li_0.6FePO₄ electrode at least 10⁴ times larger than the single-particle working microelectrode, resulting in negligible electrochemical polarization in the counter-electrode.

Because each NMC particle weighs ∼1 nano-gram, its mass cannot be accurately measured. Instead, we use the particle volume, obtained from the projected area using scanning electron microscopy (SEM). From the projected area, we compute the radius and volume of the particle assuming a spherical shape (Fig. S4, ESI†). Sensitivity analysis suggests that relaxing the spherical assumption yields nearly no change in the estimated volume (Fig. S5, ESI†).

After acquiring the SEM image for volume estimation, we placed the array in an Ar-filled glovebox (<1 ppm O₂ and H₂O) and dropped ∼3 µL of 1 M LiPF₆ in propylene carbonate on the chip, connecting the NMC particles with the counter/reference electrodes. The dropped electrolyte covers the NMC532 particles on the working electrodes and the Li_0.6FePO₄ counter/reference electrodes. Finite element analysis shows a bulk electrolyte voltage drop <1 mV for the currents used in this experiment (Fig. S6, ESI†). A stainless-steel cap reduces electrolyte evaporation to <1% per day (Fig. S7, ESI†); our experiment lasted 8 days. Unlike a previous report using microfabricated chips to conduct “dry” transport measurements on NMC particles,³¹ our design enables the electrochemical charge and discharge of individual NMC particles in liquid electrolytes.

Electrochemical cycling of single particles

After assembling the chip, we first conduct galvanostatic cycling on each of the 21 particles with a constant current of 0.22 pA µm⁻³, which is ∼50 mA g⁻¹, or a C-rate of ∼C/3. The particles were charged to a cutoff voltage of 4.2 V vs. Li/Li⁺, and discharged to a cutoff voltage of 2.9 V. The first charge, first discharge, and second charge curves of a representative particle are shown in Fig. 2a; it is overlaid with the electrochemical profile of a coin cell at the same rate in Fig. S8 (ESI†). The diameter of this particle, measured by SEM, is 10.1 µm, and the first discharge capacity was 278 pico-amp hours (pA h). In contrast, a “blank” Au microelectrode without a particle shows a capacity ∼0.2 pico-amp hours in this voltage range, suggesting negligible parasitic resistance and capacitance (Fig. S9, ESI†). Because the electrochemical profiles are essentially stable after the second charge (Fig. S10, ESI†), we limit the number of formation cycles to limit the experiment on each particle to <24 hours (see Methods).

Fig. 2 Galvanostatic cycling of individual particles on the multi-electrode arrays (a) The first charge, second discharge, and second charge curves of an NMC particle on a working electrode. This particle was (dis)charged between 2.9 and 4.2 V at a constant 120 pA, or a C-rate of approximately C/3. The inset shows an SEM image of the particle being cycled; the scale bar is 5 µm. (b) The first discharge capacity is nearly perfectly correlated with the volume estimated from the SEM image, showing the robustness and reliability of our measurements. The purple dashed line is the fit. The particle volume estimate is based on the SEM images of the uncycled particle (Fig. S1, ESI†).

In Fig. 2b, we plot the measured electrochemical discharge capacity of the 21 particles against the particles’ volume estimated from the SEM images (see Methods for details). Our results show that the discharge capacity is proportional to the volume (R² = 0.98), confirming the robustness of our single-particle electrochemistry and microscopy-based volume estimation. Our linear regression shows a volumetric capacity ∼600 mA h cm⁻³ between 2.9 V and 4.2 V. Under the assumption that the bulk density of a particle is 4.77 g cm⁻³, our measurements yield a gravimetric capacity ∼130 mA h g⁻¹ between these voltages. This number is slightly lower than past works^32–35 (∼140 mA h g⁻¹) likely due to the somewhat higher C-rates and because we did not account for internal voids and pores³⁶ and likely overestimated the mass. In addition, electrochemical impedance spectroscopy on individual particles suggests essentially negligible contact resistance between the particles and the Au microelectrodes compared to the charge-transfer resistance (Fig. S11, ESI†). The 21 particles in this experiment are much greater than past single-particle electrochemistry studies which only investigate one or a few particles for a given condition;^{6,7,10,21–25} as we show in the next section, this larger data set is essential in statistically uncovering our core results.

Quantification of exchange current density and lithium diffusion

Having established the robustness of our single-particle electrochemistry platform, we use potentiostatic intermittent titration technique (PITT) to measure the exchange current density j₀ and lithium diffusion coefficient D_Li.^6,7,37–39D_Li describes the bulk diffusion rate; j₀ provides a phenomenological descriptor for the reaction rate that encompasses several mechanisms,⁴⁰ including ion desolvation, transport in cathode–electrolyte-interphase, ion insertion from surface to bulk, and electron charge transfer. After the first discharge, the particles were again charged to 4.2 V at 0.22 pA µm⁻³ (∼C/3). Afterwards, they were discharged at the same rate to 4.1 V, placed under open-circuit voltage relaxation for 1 h for equilibration, and then discharged using PITT by −15 mV referenced to the open-circuit voltage after relaxation (see Methods and Fig. S12, ESI†). To obtain the electrochemical parameters D_Li and j₀, we fit eqn (1) and (2) to the PITT current traces to simultaneously solve for D_Li and j₀.^6,38 These equations represent solutions, with spherical boundary conditions, to Fick's First Law of diffusion under the assumption that lithium enters the secondary particle surface and diffuses into the bulk. These solutions are applicable to reaction-limited systems, diffusion-limited systems, and systems that are neither reaction nor diffusion limited.^37,38 Because our fits assume D_Li and j₀ is constant, our choice of −15 mV perturbation yields <4% change in the lithium concentration (Fig. S13c, ESI†), while obtaining enough signal to fit the data.I is the electrochemical current, t is the time, B is the Biot number, r is the radius of a particle, R is the gas constant, T is temperature, and Q is the integrated electrochemical charge during PITT. Eqn (2) shows the relation between the j₀, D_Li and B. The term , where V is the electrochemical potential and C the lithium concentration, is determined from the slope of the voltage vs. Li concentration curves for NMC532 composite electrode in a coin cell cycled at C/10 (Fig. S13a and b, ESI†). Fig. 3b shows the PITT current response and fits at 3 different target OCV. To avoid overfitting at longer times, we sample the experimental current at times evenly spaced on a square root scale (e.g., times = 1, 4, 9, 16, etc. seconds) (Fig. S14, ESI†). The current traces and fitting results for all 21 particles at all voltages are shown in Fig. S15 (ESI†). By conducting our PITT measurements at a low overpotential and during lithiation, we do not anticipate real or “fictitious” phase separation⁴¹ during the measurements; this absence of phase separation enables us to use eqn (1) and (2).

Fig. 3 Obtaining single-particle exchange current density (j₀) and lithium diffusivity (D_Li) using potentiostatic intermittent titration technique (PITT). (a) Each particle was discharged to a given voltage and held for 1 h at open-circuit voltage (OCV). Afterwards, a −15 mV PITT voltage was applied, and the electrochemical current was recorded over 1200 seconds. We fit the data to eqn (1) and (2) to obtain j₀ and D_Li. The inset image is an SEM image of the particle used in this PITT measurement. (b) Current responses of PITT measurement and fits to eqn (1) and (2) under three different target voltages. The time scale is converted to an inverse root scale. (c) and (d) The exchange current density j₀ and lithium diffusivity D_Li estimated from the PITT fitting for 21 particles at various voltages. We assume that the radius parameter in eqn (1) and (2) equals the radius of the secondary particle computed from SEM images, or r_Secondary. Each color represents a different particle.

Next, we repeat the PITT measurements for all 21 particles and measure the particle-to-particle variability in j₀ and D_Li. All quantified results are given in Table S1 (ESI†). The range of Biot numbers for all particles ranges from 0.25 to 2.5 (Table S1, ESI†), suggesting that the particles are neither reaction limited (B ≪ 1) nor diffusion limited (B ≫ 1). Table S2 (ESI†) shows that the measurements are repeatable, with ∼1% and ∼3% standard deviation in the quantified D_Li and j₀ respectively, averaged across all voltages. Fig. 3c and d plots the relationship between j₀ and D_Li against the lithium fraction (X) for the 21 particles. To obtain these results, we assume that the radius (r) parameter in eqn (1) and (2) equals the radius of the secondary particle measured by SEM, as generally assumed in this field.^6,7,10,42 Consistent with previous works,^{6,7,22,32,39,43–47}j₀ increases with more lithium extraction (higher SOC). The range of obtained values for j₀ (0.01 to 0.1 mA cm⁻²) and D_Li (10⁻¹⁰ to 10⁻⁹ cm² s⁻¹) are broadly consistent with previous reports of polycrystalline NMC particles taken at both the porous electrode^{32,39,43–47} and single-particle^6,7,22 levels (Fig. S16, ESI†). Our quantified values further show no dependence with the date that the measurements were conducted, confirming that the minimal electrolyte evaporation over 8 days has a negligible effect on our measurements (Fig. S17, ESI†). In addition, a cell with LiFePO₄ as both the working and counter electrode is also stable, showing that the counter-electrode and electrolyte do not show an increase in the electrochemical polarization after repeated cycling (Fig. S18, ESI†).

Unexpected size effects in diffusion and reaction

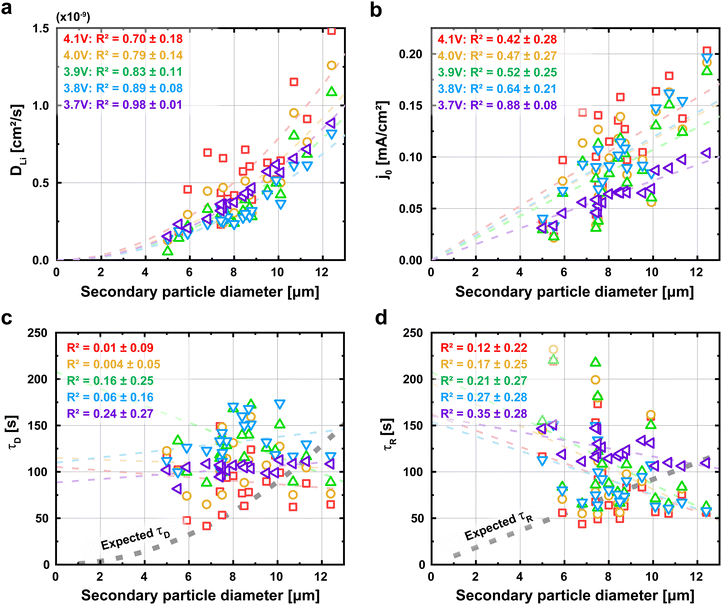
We next plot j₀ and D_Li as a function of the secondary particle diameter (Fig. 4a and b). We expect that both j₀ and D_Li, by definition, are size-independent intensive parameters. To our surprise, both j₀ and D_Li appear to increase with particle size. In particular, Fig. 4a shows that D_Li appears to be quadratically proportional with the secondary particle diameter, while Fig. 4b shows that j₀ appears to be linearly proportionally with diameter. Statistically, the coefficient of determination (R²) ranges from 0.42 to 0.98. Importantly, the 95% confidence interval for R² does not cross 0, indicating a statistically-significant correlation with particle diameter. Holistically, this result is highly surprising, it is expected that j₀ and D_Li are intensive properties that are not dependent on the geometry of the secondary particle. We note that the R² for j₀ is relatively low, especially at higher voltages. We speculate that the surface property j₀ is more sensitive to small process variations between particles than the bulk property D_Li, and that this variation is more substantial at higher voltages. However, we cannot exclude other possibilities for the relatively low R².

Fig. 4 The dependence of the measured electrochemical parameters as a function of particle diameter (a) and (b) the relation between the measured D_Li and j₀ with the diameter of each particle under five different target voltages. Dashed lines are linear (quadratic) fitting lines that pass through the origin. The R² is calculated along with its 95% confidence interval. (c) and (d) The computed diffusion τ_D and reaction τ_R times. The diffusion time is computed using τ_D = l²/4D_Li, where l equals the radius of the secondary particle. The reaction time is computed from j₀ using an effective RC time constant (detailed in Methods). The dashed lines show the linear fits for the calculated τ_D and τ_R as a function of the particle size, which show no statistically significant correlations because nearly all of the 95% confidence intervals for R² span 0.

We next interpret these results in the context of diffusion and reaction times. The diffusion time τ_D is commonly defined using τ_D = l²/4D_Li, where l is the characteristic diffusion length and assumed to equal the radius of the secondary particle. Under the standard assumption of a constant lithium diffusivity (D_Li), the diffusion time τ_D is expected to increase quadratically with the particle's diameter.^42,48 However, our quantified τ_D is essentially independent of particle size (Fig. 4c).

We apply the same analysis for reaction time, which we interpret to equal a characteristic time constant (τ_R = Res × Cap). Cap is the faradaic charge transferred per volt, and scales with the volume of the particle. Res is the charge transfer resistance, and is proportional to the inverse of j₀ multiplied by the surface area (see details in Experimental Methods). Under the assumption that j₀ is independent of size, the τ_R should be proportional to the diameter of the particle due to the volumetric scaling of the capacitance and the inverse surface area scaling of the resistance. However, our results in Fig. 4b shows that the exchange current density j₀ increases with particle size; as a result, τ_R becomes independent of particle size.

To confirm that the absence of the expected correlation between particle size with τ_D and τ_R is not an artifact of our fitting procedure, we revisit the raw current traces obtained through PITT. In Fig. 5a, we plot the current traces I of all particles normalized by the initial current I_init obtained 0.1 second after the PITT experiments at 4.1 V. We also plot the solutions to eqn (1) and (2); these equations, which represent the expected behavior, suggest that larger particles take more time for the current to decay, a result of longer reaction and diffusion times. In Fig. 5b, we plot the characteristic time, defined as when the current decays to 37%, or [exp(−1)] of the initial current. While there does exist scatter in the data, this characteristic time obtained from the raw current traces is again not correlated with particle size. Fig. S19 (ESI†) shows the characteristic times for the other voltages. In contrast, eqn (1) and (2) suggests that this characteristic time increases with particle diameter under constant D_Li and j₀. This result confirms that the lack of size-dependent τ_D and τ_R is directly reflected in the raw current traces, and is not an artifact of fitting. All of these observations: the size dependent electrochemical parameters but size-independent diffusion and reaction times, are in stark contrast to our standard understanding of ion insertion into battery materials.⁹

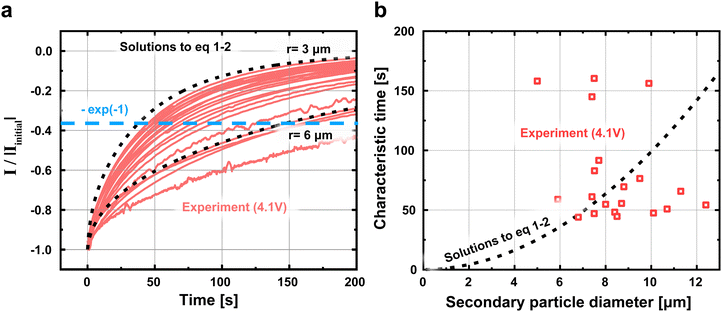Fig. 5 Direct estimates of characteristic electrochemical timescales from PITT measurements (a) The PITT current traces for all particles at 4.1 V normalized to the initial current at t = 0.1 s. The solutions to eqn (1) and (2) under the assumption that D_Li = 5.2 × 10⁻¹⁰ cm² s⁻¹ and j₀ = 0.104 mA cm⁻², which are the median of D_Li and j₀ obtained at 4.1 V (Table S1, ESI†), are plotted in black. (b) The characteristic electrochemical timescale as a function of particle diameter. The characteristic time is defined as when I/I_initial = exp(−1), and represents a convolution of τ_D and τ_R. Whereas eqn (1) and (2) suggest that large particles require longer timescales, our results show no size dependence. This result shows that the diameter-independent τ_D and τ_R found in Fig. 4 can be observed in the raw data and are not artifacts of our analysis procedure. The same trends are measured for the other voltages (Fig. S19, ESI†).

Proposed origins of size-independent j₀ and D_Li

We aim to understand why j₀ and D_Li appear to depend on secondary particle size (Fig. 4a and b), while the reaction time τ_R and diffusion time τ_D do not (Fig. 4c and d). We propose that the apparent size dependencies of j₀ and D_Li arise because the standard description of lithium transport in battery particles, whereby lithium enters the surface of the secondary particle and diffuses into the bulk,^6–17 is incorrect (Fig. 6a). Based on this model, the diffusion length of the particle increases with the secondary particle radius. If the measured diffusion time τ_D is independent of the particle size, as shown in Fig. 4c, then the lithium diffusivity would appear to increase to compensate for the increased diffusion length (Fig. 4a), even though this is physically unrealistic. A similar argument for reaction time can be constructed based on surface-area-to-volume ratios.

Fig. 6 Proposed mechanism for size-independent reaction and diffusion times (a) The standard model for particle-level lithium transport assumes that lithium enters the surface of the secondary particles and diffuses into the bulk. As a result, the effective diffusion length increases with the secondary particle diameter. (b) We propose the relevant length scale (r_Effective) is much shorter than the radius of the secondary particle, and is independent of the secondary particle diameter. One possibility is that the electrolyte penetrates the particle due to intergranular cracking. (c) and (d) We refitted the PITT data to eqn (1) and (2); however, instead of using the secondary particle radius, we assume that the radii in these equations equal 0.5 µm for all particles. Under this assumption, the quantified and becomes effectively independent of particle size, consistent with a belief that these values are intensive properties and not dependent on particle diameter. We note that the quantified values depend strongly on the assumed r_Effective; as a result, the true values require us to know the r_Effective, and is subject for future work.

We propose instead that the characteristic diffusion length is decoupled from the radius of the secondary particle (Fig. 6b). Although grain boundaries may enable faster lithium transport, they are expected to only increase the total net lithium transport by <50%.¹⁸ Instead, one likely mechanism, as suggested by Janek and colleagues,^28,29 is that the electrolyte penetrates the secondary particle due to intergranular cracking such that the electrochemical reaction occurs inside the bulk of the secondary particle along these crack surfaces. Our cross-section scanning electron microscopy shows clear evidence of intergranular cracking in particles imaged after PITT cycling (Fig. S20, ESI†). To incorporate this assumption into the PITT model, we instead assume that the radius (r) in eqn (1) and (2) is identical for all particles, regardless of the diameter of the secondary particle. In this revised model, the diffusion length and the surface-area-to-volume ratio of all particles are independent of secondary particle diameter.

In Fig. 6c and d, we plot the re-fitte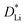d and under the assumption that r_Effective = 0.5 µm for all particles, regardless of the secondary particle diameter. Under this assumption, the extracted electrochemical parameters no longer depend on the particle size, consistent with expectations; the 95% confidence intervals for nearly all R² cross 0, which means that the correlations are too weak to be statistically significant. Because the diffusion length and the surface-area-to-volume ratio of each particle are identical, the extracted τ_R and τ_D remain independent of particle size.

We note that the quantifie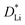d and 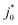values depend on the assumed effective radius, which we arbitrarily chose as 0.5 µm. As we show in Fig. S21 (ESI†), if the assumed radius r_Effective changes, the quantified and will also change, however, regardless of the r_Effective chosen, there is no size dependence for and if every particle uses the same effective radius. Instead, we find that is constant for any chosen r_Effective, and has a unit of s⁻¹ (Fig. S21b, ESI†). This is a consequence of the analytical solution to our PITT eqn (1) whereby D_Li is always paired with 1/r². For this reason, our PITT fits cannot obtain without prior knowledge of r_Effective². At the same time, we find that 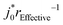is also constant (Fig. S21d, ESI†) because j₀ also cannot be computed in eqn (2) without prior knowledge of r_Effective. In other words, our PITT measurements enable us to obtain fits for D_Lir⁻² and j₀r⁻¹; however, without knowing r, we cannot compute D_Li or j₀. Measuring these values will be the subject of future work. Although we propose cracking and electrolyte penetration as a likely mechanism, our data does not allow us to exclude other possibilities.

By decoupling the characteristic diffusion length from the secondary particle radius, we eliminate the unexpected dependence of D_Li and j₀ on the secondary particle diameter from Fig. 4. In assuming that the electrochemical reactions occur within the secondary particle, and not just at the surface, the diffusion lengths and surface-area-to-volume ratios no longer depend on the secondary particle diameter. This result allows us to explain why the diffusion and reaction times are not dependent on the secondary particle diameter (Fig. 4c and d), without resorting to using size-dependent D_Li and j₀, as we had done earlier. The remaining particle-to-particle variability in these parameters can be attributed to either intrinsic differences between the particles, or to different characteristic diffusion lengths possibly due to different amounts of cracking, and can be the subject of future investigations.

Discussion

Our unexpected observations have substantial implications for the understanding and design of battery materials. We provide two major results for NMC cathodes. First, we show that smaller secondary particles do not have faster electrochemical time constants than larger ones (Fig. 4 and 5). Instead, the diffusion and reaction times are essentially independent of the secondary particle diameter in these polycrystalline particles. This result contradicts the predictions of the standard particle-level transport model given in the widely-used Doyle–Fuller–Newman-type models,⁹ where smaller particles are expected to have faster timescales. Our results are qualitatively consistent with recent work by Wagner et al.⁴² whereby the rate performance is very similar for 9 µm and 37 µm diameter polycrystalline particles. Operando imaging using X-rays²⁶ and visible light²⁷ also show that smaller NMC particles do not (de)lithiate faster than larger ones; however, such experiments were done at very low cycling rates (<C/10).^26,27 We propose two ways to account for our observations in porous electrode modeling. A simple correction is to use a size-dependent j₀ and D_Li like in Fig. 4a and b. A more complex method is to model electrochemical reactions within the secondary particles’ microstructure. Although we conducted our work for NMC-532, we anticipate these results will be widely applicable to most polycrystalline NMC particles that undergo anisotropic expansion and cracking.

Our second advance is to show that the true values of j₀ and D_Li in polycrystalline particles may be much lower than previously believed. j₀ and D_Li are usually obtained by combining an electrochemical measurement^{6,7,10,22,28,32,43–47,49} like PITT or impedance, with assumptions about the particles’ geometry, diffusion length, and surface-area-to-volume ratios as in eqn (1) and (2). If the characteristic diffusion length (Fig. 6b) is much shorter than the radius of the secondary particle, then the true diffusion coefficient would be much lower than the ones extracted using the secondary particle radius. Similarly, if the electrochemically active surface area of a particle is much higher than the outer surface area of the secondary particle (Fig. 6b), then the true exchange current density j₀ will be much lower. Characterizing the true values for j₀ and D_Li in polycrystalline particles requires additional research on the effective radius and diffusion length (Fig. S21, ESI†).

Beyond fundamental understanding, our work has implications for the design of future battery materials. Single-crystal NMC particles are highly promising for Li-ion batteries with longer cycle life. However, to achieve similar cycling rates, single-crystal NMC particles should be much smaller than polycrystalline ones.⁵⁰ Recent work shows that single-crystal particles lithiate much slower than similarly-sized polycrystalline ones.⁸ On the other hand, if we use solid electrolytes, we do not anticipate seeing size-independent reaction and diffusion times because the solid electrolyte cannot penetrate a cracked secondary particle;²⁸ as a result, both single-crystal and polycrystalline particles must be smaller.

An unresolved question is why the secondary particle size is decoupled from the characteristic diffusion length. We propose that this decoupling results from intergranular cracking, such that the electrolyte penetrates the secondary particle (Fig. S20, ESI†). However, we cannot exclude other possibilities like fast grain boundary diffusion.^18,19 The cracking plus electrolyte penetration hypothesis is strongly supported by recent studies by Janek and coworkers,^28,29 which show that polycrystalline NMC811 particles in liquid electrolytes have lower impedances and higher diffusivities after the first cycle after cracking. Indeed, our particles also show a sudden reduction in the overpotential during the first cycle (Fig. 2a, S22, ESI†), which can be attributed to electrolyte penetration and the increase in the electrochemically-active area; if true, the cracks would form when the state of charge is less than 1% (Fig. S22, ESI†). While other works have proposed electrolyte penetration in polycrystalline NMC^28,29 and LiCoO₂⁵¹ particles due to cracking, our work is the first to show that this electrolyte penetration, if true, is so substantial that the diffusion and reaction times are independent of the secondary particle size (Fig. 4).

Our results overturn the dominant picture of lithium transport^6–17 in the most widely-used cathode material. Moreover, this result occurs in a lower 50% Ni composition cathode, at a relatively low voltage, and without calendaring, all of which typically result in less cracking.^4,52 If this electrolyte cracking model is accurate, then our results show that intergranular cracking, long believed to be strongly detrimental to cycle life,^4,52–54 is in fact essential for the ability of polycrystalline particles to (dis)charge at reasonable cycling rates. Our electrolyte penetration hypothesis also motivates future research into capillary effects resulting from the ultrathin electrolyte channels formed through intergranular cracking, which may also lead to different forms of cathode electrolyte interphase. We speculate that such capillary effects may provide another crucial area of difference between single-crystal particles, which do not have these internal capillaries, and poly-crystal particles, which do.

Finally, our work opens new frontiers in precise, high-throughput measurements of electrochemical systems at the nanoscale. Unlike operando spectro-microscopic measurements using visible light²⁷ or X-rays,⁵⁵ our platform provides a direct and precise measurement of electrochemical current and voltage within a single particle with exceptional temporal (<1 s) and current (<1 pA) resolutions. Although single-particle electrochemistry for battery materials has been used for over two decades,^6,7,10,21,22 we were able to measure a statistically-significant number of particles, which enables us to show that reaction and diffusion times are decoupled from the secondary particle size in polycrystalline NMC particles.

Conclusion

In summary, we adapted the micro-electrode array to conduct electrochemical cycling of individual NMC532 particles. By cycling over 20 individual particles, we show that the reaction and diffusion times are independent of the particle diameter, which is in stark contrast to the standard model of lithium insertion^6–17 in this widely used cathode material. Such results have implications for both the design of future cathode materials as well as improved models and predictions for battery operations. Moreover, we anticipate that our high-throughput multi-electrode array can be broadly applied to solve diverse problems within batteries and other electrochemical systems. One example can be to provide highly precise, single-particle measurements for electrocatalysis.⁵⁶

Materials & methods

Multi-electrode array fabrication

The fabrication process is graphically illustrated in (Fig. S23, ESI†). The multi-electrode array introduced in this work has been fabricated on 100 mm diameter SiO₂ (500 nm)/Si wafer in the Lurie Nanofabrication Facility (LNF) at the University of Michigan. First, a 100 nm Au with 5 nm Ti adhesion for working electrodes, counter electrodes, wires, and contact pads is deposited by photolithography (0.9 µm of LOR 10B and 1 µm of S1813), electron beam evaporation (Enerjet evaporator), and lift-off (Remover PG and Isopropanol). Next, a 50 nm of SiN passivation layer is deposited by plasma enhanced chemical vapor deposition (Plasmatherm 790). The CVD pressure was 1500 mTorr and the gas was a NH₃/N₂/He/SiH₄ mixture at a ratio of 0.2 : 24:75 : 0.8 and a power of 150 W for 120 s and a setpoint temperature of 350 °C. We next use photolithography (1 µm of S1813) and dry reactive ion etching (Plasmatherm 790) is used to etch the SiN passivation layer and expose the electrical contacts for the working and counter electrodes as well as the large contact pads that lie away from the electrolyte (Fig. 1a); the wires remain passivated with SiN to minimize parasitic resistance. The room temperature reactive ion etching process used a CF₄/O₂ gaseous mixture at a ratio of 95 : 5, a total pressure of 100 mtorr, a power of 150 W, and a time of 100 s. The processed wafer is diced to 2 × 2 cm chips by dicing saw (ADT 7100). The photomask design files are given in the Data Archive.

Particle & chip assembly

A small amount of polycrystalline NMC-532 (BASF TODA) particles are dry-transferred to the center of the multi-electrode array using a cleanroom swab. Secondary particles randomly located in the center of the array are positioned on working microelectrodes using a 1 µm-wide tungsten needle (Everbeing) mounted on an XYZ micromanipulator under an optical microscope with a 20× long working distance objective lens (Fig. S3, ESI†). After the particle assembly, the array and particles are annealed together under 400 °C for 1 h in air to improve contact between microelectrodes and particles. After annealing, ∼0.1 mg of a slurry of partially delithiated Li_0.6FePO₄ mixed with PVDF is placed on the counter/reference electrode. The chip is dried on a hot plate at 70 °C to remove the solvent from the slurry. The dried chip is transferred to an Ar-filled glove box and ∼3 µL of 1 M LiPF₆ in propylene carbonate (Sigma-Aldrich) is dropped on the chip using a micropipette; the electrolyte only connects the working and counter/reference electrodes, and do not contact the pads at the edge of the chip. A stainless-steel cap is placed over the center of the chip where the particles and electrolyte are located to minimize evaporation.

Counter/reference electrode

The counter/reference electrode Li_0.6FePO₄ was created by chemically delithiating a pristine carbon-coated commercial LiFePO₄ powder from Mitsui Engineering and Shipbuilding. This process was conducted by mixing K₂S₂O₈ (Sigma Aldrich) with LiFePO₄ in water. Each K₂S₂O₈ molecule oxidizes and delithiates 2 LiFePO₄ molecules using the following reaction:

K₂S₂O_8(aq) + 2 LiFePO_4(s) → K₂SO_4(aq) + Li₂SO_4(aq) + LiFePO_4(s)

To make Li_0.6FePO₄, we use a 1 : 5 molar ratio between K₂S₂O₈ and LiFePO₄. After letting the reaction proceed for 1 hour, we centrifuge the sample in water and remove the soluble potassium and lithium sulfates. The remaining water-insoluble Li_0.6FePO₄ powder was dried overnight in an oven at ∼80 °C.

After drying, the partially delithiated Li_0.6FePO₄ was mixed with carbon black, and polyvinylidene fluoride at a mass ratio of ∼70 : 20:10, respectively. This mixture was made into a slurry by adding N-methyl-2-pyrrolidone solvent. A small amount of this slurry, ∼0.1 mg, was placed on one of the larger gold pads to form the counter/reference electrode.

Volume estimation

After NMC secondary particles are relocated on the working microelectrodes, each particle's secondary electron microscopy (SEM) is taken (Fig. S1, ESI†). The SEM was performed on JEOL IT500 SEM. Images were taken with an acceleration voltage of 3 kV and secondary electrons were detected. Next, the region of the secondary particle is identified and thresholded using Adobe Photoshop (Fig. S4, ESI†). Based on the microscope magnification, the number of pixels in this threshold region is counted and directly converted into a projected surface area. The radius (r) of the particle is calculated from the projected area from SEM (Area), whereby Area = πr². The volume of the particle is computed from Volume = 4/3 πr³. The diameter equals twice the radius.

Focused ion beam milling

We use plasma focused ion beam milling to obtain a cross-sectional image of an NMC532 particle on a microelectrode (Fig. 1e). Particles were assembled on working microelectrodes of a multi-electrode array. Thermo Fisher Helios G4 PFIB UXe was used to mill approximately half of an NMC532 particle and take an SEM image of the cross-section. Xe ion beam with a voltage of 30 kV, current of 1.0  nA was used for milling. The SEM image of the cross-section was taken using a through-lens detector at 2 kV and 0.1 nA.

Electrochemical cycling

The potentiostat and the electrodes are electrically connected through two tungsten probe-equipped micromanipulator (Quater XYZ300 series) in an Ar glovebox; the temperature was not controlled but measured to be 29 °C. We utilize a Bio-Logic VMP-300 potentiostat with ultra-low-current modules, whose lowest current range is 1 pico-amp and the ultimate resolution is 80 atto-amp. The electrochemistry is composed of 4 steps, described below and graphically illustrated in Fig. S12 (ESI†). These processes were chosen to ensure that the electrochemistry can be conducted less than 24 hours.

(1) First charge (∼4 h)

Particles are charged using a constant current rate of 0.22 pA µm⁻³ to a cutoff voltage of 4.2 V.

(2) First discharge (∼3 h)

Particles are discharged at a rate of 0.22 pA µm⁻³ to a cutoff voltage of 2.9 V.

(3) Second charge (∼3 h)

Particles are charged at a rate of 0.22 pA µm⁻³ to a cutoff voltage of 4.2 V.

(4) PITT (∼10 h)

(a) The particle is discharged at 0.22 pA µm⁻³ to a cutoff voltage of 4.1 V

(b) The particle is held at OCV for 1 h; the voltage is recorded.

(c) A-15 mV PITT against the last recorded OCV is applied for 20 min. For example, if the recorded OCV is 4.1 V, then the PITT constant voltage will be 4.085 V.

(d) Discharge the particle at 0.22 pA µm⁻³ to a cutoff voltage of 4.0 V; repeat steps (b and c)

(e) Discharge the particle at 0.22 pA µm⁻³ to a cutoff voltage of 3.9 V; repeat steps (b and c)

(f) Discharge the particle at 0.22 pA µm⁻³ to a cutoff voltage of 3.8 V; repeat steps (b and c)

(g) Discharge the particle at 0.22 pA µm⁻³ to a cutoff voltage of 3.7 V; repeat steps (b and c)

(h) Discharge the particle at 0.22 pA µm⁻³ to a cutoff voltage of 3.6 V; repeat steps (b and c)

Due to relatively low currents and high noise (Fig. S12, ESI†), we did not include the results at 3.6 V in our analyses.

Diffusion and reaction time fitting

A least-square fit in Matlab was used to fit D_Li and j₀ in accordance with eqn (1) and (2). A copy of the script is given in the Data Archive. During the data fitting, we sample points equally spaced in a square root of the time scale (Fig. S14, ESI†). We find this approach shows the best fit to eqn (1) and (2) at both short and long-time scales.

Coefficient of determination (R²)

To compute R², the diameter is the independent variable while D_Li and j₀ are the dependent variables y. After conducting a linear or quadratic regression, we calculate R² with the following equation:
y_i refers to each index of the dependent variable y. ŷ_i refers to the predicted value of the dependent variable based on the regression fit (linear or quadratic). ȳ_i represents the mean of all the actual values of y.

To compute the 95% confidence interval of R² (α = 0.025), we apply the following equation based on the Student's t test:

where α is the desired confidence interval percentage, SE_R² is the standard error for R², t is the t-value, k is the number of predictors in the model (1), and n is the total sample size (21). The t-value equals 2.1 under α = 0.025.

Reaction time calculations

The characteristic reaction time can be written as τ_R = Res × Cap. Cap, or capacitance, is the faradaic charge transferred per volt, and Res is the charge transfer resistance. We first separate the material and geometric components of Res and Cap. The particle capacitance (or pseudocapacitance) is given by the volumetric capacitance multiplied by the volume. The volumetric capacitance C_V can be obtained by differentiating the capacity–voltage curve of a coin cell (Fig. S13, ESI†) while assuming the NMC density of 4.77 g cm⁻³. While C_V depends on the voltage, it is assumed to be identical for all particles, consistent with Fig. 2b.

Next, we consider the resistance Res. The resistance relates to the exchange current density j₀ through

where R is the gas constant, T is the temperature, and F is Faraday's Constant. Combined, the reaction time is given by

NMC532/Li coin cell assembly

The porous electrode and coin cells were assembled in the Michigan Battery Laboratory using a standard process. The cathode slurry was composed of 96 wt% NMC532 (BASF TODA), 2 wt% C65 conductive additive, and 2 wt% PVDF binder. The slurry was casted onto 15 µm-thick Al foil. The slurry coated foil was dried at 60 °C an hour and calendered. The final thickness of the electrode was ∼50 µm. 2032 coin cells were assembled by punching 1/2 inch circular electrodes from the prepared foil. The electrode was placed into the coin cell housing, followed by a separator, 75 µL of electrolyte (1 M LiPF₆ in propylene carbonate, Sigma-Aldrich), a Li metal foil, a stainless steel spacer, and a washer spring. Cells were crimped at a pressure of 1000 psi. The cells were then cycled in a Land battery cycler at a constant current of 0.1 C between 2.9 V and 4.2 V for five times to obtain the capacity–voltage curve in Fig. S13 (ESI†).

Author contributions

Y. L. conceived this project. J. M. and L. M. G. developed the single-particle electrochemistry platform and obtained the data. J. M. and R. H. analyzed the data. All authors contributed to the data interpretation and writing of the manuscript.

Data availability

All electrochemical and imaging data is available at the Materials Commons Data Archive, at https://doi.org/10.13011/m3-pnh3-nj57. The photomask design files and the Matlab fitting scripts are also located in this archive.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

This work was supported by LG Energy Solution, Battery Innovation Contest (BIC), and by startup funding from the University of Michigan College of Engineering. The authors acknowledge the Michigan Center for Materials Characterization for use of the instruments and staff assistance. Fabrication of the microelectrode arrays were conducted at the University of Michigan Lurie Nanofabrication Facility. The authors acknowledge Robert Hovden & Joe Gallegos (University of Michigan) for assistance with experiments, and Steve Harris (Lawrence Berkeley National Laboratory), Kang Xu (Army Research Laboratory), William Gent (Sila Nanotechnology), Alec Talin (Sandia National Laboratories), and Vishwas Goel & Katsuyo Thornton (University of Michigan) for insightful discussions.

References

1. A. Sood, A. D. Poletayev, D. A. Cogswell, P. M. Csernica, J. T. Mefford, D. Fraggedakis, M. F. Toney, A. M. Lindenberg, M. Z. Bazant and W. C. Chueh, Nat. Rev. Mater., 2021, 6, 847–867.
2. M. Huang, M. Schwacke, M. Onen, J. del Alamo, J. Li and B. Yildiz, Adv. Mater., 2022, 2205169.
3. V. Rai, R. S. Singh, D. J. Blackwood and D. Zhili, Adv. Eng. Mater., 2020, 22, 2000082.
4. W. Li, E. M. Erickson and A. Manthiram, Nat. Energy, 2020, 5, 26–34.
5. Y. Li and W. C. Chueh, Annu. Rev. Mater. Res., 2018, 48, 137–165.
6. P.-C. Tsai, B. Wen, M. Wolfman, M.-J. Choe, M. S. Pan, L. Su, K. Thornton, J. Cabana and Y.-M. Chiang, Energy Environ. Sci., 2018, 11, 860–871.
7. B. Wen, Z. Deng, P.-C. Tsai, Z. W. Lebens-Higgins, L. F. J. Piper, S. P. Ong and Y.-M. Chiang, Nat. Energy, 2020, 5, 578–586.
8. M. Ge, S. Wi, X. Liu, J. Bai, S. Ehrlich, D. Lu, W.-K. Lee, Z. Chen and F. Wang, Angew. Chem., Int. Ed., 2021, 60, 17350–17355.
9. M. Doyle, T. F. Fuller and J. Newman, J. Electrochem. Soc., 1993, 140, 1526.
10. K. Ando, Y. Yamada, K. Nishikawa, T. Matsuda, D. Imamura and K. Kanamura, ACS Appl. Energy Mater., 2018, 1, 4536–4544.
11. A. Verma, K. Smith, S. Santhanagopalan, D. Abraham, K. P. Yao and P. P. Mukherjee, J. Electrochem. Soc., 2017, 164, A3380.
12. R. Xu, Y. Yang, F. Yin, P. Liu, P. Cloetens, Y. Liu, F. Lin and K. Zhao, J. Mech. Phys. Solids, 2019, 129, 160–183.
13. S. Li, Z. Jiang, J. Han, Z. Xu, C. Wang, H. Huang, C. Yu, S.-J. Lee, P. Pianetta, H. Ohldag, J. Qiu, J.-S. Lee, F. Lin, K. Zhao and Y. Liu, Nat. Commun., 2020, 11, 4433.
14. X. Lu, X. Zhang, C. Tan, T. M. M. Heenan, M. Lagnoni, K. O’Regan, S. Daemi, A. Bertei, H. G. Jones, G. Hinds, J. Park, E. Kendrick, D. J. L. Brett and P. R. Shearing, Energy Environ. Sci., 2021, 14, 5929–5946.
15. G. Sun, T. Sui, B. Song, H. Zheng, L. Lu and A. M. Korsunsky, Extreme Mech. Lett., 2016, 9, 449–458.
16. X. Lu, A. Bertei, D. P. Finegan, C. Tan, S. R. Daemi, J. S. Weaving, K. B. O’Regan, T. M. M. Heenan, G. Hinds, E. Kendrick, D. J. L. Brett and P. R. Shearing, Nat. Commun., 2020, 11, 2079.
17. A. Quinn, H. Moutinho, F. Usseglio-Viretta, A. Verma, K. Smith, M. Keyser and D. P. Finegan, Cell Rep. Phys. Sci., 2020, 1, 100137.
18. S. Han, J. Park, W. Lu and A. M. Sastry, J. Power Sources, 2013, 240, 155–167.
19. X. He, H. Sun, X. Ding and K. Zhao, J. Phys. Chem. C, 2021, 125, 10284–10294.
20. M. E. Spira and A. Hai, Nat. Nanotech., 2013, 8, 83–94.
21. D. J. Miller, C. Proff, J. G. Wen, D. P. Abraham and J. Bareño, Adv. Energy Mater., 2013, 3, 1098–1103.
22. X. Li, N. Li, K.-L. Zhang, J. Huang, S. Jiao, H.-S. Chen and W.-L. Song, Angew. Chem., Int. Ed., 2022, 61, e202205394.
23. L. Danis, S. M. Gateman, C. Kuss, S. B. Schougaard and J. Mauzeroll, ChemElectroChem, 2017, 4, 6–19.
24. Y. Takahashi, T. Yamashita, D. Takamatsu, A. Kumatani and T. Fukuma, Chem. Commun., 2020, 56, 9324–9327.
25. T. Yamamoto, T. Ando, Y. Kawabe, T. Fukuma, H. Enomoto, Y. Nishijima, Y. Matsui, K. Kanamura and Y. Takahashi, Anal. Chem., 2021, 93, 14448–14453.
26. C. Tan, A. S. Leach, T. M. M. Heenan, H. Parks, R. Jervis, J. N. Weker, D. J. L. Brett and P. R. Shearing, Cell Rep. Phys. Sci., 2021, 2, 100647.
27. N. Sharma, L. S. de Vasconcelos, S. Hassan and K. Zhao, Nano Lett., 2022, 22, 5883–5890.
28. R. Ruess, S. Schweidler, H. Hemmelmann, G. Conforto, A. Bielefeld, D. A. Weber, J. Sann, M. T. Elm and J. Janek, J. Electrochem. Soc., 2020, 167, 100532.
29. E. Trevisanello, R. Ruess, G. Conforto, F. H. Richter and J. Janek, Adv. Energy Mater., 2021, 11, 2003400.
30. F. La Mantia, C. D. Wessells, H. D. Deshazer and Y. Cui, Electrochem. Commun., 2013, 31, 141–144.
31. S. Burkhardt, M. S. Friedrich, J. K. Eckhardt, A. C. Wagner, N. Bohn, J. R. Binder, L. Chen, M. T. Elm, J. Janek and P. J. Klar, ACS Energy Lett., 2019, 4, 2117–2123.
32. H.-J. Noh, S. Youn, C. S. Yoon and Y.-K. Sun, J. Power Sources, 2013, 233, 121–130.
33. S.-K. Jung, H. Gwon, J. Hong, K.-Y. Park, D.-H. Seo, H. Kim, J. Hyun, W. Yang and K. Kang, Adv. Energy Mater., 2014, 4, 1300787.
34. R. Weber, C. R. Fell, J. R. Dahn and S. Hy, J. Electrochem. Soc., 2017, 164, A2992.
35. J. Li, H. Li, W. Stone, R. Weber, S. Hy and J. R. Dahn, J. Electrochem. Soc., 2017, 164, A3529.
36. E. J. Cheng, K. Hong, N. J. Taylor, H. Choe, J. Wolfenstine and J. Sakamoto, J. Eur. Ceram. Soc., 2017, 37, 3213–3217.
37. J. Li, F. Yang, X. Xiao, M. W. Verbrugge and Y.-T. Cheng, Electrochim. Acta, 2012, 75, 56–61.
38. J. Li, X. Xiao, F. Yang, M. W. Verbrugge and Y.-T. Cheng, J. Phys. Chem. C, 2012, 116, 1472–1478.
39. H. Lee, S. Yang, S. Kim, J. Song, J. Park, C.-H. Doh, Y.-C. Ha, T.-S. Kwon and Y. M. Lee, Curr. Opin. Electrochem., 2022, 34, 100986.
40. T. R. Jow, S. A. Delp, J. L. Allen, J.-P. Jones and M. C. Smart, J. Electrochem. Soc., 2018, 165, A361.
41. J. Park, H. Zhao, S. D. Kang, K. Lim, C.-C. Chen, Y.-S. Yu, R. D. Braatz, D. A. Shapiro, J. Hong, M. F. Toney, M. Z. Bazant and W. C. Chueh, Nat. Mater., 2021, 20, 991–999.
42. A. C. Wagner, N. Bohn, H. Geßwein, M. Neumann, M. Osenberg, A. Hilger, I. Manke, V. Schmidt and J. R. Binder, ACS Appl. Energy Mater., 2020, 3, 12565–12574.
43. Y. Wei, J. Zheng, S. Cui, X. Song, Y. Su, W. Deng, Z. Wu, X. Wang, W. Wang, M. Rao, Y. Lin, C. Wang, K. Amine and F. Pan, J. Am. Chem. Soc., 2015, 137, 8364–8367.
44. J. Schmalstieg, C. Rahe, M. Ecker and D. U. Sauer, J. Electrochem. Soc., 2018, 165, A3799.
45. S. Cui, Y. Wei, T. Liu, W. Deng, Z. Hu, Y. Su, H. Li, M. Li, H. Guo, Y. Duan, W. Wang, M. Rao, J. Zheng, X. Wang and F. Pan, Adv. Energy Mater., 2016, 6, 1501309.
46. R. Amin and Y.-M. Chiang, J. Electrochem. Soc., 2016, 163, A1512.
47. V. Charbonneau, A. Lasia and G. Brisard, J. Electroanal. Chem., 2020, 875, 113944.
48. R. Chen, T. Zhao, X. Zhang, L. Li and F. Wu, Nanoscale Horiz., 2016, 1, 423–444.
49. M. Ecker, T. K. D. Tran, P. Dechent, S. Käbitz, A. Warnecke and D. U. Sauer, J. Electrochem. Soc., 2015, 162, A1836.
50. I. A. Moiseev, A. A. Savina, A. D. Pavlova, T. A. Abakumova, V. S. Gorshkov, E. M. Pazhetnov and A. M. Abakumov, Energy Adv., 2022, 1, 677–681.
51. J. R. Wilson, J. S. Cronin, S. A. Barnett and S. J. Harris, J. Power Sources, 2011, 196, 3443–3447.
52. G. W. Nam, N.-Y. Park, K.-J. Park, J. Yang, J. Liu, C. S. Yoon and Y.-K. Sun, ACS Energy Lett., 2019, 4, 2995–3001.
53. H. Liu, M. Wolfman, K. Karki, Y.-S. Yu, E. A. Stach, J. Cabana, K. W. Chapman and P. J. Chupas, Nano Lett., 2017, 17, 3452–3457.
54. I. Hamam, R. Omessi, D. Rathore, C. Geng, R. Cooke, K. Plucknett, D. P. Bishop, N. Zaker, G. A. Botton, C. Yang and J. R. Dahn, Cell Rep. Phys. Sci., 2022, 3, 100714.
55. J. Lim, Y. Li, D. H. Alsem, H. So, S. C. Lee, P. Bai, D. A. Cogswell, X. Liu, N. Jin, Y. Yu, N. J. Salmon, D. A. Shapiro, M. Z. Bazant, T. Tyliszczak and W. C. Chueh, Science, 2016, 353, 566–571.
56. A. R. Akbashev, ACS Catal., 2022, 12, 4296–4301.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ee00953j

---