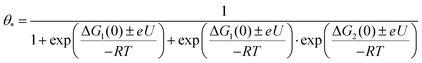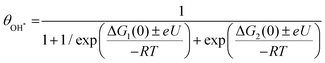Boosting electrochemical methane conversion by oxygen evolution reactions on Fe–N–C single atom catalysts

Abstract

Electrochemical methane conversion is promising for direct conversion even at ambient temperature, but requires delicate control of the competing reactions of the electrochemical oxygen evolution reaction (OER) to improve efficiency and productivity. Here we employ Fe–N–C single atom catalysts (SACs) to achieve high faradaic efficiency and ethanol conversion productivity in OER-assisted methane oxidation. We computationally identify a potential region that maintains stable active oxygen on Fe–N–C SACs where the potential limiting step for the OER is OOH* formation. We also present a reaction pathway for the spontaneous oxidation of methane by the active oxygen, production of methanol, and conversion to ethanol by deprotonation. The Fe–N–C SAC achieves methane-to-ethanol conversion with a high production rate of 4668.3 μmol g_cat⁻¹ h⁻¹ with a selectivity of 85% under the application of 1.6 V_RHE. The faradaic efficiency (FE) is 68%, far exceeding previous results. Furthermore, we demonstrate a direct gas diffusion flow cell to enhance the mass transfer of methane. Conversion in the flow cell achieves ethanol production rates of up to 11 480.6 μmol g_cat⁻¹ h⁻¹.

---

Broader context

Oxidation of methane with high bond enthalpy tends to result in complete oxidation. Recently, instead of conventional thermochemical catalysts, electrochemical catalysts have been spotlighted for their capability for the partial oxidation of methane at low temperatures. Nonetheless, many electrocatalysts exhibit relatively low faradaic efficiencies due to competition with the electrochemical oxygen evolution reaction. In this study, we achieve high faradaic efficiency methane oxidation by employing a Fe single-atom catalyst that evades the oxygen evolution reaction. The Fe single atom catalyst has the feature of making OOH* formation a potential limiting step in the oxygen evolution reaction step, allowing the potential to maintain a stable O* intermediate. We increase the Faraday efficiency with the oxidation of methane by this O*. We achieve an ethanol production rate of 4668.3 μmol g_cat⁻¹ h⁻¹ with 68% FE and 85% selectivity using the Fe single atom catalyst. Furthermore, we introduce a flow cell with a direct gas diffusion electrode to achieve continuous reaction while overcoming the low mass transfer of methane in an aqueous solution. The flow cell reaction achieves a greatly improved ethanol production rate of 11 480.6 μmol g_cat⁻¹ h⁻¹.

As methane becomes a rich resource with shale gas and natural gas development, energy-efficient use of methane or conversion to high-value-added chemicals is highly demanded.^1–3 The conversion of methane to alcohol is highly favored because alcohol is transport-efficient and can be used directly as a fuel or raw material for synthesizing plastics or various hydrocarbons.^1,4 Although indirect methane-to-methanol conversion based on syngas produced by steam reforming is commercially available, the multi-step process and high energy consumption impair the economic viability of this process.^5–7 Therefore, the direct conversion of methane to alcohol is highly pursued.^8,9

Recent electrochemical approaches have shown promising results for the direct conversion of methane-alcohol at ambient temperature.^10–12 The electrochemical approach exhibits distinctive features compared to conventional thermochemical conversion in terms of catalyst activation, conversion reaction, and product extraction.¹³ First, this approach can promote active oxygen species onto the catalyst from an aqueous medium without a separate oxidizing agent by electrochemical oxygen evolution reaction (OER).^14,15 In addition, modulation of the electrical potential lowers the barrier energy in the electrochemical reaction pathway, thus facilitating the conversion.¹⁶ Besides, the aqueous medium promotes the conversion by stabilizing the intermediate by solvation and allows the immediate extraction of the alcohol product with high solubility for alcohol.¹⁷ Zheng and co-workers have demonstrated room-temperature electrochemical methane oxidation with Mg-based metal–organic framework catalysts. They achieved a liquid product conversion rate of 126.6 μmol g_cat⁻¹ h⁻¹ at the electrode potential of 1.60 V_RHE.¹⁸ Singh and co-workers have presented electrochemical conversion by a bimetallic Cu₂O₃/TiO₂ catalyst, achieving methanol production of 3.44 μmol g_cat⁻¹ h⁻¹.¹⁹ Zheng and co-workers have achieved an electrochemical methane–ethanol conversion using a Rh/ZnO nanosheet catalyst, resulting in an ethanol production rate of 789 μmol g_cat⁻¹ h⁻¹ with a selectivity of 85%.²⁰

Despite these achievements, electrochemical methane conversion often exhibits low faradaic efficiency (FE). Indeed, electrochemical methane conversion using Rh/ZnO nanosheets, Mg-MOF-74, and bimetallic Cu₂O₃/TiO₂ catalysts reported low faradaic efficiencies of 22.5%, 10.9%, and 6%, respectively.^18–20 The lower faradaic efficiency in OER-assisted methane oxidation can be attributed to the faster OER than methane oxidation.²¹ Specifically, the rapid evolution of the OER intermediate O* to O₂ lowers the methane oxidation rate. After all, low FE causes low methane conversion rates. Therefore, an electrocatalyst that maintains stable active oxygen species without activation of the OER is a prerequisite for high methane conversion rates.

In this study, we demonstrate OER-assisted high-efficiency electrochemical methane conversion using Fe–N–C single atom catalysts (SACs) (Fig. 1). Fe–N–C SACs have been widely used as high-efficiency electrocatalysts for oxygen reduction reactions.²² Our strategy is based on the fact that the Fe–N–C SAC has the OOH* formation step as potential limiting in the OER, allowing an electrode potential that keeps the O* intermediate in the preceding step stable. As a contrasting example, the α-Fe₂O₃ catalyst has the formation of the first intermediate, OH*, as a potential limiting step (Fig. S1, ESI†), so that at any potential that makes this step spontaneous, the O* intermediate evolves rapidly to O₂. DFT calculations and microkinetic analysis confirm the electrode potential region of 1.26–1.79 V_RHE, which retains the O* intermediate on Fe–N–C SAC without OER activation. With O* stable in this potential region, we achieve methane-to-ethanol conversion with a high FE. Specifically, we reach the highest ethanol production rate of 4668.3 μmol g_cat⁻¹ h⁻¹ with a selectivity of 85% at 1.6 V_RHE. Here, the FE for methane-to-ethanol conversion is 68%, a significant improvement over previous results. Furthermore, we present a flow cell reaction using a gas diffusion electrode in electrochemical methane conversion. This reactor allows for improved mass transfer of methane to the catalyst, achieving an ethanol production rate of 11 480.6 μmol g_cat⁻¹ h⁻¹, a 2.5-fold improvement over the batch reaction.

Fig. 1 Scheme depicting oxidation of methane by O* in the OER, and its conversion to ethanol.

Preparation of Fe–N–C SACs

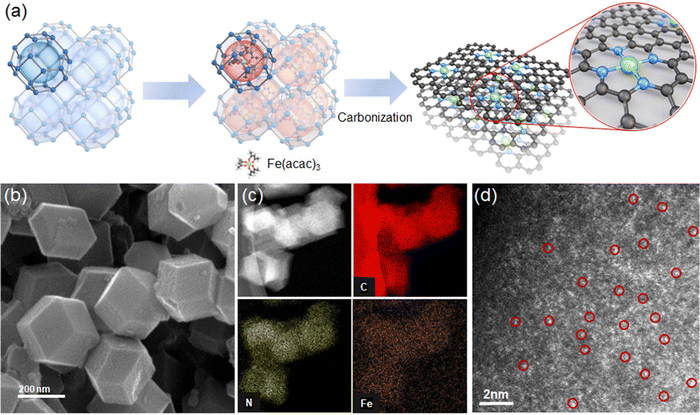
We prepare Fe–N–C SACs by impregnating Fe(acac)₃ in cages in a zeolite imidazole framework (ZIF-8) and then pyrolytic carbonization at 900 °C. During carbonization, ZIF-8 is converted to nitrogen-doped carbon, and Fe(acac)₃ in the cage is reduced to Fe and anchored onto nitrogen (Fig. 2a).

Fig. 2 Preparation of Fe–N–C SAC. (a) A scheme depicting the preparation of a Fe–N–C SAC. The cage of ZIF-8 contains one Fe(acac)₃ molecule. The carbonization of Fe(acac)₃-impregnated ZIF-8 forms the active site of single atom Fe–N_x on the N–C substrate. (b) SEM, (c) TEM/element mapping, and (d) HAADF-STEM images of the Fe–N–C SAC, respectively. Single atom Fe is highlighted in the HAADF-STEM image.

The SEM image shows Fe–N–C SAC nanoparticles with a size of 200–300 nm with a dodecahedral shape (Fig. 2b). TEM and its elemental mapping show uniform dispersion of N and Fe in C medium (Fig. 2c). The XRD pattern of Fe–N–C is consistent with that of N–C without Fe; the pattern shows broad peaks corresponding to graphitic carbon at 24° and 42° (Fig. S2, ESI†). No independent phases of Fe such as metallic Fe or Fe clusters are observed. We observe Fe–N–C SACs by high-angle annular dark-field scanning transmission electron (HAADF-STEM) analysis. The image confirms independently dispersed bright dots corresponding to Fe single atoms (Fig. 2d). The ICP-MS analysis confirms a loading of Fe of about 1.45 wt%. This content falls within the range 0.36–3.46 wt% of Fe content in prior Fe–N–C catalysts.^23–25

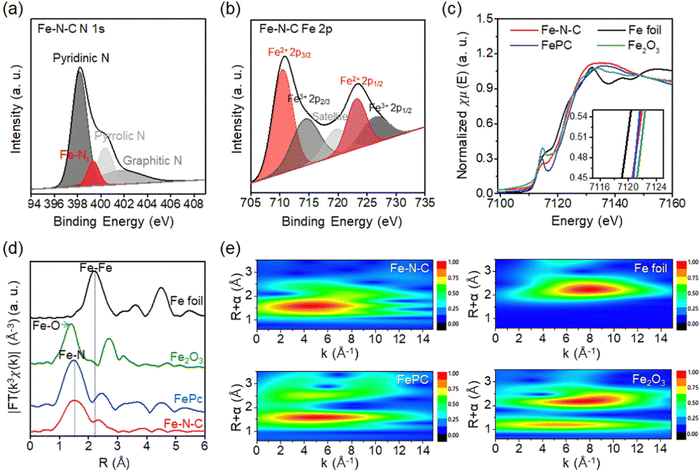
The chemical state of the nitrogen atom in Fe–N–C SAC is analyzed by the XPS spectrum (Fig. S3, ESI†). Specifically, the N 1s XPS spectrum is deconvolved into four sub-peaks. These peaks consist of pyridinic N (398.6 eV), N coordinated with Fe atoms (Fe–N_x; 400 eV), pyrrolic N (399.9 eV), and graphitic N (401.0 eV) species (Fig. 3a).^26,27 The spectrum exhibits a peak corresponding to Fe–N_x that locates between pyridinic N and pyrrolic N species, which is consistent with previous experimental and computational studies of Fe–N–C.²⁷ The Fe 2p XPS spectrum of Fe–N–C SAC is deconvolved into five peaks, which consist of peaks corresponding to Fe²⁺ (710.5 eV) and Fe³⁺ (714.4 eV) in the 2p_3/2 orbital, peaks corresponding to Fe²⁺ (723.2 eV) and Fe³⁺ (725.4 eV) in the 2p_1/2 orbital and satellite peaks (Fig. 3b).²⁸ First of all, the binding energies for the peaks of Fe 2p_3/2 and Fe 2p_1/2 (710.5 eV and 723.2 eV) are higher than those previously reported for the peaks of metallic Fe (707.4 eV and 719.7 eV).²⁹ This result indicates that the Fe is in an oxidized state rather than a metallic state. The deconvoluted peaks correspond to various valence states for the Fe species, but the strong peak for Fe²⁺ confirms that the Fe–N–C coordination is dominant.³⁰

Fig. 3 Characterization. (a) XPS N 1s and (b) Fe 2p spectra of Fe–N–C SACs. (c) Normalized Fe K-edge XANES spectrum, (d) Fe K-edge Fourier transform, and (e) wavelet transform contour plot of Fe K-edge of Fe–N–C SAC. The spectra of Fe foil, Fe₂O₃ and FePc are also displayed for comparison. The inset of (c) exhibits first-derivative curves of spectra.

To analyze the local coordination environment of Fe SAC, X-ray absorption near-edge structure (XANES) and extended X-ray absorption fine structure (EXAFS) are utilized (Fig. 3c).³¹ The Fe K-edge XANES profile of Fe–N–C SAC shows that the near-edge absorption energy is located between the Fe foil and Fe₂O₃, and is similar to that of iron phthalocyanine (FePc). This indicates that the valence state of Fe is between Fe⁰ and Fe³⁺, close to Fe²⁺.³² This result is consistent with the Fe 2p XPS result, which showed a dominant peak for Fe²⁺. The Fourier transform (FT) k²-weighted EXAFS spectrum of the Fe K-edges is presented in Fig. 3d. The spectrum of Fe–N–C SAC exhibits one strong peak without a high shell peak. Furthermore, the peak at about 1.5 Å does not overlap with the Fe–Fe bond of metallic Fe (∼2.2 Å) or the Fe–O bond of Fe₂O₃ (∼1.4 Å), but aligns with ∼1.5 Å in FePc. These results confirm the dispersion of Fe single atoms with Fe–N coordination environments. To further characterize the Fe single atom, we present a wavelet transform (WT)-EXAFS, which provides a better resolution of EXAFS in k and R space (Fig. 3e).³³ The Fe–N–C SAC exhibits only one intensity maximum at 5 Å⁻¹ (Fig. 3e). This feature is similar to FePC exhibiting one peak at 5 Å⁻¹, but distinctly different from Fe foil (8 Å⁻¹) and Fe₂O₃ (5 Å⁻¹ and 8 Å⁻¹). This comparison reconfirms a single Fe atom with Fe–N coordination.

Analysis of OER-assisted methane oxidation

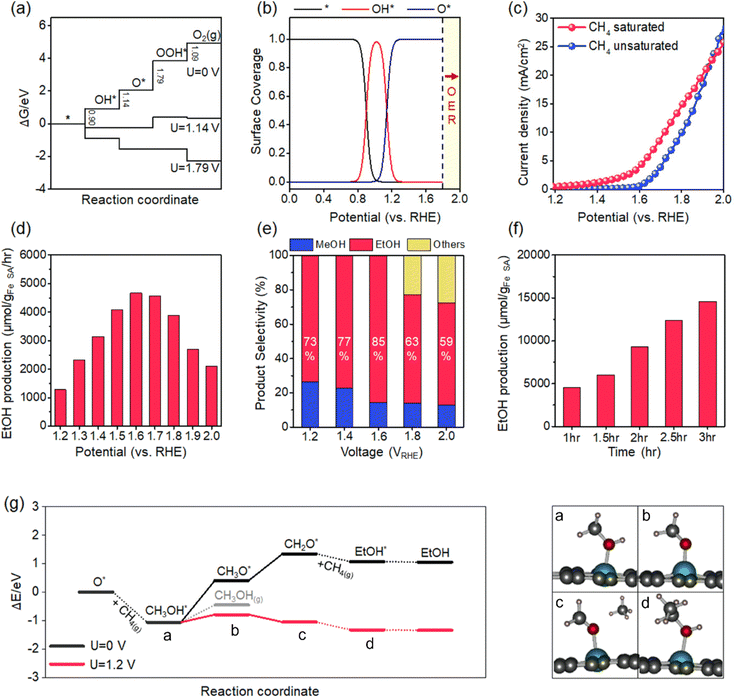
We obtained energy diagrams for the OER on Fe–N–C SAC by DFT calculation. The OER on Fe–N–C SAC consists of four typical electron transfer steps (Fig. 4a); adsorption of OH*, formation of O* by deprotonation, formation of OOH* by reaction with OH, and production of O₂ by deprotonation. Among these, the OOH* formation exhibits the largest free energy change. In this energy diagram, the formation of O* requires an anodic potential of 1.14 V_RHE. On the other hand, at a potential of 1.79 V_RHE, the energy change of the four steps goes downhill, and thus O₂ evolves spontaneously. Therefore, the Fe–N–C SAC can maintain a stable O* that is not quickly consumed by the OER in the potential range of 1.14–1.79 V_RHE. From the OER energy profile point of view, many electrocatalytic oxides do not stabilize O* either because the OH*/O* formation step is limiting (TiO₂,³⁴ LaCuO₃³⁵) or the O₂ formation step is limiting (IrO₂,³⁶ TaO₂³⁷).

Fig. 4 Methane conversion. (a) The free energy diagram for the OER on Fe–N–C SAC. The energy changes at potentials of zero (U = 0 V), 1.14 V, and 1.79 V are compared. (b) The surface coverage of OER intermediates on Fe–N–C catalysts as a function of electrode potential. (c) The LSV curves with and without methane saturation in the electrolyte. (d) The production rate for ethanol at various electrode potentials. (e) The selectivity of oxygenate products at various potentials. (f) The ethanol production as a function of reaction time. (g) Calculated energy diagrams for the reaction coordinate for methane–ethanol conversion at 0 V and 1.2 V. The solid and dashed lines represent the electrochemical and thermochemical steps, respectively. The cartoons are atomic configurations corresponding to each reaction coordinate.

To discriminate the OER intermediates on the Fe–N–C SAC surface according to the anodic potential, we further perform microkinetic analysis (see Supplementary note, ESI†). Considering that the formation of OOH* is a rate-determining step, the site coverage for free active sites (θ_*), OH* (θ_OH*) and O* (θ_O*) on the catalyst according to the electrode potential is described by the following equation, respectively.

where ΔG₁ and ΔG₂ are the Gibbs energy changes for the reaction in which OH* and O* are formed, R is the gas constant, U is the electrode potential, and T is the temperature. A plot of these equations is presented in Fig. 4b. At increasing electrode potential, OH* occupies the catalyst surface with a threshold voltage of about 0.90 V_RHE, while O* forms predominantly on the surface above about 1.14 V_RHE, and then O₂ evolves to a fast OER above 1.79 V_RHE. This result reaffirms a particular potential range with a dominant coverage of O* as analyzed in the DFT calculation.

We measure the LSV profile for Fe–N–C catalysts with and without methane saturation in the electrolyte (Fig. 4c). For this measurement, the Fe–N–C catalyst is coated onto a graphite foil; the coating is obtained by casting a dispersion of the Fe–N–C catalyst in a Nafion-dissolved ethanol solution (1% (v/v)) and subsequently drying at 100 °C for 24 hours. The Nafion binder used was found to be electrochemically inactive (Fig. S4, ESI†). The LSV for N–C without Fe is presented in Fig. S5 (ESI†). In the bare electrolyte, the curve exhibits a sharp increase with an inflection point at about 1.6 V_RHE. This oxidation current corresponds to the catalytic OER. At the potential of 2.0 V_RHE, vigorous generation of O₂ is observed at the Fe–N–C catalyst electrode along with the generation of H₂ at the Pt counter electrode (Fig. S6, ESI†). In contrast, in the methane-saturated electrolyte, the curve exhibits an earlier threshold point of the current at 1.2 V_RHE. Higher oxidation current than bare electrolytes in the range of 1.2–1.6 V_RHE is caused by methane oxidation, not the OER. We observe that the evolution of O₂ at the Fe–N–C catalytic electrode at a potential of 1.6 V_RHE is relatively weak compared to that of H₂ at Pt (Fig. S6, ESI†). On the other hand, at a potential of 2.0 V_RHE, vigorous evolution of O₂ together with H₂ similar to that in the bare electrolyte is observed. The reaction utilizing ¹³C-labeled methane at 1.6 V_RHE identifies the liquid phase product of ethanol (Fig. S7, ESI†). Briefly, the LSV analysis confirms methane oxidation by O* in the potential range where stable O* is predicted by DFT and microkinetic analyses.

We measure the ethanol production rates on Fe–N–C SACs in the electrode potential range of 1.2–2.0 V_RHE. As the potential increases, the ethanol production rate increases, achieving a maximum production rate of 4668.3 μmol g_cat⁻¹ h⁻¹ at the potential of 1.6 V_RHE. The increase in the production rate is attributed to the faster formation of O* and energetic stabilization of the electrochemical conversion pathway at higher potentials, as confirmed later. At 1.6 V_RHE, the FE represents up to 68%. The faradaic efficiency, which falls short of unity, may be associated with the generation of other oxygenates, including methanol (>10% FE), and also to the frustration of methane oxidation due to transitions to other OER intermediates (<10% FE). Nonetheless, this FE value is significantly higher than the previous results (Table S1, ESI†).^18–20 This high FE leads to a high conversion rate. The peak production rate (4668.3 μmol g_cat⁻¹ h⁻¹) surpasses previous electrochemical methane conversion results (Table S2, ESI†). Even in comparison by current density for methane oxidation, our achievement (4.9 mA cm⁻²) outperforms previous electrocatalytic results; 1.28 mA cm⁻² for NiO/ZrO₂, 3.7 mA cm⁻² for ZrO₂-NT/Co₃O₄, 4.6 mA cm⁻² for CoNiO_x and 1.0 mA cm⁻² for CuO/CeO₂. On the other hand, above the potential of 1.6 V_RHE, the production rate decreases (Fig. 4d). This range corresponds to the potential for a current increase due to the OER in LSV measurement. Thus, the decrease in ethanol production rate is aggravated by the fast OER.

The selectivity for methane conversion at various electrode potentials is shown in Fig. 4e. At 1.6 V_RHE, the selectivity to ethanol reaches 85%. As another oxygenates product, methanol is mainly detected. At lower potentials than 1.6 V_RHE, the selectivity to methanol increases. In contrast, the higher the potential, the higher the selectivity for C₃ products such as acetone. As presented later, the high selectivity to methanol at low potentials is rationalized by the relative favoring of methanol desorption due to the slow rate of methanol-to-ethanol conversion. At higher potentials, ethanol will favor deprotonation as in the methanol-to-ethanol conversion pathway, resulting in conversion to higher-order products such as acetone (see Supplementary note, ESI†). At 1.6 V_RHE, the production of ethanol as a function of reaction time increases linearly (Fig. 4f). At 3 h, the ethanol production achieves 14576.4 μmol g_cat⁻¹ (the amount of total oxygenates is 17148.7 μmol g_cat⁻¹).

We present a thermodynamically favorable reaction route for methane–ethanol conversion by DFT calculations (Fig. 4g). First, the initial state in which O* is formed on the Fe–N–C SAC is considered. The presence of active oxygen on the catalyst surface is confirmed by XPS analysis (Fig. S8, ESI†). The O* reacts with methane to form CH₃OH* with accompanying cleavage of the methane C–H bond. This process is an exothermic reaction with an energy change of −1.06 eV. This process is reminiscent of methane activation at the Fe-oxo site; it was observed that the high electron-affinity Fe-oxo site activates the C–H bond of methane even at low temperatures to form methoxy species.³⁸ Note that O*-mediated methane activation is pivotal for the highly selective partial oxidation of methane; various noble metals and noble metal oxide catalysts activate methane at low temperatures through the methane σ-complex, which causes overoxidation.^39,40 Next, the adsorbed methanol is electrochemically deprotonated. The deprotonation of CH₃OH* is an endothermic process with an energy change of 0.66 eV. The formation of CH₂O* by further deprotonation is also an endothermic process with an energy change of 0.94 eV. Since these processes proceed in an electrochemical pathway, they become favorable under the anodic electrode potential. The application of 1.2 V_RHE converts these deprotonations into spontaneous processes with limiting energy changes as low as 0.27 eV. Here, the deprotonation on the Fe–N–C catalyst appears to be distinct from that on the oxide catalyst. It has been confirmed that deprotonation on the oxides proceeds by dissociation of C–H bonds.⁴¹ The Fe–N–C catalyst induces the dissociation of O–H bonds. This may be attributed to the weak stabilizing effect of carbonic hydrogen due to the absence of O in the Fe–N–C catalyst.⁴² Furthermore, this deprotonation energy profile rationalizes the relatively high selectivity of methanol at low potentials and the high selectivity of ethanol at high potentials. At low potentials, the desorption of CH₃OH* to methanol is more favorable than the deprotonation. At an increase in potential, the deprotonation of methanol becomes relatively dominant, thereby facilitating its conversion to ethanol. Finally, CH₂O* combines with methane to form ethanol. The carbon in CH₂O* is highly electropositive and thus binds directly to methane.⁴³

Flow cell-assisted electrochemical methane conversion

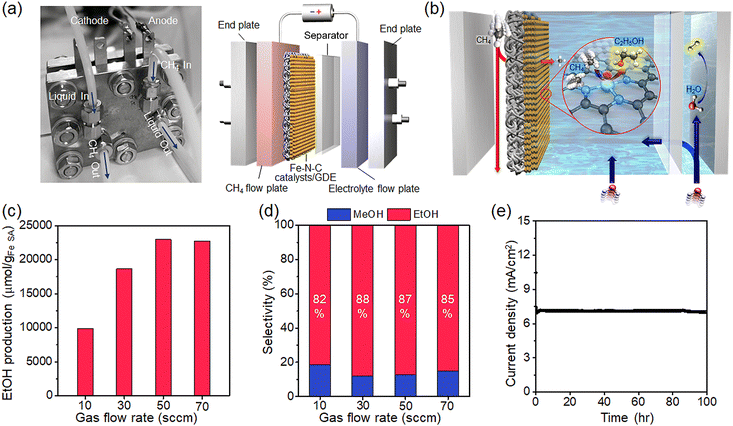
The low solubility and diffusivity of methane in aqueous media are obstacles from a process point of view for electrochemical methane conversion.⁴⁴ To address mass transfer limitations, we employ a flow cell with a gas diffusion electrode (GDE) capable of a direct gas-phase supply of methane. Such flow cells have been applied in the electrochemical reduction of CO₂ to achieve several orders of magnitude higher current densities while maintaining high selectivity compared to batch-type cells,^45,46 but have rarely been employed for methane conversion. Our custom-designed flow cell consists of a methane flow plate, a microporous carbon film immobilized with a Fe–N–C SAC, a porous separator, an electrolyte flow plate, and endplates at both ends (Fig. 5a). The Fe–N–C SAC mixed with Nafion binder is coated on hydrophobic carbon paper to prepare a GDE (Fig. S9, ESI†). The catalyst loading on the GDE was adjusted to 1 mg. The active area of the GDE is 9(3 × 3) cm². The porous separator adopted was the commercially available Zirfon separator. This membrane suppresses the crossover of H₂ formed at the counter electrode to the product flow in the Fe–N–C catalyst/GDE as much as possible.⁴⁷ The methane flow plate and the electrolyte flow plate contain a serpentine flow channel with a cross-section of 239 mm² and also serve as a current collector.

Fig. 5 Methane conversion in a flow cell. (a) The digital camera image of the flow cell. The inlet and outlet of the electrolyte and methane were specified respectively. Schematic diagram of the flow cell configuration consisting of a flow plate, catalyst-coated GDE, separator, and endplate. (b) Scheme for the flow of methane and electrolyte and the reaction at the catalyst surface in the flow cell. (c) The ethanol production as a function of methane flow. (d) The selectivity for various methane flows. (e) Current density to methane conversion versus operating time of the flow cell. The applied voltage is 1.6 V_Pt.

In operation, methane flowing through the flow plate is accompanied by methane diffusion through the GDE layer, transporting the methane to the electrode/electrolyte interface (Fig. 5b). An aqueous electrolyte containing CO₃²⁻ flows over the surface of the GDE but does not penetrate the GDE layer due to the hydrophobicity of the carbon layer (Fig. S10, ESI†). Methane diffused into the GDE dissolves in the electrolyte in contact with the electrode, diffuses into the nearby catalyst, and undergoes a conversion reaction. Here, the diffusion distance of methane to the catalytic surface is significantly shorter,^48,49 and thus the supply of methane is efficient and rapid compared to methane diffusion within the bulk electrolyte of the batch reaction.

We evaluate ethanol production under various methane flow conditions. The ethanol production rate increases as methane flow increases, but the production rate saturates at flow rates above 50 sccm (Fig. 5c). A high flow rate not only improves the solubility of methane by increasing the local pressure, but also improves mass transfer by keeping the diffusion channel constant, which in turn promotes the methane conversion reaction.⁵⁰ On the other hand, too high a flow rate may stagnate the methane conversion efficiency by reducing the area of the electrolyte/catalyst interface or/and destabilizing the electrolyte flow at the catalyst surface by high local pressure.⁵¹ The selectivity of the product at various flow conditions is presented in Fig. 5d; the selectivity maintains high values of 85.5% on average.

We achieve an ethanol production rate of 11 480.6 μmol g_cat⁻¹ h⁻¹ with a selectivity of 87% at 50 sccm. The production rate is 2.5 times higher than the maximum achieved in the batch cell, which immediately shows the effect of improved mass transfer in the flow cell. This production rate significantly improved over previous electrochemical methane conversion (Table S2, ESI†). We evaluate the operational stability of the electrochemical conversion by measuring current values under constant voltage conditions on Fe–N–C-coated GDE electrodes. The current value remains very stable, showing a decrease of only 5% over 100 h (Fig. 5e). After the operation, the HAADF-STEM image of the Fe–N–C catalyst reveals SAC features (Fig. S11, ESI†), and the XRD pattern does not reveal the presence of metallic Fe due to any agglomeration of Fe (Fig. S11, ESI†). The LSV profiles and EIS spectra for methane oxidation on Fe–N–C catalysts at 100 h also overlap the curves from the initial scan, confirming catalytic activity retention (Fig. S12, ESI†).

Conclusion

We exhibit high FE electrochemical methane-to-ethanol conversion by employing a Fe–N–C SAC. DFT analysis of the OER of the Fe–N–C SAC confirms that the formation of the OOH* intermediate is a potential limiting step, so there is an available potential to maintain stable O*. The microkinetic analysis using the calculated Gibbs energy presents an electrode potential that allows dominant O* coverage. At greater than 1.6 V_RHE of the anodic potential, the electrochemical methane conversion exhibits a decrease in the production rate for ethanol. The corresponding electrode potential matches the potential that initiates the OER on the Fe–N–C catalyst, confirming that methane conversion competes with OER at higher potentials. We achieve high production rate methane conversion with high FE by stable O* against the OER at 1.6 V_RHE. We achieve a high FE of 68% at an electrode potential of 1.6 V_RHE, achieving high productivity. The production rate for ethanol is 4668.3 μmol g_cat⁻¹ h⁻¹ with a selectivity of 85%. This productivity surpasses recent electrochemical methane-alcohol conversion results. Besides, we present an electrochemical flow cell that utilizes a gas diffusion layer electrode that enhances low mass transfer in an aqueous medium of methane. We achieve an ethanol production rate of 11 480.6 μmol g_cat⁻¹ h⁻¹ at a methane flow rate of 50 sccm and present stable operation for at least 100 h.

Author contributions

C. K., H. M., and J. K. conducted the experiments and analyzed the data. C. K. also drafted the initial manuscript. J. H. M. supervised the data acquisition and processing, and wrote and edited the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the National Research Foundation of Korea for their support (grants 2021M3D3A1A01022112 and 2022R1A2C2005228) and the Pohang Accelerator Laboratory (PAL) for access to the 7D XAFS beamline.

References

1. M. Ravi, M. Ranocchiari and J. A. van Bokhoven, Angew. Chem., Int. Ed., 2017, 56, 16464–16483.
2. E. G. Nisbet, E. J. Dlugokencky and P. Bousquet, Science, 2014, 343, 493–495.
3. D. Saha, H. A. Grappe, A. Chakraborty and G. Orkoulas, Chem. Rev., 2016, 116, 11436–11499.
4. C. Karakaya and R. J. Kee, Prog. Energy Combust. Sci., 2016, 55, 60–97.
5. P. Tang, Q. Zhu, Z. Wu and D. Ma, Energy Environ. Sci., 2014, 7, 2580–2591.
6. Z. Zhu, W. Guo, Y. Zhang, C. Pan, J. Xu, Y. Zhu and Y. Lou, Carbon Energy, 2021, 3, 519–540.
7. F. Schüth, Science, 2019, 363, 1282–1283.
8. B. E. R. Snyder, P. Vanelderen, M. L. Bols, S. D. Hallaert, L. H. Böttger, L. Ungur, K. Pierloot, R. A. Schoonheydt, B. F. Sels and E. I. Solomon, Nature, 2016, 536, 317–321.
9. P. Tomkins, M. Ranocchiari and J. A. van Bokhoven, Acc. Chem. Res., 2017, 50, 418–425.
10. M. Ma, B. J. Jin, P. Li, M. S. Jung, J. I. Kim, Y. Cho, S. Kim, J. H. Moon and J. H. Park, Adv. Sci., 2017, 4, 1700379.
11. A. H. B. Mostaghimi, T. A. Al-Attas, M. G. Kibria and S. Siahrostami, J. Mater. Chem. A, 2020, 8, 15575–15590.
12. S. Yuan, Y. Li, J. Peng, Y. M. Questell-Santiago, K. Akkiraju, L. Giordano, D. J. Zheng, S. Bagi, Y. Román-Leshkov and Y. Shao-Horn, Adv. Energy Mater., 2020, 10, 2002154.
13. X. Meng, X. Cui, N. P. Rajan, L. Yu, D. Deng and X. Bao, Chemistry, 2019, 5, 2296–2325.
14. L. Arnarson, P. S. Schmidt, M. Pandey, A. Bagger, K. S. Thygesen, I. E. Stephens and J. Rossmeisl, Phys. Chem. Chem. Phys., 2018, 20, 11152–11159.
15. Y. Kang, Z. Li, X. Lv, W. Song, Y. Wei, X. Zhang, J. Liu and Z. Zhao, J. Catal., 2021, 393, 20–29.
16. H. Wang, J. Chen, Y. Lin, X. Wang, J. Li, Y. Li, L. Gao, L. Zhang, D. Chao, X. Xiao and J.-M. Lee, Adv. Mater., 2021, 33, 2008422.
17. A. A. Latimer, A. Kakekhani, A. R. Kulkarni and J. K. Nørskov, ACS Catal., 2018, 8, 6894–6907.
18. M. Chen, X. Lv, A. Guan, C. Peng, L. Qian and G. Zheng, J. Colloid Interface Sci., 2022, 623, 348–353.
19. A. Prajapati, B. A. Collins, J. D. Goodpaster and M. R. Singh, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2023233118.
20. Z. Xie, M. Chen, Y. Chen, A. Guan, Q. Han and G. Zheng, J. Phys. Chem. C, 2021, 125, 13324–13330.
21. K. Zhang and R. Zou, Small, 2021, 17, 2100129.
22. K. Liu, J. Fu, Y. Lin, T. Luo, G. Ni, H. Li, Z. Lin and M. Liu, Nat. Commun., 2022, 13, 1–8.
23. F. Pan, B. Li, E. Sarnello, Y. Fei, X. Feng, Y. Gang, X. Xiang, L. Fang, T. Li, Y. H. Hu, G. Wang and Y. Li, ACS Catal., 2020, 10, 10803–10811.
24. L. Jiao, G. Wan, R. Zhang, H. Zhou, S.-H. Yu and H.-L. Jiang, Angew. Chem., Int. Ed., 2018, 57, 8525–8529.
25. L. Jiao, R. Zhang, G. Wan, W. Yang, X. Wan, H. Zhou, J. Shui, S.-H. Yu and H.-L. Jiang, Nat. Commun., 2020, 11, 1–7.
26. J. Woo, S. Y. Yang, Y. J. Sa, W.-Y. Choi, M.-H. Lee, H.-W. Lee, T. J. Shin, T.-Y. Kim and S. H. Joo, Chem. Mater., 2018, 30, 6684–6701.
27. J. Han, X. Meng, L. Lu, J. Bian, Z. Li and C. Sun, Adv. Funct. Mater., 2019, 29, 1808872.
28. L. Lin, Q. Zhu and A.-W. Xu, J. Am. Chem. Soc., 2014, 136, 11027–11033.
29. G. Gan, X. Li, S. Fan, Z. Yin, L. Wang and G. Chen, Nano Energy, 2021, 80, 105532.
30. Y. Zhao, K. Watanabe and K. Hashimoto, J. Am. Chem. Soc., 2012, 134, 19528–19531.
31. Y. Chen, S. Ji, Y. Wang, J. Dong, W. Chen, Z. Li, R. Shen, L. Zheng, Z. Zhuang and D. Wang, Angew. Chem., 2017, 129, 7041–7045.
32. X. Ao, Y. Ding, G. Nam, L. Soule, P. Jing, B. Zhao, J. Y. Hwang, J.-H. Jang, C. Wang and M. Liu, Small, 2022, 18, 2203326.
33. H. Fei, J. Dong, M. J. Arellano-Jiménez, G. Ye, N. Dong Kim, E. L. G. Samuel, Z. Peng, Z. Zhu, F. Qin, J. Bao, M. J. Yacaman, P. M. Ajayan, D. Chen and J. M. Tour, Nat. Commun., 2015, 6, 8668.
34. X. Huang, J. Wang, H. B. Tao, H. Tian and H. Xu, Chem. Sci., 2019, 10, 3340–3345.
35. J. S. Yoo, X. Rong, Y. Liu and A. M. Kolpak, ACS Catal., 2018, 8, 4628–4636.
36. A. Zagalskaya and V. Alexandrov, ACS Catal., 2020, 10, 3650–3657.
37. H. Y. Lim, S. O. Park, S. H. Kim, G. Y. Jung and S. K. Kwak, Front. Energy Res., 2021, 9, 606313.
38. F. Göltl, C. Michel, P. C. Andrikopoulos, A. M. Love, J. Hafner, I. Hermans and P. Sautet, ACS Catal., 2016, 6, 8404–8409.
39. S. Xie, Z. Shen, J. Deng, P. Guo, Q. Zhang, H. Zhang, C. Ma, Z. Jiang, J. Cheng and D. Deng, Nat. Commun., 2018, 9, 1–7.
40. Z. Zakaria and S. K. Kamarudin, Renewable Sustainable Energy Rev., 2016, 65, 250–261.
41. J. Yang, Y. Zhou, H. Su and S. Jiang, J. Electroanal. Chem., 2011, 662, 251–256.
42. N. Kruse, M. Rebholz, V. Matolin, G. K. Chuah and J. H. Block, Surf. Sci., 1990, 238, L457–L462.
43. N. Spinner and W. E. Mustain, J. Electrochem. Soc., 2013, 160, F1275.
44. L. C. Jacobson and V. Molinero, J. Phys. Chem. B, 2010, 114, 7302–7311.
45. D. A. Salvatore, D. M. Weekes, J. He, K. E. Dettelbach, Y. C. Li, T. E. Mallouk and C. P. Berlinguette, ACS Energy Lett., 2018, 3, 149–154.
46. D. Ma, T. Jin, K. Xie and H. Huang, J. Mater. Chem. A, 2021, 9, 20897–20918.
47. T. Naito, T. Shinagawa, T. Nishimoto and K. Takanabe, ChemSusChem, 2022, 15, e202102294.
48. D. Salvatore and C. P. Berlinguette, ACS Energy Lett., 2020, 5, 215–220.
49. X. Wu, J. W. Sun, P. F. Liu, J. Y. Zhao, Y. Liu, L. Guo, S. Dai, H. G. Yang and H. Zhao, Adv. Funct. Mater., 2022, 32, 2107301.
50. M. Yarrison, K. R. Cox and W. G. Chapman, Ind. Eng. Chem. Res., 2006, 45, 6770–6777.
51. Z. Xing, L. Hu, D. S. Ripatti, X. Hu and X. Feng, Nat. Commun., 2021, 12, 136.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ee00027c

‡ These authors equally contributed to this work.

---