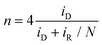A dynamic piezoelectric effect to promote electrosynthesis of hydrogen peroxide

Abstract

Physical field modulation has been regarded as a promising approach to boost the performance of various electrocatalysts and has recently received notable attention. However, such a technique by coupling an external field to controllably enable efficient and green electrosynthesis of hydrogen peroxide (H₂O₂) through a 2e⁻ oxygen reduction reaction (ORR) has not been perceived so far. In order to address the feasibility of this method, a controllable piezoelectric strategy based on the response of intrinsic electric domains to the stimulation of fluid mechanical force was exploited effectively to induce local electric fields on the polarized ceramic catalyst surface during the dynamic ORR. By adjusting the polarization degree of ceramic catalysts, the strength of the local electric field could be accordingly modulated, thus tuning the coverage of OH⁻ ions on the catalyst surface which is beneficial for optimizing the binding strength towards oxygen-containing intermediates and alleviating the disproportionation of the peroxide product.

---

Broader context

A two-electron oxygen reduction reaction (2e⁻ ORR) is considered as a viable route to convert electrical energy into an important chemical (H₂O₂); yet, it is still a formidable challenge to achieve low-cost, highly selective, and stable electrocatalysts to economically and efficiently drive hydrogen peroxide conversion. Within this context, piezoelectric lead zirconate titanate (PZT), the most widely studied commercially available ceramic, was explored as a 2e⁻ ORR electrocatalyst. Based on the piezoelectricity effect, a local electric field was induced on the surface of polarized PZT catalysts during dynamic ORR catalysis. Furthermore, by adjusting the polarization degree of ceramic catalysts, the strength of the local electric field could be accordingly modulated, thus tuning the adsorption/desorption ability of the surface towards OH⁻ and OOH⁻ ions that is beneficial for the utilization of more active sites as well as the reaction kinetics and thermodynamics for the 2e⁻ ORR. As a result, a record-breaking activity towards the 2e⁻ ORR has been achieved with optimized PZT amongst all other previously reported transition metal oxide electrocatalysts. Most notably, such a controllable piezoelectric strategy could also be extended to activate the 2e⁻ ORR performance of lead-free piezoelectric electrocatalysts.

Introduction

Efficient hydrogen peroxide (H₂O₂) production in an economic and green way is of utmost significance to energy and societal development, yet the most widely employed route to produce H₂O₂ is industrial anthraquinone cycling which suffers from intensive energy consumption, complex supportive infrastructure, and massive organic waste emissions.^1–5 Compared with such a conventional method, the electrocatalytic oxygen reduction reaction (ORR) undergoing two-electron transfer can well surmount the above-mentioned drawbacks during the synthesis of H₂O₂, being a promising alternative to the current commercial technique.^6–10 Unfortunately, achieving low-cost, highly active, and selective electrocatalysts to direct the 2e⁻ ORR pathway for realizing the massive production of H₂O₂ is still a formidable challenge. Over the past decades, non-noble metal-based catalysts such as carbonaceous materials, transition metal-based compounds, and single-atom catalysts have attracted a great deal of attention and enormous efforts have been dedicated to developing industrially applicable 2e⁻ ORR electrocatalysts.^2,11–19 Despite considerable progress having been made in recent years, the catalyst system, optimization strategy, and the correlation between the electronic structure and performance still need to be essentially improved and revolutionized in order to obtain technological breakthroughs in the field of the electrocatalytic 2e⁻ ORR.

Physical field modulation is a powerful and newly emerged approach to accelerating the (electro)catalytic reaction. In 2018, Niether et al. reported that when an external high-frequency alternating magnetic field was applied to magnetic nanocatalysts, a local heating effect was generated in their immediate vicinity, which significantly promoted alkaline water electrolysis.²⁰ Following this observation, Huang et al. claimed that an external plasmon resonance could induce a thermal effect for Pd_xAg, resulting in the generation of effective hot holes and remarkably improved the methanol oxidation activity.²¹ Recently, Gao et al. demonstrated that by introducing an external light field to a NiFe₂O₄ catalyst, its surface reconstruction into real active species during water oxidation could be tremendously accelerated, thus distinctly decreasing its reaction overpotential.²² Inspired by these appealing results, a question naturally arises as to whether some physical fields can be exerted on materials to improve the electrocatalytic 2e⁻ ORR. Previous studies have unveiled that if an electric field is locally triggered on the surface of electrocatalysts, the accumulation/diffusion tendency of charged ions involved in the electrocatalytic process will be apparently affected, thus modulating the thermodynamics and kinetics of the reaction intermediate.^23,24 Furthermore, recent theoretical calculations have also predicted that during the ORR, the local electric field can also effectively regulate the adsorption capability of active sites towards oxygen-containing intermediates, especially the surface-adsorbed OOH⁻ or OH⁻ (OOH* or OH*).^25,26 This is because an optimum binding strength between active sites and OOH* or OH* is the prerequisite to ensure the ideal 2e⁻ ORR pathway.^27–29 Consequently, the following question that needs to be addressed is whether and how the local electrical field can be controllably excited on the surface of electrocatalysts during the 2e⁻ ORR, and how such an effect influences the performance of the catalysts.

On the other hand, piezoelectric ceramics are one of the most comprehensively studied and commercially available materials, in which an electric field can be generated when an external mechanical force is imposed.³⁰ Since the high-speed rotation of the fluid is indispensable during the fundamental study of the ORR, it may be envisioned that piezoelectric ceramics can serve as the most suitable candidate to produce the local electric field by the piezoelectric effect to tune the dynamic 2e⁻ ORR catalysis. However, to the best of our knowledge, such a phenomenon in electrocatalysis has never been explored.

Bearing the above questions in mind, herein, a proof-of-concept study has been provided on the most typical piezoelectric ceramic,^31,32 Pb(Zr_0.5Ti_0.5)O₃ (PZT), which exhibits poor intrinsic 2e⁻ ORR performance.³³ The PZT ceramic was subjected to controllable piezoelectricity through altering polarizing extent under different electric fields (denoted as PZT-1.5, PZT-2, and PZT-2.5, respectively). Compared to the unpolarized one (non-piezoelectric, denoted as PZT-0), all the piezoelectric PZT ceramics displayed remarkably enhanced H₂O₂ evolution performance. Among them, the best performance was achieved for PZT-2, surpassing 90% selectivity in a wide potential range of 0.6–0.1 V vs. the reversible hydrogen electrode (RHE). Strikingly, the selectivity even reached up to ∼98% at 0.4 V vs. the RHE, outperforming those of almost all the oxides and most of the state-of-the-art catalysts reported for the alkaline 2e⁻ ORR. Moreover, the higher 2e⁻ ORR performance of PZT-2 was also verified by in situ visualizing its faster on-site tandem degradation reaction rate. Combining various ex/in situ characterization with theoretical finite element analysis (FEA), the catalytic performance enhancement was closely related to the piezoelectric properties, which was triggered by the effect of mechanical stress from the dynamic rotating fluid on polarized PZT ceramics. Among them, the unrivaled PZT-2 demonstrated the most favorable local electric field, electrostatically repulsing OH⁻ ions of the electrolyte and OOH⁻ ions from over-accumulation at its surface, and concurrently enabled their surface concentration into the balanced states, thereby realizing the optimum binding strengths of both OOH* and OH*, as well as the alleviation of the disproportionation of the produced H₂O₂. Furthermore, the universality and applicability of such a piezoelectric enhancement were further supported by boosting the 2e⁻ ORR performance of environmentally friendly lead-free barium titanate (BaTiO₃, BT).

Results and discussion

Piezoelectric behavior of PZT ceramic electrocatalysts

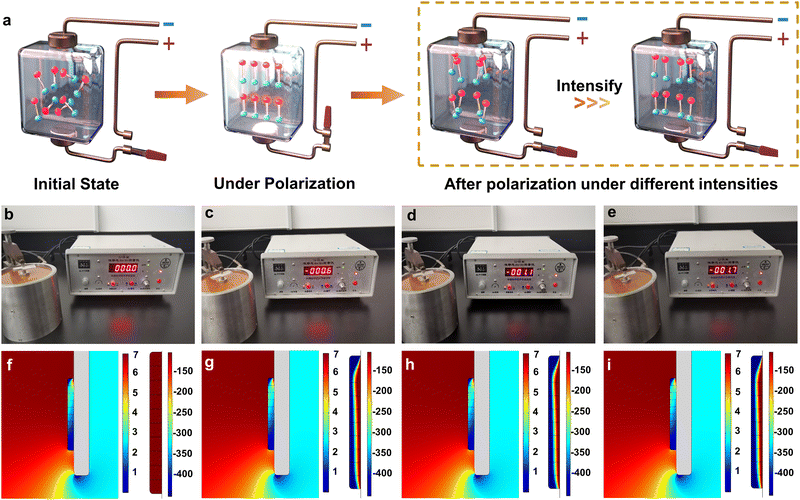
Fig. 1a schematically displays the polarization treatment towards PZT ceramics by subjecting them to the piezoelectric effect. Before polarization, the electric domains of pristine PZT ceramics were disordered, thereby their overall piezoelectricity cannot be observed. However, upon applying a polarized electric field, an ordered arrangement of the intrinsic electric domains along the strength direction of the applied electric field was induced within the pristine PZT ceramics, which is the origin of their evidently presented piezoelectricity. After polarization, although the orderly orientated electric domains were relaxed, most of them could still be preserved in an ordered model to a large extent within the PZT materials. Furthermore, the stronger the external polarizing electric field is, the more ordered the electric domains of the post-polarization PZT materials behave, thus exhibiting a better overall piezoelectric ability.^34,35 Based on this principle, the Pb(Zr_0.5Ti_0.5)O₃ ceramic tablet with a pure phase was synthesized by thermal treatment, followed by polarization under electric fields of 0, 1.5, 2, and 2.5 kV mm⁻¹ for 10 min, respectively (herein sequentially defined as PZT-0, PZT-1.5, PZT-2, and PZT-2.5, respectively). Notably, under our experimental conditions, more than 200 g of catalyst could be produced in one-batch of polarization treatment (Fig. S1, ESI†), suggesting the high potential for practical application. Hereafter, the as-ground ceramic powders were deposited as electrode films to examine their piezoelectric behavior. As expected, all PZT electrodes by polarization treatment showed a piezoelectric response compared to that of PZT-0 when the external force was applied, strongly demonstrating the successful polarization. Moreover, these four catalyst films showed different piezoelectric responses. The variation tendency is consistent with the fact that a higher electric field strength leads to a larger piezoelectric effect and in turn implies the controllable piezoelectricity of these samples (Fig. 1b–e, and Table S1, ESI†). Such an observation could also be confirmed by comparing the piezoelectric constant (d₃₃) and piezo response force in the microscopy images (PFM) of PZT-0 and PZT-2 ceramic tablets (Table S1 and Fig. S2, ESI†). To further support this point and test how they would perform in the fluid field, theoretical FEA simulations by modeling the catalysts on the RRDE at a rotation speed of 1600 rpm during ORR measurements were carried out and the surface forces, as well as the piezo-induced local electric field towards these PZT catalysts (PZT-0, 1.5, 2, and 2.5), were calculated. Note that under the conditions of typical ORR tests, the PZT powder catalysts deposited on the RRDE will unavoidably be subject to the pressures from electrolytes triggered by the rotation of the electrode. Thus, as shown in Fig. 1f–i, the stress was induced on the surface of all PZT particle models with the nearly same distribution and intensity during rotation. However, compared with charge neutrality observed on the PZT-0 surface, local negative electric fields emerged on all of the other three piezoelectric PZT models, whose surface value gradually increased in the order of PZT-1.5 (−6.98 × 10⁻⁴ V), PZT-2 (−7.07 × 10⁻⁴), and PZT-2.5 (−7.34 × 10⁻⁴) (Fig. 1f–i and Table S2, ESI†), further proving the above hypothesis. It is worth noting that the morphology, crystallinity, composition, chemical state, and elemental distribution of PZT before and after polarization treatment basically remained the same, substantiating that such features are independent of the polarization treatment (Fig. S3–S8, and Table S3, ESI†).

Fig. 1 (a) Schematic illustrations of electric domain orientation within PZT at the initial state, as well as under and after the external electric field polarizations. d₃₃ tests of the unpolarized (b) PZT-0, as well as polarized (c) PZT-1.5, (d) PZT-2, and (e) PZT-2.5 powder catalysts, which were measured after being deposited on the FTO substrate (insulating side). Stress distribution diagrams (left, unit: N m⁻²), and the associated surface electric fields (right, unit: μV) of (f) PZT-0, (g) PZT-1.5, (h) PZT-2, and (i) PZT-2.5 particle models under the fluid field at a rotating speed of 1600 rpm.

ORR performances of PZT ceramic electrocatalysts

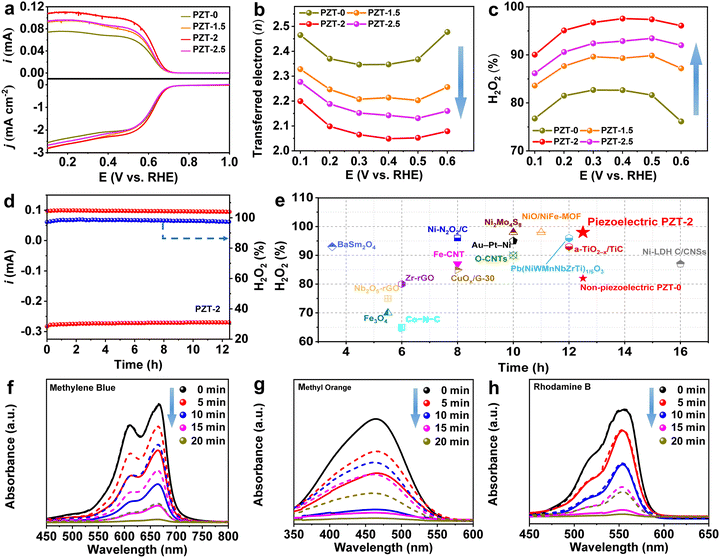
To investigate the dependence of the 2e⁻ ORR performance on the piezoelectric effect, electrochemical measurements for non-piezoelectric PZT-0 and piezoelectric PZT-1.5, 2, and 2.5 powder catalysts were conducted using an RRDE (rotating rate: 1600 rpm) in the O₂-saturated 0.1 M KOH electrolyte (see details in the ESI†).³⁶ Prior to the electrochemical test, the FESEM characterization revealed that the catalyst film with an average thickness of ∼4 μm was tightly and densely adhered to the glassy carbon (Fig. S9, ESI†), which might be conducive to delivering the robust electrode. Also, we determined the collection efficiency (N) of the employed RRDE as 0.37 (Fig. S10, ESI†). In Fig. 2a, the linear sweep voltammetry (LSV) curves recorded at a scan rate of 10 mV s⁻¹ presented both the disk current density and ring current of all the investigated electrocatalysts, in which the PZT-2 attained the best catalytic performance. Specifically, it only required an onset potential as high as ∼0.71 V vs. RHE at both the disk and ring electrodes, quite close to the theoretical equilibrium potential of 0.7 V vs. RHE.³³ Moreover, PZT-2 could afford a high current density of 1 mA cm⁻² at a potential of ∼0.627 V vs. RHE, which was not only superior to that of the non-piezoelectric PZT-0 but also outmatched those of the piezoelectric reference samples, PZT-1.5 and PZT-2.5. Intriguingly, in the case of non-rotating measurement, the most optimized PZT-2 exhibited a nearly overlapped LSV curve with that of PZT-0 (Fig. S11, ESI†), implying that the presented performance elevation arose from the piezoelectric response of PZT-2 caused by the electrode rotating in the fluid field. Additionally, the electron transfer number (n) during the ORR process for these samples was calculated and compared. As depicted in Fig. 2b, within the potential range of 0.6–0.1 V vs. RHE, all the piezoelectric PZT catalysts showed lower n than that of the non-piezoelectric PZT-0 (average value of ∼2.4), suggesting the presence of piezoelectric effect could effectively direct the PZT catalysts to be more preferable for the 2e⁻ pathway. In particular, PZT-2 exhibited the lowest average n value of only ∼2.09, indicating that it almost exclusively catalyzed O₂ to be reduced into H₂O₂, which was further validated by the selectivity of H₂O₂ production provided in Fig. 2c. In the same wide potential range, the H₂O₂ selectivity of PZT-2 exceeded 90%, reaching as high as around 98% at 0.4 V vs. the RHE. In addition, combining the n and H₂O₂ selectivity results, the preference of the 2e⁻ ORR for the probed four samples could be determined in the order of PZT-2, PZT-2.5, PZT-1.5, and PZT-0, indicating the flexibility and controllability of our piezoelectric promotion strategy, which will be elaborated in the next section. On the other hand, considering that durability is another key indicator to estimate the performance of 2e⁻ ORR electrocatalysts, a chronoamperometry (CA) test at a potential of 0.4 V vs. RHE (Fig. 2d) was therefore performed for PZT-2. Apparently, PZT-2 could robustly maintain its high ORR performance over 12 h with negligible performance decay, illustrating the continuous and stable piezoelectric effect in dynamic catalysis. To our best knowledge, the excellent 2e⁻ ORR ability of PZT-2, from the perspectives of both H₂O₂ selectivity and stability, was superior to almost all the documented transition metal oxide-based and most of the reported electrocatalysts (e.g., transition metal sulfide and selenide-based ones) in the basic environment (Fig. 2e and Table S4, ESI†). Besides, the effect of piezoelectric enhancement on ORR catalysis could be further validated using an assembled H-type electrolyzer, where the 0.1 M KOH electrolyte was stirred at 1600 rpm to produce stress on the working electrodes (powder PZT-0 and PZT-2 catalysts deposited on carbon paper, respectively, the details of which are provided in the ESI†). Fig. S12 shows the corresponding LSV curves obtained under Ar and O₂-saturated environments. Under an Ar atmosphere, negligible current densities were observed, while the devices equipped with both PZT-0 and PZT-2 exhibited obvious catalytic activity in the O₂-saturated electrolyte, between which, the H-cell integrated by carbon paper-supported PZT-2 possessed a noticeably improved oxygen reduction capability, corroborating the function of force-induced piezoelectric response. To further demonstrate that such a piezoelectric enhancement enables a better H₂O₂ yield, potassium permanganate (KMnO₄) titration experiments were performed. In line with our expectations, after the ORR at around 14.1 mA cm⁻² (CA test at a constant potential of 0.4 V vs. RHE) for 30 min, piezoelectric PZT-2 achieved a H₂O₂ production rate of ∼500 mmol g⁻¹ h⁻¹ and a Faraday efficiency (FE) of ∼91%, significantly superior to those of non-piezoelectric PZT-0 (a production rate of ∼300 mmol g⁻¹ h⁻¹ and an FE of ∼80%). On the other hand, peroxide disproportionation reaction (PDR) measurements were also conducted for both PZT-0 and PZT-2, and the results signified that the decomposition degree of H₂O₂ for these two samples where no forces were applied was almost the same (Fig. S13, ESI†), affirming that these two samples possess a similar nature. Note that the 2e⁻ ORR performance of polarized PZT ceramic catalysts gradually deteriorated with the decrease of the Zr/Ti ratio, possibly due to the intrinsically favorable nature of Ti species to the 4e⁻ ORR pathway (Fig. S14–S16 and Tables S5–S6, ESI†).³⁷ In addition, the change in pH value could also significantly alter the H₂O₂ productivity, i.e., when the pH value was lower, an inferior 2e⁻ ORR performance was attained (details are provided in Fig. S17, ESI†).

Fig. 2 (a) LSV curves of PZT-0, PZT-1.5, PZT-2, and PZT-2.5 recorded at 1600 rpm with a scan rate of 10 mV s⁻¹ (bottom part), accompanied by the associated H₂O₂ current on the ring electrode (upper part). (b) The calculated n, and (c) selectivity of H₂O₂ within the potential range from 0.6 to 0.1 V (vs. RHE). (d) CA stability test of PZT-2 at a fixed disk potential of 0.4 V vs. RHE. (e) Comparison of ORR selectivity and stability of PZT-2 with reported oxide-based and other advanced electrocatalysts. At each degradation time interval, the UV-Vis spectra of (f) MB, (g) MO, and (h) RB in the treated catholytes containing H₂O₂ on-site catalyzed by PZT-0 (dash lines) and PZT-2 (solid lines).

Encouraged by the above findings, a tandem reaction, coupling the on-site produced H₂O₂ with dye degradation, was further performed via the Fenton reaction to demonstrate the positive role of the piezoelectric effect in improving the 2e⁻ ORR capability. After the CA test at 0.4 V vs. RHE for 30 min, the catholytes containing in situ formed H₂O₂ catalyzed by PZT-0 and PZT-2 were acidified, followed by mixing with Fe²⁺ to obtain the Fenton reaction solutions. Three organic dyes, i.e., methylene blue (MB), methyl orange (MO), and rhodamine b (RB), respectively, were applied to assess the degradation ability (details are provided in the ESI†). Fig. S18 (ESI†) clearly demonstrates that compared with the Fenton reaction solution prepared using catholytes of PZT-0, the reaction solutions containing H₂O₂ produced by the PZT-2 catalyst promoted decolorization of all three organic dyes at a higher rate, which can be further corroborated by comparing the corresponding absorption peak in the ultraviolet-visible (UV-Vis) spectra of these two Fenton reaction solutions at each degradation time interval (0, 5, 10, 15, and 20 min) (Fig. 2f–h). Strikingly, the presented results elaborated that the piezoelectric effect can not only realize higher H₂O₂ production but also more effectively degrade a variety of contaminants in wastewater via an on-site tandem Fenton reaction, suggesting its high potential in practical applications.

Insights into the mechanism of piezoelectric enhancement towards the 2e⁻ ORR

In order to gain more insights into the piezoelectric promotion mechanism for the 2e⁻ ORR, comprehensive ex situ characterization, i.e., Rietveld refinement of XRD, FESEM, ICP-OES, XPS, and TEM together with HRTEM, SAED, and the HAADF-STEM patterns and the corresponding EDX mappings, was first carried out on both post-ORR (12 h of CA test at 0.4 V vs. the RHE) PZT-0 and PZT-2 (Fig. S19–S23 and Tables S7–S8, ESI†). By analyzing and comparing the attained data, it can be concluded that the original phase structure, crystallinity, lattice parameters, components, and microstructures remained intact after ORR CA for both non-piezoelectric and piezoelectric PZT samples. In addition, PZT-0 and PZT-2 at 0.4 V vs. the RHE after 12 h of ORR CA (the utilized electrolytes were continuously stirred at a speed of 1600 rpm) were also freeze-quenched for the quasi in situ Raman measurements. As a result, in agreement with the Raman bands of PZT during the 2e⁻ ORR, the peaks assigned to the Pb–O, Zr–O, and Ti–O can be well-identified for both samples (Fig. S24, ESI†),³⁴ affirming again that both piezoelectric and non-piezoelectric PZT retained their original lead zirconate titanate phase. Moreover, the polarized ceramic catalyst could well-preserve its initial piezoelectric activity after the ORR (details in Table S9, ESI†). From these observations, it could also be concluded that the improvement of catalytic performance for PZT-2 resulted from the effective piezoelectric response during dynamic catalysis.

To achieve a deeper understanding, we employed a Gouy–Chapman–Stern model of FEA (details are provided in the ESI†)^23,24 for first investigating the ion concentrations within electric double layers (EDLs) for various PZT models (PZT-0, 1.5, 2, and 2.5) in 0.1 M KOH influenced by their own piezoelectricity-induced surface local electric fields, which has been elaborated in the previous parts (Fig. 1f–i and Table S2, ESI†). Intriguingly, the different structures of EDLs were observed for these four samples, which could be specifically summarized as follows. First, the K⁺ concentrations adjacent to the electrode surface linearly increased against the polarization enhancement (i.e., the elevation of the piezoelectric activity) of ceramic catalysts (Fig. S25, ESI†). More importantly, the local electric fields enabled the negative charge to distribute on the surface of piezoelectric PZT, which was deemed to influence the concentration of OH⁻ ions in the EDLs via the charge interaction.²³ As shown in Fig. 3a, no OH⁻ ion gradient variation could be seen near the surface of non-piezoelectric PZT-0. However, the OH⁻ concentration was tremendously diluted in the immediate vicinity of all piezoelectric PZT models (Fig. 3b–d), which could be further visually substantiated by the involved parameters in terms of OH⁻ concentration, piezoelectricity-induced electric field intensity, and their distance from the surface of PZT-based models (Fig. 3e). Therefore, it could be concluded that the stronger piezoelectric response led to the lower OH⁻ coverage in the Helmholtz layer of the EDLs directly adjacent to the electrode surface (Fig. 3f) due to the charge repulsion. Notably, in the presence of the above-simulated EDLs, we have also compared the distribution of OOH⁻ density ranging from the surface to vicinity regions of ceramic samples, which displayed a trend in agreement with that of OH⁻ concentration surrounding different ceramic samples (Fig. 3g–l).

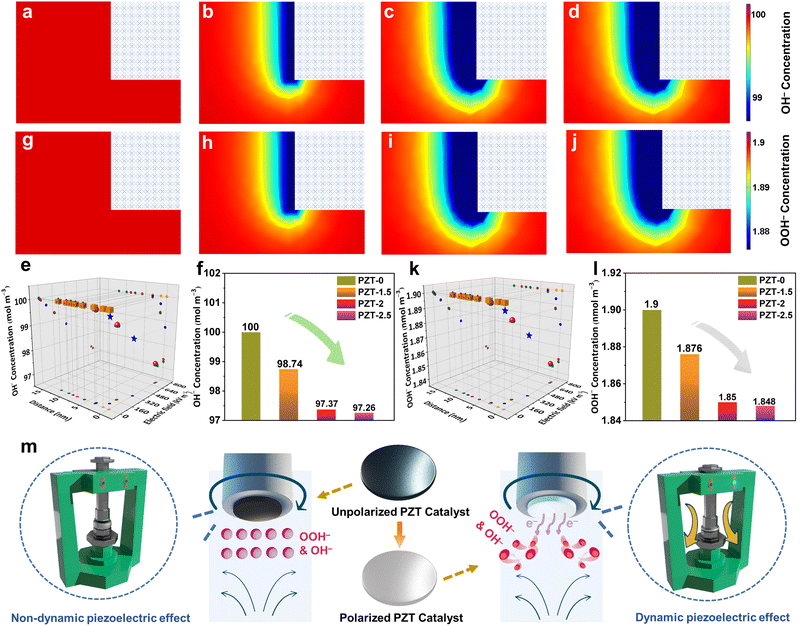Fig. 3 The FEA simulation of OH⁻ density (unit: mol m⁻³) mapping images at the immediate vicinity of (a) PZT-0, (b) PZT-1.5, (c) PZT-2, and (d) PZT-2.5. (e) The derived OH⁻ concentration distribution as a function of the piezoelectricity-induced electric field intensity and the distance from the surface of PZT-0 (cube), PZT-1.5 (star), PZT-2 (sphere), and PZT-2.5 (tetrahedron) models. (f) The corresponding specific OH⁻ concentration values in the Helmholtz layer of the EDLs directly adjacent to the surface of these four PZT models. The FEA simulation of OOH⁻ density (unit: nmol m⁻³) mapping images at the immediate vicinity of (g) PZT-0, (h) PZT-1.5, (i) PZT-2, and (j) PZT-2.5. (k) The derived OOH⁻ concentration distribution as a function of the piezoelectricity-induced electric field intensity and the distance from the surface of PZT-0 (cube), PZT-1.5 (star), PZT-2 (sphere), and PZT-2.5 (tetrahedron) models. (l) The corresponding specific OOH⁻ concentration values in the Helmholtz layer of the EDLs directly adjacent to the surface of these four PZT models. Note that the initial concentrations of OOH⁻ ions of all four PZT modeling systems (details are provided in ESI†) were assumed as the same, only suitable for comparing the general differences between unpolarized and polarized ceramic catalysts. Moreover, the rectangles in the upper right corner of mapping images represent the associated ceramic catalysts. (m) The working mechanism of the dynamic piezoelectric effect to boost the 2e⁻ ORR performance enabled by the polarized PZT ceramic catalyst.

Therefore, it can be concluded from the above analysis that catalysts with different polarization degrees would generate the EDL structure with different concentrations of OH⁻ and OOH⁻, in which the density of OH⁻ and OOH⁻ has an important effect on the ORR performance. It is well known that the fundamental reaction mechanism of the electrochemical 2e⁻ ORR in the alkaline electrolyte with a high pH value (e.g., 0.1 M KOH) undergoes the following two reaction steps:³⁸

* + O₂ + H₂O + e⁻ → OOH* + OH⁻ (Step 1)

OOH* + e⁻ → + HO₂⁻ + * (Step 2)

According to the above reactions, it is deemed that optimizing the binding strength of the key intermediate OOH⁻ adsorbed by the catalyst surface (OOH*), is the most important factor determining the final hydrogen peroxide yield via the electrochemical 2e⁻ ORR.^39,40 Intrinsically, the adsorption free energy towards OH⁻ on the surface active sites (OH*) follows a linear scaling relationship with the adsorption free energy towards OOH⁻ (ΔG_OOH* = ΔG_OH* + 3.2), and the ΔG_OH* thus can also be used to evaluate the ORR performance of the electrocatalyst.^28,38,41 On the other hand, previous findings have demonstrated that the coverage of OH⁻ on the electrode surface would greatly affect the ΔG_OH* and ΔG_OOH*, and thus the ORR performance. Furthermore, the higher surface OH⁻ coverage leads to the increased ΔG_OH* and ΔG_OOH*.^42,43 On the basis of the above premises, we can deduce how the ORR performance changes against the variation of OH⁻ concentration on the catalyst's surface.

Based on the FEA findings, in our case, the concentration of OH⁻ in the immediate vicinity of the catalyst surface gradually reduced with the polarization degree, indicating the decreased coverage of OH⁻ on the catalyst surface. On one hand, the higher surface OH⁻ coverage leads to the increased binding strength of OH*,⁴² while the over-strong *OH binding strength (i.e., PZT-0 and PZT-1.5 in our case) indicates that the ORR process would be prone to a 4e⁻ pathway.^28,41 On the other hand, the lower concentration of OH⁻ on the surface of the ceramic catalyst can lead to more active sites, which contributes to the adsorption and reduction of more O₂ molecules resulting in a higher surface coverage of the critical intermediate OOH*, and thus an improved OOH* adsorption ability.^43–45 However, as for the ceramic catalyst (i.e., PZT-2.5) with too sparse local OH⁻ concentration, its coverage and adsorption strength of OOH* were over-strong, which tend to dissociate the O–O bond and follow a 4e⁻ pathway.⁴⁶ Hence, only the polarized ceramic catalyst with the optimum dynamic piezoelectric activity (i.e., PZT-2), which was believed to attain the most moderate OH⁻ concentration close to the surface, can show the best H₂O₂ production ability through the electrochemical 2e⁻ ORR.

Moreover, the suppression of the spontaneous peroxide disproportionation reaction (PDR, 2 HO₂⁻ → 2 OH⁻ + O₂ in 0.1 M KOH) should also be considered.^38,47 It can be naturally envisioned that driving the formed OOH⁻ products away from the catalyst surface can significantly reduce the spontaneous PDR,^38,40 by which the yield of H₂O₂ electrosynthesized by the 2e⁻ ORR can be maintained for a longer time. In our case, the stronger the dynamic piezoelectric response of the ceramic catalyst, the sparser the OOH⁻ concentration in the immediate vicinity of its surface. Therefore, we can conclude the following: the spontaneous PDR degree of the product HO₂⁻ induced by polarized piezoelectric ceramic catalysts was smaller, which can also be verified by the dynamic PDR experiments between the non-piezoelectric PZT-0 and piezoelectric PZT-2 catalysts in the reaction solution which was stirred at a speed of 1600 rpm (the same as the rotating rate of RRDE during ORR measurements) (Fig. S26, ESI†).

On the basis of the above FEA simulation results on the OH⁻ and OOH⁻ density in the EDL regions of PZT models in 0.1 K KOH (Fig. 3a–l), the working mechanism of the dynamic piezoelectric effect to boost the 2e⁻ ORR performance enabled by polarized PZT ceramic catalysts can be understood from the following: first of all, the piezoelectricity-induced local electric fields can be controllably regulated through adjusting the polarization degrees towards the ceramics. An optimized local surface electric field gave rise to a 2e⁻ alkaline ORR-favourable OH⁻ concentration in the EDL region of PZT catalysts during dynamic electrochemistry, which further led to the optimum OH⁻ coverage in the Helmholtz layer directly adjacent to the catalyst surface. Based on this point, the moderate binding strengths of OH* and OOH* (neither too strong nor too weak) on the PZT surface can be achieved, and thus a satisfactory H₂O₂ generation ability via oxygen electroreduction. Besides, through the charge repulsion, the product HO₂⁻ obtained from the alkaline 2e⁻ ORR was expelled away from the polarized ceramic PZT catalyst surface, which effectively alleviated the serious occurrence of the PDR, thereby maintaining high productivity for a longer time (Fig. 3m).

Universality of the dynamic piezoelectric strategy towards lead-free piezoelectric ceramics

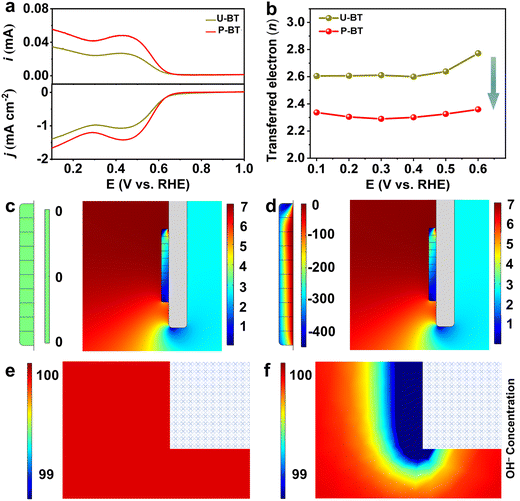
PZT ceramics are considered as one of the most widely developed and commercially available piezoelectric materials which typically exhibit a very high piezoelectric coefficient. Nevertheless, it might raise environmental concerns due to the presence of lead.^30,48,49 Hence, lead-free substitutes, which can simultaneously fulfill the performance, environment, and cost requirements, are highly desired.^48,50 Previous works have shown that barium titanate (BT)-based materials can also catalyze the ORR with an electron transfer number of around 3.2–3.5,⁵¹ displaying the poor 2e⁻ ORR. To validate the universality of the piezoelectric promotion strategy toward lead-free BT ceramics, we deliberately prepared piezoelectric BT catalyst powders by polarizing the as-sintered BT ceramic tablets followed by grinding (denoted as P-BT). On one hand, in comparison with the unpolarized ones (denoted as U-BT), the polarized P-BT presented distinct piezoelectricity both in the form of a ceramic tablet and deposited film (Fig. S27–S30 and Tables S10–S11, ESI†). Remarkably, the piezoelectric effect of P-BT enabled itself to behave more efficiently for the 2e⁻ ORR to generate H₂O₂. After depositing the BT powders on the RRDE, the better ORR ability of P-BT than that of U-BT can be reflected by their LSV curves (Fig. 4a). In analogy to the PZT catalysts and compared to the non-piezoelectric U-BT for the 2e⁻ ORR, P-BT with piezoelectricity also displayed a value of n closer to the theoretical one, higher H₂O₂ production selectivity, and superior stability (Fig. 4b and Fig. S31, ESI†) which indeed certified that the piezoelectric response-induced elevated catalytic 2e⁻ ORR performance is also feasible for lead-free piezoelectric materials. The almost identical crystalline structure and composition of P-BT before and after the ORR further confirmed its great stability during the ORR. (Fig. S27, S32 and Table S12, ESI†). Similar to PZT, such a performance enhancement for P-BT can be ascribed to the moderate surface OH⁻ and OOH⁻ concentration modulated by the piezoelectric field, enabling both optimized binding strengths of OH*/OOH*, as well as mitigated PDR tendency during the 2e⁻ ORR, and thereby delivering an exceptional catalytic performance superior to that of non-piezoelectric U-BT (Fig. 4c–f, Fig. S33–S35, and Table S13, ESI†).

Fig. 4 (a) LSV curves of U-BT and P-BT recorded at 1600 rpm at a scan rate of 10 mV s⁻¹ (bottom part), accompanied by the associated H₂O₂ current on the ring electrode (upper part). (b) The calculated n of H₂O₂ within the potential range of 0.6 to 0.1 V (vs. RHE). Stress distribution diagrams (right, unit: N m⁻²) and the associated surface electric fields (left, unit: μV) of (c) U-BT and (d) P-BT particle models under the fluid field at a rotating speed of 1600 rpm (same as the speed of the rotating RRDE for ORR measurements). The FEA simulation of OH⁻ density (unit: mol m⁻³) mapping images at the immediate vicinity of (e) U-BT and (f) P-BT, where the rectangles in the upper right corner of mapping images represent the associated ceramic catalysts.

Conclusions

In summary, lead zirconate titanate with an optimized piezoelectric effect was highly efficient towards the 2e⁻ ORR in alkaline media, resulting in higher performance than those of almost all previously reported metal oxide-based and state-of-the-art electrocatalysts. The combination of experimental with theoretical results uncovered that the accumulation of surface negative charges triggered by the mechanical force during the dynamic ORR process could be controllably modulated by polarizing lead zirconate titanate to different degrees, and thus flexibly tuning their surrounding OH⁻/OOH⁻ concentrations. This can optimize the binding strengths of both OH* and OOH*, as well as alleviate the disproportionation degrees of the formed peroxides, resulting in enhancing the 2e⁻ ORR performance. The proposed dynamic piezoelectric effect has been demonstrated to be very effective in improving the 2e⁻ ORR performance of PZT, and it could also be extended to other materials with the piezoelectric effect, unlocking opportunities for the investigation of low-cost, scalable, and transition metal-based highly efficient electrocatalytic systems. This work also innovatively introduces the local electrical field concept by bridging the piezoelectric materials with the mechanical force during ORR operation, which may serve as a novel, promising, and meaningful avenue for elevating catalytic capability in a variety of dynamic catalytic reactions.

Experimental

Preparation of ceramic catalysts

Pb(Zr_0.5Ti_0.5)O₃ ceramic tablets were synthesized by the solid-state reaction method. Raw materials including reagent-grade Pb₃O₄ (99.63%, Qingdao Zhongyuanhong Chemical Reagento Ltd, Qingdao, China), ZrO₂ (99.76%, Yixing Xinxing Zirconium Industry Co., Ltd, Yixing, China) and TiO₂ (99.38%, Sinopharm Chemical Reagent Co., Ltd, Shanghai, China) powders were mixed with a molar ratio of Pb³⁺ : Zr⁴⁺ : Ti⁴⁺ = 1 : 0.5 : 0.5, and ball milled with deionized water for 12 h. After drying, the mixture was calcined at 860 °C for 2 h in the furnace, followed by ball milling and granulation. The as-prepared powders were pressed into disks with a thickness of 1 mm and a diameter of 20 mm, which were subsequently sintered at 1240 °C for 2 h and coated with silver electrodes on both sides. The as-obtained PZT ceramic tablets were polarized under electric fields of 0, 1.5, 2, and 2.5 kV mm⁻¹ for 10 min, respectively (accordingly named PZT-0, PZT-1.5, PZT-2, and PZT-2.5). Finally, these polarized PZT tablets were polished with sandpaper to remove the silver electrode on the surface for all the experiments in this work. Besides, Pb(Zr_0.4Ti_0.6)O₃ and Pb(Zr_0.3Ti_0.7)O₃ ceramic tablets were fabricated using the same procedures, except that the molar ratio of Pb³⁺ : Zr⁴⁺ : Ti⁴⁺ was changed as 1 : 0.4 : 0.6 and 1 : 0.3 : 0.7, and denoted as U-Pb(Zr_0.4Ti_0.6)O₃ and U-Pb(Zr_0.3Ti_0.7)O₃, respectively. Then, they were polarized under an electric field of 2.7 and 3.1 kV mm⁻¹ for 10 min, respectively, attaining the same d₃₃ value (piezoelectric activity) as that of PZT-2, which were named P-Pb(Zr_0.4Ti_0.6)O₃ and P-Pb(Zr_0.3Ti_0.7)O₃, respectively. Also, BT ceramic tablets were synthesized using a similar procedure, and the required raw materials for their preparation were BaCO₃ (99%, Aladdin Biochemical Technology Co., Ltd, Shanghai, China) and TiO₂ (99.38%, Sinopharm Chemical Reagent Co., Ltd, Shanghai, China). We denoted the unpolarized BT tablets as U-BT, while those polarized under an electric field of 1.5 kV mm⁻¹ for 10 min were named P-BT. All the above-mentioned PZT and BT tablets served as the starting materials, which were ground into the form of powders using a mortar for ORR evaluation.

Characterization

To probe the piezoelectricity of the as-obtained ceramic tablets, and the associated ground powders (deposited on the substrate as a film, details of which are provided in the ESI†), we measured their piezoelectric constant d₃₃ using a quasi-static piezoelectric d₃₃ meter (ZJ-3A, China Academy of Acoustics, Shanghai, China). Moreover, the domain morphology and structure of the ceramic tablet surface were detected using a PFM (MFP-3D, Asylum Research, Oxford Instrument, the UK). In order to investigate the crystalline phases of the samples presented in our current work, powder XRD measurements were performed on a D8 ADVANCE X-ray diffractometer with Cu Kα radiation (λ = 1.5406 Å). The Rietveld refinement program RIETAN-2000 was further used to analyze the XRD profiles.⁵² The surface morphology and microstructure of the involved samples were probed by the FESEM (Zeiss G500). Also, the TEM (FEI Talos F200X) was further employed to gain more insights into the microstructures of the measured samples. The elemental content of the samples was probed by the ICP-OES (Varian 720-ES) measurements. Additionally, XPS was utilized to explore the chemical states of the presented samples with an ESCALAB 250Xi spectrometer (Thermo Scientific, USA) which was equipped with a pass energy of 30 eV with a power of 100 W (10 kV and 10 mA), as well as a monochromatized AlKα X-ray (hν = 1486.65 eV) source. All samples were characterized at a pressure of less than 1.0 × 10⁻⁹ Pa. And all the spectra were recorded through the advantage software (Version 5.979) in a step of 0.05 eV. Ex/in situ Raman spectroscopy was performed through the 458 nm emission of an Argon ion laser (Innova 70, Coherent) for excitation, as well as a confocal Raman spectrometer (Lab Ram HR-800 Jobin Yvon) which was equipped with a liquid nitrogen cooled charge-coupled device (CCD) camera as the detector. The typical laser power applied to the sample was 0.5 mW. Moreover, the measurements were carried out using a Linkam Cryostage THMS600 cryostat, during which, the temperature of the probed samples was kept at 80 K. For accuracy, the measurements were performed at three different spots of the explored catalysts. Note that for the piezoelectricity, post-ORR, and Raman measurements, all the powder samples were deposited on substrates, and the related details can be found in the ESI.†

Electrochemical measurements

To begin, around 4 mg of as-ground PZT powder samples and 1 mg of Ketjen Black were dispersed in a mixture solution comprising 300 μL of deionized water, 650 μL of ethanol, and 50 μL of 0.5 wt% Nafion. The as-prepared dispersion was then sonicated in an ice water bath for 30 min, and 6.28 μL of the ultrasonic ink was dripped on the glassy carbon of RRDE with a surface area of 0.1256 cm². In alkaline media (0.1 M KOH), an electrochemical workstation (760E, CHI) was employed to be coupled with a standard three-electrode system, where the RRDE loaded with catalysts, a Hg/HgO electrode, and a graphite rod served as the working electrode, reference electrode, and counter electrode, respectively. However, a saturated calomel electrode (SCE) was employed in both neutral (0.1 M Na₂SO4) and acid (0.05 M H₂SO₄) electrolytes. The n and H₂O₂ selectivity (H₂O₂%) can be calculated as follows:

In the above equations, i_R and i_D represent the ring current and the absolute value of disk current, respectively. The value of N for the utilized RRDE was determined as 0.37.

H-cell electrolyzer

The yield of H₂O₂ catalyzed by the catalysts in 0.1 M KOH was determined via an assembled H-cell electrolyzer, in which the catalysts (powder PZT-0 and PZT2) and commercial IrO₂-deposited carbon papers worked as the working electrode, and the counter electrode, respectively, with the same mass loading of around 0.5 mg cm⁻². The electrolyte was stirred at the rate of 1600 rpm during measurements to simulate similar pressures on the deposited catalysts to those caused by the rotation of the RRDE. The catholyte containing HO₂⁻ was acidified by adding sulfuric acid. The H₂O₂ yield was quantified through the following reaction: 2KMnO₄ + 5H₂O₂ + 3H₂SO₄ → K₂SO₄ + 2MnSO₄ + 8H₂O + 5O₂.⁵³ The organic dye degradation performance tests were also performed in the same assembled H-type cell. On one hand, three dyes, including methylene blue (MB), methyl orange (MO), and rhodamine B (RB), with a concentration of 30 ppm were prepared. On the other hand, 5 mL of catholyte was collected from the cathode area (PZT-0 and PZT-2 supported on carbon paper) after a 30 min CA test at a constant potential of 0.4 V vs. RHE. Then, 1 mL of 1 M H₂SO₄ and 1 × 10⁻³ Fe²⁺ were mixed with the as-obtained catholyte, followed by being dissolved into 10 mL of dye solutions, which were then continuously shaken to realize a sufficient Fenton reaction, i.e., 2Fe²⁺ + H₂O₂ → 2Fe³⁺ + OH⁻ + OH˙. The concentration of the dyes at each degradation time interval was determined through UV-Vis spectra (corresponding to the optical photos at the same reaction moment). The associated UV-Vis absorption peaks of MB, MO, and RB are located at 664, 463, and 553 nm, respectively.³³

Computational study

To simulate the stress on the surface of the piezoelectric ceramics with different polarization states (PZT-0, PZT-1.5, PZT-2, and PZT-2.5, as well as U-BT and P-BT) in the flow field (0.1 M KOH electrolyte where the RRDE worked at a rotating rate of 1600 rpm), as well as the associated surface electric fields enabled by their inverse piezoelectric effect, the FEA method was employed using the COMSOL Multiphysics® 5.5 software.^33,54 Considering the high complexity of the direct calculation of the real three-dimensional model, the models adopted in this work were reasonably simplified in a two-dimensional form in accordance with the actual physical process.^33,55,56 The PZT model (including PZT-0, 1, 1.5, and 2.5) size was set as 2 μm, while the electrode substrate length and width were set as 50 and 5 μm, respectively (Fig. S36, ESI†). Afterward, all of these models were endowed with the associated material properties based on the actual experimental settings. In detail, the piezoelectricity constant for PZT-0, PZT-1, PZT-1.5, PZT-2, U-BT, and P-BT was set as 0, 25, 50, 130, 0, and 25, respectively. The actual physical process was coupled by the fluid field, electrostatic field, and solid mechanic field. The fluid field was used to simulate the real electrochemical measurement environment, whose specific settings are shown in Table S14 (ESI†). The electrostatic field was applied to describe the electrostatic response of the models in the calculation, where a change in the surface potential of 0.7 V vs. RHE (thermodynamically theoretic potential of H₂O₂ formation) against the powder was used to simplify the expression. Furthermore, we also simulated the mechanical response of structural materials through the solid mechanic field.³³

The speed f of the sample and electrode was set as 1600 rpm, the radius of rotation r was set as 5 cm, and the steady-state average flow velocity U (8.38 m s⁻¹) at the inlet was solved by the following formula:

U = 2π·f·r

The division of mesh was automatically realized by the software, which is shown in Fig. S37 (ESI†). Moreover, a transient study was conducted, for which the time step and the calculation time were set as 0.05 and 4 s, respectively.

Hereafter, based on the as-calculated surface electric fields of different ceramic catalysts, we simulated the concentration distributions of different ions within the electric double layers (EDLs) using the Gouy–Chapman–Stern model,^23,24,57 which is composed of a Helmholtz layer and a diffusion layer. In the current work, a monolayer of surface-adsorbed hydrated potassium ions made up the Helmholtz layer, while the diffusion layer comprises both cations and anions presenting a free diffusion in the electrolyte, which was established on the basis of a dynamic equilibrium between electrostatic forces and diffusion. The modules of “Electrostatics” and “Transport of diluted species” were combined to solve the density of different ions in the EDLs, in which the Poisson–Nernst–Planck equations were solved in the steady state:^23,24

In these equations, d represents the distance from the electrode surface, and d_H is the thickness of the as-built Helmholtz layer (in our case, 0.33 nm, i.e., the radius of a hydrated potassium ion). Therefore, d < d_H means the Helmholtz layer, while d > d_H means the region in the diffusion layer. c_i and z_i, in which i ∈ {K⁺, OH⁻, OOH⁻}, represent the concentrations and valencies of the different ions, respectively. e and k_B are the elementary charge and Boltzmann constant, respectively. The absolute temperature T was taken as 297.3 K. D means the diffusion coefficient, which was taken as 2 × 10⁻⁹ and 5 × 10⁻⁹ m² s⁻¹ for K⁺ and OH⁻ in water, respectively (0.1 M KOH).⁵⁸ Two-dimensional models were established to represent the three-dimensional ceramic catalysts used in this work, as illustrated in Fig. S38 (ESI†). The piezoelectricity-induced surface potential (surface electric field) was applied to this model through electrical potential boundary conditions. The critical parameters set for this simulation are depicted in Table S15 (ESI†). For the post-processing, at the middle height of the ceramic catalyst model in the current simulation, the function of electric fields and ion concentrations with the distance away from the PZT (BT) model surface was obtained (Fig. S38, ESI†). The mesh division for the ion concentration calculation was also automatically provided by the software (Fig. S39, ESI†).

Author contributions

Z. K., P. M., and Z. L. C. supervised the whole project. P. M., H. Y., and Z. L. C. conceived the idea and designed the experiments. Z. R. C. synthesized the ceramic catalysts. J. W. conducted the electrochemical measurements. K. Z. performed the FEA simulations. H. Y. collected the experimental and computational data, as well as wrote the original manuscript. Z. K., P. M., and Z. L. C. revised the manuscript. All authors discussed the results and contributed to the final manuscript.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

This work is supported by the National MCF Energy R&D Program of China (2018YFE0306105), the National Key R&D Program of China (2020YFA0406104, 2020YFA0406101), the Innovative Research Group Project of the National Natural Science Foundation of China (51821002), the National Natural Science Foundation of China (52201269), the Natural Science Foundation of Jiangsu Province (BK20210735), the Natural Science Foundation of the Higher Education Institutions of Jiangsu Province (21KJB430043), the Collaborative Innovation Center of Suzhou Nano Science & Technology, the 111 Project, and the Suzhou Key Laboratory of Functional Nano & Soft Materials. This work also thanks the Beijing Institute of Nanoenergy and Nanosystems, CAS, for providing the Comsol resource for theoretical modeling. Z. L. Chen gratefully acknowledges the funding from the Alexander von Humboldt (AvH) Foundation. H. Yang thanks China Scholarship Council (CSC) for the PhD fellowship. P. W. Menezes greatly acknowledges support from the German Federal Ministry of Education and Research in the framework of the project Catlab (03EW0015A/B). The authors are greatly indebted to Mr Konstantin Laun and Dr Ingo Zebger for the Raman measurements.

References

1. C. Xia, Y. Xia, P. Zhu and H. Wang, Science, 2019, 366, 226–231.
2. H. Sheng, A. N. Janes, R. D. Ross, D. Kaiman, J. Huang, B. Song, J. R. Schmidt and S. Jin, Energy Environ. Sci., 2020, 13, 4189–4203.
3. Q. Zhao, Y. Wang, W. Lai, F. Xiao, Y. Lyu, C. Liao and M. Shao, Energy Environ. Sci., 2021, 14, 5444–5456.
4. K. Dong, J. Liang, Y. Ren, Y. Wang, Z. Xu, L. Yue, T. Li, Q. Liu, Y. Luo, Y. Liu, S. Gao, M. S. Hamdy, Q. Li, D. Ma and X. Sun, J. Mater. Chem. A, 2021, 9, 26019–26027.
5. X. Shi, S. Back, T. M. Gill, S. Siahrostami and X. Zheng, Chem, 2021, 7, 38–63.
6. Y. Xia, X. Zhao, C. Xia, Z. Wu, P. Zhu, J. Y. Kim, X. Bai, G. Gao, Y. Hu, J. Zhong, Y. Liu and H. Wang, Nat. Commun., 2021, 12, 4225.
7. Z. Lu, G. Chen, S. Siahrostami, Z. Chen, K. Liu, J. Xie, L. Liao, T. Wu, D. Lin, Y. Liu, T. F. Jaramillo, J. K. Nørskov and Y. Cui, Nat. Catal., 2018, 1, 156–162.
8. H. W. Kim, M. B. Ross, N. Kornienko, L. Zhang, J. Guo, P. Yang and B. D. McCloskey, Nat. Catal., 2018, 1, 282–290.
9. K. Dong, J. Liang, Y. Wang, L. Zhang, Z. Xu, S. Sun, Y. Luo, T. Li, Q. Liu, N. Li, B. Tang, A. A. Alshehri, Q. Li, D. Ma and X. Sun, ACS Catal., 2022, 12, 6092–6099.
10. Y. Jiang, P. Ni, C. Chen, Y. Lu, P. Yang, B. Kong, A. Fisher and X. Wang, Adv. Energy Mater., 2018, 8, 1801909.
11. E. Jung, H. Shin, W. H. Antink, Y. Sung and T. Hyeon, ACS Energy Lett., 2020, 5, 1881–1892.
12. Y. Bu, Y. Wang, G. Han, Y. Zhao, X. Ge, F. Li, Z. Zhang, Q. Zhong and J. Baek, Adv. Mater., 2021, 33, 2103266.
13. Y. Sun, L. Silvioli, N. R. Sahraie, W. Ju, J. Li, A. Zitolo, S. Li, A. Bagger, L. Arnarson, X. Wang, T. Moeller, D. Bernsmeier, J. Rossmeisl, F. Jaouen and P. Strasser, J. Am. Chem. Soc., 2019, 141, 12372–12381.
14. E. Jung, H. Shin, B. Lee, V. Efremov, S. Lee, H. S. Lee, J. Kim, W. H. Antink, S. Park, K. Lee, S. Cho, J. S. Yoo, Y. Sung and T. Hyeon, Nat. Mater., 2020, 19, 436–442.
15. C. Tang, L. Chen, H. Li, L. Li, Y. Jiao, Y. Zheng, H. Xu, K. Davey and S. Qiao, J. Am. Chem. Soc., 2021, 143, 7819–7827.
16. Z. Zhou, Y. Kong, H. Tan, Q. Huang, C. Wang, Z. Pei, H. Wang, Y. Liu, Y. Wang, S. Li, X. Liao, W. Yan and S. Zhao, Adv. Mater., 2022, 34, 2106541.
17. K. Dong, J. Liang, Y. Wang, Z. Xu, Q. Liu, Y. Luo, T. Li, L. Li, X. Shi, A. M. Asiri, Q. Li, D. Ma and X. Sun, Angew. Chem., Int. Ed., 2021, 60, 10583–10587.
18. M. Wang, X. Dong, Z. Meng, Z. Hu, Y. Lin, C. Peng, H. Wang, C. Pao, S. Ding, Y. Li, Q. Shao and X. Huang, Angew. Chem., Int. Ed., 2021, 60, 11190–11195.
19. Z. Deng, L. Li, Y. Ren, C. Ma, J. Liang, K. Dong, Q. Liu, Y. Luo, T. Li, B. Tang, Y. Liu, S. Gao, A. M. Asiri, S. Yan and X. Sun, Nano Res., 2022, 15, 3880–3885.
20. C. Niether, S. Faure, A. Bordet, J. Deseure, M. Chatenet, J. Carrey, B. Chaudret and A. Rouet, Nat. Energy, 2018, 3, 476–483.
21. L. Huang, J. Zou, J. Ye, Z. Zhou, Z. Lin, X. Kang, P. K. Jain and S. Chen, Angew. Chem., Int. Ed., 2019, 58, 8794–8798.
22. L. Gao, X. Cui, Z. Wang, C. D. Sewella, Z. Li, S. Liang, M. Zhang, J. Li, Y. Hu and Z. Lin, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2023421118.
23. P. Liu, B. Chen, C. Liang, W. Yao, Y. Cui, S. Hu, P. Zou, H. Zhang, H. J. Fan and C. Yang, Adv. Mater., 2021, 33, 2007377.
24. M. Liu, Y. Pang, B. Zhang, P. De Luna, O. Voznyy, J. Xu, X. Zheng, C. T. Dinh, F. Fan, C. Cao, F. P. G. de Arquer, T. S. Safaei, A. Mepham, A. Klinkova, E. Kumacheva, T. Filleter, D. Sinton, S. O. Kelley and E. H. Sargent, Nature, 2016, 537, 382–386.
25. Z. Duan and G. Henkelman, ACS Catal., 2019, 9, 5567–5573.
26. H. Li, S. Kelly, D. Guevarra, Z. Wang, Y. Wang, J. A. Haber, M. Anand, G. T. K. K. Gunasooriya, C. S. Abraham, S. Vijay, J. M. Gregoire and J. K. Nørskov, Nat. Catal., 2021, 4, 463–468.
27. J. Xi, S. Yang, L. Silvioli, S. Cao, P. Liu, Q. Chen, Y. Zhao, H. Sun, J. N. Hansen, J. B. Haraldsted, J. Kibsgaard, J. Rossmeisl, S. Bals, S. Wang and I. Chorkendorff, J. Catal., 2021, 393, 313–323.
28. N. Wang, S. Ma, P. Zuo, J. Duan and B. Hou, Adv. Sci., 2021, 8, 2100076.
29. K. Jiang, J. Zhao and H. Wang, Adv. Funct. Mater., 2020, 30, 2003321.
30. P. K. Panda and B. Sahoo, Ferroelectrics, 2015, 474, 128–143.
31. A. I. Kingon and S. Srinivasan, Nat. Mater., 2005, 4, 233–237.
32. T. Ibn-Mohammed, S. C. L. Koh, I. M. Reaney, A. Acquaye, D. Wang, S. Taylore and A. Genovese, Energy Environ. Sci., 2016, 9, 3495–3520.
33. Z. Chen, J. Wu, Z. Chen, H. Yang, K. Zou, X. Zhao, R. Liang, X. Dong, P. W. Menezes and Z. Kang, Angew. Chem., Int. Ed., 2022, 61, e202200086.
34. R. Ahluwalia, T. Lookman, A. Saxena and W. Cao, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 014112.
35. P. Paruch, T. Tybell and J. M. Triscone, Appl. Phys. Lett., 2001, 79, 530–532.
36. C. Xia, J. Y. Kim and H. Wang, Nat. Catal., 2020, 3, 605–607.
37. H. Niu, X. Wang, C. Shao, Y. Liu, Z. Zhang and Y. Guo, J. Mater. Chem. A, 2020, 8, 6555–6563.
38. S. Siahrostami, S. J. Villegas, A. H. B. Mostaghimi, S. Back, A. B. Farimani, H. Wang, K. A. Persson and J. Montoya, ACS Catal., 2020, 10, 7495–7511.
39. X. Yang, Y. Zeng, W. Alnoush, Y. Hou, D. Higgins and G. Wu, Adv. Mater., 2022, 34, 2107954.
40. J. Huang, J. Chen, C. Fu, P. Cai, Y. Li, L. Cao, W. Liu, P. Yu, S. Wei, Z. Wen and J. Li, ChemSusChem, 2020, 13, 1496–1503.
41. A. Kulkarni, S. Siahrostami, A. Patel and J. K. Nørskov, Chem. Rev., 2018, 118, 2302–2312.
42. K. A. Stoerzinger, W. T. Hong, G. Azimi, L. Giordano, Y. Lee, E. J. Crumlin, M. D. Biegalski, H. Bluhm, K. K. Varanasi and Y. Shao-Horn, J. Phys. Chem. C, 2015, 119, 18504–18512.
43. A. Holewinski and S. Linic, J. Electrochem. Soc., 2012, 159, H864–H870.
44. G. Wang, Z. Yang, Y. Du and Y. Yang, Angew. Chem., Int. Ed., 2019, 58, 15848–15854.
45. F. H. B. Lima, J. Zhang, M. H. Shao, K. Sasaki, M. B. Vukmirovic, E. A. Ticianelli and R. R. Adzic, J. Phys. Chem. C, 2007, 111, 404–410.
46. X. Li, S. Tang, S. Dou, H. J. Fan, T. S. Choksi and X. Wang, Adv. Mater., 2022, 34, 2104891.
47. K. Jiang, S. Back, A. J. Akey, C. Xia, Y. Hu, W. Liang, D. Schaak, E. Stavitski, J. K. Nørskov, S. Siahrostami and H. Wang, Nat. Commun., 2019, 10, 3997.
48. X. Zhou, G. Xue, H. Luo, C. R. Bowen and D. Zhang, Prog. Mater. Sci., 2021, 122, 100836.
49. H. Thong, C. Zhao, Z. Zhou, C. Wu, Y. Liu, Z. Du, J. Li, W. Gong and K. Wang, Mater. Today, 2019, 29, 37–48.
50. T. Zheng, J. Wu, D. Xiao and J. Zhu, Prog. Mater. Sci., 2018, 98, 552–624.
51. C. Chen, G. King, R. M. Dickerson, P. A. Papin, S. Gupta, W. R. Kellogg and G. Wu, Nano Energy, 2015, 13, 423–432.
52. F. Izumi and T. Ikeda, Mater. Sci. Forum, 2000, 321–323, 198–203.
53. T. M. Gill and X. Zheng, Chem. Mater., 2020, 32, 6285–6294.
54. E. J. F. Dickinson, H. Ekström and E. Fontes, Electrochem. Commun., 2014, 40, 71–74.
55. R. B. Lakshmi, N. P. Harikrishnan and A. V. Juliet, Appl. Surf. Sci., 2017, 418, 99–102.
56. M. Scaramuzza, A. Ferrario, E. Pasqualotto and A. De Toni, Procedia Chem., 2012, 6, 69–78.
57. Y. Gao, R. Yang, C. Wang, C. Liu, Y. Wu, H. Li and B. Zhang, Sci. Adv., 2022, 8, eabm9477.
58. Z. Lu, L. Zhang, R. Iwata, E. N. Wang and J. C. Grossman, Langmuir, 2020, 36, 15112–15118.

---

Footnotes

† Electronic supplementary information (ESI) available: Supplementary details of catalyst characterization before and after the ORR, as well as the electrochemical measurements and finite element analysis. See DOI: https://doi.org/10.1039/d2ee02554j

‡ H. Yang, J. Wu and Z. R. Chen contributed equally to this work.

---