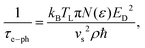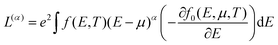Twisted grain boundary leads to high thermoelectric performance in tellurium crystals

Abstract

Identifying an ideal microstructure for efficient thermoelectric materials has been complicated by the interplay between the electrical and thermal properties. The electrical properties of thermoelectric materials are often compromised to reduce lattice thermal conductivities and increase dimensionless thermoelectric figure-of-merit (zT). However, the increase in zT achieved using this strategy has recently stagnated. For example, elemental tellurium (Te) has exhibited a degraded zT of ∼1 for several years although it has gained considerable attention as a potential high-performance thermoelectric material. In this study, we demonstrate an unprecedentedly high zT of 1.42 at 623 K for 1% Fe₂As-doped elemental Te crystals by utilizing the doping-induced twisting behavior of grain boundaries in Te. The unconventional twisted microstructure—twisted boundaries with aligned helical chains—enables an “electrically textured and thermally random” orientation. Therefore, the twisted Te crystal has a higher electrical conductivity and a comparable lattice thermal conductivity to the polycrystalline Te.

---

Broader context

Thermoelectric materials have gained great attention owing to their capability of converting heat into electricity without mechanical movements. However, their application is still limited to extremely specific areas (e.g., radioisotope thermoelectric generators) because of the low energy conversion efficiency of thermoelectric modules. Although nanostructuring has been successful in improving thermoelectric properties for more than a few decades, recent calculations and experiments showed a pessimistic future of nanostructuring, where thermal conductivities cannot be reduced below the amorphous minimum due to the quantum mechanical limit. Here, we utilized an unusual concept of “rotation” to effectively decouple electrical and thermal transport properties using elemental tellurium (Te) as a model system. It is found that the twisted grain boundaries in the Fe₂As-doped Te crystal preserve high electrical conductivities while reducing the thermal conductivities, showing superior thermoelectric performance. We believe that the strategy described in our work is expected to provide a breakthrough for improving the thermoelectric properties of various thermoelectric materials.

1. Introduction

Anisotropy is the characteristic of a material according to which properties change along a specific direction.¹ A single crystal consisting of long-range-ordered atomic planes exhibits extreme anisotropy, wherein electrical, thermal, mechanical, and optical properties vary depending on the crystallographic axis.^2–4 In contrast, polycrystalline materials having several grains without a preferred orientation typically exhibit isotropy because bulk properties are averaged along various crystallographic directions.⁵ In modern electronics applications, most materials are grown into single crystals in the anisotropically “best” direction to fully utilize their electronic performance (e.g., electron mobility).⁶ In contrast, efficient thermal insulators are often polycrystalline in nature and have extremely small grain sizes to block heat from all directions and suppress the thermal properties (e.g., phonon mean free path).⁷

This simple structure–property relationship becomes highly complicated for the design of efficient thermoelectric materials. Thermoelectric materials can directly convert heat into electricity, but their poor conversion efficiencies hindered their practical applications, necessitating further improvement.⁸ Typically, thermoelectric efficiency is proportional to the dimensionless figure-of-merit (zT), defined as zT = S²σT/κ, where S, σ, T, and κ are the Seebeck coefficient, electrical conductivity, absolute temperature, and thermal conductivity of a thermoelectric material, respectively.⁹ As discussed above, single crystals would possess superior electrical properties. However, concomitant high thermal conductivity hinders the achievement of high zT values for single crystals. Therefore, most thermoelectric materials have been synthesized in the polycrystalline form with nanograins by high-energy ball milling and spark plasma sintering (SPS) to reduce the lattice thermal conductivity (κ_L) of a material by compromising the electrical properties.^10,11 For decades, this strategy has been successful in increasing the zT values of thermoelectric materials; however, it has been found that κ_L cannot be reduced under the Ioffe–Regel limit of κ_L.¹² Consequently, the increase in zT values has stagnated recently, and a novel design rule is required to enhance the overall thermoelectric properties.

The simultaneous utilization of both high single-crystal-like electron mobility and a polycrystalline-like short phonon mean free path in a single material would be ideal for obtaining a high zT. This apparently unphysical statement has been realized in Cu₂(S,Te) mosaic crystals having tilted grains, with the translational symmetry of the lattice preserved throughout the crystal.¹³ However, the improvement in zT values mainly stems from a reduction in thermal conductivity, while the overall electrical properties remained similar or even decreased to values lower than those of polycrystalline samples. This might be ascribed to the absence of a well-defined texture in the direction of high electron mobility, which can be inferred from the X-ray diffraction profile of the mosaic crystal. Therefore, approaches for improving the electrical transport properties are necessary to achieve further improvement.

Thus, we hypothesized that a crystal with rotating grains but textured to the high-electron-mobility planes would be an ideal candidate for a novel high-performance thermoelectric material. In fact, this strategy has been experimentally realized to design a material with extremely anisotropic thermal properties. For example, a multilayer MoS₂ thin film with interlayer rotations exhibits ultralow out-of-plane thermal conductivities, while having high in-plane thermal conductivities.¹⁴ However, for thermoelectric applications, one should preserve the high electrical conductivities as well, and this was not straightforward using well-known layered thermoelectric materials (e.g., Bi₂Te₃) because of the mismatch between the direction of texturing (out-of-plane) and high electron mobility (in-plane). Therefore, we decided to use elemental tellurium (Te) which has a one-dimensional helical chain structure as a model system to align the texture direction with the high-mobility direction. To fully utilize its anisotropic properties along the c-axis and high thermoelectric performance resulting from its nested valence band,¹⁵ we incorporated iron arsenide (Fe₂As) as a p-type dopant in the Te matrix and synthesized highly textured samples using our conventional directional solidification apparatus (Fig. S1, ESI†).

In this study, we unveil an unconventional microstructure in 1% Fe₂As-doped Te to achieve an electrically single crystal with thermally polycrystalline nature and excellent thermoelectric properties. It was found that the addition of Fe₂As during the crystal growth not only increased the hole concentration, but also improved the degree of texturing compared with pure Te, and eventually led to the formation of a “twisted” microstructure. The twisted grain boundaries exhibit a highly anisotropic orientation—textured and random parallel and perpendicular to the growth direction, respectively—which enables both facile charge conduction and suppressed phonon propagation simultaneously. Therefore, an impressively high zT value of 1.42 at 623 K with zT_avg of 0.86 was achieved, which is arguably the highest value among the reported thermoelectric performances of elemental Te. This result clearly shows that the twisted microstructure can surpass a zT threshold of approximately 1, a limit that has not been easily overcome by conventional strategies in elemental Te. Ultimately, this work suggests an innovative way to decouple electron and phonon transport by controlling the structure–property relationship for developing efficient thermoelectric materials.

2. Results and discussion

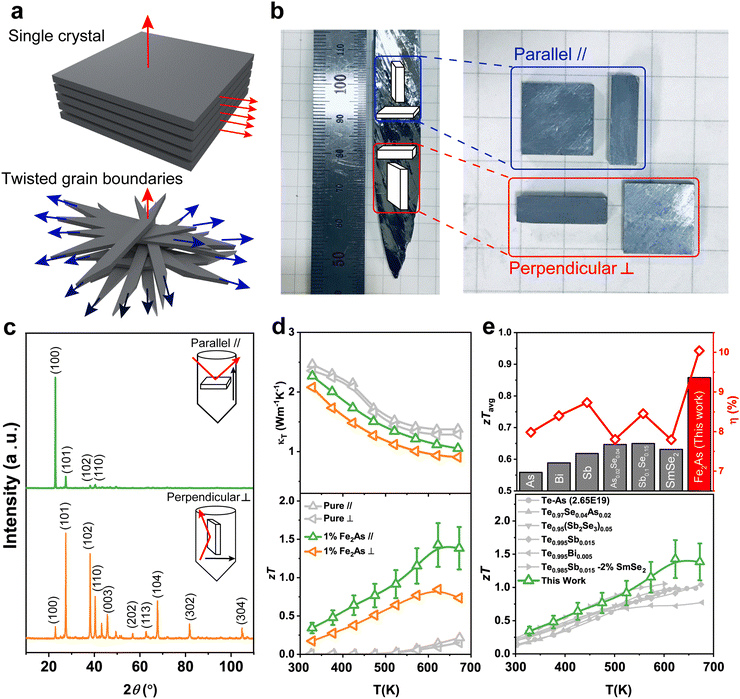
2.1 Texture-random duality of twisted grain boundaries

First, we compare the microstructure of a single crystal and a twisted Te crystal and its effect on the thermoelectric properties. Single crystals exhibit long-range-ordered atomic planes over a micron (or larger) scale, which minimizes electron scattering due to grain boundaries^16,17 (Fig. 1a, top). However, simultaneously, the absence of a phonon scattering center leads to high thermal conductivity, forestalling the achievement of high zT values for single crystals.

Fig. 1 Twisting boosts thermoelectric properties in chiral Te. (a) Schematic drawing of crystallographic orientation of a single crystal and a twisted Te crystal. The phonon transport is significantly limited while facile electron transport is conserved in the twisted crystal. (b) A digital photograph of the cleaved Te crystal and samples for electrical and thermal property measurements on top of the 5 × 5 mm grids. (c) Anisotropic XRD profile of the 1% Fe₂As doped Te crystal in parallel (‖) and perpendicular (⊥) directions to the growth direction. The red arrows show the beam path of diffracted X-rays and the black arrows show the direction along which the thermoelectric properties are measured. (d) Temperature-dependent total thermal conductivities (κ_T) and zT values of pure and 1% Fe₂As-doped Te crystals. (e) Comparison of average zT (zT_avg, bar), conversion efficiency (η, symbol), and temperature-dependent zT values of reported elemental polycrystalline Te with various dopants and twisted Te. The error bars in (e) denote the standard error of zT measurements (∼20%).

However, it was recently discovered that the propagation of transverse acoustic phonon modes can be suppressed by introducing an interlayer rotation in a textured thin film, minimizing the out-of-plane thermal conductivities (Fig. 1a, bottom).¹⁴ Furthermore, it is reasonable to assume that a small misfit in the twisted crystal would be beneficial for facile electron transport compared to that of the large-angle grain boundary of a polycrystalline material.^18,19 Therefore, we synthesized Te crystals with twisted grain boundaries to confirm the above hypothesis.

High-quality Te crystal samples doped with 1% Fe₂As were highly dense (∼99.5% of the theoretical density) and were easily cleaved. These expose a metallic luster, which is typical of single crystals (Fig. 1b). However, X-ray diffraction (XRD) measurements revealed that the samples were aligned to a (100) plane, but were randomly oriented in parallel and perpendicular directions with respect to the growth direction, respectively (Fig. 1c). As a result, an unusual sample with poly- and single-crystal duality was obtained. Surprisingly, pure Te crystals synthesized under the same condition showed nearly identical thermal conductivities (κ_T) regardless of the sample direction, while 1% Fe₂As-doped Te exhibited highly anisotropic κ_T and zT values (Fig. 1d). We attribute this anisotropic behavior to the dopant-induced texturing and twisting of the grain boundaries, which will be discussed in the next section. Compared with conventional polycrystalline Te, the twisted Te crystal exhibited excellent thermoelectric properties for both high average zT (zT_avg) and thermoelectric efficiency (η) at all operating temperatures (Fig. 1e).

2.2 Theoretical thermoelectric properties of Te

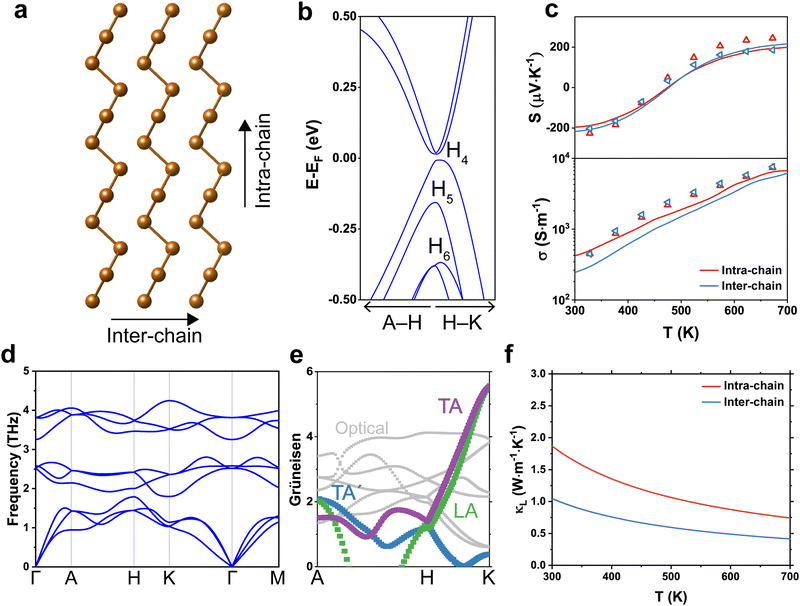
Tellurium crystallizes in a trigonal structure (space group P3₂21 or P3₁21 for left- and right-handed, respectively), showing a characteristic one-dimensional helical chain (Fig. 2a).²⁰ Owing to its highly anisotropic bonding structure, the electrical and thermal properties of Te depend on the crystallographic direction. The most prominent phenomenon is the formation of nested valence bands (i.e., multiple carrier pockets at identical valleys) at the H point (Fig. 2b). Without spin–orbit interaction (SOI), Te has a non-degenerate conduction band maximum and a doubly degenerate valence band maximum (Fig. S2, ESI†). However, the SOI of nonbonding 5p electrons in Te splits the electronic band into two spin-polarized states because of its non-centrosymmetric crystal structure.²¹ This increases the band effective mass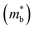 but preserves the inertial effective mass of electrons; therefore, both a high Seebeck coefficient and electrical conductivity can be achieved in p-type Te.²²

Fig. 2 Inherent anisotropic thermoelectric properties in the Te chain. (a) Crystal structure of Te along the a-axis. (b) Electronic band structure of Te along A–H and H–K directions. (c) Calculated temperature-dependent S and σ of pure Te along the inter- (red) and intra-chain (blue) directions. Experimental data of pure Te were plotted together for comparison. (d) Phonon dispersion and the corresponding (e) mode-specific Grüneisen parameter of Te. (f) Calculated temperature-dependent κ_L of pure Te along the inter- and intra-chain directions using the Boltzmann transport equation.

We calculated the theoretical S and σ values using the density functional theory (DFT) and Boltzmann transport equation under the relaxation time approximation (Fig. 2c and Fig. S3, ESI†). Theoretical S values showed n- to p-type transitions near 450 K, regardless of the direction. It is known that undoped, polycrystalline Te exhibits persistent p-type conduction properties at these temperatures,^22–25 while high-purity Te ingots with similar temperature dependence observed in this study yield negative S values.²⁶ Indeed, high-purity Te grown by TGS showed a similar polarity reversal near 450 K, and exhibited good agreement with the calculation data. This reversal in the Seebeck coefficient can be ascribed to the effect of additional holes in the valence band that arise from thermal acceptors or from the second conduction band minima located at the A point (Fig. S2, ESI†).²⁷ In addition, the theoretical σ value was higher in the parallel direction than in the perpendicular direction, while there were minor differences between the experimental σ values in the parallel and perpendicular directions because of the discrepancy of the crystal orientation.

The phonon dispersion also reveals the highly anisotropic and unique thermal properties of Te (Fig. 2d). Phonon dispersion is an indicator of the kinetic stability of the lattice because an elastic instability of the structure will appear as a form of negative phonon mode (i.e., imaginary frequency).²⁸ Therefore, the absence of an imaginary frequency in the entire Brillouin zone confirms that the helical chain structure of Te is kinetically stable. Three phonon branches, including two transverse acoustic (TA and TA′) modes and a longitudinal acoustic mode (LA), originate from the zone center (Γ point). The maximum frequency of these acoustic modes is approximately 60 cm⁻¹, which is similar to those of either Mg₃Sb₂²⁹ or Sb₂Te₃,³⁰ which are representative high-performance thermoelectric materials. This low-frequency acoustic mode implies a soft chemical bonding of Te, which is beneficial for achieving low κ_L values.³¹ Moreover, the Grüneisen parameters of TA and LA modes are as high as 5.5 at the K point. Since the Grüneisen parameter is a quantitative measure of the bonding anharmonicity, Te is expected to have low κ_L values because of the anharmonic phonon dispersion. Indeed, κ_L values at room temperature for inter-chain (1.86 W m⁻¹ K⁻¹) and intra-chain (1.04 W m⁻¹ K⁻¹) directions were considerably lower than those of elemental semiconductors (i.e., 166 and 65 W m⁻¹ K⁻¹ for Si and Ge, respectively).³² The low κ_L values along the intra-chain direction result from a high average Grüneisen parameter (1.37) compared with that along the inter-chain direction (0.92).³³

2.3 Microstructure of twisted grain boundaries in doped Te crystals

Although Te exhibits intriguing anisotropic properties, the thermoelectric performance of undoped Te is considerably lower than that of state-of-the-art thermoelectric materials. From the above calculation results, we found that Te exhibits both high electrical and thermal conductivities along the parallel direction compared with those in the perpendicular direction. Therefore, simply growing single-crystal Te along [100] or [001] does not guarantee high thermoelectric performance. In fact, the electrical properties of Te become highly anisotropic when heavily doped with p-type dopants.¹⁵ Inspired by this, we carefully grew Te crystals for various p-type dopant concentrations.

It has been reported that arsenic (As) is an effective p-type dopant in Te, thus resulting in a considerable improvement in electrical conductivity.²² However, elemental As preferentially forms arsenic trioxide owing to its high reactivity with oxygen, and thus produces toxic fumes above its boiling temperature. Hence, we chose an arsenide compound (i.e., Fe₂As) as an As source instead of elemental As for safe handling and reliable synthesis. Interestingly, the crystallographic orientation of the synthesized samples changed considerably upon increasing the dopant concentration. Multiple peaks in the XRD patterns of pure Te confirm that the sample is polycrystalline despite the slow crystallization process (Fig. S4, ESI†). In contrast, adding a small amount (0.2% or 0.8%) of Fe₂As enhances the crystal texture along the (003) plane, and eventually leads to the anisotropic XRD profile at 1% Fe₂As-doped Te, as discussed in Fig. 1c.

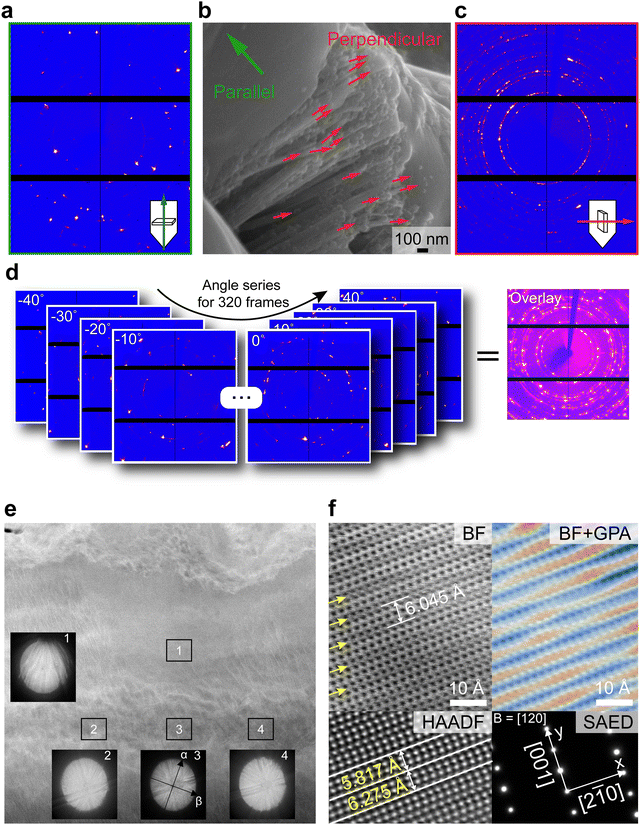
To gain an insight into the observed structural anisotropy of 1% Fe₂As-doped Te, we analyzed a scanning electron microscopy image of the sample as shown in Fig. 3b. It is found that several rod-like structures are aligned perpendicular to the growth direction. Each Te rod is pointing in a different direction as denoted by the red arrows, yielding a polycrystalline-like XRD profile in Fig. 3c. However, the sample shows well-defined diffraction spots when measured parallel to the growth direction, because these nanowires are stacked in a vertical direction, preferentially exposing the (100) plane (Fig. 3a). Interestingly, merging these diffraction spots acquired for several in-plane tilting angles produces polycrystalline-like diffraction rings (Fig. 3d). This means that each grain boundary is twisted in an in-plane direction, signposting a twisted morphology of the analyzed sample. Moreover, the strong optical activity of 1% Fe₂As-doped Te further confirms macroscopic structural chirality in the sample (Fig. S5, ESI†).

Fig. 3 Microstructure of a twisted Te crystal (a and c) 2D XRD pattern of the 1% Fe₂As-doped Te crystal measured (a) parallel and (c) perpendicular to the growth direction. Note that the diffractometer utilizes a transmission geometry. (b) Scanning electron microscopy image of 1% Fe₂As-doped Te showing grain morphologies parallel and perpendicular to the growth direction. (d) 2D XRD pattern of 1% Fe₂As-doped Te acquired at different in-plane tilting angles. Merging each pattern into a single image yields diffraction rings as shown in the right panel. (e) LAADF-STEM image revealing the twisting feature in the crystal. The insets are Kikuchi patterns corresponding to regions 1 to 4. (f) Atom-resolved BF and HAADF images and the selected area electron diffraction pattern acquired from region 3 along the [120] zone axis. The strain mapping along the yy direction (ε_yy) is overlaid with an identical scale to demonstrate the periodic lattice distortion. The yellow arrows depict positively strained planes.

We then conducted characterization by scanning transmission electron microscopy (STEM) to gain insights into the orientation and atomic structure of the twisted Te crystals. Fig. 3e shows a low-angle annular dark-field (LAADF)–STEM image with Kikuchi patterns acquired at various positions. Instead of the equiaxed grains, columnar grains with a relatively long lateral size of a few micrometers can be observed. The Kikuchi patterns of regions 2–4 were identical, thus indicating a large single grain in regions 2–4. The slightly tilted pattern of region 3 was intentionally obtained by moving the electron probe along the grain, which also supported the single-grain characteristics. The pattern of region 1 is tilted along the alpha (α) direction compared with regions 2–4, thus indicating that the zone axis of region 1 does not exist along [120], thus forming an incoherent boundary between regions 1 and 2–4. The strain originating from the misfit orientation at the grain boundary between regions 1 and 2–4 is observed in the LAADF images by comparing the contrast differences of high-angle annular dark-field (HAADF)–STEM and LAADF–STEM images (Fig. S6, ESI†). Note that the chemical homogeneity was confirmed within horizontal grains using STEM-EDX elemental mapping; thus, the contrast does not stem from elemental partitioning or precipitation (Fig. S7, ESI†).

To validate the contribution of misfit strain at the grain boundary, we performed aberration-corrected STEM and examined the area between regions 1 and 3. The atomic-resolution bright field (BF)-STEM image shows the crystal structure of Te viewed along the [120] zone axis (Fig. 3f). In the image, repeating dark contrasts appeared with a period of 6.045 Å, which is ∼2.2% higher than the c-axis lattice constant of pure Te (5.912 Å). Given that the BF imaging technique is highly sensitive to the diffraction contrast and lattice strain,¹⁹ we suspected that these periodic ripples resulted from a microstrain in the lattice. Indeed, geometric phase analysis revealed that the lattice was both stretched and compressed along the [001] direction, wherein the stretched regions had a dark contrast. Notably, the rippling contrasts disappeared in the HAADF–STEM image because HAADF detectors are sensitive to an atomic number (Z) contrast but robust to other factors.³⁴ We measured the interplanar distance between two adjacent (001) planes and found that none of these values (5.817 Å and 6.275 Å) corresponded to the c-axis lattice parameter of Te, while the average (6.046 Å) corresponded to the period of strain ripples. The lattice strain comprised compression (1.6%) and tensile (6.1%) strain. The lattice strain could be induced from the incorporation of Fe and As into Te because pure Te did not show significant lattice strain or periodic ripples in the STEM images (Fig. S8, ESI†). It should be noted that the observed strain does not affect the overall electrical transport properties, which is confirmed by DFT calculations (Fig. S2, ESI†) and FT-IR spectroscopy (Fig. S9, ESI†).

From the above observations, we speculate that the unconventional twisted microstructure of Te crystals may originate from a complex interplay of doping, growth kinetics, and strain accommodation. Doping-induced texturing has been reported previously in the bulk^35–37 or thin films,^38,39 although a detailed mechanism has not yet been fully elucidated. The formation mechanism of the twisted grain boundaries in doped Te might be nuanced because of its characteristic helical nature. Based on the previous reports, however, we propose that the Eshelby twist could be the principal mechanism for the formation of twisted microstructures. The observed twisted microstructures can be considered chiral structure because of the absence of the rotational symmetry. Unlike the conventional belief that a chiral ligand is necessary for synthesizing twisted nanostructures, chiral shaped Te spontaneously forms in the absence of the ligand.⁴⁰ Moreover, the rapid solidification process leads to an achiral shape formation even with chiral ligands.⁴⁰ This corroborates that the Eshelby twist is responsible for the chiral shape formation.

However, given the polycrystalline nature of pure Te synthesized under a slow cooling process, we speculate that adding a dopant (or solid–liquid interface) might contribute to construct a twisted morphology in a bulk scale. For example, Eshelby twisted germanium sulfide is synthesized with the aid of gold⁴¹ or bismuth⁴² catalysts via vapor–liquid–solid growth.⁴³ Similarly, we suppose that insoluble dopants act as a catalyst (or a pinning point) to increase the frequency of the twisting, not simply increasing the texturing of a given material. Indeed, adding an excess amount (2%) of Fe₂As does not exhibit textured orientation, but rather shows the polycrystalline nature in the XRD pattern (Fig. S10, ESI†). It is known that the solubility of Fe and As in the Te matrix is significantly low.^44,45 The time-of-flight–secondary ion mass spectroscopy (TOF-SIMS, Fig. S11, ESI†) and energy-dispersive X-ray spectroscopy (EDX) mapping and backscattered electron images revealed the existence of Fe- and As-rich precipitates in the matrix (Fig. S12 and S13, ESI†). We identified these precipitates as FeTe₂ and As₂Te₃ using powder XRD measurements (Fig. S14, ESI†). In addition, calorimetric analyses showed endothermic peaks, which are assigned to the glass transition temperature of As₂Te₃ and the reaction temperature of the Fe–As phases (Fig. S15, ESI†).^46,47 Therefore, these precipitates might act as a source of lattice strain, solid–liquid interface, or pinning point during the growth process. Therefore, a combination of these microstructures results in a twisted microstructure with simultaneous textured and random orientations.

2.4 Electrically textured and thermally random characteristics

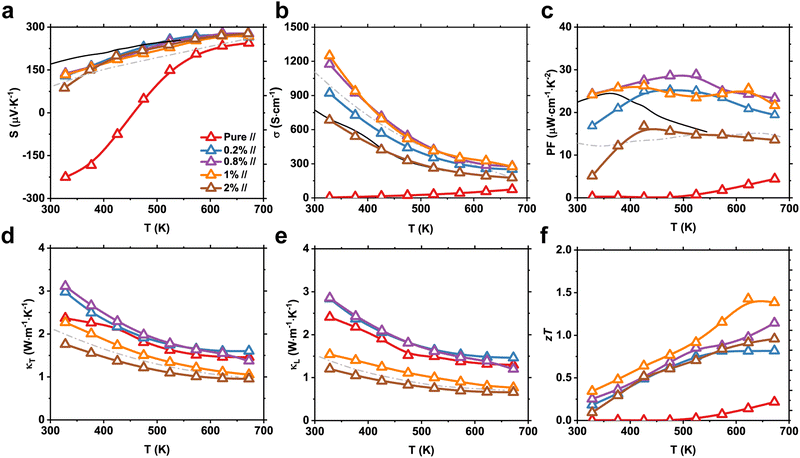
We now show that the twisted microstructure is highly beneficial for improving the thermoelectric properties. The temperature-dependent S of pure and Fe₂As-doped Te parallel to the crystal growth direction is shown in Fig. 4a. Because As is known to be an effective acceptor, adding small amounts of Fe₂As completely converts Te into a p-type degenerate semiconductor with the increase the hole concentration of Te.²² From the Hall effect measurements, we found that the hole concentration of Te increased considerably from 3.2 × 10¹⁶ to 1.6 × 10¹⁹ cm⁻³ at 300 K for pure and 1% Fe₂As-doped Te, respectively (Fig. S16, ESI†), followed by significant improvement in σ (Fig. 4b). The asymmetry ratios of the S values between the parallel and perpendicular directions (S_‖/S_⊥) were 0.86, 1.02, and 1.44 for 0.2, 0.8, and 1% Fe₂As concentrations, respectively (Fig. S17, ESI†). These values are consistent with the DFT-calculated ratio (= 1.25) for a hole concentration of 10¹⁹ cm⁻³.¹⁵ Therefore, highly anisotropic S values could be obtained by heavy p-type doping and the textured nature of the samples.

Fig. 4 Temperature-dependent thermoelectric properties parallel to the crystal growth direction Temperature-dependent (a) Seebeck coefficient, (b) electrical conductivity, (c) power factor, (d) total thermal conductivity, (e) lattice thermal conductivity, (f) and dimensionless figure of merit (zT) values for pure and Fe₂As-doped Te crystals. Data for As-doped polycrystalline Te (grey line) and Sb-doped single crystal Te (black line) were plotted together for comparison.

It is interesting to note that both S and σ values of 1% Fe₂As-doped Te surpass those of polycrystalline As-doped Te with similar carrier concentrations, and yield superior power factor (PF) values over the entire temperature range (Fig. 4c). Assuming a single parabolic band model, simultaneous improvement of S and σ by carrier concentration optimization is not possible because of their trade-off relationship.⁹ The estimated hole effective mass for Fe₂As-doped Te samples ranges from 0.25m₀ to 0.45m₀. The increase of the hole effective mass with doping might be attributed to the nested valence bands of Te, which will make holes heavier at a deeper Fermi level (Fig. S18, ESI†).²² A similar increase of the hole effective mass is observed in Sb-doped Te as well; however, it is not enough to explain the significant increase of PF by the band nesting effect alone.⁴⁸ Therefore, we attribute the superior electrical properties to the textured morphology. Indeed, the temperature dependence of the weighted mobility of 0.8% and 1% Fe₂As-doped Te shows a negligible barrier height for the charge transport, signifying that an enhanced electrical conductivity stems from the structure effect (Fig. S19, ESI†).

In fact, 0.8% Fe₂As-doped Te showed similar or higher PF values than the 1% sample because of the highly textured grains. However, a considerable drop in both total (κ_T) and lattice (κ_L) thermal conductivities was observed for 1% Fe₂As-doped Te (Fig. 4d and e). Owing to the textured orientation, κ_L values of 0.2% and 0.8% Fe₂As-doped Te (2.85 W m⁻¹ K⁻¹) at 323 K were higher than those of pure Te (2.40 W m⁻¹ K⁻¹). In contrast, 1% Fe₂As-doped Te yielded a κ_L value of 1.54 W m⁻¹ K⁻¹ at 323 K, which is comparable to the polycrystalline value (1.48 W m⁻¹ K⁻¹). The thermally polycrystalline behavior of 1% Fe₂As-doped Te is further confirmed by evaluating the phonon mean free path (Fig. S20, ESI†). The pure Te and textured Te (0.2 and 0.8% Fe₂As-doped samples) showed a similar phonon mean free path of ∼3.6 nm, implying that the point defect scattering by Fe₂As incorporation is not prominent because of its low solubility. However, 1% and 2% Fe₂As-doped Te showed a marked reduction of the phonon mean free path, which corroborates the critical role of the microstructure in suppressing phonon propagation in Te. As a result, 1% Fe₂As-doped Te exhibited single-crystal-like facile hole transport but polycrystalline-like phonon transport, which resulted in improved zT values, and reached a maximum zT value of 1.42 at 623 K (Fig. 4f and Fig. S21, ESI†). Note that the beneficial effect of the twisted microstructure vanishes when the sample is measured perpendicular to the growth direction (Fig. S17, ESI†). From this observation, we attribute the superior electrical properties to the textured (100) plane which has higher electrical conductivity than the (001) plane, as discussed in Fig. 2c. Rotating grains effectively scatter phonons similar to observations made in Cu₂(S,Te) mosaic crystals¹³ and MoS₂ multilayers,¹⁴ but textured grains preserve high electrical conductivity and lead to superior PF values. One can notice that adding 2% Fe₂As greatly reduces the lattice thermal conductivity due to the highly random orientation of grains, and the significant drop of the PF hinders zT from surpassing 1, confirming the effectiveness of constructing twisted grain boundaries in thermoelectric Te. In addition, the influence of magnetism on electrical properties of 1% Fe₂As-doped Te has been ruled out as it exhibits diamagnetic property (Fig. S22, ESI†).

Lastly, we confirmed the reproducibility and repeatability of the thermoelectric properties of 1% Fe₂As-doped Te by measuring the properties for several heating–cooling cycles (Fig. S23, ESI†) and international round-robin tests (Fig. S24, ESI†). Samples cut from various positions of the crystal exhibited excellent uniformity in thermoelectric properties, and demonstrated that the high zT values did not originate from the uneven chemical composition (Fig. S25, ESI†). Moreover, the high Vickers hardness above 1 GPa further ensures mechanical stability for practical device applications (Fig. S26, ESI†).

3. Conclusions

In summary, we successfully demonstrated the electron-passing and phonon-blocking characteristics of twisted tellurium using a temperature gradient solidification process. We observed the anisotropic orientation of crystal planes and the corresponding lattice distortions, which originate from the introduction of the Fe₂As dopant. Eventually, a highly textured microstructure enabled facile electron transport, while twisted grain boundaries significantly reduced the lattice thermal conductivity to polycrystalline values. This synergistic improvement in both electrical and thermal transport leads to a high zT of 1.42 at 623 K, which is one of the highest values among elemental Te-based thermoelectrics. These results highlight the effectiveness of constructing a twisted microstructure in thermoelectric materials for obtaining high electrical conductivities, while reducing thermal conductivities toward high zT values. This strategy can be expanded to quasi-one-dimensional thermoelectric materials (e.g., In₄Se₃) to achieve an improved thermoelectric performance compared to that of single crystals or nanostructured polycrystals.

4. Experimental section

4.1 Materials

Te shots (99.999%, 5N plus, Canada) and Fe₂As (metals basis, 99.5%, Alfa Aesar, USA) were used as received with no further purification.

4.2 Synthesis

The samples were melted in a vertical furnace as shown in Fig. S1a and b (ESI†). The crystals were obtained by heating and slowly cooling the materials in a conical evacuated sealed quartz tube. Stoichiometric amounts of Te and Fe₂As were added to the tube with the composition of Te_1−x(Fe₂As)_x (x = 0, 0.002, 0.008, 0.01, and 0.02) and flame-sealed after repeated cycles of purging with Ar. The quartz tube was loaded into a vertical furnace and the temperature was raised to 783 K and then maintained for 12 h followed by slow cooling to 603 K at 1 K h⁻¹ to prevent thermal cracks and provide avenues for nucleation at the conical tip. The quartz tube was then cooled to room temperature at 100 K h⁻¹.

4.3 Powder X-ray diffraction (XRD)

The phases of bulk and powdered samples were determined by using an X-ray diffractometer (SmartLab, Rigaku, Japan) at room temperature using a CuK_α radiation source (λ = 0.15406 nm). The texture was determined by using pole figure equipment (D/MAX-2500, Rigaku, Japan) with a CuK_α radiation source (λ = 0.15406 nm).

4.4 Scanning electron microscopy (SEM)

The fractured surface and the polished surface were analyzed by using a field emission scanning electron microscope (SU 5000, Hitachi, Japan) equipped with an energy dispersive X-ray spectrometer (X-Max, Oxford, USA) for chemical analysis. The precipitates were observed in the backscattered electron-scanning mode.

4.5 Differential scanning calorimetry (DSC)

The heat flow measurement was experimentally performed using a high temperature differential scanning calorimeter (DSC Q2000, TA Instrument, USA). The samples were sealed using aluminum Tzero hermetic pan and lid (TA Instrument, USA) and heated to 723 K with a ramping rate of 5 K min⁻¹. Experimental heat capacities of pure Te and 1% Fe₂As-doped Te were measured at Netzsch Korea Co., Ltd to exclude the possibility of overestimating zT by neglecting latent heat from a phase transition (Fig. S27, ESI†).

4.6 Time-of-flight–secondary ion mass spectroscopy (TOF-SIMS)

TOF-SIMS analysis was performed using a TOF-SIMS5 apparatus (ION-TOF GmbH, Germany). The elemental distribution of Fe₂As-doped Te was measured for 10 min using Bi₃⁺⁺ as the primary ion source with an energy of 30 keV.

4.7 X-ray photoelectron spectroscopy (XPS)

The XPS spectra for doped ingot were measured using a scanning XPS microprobe (VersaProbe PHI 5000, ULVAC-PHI, Japan) instrument under an ultrahigh vacuum chamber (<10⁻⁷ Pa) with Al K_α radiation (X-ray energy of 1486.6 eV). An XPS beam size of 100 μm was used to obtain the spectra. The adventitious carbon peak with a binding energy of 284.8 eV was used as a reference for calibration of the core level spectra.

4.8 Transmission electron microscopy (TEM)

The specimen for TEM analysis was prepared by using a focused ion beam (FIB, Helios G4, FEI Company, USA) with liquid gallium metal as an ion source. The specimen was cut parallel to the growth direction and milled to the final thickness of approximately 40 nm to ensure electron transparency. The TEM imaging was conducted by using a spherical aberration-corrected TEM (Titan Cubed G2 60-300, FEI Company, USA) at 300 kV with a spherical aberration corrector (CEOS GmbH, Germany) and a Gatan Image Filter (Quantum 965, Gatan Inc., USA). To minimize electron drift, the measurement was started at 3 h after sample loading. The size of the electron probe was approximately 1 Å and the convergence semi-angle was 25.1 mrad. Energy-dispersive X-ray spectroscopy (EDX) elemental mapping was performed with four integrated silicon-drift EDX detectors (Super X, ChemiSTEM^TM Technology, USA). The selected area electron diffraction (SAED) pattern was acquired with an aperture size of 100 nm. The Kikuchi pattern was acquired in the STEM mode for each position and directly captured from FluCam (Fig. S28, ESI†). The obtained pattern was indexed using a simulated Kikuchi pattern of Te viewed along the [120] zone axis (Kossel/Kikuchi, JCrystalSoft). The camera length was adjusted from 73 mm (HAADF imaging) to 140 mm (LAADF imaging) to manipulate the collection semi-angle. The acquired raw images were band-pass filtered to minimize background noise by using commercial software (HREM-Filters Lite, HREM Research Inc., Japan). The strain mapping was performed using the geometric phase analysis (GPA) method.

4.9 Diffuse reflectance infrared Fourier transform spectroscopy

The optical reflectance spectrum was measured with a Fourier transform-infrared spectrometer (Nicolet iS50, Thermo Fisher, USA) using diffuse reflectance infrared Fourier transform spectroscopy and the absorption coefficient was calculated using the Kubelka–Munk function, which is given by F(R) = (1 − R)²/2R, where R is the optical reflectance.

4.10 Thermoelectric property measurement

The thermoelectric properties were measured along the perpendicular and parallel directions to crystal growth. The Seebeck coefficient and electrical conductivity were measured simultaneously by using a commercial system (BS-1, BlueSys, Republic of Korea) with a dimension of 3 × 3 × 10 mm³. The measurement was performed under a weak helium backpressure and the sample was coated with a thin boron nitride layer to minimize the sample outgassing. The reproducibility of thermoelectric properties was verified using a separate commercial apparatus (ZEM-3, ULVAC, Japan) and a home-built apparatus in Northwestern University. Thermal conductivity was estimated from the product of the density (ρ), specific heat capacity (C_p), and thermal diffusivity (D). The thermal diffusivity was measured by the laser flash method (LFA 467, Netzsch. Ltd, Germany). The reproducibility of the thermal diffusivity was also confirmed by using other apparatuses at KAIST Analysis Center for Research Advancement and Northwestern University (LFA 457, Netzsch, Germany). The specific heat capacity was estimated using the Dulong–Petit law. In measuring thermal diffusivity, the samples were coated with a thin layer of graphite to reduce the tendency for errors related to the emissivity of the material. The temperature dependent Hall coefficient (R_H), carrier concentration (n_H), and mobility (μ_H) of the samples were measured to 400 °C using the Van der Pauw configuration and the high temperature Hall measurement system (ResiTest 8300, TOYO Corporation, Japan) under a magnetic field of 1 T and an excitation current of 100 mA. zT_avg was calculated by taking an integral mean of temperature-dependent zT values from 323 to 673 K.

4.11 Angle-dependent X-ray diffraction

We used the sample cut for thermoelectric property measurements for consistency. The sample was polished off to have a thickness of 300 μm for the X-ray transparency, and was mounted on a glass fiber with glue on a STOE STADIVARI diffractometer equipped with an AXO Ag K_α micro-focus sealed X-ray A-MiXS source (λ = 0.560834 Å), running at 65 kV and 0.68 mA, and a Dectris Pilatus3 R CdTe 300K Hybrid Photon Counting detector. The size of the X-ray beam was approximately 100 μm. The phi angle was changed ranging from −40° to 40° over 320 frames, and the intensity data were collected at 300 K over a period of 120 s at each frame. Data processing was performed with the X-Area software package. The measurement geometry is described in ESI† (Fig. S29).

4.12 Circular dichroism spectroscopy

The chiroptical properties of pure and Fe₂As-doped Te crystals were measured using a circular dichroism spectrophotometer (J-815, JASCO) consisting of a xenon lamp, a photoelastic modulator, and a built-in quad-channel lock-in amplifier. The absorbance and circular dichroism spectra were simultaneously acquired from 180 to 350 nm with a data pitch of 0.05 nm and a scan rate of 50 nm min⁻¹. Due to the extremely high absorbance of Te, we measured the diffuse reflectance signal instead of the transmittance using an integrating sphere coated with BaSO₄ (DRCD-575, JASCO). This enables measurement of the sample without dissolving it in a solvent, which might change the structural feature of the original sample. Spurious circular dichroism signals from linear dichroism contributions were ruled out by measuring the spectra while rotating the sample.⁴⁹

4.13 Sound velocity measurement

The speed of sound was measured by the pulse-echo method. An ultrasonic pulse was sent and received by an identical piezoelectric transducer. A longitudinal transducer with a center frequency of 5 MHz (CMR-052, ndtXducer) and a normal incidence shear transducer with an identical frequency (SM-052, ndtXducer) were used for determining longitudinal and transverse sound velocities, respectively. An ultrasonic pulser/receiver was used to manipulate the pulse characteristics (DPR 300, JSR Ultrasonics) and the resulting waveform was recorded using a digital oscilloscope (DSO-X 2022A, Keysight). The time delay, t_d, was determined by varying t_d to maximize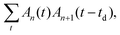 where A_n(t) is the amplitude of the n-th pulse wave.

4.14 Mechanical property measurement

The nano-mechanical properties were measured using the nanoindentation technique (STeP4-UNHT3 & MST3, Anton Paar). We used a standard Berkovich diamond indenter with a load of 20 mN with a loading rate of 40 mN min⁻¹. The tests were repeated 8 times to check the repeatability of the measurement. The estimated uncertainty of the measurement is within 10%.

4.15 Magnetic property measurement

The magnetization of the pure and Fe₂As-doped Te powder samples at different magnetic fields was measured using a magnetic property measurement system (MPMS3-Evercool, Quantum Design) equipped with a superconducting quantum interference device vibrating-sample magnetometer (SQUID VSM) whose sensitivity is better than 10⁻⁸ emu. The magnetic field was swept between ±0.5 T with a sweeping rate of 2 mT s⁻¹. The powder samples were kept in gelatin capsules whose background diamagnetic property was measured independently and subtracted later.

4.16 Density functional theory (DFT) calculations

First-principles calculations of Te were performed based on density functional theory with the generalized gradient approximation⁵⁰ parametrized by Perdew, Burke, and Ernzerhof (PBE-GGA) implemented in the Vienna ab initio simulation package (VASP) code.⁵¹ The cutoff energy for the plane wave basis was 520 eV. The lattice parameters after structure optimization were a = b = 4.5123 Å, and c = 5.9598 Å.

The electrical transport properties were calculated using the Boltzmann transport theory within the relaxation time approximation. The relaxation time for electron–phonon scattering was calculated as^52,53

where N(ε) is the electronic density of states, k_B is the Boltzmann constant, T_L is the lattice temperature, ρ is the density of Te (= 6.050 g cm⁻³), ν_s is the speed of sound (= 2000 m s⁻¹) and E_D is the deformation potential of the electronic band (= 4.0 eV). The thermoelectric coefficients were calculated from the transport distribution function given by⁵⁴
where ν_k is the component of the group velocity of each carrier in the transport direction, E_k is the energy of that electronic state, and τ_k is total relaxation time. The moments of generalized transport coefficients are given by
Using boundary conditions, the thermoelectric coefficients are calculated as
The force constants and thermal properties were calculated using the real-space approach included in the PHONOPY package⁵⁵ and the finite displacement method. A 5 × 5 × 4 sized supercell was used and a displacement of 0.01 Å was applied in DFT calculations. The lattice thermal conductivity was obtained using the Boltzmann transport equation under the relaxation time approximation as⁵⁶
where the sum is over all phonon bands b, the integral is over the Brillouin zone, ν_b,q is the group velocity of the phonon mode, τ_b,q is the phonon relaxation time, and C_b,q is the mode heat capacity. The relaxation time was obtained by considering anharmonic scattering using the quasi-harmonic approximation, which is expressed as⁵⁶
where M is the average atomic mass, V is the unit cell volume, ν_s is the speed of sound, and θ_D is the Debye temperature.

Author contributions

S. A. and H. J. contributed equally to this work. M.-W. O. conceived the project and designed the experiments. V. Q. N. and S. C. designed the temperature gradient solidification furnace. S. A., H. J., and B. F. synthesized ingots and measured the transport properties. N. K. and C. B. performed DFT calculations on electrical and thermal properties of tellurium. W. H. N. performed the high temperature Hall measurements. J. H. P. and S. D. P. measured the thermal diffusivity. C. V. N., H. S., and J. Y. S. synthesized the polycrystalline ingots. H. J., M. A. M. and G. J. S. confirmed the reproducibility of thermoelectric properties and analyzed the microstructure. J. K. and B.-G. P. measured the magnetic properties. K. H. H. and Y. S. J. reviewed the manuscript. S. A., H. J., and M.-W. O. wrote the manuscript with discussion and input from all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Creative Materials Discovery Program through the National Research Foundation of the Republic of Korea (NRF) funded by the Ministry of Science and ICT (No. 2020M3D1A1070053). N. Kumar acknowledges a PhD fellowship from CSIR, India (Grant no. 09/1129(0017)/2019-EMR-I). This research was supported by the research fund of Hanbat National University in 2019. M.-W. Oh and C. Bera also acknowledge the India-Korea Joint Network Center on Computational Materials supported by DST India (INT/Korea/JNC/CMS). This work made use of the IMSERC Crystallography facility at Northwestern University, which has received support from the Soft and Hybrid Nanotechnology Experimental (SHyNE) Resource (NSF ECCS-2025633), and Northwestern University. Purchase of the Ag-microsource diffractometer used to obtain results included in this publication was supported by the Major Research Instrumentation Program from the National Science Foundation under the award CHE-1920248.

References

1. B. He, et al., The Fermi surface geometrical origin of axis-dependent conduction polarity in layered materials, Nat. Mater., 2019, 18, 568–572,  DOI:10.1038/s41563-019-0309-4.
2. L.-D. Zhao, et al., Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals, Nature, 2014, 508, 373–377,  DOI:10.1038/nature13184.
3. R. Zhuang, et al., Highly sensitive X-ray detector made of layered perovskite-like (NH4)₃Bi₂I₉ single crystal with anisotropic response, Nat. Photonics, 2019, 13, 602–608,  DOI:10.1038/s41566-019-0466-7.
4. C. Kearney, et al., Nanoscale Anisotropic Plastic Deformation in Single Crystal Aragonite, Phys. Rev. Lett., 2006, 96, 255505,  DOI:10.1103/PhysRevLett.96.255505.
5. Y. Luo, et al., High-Performance Thermoelectrics from Cellular Nanostructured Sb₂Si₂Te₆, Joule, 2020, 4, 159–175,  DOI:10.1016/j.joule.2019.10.010.
6. J. Feng, et al., Single-crystalline layered metal-halide perovskite nanowires for ultrasensitive photodetectors, Nat. Electron., 2018, 1, 404–410,  DOI:10.1038/s41928-018-0101-5.
7. R. Wordsworth, L. Kerber and C. Cockell, Enabling Martian habitability with silica aerogel via the solid-state greenhouse effect, Nat. Astron., 2019, 3, 898–903,  DOI:10.1038/s41550-019-0813-0.
8. J. He and T. M. Tritt, Advances in thermoelectric materials research: Looking back and moving forward, Science, 2017, 357, eaak9997,  DOI:10.1126/science.aak9997.
9. G. J. Snyder and E. S. Toberer, Complex thermoelectric materials, Nat. Mater., 2008, 7, 105–114,  DOI:10.1038/nmat2090.
10. B. Poudel, et al., High-Thermoelectric Performance of Nanostructured Bismuth Antimony Telluride Bulk Alloys, Science, 2008, 320, 634–638,  DOI:10.1126/science.1156446.
11. A. J. Minnich, M. S. Dresselhaus, Z. F. Ren and G. Chen, Bulk nanostructured thermoelectric materials: current research and future prospects, Energy Environ. Sci., 2009, 2, 466–479,  10.1039/B822664B.
12. M. T. Agne, R. Hanus and G. J. Snyder, Minimum thermal conductivity in the context of diffuson-mediated thermal transport, Energy Environ. Sci., 2018, 11, 609–616,  10.1039/C7EE03256K.
13. Y. He, et al., Ultrahigh Thermoelectric Performance in Mosaic Crystals, Adv. Mater., 2015, 27, 3639–3644,  DOI:10.1002/adma.201501030.
14. S. E. Kim, et al., Extremely anisotropic van der Waals thermal conductors, Nature, 2021, 597, 660–665,  DOI:10.1038/s41586-021-03867-8.
15. H. Peng, N. Kioussis and G. J. Snyder, Elemental tellurium as a chiral p-type thermoelectric material, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 195206,  DOI:10.1103/PhysRevB.89.195206.
16. K. Imasato, et al., Metallic n-Type Mg₃Sb₂ Single Crystals Demonstrate the Absence of Ionized Impurity Scattering and Enhanced Thermoelectric Performance, Adv. Mater., 2020, 32, 1908218,  DOI:10.1002/adma.201908218.
17. J. J. Kuo, et al., Grain boundary dominated charge transport in Mg₃Sb₂-based compounds, Energy Environ. Sci., 2018, 11, 429–434,  10.1039/C7EE03326E.
18. S. I. Kim, et al., Dense dislocation arrays embedded in grain boundaries for high-performance bulk thermoelectrics, Science, 2015, 348, 109–114,  DOI:10.1126/science.aaa4166.
19. K. Biswas, et al., Strained endotaxial nanostructures with high thermoelectric figure of merit, Nat. Chem., 2011, 3, 160–166,  DOI:10.1038/nchem.955.
20. Z. Dong and Y. Ma, Atomic-level handedness determination of chiral crystals using aberration-corrected scanning transmission electron microscopy, Nat. Commun., 2020, 11, 1588,  DOI:10.1038/s41467-020-15388-5.
21. M. Sakano, et al., Radial Spin Texture in Elemental Tellurium with Chiral Crystal Structure, Phys. Rev. Lett., 2020, 124, 136404,  DOI:10.1103/PhysRevLett.124.136404.
22. S. Lin, et al., Tellurium as a high-performance elemental thermoelectric, Nat. Commun., 2016, 7, 10287,  DOI:10.1038/ncomms10287.
23. Y. Wu, et al., Scattering Mechanisms and Compositional Optimization of High-Performance Elemental Te as a Thermoelectric Material, Adv. Electron. Mater., 2020, 6, 2000038,  DOI:10.1002/aelm.202000038.
24. M. Yang, et al., High-pressure synthesis and thermoelectric performance of tellurium doped with bismuth, J. Mater. Sci., 2017, 52, 10526–10532,  DOI:10.1007/s10853-017-1180-9.
25. M. Yang, et al., Electrical transport and thermoelectric properties of Te–Se solid solutions, Phys. Lett. A, 2019, 383, 2615–2620,  DOI:10.1016/j.physleta.2019.05.019.
26. F. Tadao, T. Seiichi and T. Shotaro, Electrical properties of antimony-doped tellurium crystals, Sci. Rep. Res. Inst., Tohoku Univ., Ser. A, 1952, 4, 283–297.
27. R. Link, Zur anomalen Vorzeichenumkehr des Hallkoeffizienten in Tellur, Phys. Status Solidi B, 1965, 12, 81–92,  DOI:10.1002/pssb.19650120105.
28. S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Phonons and related crystal properties from density-functional perturbation theory, Rev. Mod. Phys., 2001, 73, 515–562,  DOI:10.1103/RevModPhys.73.515.
29. W. Peng, G. Petretto, G.-M. Rignanese, G. Hautier and A. Zevalkink, An Unlikely Route to Low Lattice Thermal Conductivity: Small Atoms in a Simple Layered Structure, Joule, 2018, 2, 1879–1893,  DOI:10.1016/j.joule.2018.06.014.
30. D. Das, et al., Defect induced structural and thermoelectric properties of Sb₂Te₃ alloy, J. Appl. Phys., 2015, 118, 045102,  DOI:10.1063/1.4927283.
31. Z. Chen, X. Zhang and Y. Pei, Manipulation of Phonon Transport in Thermoelectrics, Adv. Mater., 2018, 30, 1705617,  DOI:10.1002/adma.201705617.
32. Z. Chen, X. Zhang, S. Lin, L. Chen and Y. Pei, Rationalizing phonon dispersion for lattice thermal conductivity of solids, Natl. Sci. Rev., 2018, 5, 888–894,  DOI:10.1093/nsr/nwy097.
33. H. Peng, N. Kioussis and D. A. Stewart, Anisotropic lattice thermal conductivity in chiral tellurium from first principles, Appl. Phys. Lett., 2015, 107, 251904,  DOI:10.1063/1.4938203.
34. W. He, et al., High thermoelectric performance in low-cost SnS_0.91Se_0.09 crystals, Science, 2019, 365, 1418–1424,  DOI:10.1126/science.aax5123.
35. Y. Zhang, H. Zhang, Y. Xu and Y. Wang, Significant effect of lanthanide doping on the texture and properties of nanocrystalline mesoporous TiO₂, J. Solid State Chem., 2004, 177, 3490–3498,  DOI:10.1016/j.jssc.2004.05.026.
36. A. Chen, et al., Effects of nickel doping on the preferred orientation and oxidation potential of Ti/SbSnO₂ anodes prepared by spray pyrolysis, J. Alloys Compd., 2016, 684, 137–142,  DOI:10.1016/j.jallcom.2016.05.076.
37. Z. Yao, et al., Influences of rare earth element Ce-doping and melt-spinning on microstructure and magnetostriction of Fe83Ga17 alloy, J. Alloys Compd., 2015, 637, 431–435,  DOI:10.1016/j.jallcom.2015.03.009.
38. Y. Morinaga, K. Sakuragi, N. Fujimura and T. Ito, Effect of Ce doping on the growth of ZnO thin films, J. Cryst. Growth, 1997, 174, 691–695,  DOI:10.1016/S0022-0248(97)00045-6.
39. S. Q. Zhang, L. D. Wang, W. L. Li, N. Li and W. D. Fei, Effects of lanthanum doping on the preferred orientation, phase structure and electrical properties of sol–gel derived Pb_1–3x/2La_x (Zr_0.6Ti_0.4)O₃ thin films, J. Alloys Compd., 2011, 509, 2976–2980,  DOI:10.1016/j.jallcom.2010.11.177.
40. A. Ben-Moshe, et al., The chain of chirality transfer in tellurium nanocrystals, Science, 2021, 372, 729–733,  DOI:10.1126/science.abf9645.
41. Y. Liu, et al., Helical van der Waals crystals with discretized Eshelby twist, Nature, 2019, 570, 358–362,  DOI:10.1038/s41586-019-1308-y.
42. E. Sutter and P. Sutter, Ultrathin Twisted Germanium Sulfide van der Waals Nanowires by Bismuth Catalyzed Vapor–Liquid–Solid Growth, Small, 2021, 17, 2104784,  DOI:10.1002/smll.202104784.
43. P. Sutter, S. Wimer and E. Sutter, Chiral twisted van der Waals nanowires, Nature, 2019, 570, 354–357,  DOI:10.1038/s41586-019-1147-x.
44. H. Ipser, K. L. Komarek and H. Mikler, Transition metal—Chalcogen systems, V, Monatsh. Chem., 1974, 105, 1322–1334,  DOI:10.1007/BF00909870.
45. J. C. Rouland, R. Ollitrault-Fichet, J. Flahaut, J. Rivet and R. Ceolin, The As-Te system: phase diagram and glass separation, Thermochim. Acta, 1990, 161, 189–200,  DOI:10.1016/0040-6031(90)80300-N.
46. D. Brandová and R. Svoboda, Thermo-structural characterization of (As₂Se₃)_100−x-(As₂Te₃)_x glasses for infrared optics, J. Am. Ceram. Soc., 2019, 102, 382–396,  DOI:10.1111/jace.15919.
47. A. Seitkan, G. I. Lampronti, R. N. Widmer, N. P. M. Casati and S. A. T. Redfern, Thermal Behavior of Iron Arsenides Under Non-Oxidizing Conditions, ACS Omega, 2020, 5, 6423–6428,  DOI:10.1021/acsomega.9b03928.
48. S. Q. Lin, et al., Sb induces both doping and precipitation for improving the thermoelectric performance of elemental Te, Inorg. Chem. Front., 2017, 4, 1066–1072,  10.1039/c7qi00138j.
49. C. H. Huang, et al., Extraction of magnetic circular dichroism effects from blended mixture of magnetic linear dichroism signals in the cobalt/Scotch tape system, Sci. Rep., 2019, 9, 17192,  DOI:10.1038/s41598-019-53880-1.
50. P. E. Blochl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979,  DOI:10.1103/physrevb.50.17953.
51. G. Kresse and J. Furthmuller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186,  DOI:10.1103/physrevb.54.11169.
52. R. Gupta, N. Kumar, P. Kaur and C. Bera, Theoretical model for predicting thermoelectric properties of tin chalcogenides, Phys. Chem. Chem. Phys., 2020, 22, 18989–19008,  10.1039/d0cp03117h.
53. N. Kumar and C. Bera, Theoretical prediction of thermoelectric properties of n-type binary Zintl compounds (KSb and KBi), Phys. B, 2021, 619, 413206,  DOI:10.1016/j.physb.2021.413206.
54. G. K. H. Madsen, J. Carrete and M. J. Verstraete, BoltzTraP2, a program for interpolating band structures and calculating semi-classical transport coefficients, Comput. Phys. Commun., 2018, 231, 140–145,  DOI:10.1016/j.cpc.2018.05.010.
55. A. Togo, F. Oba and I. Tanaka, First-principles calculations of the ferroelastic transition between rutile-type and CaCl₂-type SiO₂ at high pressures, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106,  DOI:10.1103/PhysRevB.78.134106.
56. P. Kaur and C. Bera, Effect of alloying on thermal conductivity and thermoelectric properties of CoAsS and CoSbS, Phys. Chem. Chem. Phys., 2017, 19, 24928–24933,  10.1039/c7cp05170k.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ee02169b

‡ These authors contributed equally.

---