Effect of hydration equilibria on the relaxometric properties of Gd(III) complexes: new insights into old systems

Abstract

We present a detailed relaxometric and computational investigation of three Gd(III) complexes that exist in solution as an equilibrium of two species with a different number of coordinated water molecules: [Gd(H₂O)_q]³⁺ (q = 8, 9), [Gd(EDTA)(H₂O)_q]⁻ and [Gd(CDTA)(H₂O)_q]⁻ (q = 2, 3). ¹H nuclear magnetic relaxation dispersion (NMRD) data were recorded from aqueous solutions of these complexes using a wide Larmor frequency range (0.01–500 MHz). These data were complemented with ¹⁷O transverse relaxation rates and chemical shifts recorded at different temperatures. The simultaneous fit of the NMRD and ¹⁷O NMR data was guided by computational studies performed at the DFT and CASSCF/NEVPT2 levels, which provided information on Gd⋯H distances, ¹⁷O hyperfine coupling constants and the zero-field splitting (ZFS) energy, which affects electronic relaxation. The hydration equilibrium did not have a very important effect in the fits of the experimental data for [Gd(H₂O)_q]³⁺ and [Gd(CDTA)(H₂O)_q]⁻, as the hydration equilibrium is largely shifted to the species with the lowest hydration number (q = 8 and 2, respectively). The quality of the analysis improves however considerably for [Gd(EDTA)(H₂O)_q]⁻ upon considering the effect of the hydration equilibrium. As a result, this study provides for the first time an analysis of the relaxation properties of this important model system, as well as accurate parameters for [Gd(H₂O)_q]³⁺ and [Gd(CDTA)(H₂O)_q]⁻.

---

Introduction

Relaxometry plays a key role among the techniques for the characterisation of paramagnetic species in solution.^1,2 The technique is based on the measurement of properties of solvent molecules in order to obtain information on the metal complex with which they interact chemically and magnetically. Typically, relaxometric studies involve measuring the ¹H longitudinal (T₁) and/or transverse relaxation times (T₂) of solvent water molecules, which are shortened by the presence of the paramagnetic solute.^3,4 Relaxometric data can be acquired at different temperatures to gain information on the dynamics of the system. Furthermore, the fast field cycling relaxometric technique allows recording relaxation data over a rather wide range of magnetic field strengths, typically from 0.01 MHz up to 60 or even 120 MHz.⁵ The effect of the applied magnetic field is generally analysed using nuclear magnetic relaxation dispersion (NMRD) profiles, which are plots of the relaxation rates (R_1,2) or relaxivities (r_1,2) versus the proton Larmor frequency. The r_1,2 values correspond to the relaxation rate enhancement effect of bulk water protons normalized to a 1 mM concentration of the paramagnetic solute, expressed in mM⁻¹ s⁻¹ units.⁶

Relaxometry has played a critical role in developing and characterizing contrast agents for magnetic resonance imaging (MRI) based on paramagnetic ions such as Gd(III),^4,7,8 Fe(III),^9–11 V(IV)^12,13 or Mn(II).^14–16 MRI contrast agents used in clinical practice enhance image contrast by shortening the longitudinal relaxation times of water nuclei present in the tissues where the agent is distributed. The shortening of T₁ enhances signal intensity when using short repetition times in the MRI experiment, which facilitates the diagnoses of different pathologies.¹⁷ Many fundamental studies were devoted over the last two decades to understand the correlation between the structure of the complex and the dynamic and structural parameters that determine the observed relaxivity.¹⁸ As a result, we have now a rather accurate understanding of the relationship between the coordination chemistry of these paramagnetic metal ions and their relaxation properties. Besides the use of relaxometry in the MRI field, this technique is very appropriate to undertake more fundamental studies on paramagnetic species in solution.

The relaxivity of a paramagnetic complex experiences contribution from both inner-sphere (IS) and outer-sphere (OS) mechanisms.^19,20 The latter arises from the diffusion of water molecules in the vicinity of the paramagnetic centre,²¹ and can be barely affected by changing ligand design. The IS mechanism is directly proportional to the number of water molecules present in the inner coordination sphere q, as well as on the mean residence time of water molecules in the first coordination sphere (τ_M = 1/k_ex, where k_ex is the exchange rate), and their relaxation time T_1M:

here, c is the concentration of the complex in mol L⁻¹. Thus, an obvious strategy that can be used to enhance relaxivity is to increase the number of water molecules coordinated to the metal ion.^22–29 The analysis of NMRD data often relies on the independent determination of q using a variety of methods. Most commonly, the value of q for Gd(III) complexes is obtained from the analysis of luminescence lifetimes of Eu(III) or Tb(III) analogues, with the use of empirical expressions developed for this purpose.^30,31 Alternatively, ¹⁷O NMR studies on the Dy(III) analogues can be used for hydration number determination.³² However, in some instances these studies afford non-integer numbers that suggest the presence of a hydration equilibrium in solution involving species with a different number of coordinated water molecules. In a few cases, the thermodynamic parameters that characterize the hydration equilibrium were obtained by analysing the ⁵D₀ ← ⁷F₀ absorption band of the Eu(III) analogue, which displays separate absorption maxima for the two species at equilibrium.^33–38 However, the application of this method is limited by the low extinction coefficient of this absorption, which requires large amounts of sample. More recently, the hydration equilibrium of different complexes were studied by Janicki using the absorption spectra of Gd(III) complexes in the UV-region, among them the aqua-ion [Gd(H₂O)_q]³⁺ (q = 8, 9) and the [Gd(EDTA)(H₂O)_q]⁻ and [Gd(CDTA)(H₂O)_q]⁻ complexes (q = 2, 3).³⁹

The presence of a hydration equilibrium is likely to affect significantly relaxometric studies, as q affects both relaxivity and the ¹⁷O NMR relaxation and chemical shift data used to evaluate water exchange dynamics. Thus, herein we have undertaken a detailed relaxometric characterization of the [Gd(H₂O)_q]³⁺, [Gd(EDTA)(H₂O)_q]⁻ and [Gd(CDTA)(H₂O)_q]⁻ complexes to assess the relevance of considering hydration equilibria in the analysis of relaxometric data.

Results and discussion

¹⁷O NMR studies

The hydration equilibrium may be expressed as:

[GdL(H₂O)_N] + H₂O ⇄ [GdL(H₂O)_N+1] (2)

where the charges are omitted for simplicity and L represents a ligand other than water. The thermodynamic parameters obtained for these complexes are summarized in Table 1, which also reports the effective q values obtained from the corresponding equilibrium constants K_eq using the following equation:

Table 1 Thermodynamic parameters reported for hydration equilibrium (1) and values of q at different temperatures^a

Complex	ΔH/kJ mol^−1	ΔS/J mol^−1 K^−1	q ^278	q ^298	q ^353
a ΔH and ΔS values from ref. 39.
[Gd(H2O)q]^3+	+6	+11	8.22	8.25	8.33
[Gd(EDTA)(H2O)q]^−	−18.2	−66	2.48	2.36	2.15
[Gd(CDTA)(H2O)q]^−	−15.8	−75	2.10	2.07	2.03

---

These data show that the hydration number of the aqua-ion is rather insensitive to temperature within the range used for relaxometric studies (ca. 278–353 K), with the population of the nine coordinated species varying in the range 22–33%. This is in line with the general view that the main aqua complex present in solution for Gd(III) is the eight-coordinate form.^40,41 On this basis, NMRD and ¹⁷O NMR studies considered a value of q = 8 for the analysis of the data,⁴ though earlier work assumed q = 9,^42,43 affording k_ex values that differed by ∼20%. For the complex with EDTA⁴⁻ both the populations of q = 2 and q = 3 species are significant over the 278–353 K temperature range, with nearly equal populations of the two species at 278 K. However, the CDTA⁴⁻ analogue displays q values close to 2, with the tris-hydrated species accounting for 10% or less of the overall population.

With the hydration parameters in hand, we have undertaken a variable temperature ¹⁷O NMR study in which transverse relaxation rates and chemical shifts were measured. These data are generally expressed as reduced relaxation rates (1/T_2r) and chemical shifts (Δω_r) by normalizing the data to the mole fraction of bound water molecules P_m. The latter can be calculated from the values of q at the given temperature as P_m = (cq)/55.55. The values of 1/T_2r measured for the three complexes decrease with temperature, a behaviour that is characteristic of the fast exchange regime (Fig. 1).⁴⁴ Under these conditions, the values of 1/T_2r are mainly determined by the ¹⁷O relaxation rate (1/T_1M) of coordinated water molecules, which is proportional to the square of the ¹⁷O hyperfine coupling constant A/ħ and is affected by both water exchange and electron relaxation. One can notice that the 1/T_2r values at a given temperature follow the order [Gd(H₂O)_q]³⁺ < [Gd(EDTA)(H₂O)_q]⁻ ∼ [Gd(CDTA)(H₂O)_q]⁻, which implies that [Gd(H₂O)_q]³⁺ has the fastest water exchange within this series.

Fig. 1 Reduced ¹⁷O NMR transverse relaxation rates (1/T_2r) and chemical shifts (Δω_r). The solid lines correspond to the fits of the data as described in the text. [Gd(H₂O)_q]³⁺, 18.9 mM, pH 4.0; [Gd(EDTA)(H₂O)_q]⁻, 10.8 mM, pH 7.4; [Gd(CDTA)(H₂O)_q]⁻, 10.5 mM, pH 7.1.

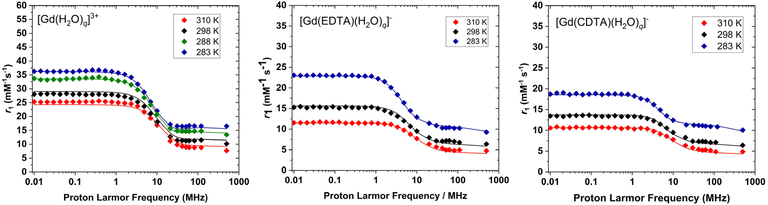
¹H NMRD profiles

The relaxivities of the three Gd(III) complexes were measured over a wide range of proton Larmor frequencies using fast field cycling relaxometry (ca. 0.01–120 MHz), with additional points recorded using a high resolution instrument operating at 500 MHz (Fig. 2). The NMRD profiles have the typical shape observed for solutions of small Gd(III) complexes, with a plateau at low field (<1 MHz), a dispersion at intermediate fields (ca. 1–10 MHz) and a second region of fairly constant relaxivity at high field (>20 MHz).¹ The NMRD profiles recorded for [Gd(H₂O)_q]³⁺ and [Gd(EDTA)(H₂O)_q]⁻ agree with those measured earlier up to 60 MHz.^4,45 The higher relaxivities observed for [Gd(H₂O)_q]³⁺ are simply a consequence of the high hydration number. The NMRD profiles of [Gd(EDTA)(H₂O)_q]⁻ display higher relaxivities at low field compared with [Gd(CDTA)(H₂O)_q]⁻, which is likely reflecting some differences in electron spin relaxation. The relaxivities of all three complexes increase when the temperature is lowered. This is a consequence of an increased outer-sphere contribution due to a lower diffusion coefficient at lower temperatures. Furthermore, the IS contribution increases as well at high fields (>2 MHz) due to the longer rotational correlation times (τ_R) observed at low temperatures.

Fig. 2 ¹H Nuclear Magnetic Relaxation Dispersion (NMRD) profiles recorded in aqueous solutions at different temperatures. [Gd(H₂O)_q]³⁺, 3.3 mM, pH 4.0; [Gd(EDTA)(H₂O)_q]⁻, 10.8 mM, pH 7.4; [Gd(CDTA)(H₂O)_q]⁻, 10.5 mM, pH 7.1.

Theoretical calculations

A rather large number of parameters affects the ¹H NMRD profiles and ¹⁷O NMR data, some of which are common to both sets of data.⁴⁶ The presence of two complex species in solution with different hydration numbers complicates further the analysis, as it requires incorporating additional parameters. For instance, the two species at equilibrium may have significantly different values of the hyperfine coupling constant A/ħ, or the electronic relaxation times, as a result of differences in zero field splitting (ZFS) energies. Incorporating additional parameters into the model is likely to improve the quality of the fits, but not necessarily be more meaningful. We therefore performed a computational study to guide the strategy to fit the experimental data.

We started our computational study by modelling the [Gd(H₂O)₈]³⁺ and [Gd(H₂O)₉]³⁺ systems. Previous studies on these small complexes were conducted using polarizable continuum models (PCM) to account for solvent effects.⁴⁰ However, geometry optimizations using PCM suffer from convergence issues, and furthermore they cannot be used to study water exchange reactions. Thus, we started our calculations using a cluster/continuum approach,^47,48 in which an explicit second sphere solvation shell is added to the model, while the effects of bulk water are considered with the PCM model.⁴⁹ The starting geometry had nine coordinated water molecules and 18 second-sphere water molecules (Fig. 3). The hydrogen bond pattern in this cluster is such that the coordinated water molecules are connected by hydrogen bonds through two second sphere water molecules, providing a complete second-sphere shell. This hydrogen bond structure was used previously to study octahedral aqua-complexes.^50–52 Our calculations provide a tricapped trigonal prismatic coordination polyhedron (TTP), as observed by X-ray diffraction studies. A potential energy surface scan was subsequently performed by elongating one of the Gd–O_w bonds, leading to a second energy minimum that corresponds to the eight-coordinate complex. The latter displays a square antiprismatic (SAP) coordination environment, as would be expected. The relative free energy of the [Gd(H₂O)₉]³⁺·18H₂O and [Gd(H₂O)₈]³⁺·19H₂O systems (at 298.15 K) favour the latter by 4.37 kJ mol⁻¹, in qualitative agreement with the experimental data.

Fig. 3 DFT structures of the [Gd(H₂O)₉]³⁺·18H₂O (top, oxygen atoms defining the upper and lower tripods of the TTP coordination polyhedron are shown in green, while capping positions are shown in blue) and [Gd(H₂O)₈]³⁺·19H₂O (bottom, the upper and lower quadrangular faces of the SAP coordination polyhedron are shown in green and blue, respectively).

The TTP coordination polyhedron in [Gd(H₂O)₉]³⁺·18H₂O is characterized by Gd–O bonds involving capping water molecules (Gd–O_c, average at 2.509 Å) being slightly longer than those at the vertexes of the prism (Gd–O_p at 2.469 Å). This is in good agreement with the available crystallographic data.⁵³ The average Gd–O distance decreases slightly upon lowering the coordination number from nine to eight, as would be expected (Table 2). This has a slight impact on the Gd⋯H distances involving coordinated water molecules (r_GdH), which nevertheless are very close to the value of 3.1 Å obtained using ENDOR measurements.⁵⁴ The values of the isotropic hyperfine coupling constants A/ħ are also slightly affected by the coordination number, with the shorter Gd–O bonds in the eight-coordinate form resulting in somewhat higher values of A/ħ compared with the nine-coordinate form.⁵⁵ Nevertheless, the average values of A/ħ calculated for the two eight- and nine-coordinate forms differ by <10% (Table 2).

Table 2 Distances, hyperfine coupling constants and ZFS energies obtained with computational studies

	r GdO /Å	r GdH /Å	^17O A/ħ^a/10^6 rad s^−1	D/cm^−1	E/D	Δ S/cm^−1	Δ S ^2/10^19 s^−2
a Average values within parenthesis.
[Gd(H2O)8]^3+·19H2O	2.407–2.533 (2.460)	2.974–3.158 (3.085)	3.41–6.11 (4.80)	0.0659	0.042	0.0539	10.3
[Gd(H2O)9]^3+·18H2O	2.449–2.543 (2.482)	3.054–3.214 (3.119)	3.73–5.18 (4.40)	−0.0098	0.064	0.0081	0.232
[Gd(EDTA)(H2O)2]^−·5H2O	2.529; 2.540 (2.535)	3.011–3.111 (3.062)	3.15; 3.46 (3.31)	−0.0322	0.223	0.0282	2.82
[Gd(EDTA)(H2O)3]^−·4H2O	2.561–2.671 (2.598)	3.025–3.163 (3.091)	2.57–2.92 (2.75)	−0.0335	0.281	0.0304	3.29
[Gd(CDTA)(H2O)2]^−·5H2O	2.513; 2.552 (2.533)	3.024–3.176 (3.095)	2.94; 2.85 (2.90)	−0.0380	0.327	0.0357	4.52
[Gd(CDTA)(H2O)3]^−·4H2O	2.561–2.570 (2.562)	3.025–3.177 (3.100)	2.59–2.94 (2.79)	0.0377	0.294	0.0345	4.24

---

Cluster-continuum calculations were also performed on the [Gd(EDTA)(H₂O)₃]⁻·5H₂O and [Gd(CDTA)(H₂O)₃]⁻·5H₂O systems, with subsequent relaxed potential energy surface scans leading to the corresponding eight-coordinate species (see ESI†). In the case of CDTA, the bis-hydrated form is more stable than the tris-hydrated species, with the relative free energy of the latter being +7.81 kJ mol⁻¹. However, the q = 2 and q = 3 forms possess very similar free energy values (ΔG° ∼ 0.11 kJ mol⁻¹) in the case of EDTA. This is in good qualitative agreement with the experimental data shown in Table 1, which evidence that the tris-hydrated form is more stable for EDTA than CDTA complexes. The average A/ħ vales calculated for EDTA and CDTA complexes are somewhat lower than those obtained for the [Gd(H₂O)₉]³⁺·18H₂O and [Gd(H₂O)₈]³⁺·19H₂O systems, which is expected considering the shorter Gd–O bond distances observed for the latter. Of note, the calculated values of A/ħ = A^iso × 2π are all positive, though values obtained from ¹⁷O NMR studies are often incorrectly reported as negative.⁵⁶ The calculated r_GdH values are again very close to the of 3.1 Å, which confirms that this parameter is rather insensitive to the nature of the co-ligands present in the Gd(III) coordination environment.

Electron relaxation in Gd(III) complexes is generally attributed to fluctuations of the zero field splitting (ZFS) energy due to transient distortions of the coordination environment, caused by vibrations and collisions with solvent molecules.^57,58 Electron relaxation is believed to receive contributions from both static and transient ZFS effects.^59,60 The ZFS energy was calculated using the complete active space self-consistent field (CASSCF) approach, with electron correlation incorporated using N-electron valence state perturbation theory (NEVPT2). This multiconfigurational method provides ZFS energies of Gd(III) complexes of the correct order of magnitude, while the results obtained with DFT are heavily dependent on the functional used.^58,61 The ZFS can be defined using the common axial (D) and rhombic (E/D) parameters,⁶² which are listed in Table 2.

The values of D and E/D obtained with NEVPT2 calculations define highly rhombic ZFS tensors, with E/D being close to its maximum value of 1/3. It has been shown that for E/D values >0.2 the prediction of the sign of D becomes problematic for Mn(II) complexes.⁶² While this may be the case also for the Gd(III) complexes investigated here, we note that electron relaxation is related to fluctuations in the value of Δ², and thus only the absolute value of Δ is relevant.

The values of |D| obtained for the complexes of EDTA⁴⁻ and CDTA⁴⁻ are relatively similar, being close to those obtained for other Gd(III) complexes using CASSCF-based approaches.^58,61,63 We note that the pairs of species involved in hydration equilibrium, for the complexes of EDTA⁴⁻ and CDTA⁴⁻, display very similar values of |D| and E/D, and thus very likely similar electronic relaxation times. The aqua complexes [Gd(H₂O)₉]³⁺ and [Gd(H₂O)₈]³⁺ are characterized by lower E/D values than the EDTA⁴⁻ and CDTA⁴⁻ complexes, which can be ascribed to the more symmetrical coordination environments in the former.⁶⁴ The value of |D| calculated for the eight-coordinate species is one order of magnitude higher than that of the nine-coordinated species. Conversely, the eight-coordinate form [Gd(H₂O)₈]³⁺ displays a |D| value that is comparable to those of the CDTA⁴⁻ and EDTA⁴⁻ complexes. This suggests that the TTP coordination environment results in particularly small ZFS energies. This is in line with previous studies, which showed that lanthanide complexes with this coordination environment display particularly sharp EPR lines, which is associated to slow electron spin relaxation due to a nearly zero static ZFS.^64,65

The static ZFS energy can be approximated using the following expression:^20,60

The trend observed for the values of |D| calculated for this series of complexes is associated with the splitting of the Kramer's doublets arising from the ⁸S configuration of Gd(III) (Fig. 4). For axially symmetric systems, the Kramer doublets are separated by energies equal to 2D, 4D and 6D with respect to the lowest energy level if D > 0, while the situation is reversed if D < 0.⁶¹ For the rhombic systems investigated here, a D > 0 value is obtained when the separation of the Kramer doublets increases on increasing energy (i.e. [Gd(H₂O)₈]³⁺), while a negative D value is observed in the opposite case.

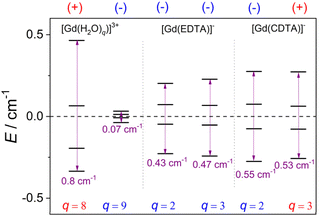Fig. 4 Splitting of the Kramers doublets obtained with CASSCF/NEVPT2 calculations and the signs of D.

Simultaneous fit of the ¹H NMRD and ¹⁷O NMR data

The simultaneous fit of the experimental relaxation and chemical shift data is the most convenient approach to estimate the parameters that determine the relaxivity of a given complex.⁴⁶ The ¹H relaxivity data were fit to the standard Solomon–Bloembergen–Morgan theory of paramagnetic relaxation,^66–68 while the Swift–Connick⁶⁹ equations were used for ¹⁷O NMR. The two sets of data are affected by several common parameters: the exchange rate of the coordinated water molecules expressed by k²⁹⁸_ex and its activation enthalpy ΔH^‡, and the parameters describing electron relaxation, namely the correlation time for the fluctuation of the ZFS interaction, τ_V, and the mean-square zero field splitting energy, Δ². Separate fits of the data generally improve the agreement between experimental and calculated data, but do not necessarily yield more accurate parameters.

The equilibrium expressed by eqn (2) implies that the rate constants for the forward (k₊) and reverse (k₋) processes are related by the equilibrium constant, so that K_eq = k₊/k₋. Thus, we used a single set of k²⁹⁸_ex and ΔH^‡ parameters for the fits, corresponding to the process in which a water molecule enters the coordination sphere. The number of coordinated water molecules q was expressed by eqn (3), using the thermodynamic data shown in Table 1. The values of 1/T_2r and Δω_r were also calculated at each temperature from the molar fraction of coordinated water molecules obtained as P_m = (cq)/55.55.

Some parameters had to be fixed to reasonable values for a reliable analysis. The distance between proton nuclei of coordinated water molecules and the metal ion was fixed to 3.0 Å, a value that is close to those obtained by the DFT calculations described above and within the range afforded by ENDOR studies (3.1 ± 0.1 Å).^54,70 The distance of closest approach of an outer-sphere water molecule was fixed to 4.0 Å on the grounds of previous studies.⁷¹ The parameters related to diffusion were also fixed to reasonable values: the diffusion coefficient was set to D²⁹⁸_GdH = 2.3 × 10⁻⁹ m² s⁻¹ and its activation energy was constrained to E_D = 20 kJ mol⁻¹.⁷² Finally, we had to fix the value of the activation energy for the modulation of the zero field splitting (E_v = 1 kJ mol⁻¹), as otherwise unreasonable values were obtained. We fitted a single value for A/ħ, τ_V and Δ² to avoid over-parametrization of the model. This approach is supported by our theoretical calculations, which indicate that these parameters differ only slightly for the eight- and nine-coordinate species in the case of EDTA⁴⁻ and CDTA⁴⁻ complexes (Table 2). For the aqua complex, the nine-coordinate species accounts for ∼20–35% of the overall population in the temperature range investigated (Table 1). Thus, we performed the fits of the data assuming different values of Δ² for the eight- and nine-coordinate species.

The agreement between the experimental and calculated 1/T_2r and Δω_r data is excellent for the three complexes investigated here, as shown in Fig. 1. The calculated ¹H NMRD data are also in good agreement with the experiment, considering the large number of parameters fitted and the assumptions made to perform the analysis (Fig. 2). For [Gd(H₂O)_q]³⁺ and [Gd(CDTA)(H₂O)_q]⁻ the eight-coordinate species is either largely dominant ([Gd(CDTA)(H₂O)_q]⁻), or its population is barely affected by temperature ([Gd(H₂O)_q]³⁺). As a result, the simultaneous fits performed including the hydration equilibrium, or assuming coordination number 8, provide very similar fitted parameters and R² values (Table 3). The most important difference is the k²⁹⁸_ex of [Gd(H₂O)_q]³⁺, which decreases by ∼22% upon considering the hydration equilibrium.

Table 3 Parameters obtained from the simultaneous fit of ¹H NMRD profiles and ¹⁷O NMR data

	[Gd(H2O)q]^3+		[Gd(EDTA)(H2O)q]^−		[Gd(CDTA)(H2O)q]^−
q	8 ⇄ 9	8	2 ⇄ 3	2	2 ⇄ 3	2
a Parameters fixed during the fitting procedure. b This value corresponds to [Gd(H2O)8]^3+. For the minor [Gd(H2O)9]^3+ species the fit affords Δ^2 = 0.6 × 10^19 s^−2 with a large statistical error (see text).
^298 Δ ^2/10^19 s^−2	19.2 ± 3.2^b	11.3 ± 2.0	1.61 ± 0.16	0.79 ± 0.07	2.49 ± 0.13	2.23 ± 0.12
^298 τ V/ps	6.7 ± 0.9	7.1 ± 1.0	30.7 ± 2.7	54.3 ± 4.7	32.4 ± 1.6	34.9 ± 1.8
E V/kJ mol^−1	1.0^a	1.0^a	1.0^a	1.0^a	1.0^a	1.0^a
A O/ħ/10^6 rad s^−1	4.5 ± 0.6	4.6 ± 0.6	4.0 ± 0.3	4.0 ± 0.3	4.0 ± 0.2	4.0 ± 0.2
C os	0.1^a	0.1^a	0.1^a	0.1^a	0.1^a	0.1^a
τ ^298M/ns	2.0 ± 0.7	1.6 ± 0.5	7.5 ± 1.2	5.9 ± 1.0	5.8 ± 0.8	5.4 ± 0.8
k ^298ex/10^6 s^−1	490 ± 166	632 ± 212	134 ± 21	169 ± 30	173 ± 23	184 ± 26
ΔH^‡/kJ mol^−1	16.5 ± 6.1	16.1 ± 6.1	24.4 ± 2.6	23.5 ± 3.0	21.9 ± 2.3	21.0 ± 2.4
ΔS^‡/J mol^−1 K^−1	−23.0 ± 5.0	−22.0 ± 5.0	−8.0 ± 2.0	−9.0 ± 3.0	−14.0 ± 2.0	−16.0 ± 2.0
^298 τ R/ps	32.8 ± 0.6	33.4 ± 0.6	50.8 ± 0.8	59.4 ± 0.6	64.0 ± 0.6	64.7 ± 0.6
E R/kJ mol^−1	14.5 ± 0.4	14.0 ± 0.6	24.3 ± 0.3	26.9 ± 0.4	25.7 ± 0.4	26.5 ± 0.4
r GdH/Å	3.0^a	3.0^a	3.0^a	3.0^a	3.0^a	3.0^a
a GdH/Å	4.0^a	4.0^a	4.0^a	4.0^a	4.0^a	4.0^a
^298 D/10^−9 m^2 s^−1	2.3^a	2.3^a	2.3^a	2.3^a	2.3^a	2.3^a
E D/kJ mol^−1	20.0^a	20.0^a	20.0^a	20.0^a	20.0^a	20.0^a
R ^2	0.99657	0.99648	0.99808	0.99748	0.99787	0.99761

---

The quality of the fit for [Gd(EDTA)(H₂O)_q]⁻ deteriorates significantly if the hydration equilibrium is neglected. Furthermore, the values of τ_V and Δ² experience a strong impact if neglecting the hydration equilibrium. In particular, τ_V is an effective correlation time that should be intermediate between that expected for the transient ZFS (<1 ps) and that of the static ZFS, which is modulated by τ_R.⁶⁰ The value of τ_V obtained assuming q = 2 (54.3 ps, Table 3) is virtually identical to that of τ²⁹⁸_R (59.4 ps). This would imply that transient ZFS does not contribute to the relaxation of the electron spin, a situation that is extremely unlikely. When considering the hydration equilibrium, τ_V assumes a more reasonable value of 31 ps, which is close to that obtained for [Gd(CDTA)(H₂O)_q]⁻. The values of τ²⁹⁸_R and its activation energy E_R also vary significantly depending on whether the hydration equilibrium is taken into account or not. In particular, the value of E_R for small Gd(III) complexes should be close to 20 kJ mol⁻¹.^4,73 Taking this value as a reference, it is clear that the fit of the data neglecting the hydration equilibrium worsens the quality of the value obtained for E_R. Thus, we conclude that considering the hydration equilibrium provides more reliable fitted parameters. This appears to be particularly important in cases where the two species at equilibrium present similar populations in solution. Of note, the value of k²⁹⁸_ex increases by ∼26% when neglecting the hydration equilibrium.

Rotational dynamics

The ²⁹⁸τ_R values obtained from the fits of the data and the corresponding activation energies E_R are very similar to those determined for small Gd(III) complexes.^4,73 For [Gd(H₂O)_q]³⁺, different EPR studies afforded ²⁹⁸τ_R values of 32 ⁷⁴ and 23 ps,⁷⁵ in good agreement with the present study. Previous NMRD studies gave a somewhat longer ²⁹⁸τ_R value of 41 ps.⁴ However, the latter study involved simultaneous fit of NMRD and T₁¹⁷O relaxation data. It was later found that the correlation time for the Gd–O_water vector is sensibly longer than that of the Gd–H_water vector (τ_RH/τ_RO = 0.65),⁷⁶ explaining the longer τ_R. The ²⁹⁸τ_R values obtained for the EDTA⁴⁻ and CDTA⁴⁻ complexes are longer than for the aqua ion, as their molecular masses are greater.

Hyperfine coupling constants

The value of A_O/ħ determined for the aqua ion (4.5 × 10⁶ rad s⁻¹) is somewhat lower than those obtained in previous ¹⁷O NMR studies (5.3 × 10⁶ rad s⁻¹).^4,77 Our value is in turn in excellent agreement with different computational studies,^55,78 including the average values obtained with DFT in this work (Table 2). The values of A_O/ħ are somewhat lower for the complexes of EDTA⁴⁻ and CDTA⁴⁻ (4.0 × 10⁶ rad s⁻¹). This value of A_O/ħ is very similar to those obtained for Gd(III) complexes other than the aqua-ion: (3.9 ± 0.3) × 10⁶ rad s⁻¹.⁵⁵ Our DFT calculations (Table 2) provide A_O/ħ values that are somewhat lower than the experimental ones. We attribute this effect to the functional used for geometry optimization (wB97XD), which was chosen for this work because it provides good estimates for activation energies of water exchange reactions.⁷⁹ In comparison with other functionals like TPPSh, wB97XD affords slightly longer Gd–O_water distances,⁸⁰ resulting in lower A_O/ħ values.

Electron relaxation

The fits reported in Table 3 and performed considering hydration equilibria, provide very reasonable values of τ_V and Δ². The correlation time τ_V takes values intermediate between τ_R and the correlation time expected for the transient ZFS (<1 ps),^58,60 suggesting that both the transient and static ZFS have a significant contribution to electron relaxation. Interestingly, the values of Δ² estimated using theoretical calculations (Table 2) follow very well the trend of the experimental values. In the case of [Gd(H₂O)_q]³⁺ the eight-coordinate species is the most abundant one in solution. The fits and NEVPT2 calculations give Δ² values for [Gd(H₂O)₈]³⁺ in good mutual agreement (19.2 × 10¹⁹ and 10.3 × 10¹⁹ s⁻²), considering the difficulties associated with the calculation of ZFS parameters.⁶² Our fits give a Δ² value for [Gd(H₂O)₉]³⁺ that is one order of magnitude lower (Δ² = 0.6 ± 1.4 × 10¹⁹ s⁻²), though the low abundance of this species resulted in a large statistical error. Nevertheless, these results support the fact that two aqua complexes at equilibrium have very different ZFS energies, in agreement with the theoretical study. The value of Δ² obtained from the fits for [Gd(CDTA)(H₂O)_q]⁻ is slightly higher than that of [Gd(EDTA)(H₂O)_q]⁻ by a factor of ∼1.5, a trend that is also reproduced by the theoretical data.

Water exchange rates

The best estimate of [Gd(H₂O)_q]³⁺k²⁹⁸_ex (804 × 10⁶ s⁻¹) reported to date was obtained from a combined NMRD, ¹⁷O NMR and EPR study, assuming that q = 8.⁴ The analysis of our data incorporating the hydration equilibrium indicates that this value is somewhat lower (k²⁹⁸_ex = 490 × 10⁶ s⁻¹), but remains one of the fastest water exchange rates reported to date for a Gd(III) complex.⁸¹ Water exchange is somewhat lower for [Gd(EDTA)(H₂O)_q]⁻ and [Gd(CDTA)(H₂O)_q]⁻, following the general trend that coordination of polyaminocarboxylate ligands slows down water exchange with respect to the aqua ion. Water exchange is slightly faster for [Gd(CDTA)(H₂O)_q]⁻ than for [Gd(EDTA)(H₂O)_q]⁻. This is in contrast with previous studies on q = 1 Gd(III) complexes, which showed that rigidifying the ligand structure by replacing an ethyl group by a cyclohexyl moiety slowed water exchange considerably.^35,82

The values of the entropy of activation (ΔS^‡) for water exchange are negative, suggesting associatively activated water exchange mechanisms for the eight-coordinate complexes.⁸³ In the case of [Gd(H₂O)_q]³⁺ this was confirmed by variable pressure ¹⁷O NMR measurements, which afforded a negative activation volume of ΔV^‡ = −3.3 cm³ mol⁻¹.⁴ The same study reported a ΔS^‡ value identical to that obtained in this work. Given the negative ΔS^‡ value obtained for [Gd(H₂O)_q]³⁺, it may be somewhat surprising the positive reaction entropy reported for the hydration equilibrium expressed as in eqn (2). Most likely this positive ΔS is related to more ordered second-sphere hydration shell in the eight-coordinate [Gd(H₂O)₈]³⁺ species.

The water exchange mechanism for [Gd(H₂O)₈]³⁺ and [Gd(EDTA)(H₂O)₂]⁻ were further investigated by computing the transition states responsible for the interconversion between eight- and nine-coordinate species. For the [Gd(H₂O)₈]³⁺·19H₂O system, one of the second sphere water molecules with a Gd⋯O_water distance of 4.21 Å approaches the Gd(III) ion to 3.43 Å to reach the transition state, while the coordinated water molecules experience very minor changes in Gd–O_water distances. The values of ΔH^‡ and ΔS^‡ obtained by DFT are 8.4 kJ mol⁻¹ and −14.8 J mol⁻¹ K⁻¹, respectively. For [Gd(EDTA)(H₂O)₂]⁻·7H₂O DFT affords ΔH^‡ = 8.7 kJ mol⁻¹ and ΔS^‡ = −30.2 J mol⁻¹ K⁻¹, with a Gd⋯OH₂ distance in the transition state involving the entering water molecule of 3.30 Å. Thus, DFT affords activation parameters in qualitative good agreement with the experimental data, and confirms that water exchange in this family of eight-coordinated species is associatively activated.

Conclusions

Over the last twenty years, the increasing availability of commercial instruments for the accurate measurement of the frequency dependence of nuclear magnetic relaxation times of solvent protons in solutions of paramagnetic metal complexes has made the fast field-cycling relaxometry technique a relevant tool for coordination chemists. The most striking example concerns the remarkable knowledge acquired of the properties of metal complexes of Gd(III), Mn(II) and Fe(III) in aqueous solution, which are investigated as MRI probes. The measurement and analysis of NMRD profiles allows obtaining reliable information on the hydration state, the metal–water protons distance, the rotational dynamics, the exchange rate of metal–bound water molecules and the electronic relaxation times of the paramagnetic ion.

By simultaneously analysing ¹H NMRD profiles with R₂ and shift ¹⁷O NMR data, measured at high field on a high-resolution spectrometer, more accurate and meaningful results are obtained. However, in the not an uncommon case in which the complexes exist in solution as a mixture of species differing in the hydration state (fractional effective q value), the application of this procedure only provides values of the molecular parameters that are the weighted average of the two forms with different q. The knowledge of the thermodynamic parameters of the exchange process between the two species, obtained via UV-Vis spectroscopy, and the results of computational techniques allow the relaxometric analysis to evaluate with high accuracy the separate contributions of the two species, if their relative populations do not differ excessively. We have used this approach for the first time, applying it to the case of the Gd(III) aqua ion and to complexes with EDTA⁴⁻ and CDTA⁴⁻. The results obtained are very satisfactory both for the better quality of the best-fitting parameters of the relaxometric data and for the new insights into the property–structure relationship, with particular regard to the exchange process of inner-sphere water molecules and electronic relaxation. We think that this approach can provide considerable help to better understand the structure and dynamics in aqueous solution of the numerous paramagnetic Gd(III) complexes characterized by fractional q.

Experimental and computational section

General considerations

All reagents used were purchased from commercial sources and were of reagent grade quality. The [Gd(H₂O)_q]³⁺ sample was prepared by dissolving GdCl₃·6H₂O in water at pH = 4. The [GdL(H₂O)_q]⁻ (L = EDTA, CDTA) complexes were prepared by adding 1.1 equiv. of the Gd(III) salt to an aqueous solution of the L ligand at pH = 6. After the addition, the pH was adjusted to 6.0 with a diluted NaOH solution and the solution was stirred at room temperature for 5 h. Then, the pH was increased to 10 with 0.1 M NaOH, and the solution was stirred for 3 h, to promote the precipitation of the free Gd(III) as hydroxides. The solution was finally filtered through 0.2 μm filters and neutralized with 0.1 M HCl.

¹H NMRD and ¹⁷O NMR measurements

1/T₁¹H Nuclear Magnetic Relaxation Dispersion (NMRD) profiles were collected with a Fast-Field Cycling (FFC) Stelar SmarTracer Relaxometer (Stelar s.r.l., Mede, PV, Italy) over a continuum of proton Larmor frequencies from 9.97 × 10⁻³ to 10 MHz. Additional data in the range 20–120 MHz proton Larmor frequency were measured with a High Field Relaxometer (Stelar) equipped with the HTS-110 3T Metrology Cryogen-free Superconducting Magnet. The analyses were carried out by using the standard inversion recovery sequence (20 experiments, 2 scans) with a typical 90° pulse width of 3.5 μs and the reproducibility of the data was within ±0.5%. The temperature was controlled with a Stelar VTC-91 heater airflow equipped with a copper–constantan thermocouple (uncertainty of ±0.1 K). R₁ values at 500 MHz were measured with Bruker Avance III spectrometer (11.7 T) equipped with a 5 mm probe.

¹⁷O NMR measurements were recorded on a Bruker Avance III spectrometer (11.7 T) equipped with a 5 mm probe and standard temperature control unit. Aqueous solutions of the complexes were enriched to reach 2.0% of the ¹⁷O isotope (Cambridge Isotope). The transverse relaxation rates were calculated at different temperatures (278–353 K) from the signal width at a half-height. The concentration of the metal complexes was assessed by ¹H-NMR measurements (Bruker Avance III Spectrometer equipped with a wide bore 11.7 Tesla magnet), by using the well-established bulk magnetic susceptibility method.⁸⁴

Computational details

The geometries of the Gd(III) complexes were optimized with the Gaussian 16 program package (revision C.01)⁸⁵ using the wB97XD functional, which is a long-range corrected hybrid density functional incorporating atom–atom dispersion corrections.⁸⁶ In these calculations we employed a large-core effective core potential for the lanthanide (LCECP) including 53 electrons in the core for Gd(III)⁸⁷ and the Def2-TZVPP basis set for all ligand atoms.⁸⁸ The integration grid was set with the integral = superfinegrid command. Bulk water solvent effects were considered using a polarizable continuum model⁴⁹ using scrf = (pcm, solvent = water) and the default options implemented in Gaussian, except the radii of O and H, which were taken as 1.925 and 1.5873 Å, respectively.⁵² Frequency calculations were used to confirm that the optimized structures correspond to stationary points on the potential energy surface. Transition states were located using the Transit-Guided Quasi-Newton (STQN3) method,⁸⁹ and characterized by a single negative frequency with atom displacements that signal the approach of the entering water molecule to the eight-coordinate complex.

The ORCA program package (version 5.0.3)^90,91 was used to calculate isotropic ¹⁷O hyperfine coupling constants and the ZFS tensor. Relativistic effects were incorporated using the Douglas–Kroll–Hess (DKH2) approximation.^92,93 The SARC2-DKH-QZVP⁹⁴ and DKH-def2-TZVPP⁹⁵ basis sets were used for Gd and ligand atoms, respectively. The resolution of identity and chain of spheres (RIJCOSX) method^96–98 was used throughout with the SARC2-DKH-QZVP/JK⁹⁴ auxiliary basis set for Gd and auxiliary basis sets generated with the Autoaux⁹⁹ method for ligand atoms. Hyperfine coupling constants were obtained using DFT with the TPSSh functional,¹⁰⁰ which was found to perform well for this specific problem.^55,101,102 The quasi-restricted orbitals¹⁰³ generated from these calculations were used as starting orbitals for complete active space self-consistent field (CASSCF) calculations,^104,105 in which dynamic correlation was incorporated using the quasi-degenerate¹⁰⁶ strongly contracted variant of N-electron valence state perturbation theory (SC-NEVPT2).^106,107 Spin–orbit coupling effects were introduced using quasi-degenerate perturbation theory (QDPT).^108,109 The active space of the state-averaged CASSCF calculations consisted of seven electrons distributed over the seven Gd-based 7f orbitals CAS(7,7), including one octet and 48 sextet roots. Bulk water solvent effects in all ORCA calculations were included with the SMD solvation model.¹¹⁰

Author contributions

A. N.: synthesis, purification, and characterization of the complexes; NMRD profiles. F. C.: ¹⁷O NMR data, relaxivity measurements, data analysis. C. P.-I.: DFT calculations, NMR data analysis, resources, conceptualization and manuscript preparation. M. B.: project supervision, conceptualization, data analysis resources and manuscript preparation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

A. N. acknowledges Università del Piemonte Orientale for the PhD grant. C. P.-I. thanks Ministerio de Ciencia e Innovación (grants PID2019-104626GB-I00 and PID2022-138335NB-I00) and Xunta de Galicia (grant ED431C 2023/33) for generous financial support. C. P.-I. also thanks Centro de Supercomputación de Galicia (CESGA) for providing the computer facilities.

References

1. S. Aime, M. Botta, D. Esteban-Gómez and C. Platas-Iglesias, Characterisation of magnetic resonance imaging (MRI) contrast agents using NMR relaxometry, Mol. Phys., 2019, 117, 898–909.
2. G. Parigi, E. Ravera, M. Fragai and C. Luchinat, Unveiling protein dynamics in solution with field-cycling NMR relaxometry, Prog. Nucl. Magn. Reson. Spectrosc., 2021, 124–125, 85–98.
3. S. H. Koenig, C. M. Baglin and R. D. Brown, Magnetic field dependence of solvent proton relaxation in aqueous solutions of Fe³⁺ complexes, Magn. Reson. Med., 1985, 2, 283–288.
4. D. H. Powell, O. M. N. Dhubhghaill, D. Pubanz, L. Helm, Y. S. Lebedev, W. Schlaepfer and A. E. Merbach, Structural and Dynamic Parameters Obtained from ¹⁷O NMR, EPR, and NMRD Studies of Monomeric and Dimeric Gd³⁺ Complexes of Interest in Magnetic Resonance Imaging: An Integrated and Theoretically Self-Consistent Approach, J. Am. Chem. Soc., 1996, 118, 9333–9346.
5. Y. Gossuin, Z. Serhan, L. Sandiford, D. Henrard, T. Marquardsen, R. T. M. De Rosales, D. Sakellariou and F. Ferrage, Sample Shuttling Relaxometry of Contrast Agents: NMRD Profiles above 1 T with a Single Device, Appl. Magn. Reson., 2016, 47, 237–246.
6. S. Dumas, V. Jacques, W.-C. Sun, J. S. Troughton, J. T. Welch, J. M. Chasse, H. Schmitt-Willich and P. Caravan, High Relaxivity Magnetic Resonance Imaging Contrast Agents Part 1 Impact of Single Donor Atom Substitution on Relaxivity of Serum Albumin-Bound Gadolinium Complexes, Invest. Radiol., 2010, 45, 13.
7. S. Aime, A. Barge, J. I. Bruce, M. Botta, J. A. K. Howard, J. M. Moloney, D. Parker, A. S. de Sousa and M. Woods, NMR, Relaxometric, and Structural Studies of the Hydration and Exchange Dynamics of Cationic Lanthanide Complexes of Macrocyclic Tetraamide Ligands, J. Am. Chem. Soc., 1999, 121, 5762–5771.
8. S. Aime, M. Botta, G. Ermondi, F. Fedeli and F. Uggeri, Synthesis and NMRD studies of gadolinium(3+) complexes of macrocyclic polyamino polycarboxylic ligands bearing .beta.-benzyloxy-alpha-propionic residues, Inorg. Chem., 1992, 31, 1100–1103.
9. I. Bertini, F. Capozzi, C. Luchinat and Z. Xia, Nuclear and electron relaxation of hexaaquairon(3+), J. Phys. Chem., 1993, 97, 1134–1137.
10. Z. Baranyai, F. Carniato, A. Nucera, D. Horváth, L. Tei, C. Platas-Iglesias and M. Botta, Defining the conditions for the development of the emerging class of Fe^III-based MRI contrast agents, Chem. Sci., 2021, 12, 11138–11145.
11. R. Uzal-Varela, F. Lucio-Martínez, A. Nucera, M. Botta, D. Esteban-Gómez, L. Valencia, A. Rodríguez-Rodríguez and C. Platas-Iglesias, A systematic investigation of the NMR relaxation properties of Fe(III)-EDTA derivatives and their potential as MRI contrast agents, Inorg. Chem. Front., 2023, 10, 1633–1649.
12. I. Bertini, Z. Xia and C. Luchinat, Solvent water ¹H NMRD study of oxovanadium(IV) aquo ion, J. Magn. Reson. (1969–1992), 1992, 99, 235–246.
13. V. Lagostina, F. Carniato, D. Esteban-Gómez, C. Platas-Iglesias, M. Chiesa and M. Botta, Magnetic and relaxation properties of vanadium(IV) complexes: an integrated ¹H relaxometric, EPR and computational study, Inorg. Chem. Front., 2023, 10, 1999–2013.
14. E. Balogh, Z. He, W. Hsieh, S. Liu and É. Tóth, Dinuclear Complexes Formed with the Triazacyclononane Derivative ENOTA⁴⁻: High-Pressure ¹⁷O NMR Evidence of an Associative Water Exchange on [Mn^II₂(ENOTA)(H₂O)₂], Inorg. Chem., 2007, 46, 238–250.
15. I. Bertini, F. Briganti, Z. Xia and C. Luchinat, Nuclear Magnetic Relaxation Dispersion Studies of Hexaaquo Mn(II) ions in Water-Glycerol Mixtures, J. Magn. Reson., Ser. A, 1993, 101, 198–201.
16. D. Esteban-Gómez, C. Cassino, M. Botta and C. Platas-Iglesias, ¹⁷O and ¹H relaxometric and DFT study of hyperfine coupling constants in [Mn(H₂O)₆]²⁺, RSC Adv., 2014, 4, 7094.
17. B.-T. Doan, S. Meme and J.-C. Beloeil, in The Chemistry of Contrast Agents in Medical Magnetic Resonance Imaging, ed. A. Merbach, L. Helm and É. Tóth, John Wiley & Sons, Ltd, Chichester, UK, 2013, pp. 1–23.
18. J. Wahsner, E. M. Gale, A. Rodríguez-Rodríguez and P. Caravan, Chemistry of MRI Contrast Agents: Current Challenges and New Frontiers, Chem. Rev., 2019, 119, 957–1057.
19. P. Caravan, J. J. Ellison, T. J. McMurry and R. B. Lauffer, Gadolinium(III) Chelates as MRI Contrast Agents: Structure, Dynamics, and Applications, Chem. Rev., 1999, 99, 2293–2352.
20. L. Helm, Relaxivity in paramagnetic systems: Theory and mechanisms, Prog. Nucl. Magn. Reson. Spectrosc., 2006, 49, 45–64.
21. J. H. Freed, Dynamic effects of pair correlation functions on spin relaxation by translational diffusion in liquids. II. Finite jumps and independent T₁ processes, J. Chem. Phys., 1978, 68, 4034–4037.
22. A. Vágner, E. Gianolio, S. Aime, A. Maiocchi, I. Tóth, Z. Baranyai and L. Tei, High kinetic inertness of a bis-hydrated Gd-complex with a constrained AAZTA-like ligand, Chem. Commun., 2016, 52, 11235–11238.
23. S. Aime, L. Calabi, C. Cavallotti, E. Gianolio, G. B. Giovenzana, P. Losi, A. Maiocchi, G. Palmisano and M. Sisti, [Gd-AAZTA]⁻: A New Structural Entry for an Improved Generation of MRI Contrast Agents, Inorg. Chem., 2004, 43, 7588–7590.
24. C. Ferroud, H. Borderies, E. Lasri, A. Guy and M. Port, Synthesis of a novel amphiphilic GdPCTA-[12] derivative as a potential micellar MRI contrast agent, Tetrahedron Lett., 2008, 49, 5972–5975.
25. C. S. Bonnet, S. Laine, F. Buron, G. Tircsó, A. Pallier, L. Helm, F. Suzenet and É. Tóth, A Pyridine-Based Ligand with Two Hydrazine Functions for Lanthanide Chelation: Remarkable Kinetic Inertness for a Linear, Bishydrated Complex, Inorg. Chem., 2015, 54, 5991–6003.
26. J. Costa, É. Tóth, L. Helm and A. E. Merbach, Dinuclear, Bishydrated Gd^III Polyaminocarboxylates with a Rigid Xylene Core Display Remarkable Proton Relaxivities, Inorg. Chem., 2005, 44, 4747–4755.
27. Z. Baranyai, M. Botta, M. Fekete, G. B. Giovenzana, R. Negri, L. Tei and C. Platas-Iglesias, Lower Ligand Denticity Leading to Improved Thermodynamic and Kinetic Stability of the Gd³⁺ Complex: The Strange Case of OBETA, Chem. – Eur. J., 2012, 18, 7680–7685.
28. J. Hao, P. Bourrinet and P. Desché, Assessment of Pharmacokinetic, Pharmacodynamic Profile, and Tolerance of Gadopiclenol, A New High Relaxivity GBCA, in Healthy Subjects and Patients With Brain Lesions (Phase I/IIa Study), Invest. Radiol., 2019, 54, 396–402.
29. C. Robic, M. Port, O. Rousseaux, S. Louguet, N. Fretellier, S. Catoen, C. Factor, S. Le Greneur, C. Medina, P. Bourrinet, I. Raynal, J.-M. Idée and C. Corot, Physicochemical and Pharmacokinetic Profiles of Gadopiclenol: A New Macrocyclic Gadolinium Chelate With High T1 Relaxivity, Invest. Radiol., 2019, 54, 475–484.
30. A. Beeby, I. M. Clarkson, R. S. Dickins, S. Faulkner, D. Parker, L. Royle, A. S. de Sousa, J. A. G. Williams and M. Woods, Non-radiative deactivation of the excited states of europium, terbium and ytterbium complexes by proximate energy-matched OH, NH and CH oscillators: an improved luminescence method for establishing solution hydration states, J. Chem. Soc., Perkin Trans. 2, 1999, 493–504.
31. R. M. Supkowski and W. D. Horrocks, On the determination of the number of water molecules, q, coordinated to europium(III) ions in solution from luminescence decay lifetimes, Inorg. Chim. Acta, 2002, 340, 44–48.
32. K. Djanashvili and J. A. Peters, How to determine the number of inner-sphere water molecules in lanthanide(III) complexes by ¹⁷O NMR spectroscopy. A technical note, Contrast Media Mol. Imaging, 2007, 2, 67–71.
33. N. Graeppi, D. Hugh Powell, G. Laurenczy, L. Zékány and A. E. Merbach, Coordination equilibria and water exchange kinetics of lanthanide(III) propylenediaminetetraacetates and other magnetic resonance imaging related complexes, Inorg. Chim. Acta, 1995, 235, 311–326.
34. É. Tóth, O. M. N. Dhubhghaill, G. Besson, L. Helm and A. E. Merbach, Coordination equilibrium—a clue for fast water exchange on potential magnetic resonance imaging contrast agents?, Magn. Reson. Chem., 1999, 701–708.
35. E. Balogh, M. Mato-Iglesias, C. Platas-Iglesias, É. Tóth, K. Djanashvili, J. A. Peters, A. de Blas and T. Rodríguez-Blas, Pyridine- and Phosphonate-Containing Ligands for Stable Ln Complexation. Extremely Fast Water Exchange on the Gd^III Chelates, Inorg. Chem., 2006, 45, 8719–8728.
36. M. Mato-Iglesias, A. Roca-Sabio, Z. Pálinkás, D. Esteban-Gómez, C. Platas-Iglesias, É. Tóth, A. de Blas and T. Rodríguez-Blas, Lanthanide Complexes Based on a 1,7-Diaza-12-crown-4 Platform Containing Picolinate Pendants: A New Structural Entry for the Design of Magnetic Resonance Imaging Contrast Agents, Inorg. Chem., 2008, 47, 7840–7851.
37. C. Platas-Iglesias, D. M. Corsi, L. V. Elst, R. N. Muller, D. Imbert, J.-C. G. Bünzli, É. Tóth, T. Maschmeyer and J. A. Peters, Stability, structure and dynamics of cationic lanthanide(III) complexes of N,N′-bis(propylamide)ethylenediamine-N,N′-diacetic acid, Dalton Trans., 2003, 727–737.
38. F. Yerly, F. A. Dunand, É. Tóth, A. Figueirinha, Z. Kovács, A. D. Sherry, C. F. G. C. Geraldes and A. E. Merbach, Spectroscopic Study of the Hydration Equilibria and Water Exchange Dynamics of Lanthanide(III) Complexes of 1,7-Bis(carboxymethyl)-1,4,7,10-tetraazacyclododecane (DO2A), Eur. J. Inorg. Chem., 2000, 1001–1006.
39. R. Janicki and A. Mondry, Structural and thermodynamic aspects of hydration of Gd(III) systems, Dalton Trans., 2019, 48, 3380–3391.
40. K. Djanashvili, C. Platas-Iglesias and J. A. Peters, The structure of the lanthanide aquo ions in solution as studied by ¹⁷O NMR spectroscopy and DFT calculations, Dalton Trans., 2008, 602–607.
41. C. Cossy, L. Helm, D. H. Powell and A. E. Merbach, A change in coordination number from nine to eight along the lanthanide(III) aqua ion series in solution: a neutron diffraction study, New J. Chem., 1995, 19, 27–35.
42. C. Cossy, L. Helm and A. E. Merbach, Oxygen-17 nuclear magnetic resonance kinetic study of water exchange on the lanthanide(III) aqua ions, Inorg. Chem., 1988, 27, 1973–1979.
43. R. V. Southwood-Jones, W. L. Earl, K. E. Newman and A. E. Merbach, Oxygen-17 NMR and EPR studies of water exchange from the first coordination sphere of gadolinium(III) aquoion and gadolinium(III) propylenediaminetetra-acetate, J. Chem. Phys., 1980, 73, 5909–5918.
44. J. Maigut, R. Meier, A. Zahl and R. van Eldik, Triggering Water Exchange Mechanisms via Chelate Architecture. Shielding of Transition Metal Centers by Aminopolycarboxylate Spectator Ligands, J. Am. Chem. Soc., 2008, 130, 14556–14569.
45. S. H. Koenig, C. Baglin, R. D. Brown and C. Fred Brewer, Magnetic field dependence of solvent proton relaxation induced by Gd³⁺ and Mn²⁺ complexes, Magn. Reson. Med., 1984, 1, 496–501.
46. J. A. Peters, The reliability of parameters obtained by fitting of ¹H NMRD profiles and ¹⁷O NMR data of potential Gd³⁺-based MRI contrast agents: Fitting of ¹H NMRD profiles and ¹⁷O NMR data, Contrast Media Mol. Imaging, 2016, 11, 160–168.
47. D. Riccardi, H.-B. Guo, J. M. Parks, B. Gu, L. Liang and J. C. Smith, Cluster-Continuum Calculations of Hydration Free Energies of Anions and Group 12 Divalent Cations, J. Chem. Theory Comput., 2013, 9, 555–569.
48. K. E. Gutowski and D. A. Dixon, Predicting the Energy of the Water Exchange Reaction and Free Energy of Solvation for the Uranyl Ion in Aqueous Solution, J. Phys. Chem. A, 2006, 110, 8840–8856.
49. J. Tomasi, B. Mennucci and R. Cammi, Quantum Mechanical Continuum Solvation Models, Chem. Rev., 2005, 105, 2999–3094.
50. C. W. Bock, G. D. Markham, A. K. Katz and J. P. Glusker, The Arrangement of First- and Second-shell Water Molecules Around Metal Ions: Effects of Charge and Size, Theor. Chem. Acc., 2006, 115, 100–112.
51. G. D. Markham, J. P. Glusker and C. W. Bock, The Arrangement of First- and Second-Sphere Water Molecules in Divalent Magnesium Complexes: Results from Molecular Orbital and Density Functional Theory and from Structural Crystallography, J. Phys. Chem. B, 2002, 106, 5118–5134.
52. M. Regueiro-Figueroa, D. Esteban-Gómez, R. Pujales-Paradela, L. Caneda-Martínez, A. De Blas and C. Platas-Iglesias, Water exchange rates and mechanisms in tetrahedral [Be(H₂O)₄]²⁺ and [Li(H₂O)₄]⁺ complexes using DFT methods and cluster-continuum models, Int. J. Quantum Chem., 2016, 116, 1388–1396.
53. I. Persson, P. D'Angelo, S. De Panfilis, M. Sandström and L. Eriksson, Hydration of Lanthanoid(III) Ions in Aqueous Solution and Crystalline Hydrates Studied by EXAFS Spectroscopy and Crystallography: The Myth of the “Gadolinium Break”, Chem. – Eur. J., 2008, 14, 3056–3066.
54. A. V. Astashkin, A. M. Raitsimring and P. Caravan, Pulsed ENDOR Study of Water Coordination to Gd³⁺ Complexes in Orientationally Disordered Systems, J. Phys. Chem. A, 2004, 108, 1990–2001.
55. D. Esteban-Gómez, A. de Blas, T. Rodríguez-Blas, L. Helm and C. Platas-Iglesias, Hyperfine Coupling Constants on Inner-Sphere Water Molecules of Gd^III-Based MRI Contrast Agents, ChemPhysChem, 2012, 13, 3640–3650.
56. O. V. Yazyev, L. Helm, V. G. Malkin and O. L. Malkina, Quantum Chemical Investigation of Hyperfine Coupling Constants on First Coordination Sphere Water Molecule of Gadolinium(III) Aqua Complexes, J. Phys. Chem. A, 2005, 109, 10997–11005.
57. P. H. Fries, Computing Electronic Spin Relaxation for Gd³⁺-Based Contrast Agents – Practical Implementation, Eur. J. Inorg. Chem., 2012, 2156–2166.
58. S. Khan, R. Pollet, R. Vuilleumier, J. Kowalewski and M. Odelius, An ab initio CASSCF study of zero field splitting fluctuations in the octet ground state of aqueous [Gd(III)(HPDO3A)(H₂O)], J. Chem. Phys., 2017, 147, 244306.
59. E. Belorizky and P. H. Fries, Simple analytical approximation of the longitudinal electronic relaxation rate of Gd(III) complexes in solutions, Phys. Chem. Chem. Phys., 2004, 6, 2341.
60. P. H. Fries and E. Belorizky, Determination of the Static Zero-Field Splitting of Gd³⁺ Complexes in Solution from the Shifts of the Central Magnetic Fields of Their EPR Spectra, ChemPhysChem, 2012, 13, 2074–2081.
61. S. Khan, A. Kubica-Misztal, D. Kruk, J. Kowalewski and M. Odelius, Systematic theoretical investigation of the zero-field splitting in Gd(III) complexes: Wave function and density functional approaches, J. Chem. Phys., 2015, 142, 034304.
62. S. Zein and F. Neese, Ab Initio and Coupled-Perturbed Density Functional Theory Estimation of Zero-Field Splittings in Mn^II Transition Metal Complexes, J. Phys. Chem. A, 2008, 112, 7976–7983.
63. C. Charpentier, J. Salaam, A. Nonat, F. Carniato, O. Jeannin, I. Brandariz, D. Esteban-Gómez, C. Platas-Iglesias, L. J. Charbonnière and M. Botta, pH-Dependent Hydration Change in a Gd-Based MRI Contrast Agent with a Phosphonated Ligand, Chem. – Eur. J., 2020, 26, 5407–5418.
64. A. Borel, H. Kang, C. Gateau, M. Mazzanti, R. B. Clarkson and R. L. Belford, Variable Temperature and EPR Frequency Study of Two Aqueous Gd(III) Complexes with Unprecedented Sharp Lines, J. Phys. Chem. A, 2006, 110, 12434–12438.
65. E. A. Suturina, K. Mason, M. Botta, F. Carniato, I. Kuprov, N. F. Chilton, E. J. L. McInnes, M. Vonci and D. Parker, Periodic trends and hidden dynamics of magnetic properties in three series of triazacyclononane lanthanide complexes, Dalton Trans., 2019, 48, 8400–8409.
66. I. Solomon, Relaxation Processes in a System of Two Spins, Phys. Rev., 1955, 99, 559–565.
67. N. Bloembergen, Proton Relaxation Times in Paramagnetic Solutions, J. Chem. Phys., 1957, 27, 572–573.
68. N. Bloembergen and L. O. Morgan, Proton Relaxation Times in Paramagnetic Solutions. Effects of Electron Spin Relaxation, J. Chem. Phys., 1961, 34, 842–850.
69. T. J. Swift and R. E. Connick, NMR-Relaxation Mechanisms of O¹⁷ in Aqueous Solutions of Paramagnetic Cations and the Lifetime of Water Molecules in the First Coordination Sphere, J. Chem. Phys., 1962, 37, 307–320.
70. S. G. Zech, W.-C. Sun, V. Jacques, P. Caravan, A. V. Astashkin and A. M. Raitsimring, Probing the Water Coordination of Protein-Targeted MRI Contrast Agents by Pulsed ENDOR Spectroscopy, ChemPhysChem, 2005, 6, 2570–2577.
71. L. Leone, G. Ferrauto, M. Cossi, M. Botta and L. Tei, Optimizing the Relaxivity of MRI Probes at High Magnetic Field Strengths With Binuclear GdIII Complexes, Front. Chem., 2018, 6, 158.
72. L. Vander Elst, A. Sessoye, S. Laurent and R. N. Muller, Can the Theoretical Fitting of the Proton-Nuclear-Magnetic-Relaxation-Dispersion (Proton NMRD) Curves of Paramagnetic Complexes Be Improved by Independent Measurement of Their Self-Diffusion Coefficients?, Helv. Chim. Acta, 2005, 88, 574–587.
73. H. Lammers, F. Maton, D. Pubanz, M. W. van Laren, H. van Bekkum, A. E. Merbach, R. N. Muller and J. A. Peters, Structures and Dynamics of Lanthanide(III) Complexes of Sugar-Based DTPA-bis(amides) in Aqueous Solution: A Multinuclear NMR Study, Inorg. Chem., 1997, 36, 2527–2538.
74. S. Rast, P. H. Fries and E. Belorizky, Static zero field splitting effects on the electronic relaxation of paramagnetic metal ion complexes in solution, J. Chem. Phys., 2000, 113, 8724–8735.
75. S. Rast, A. Borel, L. Helm, E. Belorizky, P. H. Fries and A. E. Merbach, EPR Spectroscopy of MRI-Related Gd(III) Complexes: Simultaneous Analysis of Multiple Frequency and Temperature Spectra, Including Static and Transient Crystal Field Effects, J. Am. Chem. Soc., 2001, 123, 2637–2644.
76. F. A. Dunand, A. Borel and A. E. Merbach, How Does Internal Motion Influence the Relaxation of the Water Protons in Ln^III DOTA-like Complexes?, J. Am. Chem. Soc., 2002, 124, 710–716.
77. K. Micskei, D. H. Powell, L. Helm, E. Brücher and A. E. Merbach, Water exchange on [Gd(H₂O)₈]³⁺ and [Gd(PDTA)(H₂O)₂]⁻ in aqueous solution: A variable-pressure, -temperature and -magnetic field ¹⁷O NMR study, Magn. Reson. Chem., 1993, 31, 1011–1020.
78. O. V. Yazyev and L. Helm, Gadolinium(III) ion in liquid water: Structure, dynamics, and magnetic interactions from first principles, J. Chem. Phys., 2007, 127, 084506.
79. L. Leone, S. Camorali, A. Freire-García, C. Platas-Iglesias, D. Esteban Gomez and L. Tei, Scrutinising the role of intramolecular hydrogen bonding in water exchange dynamics of Gd(III) complexes, Dalton Trans., 2021, 50, 5506–5518.
80. A. Roca-Sabio, M. Regueiro-Figueroa, D. Esteban-Gómez, A. de Blas, T. Rodríguez-Blas and C. Platas-Iglesias, Density functional dependence of molecular geometries in lanthanide(III) complexes relevant to bioanalytical and biomedical applications, Comput. Theor. Chem., 2012, 999, 93–104.
81. P. Caravan, D. Esteban-Gómez, A. Rodríguez-Rodríguez and C. Platas-Iglesias, Water exchange in lanthanide complexes for MRI applications. Lessons learned over the last 25 years, Dalton Trans., 2019, 48, 11161–11180.
82. F. Lucio-Martínez, Z. Garda, B. Váradi, F. K. Kálmán, D. Esteban-Gómez, É. Tóth, G. Tircsó and C. Platas-Iglesias, Rigidified Derivative of the Non-macrocyclic Ligand H₄OCTAPA for Stable Lanthanide(III) Complexation, Inorg. Chem., 2022, 61, 5157–5171.
83. L. Helm and A. E. Merbach, Inorganic and Bioinorganic Solvent Exchange Mechanisms, Chem. Rev., 2005, 105, 1923–1960.
84. D. M. Corsi, C. Platas-Iglesias, H. van Bekkum and J. A. Peters, Determination of paramagnetic lanthanide(III) concentrations from bulk magnetic susceptibility shifts in NMR spectra, Magn. Reson. Chem., 2001, 39, 723–726.
85. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 (revision C.01), Gaussian, Inc., 2016.
86. J.-D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
87. M. Dolg, H. Stoll, A. Savin and H. Preuss, Energy-adjusted pseudopotentials for the rare earth elements, Theor. Chim. Acta, 1989, 75, 173–194.
88. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
89. C. Peng and H. B. Schlegel, Combining Synchronous Transit and Quasi-Newton Methods to Find Transition States, Isr. J. Chem., 1993, 33, 449–454.
90. F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
91. F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327.
92. M. Reiher, Douglas–Kroll–Hess Theory: a relativistic electrons-only theory for chemistry, Theor. Chem. Acc., 2006, 116, 241–252.
93. M. Barysz and A. J. Sadlej, Two-component methods of relativistic quantum chemistry: from the Douglas–Kroll approximation to the exact two-component formalism, J. Mol. Struct.: THEOCHEM, 2001, 573, 181–200.
94. D. Aravena, F. Neese and D. A. Pantazis, Improved Segmented All-Electron Relativistically Contracted Basis Sets for the Lanthanides, J. Chem. Theory Comput., 2016, 12, 1148–1156.
95. D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, All-Electron Scalar Relativistic Basis Sets for Third-Row Transition Metal Atoms, J. Chem. Theory Comput., 2008, 4, 908–919.
96. F. Neese, An improvement of the resolution of the identity approximation for the formation of the Coulomb matrix, J. Comput. Chem., 2003, 24, 1740–1747.
97. S. Kossmann and F. Neese, Comparison of two efficient approximate Hartee–Fock approaches, Chem. Phys. Lett., 2009, 481, 240–243.
98. R. Izsák and F. Neese, An overlap fitted chain of spheres exchange method, J. Chem. Phys., 2011, 135, 144105.
99. G. L. Stoychev, A. A. Auer and F. Neese, Automatic Generation of Auxiliary Basis Sets, J. Chem. Theory Comput., 2017, 13, 554–562.
100. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Climbing the Density Functional Ladder: Nonempirical Meta-Generalized Gradient Approximation Designed for Molecules and Solids, Phys. Rev. Lett., 2003, 91, 146401.
101. S. Karimi and L. Helm, Water Exchange on [Ln(DO3A)(H₂O)₂] and [Ln(DTTA–Me)(H₂O)₂]⁻ Studied by Variable Temperature, Pressure, and Magnetic Field NMR, Inorg. Chem., 2016, 55, 4555–4563.
102. M. Regueiro-Figueroa and C. Platas-Iglesias, Toward the Prediction of Water Exchange Rates in Magnetic Resonance Imaging Contrast Agents: A Density Functional Theory Study, J. Phys. Chem. A, 2015, 119, 6436–6445.
103. F. Neese, Importance of Direct Spin–Spin Coupling and Spin-Flip Excitations for the Zero-Field Splittings of Transition Metal Complexes: A Case Study, J. Am. Chem. Soc., 2006, 128, 10213–10222.
104. P.-Å. Malmqvist and B. O. Roos, The CASSCF state interaction method, Chem. Phys. Lett., 1989, 155, 189–194.
105. C. Kollmar, K. Sivalingam, B. Helmich-Paris, C. Angeli and F. Neese, A perturbation-based super-CI approach for the orbital optimization of a CASSCF wave function, J. Comput. Chem., 2019, 40, 1463–1470.
106. C. Angeli, S. Borini, M. Cestari and R. Cimiraglia, A quasidegenerate formulation of the second order n-electron valence state perturbation theory approach, J. Chem. Phys., 2004, 121, 4043–4049.
107. C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, Introduction of n-electron valence states for multireference perturbation theory, J. Chem. Phys., 2001, 114, 10252–10264.
108. D. Maganas, S. Sottini, P. Kyritsis, E. J. J. Groenen and F. Neese, Theoretical Analysis of the Spin Hamiltonian Parameters in Co^(II)S₄ Complexes, Using Density Functional Theory and Correlated ab initio Methods, Inorg. Chem., 2011, 50, 8741–8754.
109. M. Atanasov, D. Aravena, E. Suturina, E. Bill, D. Maganas and F. Neese, First principles approach to the electronic structure, magnetic anisotropy and spin relaxation in mononuclear 3d-transition metal single molecule magnets, Coord. Chem. Rev., 2015, 289–290, 177–214.
110. A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113, 6378–6396.

---

Footnote

† Electronic supplementary information (ESI) available: Additional relaxometric data and optimized geometries obtained with DFT. See DOI: https://doi.org/10.1039/d3dt03413e

---