Activation of the N₂ molecule by means of low-valence complexes of calcium and magnesium

Abstract

Nitrogen gas is a highly inert molecule and its activation under mild conditions represents a crucial goal in current research. In a recent study, the discovery of low-valence Ca(I) compounds capable of coordinating and reducing N₂ was reported [B. Rösch, T. X. Gentner, J. Langer, C. Färber, J. Eyselein, L. Zhao, C. Ding, G. Frenking and S. Harder, Science, 2021, 371, 1125]. The study of low-valence alkaline earth complexes represents a new horizon in inorganic chemistry and demonstrates examples of spectacular reactivity. For example, complexes of the [BDI]₂Mg₂ type are selective reducing reagents in both organic and inorganic synthesis reactions. To date, however, no activity of Mg(I) complexes in the activation of the nitrogen molecule has been reported. By computational studies, in the present work, we investigated the analogies and differences of low-valence Ca(I) and Mg(I) complexes in the coordination, activation and protonation of N₂. We have shown that the possibility of alkaline earth metals to employ atomic orbitals of the d type is reflected in the differences in the N₂ binding energy and its coordination mode (end-on vs. side-on), as well as in the spin state of the resulting adduct (singlet vs. triplet). These divergences are finally observed in the subsequent protonation reaction, which turned out to be prohibitive in the presence of Mg.

---

1. Introduction

Dinitrogen (N₂) is one of the most abundant molecules on our planet, forming almost 78% of the Earth's atmosphere, but at the same time, it is also one of the most difficult gases to exploit in chemical processes.¹ Indeed, the strong triple bond, the low proton and electron affinity, the absence of polarisation and the high HOMO–LUMO gap (10.82 eV) govern the scarce reactivity of N₂ and pose serious challenges for its industrial and biological conversion. The continuous growth in ammonia demand from humanity is industrially fulfilled by the Haber–Bosch process, which requires harsh conditions (400–600 °C/200–600 bar) to overcome N₂ inertness.² Besides being energy-intensive, the Haber–Bosch reaction uses H₂ as a reductant which, in turn, is mainly produced via the unsustainable steam reforming of natural gas. Biological N₂ fixation into bio-available ammonia is instead performed by metalloenzymes, known as nitrogenases, that couple protons and electrons for substrate reduction and that need considerable amounts of ATP to work.^3,4

Although the well-established and productive Haber–Bosch process is unlikely to be replaced in the near future, the fact that both industry and nature rely on d-block metals as catalysts for the N₂ reduction reaction (N₂RR) has triggered the development of alternative strategies based on transition metals, starting in the mid-1960s.^5–8 The main reason is that ammonia is fundamental to sustaining human life and society's progress, so discovering the requirements for efficient N≡N splitting under mild conditions and with minimal energy input is a primary goal for chemists. Furthermore, besides the “conventional” use of NH₃, it has recently emerged as a promising green fuel for fuel cells, pushing forward academic and industrial interest in its fully sustainable production.^9,10

Examples of homogeneous systems based on d-block metals for the N₂RR have increased over the past decades, with crucial contributions by the groups of Chatt,^11–13 Hidai,¹⁴ Schrock,^15–20 Peters,^{21,22,23–25} Nishibayashi,^26–30 Ashley³¹ and others.^5,32,33 The partially filled d orbitals of transition metals are suited in terms of both energy and symmetry to weaken the triple bond of N₂, although the latter is notably a poorly coordinating molecule. Interestingly, it has also been found that transition metals are not indispensable for N₂ activation, since it can also be accomplished by f-block elements (e.g. La and Ce),^34,35 by the p-block half-metal B,^36–38 and by the s-block alkali metal (Li)^39,40 and alkaline earth (AE) metals (Be, Ca, Sr, Ba).^41–46 Activation of N₂ by AE metals, in particular, has experienced huge progress in recent years thanks to several investigations performed under matrix isolation conditions. Zhou, Frenking and collaborators reported different Be-dinitrogen complexes, including the first example of the N₂ side-on adduct for main group elements.⁴² They also isolated and spectroscopically characterized octahedral complexes of AE metals of the types M(CO)₈ and M(N₂)₈ (M = Ca, Sr, and Ba).^44,47 Here, an (n − 1)d²(n)s⁰(n)p⁰ configuration has been assigned to M, which fulfills the 18 electron rule upon coordination, behaving as a d-block element. The ability of heavier alkaline earth atoms (Ca, Sr and Ba) to employ their (n − 1)d atomic orbitals in covalent interactions has already been suggested by earlier theoretical investigations which showed how these orbitals lie close in energy to the valence np orbitals, opposite to the lighter atoms Be and Mg.^48,49 Later, Harder, Frenking and coworkers showed that low valent Ca(I) is also capable of reducing N₂ to give N₂H₂ (which then disproportionates to give 0.5N₂ and 0.5N₂H₄), although only under very peculiar conditions.⁴⁵ In particular, starting from a stable binuclear Ca(I) iodide precursor (1_Ca, Fig. 1), featuring one very bulky β-diketiminate ligand (BDI = HCC(Me)N[2,6-3-pentyl-phenyl]₂) per Ca(I), it was possible to serendipitously bind and activate N₂ at −60 °C by (i) treatment with K/KI as the reducing agent, (ii) using an aliphatic solvent and (iii) adding tetrahydropyran (THP) or tetrahydrofuran (THF) to the solution. In this way, the crystal structures of both [(BDI)Ca(THP)]₂N₂ (2_Ca–N2) and [(BDI)Ca(THF)]₂N₂ (3_Ca–N2) (Fig. 1) were obtained, revealing the side-on coordination of N₂, which is bound in a sandwich fashion between the two Ca atoms. DFT calculations confirmed that N₂ is doubly reduced, as N₂²⁻, with each Ca(I) contributing one electron to its reduction. Interestingly, heating up 3_Ca–N2 (but not 2_Ca–N2) to 60 °C led to the degradation of coordinated THF molecules, i.e. the transfer of two protons from one of the OCH₂ units of each THF to both N atoms of the activated N₂²⁻, resulting in N₂H₂ formation. All the above-described processes, if carried out in aromatic solvents such as benzene or p-xylene, lead to solvent reduction (instead of the N₂ one) by their fitting between the two Ca(I) atoms. Interestingly, the same behaviour towards aromatic molecules has been previously observed for the highly reducing Mg(I) analogue [(BDI)Mg]₂ (1_Mg).^50,51 The latter shows two important differences with respect to the Ca counterpart: (i) 1_Mg features a stable and well-characterised Mg(I)–Mg(I) bond,⁵² while the same Ca(I)–Ca(I) interaction (as in 2_Ca, Fig. 1) has not been detected, so it should form only transiently^53,54 and (ii) 1_Mg does not bind or reduce N₂.^45,55 This suggests that apparently, tiny differences among the electronic structures of the AE metals (such as between closely related Ca and Mg) may result in very different reactivities. Previous theoretical investigations indicated that in the cases of Ca, Sr and Ba, back-donation from their d orbitals to the empty π* ones of N₂ is crucial for the coordination of the latter, while in the case of Be, back-donation to N₂ has been ascribed to the metal p orbitals.⁴⁶ Although all these elements can bind N₂, only Ca(I) can effectively reduce it.

Fig. 1 Schematic representation of different monovalent Ca and Mg species. Species 1_Ca and 1_Mg have been experimentally characterized while 2_Ca and 3_Ca are only postulated.

Furthermore, it is intriguing and puzzling at the same time that no Mg–N₂ interaction has ever been detected or characterised, and so the nature of such interaction also remains completely unexplored from a theoretical standpoint. In this scenario, this work aims at shedding light on the differences between low-valent Ca(I) and Mg(I) BDI complexes in terms of their electronic structure and reactivity towards N₂. In particular, we present a detailed characterisation of the N₂ binding mode and energy for different M-BDI complexes (M = Ca(I), Mg(I)), accounting for the presence of both THF and THP. Then, we analysed the different Ca vs. Mg orbital contributions to the bond with N₂ and investigated the effect of the two AE metals on the subsequent N₂ protonation step by THF/THP degradation. Overall, our contribution will generate new knowledge on the role of different AEs in N₂ activation and reduction, hopefully providing new hints for future advancements in the use of AE-based catalysts for the N₂RR.

2. Results and discussion

2.1. N₂ coordination to the low-valence Ca and Mg complexes

The [(BDI)Ca(THP)]₂N₂ and [(BDI)Ca(THF)]₂N₂ species (2_Ca–N2 and 3_Ca–N2, Fig. 1) had been crystallised and analysed through X-ray analysis (CCDC 2036242 and 2036243) in a previous experimental–theoretical work.⁴⁵ We compared the two geometries stored in the CCDC database with those obtained through geometry optimisation calculations at the BP86-D3(BJ)/def2-SVP level of theory. The chosen level of theory turned out to be eligible for the description of the geometric parameters of the centrosymmetric alkaline earth metal structures. Concerning the atomic distances of the first coordination sphere of Ca(I), the maximum deviation observed is 0.02 Å for the Ca(I)–O(THP) distance in 2_Ca–N2 and 0.03 Å for the Ca(I)–N(BDI) distance in 3_Ca–N2 (see Fig. 2). A larger basis set – def2-TZVP – for the description of the calcium atoms and of their first coordination sphere was tested; however, the bond distance analysis showed that the use of a broader basis set gives similar results with respect to the use of a smaller def2-SVP one (see Table S1†).

Fig. 2 Optimized structures of 2_Ca–N2 and 3_Ca–N2. Most significant calculated and experimental (in brackets) geometry parameters are reported below each species. Colour pattern: grey, C; blue, N; red, O; green, Ca. Hydrogen atoms are omitted for clarity.

In the optimised LCa(N₂)CaL species (Fig. 2), the nitrogen molecule bound between the two calcium atoms shows an elongated N–N bond (1.26 Å for both 2_Ca–N2 and 3_Ca–N2), corresponding to the strong activation of N₂.⁵⁶

The natural bond orbital (NBO) analysis was carried out to study the electronic structures of the LCa(N₂)CaL species. Natural atomic orbital occupancies and natural atomic charges (Table 1) indicate that the side-on bridging N₂ unit is activated to an N₂²⁻ anion which interacts with two Ca²⁺ cations. The accumulation of negative charge on the activated N₂ molecule and the concomitant oxidation of Ca ions were previously observed by means of different population analysis schemes – e.g. NBO analysis and quantum theory of atoms in molecules (QTAIM) – in the Ca₂N₂ system.⁴⁵ The resulting Ca–N(N₂) distances are all equal to 2.29 Å in the presence of THF while each Ca ion lies at a distance of 2.32 and 2.30 Å from each nitrogen atom of the N₂ molecule in the presence of THP, respectively (see Fig. 2).

Table 1 Natural atomic charges and natural atomic orbital occupancies (in brackets) computed on the LAE(N₂)AEL optimised geometries

	2 Ca–N2	3 Ca–N2		e^32Mg–N2	e^33Mg–N2
Ca1	1.74 (18)	1.74 (18)	Mg1	1.80 (10)	1.80 (10)
Ca2	1.74 (18)	1.74 (18)	Mg1	1.80 (10)	1.80 (10)
N1	−0.82 (8)	−0.82 (8)	N1	−0.83 (8)	−0.83 (8)
N2	−0.82 (8)	−0.83 (8)	N1	−0.83 (8)	−0.83 (8)

---

Despite the observed structural similarity of the complexes containing THP or THF, the two compounds have experimentally shown different stability over time. In fact, while at room temperature the THF complex decomposes overnight, the THP analogue remains stable for 24 hours before, also decomposing through the evolution of H₂ and N₂. The difference in stability observed experimentally can be correlated to the bond strength established between the calcium ions and the dinitrogen molecule in the two complexes. The binding energy of the N₂ molecule to the neutral fragment [(BDI)Ca(THP)]₂ or [(BDI)Ca(THF)]₂ (2_Ca and 3_Ca in Fig. 1) was calculated at the B3LYP-D3(BJ)/def2-TZVPP level of theory considering the species solvated in a continuum solvent. We will refer exclusively to relative binding energies (ΔΔE) for two main reasons: (i) DFT generally performs poorly in calculating absolute energies for ligand association to large metal complexes⁵⁷ and (ii) the focus of the present work is to highlight eventual differences among the considered compounds in their reactivity towards N₂. In the case of Ca–N₂ adducts (2_Ca–N2 and 3_Ca–N2), we observed that N₂ binds more favorably (by 6.7 kcal mol⁻¹) to 2_Ca than to 3_Ca, indicating that the reaction can be favored in the presence of THP. Triplet states were investigated for the Ca–Ca reagents (2_Ca and 3_Ca) and the Ca–N₂ products ((2_Ca–N2 and 3_Ca–N2) by running optimisation calculations. The results indicate that the singlet state geometries are retained in the triplet states. In any case, single states were found to be the most energetically favourable ones (energy differences between triplet and single states are 10.3 kcal mol⁻¹ and 7.4 kcal mol⁻¹ for 2_Ca–N2 and 2_Ca species and 9.7 kcal mol⁻¹ and 13.1 kcal mol⁻¹ for 3_Ca–N2 and 3_Ca species, respectively).

The BDI ligand was reported to be able to stabilise the Mg(I)–Mg(I) bond and it was proposed that Mg(BDI) systems are less reducing than their Ca(BDI) counterparts. Furthermore, Mg(BDI) complexes have not shown (so far) any reactivity towards N₂. In order to verify and rationalise this Mg vs. Ca difference, we replaced the Ca(I) with Mg(I) atoms in our models. First, we verified the plausible existence of compounds of the [(BDI)Mg(THP)]₂N₂ or [(BDI)Mg(THF)]₂N₂ type (2_Mg–N2 and 3_Mg–N2 shown in Fig. 3). For each species, we obtained a minimum with a geometry resembling the one obtained for the Ca-containing analogues. The N₂ molecule is coordinated between two Mg ions in a side-on manner, with resulting Mg–N(N₂) distances of 2.15 Å and 2.18 Å in 2_Mg–N2 and 2.12, 2.16 Å and 2.13, 2.15 Å in 3_Mg–N2 (see Fig. 4, S1† and Table 2). Analogously to what was observed for the Ca-containing species, the two Mg atoms were oxidised to Mg(II) while the nitrogen molecule was 2-electron reduced (Table S2†). Exploration of alternative spin states led to the localisation of geometries that are significantly more stable in energy. These complexes exhibit a paramagnetic character and the nitrogen molecule is inserted between the two Mg ions in an end-on manner (e³2_Mg–N2 and e³3_Mg–N2, Fig. 4 and Fig. S1†). In more detail, these high spin (triplet) complexes with a coordinated end-on N₂ molecule are much more stable with respect to the low spin (singlet) ones with a side-on N₂ molecule, irrespective of the solvent. Indeed, e³2_Mg–N2 turned out to be 16.3 and 19.1 kcal mol⁻¹ more stable than 2_Mg–N2 and e¹2_Mg–N2, respectively, while e³3_Mg–N2 is 11.8 and 17.4 kcal mol⁻¹ more stable than 3_Mg–N2 and e¹2_Mg–N2, respectively. The end-on bridging mode of N₂ shows a lower elongation of the N–N bond than the side-on coordination mode (1.22 Å and 1.23 Å for e³2_Mg–N2 and e³3_Mg–N2, respectively). Interestingly, in both e³2_Mg–N2 and e³3_Mg–N2 a contraction of the bonds between the magnesium ions and the coordinating atoms from BDI and solvent (N and O atoms) is observed, as evidenced in Table 2. Similarly to the side-on species, the end-on ones exhibit an interaction between two Mg²⁺ cations and a N₂²⁻ anion (Table 1).

Fig. 3 Scheme of the N₂ coordination compounds formed after insertion between the two AE(I) ions.

Fig. 4 Optimized structures of the characterized N₂ coordination modes to 2_Mg. Colour pattern: grey, C; blue, N; red, O; magenta, Mg. Hydrogen atoms are omitted for clarity.

Table 2 Distance values between the nitrogen atoms of the N₂ molecule and between magnesium ions and atoms in their coordination sphere for the [(BDI)Mg(THP)]₂N₂ and [(BDI)Mg(THF)]₂N₂ species (2_Mg–N2 and 3_Mg–N2)and for e³[(BDI)Mg(THP)]₂N₂ and e³[(BDI)Mg(THF)]₂N₂ species (e³2_Mg–N2 and e³2_Mg–N2). All distances in Å. Atom labels are shown in Fig. 4 and S1†

	2 Mg–N2	3 Mg–N2	e^32Mg–N2	e^33Mg–N2
N1–N2	1.29	1.29	1.22	1.23
Mg1–N1	2.15	2.12	1.96	1.94
Mg1–N2	2.18	2.16	—	—
Mg2–N1	2.18	2.15	—	—
Mg2–N2	2.15	2.13	1.96	1.94
Mg1–N3	2.20	2.13	2.08	2.07
Mg1–N4	2.16	2.16	2.10	2.07
Mg2–N5	2.20	2.13	2.08	2.06
Mg2–N6	2.16	2.15	2.10	2.07
Mg1–O	2.23	2.16	2.12	2.09
Mg2–O	2.23	2.18	2.12	2.10

---

In order to evaluate the effect of Ca substitution with Mg on N₂ activation, we calculated N₂ binding energies for LMg(I)–Mg(I)L systems (2_Mg and 3_Mg), as previously done for the Ca-complexes. The singlet states of 2_Mg and 3_Mg turned out to be much more stable with respect to their triplet state counterparts (−17.7 kcal mol⁻¹ and −27.2 kcal mol⁻¹, respectively), therefore they were considered as the reagents in the N₂ coordination reaction. Interestingly, also for Mg(I) systems it is observed that N₂ binding is favored in THP rather than in THF (by −7.7 kcal mol⁻¹), as evidenced for the Ca(I) complexes.

Although the compounds reported by Rösch et al.⁴⁵ did not show any paramagnetic character, our results for the Mg compounds motivated us to investigate the formation of a possible end-on coordination mode of N₂ to both 2_Ca and 3_Ca. We found that only 2_Ca can coordinate with N₂ in an end-on fashion, forming e³2_Mg–N2, while in the presence of THF (i.e. for 3_Ca) this binding mode is not accessible. As observed for Mg systems, e³2_Ca–N2 is characterised by a triplet ground state, but in this case, it is much more unstable with respect to the low spin side-on complex 2_Ca–N2 (by 17.4 kcal mol⁻¹).

Finally, considering the formation of the most stable Ae(I)–N₂ adducts for both Mg (end-on coordination, triplet) and Ca (side-on coordination, singlet), it has been found that N₂ binding energies are more energetically favoured in the case of Ca(I) than those in Mg(I) complexes. Indeed, considering THP solvent, the formation of 2_Ca–N2 is 6.6 kcal mol⁻¹ more favored than that of e³2_Mg–N2, while in THF, the formation of 3_Ca–N2 is 7.6 kcal mol⁻¹ more favored than that of 3_Mg–N2.

2.2. Molecular orbital analysis

Given the unexpected differences observed between Mg and Ca compounds in terms of the coordination mode of the nitrogen molecule and the related electronic configuration, we analysed in more detail both AE(I)–AE(I) and AE(I)–N₂–AE(I) interactions. As reported above, the AE(I)–AE(I) type compounds proved to be more stable in the singlet ground state for both the metal-alkaline earth elements considered in the present study.

As for the Ca compounds, the computed Ca(I)–Ca(I) distance was found to be 3.93 and 3.80 Å for 2_Ca and 3_Ca, respectively. The molecular orbital analysis of 2_Ca and 3_Ca indicated that their HOMO orbitals are characterised by a σ-like bond among the two Ca ions (see Fig. 5) that contribute equally to the formation of the Ca–Ca bond by means of their s and p orbitals, as well as with a little contribution from the d orbitals. As reported in Table 3, the percentage contribution to the HOMO of the d orbitals of each Ca is around 10% for both 2_Ca and 3_Ca. Also in the case of the LMg(I)–Mg(I)L species the dominant interaction is characterised by a sigma bond between the two Mg atoms, in which both metal ions contribute equally almost by means of their s and p orbitals (see Fig. 5) and with a negligible (4%) participation of d orbitals.

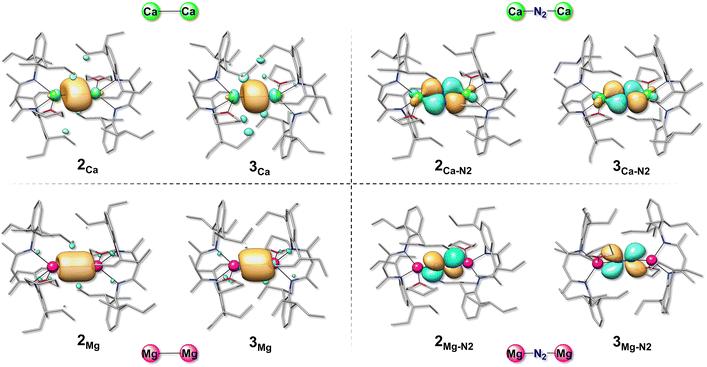Fig. 5 Graphical representation of HOMOs (isosurface cutoff = 0.05 a.u.) of the LCa(I)–Ca(I)L and LMg(I)–Mg(I)L species as well as for their energetically most stable N₂ bearing complexes.

Table 3 Percentage contribution of orbital type (s, p, d and f) for each atom participating to the HOMO of the most representative species. Values were obtained by computing the Mulliken contributions of each atom for the selected MO

	% s	% p	% d	% f
2 Ca
Ca1	58.7	31.7	9.6
Ca2	58.4	31.8	9.8
3 Ca
Ca1	62.0	29.7	8.3
Ca2	59.9	30.5	9.6
2 Mg
Mg1	56.1	39.5	4.4
Mg2	56.1	39.5	4.4
3 Mg
Mg1	55.6	40.1	4.3
Mg2	54.0	41.7	4.3
2 Ca–N2
Ca1	6.7	3.4	89.9
Ca2	5.3	4.0	90.7
N1		100
N2		100
3 Ca–N2
Ca1	0.9	2.9	96.2
Ca2	1.7	3.3	95.0
N1		100
N2		100
e^32Mg–N2
Mg1
Mg2
N1		96.7	3.3
N2		96.7	3.3
e^33Mg–N2
Mg1
Mg2
N1	0.1	96.7	3.1	0.1
N2	0.2	96.6	3.1	0.1

---

The HOMO–LUMO gap of 2_Ca is 24.2 kcal mol⁻¹ and 6.2 kcal mol⁻¹ smaller than that of 3_Ca. Interestingly, the calculated HOMO–LUMO gaps for the LMg(I)–Mg(I)L species are significantly larger (53.3 kcal mol⁻¹ and 58.3 kcal mol⁻¹ for 2_Mg and 3_Mg, respectively), and this may justify the higher stability of the systems featuring an Mg(I)–Mg(I) bond, with respect to the ones with a (hypothetical) Ca(I)–Ca(I) interaction, as suggested by previous experimental and theoretical investigations.⁴⁵

We subsequently analysed the shape of the bonding orbitals in the most stable AE(I)–N₂–AE(I) compounds as well as the contribution of the AE atomic orbitals to the bonding molecular orbitals. The Ca species containing a μ₂-N₂ molecule evidence a molecular orbital (HOMO) involving the monovalent ions and the nitrogen atoms of N₂, where the latter contribute 85% to the formation of the bond thanks to the sole participation of their p orbitals (see Fig. 5). On the other hand, the two Ca ions intervene symmetrically in the formation of the bond mostly by means of their d orbitals. This contribution exceeds 95% in the case of compound 2_Ca–N2 and it is around 90% in compound 3_Ca–N2 (see Table 3). Our results are in accordance with what was previously reported for [(BDI)Ca(THF)]₂N₂ through energy decomposition with natural orbitals for chemical valence (EDA-NOCV) analysis, which showed that the interaction between the calcium complex and N₂ essentially relies on Ca(I) d orbitals and N₂ p orbitals.⁴⁵ Interestingly, N₂ binding to 2_Ca and 3_Ca causes an increase in HOMO–LUMO gaps by 17.8 kcal mol⁻¹ in the presence of THP (2_Ca–N2) and by 15.8 kcal mol⁻¹ in the presence of THF (3_Ca–N2), plausibly explaining why the LCa(N₂)CaL species, but not the LCa–CaL ones, have been experimentally isolated and characterized.

The situation is completely different in the case of Mg complexes characterised by an N₂ end-on interaction and a triplet ground state. In this case, in fact, there is no molecular orbital formed by the atomic orbitals of both Mg and N. In compounds e³2_Mg–N2 and e³3_Mg–N2, HOMO and HOMO−1 are constituted by the p orbitals of the two atoms of the N₂ molecule as shown in Fig. 5. This result therefore suggests that the covalent contribution to the AE–N₂ bond is larger for Ca(I) than for Mg(I), since the former can participate with its d orbitals in N₂ activation (see Table 3).

2.3. N₂ protonation reaction

As aforementioned, protonation of the activated N₂ molecule has been experimentally observed, and it occurs by proton transfer from one of the OCH₂ units of the THF ligand.⁴⁵ The reaction leads to the formation of diazene (N₂H₂) and elimination products such as ethylene and enolate. Subsequently, diazene disproportionates at temperatures lower than −150 °C in N₂ and hydrazine (N₂H₄). In 3_Ca–N2, the protonation of N₂²⁻ by one THF ligand begins with the formation of a hydrogen bond between one nitrogen of the N₂ molecule and one of the two alpha protons of the spatially closest THF OCH₂ unit. A similar mechanism can be envisioned for the THP counterpart which, although reported to be more stable than 3_Ca–N2, decomposes unselectively at elevated temperatures. In order to highlight the effect of the Ca to Mg substitution on N₂²⁻ protonation properties, we calculated the associated reaction mechanism in both cases.

We started analysing the reactivity of compound 3_Ca–N2, which was previously investigated through theoretical investigations using a simpler model and the pure functional BP86.⁴⁵ In 3_Ca–N2 the N(N₂)–H(OCH₂) distance is 2.67 Å while the C–H distance is 1.11 Å. As the reaction occurs, the N(N₂)–H(OCH₂) distance shortens up to 1.10 Å in the final product 3P_Ca, while the C–H distance elongates to 2.01 Å. The reaction energy was found to be 32.4 kcal mol⁻¹, with an associated energy barrier of 36.5 kcal mol⁻¹. The transition state structure is characterised by a geometry that is very similar to 3P_Ca (N(N₂)–H(OCH₂) = 1.25 Å, C–H = 1.57 Å, see Fig. S2†). These results are consistent with what is reported in the literature – i.e. a reaction energy of 29.0 kcal mol⁻¹ with an activation energy of 32.1 kcal mol⁻¹. As expected, considering 2_Ca–N2, we individuated a similar reaction path. In this case, the reaction turned out to be almost isoenergetic to that of 3_Ca–N2 (reaction energy equal to 30.7 kcal mol⁻¹) but with a higher transition state energy (activation energy equal to 38.8 kcal mol⁻¹). The starting N(N₂)–H(OCH₂) distance in 2_Ca–N2 is 2.76 Å, which shortens to 1.08 Å in the product 2P_Ca, while the initial C–H distance of 1.11 Å becomes 2.35 Å in 2P_Ca. As for the THF case, the transition state 2TS geometry is close to the final product with an N(N₂)–H(OCH₂) distance of 1.28 Å and a C–H distance of 1.62 Å. In both cases, as the solvent ligand becomes deprotonated, its interaction mode with the Ca ion changes. As previously described, in the initial coordination, the oxygen atom of the solvent molecule is pointed towards the metal ions, with a corresponding distance of 2.39 Å and 2.38 Å for 2_Ca–N2 and 3_Ca–N2, respectively. However, once the molecule has been deprotonated by the N₂²⁻ unit, the resulting electron-rich C atom approaches (Ca–C distance equals 3.42 Å and 3.39 Å in 2_Ca–N2 and 3_Ca–N2, respectively; 2.54 Å and 2.56 Å in 2P_Ca and 3P_Ca, respectively).

Then, we investigated the reactivity of the Mg systems, namely e³2_Mg–N2 and e³3_Mg–N2, towards N₂ protonation. As previously reported, no reactivity toward N₂ reduction from Mg(I) compounds has ever been reported so far. The research for a protonation product of the N₂ molecule by one THP/THF ligand led to the identification of an intermediate species in both cases that only exists in the singlet state (e¹2I_Mg/e¹3I_Mg, shown in Fig. S3†) and in which the oxygen atom of THP/THF still interacts with Mg. In more detail, in e¹2I_Mg both the oxygen and deprotonated carbon atoms coordinate to the Mg ion (Mg–C(THP) = 2.20 Å, Mg–O(THP) = 2.24 Å), in analogy to the Ca-based systems, while in e¹3I_Mg only the oxygen atom of THF binds to the metal (Mg–O(THF) = 2.02 Å). Such an intermediate structure is rather unstable for both THP and THF systems (38.9 and 41.6 kcal mol⁻¹ less stable than the reagents e³2_Mg–N2 and e³3_Mg–N2, respectively, see Fig. 6). So both e¹2I_Mg and e¹3I_Mg can evolve to a more stable product (e¹2P_Mg and e¹3P_Mg, shown in Fig. 6) in which only the deprotonated carbon atom of THP/THF coordinates with the Mg ion (Mg–C(THP) = 2.20 Å, Mg–O(THP) = 2.83 Å; Mg–C(THF) = 2.18 Å, Mg–O(THF) = 2.82). In this product, the proton of the newly formed NNH⁻ unit points opposite to the proton-donating solvent molecule, with a C(THP)–H(NNH) distance of 4.42 Å in e¹2P_Mg and a C(THF)–H(NNH) distance of 4.57 Å in e¹3P_Mg This species is represented by a singlet ground state, which turned out to be 12–13 kcal mol⁻¹ more stable than its triplet state counterpart (see Fig. S4†). The overall protonation reaction to form e¹2P_Mg or e¹3P_Mg is 26.8 and 32.2 kcal mol⁻¹ endergonic, respectively. Overall, these results indicate that the reaction coordinate associated with N₂ protonation for the Mg-containing systems is more complicated and more energy-demanding than for their Ca counterparts. Indeed, in Mg systems, on scanning the triplet potential energy surface along the reaction coordinate for the solvent-to-N₂ proton transfer, it can be assumed that the reaction requires an activation energy of at least 40 kcal mol⁻¹ in the case of THP and of at least 45 kcal mol⁻¹ in the case of THF. These barriers are substantially higher than those seen for Ca compounds. On the singlet potential energy surface, instead, along the reaction coordinate for each Mg system we find an intermediate (which does not exist in the triplet state) that is 38.9 or 41.6 kcal mol⁻¹ less stable than the reactants for THP and THF, respectively, so for the presence of both THF and THP, the reactions are more unfavorable than for the Ca complexes.

Fig. 6 Energy profiles associated with the N₂ protonation reaction for e2_Mg–N2 and e3_Mg–N2, considering both singlet and triplet states. Reaction energies (top) and the final product (bottom) are reported for each species.

3. Conclusion

In the present work we performed a computational analysis of N₂ binding and activation by low valent Mg(I) or Ca(I) BDI complexes. The main observations can be summarized as follows:

- The N₂ coordination mode to the Ca(I) and Mg(I) complexes is substantially different. Ca(I) systems bind N₂ in a side-on manner. Here, the nitrogen molecule is equidistant from the two Ca(I) atoms, and the N–N axis is perpendicular to the Ca–Ca one. Instead, in the case of Mg(I) systems, the nitrogen molecule bridges the two metal-alkaline earth atoms with an end-on type configuration, and these species are characterised by a triplet ground state. Interestingly, coupling of the structural properties of end-on bridging nitrogen complexes to the preference of a triplet ground state has already been evidenced in the literature for Mo-containing or Sc-containing compounds.^58,59

- N₂ binding to Ca(I) systems is predicted to be more energetically preferred than to Mg(I). Molecular orbital analysis allowed the rationalization of this difference, which can be mainly ascribed to the participation of d orbitals in the Ca(I)–N₂ interaction, but not in the Mg(I)–N₂ one. This suggests a higher covalent character for the AE(I)–N₂ interaction in the case of Ca than Mg.

- While in the case of Ca(I) both N₂ binding and subsequent protonation occur on the singlet potential energy surface, a marked spin-crossover behavior (singlet–triplet–singlet) has been observed in the case of Mg(I) reactivity. Indeed, a first change in the spin-state (from singlet to triplet) occurs upon N₂ binding, and a second one (from triplet to singlet) occurs upon N₂ protonation by either THF or THP. Furthermore, we showed that N₂ protonation by either THP or THF ligands is energetically prohibited for Mg systems, in contrast to what has been observed for Ca.

Overall, these results added novel insights into the current (limited) knowledge on the role of different AE metals in N₂ activation/protonation, with potential implications for future innovative AE metal-based N₂RR strategies. The present work is specific and limited to the Mg vs. Ca comparison, but upcoming investigations on other low valent alkaline earth metals (such as Sr and Ba) would help to further rationalize the relationship between the electronic structures of AE metals and their reactivity towards the activation and conversion of recalcitrant small molecules. Moreover, compounds of the Mg(0) type as well as low-valent magnesium–calcium complexes will be the object of future theoretical investigations since these systems with BDI seem to be able to activate inert molecules.^60,61

4. Computational methods

Calculations were performed within the framework of density functional theory (DFT) with the TURBOMOLE suite of programs,⁶² and in particular with the 7.1 version of such software. Geometry optimisations were obtained using the BP86^63,64 functional together with the def2-SVP basis set.⁶⁵ Dispersion correction was taken into account by using the Grimme DFT-D3 method with Becke–Johnson damping (BJ).⁶⁶ The nature of each optimized structure as the genuine minimum was confirmed by vibrational frequency calculations. As expected (in light of the large size and complexity of the molecular systems considered), some spurious imaginary vibrations, close to or below 100i cm⁻¹, occurred. These soft modes (all corresponding to the torsional motions of the terminal methyl groups belonging to BDI ligands) are products of inaccuracies derived from numerical integration procedures employed in actual DFT methods and were thus ignored.⁶⁷ Solvent effects were included by running single-point calculations on the optimised models soaked in the COSMO continuum solvent representation⁶⁸ at the dielectric constant of the apolar THF solvent (ε = 7.4257). The energetics reported in the main text were refined at the B3LYP-D3(BJ)/def2-TZVPP level.^69,70 For all the optimised models, atomic charges were computed by means of the natural population analysis approach.⁷¹ Orbital visualizations were produced using Chimera.⁷²

Author contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The computations were performed on computer resources provided by CINECA as part of the agreement with the University of Milano-Bicocca.

References

1. H.-P. Jia and E. A. Quadrelli, Chem. Soc. Rev., 2014, 43, 547–564.
2. A. J. Martín, T. Shinagawa and J. Pérez-Ramírez, Chem, 2019, 5, 263–283.
3. S. F. McWilliams and P. L. Holland, Acc. Chem. Res., 2015, 48, 2059–2065.
4. L. C. Seefeldt, Z.-Y. Yang, D. A. Lukoyanov, D. F. Harris, D. R. Dean, S. Raugei and B. M. Hoffman, Chem. Rev., 2020, 120, 5082–5106.
5. Y. Roux, C. Duboc and M. Gennari, ChemPhysChem, 2017, 18, 2606–2617.
6. R. R. Schrock, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 17087–17087.
7. A. Allen and C. Senoff, Chem. Commun., 1965, 621–622.
8. A. D. Allen, F. Bottomley, R. O. Harris, V. Reinsalu and C. Senoff, J. Am. Chem. Soc., 1967, 89, 5595–5599.
9. G. Jeerh, M. Zhang and S. Tao, J. Mater. Chem. A, 2021, 9, 727–752.
10. F. Du, W. Sun, H. Luo and C. M. Li, Mater. Rep.: Energy, 2022, 100163.
11. J. Chatt, A. Pearman and R. Richards, Nature, 1975, 253, 39–40.
12. J. Chatt, A. J. Pearman and R. L. Richards, J. Chem. Soc., Dalton Trans., 1977, 1852–1860.
13. J. Chatt, J. R. Dilworth and R. L. Richards, Chem. Rev., 1978, 78, 589–625.
14. M. Hidai, K. Tominari, Y. Uchida and A. Misono, J. Chem. Soc. D, 1969, 1392–1392.
15. D. V. Yandulov and R. R. Schrock, Science, 2003, 301, 76–78.
16. N. C. Smythe, R. R. Schrock, P. Müller and W. W. Weare, Inorg. Chem., 2006, 45, 7111–7118.
17. W. W. Weare, R. R. Schrock, A. S. Hock and P. Müller, Inorg. Chem., 2006, 45, 9185–9196.
18. R. R. Schrock, Acc. Chem. Res., 2005, 38, 955–962.
19. R. R. Schrock, Catalysis Without Precious Metals, 2010, pp. 25–50.
20. L. A. Wickramasinghe, T. Ogawa, R. R. Schrock and P. Muller, J. Am. Chem. Soc., 2017, 139, 9132–9135.
21. M. J. Chalkley, M. W. Drover and J. C. Peters, Chem. Rev., 2020, 120, 5582–5636.
22. J. S. Anderson, J. Rittle and J. C. Peters, Nature, 2013, 501, 84–87.
23. J. Rittle and J. C. Peters, J. Am. Chem. Soc., 2016, 138, 4243–4248.
24. C. M. Johansen, E. A. Boyd and J. C. Peters, Sci. Adv., 2022, 8, eade3510.
25. J. Fajardo Jr. and J. C. Peters, J. Am. Chem. Soc., 2017, 139, 16105–16108.
26. S. Kuriyama, K. Arashiba, H. Tanaka, Y. Matsuo, K. Nakajima, K. Yoshizawa and Y. Nishibayashi, Angew. Chem., Int. Ed., 2016, 55, 14291–14295.
27. Y. Nishibayashi, Nitrogen fixation, Springer, 2017, vol. 60.
28. Y. Nishibayashi, Transition Metal-Dinitrogen Complexes: Preparation and Reactivity, John Wiley & Sons, 2019.
29. H. Tanaka, K. Arashiba, S. Kuriyama, A. Sasada, K. Nakajima, K. Yoshizawa and Y. Nishibayashi, Nat. Commun., 2014, 5, 1–11.
30. K. Arashiba, E. Kinoshita, S. Kuriyama, A. Eizawa, K. Nakajima, H. Tanaka, K. Yoshizawa and Y. Nishibayashi, J. Am. Chem. Soc., 2015, 137, 5666–5669.
31. P. J. Hill, L. R. Doyle, A. D. Crawford, W. K. Myers and A. E. Ashley, J. Am. Chem. Soc., 2016, 138, 13521–13524.
32. K. C. MacLeod and P. L. Holland, Nat. Chem., 2013, 5, 559–565.
33. C. J. Van der Ham, M. T. Koper and D. G. Hetterscheid, Chem. Soc. Rev., 2014, 43, 5183–5191.
34. A. J. Ryan, S. G. Balasubramani, J. W. Ziller, F. Furche and W. J. Evans, J. Am. Chem. Soc., 2020, 142, 9302–9313.
35. H. Xie, L. Shi, X. Xing and Z. Tang, Phys. Chem. Chem. Phys., 2016, 18, 4444–4450.
36. M.-A. Légaré, G. Bélanger-Chabot, R. D. Dewhurst, E. Welz, I. Krummenacher, B. Engels and H. Braunschweig, Science, 2018, 359, 896–900.
37. M.-A. Légaré, M. Rang, G. Bélanger-Chabot, J. I. Schweizer, I. Krummenacher, R. Bertermann, M. Arrowsmith, M. C. Holthausen and H. Braunschweig, Science, 2019, 363, 1329–1332.
38. M.-A. Légaré, G. Bélanger-Chabot, M. Rang, R. D. Dewhurst, I. Krummenacher, R. Bertermann and H. Braunschweig, Nat. Chem., 2020, 12, 1076–1080.
39. P. Schenk and G. Brauer, Handbook of Preparative Inorganic Chemistry, 1963, vol. 3.
40. R. C. Spiker Jr., L. Andrews and C. Trindle, J. Am. Chem. Soc., 1972, 94, 2401–2406.
41. C. A. Thompson, L. Andrews and R. D. Davy, J. Phys. Chem., 1995, 99, 7913–7924.
42. G. Deng, S. Pan, G. Wang, L. Zhao, M. Zhou and G. Frenking, Angew. Chem., Int. Ed., 2020, 59, 10603–10609.
43. G. Deng, S. Pan, G. Wang, L. Zhao, M. Zhou and G. Frenking, Angew. Chem., Int. Ed., 2020, 59, 18201–18207.
44. Q. Wang, S. Pan, S. Lei, J. Jin, G. Deng, G. Wang, L. Zhao, M. Zhou and G. Frenking, Nat. Commun., 2019, 10, 1–8.
45. B. Rösch, T. Gentner, J. Langer, C. Färber, J. Eyselein, L. Zhao, C. Ding, G. Frenking and S. Harder, Science, 2021, 371, 1125–1128.
46. T.-T. Liu, D.-D. Zhai, B.-T. Guan and Z.-J. Shi, Chem. Soc. Rev., 2022, 51, 3846–3861.
47. X. Wu, L. Zhao, J. Jin, S. Pan, W. Li, X. Jin, G. Wang, M. Zhou and G. Frenking, Science, 2018, 361, 912–916.
48. I. Fernández, N. Holzmann and G. Frenking, Chem. – Eur. J., 2020, 26, 14194–14210.
49. M. Zhou and G. Frenking, Acc. Chem. Res., 2021, 54, 3071–3082.
50. C. Jones, Nat. Rev. Chem., 2017, 1, 1–9.
51. A. Stasch and C. Jones, Dalton Trans., 2011, 40, 5659–5672.
52. S. P. Green, C. Jones and A. Stasch, Science, 2007, 318, 1754–1757.
53. Y. Xie, H. F. Schaefer III and E. D. Jemmis, Chem. Phys. Lett., 2005, 402, 414–421.
54. S. Krieck, L. Yu, M. Reiher and M. Westerhausen, Eur. J. Inorg. Chem., 2010, 2010, 197–216.
55. T. X. Gentner, B. Rösch, G. Ballmann, J. Langer, H. Elsen and S. Harder, Angew. Chem., 2019, 131, 617–621.
56. F. Studt and F. Tuczek, J. Comput. Chem., 2006, 27, 1278–1291.
57. T. Husch, L. Freitag and M. Reiher, J. Chem. Theory Comput., 2018, 14, 2456–2468.
58. J. J. Curley, T. R. Cook, S. Y. Reece, P. Muller and C. C. Cummins, J. Am. Chem. Soc., 2008, 130, 9394–9405.
59. D. H. Woen, G. P. Chen, J. W. Ziller, T. J. Boyle, F. Furche and W. J. Evans, J. Am. Chem. Soc., 2017, 139, 14861–14864.
60. C. Jones, Nature, 2021, 592, 687–688.
61. J. Mai, B. Rösch, N. Patel, J. Langer and S. Harder, Chem. Sci., 2023, 14, 4724–4734.
62. F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91–100.
63. A. D. Becke, Phys. Rev. A, 1988, 38, 3098.
64. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822.
65. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
66. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
67. Y. Xie, H. F. Schaefer and R. B. King, J. Am. Chem. Soc., 2000, 122, 8746–8761.
68. A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235.
69. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
70. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
71. A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746.
72. E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dt00945a

---