 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantitative Raman microscopy to describe structural organisation in hollow microcrystals built from silicon catecholate and amines†
Victor V.
Volkov
 a,
Toby J.
Blundell
a,
Toby J.
Blundell
 b,
Stephen
Argent
b,
Stephen
Argent
 c and
Carole C.
Perry
c and
Carole C.
Perry
 *a
*a
aInterdisciplinary Biomedical Research Centre, School of Science and Technology, Nottingham Trent University, Clifton Lane, Nottingham NG11 8NS, UK. E-mail: carole.perry@ntu.ac.uk
bDepartment of Chemistry and Forensics, School of Science and Technology, Nottingham Trent University, Clifton Lane, Nottingham NG11 8NS, UK
cSchool of Chemistry, University of Nottingham, University Park, Nottingham NG7 2RD, UK
First published on 4th May 2023
Abstract
Macroscopic scale hollow microcrystals are a promising group of materials for gas and liquid uptake as well as sensing. In this contribution we describe the structure of hollow hexagonal cross-section crystals formulated as salts of a silicon catecholate anion and a tetramethylenediamine (TEMED) cation. Using a combination of X-ray single crystal diffraction, Raman spectroscopy and quantum chemistry we explore the structural properties of the hollow microcrystals. With the X-ray structural data as a starting point and assisted with quantum chemistry we compute Raman tensors to fit polarisation sensitive spectral responses and predict the orientation and packing of unit cells in respect to the long and short axis of the synthesised microcrystals. Using these newly developed methods for predicting molecular Raman responses in space with dependence on local orientation, we present the quantitative analysis of experimental Raman images of both hexagonal and tetragonal cross section hollow microcrystals formed from silicon catecholate anions using different amines as counterions. We describe the distributions of chemical components at the surfaces and edges of microcrystals, address the effect of catcholate hydrophobicity on water uptake and discuss possible strategies in chemical and post-assembly modifications to widen the functional properties of this group of environmentally friendly silicon organic framework (SOF) materials.
Introduction
As molecular porosity can be used to provide storage, separation and opportunities for controlled catalysis, there are many materials being investigated for these applications. One such material of continued interest is metal–organic frameworks (MOFs).1,2 At the same time, in the search for sustainability, green molecular self-assembly is one of the fastest growing areas of research in materials chemistry leading to the production of biologically inspired nanomaterials.3 Within this context, self-assembly of organic components has proved important in the generation of structurally organised amorphous silicas.4 Extensive studies of silica formation have been performed using biomolecule isolates (proteins and long chain polyamines) as well as simpler chemical mimics such as amino acids, peptides and amines.5,6Among various chelators, azamacrocycles are of a special attention: they form stable complexes with transition metals and lanthanide ions.7,8 Furthermore, research on azamacrocycle complexes has led to the development of a new generation of abiotic host molecules that contain a signalling or responsive functional group enabling the development of molecular sensors.8,9 Such complexes are reported to demonstrate metallo–organic frameworks with rich diversity in zeolite-like architectures,10–14 hollow spheres,15 hollow nano-fibres,16 and tubular structures,17,18 which may offer functional modular porosity to compete with transition and rare metal containing MOFs. In this respect, it is important to note that azamacrocyles are able to form complex architectures when complexed with silicon catecholate anions.19
In a previous study,19 we investigated the effect of amine molecular architecture on the formation of novel silica morphologies. We showed that, using the precursors 1,4,8,11-tetraazacyclotetradecane (cyclam) and dipotassium tris(1,2-benzenediolato-O,O′)silicate (KSicat), a novel layered crystalline structure in the form of hollow tetragonal needles can be obtained. We further showed that when the nitrogen containing component was changed to a diamine with different linker lengths, hexagonal hollow rods, hexagonal rods or hexagonal plates could be formed.
The azamacrocycle hollow microcrystals are a rich group of novel materials with varied macroscopic structural expressions, whose structure is readily controlled during their preparation. However, to gain a systematic perspective in the engineering of novel absorbing or sensory porous systems based on azamacrocycles, it is important to learn how to relate macroscopic structural properties with local molecular orientation, the character of assembly and the chemical nature of surfaces. This is necessary for better prediction of sizes and morphology of microstructures, controlling the degree of crystallinity/poly-crystallinity, and regulate uptake capacity as well as structural stability (upon uptake of gases and/or liquids). To answer the challenge, in the present contribution we use experimental Raman spectroscopy and microscopy to explore structural properties of tris-catecholate silicon N,N,N′N′-tetramethylethylenediamine (TCS-TEMED) and TCS-cyclam hollow microcrystals.
Examination of polarization properties of nonelastic scattering of light in crystals20 accompanied the first report on Raman in gasses and in liquids.21 In recent years, there has been systematic progress in Raman microscopy techniques to characterise poly-crystalline matter,22 and in analytical applications of Raman mapping to identify functionality, for example, in hydration diffusion within MOF microcrystals.23 Based on previous studies, to develop an understanding of the orientation of molecular components within the microcrystals studied here, we (i) use a quantum mechanics/molecular mechanics (QMMM) approach to compute Raman polarization tensors for structural elements specific to the unit cell as identified from our X-ray studies; (ii) express Raman intensities as functions of {θ,ϕ,ψ} Euler orientation angles to operate on the unit cell until there is a match of relative intensities, as observed in polarization specific Raman experiments; (iii) build a macroscopic hexagonal hollow assembly using the unit cells oriented according to the extracted Euler angles to confirm that images modelled for such structures using computed Raman tensors would agree with experimental Raman microscopy images; and (iv) discuss the nature of the vibrations we image using Raman microscopy. The outcome of these studies is that we describe molecular properties at the surfaces and edges of the crystals, address hydration when microcrystals are exposed to water and discuss further efforts in functional engineering.
Materials and methods
Synthesis
To prepare microcrystals, first, KSiCat (TCS for short) (0.14 g) was dissolved in 7.76 mL of distilled and deionised (dd) ice-cold water to give a 30 mM solution. Second, we prepare 2 ml solutions of TEMED or cyclam in ice cold dd water at a Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N ratio of 10
N ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (0.0015 g, 7.5 μM), and the pH of the TEMED and cyclam solutions was adjusted to pH 6.8 using 2 M HCl (240 μL). Then, we mixed TCS with TEMED or cyclam solutions and kept the mixtures at a temperature between 5 and 20 °C. The lower temperature was used to generate crystals of the required quality for single crystal X-ray structure determination. Any precipitate was isolated by centrifugation (5000g) after 60 minutes, washed with water (40 mL) followed by centrifugation 3 times (5000g) and the material lyophilised (Virtis freeze dryer).
1 (0.0015 g, 7.5 μM), and the pH of the TEMED and cyclam solutions was adjusted to pH 6.8 using 2 M HCl (240 μL). Then, we mixed TCS with TEMED or cyclam solutions and kept the mixtures at a temperature between 5 and 20 °C. The lower temperature was used to generate crystals of the required quality for single crystal X-ray structure determination. Any precipitate was isolated by centrifugation (5000g) after 60 minutes, washed with water (40 mL) followed by centrifugation 3 times (5000g) and the material lyophilised (Virtis freeze dryer).
Single crystal structure determination
Single crystal X-ray diffraction measurements were performed in Experimental Hutch 1 (EH1) of Beamline I19, at Diamond Light Source.24 The data were collected at a wavelength of 0.6889 Å on a Fluid Film Devices 3-circle fixed-chi diffractometer using a Dectris Pilatus 2M detector. The crystal was mounted on a MiTeGen micromount using a perfluoropolyether oil, and cooled for data collection by a Cryostream nitrogen-gas stream.25 The collected frames were integrated using XIA2 software,26–30 and the data were corrected for absorption effects using AIMLESS,31 an empirical method.All non-H atoms were located using direct methods,32 and difference Fourier syntheses. Hydrogen atoms were placed and refined using a geometric riding model. All fully occupied non-H atoms were refined with anisotropic displacement parameters, unless otherwise specified. Crystal structures were solved and refined using the Olex2 software package33,34 with SHELXL (structure refinement)35 and SHELXT (structure solution).36 CIF files were checked using checkCIF37 CCDC 2245748† contains the supplementary data for TCS-TEMED. The previously published data for the corresponding cyclam complex19 can be obtained free of charge following the on-line data request service of the Cambridge Crystallographic Data Centre. Further details are provided in the ESI.†
Polarised Raman spectroscopy
Raman spectra were obtained for TCS-TEMED crystals using a LabRAM HR Evolution confocal Raman microscope (HORIBA UK Ltd at Northampton) with a 100× (0.8 NA, 3.4 mm working distance) and excitation at 530 nm. The spectra are taken with the polarisation along and across the long axis of a selected microcrystal. Nine (parallel and perpendicular spectra) datasets were taken at different positions of three microcrystals.Raman microscopy
Raman studies were conducted on both TCS-TEMED and TCS-cylcam crystals using a DXR microscope (Thermo Fisher Scientific, Madison, Wisconsin), equipped with 100× microscopy objectives. The spectral resolution was 2 cm−1 according to the instrumental limit of the microscope operated with a 25 μm confocal pin-hole. Raman measurements were made using 532 nm excitation radiation of 2 mW. Raman activities of the selected microcrystals were sampled with a spatial resolution of 1 micron in both directions of the imaging plane. As a Raman microscopy scan collects a set of spectra specific for specified positions in the image plane; to present Raman microscopy images specific to spectral signatures of interest, we processed each spectrum to extract amplitudes of spectral components of interest. Being dependent on the nature of the vibration (normal) modes, abundance of contributing structural species, orientation and degree of orientational variance at the sampling sites, the extracted amplitudes are informative on molecular structural distributions at interfaces. To approach this, we conducted reconstructions of Raman activity microscopy images (RAM) specific to selected vibrations according to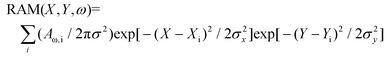 | (1) |
Here, we sum image projections of two-dimensional Gaussian source functions over all the defined sites i. Setting σx2 = σy2 = 0.5 μm2 provides the spatial full width of a source function. Xi and Yi describe the position of the projection of the site i into the image plane. X and Y variables are sample distances from the site i in terms of the dimensions of detector pixels or displacements of a pinhole. Raman difference images are taken after normalizing the images (reconstructed for different wavelengths) by the sums of amplitudes at the sites i, in the image plane. As a result, the difference images describe spatial anti-correlation tendencies: intensity is zero at a site where the selected Raman activities contribute equally.
Computational (Density functional theory (DFT)) studies were conducted using the B3LYP functional38,39 within the Gaussian 09 program package.40 For quantum chemistry studies we use atomic coordinates in respect to monoclinic unit cells as anticipated from the current study (TCS-TEMD) and from our previous X-ray studies (TCS-cyclam).19 To model structural, electronic and optical properties of TCS-TEMED and TCS-CYCLAM microstructures, we adopted a two-layer ONIOM approach.41,42 Specifically, for the TCS-TEMED system, the monoclinic supercell is constructed to include 3, 3 and 4 unit-cells along the three dimensions of the monoclinic space. The paired stack of unit cells to occupy the internal part of the supercell is selected to employ b3lyp/6-31G(d) level of theory, while the rest of the units are treated using amber parametrization.40 The frequencies of the computed normal modes are scaled with factor to vary from 0.95 to 0.97, depending on the frequency range of the corresponding resonances, as detected experimentally.
Theory of Raman responses under microscopic resolution DFT calculations allow extraction of the Raman tensor, α′q = ∂qα, of a generic normal mode q (α is the polarizability tensor), expressed with respect to the molecular frame reference system. With an initial orientation, in which the long structural axis is along the Z-axis of the laboratory frame, the Raman response of a normal mode can be expressed as an orientation function using a rotation transformation with Euler angles {θ, ϕ, ψ}:43,44
 | (2) |
 | (3) |
| RtM = (RMx, RMy, RMz) | (4) |
Results
In a previous study we investigated the role of cyclam in the formation of novel TCS-CYCLAM tetragonal hollow crystalline structures, where we were able to tune the dimensions according to the pH of the reaction medium.19 X-ray studies of TCS-CYCLAM showed the asymmetric unit consists of one slightly distorted octahedral silicon(IV) atom coordinated by three catechol ligands as well as one doubly protonated cyclam and one water molecule: [(C6H4O2)3Si][C10H26N4]·H2O. We now confirm analogous, but hexagonal hollow structuring for TCS microcrystals with N,N,N′N′-tetramethylethylenediamine, TCS-TEMED.In Fig. 1 and 2 we present results of X-ray studies: TCS-TEMED crystallised in the monoclinic crystal system in the space group C2/c, as specified in Fig. 2. The solid-state structure consists of a six-coordinate silicon atom with three catechol ligands connected via hydrogen bonds to TEMED. The structure is similar to our previously reported cyclam containing analogue [(C6H4O2)3Si][C10H26N4]·H2O,19 albeit with considerable differences in crystal packing due to the smaller size of TEMED compared to cyclam (see below). The silicon catecholate cations are connected through hydrogen bonds from each of the TEMED nitrogen atoms N(1)–H(1)⋯O(3) and N(2)–H(2)⋯O(3), Fig. 1. Both ionic components of the structure are positioned over symmetry elements with half of each in the asymmetric unit. There is also disorder of the TEMED molecule over two positions resulting in the two similar hydrogen bond distances, Table 1. Bond lengths and angles are similar to those previously reported,19 for details see Table S1.† In an almost analogous arrangement as Si–Cyclam the structure of [(C6H4O2)3Si][C6H18N2] consists of distinct layers of silicate and TEMED molecules along the crystallographic a/b axes, with a hydrogen bond network between the TEMED and silicate molecules of individual layers. A hydrogen bond network exists along the crystallographic c axis between the TEMED amine N–H and catechol oxygen atoms with the difference from Cyclam being that only a single hydrogen bonding interactions exists from either side of the silicate (as opposed to two for Cyclam). The crystals of TSC-TEMED and TSC-cyclam both contain macroscopic pores: while the complex with cyclam is tetragonal, Fig. S1,† the TEMED assembly is of hexagonal shape, Fig. 3B. At the same, sub-micron granulation at the microcrystal wall suggests the presence of amorphous and tetragonal nucleating domains. The role of a kinetically favourable metaphase has been discussed for zeolite structuring.47 Further, competition of a kinetically favourable tetragonal phase with a thermodynamically stable hexagonal phase has been reported for polymeric crystallite structures.48 Competition of tetragonal and hexagonal phases depends on lateral chain interactions, according to possible structural mismatches and polar interactions. In respect to the latter, X-ray data indicate a two-fold larger number of Hydrogen bonds for TCS-CYCLAM than for TCM-TEMED, while theory predicts a larger polarity on atoms of TCS-CYCLAM than for the TCS-TEMED system (see Chart S1 in the ESI† while comparing to data as reported in ref. 19). These may suggest stronger inter-unit bindings in the TCS-CYCLAM structure formed upon kinetically driven nucleation, and perhaps explains why TCS-CYCLAM can be formed over a wider pH range than TCS-TEMED.19
 | ||
| Fig. 2 (A) Crystal packing for a single layer of [(C6H4O2)3Si][C6H18N2] viewed along the crystallographic c axis. Both disordered components for TEMED are shown. (B) TCS-TEMED crystal and (C) TCS-cyclam crystal packing viewed face on to the Si-catecholate moiety. As a result of the smaller size of TEMED compared to cyclam considerable differences in crystal packing arrangements are observed. Whereas the previously reported cyclam19 containing compound crystallised with face-to-face stacks of Si-catecholate and cyclam in an ordered arrangement, the smaller size of TEMED results in a more staggered orientation: see panel (A). | ||
 | ||
| Fig. 3 (A) TCS-TEMED molecular structure from X-ray diffraction, (B) SEM of TCS-TEMED typical microcrystals, scale bar = 4 micron; (C) graphical representation for the two-layer ONIOM crystalline clusters; thin grey lines and thicker black lines show the structural units treated at classical and quantum levels respectively; (D) comparison of experimentation-polarized Raman response with ONIOM DFT analysis for TCS-TEMED in the low, middle and high frequency range. Indices at experimental resonances indicate spectral modes used for Raman microscopy imaging; (E1) light microscope image (collected on crystals used for Raman microscopy) of hollow TCS-TEMED microcrystal, scale bar = 10 micron. (E2–E9) Differences of normalised Raman microscopy images reconstructed at Raman wavenumbers, as indicate. Fig. S4 and S5 in the ESI† present more detailed data on Raman imaging for TCS-TEMED and TCS-cyclam, respectively. | ||
| Donor–acceptor | Distance (esd) | Acceptor–H | Distance | Donor–H–acceptor | Angle |
|---|---|---|---|---|---|
| N(1)–O(3) | 2.76(4) Å | O(3)–H | 1.84 Å | ∠N(1)HO(3) | 152.21° |
| N(2)–O(3)2 | 2.87(3) Å | O(3)2–H | 1.92 Å | ∠N(2)HO(3)2 | 157.11° |
To approach structural analysis using spectral diagnostics, in Fig. 3D we compare experimental non-polarised Raman spectra of TCS-TEMED with computed isotropic spectra. In the ESI†, we provide graphical presentations of the computed normal modes of TCS-TEMED and TCS-cyclam, see Fig. S2 and S3,† respectively. Most of the peaks arise from the aromatic complexing with Si-catecholate ion. Specifically, theory predicts that Raman scattering at 825 cm−1, is due to antisymmetric deformations of aromatic rings admixed with in-plane CCH bendings. Raman scattering at 1020 cm−1 arises from localized deformations of aromatic rings admixed with CCH bendings. This peak is narrow and thus makes it suitable as a reference marker for theoretical studies. Next, our computations suggest that Raman scattering at 1590 cm−1 involves symmetric deformations of aromatic rings. In the higher frequency range, the scattering peak 2970 cm−1 is ascribed to CH stretchings of the amine component, while the activities at 3035 and 3060 cm−1 are due to antisymmetric and symmetric CH stretchings of aromatic moieties. In Fig. 3D we index these six resonances and use the intensities of these transitions to reconstruct Raman images and Raman difference images (Fig. 3E), using approaches as described in the Materials and Methods.
To model molecular orientations and relative packing in respect to the physical shape of the micro-crystals, we explore the results of polarisation specific Raman studies: see Fig. 4. To account for variations in structure within and between individual crystals, we took 9 acquisitions of polarization specific Raman spectra for three TCS-TEMED microcrystals at three different spots. Each acquisition (taken at the same spot) consists of two spectra: the first spectrum is for polarization planes of the exciting and of the sampled field along the long axis of a microcrystal (II); the second spectrum is when polarization planes of the exciting and of the sampled fields are at right angles to the long axis of a microcrystal (⊥). Taking several spectra is important because we attempt to characterise complex crystalline objects.
 | ||
| Fig. 4 (A) Polarization Raman studies of TCS-TEMED hollow microcrystals. Pink and cyan regions describe the variance of Raman activities sampled at the indicated frequencies under parallel and perpendicular experimental geometries respectively. Black and blue lines are the mean intensities sampled under parallel and perpendicular geometries respectively; see description in the main text. Black circles show intensities computed to compare with the experimental data. (B) graphical representations of a single cell with a modelled TCS-TEMED structural components oriented in line with the results of the polarisation sensitive Raman studies; (C) a three layered horizonal slab of cells (magenta colored) packed under the extracted orientation; (D) computed hollow hexagonal assembly using cells packed under the extracted orientation, where the top magenta colored region is to simulate Raman difference images as shown in Fig. 3E2–E9; (E) modelling of Raman difference images using computed Raman responses for the top (magenta colour) region of a theoretical hexagonal hollow assembly constructed using packing of unit cells under orientation as predicted by polarisation sensitive Raman studies. | ||
To describe variance ranges, each pair of spectra was normalised by the intensity of the Raman signal at 1021 cm−1 sampled under parallel setting. Accordingly, as one may see in Fig. 4A, the III intensity at 1021 cm−1 is equal to 1 and without variance. In respect to this reference, the pink and the cyan colored regions describe the variance regions of Raman activities sampled at the indicated frequencies under parallel and perpendicular experimental geometries, respectively. The black and blue lines in Fig. 4A are the mean intensities sampled under parallel and perpendicular geometries, respectively.
Making the Raman scattering at 1021 cm−1 as a reference is due to the more conservative and resolved nature of this response: DFT studies for the model system of a stack of two units embedded in a crystalline environment, as described in the Materials and Methods, suggest just one mode dominates in the response of the modelled structure: we show graphical presentation of the mode (number 193) in the ESI.† In reality, in a crystal there are many Raman modes active at the frequency. However, since the experiment shows the resonance is narrow, we anticipate the theoretical prediction to be representative as a helpful reference.
Next, we use eqn (2)–(4), to compute Ixx and Iyy Raman intensities of normal modes of interests in the {Ψ, Φ} angular space of orientation for Θ to vary from 0° to 90°. Different normal modes demonstrate different intensity ratios (of Ixx/Iyy), when excited and detected under orthogonal directions in respect to a selected structural orientation. Here, we keep in mind the parallel and perpendicular polarization setting in respect to the long axis of a crystal as for the polarization sensitive experiment. The three Euler angles are varied in the search for such an orientation, when the intensity ratio Ixx/Iyy computed for several normal modes would best match the tendencies for the corresponding resonances as demonstrated by experiment. For the task, initially we choose normal modes, which demonstrate high contrast, a high ratio I⊥/III. The strong difference of intensities under parallel and perpendicular polarisation for the Raman resonances at 3035 and 3060 cm−1 were particularly helpful. Furthermore, in Fig. S7A–S7D (the ESI†), we use color filled regions to indicate the {Ψ, Φ} angular regions for Θ = 60°, where the ratio IXX/IYY for the computed intensities at 825, 1020, 3035 and 3060 cm−1, respectively, are close to the observed experimental data (and would fall within the variance ranges denoted by the pink and cyan coloring in Fig. 4A).
Following the procedure, we extract a plausible orientation according to Θ = 60° ± 10°, Ψ = 40° ± 10°, and Φ = 250° ± 10°. Black circles in Fig. 4A present computed intensities specific to the orientation. Here it is important to note that the suggested extract is a best match to explain the general tendencies but is not perfect and cannot be for two reasons: azamacrocycle hollow structures are not single crystals but polycrystalline assemblies; Raman tensors are computed according to the level of theory and, in our case, for example, may not account the effects of electronic resonances. Specifically, the crystals have greyish-blue colorations. Therefore, the onset of UV electronic resonances may influence expressions of Raman tensors. Such higher order effects, however, are outside the scope of this study.
The extracted orientation instructs that for a crystal with its long axis parallel to the to the laboratory XY plane, the nitrogen–nitrogen structural vector of the two TEMED components (which are part of the representative structural component: as shown in Fig. 3C) should be nearly parallel to the laboratory XY plane; and the silicon–silicon axis to direct the TCS aromatic groups slightly upward (Θ = 60°) along the positive directions of the X and Y laboratory axes, and toward the edge of a crystal: see the graphical presentation at the right side in Fig. 4. The described orientation tendency is important to discuss model images and structure–function consequences. To approach this, next, using the extracted orientation, we pack unit cells in a miniature 3D block and trim out those which do not fit a hexagonal hollow structure geometry as observed experimentally: see Fig. 3B. Imposing geometric limits, we may select the cells of the upper layer of the modelled structure (see the magenta-colored segment in Fig. 4) to compute Raman difference images according to DFT Raman tensors and intensities for the extracted orientation. Here, practically, the upper region of the modelled hexagonal structure (the magenta-colored slab in Fig. 4) is the main component contributing into imaging due to reflection and scattering. According to both the extracted orientation and the modelled structural region, in Fig. 4E2–4E9 we present computed Raman difference images reconstructed using narrow source functions to discuss the experimental Raman difference images, Fig. 3E2–3E9.
To distinguish roles of molecular moieties at different structural sites according to the computed Raman images, we need to model the spatial distribution of Raman intensity projected onto the image XY plane for a selected normal mode of a molecule under a pre-selected orientation. For this task we adopt that experimentally a spatial distribution of Raman intensity in space relates to atomic displacements specific to a normal mode.46 Hence, in Fig. 5 we present images of the relevant Raman active modes of the modelled structural components of TCS-TEMD under the extraction orientation. The positive (red) intensity at the tip-edges of the microstructure as shown in Fig. 3E2–3E5 may be assigned to the antisymmetric deformations of aromatic rings admixed with in-plane CCH bendings of the aromatic moieties of Raman mode 159 as described in Fig. 5A. Also, the negative (blue) signatures at the left edge of the side walls in Fig. 3E2–3E4 can be assigned to localized deformations of aromatic rings admixed with CCH bendings and symmetric deformations of aromatic rings specific to the modes 193, 310 and 350 as shown in Fig. 5B–D. Consistently, the dominance of the negative (blue) intensities at the tip edge in Fig. 3E6, 3E8 and 3E9 are due to the symmetric CH stretchings of aromatic moieties described by the computed mode 370 that contributes into the response at 3060 cm−1, see Fig. 5G. The positive signatures in the images are due to the antisymmetric CH stretchings of aromatic moieties and CH stretching of TEMED of the modes like 330, 350 and 351: Fig. 5D–F. Here it is important to stress that even though TCS-cyclam and TCS-TEMED demonstrate slightly different unit cells and assemblies (see Fig. 2, 3 and S1 in the ESI†), the general character in the Raman difference images (Fig. 3 and S1†) confirms a similarity of unit cell orientations in respect to the long axes of the two microstructures.
Regardless of the apparent consistency, however, one may question how specific or sensitive the computed images may be in dependence on the orientation of the crystal: if Raman difference patterns should vary if we sample another of the six sides. This concerns testing the structural model we selected to build the model micro-assembly. In the current report we rely on the hexagonal profile sorted from a single crystal block, where unit cells are oriented the same in respect to the top surface and the selected long axis according to the results of polarized Raman spectroscopy. In the ESI in Fig. S9,† we present difference images computed in the XY plane (of the laboratory frame) for a microcrystal with its long axis oriented along the Y axis of the laboratory frame after the crystal was turned by 60° about its long axis (parallel to the Y axis of the laboratory frame). The rotation brings about a different side to be used for image modelling. The computed images are not identical but analogous, consistent in terms of the character of the difference patterns. This may suggest both, that the approach we adopt (starting from a single crystal block of the specified arrangement) is plausible in applications of the material and that polycrystalline domains do not dominate. Additionally, in the ESI in Fig. S10,† we present computed XZ plane Raman difference images of the hexagonal opening. For this case, the interplay of the special relative arrangement of the Raman active moieties in dependence on the unit cell packing is particularly sensitive to the orientation of the unit cells and may stimulate further experimental efforts and computational studies assisted with machine learning to understand the subtle differences suggested from the computational studies.
According to Raman microscopy data, aromatic hydrophobic structural components in both microcrystals dominate edges at the sides of the hollow opening. Our results indicate that when exposed to water, the microcrystals hollow cavity remains dry with only moderate absorption of water by the walls, Fig. S8 (given in the ESI†) indicate that these hollow microcrystals should have promising adsorption properties for hydrophobic chemical species. Considering the results, how can we diversify the functional properties of these polycrystalline micro-assemblies? The most obvious would be to attempt assemblies with TCS units that include a hydrophilic or a polar residue. This would help to manage two aspects: (a) variation of the Si–Si structural vector in respect to the corresponding unit cell axis; (b) stimulation of interactions with a polar environment to promote uptake of a wider range of molecules by the hollow volume. Alternatively, one may consider a post assembly surface functionalization.
Conclusions
In this study we explore structural properties of TCS-TEMED and TCS-cyclam microcrystalline hollow structures, which are promising materials for gas and liquid transport as well as the engineering of silica based molecular sensors. Using the X-ray crystal structure as a starting point, coupled with theoretical and experimental Raman studies we can describe the orientation of the molecular complex in relation to the macroscopic hollow structures. We show that the molecular components organise themselves with the hydrophobic components at both internal and external interfaces where they interact with the environment. We discuss approaches that might lead to modifications of the functional properties of the materials, thereby expanding their potential for application in storage and sensing applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funding from AFOSR FA9550-16-1-0213 and FA9550-20-1-0206 is gratefully acknowledged. The authors are grateful to Dr Nathan Cumberbatch and Dr David Sheppard for assistance in Raman microscopy studies using the research infrastructure of HORIBA UK Ltd at Northampton, United Kingdom. We thank Diamond Light Source, Dr Sarah Barnett and Dr Dave Allan for access to beamline I19 under BAG proposal CY298766.References
- H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef PubMed.
- B. E. R. Snyder, A. B. Turkiewicz, H. Furukawa, M. V. Paley, E. O. Velasquez, M. N. Dods and J. R. Long, Nature, 2023, 613, 287–291 CrossRef CAS PubMed.
- S. Mann and G. A. Ozin, Nature, 1996, 382, 313–318 CrossRef CAS.
- M. R. Knecht and D. W. Wright, Chem. Commun., 2003, 3038–3039 RSC.
- S. V. Patwardhan, Chem. Commun., 2011, 7567–7582 RSC.
- M. J. Limo, A. Sola-Rabada, E. Boix, V. Thota, Z. C. Westcott, V. Puddu and C. C. Perry, Chem. Rev., 2018, 22, 11118–11193 CrossRef PubMed.
- P. D. Beer, Acc. Chem. Res., 1998, 31, 71–80 CrossRef CAS.
- P. D. Beer, Chem. Soc. Rev., 1989, 18, 409–450 RSC.
- I. Lukes, J. Kotek, P. Vojtisek and P. Hermann, Coord. Chem. Rev., 2001, 216, 287–312 CrossRef.
- D. S. Wragg, G. B. Hix and R. E. Morris, J. Am. Chem. Soc., 1998, 120, 6822–6823 CrossRef CAS.
- T. Wessels, L. B. McCusker, C. Baerlocher, P. Reinert and J. Patarin, Microporous Mesoporous Mater., 1998, 23, 67–77 CrossRef CAS.
- P. S. Wheatley and R. E. Morris, J. Solid State Chem., 2002, 167, 267–273 CrossRef CAS.
- V. Patinec, P. A. Wright, P. Lightfoot, R. A. Aitken and P. A. Cox, J. Chem. Soc., Dalton Trans., 1999, 3909–3911 RSC.
- D. S. Wragg, A. M. Z. Slawin and R. E. Morris, J. Mater. Chem., 2001, 11, 1850–1857 RSC.
- D. J. Belton, S. V. Patwardhan, V. V. Annenkov, E. N. Danilovtseva and C. C. Perry, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 5963–5968 CrossRef CAS PubMed.
- J. J. Yuan, P. X. Zhu, N. Fukazawa and R. H. Jin, Adv. Funct. Mater., 2006, 16, 2205–2212 CrossRef CAS.
- C. Gautier, P. J. Lopez, M. Hemadi, J. Livage and T. Coradin, Langmuir, 2006, 22, 9092–9095 CrossRef CAS PubMed.
- J. J. E. Moreau, L. Vellutini, M. W. C. Man and C. Bied, Chem. – Eur. J., 2003, 9, 1594–1599 CrossRef CAS PubMed.
- G. E. Tilburey, T. J. Blundell, S. P. Argent and C. C. Perry, Dalton Trans., 2019, 48, 15470–15479 RSC Correction published as G. E. Tilburey, T. J. Blundell, S. V. Patwardhan, S. Argent and C. C. Perry, Dalton Trans., 2020, 49, 1334 RSC.
- G. S. Landsherg and L. I. Mandelstam, Z. Phys., 1928, 50, 769–780 CrossRef.
- C. V. Raman, Nature, 1928, 121, 619, DOI:10.1038/121619b0.
- O. Ilchenko, Y. Pilgun, A. Kutsyk, F. Bachmann, R. Slipets, M. Todeschini, P. O. Okeyo, H. F. Poulsen and A. Boisen, Nat. Commun., 2019, 10, 5555 CrossRef CAS PubMed.
- M. Rivera-Torrente, M. Filez, C. Schneider, E. C. van der Feltz, K. Wolkersdorfer, D. H. Taffa, M. Wark, R. A. Fischer and B. M. Weckhuysen, Phys. Chem. Chem. Phys., 2019, 21, 25678–25689 RSC.
- D. R. Allan, H. Nowell, S. A. Barnett, M. R. Warren, A. Wilcox, J. Christensen, L. K. Saunders, A. Peach, M. T. Hooper, L. Zaja, S. Patel, L. Cahill, R. Marshall, S. Trimnell, A. J. Foster, T. Bates, S. Lay, M. A. Williams, P. V. Hathaway, G. Winter, M. Gerstel and R. W. Wooley, Crystals, 2017, 7, 22 CrossRef.
- J. Cosier and A. M. Glazer, J. Appl. Crystallogr., 1986, 19, 105–107 CrossRef CAS.
- P. Evans, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2006, 62, 72–82 CrossRef PubMed.
- G. Winter, J. Appl. Crystallogr., 2010, 43, 186–190 CrossRef CAS.
- P. R. Evans and G. N. Murshudov, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2013, 69, 1204–1214 CrossRef CAS PubMed.
- G. Winter, D. G. Waterman, J. M. Parkhurst, A. S. Brewster, R. J. Gildea, M. Gerstel, L. Fuentes-Montero, M. Vollmar, T. Michels-Clark, I. D. Young, N. K. Sauter and G. Evans, Acta Crystallogr., Sect. D: Struct. Biol., 2018, 74, 85–97 CrossRef CAS PubMed.
- M. D. Winn, C. C. Ballard, K. D. Cowtan, E. J. Dodson, P. Emsley, P. R. Evans, R. M. Keegan, E. B. Krissinel, A. G. W. Leslie, A. McCoy, S. J. McNicholas, G. N. Murshudov, N. S. Pannu, E. A. Potterton, H. R. Powell, R. J. Read, A. Vagin and K. S. Wilson, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2011, 67, 235–242 CrossRef CAS PubMed.
- CCP4 2018, 7.0.072: AIMLESS version 0.7.4: 13/12/18.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- O. V. Dolomanov, A. J. Blake, N. R. Champness and M. Schroder, J. Appl. Crystallogr., 2004, 36, 1283–1284 CrossRef.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- D. Kratzert, FinalCif V115, Freiburg 2023, https://dkratzert.de/finalcif.html.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, et al., Gaussian 09, revision B.01, 2010 Search PubMed.
- S. Dapprich, I. Komáromi, K. S. Byun, K. Morokuma and M. J. Frisch, J. Mol. Struct., 1999, 462, 1–21 Search PubMed.
- F. Clemente, T. Vreven and M. J. Frisch, in Quantum Biochemistry, ed. C. Matta, Wiley VCH, Weinheim, 2010, pp. 61–84 Search PubMed.
- P. Maker, Phys. Rev. A, 1970, 1, 923 CrossRef CAS.
- C. Hirose, N. Akamatsu and K. Domen, Appl. Spectrosc., 1992, 46, 1051–1072 CrossRef.
- V. Volkov, J. Chem. Phys., 2014, 141, 134121 CrossRef PubMed.
- Z. Xie, S. Duan, C.-K. Wang and Y. Luo, Nanoscale, 2017, 9, 18189–18193 RSC.
- H. Ghobarkar, O. Schaf and U. Guth, Prog. Solid State Chem., 1999, 27, 29–73 CrossRef CAS.
- L. Zheng, L. Liu, C. Shao, W. Wang, B. Wang, L. Pan, Y. Li and Z. Ma, Macromolecules, 2019, 52, 1188–1199 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2245748. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3dt00856h |
| This journal is © The Royal Society of Chemistry 2023 |


