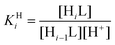Open Access Article
Open Access ArticleA seven-coordinate Mn(II) complex with a pyridine-based 15-membered macrocyclic ligand containing one acetate pendant arm: structure, stability and relaxation properties†
Marie
Pražáková
 a,
Daouda
Ndiaye
b,
Éva
Tóth
a,
Daouda
Ndiaye
b,
Éva
Tóth
 *b and
Bohuslav
Drahoš
*b and
Bohuslav
Drahoš
 *a
*a
aDepartment of Inorganic Chemistry, Faculty of Science, Palacký University Olomouc, 17. listopadu 12, 771 46 Olomouc, Czech Republic. E-mail: bohuslav.drahos@upol.cz; Fax: +420 585 634 954; Tel: +420 585 634 429
bCentre de Biophysique Moléculaire, CNRS-UPR 4301, Université d'Orléans, rue Charles Sadron, 45071 Orléans, France. E-mail: eva.jakabtoth@cnrs-orleans.fr; Fax: +33-23863151
First published on 10th May 2023
Abstract
A new 15-membered pyridine-based macrocyclic ligand containing one acetate pendant arm (N-carboxymethyl-3,12,18-triaza-6,9-dioxabicyclo[12.3.1]octadeca-1(18),14,16-triene, L1) was synthesized and its Mn(II) complex MnL1 was investigated in the context of MRI contrast agent development. The X-ray molecular structure of MnL1 confirmed a coordination number of seven with an axially compressed pentagonal bipyramidal geometry and one coordination site available for an inner-sphere water molecule. The protonation constants of L1 and the stability constants of Mn(II), Zn(II), Cu(II) and Ca(II) complexes were determined by potentiometry, and revealed higher thermodynamic stabilities in comparison with complexes of 15-pyN3O2, the parent macrocycle without an acetate pendant arm. The MnL1 complex is fully formed at physiological pH 7.4, but it shows fast dissociation kinetics, as followed by relaxometry in the presence of an excess of Zn(II). The short dissociation half-life estimated for physiological pH (ca. 3 minutes) is related to fast spontaneous dissociation of the non-protonated complex. At lower pH values, the proton-assisted dissociation pathway becomes important, while the Zn(II) concentration has no effect on the dissociation rate. 17O NMR and 1H NMRD data indicated the presence of one inner-sphere water molecule with a rather slow exchange (k298ex = 4.5 × 106 s−1) and provided information about other microscopic parameters governing relaxation. The relaxivity (r1 = 2.45 mM−1 s−1 at 20 MHz, 25 °C) corresponds to typical values for monohydrated Mn(II) chelates. Overall, the acetate pendant arm in L1 has a beneficial effect with respect to 15-pyN3O2 in increasing the thermodynamic stability and kinetic inertness of its Mn(II) complex, but leads to a reduced number of inner-sphere water molecules and thus lower relaxivity.
Introduction
Magnetic Resonance Imaging (MRI) is one of the most powerful non-invasive diagnostic techniques in medicine for the visualization of soft tissues without radiation load. Since the description of the theory and the first MR images in 1971 reported by Paul C. Lauterbur and later by P. Mansfield,1,2 and the first animal tumor imaging in 1976,3 huge progress has been made in MRI physics, instrumentation, and the chemistry of contrast agents (CAs) that are injected into patients to improve image quality.Due to the low sensitivity and insufficient image contrast, the use of CAs is often required in MRI. These paramagnetic substances reduce the longitudinal (T1) and transverse (T2) relaxation times of water protons,4 and enhance image contrast between different tissues. The majority of CAs are based on paramagnetic metal ions, which are chelated in stable complexes to prevent in vivo toxicity of the free metal. Paramagnetic metal complexes affect mainly the longitudinal relaxation of tissue water protons, leading to an increased signal intensity (positive contrast) on T1-weighted MR images (T1-CAs).
For over 35 years, Gd(III) chelates have been used in millions of human examinations and are considered as safe diagnostic drugs. However, recent findings associated Nephrogenic Systemic Fibrosis (NSF), a potentially lethal disease, with the use of Gd(III) agents in kidney impaired patients.5,6 Furthermore, gadolinium deposits, although without toxic effects, have been identified after Gd-enhanced MRI in the bones or the brain of patients even without renal problems.7,8 As a consequence, the clinical use of Gd(III) chelates formed with linear chelators has been stopped or restricted by control authorities both in Europe and the US. In parallel, the development of more biocompatible alternatives to Gd(III)-based agents has become an active area of research. In this context, complexes of paramagnetic transition metal ions, in particular Mn(II), have been widely investigated, and one Mn(II) chelate is currently in clinical trials.9 Indeed, the d5 high spin configuration, slow electron spin relaxation and fast water exchange make Mn(II) the most promising substitute for Gd(III).10–12
In general, six- or seven-coordinate Mn(II) chelates, formed with penta- or hexadentate ligands and containing at least one hydration water, can be considered as good contrast agent candidates. The presence of inner sphere water is indispensable in order to achieve good relaxivities. Relaxivity, r1, is the paramagnetic enhancement of the longitudinal water proton relaxation rates in the presence of 1 mM concentration of the paramagnetic probe, and it directly translates to MRI efficacy. High thermodynamic and redox stability, as well as kinetic inertness, are also required properties for Mn(II) complexes, due to the potential risk associated with the administration of the Mn(II) ion in high concentrations.13 A major issue could be brain accumulation of Mn(II) causing a neurological disorder (“manganism”) with symptoms similar to Parkinson's disease.14 Macrocyclic ligands are typically better candidates for Mn(II) complexation than non-cyclic analogues, since they allow higher thermodynamic stability and kinetic inertness.10,15,16 The thermodynamic stability of Mn(II) complexes is lower in comparison with other transition metal analogues due to the lack of ligand-field stabilization energy for the high spin d5 configuration, as well as in comparison with Gd(III) chelates due to the smaller charge of Mn2+. Few Mn(II) chelates were found to be inert to Zn2+ or Cu2+ transmetalation,17,18 although recent examples of Mn(II) bispidine complexes evidence that extraordinary inertness might be possible with highly preorganized and rigid ligand structures.19
Pyridine-based macrocycles have been extensively explored for Mn(II) complexation. In 2010, we reported 15-pyN5 and 15-pyN3O2,20 the pyridine containing analogues of previously studied ligands 15-aneN5 and 15-aneN3O2 (Scheme 1).21–24 We confirmed that the incorporation of a pyridine moiety into the polyaza macrocycle scaffold leads to higher thermodynamic stability and kinetic inertness. This was particularly true for 15-pyN5, where the two additional nitrogen atoms result in higher basicity and higher thermodynamic stability for Mn(II), while thanks to the two inner sphere water molecules (q = 2 for an overall coordination number of 7), high relaxivity is retained. More recently, the 15-pyN3O2Ph derivative containing a pyridine and an ortho-phenylene unit has been prepared and its Mn(II) complexation has been investigated.25 This ligand forms a surprisingly flat Mn(II) complex with two coordinated water molecules in the solid state structure; however, due to low stability even under mildly acidic conditions, this complex is unsuitable for further investigation.
In the family of 12-membered macrocycles, pyclen-based 3,9-PC2A and 3,6-PC2A (Scheme 1) and their derivatives are among the most promising ligands for Mn(II) chelation for MRI purposes.17 Independent of the position of the acetate pendant arms, both 3,9-PC2A and 3,6-PC2A form seven-coordinated Mn(II) complexes which are sufficiently stable and kinetically inert, though they have only one water molecule in the inner coordination sphere, providing lower relaxivity than the above-mentioned 15-membered macrocyclic Mn(II) complexes. The Mn(II) chelates of 3,9-PC2A and 3,6-PC2A possess modest superoxide-dismutase activity as well.17
Mn(PC2A-EA), formed with the pyclen-based derivative containing two acetic and one ethylamine pendant arm (Scheme 1), is among the most thermodynamically stable and kinetically inert monohydrated Mn(II) systems.26 The pH-dependent metal coordination of the ethylamine function, which occurs in the pH range 6–8, results in pH-sensitive relaxivities, making Mn(PC2A-EA) a potential smart CA. Another PC2A derivative bearing a biphenyl pendant arm, PC2A-BP (Scheme 1), also forms a thermodynamically stable and kinetically inert Mn(II) complex.27 Mn(PC2A-BP) interacts with human serum albumin (HSA) which is accompanied by a remarkable relaxivity increase. This agent could thus be used in angiographic imaging, providing significant MRI signal enhancement in the vasculature.
3,9-OPC2A (Scheme 1) is a less basic analogue of 3,9-PC2A, containing a non-protonable O-atom in the macrocyclic scaffold.18 Despite a lower ligand basicity, the conditional stability of the Mn(II) complex at pH 7.4 remains unaffected as compared to Mn(3,9-PC2A), while the acid assisted dissociation becomes considerably slower. 3,9-OPC2A could also be efficiently labeled with the PET isotope 52Mn. All these advantageous features make this ligand interesting for further design of bifunctional chelators.
In contrast to PC2A and its derivatives, the monofunctionalized pyclen ligands PC1A and PC1P, which bear a single acetate or phosphonate pendant (Scheme 1), form hexacoordinate and monohydrated Mn(II) complexes (CN = 6; q = 1).28 Full complexation of Mn(II) occurs at physiological pH and a metal to ligand ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1; however, the complexes are very labile and undergo oxidation to the Mn3+ form.
1; however, the complexes are very labile and undergo oxidation to the Mn3+ form.
We should also mention that many linear ligands comprising pyridine or picolinate coordinating functions have also been explored for Mn(II) complexation;29–31 the ligand PyC3A32 and its derivatives are likely the most investigated, including clinical trials.
Herein we report a novel 15-membered pyridine-based macrocyclic chelator (L1, Scheme 1), where one acetate pendant arm is appended on 15-pyN3O2. This modification should lead to higher stability and kinetic inertness, and improved solubility of MnL1, all important for potential biological applications. On the other hand, the metal coordination of the acetate group is expected to reduce the hydration number to q = 1, thus resulting in lower relaxivity. We have determined the molecular structure of MnL1 by single-crystal X-ray diffraction. The protonation constants of the ligand and thermodynamic stability of the complex have been measured in aqueous solution by potentiometry, and kinetic inertness has been assessed in transmetallation experiments of MnL1 with an excess of Zn2+ using T2 relaxation time measurements. Proton relaxivities, r1, and the microscopic parameters influencing the relaxivity of MnL1 have been determined from a combined 1H NMRD and 17O NMR study. Although MnL1 is not appropriate for further contrast agent development, the comparison of these data to the results on previously reported Mn(II) analogues provides a better understanding of structure–activity relationships in the family of pyridine-containing macrocyclic Mn(II) chelates.
Experimental section
Materials and methods
All solvents (VWR International, Lach-ner, Penta) and chemicals were purchased from commercial sources (Acros Organics, Merck) and used as received. The parent ligand 15-pyN3O2 was synthesized as previously described in the literature.20,33Mass spectra were recorded using an LCQ Fleet mass spectrometer (Thermo Scientific, Waltham, MA, USA) equipped with an electrospray source and a three-dimensional (3D) ion-trap detector in the positive/negative mode (Fig. S1†). 1H and 13C NMR spectra (Fig. S2 and S3†) were obtained using a 400-MR NMR spectrometer (Varian, Palo Alto, CA, USA) at 25 °C and 60 °C: 1H 399.95 MHz dimethylsulfoxide-d6 (DMSO-d6, residual solvent peak) and 13C 100.60 MHz (DMSO-d6, residual solvent peak). The multiplicity of the signals is indicated as follows: s – singlet, d – doublet, t – triplet, m – multiplet, and bs – broad singlet. Deuterated solvent DMSO-d6 (99.9% of D) was purchased from Sigma Aldrich and used as received. The atom numbering scheme used for NMR data interpretation is shown in Scheme 2. The carbon and hydrogen atoms were assigned according to the spectra obtained from two-dimensional correlation experiments 1H–1H gs-COSY, 1H–13C gs-HMQC (Fig. S4†) and 1H–13C gs-HMBC (Fig. S5†).
Synthesis
15-pyN3O2 (1.70 g, 6.77 mmol) was dissolved in a mixture of EtOH (25 ml) and distilled water (5 ml). Meanwhile, BrCH2COOH (157.0 mg, 1.13 mmol) and LiOH·H2O (168.0 mg, 4.00 mmol) were dissolved in cooled distilled water (<9 °C) and this resulting solution was added slowly dropwise to a stirred solution of 15-pyN3O2. The reaction mixture was then heated to reflux and refluxed for 4 h. Afterwards, the obtained mixture was filtered via a glass frit and the filtrate was evaporated to dryness. The residue was dissolved in distilled water and extracted seven times with 50 ml of CHCl3 (the organic phase contained the starting macrocycle 15-pyN3O2). The water phase was filtered and evaporated to dryness, and washed several times with hot acetone containing a small amount of 36% hydrochloric acid to dissolve the remaining lithium salt and to get the product in the form of hydrochloride. The residue was then dried under reduced pressure to give a slightly hygroscopic dark orange oil (718 mg of product in the form of hydrochloride/hydrobromide). According to the potentiometric titration of the ligand, the amount of L1 was 43%, and the rest corresponds to residual solvents and HCl/HBr content, and thus the yield based on BrCH2COOH was 88.3%. 1H NMR (400 MHz, DMSO-d6, 60 °C): δ 3.22 (t, 3JHH = 4.9 Hz, 2H, H9); 3.60 (s, 4H, H12/13); 3.64 (m, 2H, H8); 3.78 (m, 2H, H11); 3.85 (t, 2H, 3JHH = 4.9 Hz, H10); 4.19 (s, 2H, H14); 4.40 (bs, 2H, H7); 4.78 (s, 2H, H6); 7.49 (t, 2H, 3JHH = 7.8 Hz H2/H3); 7.95 (t, 1H, 3JHH = 7.8 Hz, H1). 13C NMR (400 MHz, DMSO-d6, 25 °C): δ 46.83 (C9); 49.49 (C7); 53.71 (C14); 54.54 (C8); 57.5 (C6); 64.13 (C10); 65.11 (C11); 69.53/69.73 (C12/C13); 123.0 (C2/C3); 123.31 (C2/C3); 139.41 (C1); 149.84 (C4); 151.74 (C5); 167.7 (C15). MS m/z (+): 310.26 ([L + H+]+ calcd 310.17), 332.22 ([L + Na+]+ calcd 332.16).Crystal structure determination
Single crystals suitable for X-ray diffraction were prepared by mixing an aqueous/methanol solution of the ligand (cL = 56 mM) and manganese(II) perchlorate (cMn = 113 mM) in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.10 Mn/L molar ratio. Several drops of Et3N were added to this solution. Colorless crystals of the complex were obtained by diffusion of acetone at 25 °C and by additional slow diffusion of Et2O at 6 °C into the aqua/methanol solution.
1.10 Mn/L molar ratio. Several drops of Et3N were added to this solution. Colorless crystals of the complex were obtained by diffusion of acetone at 25 °C and by additional slow diffusion of Et2O at 6 °C into the aqua/methanol solution.
X-ray diffraction data were collected on an XtaLAB Synergy-i (Rigaku) diffractometer equipped with a HiPix3000 Bantam detector and a monochromatized microfocus PhotonJet-i CuKα radiation source (λ = 1.54184 Å) at 90 K. The molecular structure of the complex was solved by direct methods and refined by full matrix least squares based on F2 (SHELXL 2014/07).34 Program Olex2 1.3 was used for the final refinement.35 The hydrogen atoms on carbon atoms were fixed into idealized positions (riding model) and assigned temperature factors either Hiso(H) = 1.2Ueq (pivot atom) for CH and CH2 moieties or Hiso(H) = 1.5Ueq (pivot atom) for CH3 groups. A solvent mask procedure was employed during the refinement process and the residual electron density corresponded to unresolved 1.5H2O molecules. The molecular and crystal structures of the complex, depicted in Fig. 1 and S3,† were drawn using the Mercury software.36
 | ||
| Fig. 1 Molecular structure of the [MnL1]+ complex unit found in the 1D polymeric structure of [MnL1]n[MnBrCl3]n/2·2H2O. | ||
Thermodynamic stability studies
Metal stock solutions were prepared from the highest analytical-grade chemicals, and their concentration was determined by complexometric titration with standardized Na2H2EDTA, using a xylenol orange indicator in the presence of urotropine buffer (ZnCl2 and MnCl2); the Eriochrome black T indicator in the presence of ammonium acetate buffer (CaCl2) or a murexide indicator in ammonium solution (CuCl2). The concentration of the ligand stock solution was determined by pH-potentiometric titrations (the difference between the two inflection points of the ligand titration curve corresponds to two ligand equivalents). To determine the protonation constants of the ligand and stability constants of the metal complexes with selected divalent metal ions, pH-potentiometric titrations were carried out with 0.1 M NaOH using 2 mM ligand solution (protonation constant of the ligand) and then a metal-to-ligand molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, with a waiting time of 2 minutes between successive points (V0 = 5 mL). The temperature (25.0 ± 0.1 °C) was controlled with a circulating water bath. The ionic strength was set to I = 0.15 M NaCl. All titrations were performed under a nitrogen atmosphere to avoid the effect of CO2. Titrations were carried out in the pH range from 1.9 (after the addition of 1 M HCl solution to the starting ligand solution in the titration cell) to pH 11.2 (or until precipitation of the metal hydroxide).
1, with a waiting time of 2 minutes between successive points (V0 = 5 mL). The temperature (25.0 ± 0.1 °C) was controlled with a circulating water bath. The ionic strength was set to I = 0.15 M NaCl. All titrations were performed under a nitrogen atmosphere to avoid the effect of CO2. Titrations were carried out in the pH range from 1.9 (after the addition of 1 M HCl solution to the starting ligand solution in the titration cell) to pH 11.2 (or until precipitation of the metal hydroxide).
All pH-potentiometric titrations were performed using a 785 DMP Titrino titration workstation with a combined electrode (Metrohm). The p[H] (p[H] = −log[H+], concentration in molarity) was measured in each titration with a combined pH glass electrode (Metrohm) filled with 3 M KCl. The electrode was calibrated in hydrogen ion concentration by titration of HCl with KOH in 0.1 M electrolyte solution.37 A plot of potential versus p[H] allows the determination of the electrode standard potential (E°) and the slope factor (f).
The protonation constants of the ligand (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KHi) are defined as follows:
KHi) are defined as follows:
For the calculation of equilibrium constants, the HYPERQUAD program was used.38 The number of fitted data pairs was between 230 and 280. The ionic product of water at 25 °C and 0.1 M ionic strength is pKw = 13.77.39 Fixed values were used for pKw, ligand acidity constants and total concentrations of the metal, ligand, and acid. All values and errors (one standard deviation) reported are at least the average of three independent experiments.
Sample preparation
MnL1 complex samples for kinetic and relaxometry studies have been prepared by mixing MnCl2 and L1 solutions of known concentrations in a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.05 and by adjusting the pH to 7.4. Mn(II) concentration in each sample was checked by bulk magnetic susceptibility measurements.
1.05 and by adjusting the pH to 7.4. Mn(II) concentration in each sample was checked by bulk magnetic susceptibility measurements.
Kinetic studies
The transmetalation reaction of MnL1 (1.4 mM solution) was monitored in the presence of 10, 20, 30, 40 and 50 molar equivalents of Zn(II) ions, by measuring water proton T2 relaxation times (60 MHz) as a function of time at 25 °C and in 0.15 M NaCl, in the pH range 4.9–6.1 (4.9; 5.0; 5.2; 5.5; 5.7; 6.1). To control pH, 50 mM N-methyl-piperazine (pH 4.9–5.5) or 50 mM MES buffer (pH 5.7–6.1) was used. No oxidation of the sample was observed.Relaxation properties
At 60 MHz, 1H longitudinal (T1) and transverse (T2) relaxation times were measured with a Bruker Minispec MQ-60 NMR analyzer. The temperature was set to 25.0 °C and controlled with a circulating water bath. T1 and T2 values were determined, respectively, by the inversion recovery method (180° − τ − 90°) and the Carl–Purcell–Meiboom–Gill (CPMG) spin-echo pulse sequence. pH-Dependent relaxivities (pH 1.75–11.8) were acquired at a MnL1 concentration of 2 mM, and the pH was adjusted by 0.045 M MES (2-(4-morpholino)ethane-sulfonic acid), HEPES (4-(2-hydroxyethyl)piperazine-1-ethanesulfonic acid), DMP (dimethyl piperazine), or NMP (N-methyl piperazine) buffers.The 1H NMRD profiles of aqueous MnL1 solution (cMn2+ = 0.99 mM; pH = 7.23) were recorded at 25 and 37 °C on a SMARTracer Fast Field Cycling NMR relaxometer (Stelar; 0.00024–0.24 T, 0.01–10 MHz 1H Larmor frequency) and a WP80 NMR electromagnet adapted to variable-field measurements (Bruker; 0.47–1.88 T, 20–80 MHz 1H Larmor frequency). The temperature was maintained by a gas flow and monitored using a VTC91 temperature control unit, based on previous calibration with a Pt resistance temperature probe.
17O NMR measurements
Variable-temperature 17O NMR measurements of an aqueous solution of MnL1 (cMnL = 4.01 mmol kg−1, pH = 7.39) were performed using a Bruker Avance III 400 MHz spectrometer (9.4 T, 54.2 MHz) in the temperature range of 5–75 °C. The temperature was calculated after calibration with ethylene glycol and MeOH. Acidified water (HClO4, pH = 3.3) was used as a diamagnetic reference. The 17O transverse relaxation times (T2) were obtained using the CPMG spin-echo technique. To eliminate susceptibility contributions to the chemical shift, the sample was in a glass sphere placed in a 10 mm NMR tube. To improve sensitivity, 17O-enriched water (11.10% H217O, Cortecnet) was added to the solution to yield approximately 1% 17O enrichment.The 17O NMR and NMRD data have been treated according to the Solomon–Bloembergen–Morgan theory of paramagnetic relaxation.40 The least squares fit was performed using Visualiseur/Optimiseur running on a MATLAB 8.3.0 (R2014a) platform.
Results and discussion
Synthesis
The 15-pyN3O2 macrocycle was obtained first via template synthesis as previously described.20,33 Two procedures were tested for the preparation of L1.The first one used BrCH2COOH and 15-pyN3O2 in a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6; lower excess of 15-pyN3O2 led to higher amounts of the disubstituted side-product. The reaction was performed in MeOH and the product was purified by successive anion and cation exchange chromatography. The resulting product, obtained in zwitterionic form, contained ca. 5–20% of the disubstituted side-product (based on NMR analysis and MS). The reaction yield (50–60%) and the purity (ranging from 60 to 90%) were strongly dependent on the temperature during BrCH2COOH addition (room temperature vs. 60 °C), the speed and the form of BrCH2COOH addition (in the form of solid or solution, and the addition of the solution takes place via a dropping funnel or linear pump) and the reflux time ranging from 1.5 to 12 h. Further optimization seemed difficult in the case of this procedure.
6; lower excess of 15-pyN3O2 led to higher amounts of the disubstituted side-product. The reaction was performed in MeOH and the product was purified by successive anion and cation exchange chromatography. The resulting product, obtained in zwitterionic form, contained ca. 5–20% of the disubstituted side-product (based on NMR analysis and MS). The reaction yield (50–60%) and the purity (ranging from 60 to 90%) were strongly dependent on the temperature during BrCH2COOH addition (room temperature vs. 60 °C), the speed and the form of BrCH2COOH addition (in the form of solid or solution, and the addition of the solution takes place via a dropping funnel or linear pump) and the reflux time ranging from 1.5 to 12 h. Further optimization seemed difficult in the case of this procedure.
The second synthetic route was based on a procedure previously described in the literature for the preparation of mono-N-substituted cyclam (1,4,8,11-tetraaza-cyclotetradecane) using LiOH·H2O and a large excess of the macrocycle.41 Therefore, we used a BrCH2COOH/15-pyN3O2 molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, and according to NMR and MS/HPLC characterization, this synthetic procedure led to high ligand purity without side product(s). Attempts (e.g. dissolving the product in a minimum amount of distilled water and HCl, followed by the addition of acetone/ether) to obtain a solid crystallized ligand were unsuccessful. Therefore, solvents were evaporated under reduced pressure to obtain the ligand as an orange oil. Subsequent potentiometric titration of this product revealed the amount of L1 to be 43%, and the rest corresponding to HCl/HBr and the water content. The calculated yield, based on BrCH2COOH and the 43% purity, was 88.3% which can be considered as high and superior to that of the above-described first approach.
7, and according to NMR and MS/HPLC characterization, this synthetic procedure led to high ligand purity without side product(s). Attempts (e.g. dissolving the product in a minimum amount of distilled water and HCl, followed by the addition of acetone/ether) to obtain a solid crystallized ligand were unsuccessful. Therefore, solvents were evaporated under reduced pressure to obtain the ligand as an orange oil. Subsequent potentiometric titration of this product revealed the amount of L1 to be 43%, and the rest corresponding to HCl/HBr and the water content. The calculated yield, based on BrCH2COOH and the 43% purity, was 88.3% which can be considered as high and superior to that of the above-described first approach.
Crystal structure determination
For single-crystal preparation, a solution of manganese perchlorate was mixed with ligand solution in MeOH/H2O (1/1) in a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (before the addition of the manganese(II) solution, a small amount of triethylamine in methanol was dropped to the ligand solution to adjust the pH and to deprotonate the ligand). Only a few crystals were suitable for X-ray diffraction analysis. Many attempts were made, by using various solvents, to prepare single crystals of the complex with coordinated water molecules. They all gave crystals of very bad quality; nevertheless, the polymeric structure could be always confirmed. In the crystal structure of [MnL1]n[MnBrCl3]n/2·2H2O (1), the [MnL1]+ units were found to form a 1D polymeric chain in which the pendant carboxylate group acts as a bridging ligand between two [MnL1]+ units (Fig. 1). The positive charge is compensated by [MnBrCl3]2− counter anions.
1 (before the addition of the manganese(II) solution, a small amount of triethylamine in methanol was dropped to the ligand solution to adjust the pH and to deprotonate the ligand). Only a few crystals were suitable for X-ray diffraction analysis. Many attempts were made, by using various solvents, to prepare single crystals of the complex with coordinated water molecules. They all gave crystals of very bad quality; nevertheless, the polymeric structure could be always confirmed. In the crystal structure of [MnL1]n[MnBrCl3]n/2·2H2O (1), the [MnL1]+ units were found to form a 1D polymeric chain in which the pendant carboxylate group acts as a bridging ligand between two [MnL1]+ units (Fig. 1). The positive charge is compensated by [MnBrCl3]2− counter anions.
For each [MnL1]+ unit of the 1D polymeric chain, the coordination sphere has a pentagonal bipyramidal geometry, with the three nitrogen and two oxygen atoms of the macrocycle coordinated in the equatorial plane and the two oxygen atoms of the acetate pendant arms in apical positions, resulting in a coordination number of seven for Mn(II). The crystal data and structural refinements are summarized in Table 1.
| a R int = ∑|Fo2 − Fo,mean2|/∑Fo2. b R 1 = ∑(||Fo| − |Fc||)/∑|Fo|; wR2 = [∑w(Fo2 − Fc2)2/∑w(Fo2)2]1/2. | |
|---|---|
| Compound | 1 |
| Formula | C30H50BrCl3Mn3N6O11 |
| M r | 1021.84 |
| Temperature (K) | 90.15 |
| Wavelength (Å) | 1.54184 |
| Crystal system | Orthorhombic |
| Space group | Pnma |
| a (Å) | 11.7529(2) |
| b (Å) | 20.8862(4) |
| c (Å) | 18.2988(3) |
| α (°) | 90 |
| β (°) | 90 |
| γ (°) | 90 |
| V, Å3 | 4491.87(14) |
| Z | 4 |
| D calc. (g cm−3) | 1.511 |
| μ (mm−1) | 9.923 |
| F(000) | 2084 |
| R(int)a | 0.0526 |
| Data/restraints/parameters | 4181/6/256 |
| Completeness to θ (%) | 99.4 |
| Goodness-of-fit on F2 | 1.046 |
| R 1, wR2b (I > 2σ(I)) | 0.0532/0.1485 |
| R 1, wR2b (all data) | 0.0551/0.1505 |
| Largest diff. peak and hole (A−3) | 1.067 and −0.849 |
| CCDC | 2244643 |
Among all Mn–N distances (2.298 and 2.355 Å), the Mn1–N1(pyridine) distance (2.216 Å) is the shortest and the Mn1–N2 distance (2.355 Å) is the longest, where N2 bears the acetate pendant arm. The bond distances between the oxygen atoms of the macrocyclic cavity and the central Mn are 2.280 and 2.329 Å. The distances between the oxygen atoms of the pendant arm (O3/O4) and the central Mn atom are ca. 0.1–0.2 Å shorter compared to the Mn–O1/O2 distances as well as all other distances (see Table 2), and thus, the pentagonal bipyramidal geometry is slightly axially compressed.
| Distances | |
| Mn1–N1 | 2.216(3) |
| Mn1–N2 | 2.355(3) |
| Mn1–N3 | 2.298(3) |
| Mn1–O1 | 2.329(2) |
| Mn1–O2 | 2.280(2) |
| Mn1–O3 | 2.159(2) |
| Mn1–O4 | 2.134(2) |
| Angles | |
| N1–Mn1–N2 | 71.90(10) |
| N1–Mn1–N3 | 72.66(11) |
| N3–Mn1–O2 | 73.59(10) |
| O1–Mn1–O2 | 70.37(9) |
| N2–Mn1–O1 | 73.70(9) |
| O3–Mn1–O4 | 165.66(10) |
The positive charge of the 1D coordination polymer is compensated by [MnBrCl3]2− anions (Br− anions are retained from the ligand synthesis) which have a distorted tetrahedral structure. Mn–Br distances are ca. 0.1 Å longer in comparison with Mn–Cl ones. Moreover, this anion has occupational disorder because the Br atom is situated in two positions of the tetrahedron (occupancy factors of 0.55 and 0.45).
Furthermore, in the crystal structure of 1, there are two co-crystallized solvent water molecules for every [MnL1]+ unit which form hydrogen bonds between each other (O–H⋯O(water)), with the carboxylate bridge (O–H⋯O(COOH)), the macrocyclic NH group (N–H⋯O(water)) or the Cl atom from the [MnBrCl3]2− anion (O–H⋯Cl); see Table S1 and Fig. S6 in the ESI.† One of the water molecules also has positional disorder.
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KH1 KH1 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KH2 KH2 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KH3 KH3 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KH4 KH4 |
|
|---|---|---|---|---|
| a Ref. 20 (0.1 M NMe4Cl). b Ref. 21 (0.1 M NaClO4). c Ref. 22 (0.1 M NaClO4). d Ref. 25 (0.15 M NaCl). e Ref. 17 (0.15 M NaCl). f Ref. 43 (0.1M KCl). g Ref. 17 (1.0 M NaCl). h Ref. 26 (0.15 M NaCl). i Ref. 27 (0.15 M NaCl). j Ref. 18 (0.15 M NaCl). k Ref. 28 (0.1 M NMe4Cl). | ||||
| L1 | 8.86(1) | 8.03(1) | 1.9(1) | |
15-pyN3O2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
8.82 | 7.8 | ||
15-pyN5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
9.40a (9.43b; 9.11c) | 8.54a (8.80b; 8.82c) | 5.28a (5.28b; 5.27c) | |
| 15-pyN3O2Phd | 8.53 | 7.63 | ||
| 3,9-PC2A | 12.25e/12.50f | 5.97e/5.75f | 3.47e/3.28f | 1.99e/2.38f |
| 3,6-PC2A | 10.72e/10.31g | 8.37e/8.59g | 3.81e/3.92g | 1.26e/1.56g |
| PC2A-EAh | 11.34 | 8.93 | 6.91 | 1.97 |
| PC2A-BPi | 10.45 | 6.93 | 2.36 | 1.64 |
| 3,9-OPC2Aj | 7.73 | 7.66 | 2.13 | |
| PC1Ak | 10.47 | 8.71 | 2.79 | |
| PC1Pk | 11.84 | 9.64 | 6.23 | 0.99 |
| Constant | Ca(II) | Mn(II) | Zn(II) | Cu(II) |
|---|---|---|---|---|
| a Calculated using pMn = −log[Mn], cMn(II) = clig = 0.01 mM at pH 7.4. b Ref. 20 (0.1 M NMe4Cl). c Ref. 21 (0.1 M NaClO4). d Ref. 22 (0.1 M NaClO4). e Ref. 25 (0.15 M NaCl). f Ref. 17 (0.15 M NaCl). g Ref. 17 (1.0 M NaCl; determined by simultaneous fitting of the pH-potentiometric and UV-Vis data). h Ref. 26 (0.15 M NaCl). i Ref. 27 (0.15 M NaCl). j Ref. 18 (0.15 M NaCl). k Ref. 28 (0.1 M NMe4Cl). | ||||
| L1 | ||||
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KML KML |
5.51(2) | 11.06(2) | 13.12(1) | 15.86(2) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KHML KHML |
6.37(2) | 3.82(3) | 2.80(6) | 2.67(3) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KML(OH) KML(OH) |
−9.7(1) | |||
| pMna | 6.95 | |||
| 15-pyN 3 O 2 | ||||
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KML KML |
2.04 | 7.18 | 8.58 | 13.91 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KML(OH) KML(OH) |
−11.92 | −11.69 | −10.31 | −8.34 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KML(OH)2 KML(OH)2 |
−12.57 | |||
| pMn | 5.28 | |||
| 15-pyN 5 | ||||
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KML KML |
2.97 | 10.89 (11.64c, 11.12d) | 16.27 | 21.84 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KHML KHML |
4.27 (4.20c, 4.51d) | 2.45 | ||
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KML(OH) KML(OH) |
−11.52 (11.54c) | −11.18 | −12.30 | |
| pMn | 6.37 (6.60c, 6.59d) | |||
| 15-pyN 3 O 2 Ph | ||||
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KML KML |
1.85 | 5.62 | 7.70 | 13.97 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KML(OH) KML(OH) |
−10.50 | −9.62 | −8.95 | |
| pMna | 5.04 | |||
| 3,9-PC2A | ||||
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KML KML |
9.92 | 17.09 | 19.49 | 23.58g |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KHML KHML |
5.08 | 2.14 | 2.74 | 2.12g |
| pMn | 8.64 | |||
| 3,6-PC2A | ||||
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KML KML |
9.57 | 15.53 | 20.37 | 24.09g |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KHML KHML |
5.27 | 3.06 | 2.36 | 2.37g |
| pMn | 8.09 | |||
| PC2A-EAh | ||||
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KML KML |
19.01 | |||
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KHML KHML |
6.88 | |||
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KH2ML KH2ML |
2.50 | |||
| pMn | 9.27 | |||
| PC2A-BP | ||||
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KML KML |
7.94 | 14.86 | 18.05 | 22.30 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KHML KHML |
1.71 | 1.04 | ||
| pMn | 8.35 | |||
| 3,9-OPC2A | ||||
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KML KML |
8.27 | 13.03 | 14.81 | 18.41j |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KHML KHML |
2.40 | 2.08 | 1.92j | |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KML(OH) KML(OH) |
−11.49 | −10.95 | −10.50 | |
| pMn | 8.69 | |||
| PC1Ak | ||||
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KML KML |
6.04 | 11.54 | 17.01 | 18.62 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KHML KHML |
7.39 | 4.95 | 3.03 | 2.09 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KML(OH) KML(OH) |
10.46 | 11.35 | ||
| pMn | 8.10 | |||
| PC1Pk | ||||
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KML KML |
6.85 | 14.06 | 19.66 | 22.63 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KHML KHML |
5.35 | 5.19 | 4.89 | |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KML(OH) KML(OH) |
−11.97 | 12.33 | 13.12 | |
| pMn | 8.30 | |||
The first protonation constant, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KH1, is similar for L1 and the parent ligand 15-pyN3O2, but it is lower than log
KH1, is similar for L1 and the parent ligand 15-pyN3O2, but it is lower than log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KH1 for 15-pyN5 or the other cyclic ligands (Table 3). This lower basicity is related to the electron-withdrawing effect of the highly electronegative oxygen atoms in the macrocyclic scaffold. The second protonation constants are similar for L1 and 15-pyN3O2, while the third constant of L1 corresponds to the additional acetate function. Protonation of the pyridine unit is not observable above pH 1.9.
KH1 for 15-pyN5 or the other cyclic ligands (Table 3). This lower basicity is related to the electron-withdrawing effect of the highly electronegative oxygen atoms in the macrocyclic scaffold. The second protonation constants are similar for L1 and 15-pyN3O2, while the third constant of L1 corresponds to the additional acetate function. Protonation of the pyridine unit is not observable above pH 1.9.
According to the stability constants (Table 4), the most stable complex is formed with Cu(II), and then the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KML values decrease in the order Cu(II) > Zn(II) > Mn(II) > Ca(II). Protonated HML1 complexes exist for all four metals investigated, while a hydroxo complex is detected only for CuL1 at basic pH.
KML values decrease in the order Cu(II) > Zn(II) > Mn(II) > Ca(II). Protonated HML1 complexes exist for all four metals investigated, while a hydroxo complex is detected only for CuL1 at basic pH.
As expected, the modification with the acetate pendant arm leads to higher stability for L1vs. 15-pyN3O2 analogues, with an increase of ca. 4 units in the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KML values. Recently, an empirical approach, based on various structural descriptors, has been proposed to estimate stability constants for Mn(II) complexes.42 Considering the stabilization effect of the additional acetate in comparison with the parent 15-pyN3O2, this method predicts log
KML values. Recently, an empirical approach, based on various structural descriptors, has been proposed to estimate stability constants for Mn(II) complexes.42 Considering the stabilization effect of the additional acetate in comparison with the parent 15-pyN3O2, this method predicts log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KML = 9.64 for MnL1, ca. 1.4 units lower than the experimental value. For a more direct comparison of MnL stabilities between ligands with different protonation constants, pMn (pMn = −log[Mn(II)]free at pH 7.4, cMn = clig = 10−5 M) was calculated for MnL1 and compared to those of other systems (Table 4). This comparison reflects again an important stability increase brought by the introduction of the additional carboxylate donor in L1. Nevertheless, the stability of MnL1 remains low as compared to Mn(II) complexes of 12-membered pyclen derivatives (Table 4), mainly because of the too large size of the macrocyclic cavity and the lower number of pendant acetates.
KML = 9.64 for MnL1, ca. 1.4 units lower than the experimental value. For a more direct comparison of MnL stabilities between ligands with different protonation constants, pMn (pMn = −log[Mn(II)]free at pH 7.4, cMn = clig = 10−5 M) was calculated for MnL1 and compared to those of other systems (Table 4). This comparison reflects again an important stability increase brought by the introduction of the additional carboxylate donor in L1. Nevertheless, the stability of MnL1 remains low as compared to Mn(II) complexes of 12-membered pyclen derivatives (Table 4), mainly because of the too large size of the macrocyclic cavity and the lower number of pendant acetates.
The species distribution curves calculated for MnL1 with the stability constants as obtained by pH-potentiometry were corroborated with pH-dependent 1H-relaxometry data (Fig. 2). Full complex formation is achieved above pH 6.5. The relaxivity decrease observed between pH 6 and 7 might be the consequence of a small quantity of an additional protonated species present, not detectable in the pH potentiometric titration. From pH 7 and up to pH 11, MnL1 exhibits constant relaxivity (2.30 mM−1 s−1, at 0.49 T and 25 °C), evidencing the lack of substantial hydrolysis. Below pH 6, the relaxivity increase corresponds to complex protonation followed by dissociation, to reach r1 = 6.7 mM−1 s−1, characteristic of [Mn(H2O)6]+.44
Dissociation kinetics
The resistance of Mn(II) complexes to dissociation or transmetalation by endogenous ions such as Cu(II) or Zn(II) is another important parameter for safe in vivo administration. In order to describe the kinetic inertness of MnL1, we have evaluated the rate of transmetalation in the presence of Zn(II) which forms more stable complexes than Mn(II), and thus can induce dissociation. Dissociation was followed by monitoring Mn(II) release by water proton T2 measurements, at pH 4.9–6.1, in the presence of 10–50 fold excess of Zn(II) to ensure pseudo-first order conditions.The observed dissociation rate constants, kobs, increase with an increase in H+ ion concentration (Fig. 3), while remain independent of the Zn(II) concentration (Fig. S8†).
In the excess of the exchanging metal, the reaction is of pseudo-first order, and the rate is proportional to the total MnL1 concentration (eqn (1)), where kobs is the pseudo-first order rate constant.
 | (1) |
In general, different dissociation pathways can co-exist, implying the participation of protons and/or the exchanging metal ion,45 as illustrated in Fig. 4.
Based on this scheme, the overall dissociation rate can be given using eqn (2) (for clarity, charges of complexes are omitted).
 | (2) |
Here the first and second terms correspond to the spontaneous dissociation of the non-protonated and the monoprotonated complexes, respectively, the third term describes the proton-assisted dissociation of the monoprotonated complex, and the last two terms refer to the metal-assisted dissociation of the non-protonated and the monoprotonated MnL1 complex. [MnL]tot is the total concentration of Mn(II) chelates ([MnL]tot = [MnL] + [MnHL] + [ZnLMn]). Since no Zn(II) dependence is observed, only the spontaneous and the proton-assisted dissociation pathways are considered, and thus the observed rate constants can be expressed as in eqn (3), with k0 = kMnL, k1 = kMnHL·KMnHL, and k2 = HkMnHL·KMnHL.
 | (3) |
The rate constants were thus fitted to eqn (3) (Fig. 3), and the calculated parameters are listed in Table 5. In the fit, the protonation constant, KMnHL, was fixed to the value obtained from pH-potentiometric titrations. The k0 value determined is (4.1 ± 0.3) × 10−3 s−1 which shows that the spontaneous dissociation of MnL1 has a significant contribution to the overall dissociation, even if the fitted curve indicates that the k0 value is overestimated. The other important pathway is the spontaneous dissociation of the monoprotonated complex, characterized by k1 = (1691 ± 41) M−1 s−1. k2 was fixed to zero during the fitting procedure; otherwise, very low values were obtained with large errors, indicating that the proton-catalyzed dissociation of the monoprotonated complex is negligible in the pH range investigated. We should note that the pH range of this study is relatively limited (4.9–6.1; below 4.9 the dissociation becomes too fast to be followed by relaxometry), which likely leads to higher errors on the rate constants calculated. When the observed rate constants have been analyzed by also fitting the protonation constant of the complex, KMnHL, we obtained an unreasonably high value, 10-fold higher than that calculated from the potentiometric data, and on the other hand, k0 was about 50% smaller in this fit. We believe that the potentiometric determination of the protonation constant is highly reliable; therefore, we prefer keeping it fixed in the fit.
| k 0 (s−1) | k 1 (M−1 s−1) | k 2 (M−2 s−1) | k 3 (M−1 s−1) | k 4 (M−2 s−1) | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMnHLa KMnHLa |
t 1/2 (h) | Metal used in transmetalation | |
|---|---|---|---|---|---|---|---|---|
| a Obtained via pH-potentiometric titration and fixed during the calculations. b Ref. 20. c Ref. 17. d Ref. 26. e Ref. 27. f Ref. 18. g Ref. 28. | ||||||||
| L1 | (4.1 ± 0.3) × 10−3 | 1691 ± 41 | 3.82 | 2.8 min | ||||
15-pyN5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
423 | 1.0 × 107 | 1.7 × 104 | 4.27 | 11.0 | Zn(II) | ||
| 3,9-PC2Ac | 221 ± 5 | (3.6 ± 0.5) × 10−2 | 2.14 | 21.0 | Zn(II) | |||
| 3,6-PC2Ac | 70 ± 1 | (1.5 ± 0.4) × 105 | (2.6 ± 0.7) × 10−2 | 3.06 | 63.2 | Cu(II) | ||
| PC2A-EAd | 0.6 | 6.88 | 8.00 × 103 | Cu(II) | ||||
| PC2A-BPe | 16.9 ± 0.2 | 286.2 | Cu(II) | |||||
| 3,9-OPC2Af | (8.6 ± 1.1) × 10−6 | 2.81 ± 0.07 | (2.40) | 21.9 | Cu(II) | |||
| PC1Ag | 2020 ± 40 | (8.0 ± 0.3) × 107 | 4.95 | 2.4 | Cu(II) | |||
Overall, the introduction of an acetate pendant arm in the ligand results in slower dissociation for MnL1 as compared to the 15-pyN3O2 analogue, for which the dissociation was too fast and not measurable using relaxometry. Similarly, very fast dissociation was reported for Mn(15-pyN3O2Ph).25 Interestingly, the Mn(II) complex of the 15-membered analogue 15-pyN5 undergoes slower proton-assisted dissociation (k1 is four times lower than for MnL1).20 For Mn(15-pyN5), as well as for pyclen derivative complexes, k0 could not be assessed; it had to be fixed to zero in the fitting; otherwise small values were obtained with large errors (Table 5). For the pyclen derivatives, the zinc-assisted pathway that proceeds via the formation of a dinuclear Zn(L)Mn complex, characterized by k3, also contributes to a small extent to the overall dissociation, while zinc-assisted dissociation of the monoprotonated complex characterized by k4 was found for Mn(15-pyN5).20
The dissociation half-life of MnL1 was estimated at pH 7.4 and compared to those of other complexes (Table 5). MnL1 has the shortest half-life, related to the important contribution of spontaneous dissociation. Since in most of the other cases this pathway was not considered, this comparison should be taken with caution. Nevertheless, the high lability of MnL1 is obvious. In the family of these fifteen-membered macrocycles which form seven-coordinate pentagonal-bipyramidal complexes, the presence of labile Mn–ether O bonds disfavors kinetic inertness, as it was also found previously in comparing the dissociation of Mn(15-pyN5) and Mn(15-pyN3O2), where the all-nitrogen-donor ligand better prevented decomplexation.10,20 The situation might be different for more rigid 12-membered macrocycles. For instance, the rate constant characterizing the acid-assisted dissociation decreased by two orders of magnitude for MnOPC2A in comparison with the N-containing 3,9-PC2A analog.17,18 On the other hand, MnL1 has the slowest dissociation among Mn(II) complexes of 15-membered N3O2 macrocyclic ligands, pointing out the beneficial effect of the acetate pendant arm.
17O NMR and 1H NMRD
The nuclear relaxation enhancement effect of paramagnetic metal ions is described by Solomon–Bloembergen–Morgan theory of paramagnetic relaxation.4 This model relates relaxivity to the dynamic and structural parameters of the metal complexes. The 1H NMRD profiles represent the magnetic field dependency of relaxivity and are crucial to determining microscopic parameters governing relaxivity and distinguishing between different relaxation mechanisms. 1H NMRD measurements are often complemented by 17O NMR data that give direct access to the water exchange process, important for the description of relaxivity.Variable-temperature transverse 17O relaxation times were measured in aqueous MnL1 solution at pH 7.4, where the complexation is complete (Fig. 2). Longitudinal 17O relaxation rates and chemical shifts were also measured, but because of large errors, they were not further analyzed. The rate, k298ex, and the activation enthalpy, ΔH‡, and the entropy, ΔS‡, of water exchange can be determined from the temperature dependence of the 17O transverse relaxation rates, which are dominated by the scalar mechanism.47 In the slow exchange regime, where the 1/T2r values increase with an increase in temperature, only water exchange is important for transverse 17O relaxation. In the fast exchange regime, where the 1/T2r values decrease with an increase in temperature, transverse 17O relaxation rates depend also on electronic relaxation and the hyperfine coupling constant AO/ℏ; however, this regime is not observable for MnL1.
1H NMRD profiles were recorded at 25 and 37 °C in the magnetic field range 0.01–80 MHz (Fig. 5). The reduced transverse 17O relaxation rates were simultaneously fitted with 1H NMRD data according to Solomon–Bloembergen–Morgan theory (equations for this analysis are given in ESI†). Fitted parameters are summarized in Table 6 and compared to selected seven-coordinate Mn(II) complexes and [Mn(H2O)6]2+.
| Parametere | [Mn(L1)(H2O)]+ | [Mn(15-pyN3O2)(H2O)2]2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
[Mn(15-pyN5)(H2O)2]2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
[Mn(15-pyN3O2Ph)(H2O)2]+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
[Mn(H2O)6]2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
|---|---|---|---|---|---|
| a Ref. 20. b Ref. 25. c Ref. 46. d Fixed during the fitting procedure. e r 1: relaxivity, k298ex: water exchange rate, ΔH‡: activation enthalpy for water exchange, ΔS‡: activation entropy for water exchange, ErH: activation energy for the rotational motion of the complex, τRH: rotational correlation time of the Mn2+–Hwater vector, τ298v: correlation time for the modulation of zero-field splitting (ZFS), Δ2: trace of the square of the transient ZFS tensor, AO/ℏ: scalar coupling constant. | |||||
| CN/q | 7/1 | 7/2 | 7/2 | 7/2 | — |
| r 1 at 25/37 °C /mM−1 s−1 (20 MHz) | 2.45/2.08 | 4.48/3.61 | 3.56/3.13 | 5.16/— | 8.36/— |
| k 298ex/107 s−1 | 0.45 ± 0.02 | 0.38 | 6.9 | 0.64 ± 0.05 | 2.1 |
| ΔH‡/kJ mol−1 | 28.1 ± 2.1 | 35.3 | 37.7 | 34.0 ± 3 | 32.9 |
| ΔS‡/J mol−1 K−1 | −23 ± 6 | −1.0 | +32 | −1.0 ± 10 | +5.7 |
| E rH/kJ mol−1 | 15.0 ± 0.5 | 16.1 | 23.1 | — | — |
| τ 298rH/ps | 35 ± 5 | 40.3 | 28.3 | — | 30e |
| τ 298v/ps | 8 ± 1 | 3.3 | 3.9 | — | 3.3 |
| Δ 2/1018 s−2 | 160 ± 10 | 6.6 | 4.6 | — | 5.6 |
| A O/ℏ/106 rad s−1 | 38.6d | 38.6 | 38.6 | 43 ± 14 | 33.3 |
The shape of the 1H NMRD curves corresponds to low-molecular-weight complexes and shows one dispersion between 1 and 10 MHz as has been previously described for other complexes except [Mn(H2O)6]2+.48,49 The hydration number of MnL1 was assumed to be q = 1 for a total coordination number of CN = 7, based on the X-ray crystal structure. In aqueous solution, the oxygen of one acetate pendant arm which coordinates to Mn(II) to form a 1D polymeric chain in the solid-state is expected to be replaced by a water molecule to complete the coordination sphere of Mn(II). As proposed by Gale et al.,50 the 17O T2 values can also give an estimate of the hydration number, provided the 1/T2rvs. temperature curve has a maximum. As MnL1 is in the slow exchange regime in the entire temperature range studied, this approach to assess the hydration number is not applicable. We note also that the lack of a fast exchange regime prevents the fit of the scalar coupling constant, AO/ℏ, as well which was fixed to the value of 38.6 MHz.20 On the other hand, the relaxivity of MnL1 is comparable to those of other monohydrated Mn(II) chelates, and thus they support q = 1 (Table 7), but it is about 40% lower for MnL1 than for the bishydrated Mn(15-pyN3O2) (Table 6). A semi-empirical method was recently proposed for the estimation of the hydration number for Mn(II) complexes,51 based on the molecular weight of the chelate and the low field relaxivity (0.01 MHz if the NMRD profile has one dispersion). This method gave q = 0.8, in accordance with the assumed q = 1.
| [Mn(L1)(H2O)]+ | [Mn(3,9-PC2A)(H2O)]a | [Mn(3,6-PC2A) (H2O)]a | [Mn(PC1A)(H2O)]+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
[Mn(PC1P)(H2O)]b | [Mn(3,9-OPC2A)(H2O)]c | [Mn(PC2A-EA)(H2O)]d | [Mn(PC2A-BP)(H2O)]e | |
|---|---|---|---|---|---|---|---|---|
| a Ref. 17. b Ref. 28. c Ref. 18. d Ref. 26. e Ref. 27. f Ref. 26 at pH values above 8.0. g Determined at 298 K and 0.49 T. h Determined at pH 6.0. i Determined at pH 8.4. j Ref. 53 measured in the presence of HSA. k Fixed during the fitting procedure. | ||||||||
| CN/q | 7/1 | 7/1 | 7/1 | 6/1 | 6/1 | 7/1 | 7/0 | 7/1 |
| 7/1f | ||||||||
| r 2981p | 2.45 | 2.91 | 2.72 | 2.39 | 2.84 | 3.09 | 2.1h/3.5i | 4.96/35.7j |
| k 298ex/107 s−1 | 0.45 ± 0.02 | 12.5 ± 1.2 | 14 ± 2.5 | 303 ± 19 | 177 ± 9 | 5.3 ± 0.4 | 4.0 ± 0.2 | 6.3 ± 0.2 |
| ΔH‡/kJ mol−1 | 28.1 ± 2.1 | 37.5 ± 2.4 | 38.2 ± 3.9 | 13.0 ± 1.6 | 14.0 ± 1.2 | 28.5 ± 1.7 | — | 35.7 ± 0.1 |
| A O/ℏ/106 rad s−1 | 38.6k | −42.4 ± 1.9 | −44.6 ± 1.8 | 36.6 ± 1.3 | 39.9 ± 1.7 | — | — | 40.0 |
The water exchange rate calculated for MnL1, k298ex = 0.45 × 107 s−1, is higher than the value previously obtained for Mn(15-pyN3O2), but it remains one of the lowest ever observed for a Mn(II) chelate; it is slightly below that reported for Mn(15-pyN3O2Ph) (k298ex = 0.64 × 107 s−1).25
We note that the negative activation entropy, ΔS‡, is in accordance with a dissociative water exchange mechanism, as we expect for a seven-coordinated Mn(II) complex.
Given the slow water exchange of MnL1, and thus the lack of a fast exchange regime, in our analysis, the electronic relaxation parameters are determined by the NMRD data, essentially at low magnetic fields. These low field relaxivities are remarkably low (<5 mM−1 s−1) as compared to those for the parent Mn(15-pyN3O2) (∼11.8 mM−1 s−1), even considering the lower hydration number of MnL1. These differences indicate faster electron spin relaxation of MnL1 reflected in higher values of τ298v and Δ2 which might be related to the different symmetry of the two complexes; nevertheless any deeper interpretation is difficult, although some recent efforts have been made to relate the structure and the electron spin relaxation of Mn(II) complexes.52 Finally, the rotational correlation time, τ298RH and the activation energy for the rotational motion of the complex, ErH, as determined from the relaxivities, are similar to other data reported for complexes of similar size.
Conclusions
In the family of 15-membered pyridine-based macrocycles, we have prepared in a high yield a novel ligand, L1, which bears one acetate pendant arm in addition to macrocycle N and O donors in order to reinforce metal coordination. Its Mn(II) complex was characterized in the general context of MRI contrast agent development. pH-potentiometric studies evidence that the coordinating acetate function leads to higher thermodynamic stability for Mn(II), Zn(II), Cu(II) and Ca(II) complexes, in comparison with the parent 15-pyN3O2 macrocycle. The Mn(II) complex is fully formed at pH 7, as also confirmed by pH-dependent 1H-relaxometry data. Despite the slower dissociation of MnL1 with respect to Mn(15-pyN3O2), the kinetic inertness remains very modest.While the addition of the acetate function on the macrocycle is beneficial for complex stability and resistance to dissociation, it has negative consequences in reducing the hydration number, and thus the relaxivity of MnL1. r1 values are comparable to those of typical small Mn(II) chelates with q = 1, but about 40% lower than for bishydrated Mn(II) complexes such as Mn(15-pyN3O2). The water exchange rate is among the lowest ever measured for a Mn(II) complex, but it does not have a limiting effect on relaxivity.
Overall, these results indicate that MnL1 is not suitable for in vivo applications, but they provide a better insight into the relationships between the structure of pyridine-based macrocyclic ligands and the MRI activity of their Mn(II) chelates.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the financial support from the Palacký University Olomouc projects IGA_PrF_2021_009, IGA_PrF_2022_006, Palacký Endowement fund scholarship 2020 and 2022. The authors also thank Dr I. Nemec for the measurement of X-ray data and their analysis, and Dr A. Pallier for helping with 1H NMRD profile measurements.Notes and references
- P. C. Lauterbur, Nature, 1973, 242, 190–191 CrossRef CAS.
- P. Mansfield and P. Grannell, Phys. Rev. B: Solid State, 1975, 12, 3618–3634 CrossRef CAS.
- R. Damadian, L. Minkoff, M. Goldsmith, M. Standford and J. Koutcher, Science, 1976, 194, 1430–1432 CrossRef CAS PubMed.
- A. Merbach, E. Tóth and L. Helm, The Chemistry of Contrast Agents in Medical Magnetic Resonance Imaging, Wiley, 2013 Search PubMed.
- T. Grobner, Nephrol., Dial., Transplant., 2006, 21, 1104–1108 CrossRef CAS PubMed.
- R. Agarwal, S. M. Brunelli, K. Williams, M. D. Mitchell, H. I. Feldman and C. A. Umscheid, Nephrol., Dial., Transplant., 2008, 24, 856 CrossRef PubMed.
- E. Di Gregorio, G. Ferruato, C. Furlan, S. Lanzardo, R. Nuzzi, E. Gianolio and S. Aime, Invest. Radiol., 2018, 53, 167–172 CrossRef CAS PubMed.
- E. Kanal and M. F. Tweedle, Radiology, 2015, 275, 630–634 CrossRef PubMed.
- ClinicalTrials.gov., https://clinicaltrials.gov/ct2/show/NCT05413668, date of access: 16 February 2023.
- B. Drahos, I. Lukes and E. Toth, Eur. J. Inorg. Chem., 2012, 1975–1986 CrossRef CAS.
- A. Gupta, P. Caravan, W. S. Price, C. Platas-Iglesias and E. M. Gale, Inorg. Chem., 2020, 59, 6648–6678 CrossRef CAS PubMed.
- M. Botta, F. Carniato, D. Esteban-Gómez, C. Platas-Iglesias and L. Tei, Future Med. Chem., 2019, 11, 1461–1483 CrossRef CAS PubMed.
- T. Inoue, T. Majid and R. G. Pautler, Rev. Neurosci., 2011, 22, 675–694 Search PubMed.
- S. Rivera-Mancía, C. Rios and S. Montes, BioMetals, 2011, 24, 811–825 CrossRef PubMed.
- Z. Garda, A. Forgacs, Q. N. Do, F. K. Kalman, S. Timari, Z. Baranyai, L. Tei, I. Toth, Z. Kovacs and G. Tircso, J. Inorg. Biochem., 2016, 163, 206–213 CrossRef CAS PubMed.
- M. Kueny-Stotz, A. Garofalo and D. Felder-Flesh, Eur. J. Inorg. Chem., 2012, 1987–2005 CrossRef CAS.
- Z. Garda, E. Molnar, N. Hamon, J. L. Barriada, D. Esteban-Gomez, B. Varadi, V. Nagy, K. Pota, F. K. Kalman, I. Toth, N. Lihi, C. Platas-Iglesias, E. Toth, R. Tripier and G. Tircso, Inorg. Chem., 2021, 60, 1133–1148 CrossRef CAS PubMed.
- T. Csupasz, D. Szucs, F. K. Kalman, O. Holloczki, A. Fekete, D. Szikra, E. Toth, I. Toth and G. Tircso, Molecules, 2022, 27, 371 CrossRef CAS PubMed.
- (a) D. Ndiaye, M. Sy, A. Pallier, S. Meme, I. de Silva, S. Lacerda, A. M. Nonat, L. J. Charbonnière and E. Toth, Angew. Chem., Int. Ed., 2020, 59, 11958–11963 CrossRef CAS PubMed; (b) P. Cieslik, P. Comba, B. Dittmar, D. Ndiaye, É. Tóth, G. Velmurugan and H. Wadepohl, Angew. Chem., Int. Ed., 2022, 61, e202115580 CrossRef CAS PubMed; (c) D. Ndiaye, P. Cieslik, H. Wadepohl, A. Pallier, S. Même, P. Comba and É. Tóth, J. Am. Chem. Soc., 2022, 144, 22212–22220 CrossRef CAS PubMed.
- B. Drahos, J. Kotek, P. Hermann, I. Lukes and E. Toth, Inorg. Chem., 2010, 49, 3224–3238 CrossRef CAS PubMed.
- D. P. Riley, S. L. Henke, P. J. Lennon, R. H. Weiss, W. L. Neumann, W. J. Rivers, Jr., K. W. Aston, K. R. Sample, H. Rahman, C. S. Ling, J. J. Shieh, D. H. Busch and W. Szulbinski, Inorg. Chem., 1996, 35, 5213–5231 CrossRef CAS.
- A. Dees, A. Zahl, R. Puchta, N. J. R. van Eikema Hommes, F. W. Heinemann and I. Ivanovic-Burmazovic, Inorg. Chem., 2007, 46, 2459–2470 CrossRef CAS PubMed.
- M. F. Cabral and R. Delgado, Helv. Chim. Acta, 1994, 77, 515–524 CrossRef CAS.
- J. E. Newton and S. C. Jackels, J. Coord. Chem., 1988, 19, 265–277 CrossRef CAS.
- K. Pota, E. Molnar, F. K. Kalman, D. M. Freire, G. Tircso and K. N. Green, Inorg. Chem., 2020, 59, 11366–11376 CrossRef CAS PubMed.
- R. Botar, E. Molnar, G. Trencsenyi, J. Kiss, F. K. Kálmán and G. Tircsó, J. Am. Chem. Soc., 2020, 142, 1662–1666 CrossRef CAS PubMed.
- F. K. Kalman, V. Nagy, B. Varadi, Z. Garda, E. Molnar, G. Trencsenyi, J. Kiss, S. Meme, W. Meme, E. Toth and G. Tircso, J. Med. Chem., 2020, 63, 6057–6065 CrossRef CAS PubMed.
- B. Drahos, J. Kotek, I. Cisarova, P. Hermann, L. Helm, I. Lukes and E. Toth, Inorg. Chem., 2011, 50, 12785–12801 CrossRef CAS PubMed.
- S. Anbu, S. H. L. Hoffmann, F. Carniato, L. Kennig, T. W. Price, T. J. Prior, M. Botta, A. F. Martins and G. J. Stasiuk, Angew. Chem., Int. Ed., 2021, 60(19), 10736–10744 CrossRef CAS PubMed.
- S. Laine, C. S. Bonnet, F. K. Kálmán, Z. Garda, A. Pallier, F. Caillé, F. Suzenet, G. Tircsó and É. Tóth, New J. Chem., 2018, 42, 8012 RSC.
- A. Forgács, R. Pujales-Paradela, M. Regueiro-Figueroa, L. Valencia, D. Esteban-Gómez, M. Botta and C. Platas-Iglesias, Dalton Trans., 2017, 46, 1546 RSC.
- E. M. Gale, I. P. Atanasova, F. Blasi, I. Ay and P. Caravan, J. Am. Chem. Soc., 2015, 137, 15548–15557 CrossRef CAS PubMed.
- P. Antal, B. Drahos, R. Herchel and Z. Travnicek, Inorg. Chem., 2016, 55, 5957–5972 CrossRef CAS PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. van de Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466–470 CrossRef CAS.
- A. E. Martell and R. J. Motekaitis, Determination and use of stability constants, VCH Publishers, 1992 Search PubMed.
- P. Gans, A. Sabatini and A. Vacca, Talanta, 1996, 43, 1739–1753 CrossRef CAS PubMed.
- D. S. Raiford, C. L. Fisk and E. D. Becker, Anal. Chem., 1979, 51, 2050–2051 CrossRef CAS.
- E. Toth, L. Helm and A. Merbach, in The Chemistry of Contrast Agents in Medical Magnetic resonance Imaging, ed. A. Merbach, L. Helm and E. Toth, John Wiley & Sons, Chichester, 2nd edn, 2013, pp. 25–81 Search PubMed.
- I. Meunier, A. K. Mishra, B. Hanquet, P. Cocolios and R. Guilard, Can. J. Chem., 1995, 73, 685–695 CrossRef CAS.
- R. Uzal-Varela, F. Pérez-Fernández, L. Valencia, A. Rodríguez-Rodríguez, C. Platas-Iglesias, P. Caravan and D. Esteban-Gómez, Inorg. Chem., 2022, 61, 14173–14186 CrossRef CAS PubMed.
- W. D. Kim, D. C. Hrncir, G. E. Kiefer and A. D. Sherry, Inorg. Chem., 1995, 34, 2225–2232 CrossRef CAS.
- D. Esteban-Gomez, C. Cassino, M. Botta and C. Platas-Iglesias, RSC Adv., 2014, 4, 7094–7103 RSC.
- B. Drahoš, V. Kubíček, C. S. Bonnet, P. Hermann, I. Lukeš and E. Tóth, Dalton Trans., 2011, 40, 1945–1951 RSC.
- Y. Ducommun, K. E. Newmann and A. E. Merbach, Inorg. Chem., 1980, 19, 3696–3703 CrossRef CAS.
- J. Maigut, R. Meier, A. Zahl and R. van Eldik, Inorg. Chem., 2008, 47, 5702–5719 CrossRef CAS PubMed.
- S. H. Koenig, C. Baglin, R. D. Brown III and C. F. Brewer, Magn. Reson. Med., 1984, 1, 496–501 CrossRef CAS PubMed.
- I. Bertini, F. Briganti, Z. Xia and C. Luchinat, J. Magn. Reson., Ser. A, 1993, 101, 198–201 CrossRef CAS.
- E. M. Gale, J. Zhu and P. Caravan, J. Am. Chem. Soc., 2013, 135, 18600 CrossRef CAS PubMed.
- J. A. Peters and C. F. G. C. Geraldes, Inorganics, 2018, 6(4), 116 CrossRef CAS.
- R. Uzal-Varela, L. Valencia, D. Lalli, M. Maneiro, D. Esteban-Gómez, C. Platas-Iglesias, M. Botta and A. Rodríguez-Rodríguez, Inorg. Chem., 2021, 60, 15055–15068 CrossRef CAS PubMed.
- G. Rolla, V. de Biasio, G. B. Giovenzana, M. Botta and L. Tei, Dalton Trans., 2018, 47, 10660–10670 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: 2D NMR spectra, more X-ray analysis details, dissociation kinetics results, potentiometric titration curves and equations for analysis of 17O NMR and 1H NMRD data. CCDC 2244643. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3dt00701d |
| This journal is © The Royal Society of Chemistry 2023 |