Inorganic anion recognition in aqueous solution by coupling nearby highly hydrophilic and hydrophobic moieties in a macrocyclic receptor

Abstract

Receptor L, composed of a tripropylenetetramine chain linking the 2 and 7 positions of an acridine unit via methylene bridges, behaves as a pentaprotic base in aqueous solution. The first four protonation steps occur on the tetra-amine chain, while the acridine nitrogen protonates only below pH 4. The penta-protonated receptor assumes a folded conformation, resulting in a cleft delimited by the aliphatic tetramine and acridine moieties, in which anions of appropriate size can be hosted. Potentiometric titrations reveal that F⁻ forms the most stable complexes, although the stability constants of the Cl⁻ and Br⁻ adducts are unusually only slightly lower than those observed for F⁻ complexes. A remarkable drop in stability is observed in the case of I⁻ adducts. Oxo-anions, including H₂PO₄⁻, NO₃⁻ and SO₄²⁻, are not bound or weakly bound by the protonated receptor, despite the known ability of charged oxygens to form stable O⁻⋯HN⁺ salt bridges. This unexpected stability pattern is explained in the light of the X-ray crystal structures of H₅LCl₅·4H₂O, H₅LBr₅·4H₂O, H₅L(NO₃)₅·3H₂O and H₅L(H₂PO₄)₅·(H₃PO₄)₂·4H₂O complexes, coupled with MD simulations performed in the presence of explicit water molecules, which reveal that Cl⁻ and, overall, Br⁻ possess the optimal size to fit the receptor cleft, simultaneously forming strong salt bridging interactions with the ammonium groups and anion⋯π contacts with protonated acridine. I⁻ and oxo-anions are too large to conveniently fit the cavity and are only partially enclosed in the receptor pocket, remaining exposed to solvent, with a lower entropic stabilization of their complexes. Although F⁻ could be enclosed in the cavity, its smaller size favours the F⁻⋯HN⁺ salt bridging interaction from outside the receptor pocket. The fluorescence emission of the acridinium unit is quenched by anion binding. The quenching ability parallels the stability of the complexes and is related to the relevance of the anion⋯π contacts in the overall host–guest interaction.

---

Introduction

Recognition of inorganic anions has become a research area of increased interest in the field of both environmental and biological chemistry.^1,2 In fact, anions play a major role in a number of environmental fates and industrial processes as well as in the biological metabolism of living beings, where phosphate, carbonate, sulphate, nitrate, and halide anions are the species most frequently found. Among halides, fluoride and bromide, though naturally occurring, can be of environmental concern, both of them being toxic at high concentration levels.^3–6 Besides its release in the environment from industrial processes, fluoride is also found in natural fresh water in high concentrations and its abatement is a current challenge in water treatment in several areas of the world.^5,6 Bromide is an undesired by-product of a number of industrial chemical processes.⁴ Conversely, chloride is essential for human health and is transported across cell membranes by various Cl⁻ intracellular channel proteins, often in conjunction with cation transportation, while iodide is involved in thyroid physiology.⁷ Sulphates are used in a variety of human activities and are formed in the atmosphere by oxidation of low valent sulphur compounds.^8,9 As such, they are one of the major components of fine particulate matter, a currently recognized public health hazard.⁹ Phosphates are involved in a number of biological processes, many of them related to signal transduction chains,⁷ but their salts are also commonly present in a variety of products for human consumption,¹⁰ and, together with nitrates,¹¹ are one of the main components of fertilizers,¹² whose excessive use leads to water eutrophication.¹³ In this context, in recent years a number of molecular receptors have been developed for inorganic anion binding with different purposes, including their sequestration for environmental remediation¹⁴ and detection in biological or environmental matrices.² In particular, fluorescence chemosensing using receptors equipped with luminescent units stands as a spectroscopic tool capable of signalling the presence of these anions in real matrices in small concentrations and in a real-time and non-destructive mode thanks to the change of emission properties upon a selective host–guest interaction.² Usually a fluorescent chemosensor for anion recognition and sensing is structured following the “binding-site signalling subunit” protocol: the binding site is covalently linked to the signalling unit through an appropriate spacer so that the host–guest interaction of the target species with the binding unit modulates the fluorescence of the signalling unit. The binding site is designed to achieve spatial optimization of non-covalent interactions through topological complementarity.^1,2 The task is particularly difficult in aqueous media as inorganic anion solvation by water molecules can strongly compete with the binding to the receptor unit, requiring the use of hosts containing clefts or cavities of the appropriate size to lodge the anions.^1,2,15–22

Polyamines are appealing receptors for anions, including inorganic anions, in water. In fact, polyamines normally occur as polycharged cations in water solution, even at neutral pH values, establishing strong charge–charge and hydrogen bonding interactions with the anionic species, which are a necessary pre-requisite for complex coordination in a solvating protic medium. Several examples of inorganic anion binding through encapsulation within cavities or clefts of protonated polyamine receptors in aqueous solution have been recently reported;^2,23–45 however, studies on metal-free fluorescent receptors of polyammonium type in pure water are still less common^38–45 and most of them are related to fluoride or phosphate anion recognition. Specific binding of fluoride is generally obtained by exploiting its high negative charge density and the consequent ability to form strong hydrogen bonding interactions with appropriate H-bonding donor groups, much higher than that found for other halides. From this point of view, oxo-anions are also able to strongly interact via charge–charge interactions and hydrogen bonding, thanks to the negatively charged oxygens that can act as strong hydrogen bonding acceptors. Typical examples can be phosphates and sulphates, which are able to form stable adducts in aqueous solution with appropriately tailored receptors, including polyammonium-based ones.^28–37 Cl⁻, Br⁻ and I⁻ are the anions most difficult to target with polyammonium receptors, due to their lower charge density and tendency to behave as H-bonding acceptors. Nevertheless, examples of macropolycyclic polyammonium cations able to form stable complexes with these elusive anions have been reported. They possess cage-like structures in which the anion can be conveniently hosted from the dimensional point of view and exploit the stabilizing effects of both formation of salt bridge interactions and anion desolvation upon encapsulation within the receptor cavity. They include katapinates,⁴⁶ tren²³ and bis-tren⁴⁷ derivatives, and macrotricyclic oxa–aza receptors.⁴⁸ In particular, the bis-tren derivative L_A,⁴⁷ the tren-based azaphane L_B ²³ and the oxa–aza cryptand L_C (Scheme 1)⁴⁸ display a relevant binding affinity for Cl⁻, the stability constants of their complexes being greater than 4 log units. Br⁻ is generally more difficult to target. Among the receptors cited above, L_A shows the highest binding ability for this anion. Recently, new types of receptors have been proposed for anion binding. However, among them only a few receptors can form stable complexes with Cl⁻, Br⁻ and/or I⁻ in pure water. They come from the families of bambus[6]uril⁴⁹ or biotin[6]uril⁵⁰ receptors (macrocycles composed of 6 2,4-substituted glycoluril or 6 biotin units connected to each other via methylene bridges), dicyclopeptides,⁵¹ rotaxanes,⁵² macropolycyclic quaternary polyammonium cations,⁵³ triangular cages containing pyridinium units,⁵⁴ and Pd(II)-based coordination cages.⁵⁵ These receptors feature a three-dimensional cavity able to encapsulate anions of appropriate size, held mainly by hydrogen and/or halogen bonds or electrostatic interactions. In this context, examples of metal-free fluorescent receptors in which Cl⁻, Br⁻ or I⁻ binding generates a change in their emission properties in pure water remain extremely limited.^43,52

Recently, we have reported on receptor L_D (Scheme 1),^56,57 containing a triethylenetetramine chain linking the 4 and 5 positions of an acridine unit. The receptor forms protonated species H_xL_D^x+ (x = 1–4), in which the acidic protons are localized on the aliphatic nitrogen atoms, while the acridine nitrogen cannot be protonated even at strongly acidic pH values. Among halide anions, fluoride is almost encapsulated within the receptor cavity, while chloride is placed somewhat above the plane of the macrocyclic ring.⁵⁷ This would enable the formation of strong hydrogen bonding and charge–charge interactions with the ammonium groups of the receptor. In consequence, F⁻ and Cl⁻ complexes are more stable than those formed by the larger Br⁻ and I⁻.

Scheme 1 Ligand drawings.

Receptor L, originally synthesized in the course of study on new polyamine-based intercalating agents for DNA,⁵⁸ presents a tripropylenetetramine chain linking the 2 and 7 positions of an acridine unit. In principle, the presence of propylenic chains between the amine groups would ensure larger flexibility. At the same time, the acridine nitrogen points outside the macrocyclic cavity. Despite the lower basicity of the heteroaromatic nitrogen atom, the larger distance from the aliphatic amine groups could favor its protonation, at least in the receptor species with a higher protonation degree. While the tetramine chain, when protonated, can enable the formation of salt bridges between the anions and the ammonium groups, protonation of acridine could favor anion⋯π contacts with the aromatic system. Anion⋯π interactions are often present in host–guest adducts between halide anions and receptors containing electron-poor aromatic moieties.⁵⁹ This interaction mode could not only enhance the stability of the complexes, but also generate an optical signal upon anion binding. Finally, acridine also has marked hydrophobic characteristics, which can favor anion desolvation, leading to an entropic energetic gain upon binding. In this context, we have now analyzed the binding and sensing properties of L towards the halide anions F⁻, Cl⁻, Br⁻ and I⁻, and the commonly occurring oxo-anions H₂PO₄⁻, and SO₄²⁻ and NO₃⁻.

In particular, we wanted to explore the effects of the receptor structural changes that occur on passing from L_D to L on the binding and sensing properties towards the considered anions (especially halides), in order to gain useful information to improve the structure-based design of artificial polyamine receptors and achieve the best possible performances in halide binding and sensing in aqueous media by optimizing different types of non-covalent interactions via the appropriate spatial organization of the binding groups.

Results and discussion

Receptor protonation in aqueous solution

Analysis of the basicity of polyamine receptors is a necessary pre-requisite to investigate their binding ability to anions in aqueous solution. Therefore, we first performed potentiometric titrations of L at 298 K in 0.1 M NaCF₃SO₃ aqueous solution, to determine the receptor protonation constants. Sodium trifluoromethanesulphonate ionic medium was used considering the poor ability of the organic sulphonate to interact via hydrogen bonding with polyammonium cations, which could compete with binding to the relevant anions considered in this study. The determined protonation constants are given in Table 1, together with those of the fluoride and phosphate anions.

Table 1 Protonation constants of L, F⁻ and PO₄³⁻ (298 K, NaCF₃SO₃ 0.1 M)

Equilibrium	log K
L + H^+ = HL^+	9.98(5)
HL^+ + H^+ = H2L^2+	9.22(4)
H2L^2+ + H^+ = H3L^3+	7.71(4)
H3L^3+ + H^+ = H4L^4+	7.09(4)
H4L^4+ + H^+ = H5L^5+	4.8(1)
F^− + H^+ = HF	3.0(1)
PO4^3− + H^+ = HPO4^2−	11.20(4)

---

The first four protonation constants range between 9.98 and 7.09 log units and strongly resemble those reported for linear tripropylenetetramine. The last protonation constant is by far lower and can be attributed to the protonation of the acridine nitrogen. Its value is just somewhat lower than that of acridine (log K = 5.3),^60,61 indicating that the basicity of the heteroaromatic nitrogen is slightly affected by the presence of the tetra-protonated polyamine chain, likely due to the rather long distance between the two moieties.

To verify that acridine protonation occurs only in the last protonation step of L and to analyse the effects of protonation on the photophysical properties of the ligand, we recorded its UV-vis absorption and fluorescence emission spectra at different pH values (Fig. 1). The UV-vis spectrum of L from alkaline to slightly acidic pH values resembles that of acridine, displaying a structured band with a maximum at 361 nm, whose intensity remains almost constant up to pH 6.

Fig. 1 pH dependence of the UV-vis absorption spectrum of L (a), absorbance at 361 nm at different pH values (black dot) superimposed to the distribution diagram of the protonated species of L (b), pH dependence of the fluorescence emission spectrum of L (the spectra recorded between pH 6 and 8.7 are reported in dotted lines) (c) and emission intensities at 420 (red dots) and 470 (black dots) nm superimposed to the distribution diagram of the protonated species of L (d) (aqueous solution, 298 K, λ_exc = 370 nm).

An enhancement of the absorbance can be observed below pH 6, accompanied by the formation of a shoulder at 400 nm (Fig. 1a). As a matter of fact, superimposition of the absorbance values at 361 nm with the distribution curves of the receptor protonated species points out that the observed spectral changes, normally attributed to the protonation of acridine,⁶⁰ occur upon the formation of the penta-protonated H₅L⁵⁺ species, in agreement with hypothesis made on the basis of the potentiometric titrations (Fig. 1b).

The emission spectrum of L shows a much more marked pH dependence. L is basically not emissive above pH 9. At lower pH values a band centred at 420 nm, attributable to the emission of unprotonated acridine, appears in the spectra. Its intensity increases up to pH 5.7. Below this pH value, the emission at 420 nm starts decreasing, and the spectra feature a new red-shifted structured band centred at 470 nm, whose intensity increases with decreasing pH (Fig. 1c). The latter band can be attributed to the acridinium emission.^56,57,60

A comparison of the emission intensity recorded at 420 and 470 nm (Fig. 1d) points out that the acridine band at a lower wavelength is due to the formation of the tetra-protonated H₄L⁴⁺ form of the receptor. This result confirms that in this species the four acidic protons are localized on the aliphatic nitrogen atoms. This would also inhibit any photo-induced electron transfer (PET) process from the unprotonated amine groups to the fluorophore, which is likely the origin of the lack of the emission observed for the less protonated species of the receptor (HL⁺, H₂L²⁺ and H₃L³⁺). Protonation of acridine occurs below pH 5.7 upon the formation of the fully protonated H₅L⁵⁺ species, in agreement with the hypothesis made on the basis of the results from potentiometric and UV-vis measurements.

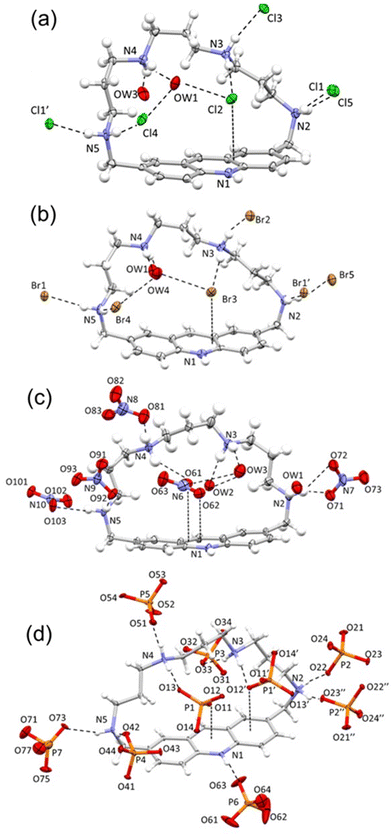
Crystal structures of the H₅L⁵⁺ salts with Cl⁻, Br⁻, NO³⁻ and H₂PO⁴⁻

Slow evaporation of aqueous solutions containing receptor L (10⁻³ M) and hydrochloride, hydrobromide, nitric or orthophosphoric acid at pH 2 afforded crystals corresponding to formulations H₅LCl₅·4H₂O (1), H₅LBr₅·4H₂O (2), H₅L(NO₃)₅·3H₂O (3) and H₅L(H₂PO₄)₅·(H₃PO₄)₂·4H₂O (4), respectively. An X-ray diffraction analysis was undertaken to understand the structure and ligation patterns in the isolated compounds. The obtained crystals were not of the best quality. Nonetheless, a description of their crystal structures can be provided, and the disposition of the ligand, anions and water molecules can be definitively confirmed. ORTEP drawings with atom labelling schemes of the four structures are shown in Fig. 2, while selected interesting contacts are summarized in Table 2.

Fig. 2 ORTEP drawing of the H₅LCl₅·4H₂O (1) (a), H₅LBr₅·4H₂O (2) (b), H₅L(NO₃)₅·3H₂O (3) (c), and H₅L(H₂PO₄)₅·(H₃PO₄)₂·4H₂O (4) (d) complexes. Displacement ellipsoids are drawn at 50% probability level. Only water molecules inside the receptor cleft are shown.

Table 2 Selected contacts for the H₅LCl₅·4H₂O (1), H₅LBr₅·4H₂O (2), H₅L(NO₃)₅·3H₂O (3) and H₅L(H₂PO₄)₅·(H₃PO₄)₂·4H₂O (4) complexes

Formula (compound)	Dihedral angle^a (°)	Acridine mean plane ⋯X distance (d) (Å) and ∑rvdW(C, X) − d^b	H-bond distances (Å) (species close or inside the pocket)
a Dihedral angle between the plane defined by the acridine system and the plane defined by the four protonated secondary nitrogen atoms in H5L^5+. b X = Cl, Br or closest O for polyatomic anions inside the receptor pocket.
H5LCl5·4H2O (1)	108.5(1)	3.363(2)	3.150(5) N3⋯Cl2
		0.227	3.175(4) Cl2⋯OW1
			3.102(4) Cl4⋯OW1
H5LBr5·4H2O (2)	108.3(2)	3.429(1)	3.296(8) N3⋯Br3
		0.201	3.300(7) Br3⋯OW4
			3.248(7) Br4⋯OW4
H5L(NO3)5·3H2O (3)	112.9(2)	2.972(7)–O61	2.99(1) N4⋯O61
		0.298	3.10(1) O61⋯OW2
		3.022(9)–O62	3.15(1) O61⋯OW3
H5L(H2PO4)5·(H3PO4)2·4H2O (4)	104.2(2)	3.143(6)–O11	2.800(8) N4⋯O13
		0.129	2.830(9) N3⋯O12′
		3.451(6)–O12′

---

The four complexes are characterized by common structural features, which are better analyzed together comparatively. In fact, the ligand always assumes a bent conformation with the plane defined by the acridine system almost perpendicular to the plane defined by the four protonated secondary nitrogens. The dihedral angles given by the two planes range from a minimum of 104.2(2)° for the phosphate complex, to a maximum value of 112.9(2)° for the nitrate one (Table 2). Similar bent arrangements have often been found in the crystal structures of aza-macrocycles and thia–aza-macrocycles containing aromatic systems with fused rings, especially in connection with short aliphatic chains.⁶²

An apparent exception to this rule is ligand L_D (Scheme 1). In fact, in the crystal structure of its tetra-bromide salt H₄L_DBr₄·2H₂O,⁵⁶ L_D was found to assume an almost planar arrangement. It is to be underlined, however, that in this ligand the aliphatic chain, although shorter than that present in L, was attached to the 4 and 5 positions of the acridine moiety, so indicating an overall lower degree of flexibility as compared to macrocycle L, which is the object of study.

Interestingly, in all herein reported structures, the pocket defined by the aromatic and the aliphatic moiety of the ligand seems to constitute a preferential binding site, wherein the hosted anions are firmly held in place by the cooperative action of H-bonds and anion⋯π interactions (Fig. 2), at least in the solid state. The other anion units present in each compound generally interact via a single H-bond with a protonated nitrogen atom staying outside the receptor cleft.

As shown in Fig. 2a–c, in the case of the monoatomic chloride and bromide and polyatomic nitrate anions a water molecule helps fill the pocket and stabilizes the complex via H-bond interactions (Table 2; for a complete list of H-bond contacts see Tables S2–S5 in the ESI†). This additional water molecule is missing in 4, being replaced by a second symmetry related phosphate (Fig. 2d). The anion⋯π contacts found in these structures indicate that the four anions establish strong interactions with the protonated acridine moiety. Actually, the differences between the sum of van der Waals radii (r_vdWC + r_vdWX)⁶³ and the measured acridine mean plane⋯X distances (d, X = Cl, Br, closest O for polyatomic anions) are never lower than 0.129 Å, demonstrating that halide anions or a single oxygen from oxo-anions are sitting within the receptor cleft. The maximum ∑r_vdW(C, X) − d difference observed for the nitrate anion oxygen (0.30 Å) can be related to its flat nature that may promote π-type interactions.

The crystal packings (see the ESI, Fig. S1†) look affected by the strength of the anion⋯π interactions, the shape and dimensions of anions, and the π–π stacking interactions between acridine moieties. In fact, in the case of the spherical monoatomic ions, couples of [H₅LCl]⁴⁺ or [H₅LBr]⁴⁺, symmetry related by an inversion center, tightly interact via a cooperative network of NH⁺⋯X⁻ salt bridges and anion⋯π interactions between the protonated acridine groups. The so-formed {[H₅LCl]⁴⁺}₂ or {[H₅LBr]⁴⁺}₂, pairs then interact via π–π stacking with adjacent centrosymmetric pair units giving rise to infinite columns which represent the main structural features of these structures (Fig. S1a and S1b†). On the other hand, the larger phosphate anion is not able to give so tightly linked pairs as chloride and bromide anions do, but the {[H₅L(H₂PO₄)]⁴⁺}₂ couples must rearrange losing the acridine involving salt bridges. Nevertheless, even the phosphate complex features columns of centrosymmetric couples interacting via π–π stacking in its crystal packing (Fig. S1d†). This type of arrangement, arising from the interplay of different non-covalent forces, yet ending up in closely related ordered columns apparently due to ligand geometry and its interaction preferences, reminds us of the recently reported self-assembly case of Blue Box with iodide anions.⁶⁴

The crystal packing of the nitrate complex presents the most significant difference in comparison with the other three structures, as the {[H₅L(NO₃)]⁴⁺}₂ pairs are not formed, yet each [H₅L(NO₃)]⁴⁺ species interacts via π–π stacking with the acridine group of the closest symmetry related adduct unit.

Given their relevance in supporting solution data, the two crystal structures featuring halides (Cl⁻, Br⁻) have been subjected to further examination. For instance, it can be shown that the ligand is almost perfectly superimposable between the two structures (the root mean square displacement computed on all atoms is 0.033 Å) and also surrounding anions (in contact within the sum of the van der Waals radii, ∑r_vdW(C, X); X = Cl, Br) come to occupy almost the same positions, this is especially true for the anions inside the ligand pocket (Fig. 3).

Fig. 3 Superposition of ligands in structures 1 and 2 and resulting distribution of anions in contact with them (a), side view and (b) front view (chloride and bromide anions are in green and brown colors, respectively). Displacement ellipsoids are drawn at 80% probability level to highlight differences.

Hirshfeld surface analysis,^65,66 oftentimes used to highlight subtle structural differences,⁶⁴ also confirms that the ligands are found in almost identical environments. Given that ligands’ Hirshfeld surface total area is practically invariant between the Cl⁻ and Br⁻ complex (454.47 vs. 455.67 Ų), their percentage compositions can be directly confronted: they also hardly vary (full information is provided in the ESI, Table S6†). The only difference is a mere 2% extra ligand⋯Br contacts (with respect to ligand⋯Cl ones) formed at the expense of ligand units touching each other (H–H contacts); such small differences are probably due to the different sizes (or electronic density for which the Hirshfeld surface method is concerned) of the two anions.

Hirshfeld surfaces can be used to generate insightful images of the portions of ligands in contact with anions (see Fig. 4 and S2† for the chloride and bromide salts, respectively). Beyond obvious and prominent H-bonds (see also tip-like feature in the fingerprint plot, Fig. S3†), the typical swoosh due to strong and centered anion⋯π contacts⁶⁷ is also clearly observed. The Hirshfeld surface of the ligand with C⋯X contacts highlighted clearly shows that the whole central ring of the acridinium unit takes part in complex stabilization (Fig. 4 and S2†).⁶⁸

Fig. 4 Ligand Hirshfeld surface in compound 1: contact distance (d_norm) standard coloring (a), shape index coloring (b), visualization of H⋯Cl contacts, corresponding to CH⋯anion (weak interactions) and ⁺NH⋯Cl salt-bridges (red interaction hotspots, Cl⁻ anions in contact shown) (c), and visualization of C⋯Cl contacts (anion⋯π interactions) which highlight the involvement of the whole central heterocycle (d).

While coloring of the Hirshfeld surface with contact (d_norm), internal (d_i) or external (d_e) distances are generally the most useful, in this case we also took advantage of the shape index descriptor.^68,69 Shape index,⁶⁸ defined as S = (2/π) arctan[(k₂ + k₁)/(k₂ − k₁)], with k₂ and k₁ principal curvatures of the surface (k₂ ≥ k₁), is a descriptor rendering the qualitative shape of a molecule: for our purpose, it can be viewed as a measure of the bulging out (blue) or in (red) of our ligand, with the caveat that two surfaces whose shape indexes only differ by a sign represent a complementary stamp/mould pair.

It is manifested, from Fig. 4b and S2b,† that the bulging in of the ligand defines the anion binding pocket. Red shape index pit of the ligand (−0.9926 for Cl⁻ complex, −0.9987 for Br⁻ complex) is found mirrored by blue shape index maxima of the anion (Cl⁻ 0.9911, Br⁻ 0.9962), thus providing a semi-quantitative view of the concept of complementarity. Even without such an attempt at formalization, the ability of the ligand to engulf halides for a significant portion of their volume can easily be shown (Fig. 5), in particular in the case of Cl⁻ and Br⁻ anions. The same considerations, however, can be qualitatively extended to oxo-anions. Due to the fact that the smaller oxygen might be able to fit into the receptor pocket, at most one polar head of these polyatomic anions can be slotted into the cavity, leaving most of the anions exposed.

Fig. 5 Visual comparison of the ability of H₅L⁵⁺ to engulf Cl⁻ (1, water molecule in red) (a), Br⁻ (2, water molecule in red) (b), NO₃⁻ (3, water molecule in cyan) (c), and H₂PO₄⁻ (4, second less interacting anion in pink) (d).

Anion binding in aqueous solution

Crystal structures described above show how a single halide anion, or a single oxygen atom in the case of nitrate and dihydrogen-phosphate, is firmly bound in the receptor cleft, held by salt NH⁺⋯X (X = Cl, Br, O) bridges coupled to anion⋯π contacts. Accordingly, we tested the ability of the ligand to bind in solution, and possibly to sense via fluorescence emission changes, the inorganic anions considered, in particular halide anions. In fact, the latter represent difficult targets in aqueous solution, due to their high solvation free energies, which can efficiently compete with anion binding by artificial receptors. We also analysed the coordination of relevant inorganic mono- and di-charged oxo-anions (nitrates, phosphates, and sulphates). The receptor is present in solution, depending on pH, in different protonated species potentially able to bind anions. Therefore, we performed potentiometric titrations to determine for each anion the species formed at different pH values and their stability constants. The results are given in Table 3.

Table 3 Stability constants of the anion complexes formed in solution with L (298 K, NaCF₃SO₃ 0.1 M)

Equilibrium	log K
H4L^4+ + F^− = [H4LF]^3+	4.0(1)
H5L^5+ + F^− = [H5LF]^4+	5.2(1)
H4L^4+ + Cl^− = [H4LCl]^3+	3.8(1)
H5L^5+ + Cl^− = [H5LCl]^4+	4.7(1)
H4L^4+ + Br^− = [H4LBr]^3+	3.4(1)
H5L^5+ + Br^− = [H5LBr]^4+	4.4(1)
H4L^4+ + I^− = [H4LI]^3+	—
H5L^5+ + I^− = [H5LI]^4+	2.9(1)
H4L^4+ + H2PO4^− = [H4L(H2PO4)]^3+	2.6(1)
H5L^5+ + H2PO4^− = [H5L(H2PO4)]^4+	2.9(1)

---

All measurements were performed at 298 K in the 0.1 M NaCF₃SO₃ ionic medium. The use of this ionic medium is justified by the poor ability of the sulphonate anion to interact with polyammonium receptors and by the low tendency of CF₃SO₃⁻ to interfere with the binding of the selected anions.

The data in Table 3 point out that, among the anions considered, only halides and, to a less extent, phosphates, show detectable interactions with the receptor, forming complexes with a 1 : 1 anion to receptor stoichiometry. At the same time, potentiometric measurements show that only H₄L⁴⁺ and H₅L⁵⁺ form stable complexes with the anions. Most likely, the stability of the adducts with less protonated forms of L is too low to be potentiometrically detected. The complexes formed by H₅L⁵⁺ are more stable than those formed by H₄L⁴⁺ likely due to both the difference of the net charge on the macrocycle and the presence, in H₅L⁵⁺, of the acridinium moiety, which can show stabilizing anion⋯π interactions. Considering the various halide anions, the stability of their complexes decreases from the smaller fluoride to the larger iodide anion. Fluoride is known for its ability to form strong hydrogen bonds with respect to the other halide anions, and this would explain the higher stability of its complexes. A drop in stability is indeed observed for Cl⁻ and Br⁻ adducts; nevertheless, for the complexes with H₅L⁵⁺ the drop in stability is only ca. 0.5 and 0.8 log unit for Cl⁻ and Br⁻, respectively, with respect to the fluoride adduct. Finally, I⁻ forms remarkably less stable complexes with H₅L⁵⁺; the drop in stability with respect to F⁻ is more than 2 log units, and no interaction is detected with H₄L⁴⁺. The stability of the H₂PO₄⁻ complexes is similar to that of iodide ones. Nitrate and sulphate do not appear to form complexes in aqueous solution. This result may appear surprising considering that phosphate and sulphate often show stronger interactions with protonated polyamines than chloride, bromide and iodide, thanks to their higher ability to act as hydrogen bond acceptor sites, and, in the case of SO₄²⁻, to its higher charge. The absence of any interaction with HPO₄²⁻ is likely due to its formation above pH 6, where H₄L⁴⁺ and H₅L⁵⁺ are not formed in aqueous solution. Among halides, fluoride normally forms remarkably more stable complexes with polyammonium receptors in water, thanks to its high charge density and strong H-bond acceptor behaviour. In contrast, larger halide anions generally show weaker interactions with polyammonium hosts in aqueous solution.^1,2 This would suggest that besides charge–charge and H-bonding interactions, which normally constitute the most relevant driving forces in the formation of anion complexes with polyammonium receptors, other interactions can give important contributions to the stability of the present complexes with Cl⁻ and Br⁻, including the possible formation of anion⋯π interactions involving the electron-poor acridine moiety, in particular in its protonated form. At the same time, structural factors related to the receptor conformation in its protonated forms can influence the stability of the complexes with anions of different sizes and/or structures. From this point of view, the crystal structures of the chloride, bromide, dihydrogen-phosphate and nitrate salts of H₅L⁵⁺ shows that in each compound, a single anion is partially enclosed within the cleft generated by the protonated tetramine chain and the acridine unit, held by NH⁺⋯X (X = Cl, Br, O) salt bridges with at least one aliphatic polyammonium group, and an anion⋯π contact. The spherical chloride and bromide anions are deeply enclosed in the receptor cleft, while the larger oxo-anions show just a single oxygen atom embedded in the cavity, while the remaining 2 (in the case of NO₃⁻) or 3 oxygen atoms (in the case of H₂PO₄⁻) remain outside the receptor cleft. The similar positioning of Cl⁻ and Br⁻ within the receptor cleft would explain the small difference in stability for the complexes of these anions, which, in turn, are also remarkably more stable than the adducts formed by I⁻ and H₂PO₄⁻ anions. Of note, no interaction is detected for SO₄²⁻ and NO₃⁻, whose dimensions are likely too large to fit the receptor cleft.

Remarkably, although the stability of the Cl⁻ and Br⁻ complexes with this monocyclic receptor is comparable or even higher than that reported for polyammonium cryptands L_A, L_B and L_C (Scheme 1), the latter encapsulate these anions within their cavity allowing their complete desolvation. The most stable complexes with chloride and bromide are formed by the hexa-protonated form of the bis-tren derivative L_A (log K = 5.75 and 4.40 for the equilibrium H₆L_A⁶⁺ + X⁻ = [H₆L_AX]⁵⁺, with X = Cl⁻ and Br⁻, respectively), while the penta-protonated species H₅L_A⁵⁺ forms less stable complexes with Cl⁻ and Br⁻ compared to the penta-charged H₅L⁵⁺ cation.⁴⁷ These observations point out the relevance of the acridinium moiety in complex stabilization. Indeed, the simultaneous formation of both salt bridging and anion⋯π interactions enhances the stability of the complex with anions, like Cl⁻ and Br⁻, which optimally fit the binding cleft of receptor L.

Both acridine and the acridinium cation are fluorescent and their emission has been found to be affected by the coordination of anions by appropriate receptors, such as L_D.⁵⁷ Therefore, we also performed an analysis of their emission properties in the presence of the anions under investigation. As discussed above, the receptor is emissive only at acidic pH values, where the H₄L⁴⁺ and H₅L⁵⁺ protonated forms are the most abundant species in solution. Therefore, we performed fluorimetric titrations by adding increasing amounts of each anion at pH 6, where the most abundant species is the tetra-protonated receptor H₄L⁴⁺ and at pH 3.5, where the H₅L⁵⁺ species is predominant in solution.

Interestingly enough, the addition of increasing amounts of the selected anions to solution of the receptor at pH 6 does not remarkably quench the emission of the receptor. Only in the case of F⁻ a minor decrease in the emission intensity of acridine at 420 nm can be observed (see Fig. 6a). In contrast, the emission of acridinium at 470 nm, measured at pH 3.5, is remarkably affected by the addition of halide anions and phosphate, mainly present as H₂PO₄⁻ species at this pH value. As shown in Fig. 6b and 6c, the addition of increasing amounts of F⁻ induces a linear decrease of the emission up to a 1 : 0.75 L to fluoride molar ratio. At higher molar ratios a smoother decrease is observed, up to ca. 70% reduction of the emission in the presence of 10 equiv. of fluoride. Similar trends are observed for other halides and H₂PO₄⁻ (Fig. 6c and Fig. S4, ESI†), although in the cases of I⁻ and H₂PO₄⁻ the emission quenching is less marked. The data in Fig. 6c suggest the formation of complexes with a 1 : 1 receptor to anion stoichiometry. From this point of view, the quenching ability of the anions decreases in the order F⁻ < Cl⁻ < Br⁻ < I⁻ < H₂PO₄⁻, which is quite the same trend as that observed for the stability constants of the complexes with the penta-protonated receptor, thus suggesting that the observed emission changes depend on the stability of the complex.

Fig. 6 Fluorescence emission spectra of L in the presence of increasing amounts of fluoride at pH 6 (a) and at pH 3.5 (b) and plot of the emission intensity at 470 nm in the presence of increasing amounts of different anions at pH 3.5 (T = 298 K, λ_exc = 370 nm) (c). Addition of nitrate and sulphate does not appreciably change the emission (observed changes lower than 3%); these data are not reported for clarity.

In the case of L_D, F⁻ and Cl⁻ form complexes with similar stability, while Br⁻ and I⁻ form remarkably less stable complexes. F⁻ and Cl⁻ induce emission enhancement of non-protonated acridine thanks to a photoinduced proton transfer process from an ammonium group of the aliphatic chain to the heteroaromatic nitrogen, generating an emissive acridinium cationic moiety. Conversely, Br⁻ and I⁻ favour quenching of the acridine emission.⁵⁷ Receptor L_D in its protonated forms assumes an almost flat conformation and the smaller F⁻ and Cl⁻ anions are almost encapsulated within its cavity, thus favouring the proton transfer process. In the case of L, all anions under investigation essentially do not affect the emission of the acridine moiety in the H₄L⁴⁺ species, ruling out possible proton transfer processes. Conversely quenching of the emission is observed in the H₅L⁵⁺ species, in which, as shown by the crystal structures of the chloride and bromide salts, the acridinium cation can interact via anion⋯π pairing with halide anions, an interaction mode known for its ability to quench the emission of an acridinium moiety.^70,71

Molecular dynamics simulations

To rationalize the interaction mode of receptor L in its protonated forms toward different anions, we performed full-atom molecular dynamics (MD) simulations, whose technical details are reported in the Experimental section. Considering that the potentiometric titrations have shown the formation of complexes in solution with a 1 : 1 receptor to anion stoichiometry, in which the receptor is in its tetra- or penta-protonated forms, we paid specific attention to the 1 : 1 complexes formed by H₄L⁴⁺ and H₅L⁵⁺ species with the purpose of obtaining structural and thermodynamic data of the complexes. Specifically, we have investigated the mutual arrangement of macrocycle and anions and evaluated the binding free energy (i.e., complexation constant), in order to rationalize the interaction mode of the anions. Among oxo-anions, H₂PO₄⁻ and SO₄²⁻ were chosen considering that the complexes with the former show unusual low stability compared to the complexes formed with halides, while the interaction with the latter is likely to be too low to be detected by potentiometric titrations.

Exploiting MD simulations supplied by the so-called alchemical transformation method,^72,73 we also determined the binding free energies of the complexes and hence their equilibrium constants, which are compared to the experimental ones in the ESI (Table S7†).

In general, considering the presence of multiple poses of the complexes (see below), and hence the complexity of the statistical sample, the calculated values are in satisfactory agreement with the experimental data. In fact, the differences between the calculated and experimental binding free energies, are often of the order of the chemical accuracy of the theoretical approach, i.e., 1 kcal mol⁻¹. However, in some cases, in particular for the H₄L⁴⁺ complexes, the discrepancy from the experimental values is greater.

From the structural point of view, it is worth noting that, in solution, both H₄L⁴⁺ and H₅L⁵⁺ forms of the complexed macrocycle assume folded conformations, in which the plane of the acridine moiety is almost perpendicular to the mean plane defined by the protonated four amine groups of the alkyl chain (Fig. S5†), in agreement with the results derived from the analysis of the X-ray crystal structures. In fact, the average angle formed by the two planes ranges between 72 and 86 degrees in the complexes of H₄L⁴⁺, while it falls between 72 and 76 degrees in the complexes of H₅L⁵⁺.

Despite the presence of four charged ammonium groups, whose electrostatic repulsion imparts rigidity to the alkyl chain, the latter maintains a certain degree of flexibility in both H₄L⁴⁺ and H₅L⁵⁺. Through the calculation of the root-mean-square displacement, whose technical details are summarized in the ESI,† we have performed a conformational analysis of all complexes.

In the case of the F⁻ and Cl⁻ complexes with both H₄L⁴⁺ and H₅L⁵⁺, four different conformations of the alkyl chain are found by MD simulations.

As an example, in Fig. 7 we report the conformations obtained for H₄L⁴⁺ in the simulation of the [H₄LCl]³⁺ complex.

Fig. 7 Ball and stick representations of the conformers found by MD simulation for complex [H₄LCl]³⁺, showing the most abundant conformation A with nearly C_s symmetry (a), the two specular forms B1 and B2 (b and c) and the less abundant conformer with C_s-like symmetry C (d). Cyan: C atoms; blue: N atoms.

The root mean square displacement of H₄L⁴⁺ determined during the simulation of the [H₄LCl]³⁺ complex is reported in Fig. S6 of the ESI† together with the conformational assignment. The conformations found in the cases of the [H₅LCl]⁴⁺, [H₄LF]³⁺ and [H₅LF]⁴⁺ complexes are similar to those of [H₄LCl]³⁺, as it can be inferred from the time dependence of the root mean square displacements of those complexes reported in Fig. S7 of the ESI.†

The most abundant conformation, roughly amounting to 70% in the [H₄LCl]³⁺ case, has an average arrangement of nearly C_s symmetry (structure A in Fig. 7a). The specular forms B1 and B2 (Fig. 7b and c) amount to about 20%, while structure C (Fig. 7d), which, similarly to A, presents a C_s-like symmetry is less abundant (<10%). The difference in the abundance between the A and C conformations, also observed for other complexes in a slightly different ratio, can be ascribed to the fact that, in the former conformation at variance with the latter, H atoms of the ammonium groups point towards the aromatic plane. This arrangement favors the formation of more stable adducts exhibiting a simultaneous interaction of the anion with the aromatic ring and the ammonium groups of the alkyl chain. In the X-ray crystal structure of H₅LCl₅·4H₂O, the macrocycle has a B1-like geometry (Fig. 7b), which is not the most abundant. These results suggest that the presence of explicit water molecules and consequent solvation can play an important role in determining the structural arrangement of the polyammonium moiety in solution.

To better rationalize the different stability of the anion complexes with H₄L⁴⁺ and H₅L⁵⁺ in aqueous solution, we performed an analysis of the geometrical arrangement of the anions within the complex and of the interactions between the poly-protonated macrocyclic host and the anionic guest. In particular, we computed the two-dimensional distribution function of R and θ, namely the distance of the anion from the centroid of the aromatic plane and the angle formed by the vector position of the anion with respect to the centroid, and the vector normal to the aromatic plane, respectively. Fig. 8 shows the different poses, represented by the peaks in the distributions, found for the [H₄LF]³⁺ and [H₅LF]⁴⁺ complexes, together with their relative population percentages. Each pose, represented schematically in Fig. 8, corresponds to a different interaction mode, in which the small F⁻ anion is unequivocally enclosed within the cavity delimited by the acridine/acridinium unit and the polyammonium chain. In the A1 and A2 poses (Fig. 8c and d), F⁻ appears to establish a double interaction with the macrocycle, specifically a H-bonding contact with one of the two central ammonium groups of the aliphatic chain and an anion⋯π interaction with the acridine ([H₄LF]³⁺, pose A1) or acridinium ([H₅LF]⁴⁺, pose A2) moieties. Conversely, in the B and C poses (Fig. 8e and f), which are found to be nearly identical in both [H₄LF]³⁺ and [H₅LF]⁴⁺ adducts, the anion interacts either only via H-bonding with a benzylic ammonium group, adjacent to the heteroaromatic unit (pose C), or with a central ammonium function of the aliphatic chain (pose B). Of note, in the case of the adduct with H₄L⁴⁺, the B pose is the most abundant and, therefore, it best describes the structural arrangement of the adducts and the interaction mode of the anion. Conversely, in the adduct with H₅L⁵⁺ all three conformers A2, B and C represent, almost equally, the structure of the complex.

Fig. 8 Two-dimensional distribution functions of R and θ (see text for definition) for the [H₄LF]³⁺ (a) and [H₅LF]⁴⁺ (b) adducts (the peaks represent different poses of the complex, whose relative populations, in percentage, are displayed on the panels) and ball and stick representations of the A1 for the [H₄LF]³⁺ adduct (c), A2 for the [H₅LF]⁴⁺ adduct (d), and B (e) and C (f) poses only for the [H₅LF]⁴⁺ adduct, highlighting the main interactions of the anion with the macrocycle (dashed lines with the distances in Å). The B and C poses of [H₄LF]³⁺ are quite similar to those for [H₅LF]⁴⁺, and, hence, they are not displayed here; for completeness, they are reported in Fig. S8.† Populations are computed according to the geometrical definitions of the poses reported in Tables S8 and S9 (ESI).†

The greater contribution of A2 and C is probably related to the presence of the acridinium charged unit, which interacts via anion⋯π direct contact in A2 or via simple electrostatic forces in C. The complete structural information of the [H₄LF]³⁺ complex in the B and C poses, is provided in Fig. S8 (ESI).†

A different behaviour is found in the complexes with Cl⁻, Br⁻ and I⁻, which feature two prevalent poses, shown in Fig. 9 for the [H₅LX]⁴⁺ complexes (X = Cl, Br or I). Similar poses are also observed for the tetra-protonated forms of the complexes (see Fig. S9† for the representative Cl⁻ case).

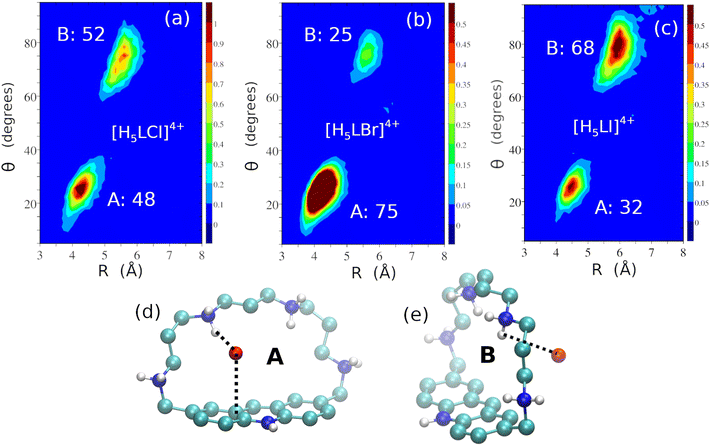Fig. 9 Two-dimensional distribution functions of R and θ for the [H₅LCl]⁴⁺ (a), [H₅LBr]⁴⁺ (b) and [H₅LI]⁴⁺ (c) adducts and ball and stick representations of the A (d) and B (e) poses for the complexes (these poses are similar in the three complexes), highlighting the main interactions of the anions with the macrocycle (dashed lines, distances for [H₅LCl]⁴⁺, [H₅LBr]⁴⁺ and [H₅LI]⁴⁺: 2.50, 2.87 and 3.28 Å for the NH⁺⋯X interaction and 3.48, 3.72 and 3.95 Å for the anion⋯π contact, respectively, in the A pose and 2.50, 2.90 and 3.35 Å for the NH⁺⋯X interaction, respectively, in the B pose). Populations are computed according to the geometrical definitions of the poses reported in Table S9 of the ESI.†

In all complexes, the anion can be engulfed within the receptor cleft (pose A), and simultaneously interact with the polyammonium chain and with acridinium heterocycle or it can remain outside the cavity, interacting only with the charged aliphatic chain (pose B). Interestingly, the contribution of pose A to the overall description of the complex increases from Cl⁻ to Br⁻ and sharply decreases from Br⁻ to I⁻. A reverse trend is obviously observed for the B pose (Fig. 9a–c). The conformational features observed for the complexes with halide anions can be interpreted in terms of their size, charge density and consequent solvation and H-bonding acceptor ability as well.

The ionic radius shows a remarkable increase from F⁻ to Cl⁻ (1.3 and 1.8 Å, respectively). A further, but less marked increase is observed on passing from Cl⁻ to I⁻ (2.2 Å) through Br⁻ (1.95 Å).

The simulated structure of the F⁻ complexes (Fig. 8) shows the anion located inside the receptor cavity, but in different positions. This would suggest that F⁻ is too small to dimensionally fit the receptor cleft. However, its localization within the cleft can ensure high de-solvation (and consequent entropic stabilization of the complex) and formation of strong H-bonds and/or anion⋯π interactions. As a result, the [H₄LF]³⁺ and [H₅LF]⁴⁺ complexes show the largest stability among those investigated in this study. The Cl⁻ and Br⁻ anions can be localized inside or outside the receptor cavity, the former position being largely prevalent in the case of Br⁻. This would suggest that bromide possesses the optimal dimension, among halide anions, to be hosted within the cleft of the protonated receptor. This ensures a larger desolvation and entropy gain in the complex formation, that would stabilize the Br⁻ adduct. The latter complex is, however, slightly less stable than that with Cl⁻ (Table 3), likely due to the poorer H-bonding acceptor ability of Br⁻. Finally, I⁻ is too large to optimally fit the receptor cleft. As a consequence, the anion preferentially binds outside the cavity, thus favouring the formation of the B pose. This localization, together with the poorest ability of I⁻ to give H-bonding, can justify the remarkable drop in the stability constant observed for the formation of its adduct with the protonated receptor with respect to the Cl⁻ and Br⁻ complexes (Table 3).

The present computational approach can also rationalize the poor binding affinity of dihydrogen phosphate for the polyammonium receptor as well as the fact that no interaction is detected with sulphate, which, similarly to phosphate anions, often gives stable adducts with polyammonium receptors. Fig. 10 shows the poses found for the complexes formed by H₄L⁴⁺ and H₅L⁵⁺ with H₂PO₄⁻, together with their relative abundance. As far as the penta-protonated receptor is concerned, the most abundant pose is the A1 type (Fig. 10c). In this pose, the complex features the anion partially enclosed within the receptor cavity, an oxygen atom interacting with both the ammonium group via H-bonding and the acridinium ring via an anion⋯π contact. The remaining oxygen or OH groups remain outside the cavity and exposed to water solvation. In the less abundant B1 pose (Fig. 10d), H₂PO₄⁻ forms a single H-bond, basically remaining outside the cavity. In the adduct with the tetra-protonated receptors (Fig. 10b), the B2 pose (Fig. 10g) becomes the most abundant, justifying its even lower stability.

Fig. 10 Two-dimensional distribution functions of R and θ for the [H₅L(H₂PO₄)]⁴⁺ (a) and [H₄L(H₂PO₄)]³⁺ (b) adducts and ball and stick representations of the A1 (c) and B1 (d) poses found for [H₅L(H₂PO₄)]⁴⁺and of the A2 (e), C2 (f) and B2 (g) ones obtained for [H₄L(H₂PO₄)]³⁺, highlighting the main interactions of the anion with the macrocycle (dashed lines, with distances in Å). Populations are computed according to the geometrical definitions of the poses reported in Tables S8 and S9 of the ESI.†

Considering SO₄²⁻ complexation, the two-dimensional distribution function of R and θ for the [H₅L(SO₄)]³⁺ adduct is reported in Fig. 11a. Analysis of the host–guest interaction reveals the presence of three different poses, A, B and C (Fig. 11b–d), whose relative abundance is also shown in Fig. 11a. Among them, only the A pose (Fig. 11b) features the SO₄²⁻ anion partially embedded inside the receptor cleft, while in the B and C poses (Fig. 11c and d), the anion is placed outside the cavity of the macrocycle.

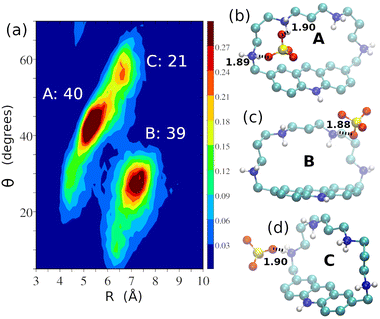Fig. 11 Two-dimensional distribution function of R and θ for the [H₅L(SO₄)]³⁺ adduct (a) and ball and stick representations of its A (b), B (c) and C (d) poses showing the main interactions of the anion with the macrocycle (dashed lines, with distances in Å). Populations are computed according to the geometrical definitions of the poses reported in Table S9 of the ESI.†

Differently from the other anions, in this case no pose displays interactions with the acridinium anion. Despite the higher charge of SO₄²⁻, these structural features can account for lower anion desolvation upon binding, accompanied by the absence of relevant anion⋯π contacts in the complex and, as a matter of fact, no interaction is experimentally detected in aqueous solution between SO₄²⁻ and H₅L⁵⁺.

The two-dimensional distribution functions of R and θ for the [H₄L(SO₄)]²⁺ adduct and the structural representations of the observed poses are reported in Fig. S10.† The SO₄²⁻ anion forms a single salt bridge interaction with an ammonium group from the aliphatic chain, analogously to [H₅L(SO₄)]³⁺.

Experimental

General procedures

Receptor L was synthesized as previously described.⁵⁸ Absorption and fluorescence spectra were recorded on a PerkinElmer Lambda 6 spectrophotometer and on a PerkinElmer LS55 spectrofluorimeter, respectively. In the spectrophotometric/spectrofluorimetric titrations a 0.1 M solution of the anions was added to a 5 × 10⁻⁶ M solution of L, adjusting the pH with small addition of 0.1 M NaOH or 0.1 M NaCF₃SO₃ aqueous solution. The pH was measured with a glass electrode. All measurements were performed at 298.0 ± 0.1 K.

Potentiometric measurements

All pH measurements (pH = −log[H⁺]) employed for the determination of the constants for ligand protonation and anion complex formation were carried out in a 0.1 M NaCF₃SO₃ aqueous solution at 298.0 ± 0.1 K by means of conventional titration experiments under an inert atmosphere. The used equipment and procedures have previously been described.³⁰ The standard potential E° and the ionic product of water (pK_w = 13.61(1) at 298.1 ± 0.1 K in 0.1 M NaCF₃SO₃) were determined by Gran's method.⁷⁴ At least three measurements (with about 100 data points for each) were performed for each system. In all experiments the ligand concentration [L] was about 1 × 10⁻³ M, while the anion concentration was varied from 0.5 × 10⁻³ M to 5 × 10⁻³ M. The computer program HYPERQUAD⁷⁵ was used to calculate the equilibrium constants from the emf data.

Crystal structure determination

Colorless crystals of H₅LCl₅·4H₂O (1) (a), H₅LBr₅·4H₂O (2) (b), H₅L(NO₃)₅·3H₂O (3) (c), and H₅L(H₂PO₄)₅·(H₃PO₄)₂·4H₂O (4) were used for X-ray diffraction analysis. A summary of the crystallographic data is reported in Table S1 (ESI),† while H-bond contacts in the crystal structure of 1–4 are reported in Tables S2–S5 (ESI).† For each compound reflections were recorded up to 2θ = 100 deg (1.0 Å), due to the significant lowering of intensity with an increasing θ value. However, the reached resolution and the reflections/refined parameter ratio, about 9 for all the compounds, with the only exception of the nitrate salt, where it is ca. 7, ensure that the overall geometry of the ligand and intermolecular distances are confidently defined.

The integrated intensities were corrected for Lorentz and polarization effects and an empirical absorption correction SCALE3 ABSPACK was applied.⁷⁶ Crystal structures were solved by direct methods (SIR97)⁷⁷ and refinements were performed by means of full-matrix least-squares using SHELXL Version 2014/7.⁷⁸ Non H atoms were anisotropically refined. H atoms were introduced as riding atoms with thermal parameter calculated in agreement with the linked atom. The water H atoms were not localized in the ΔF maps and not introduced in the calculations. Molecular plots were obtained using the software CCDC Mercury⁷⁹ and UCSF Chimera.⁸⁰

Hirshfeld surface analysis

The Hirshfeld surface of a molecule can be defined as a surface enclosing the region of space where the electron density of the molecule under consideration (or more correctly of its pro-molecule) dominates the electron density of the crystal. The mathematical definition, properties and usefulness of the Hirshfeld surface are found in the dedicated literature.⁶⁵ The same treatment allows for the visualization of the crystal structure through the lens of the so-called fingerprint plots.⁶⁶ These are complete maps of external distance (d_e) (i.e., the point-by-point distance of the nearest atom belonging to another molecule to the Hirshfeld surface of the considered species) vs. internal distance (d_i) (i.e., the point-by-point distance from a molecule's Hirshfeld surface and the nearest atom belonging to the molecule itself) from the Hirshfeld surface under consideration, they are color-coded to show relative abundance (from blue: few contacts to red: many contacts) of intermolecular contacts occupying d_i × d_e square bins of 0.01 × 0.01 Ų. The Hirshfeld surface and fingerprint plots were calculated using the Crystalexplorer21 software.⁸¹ The H₅L⁵⁺ Hirshfeld surface percent composition in compounds 1 and 2 is reported in Table S6 (ESI).†

Molecular dynamics simulations

The macrocyclic ligand L was simulated in the tetra-protonated and penta-protonated forms, H₄L⁴⁺ and H₅L⁵⁺, respectively. In both forms, all N atoms of the alkyl chain are protonated, while the aromatic N atom is protonated only in the H₅L⁵⁺ species. MD simulations of both H₄L⁴⁺ and H₅L⁵⁺ were carried out in aqueous solution with the following anions: F⁻, Cl⁻, Br⁻, I⁻, H₂PO₄⁻ and SO₄²⁻. In particular, each simulation was performed on a system formed by the macrocycle, one anion unit and 948 water molecules into a cubic simulation box. The constant-pressure (1 atm), constant-temperature (298 K) thermodynamic ensemble is adopted with standard periodic boundary conditions. The temperature control is achieved using a Nosé–Hoover thermostat,⁸² while the pressure is kept constant by the Parrinello–Rahman method with uniform scaling of the simulation box volume.⁸³ A full-atom potential model was adopted. Intermolecular interactions are treated according to the Lennard–Jones potential together with the Coulomb potential between point net charges localized on the atoms. The intramolecular interactions include harmonic stretching, harmonic bending, proper torsions, improper torsions and electrostatic and Lennard–Jones interactions between non-bonded atoms (i.e., atoms separated by more than two covalent bonds). Specifically, the AMBER-like ff99sb force field⁸⁴ in combination with atomic net charges computed through a RESP fit⁸⁵ at the HF/6-31G* level of theory was used to model the macrocycle and the H₂PO₄⁻ and SO₄²⁻ anions. For halides, we used the force field of Jensen and Jorgensen.⁸⁶ The TIP3P model⁸⁷ has been adopted for water. The atomic charges as well as the AMBER atom-types assigned to the atoms of the macrocycle in the two protonation states are reported in Tables S10 and S11 (ESI).† Lorentz–Berthelot mixing rules have been used for Lennard–Jones interactions. Constraints are enforced to covalent bonds involving H atoms. Electrostatic forces are treated by the smooth particle mesh Ewald method⁸⁸ using a fourth order B-spline interpolation polynomial for the charges, an Ewald parameter of 0.43 Å⁻¹ and a grid spacing smaller than 1 Å for the fast Fourier transform calculation of the charge weighted structure factor. The cutoff distance for the non-bonding interactions is 10 Å. A five time-step r-RESPA integrator⁸⁹ is employed for integrating the equations of motion, with the largest time step of 6 fs. Simulations lasting about 50 ns have been carried out. The binding free energies for the macrocycle–anion complex formation were estimated by means of MD simulations supplied with the alchemical transformation method proposed in ref. 72 and 73. In these simulations, the setup described above (number of water molecules, force field, temperature, pressure, etc.) was applied. The alchemical transformation method is briefly summarised in the ESI.† MD simulations have been performed using the ORAC program.^90,91

Conclusions

These results demonstrate that suitably designed polyammonium receptors, featuring a cleft for anion encapsulation equipped with a hydrophobic moiety, are able to form both salt bridges and anion⋯π contacts with embedded anionic hosts of appropriate size, inducing their de-solvation. These characteristics can be exploited to form stable complexes with ‘elusive’ anions, such as Cl⁻ and Br⁻, thus giving rise to unexpected selectivity patterns. Macrocycle L, designed to achieve a longer distance between the protonated polyamine chain and the acridine nitrogen with respect to L_D, forms a fully protonated H₅L⁵⁺ species in aqueous solution. The higher flexibility of the tetraamine chain, which links the 2 and 7 positions of an acridine moiety, allows the macrocycle to assume a folded conformation, thus defining a cleft, in which the F⁻, Cl⁻, and Br⁻ anions can be encapsulated. Among these, bromide shows better fitting with the cavity dimensions. Despite the by far lower ability of chloride and, overall, bromide to form strong hydrogen bonding interactions with ammonium groups with respect to the highly charge-dense F⁻ anion, the stability constant of their complexes is only slightly lower (log K = 5.2, 4.7 and 4.4 for [H₅LCl]⁴⁺, [H₅LBr]⁴⁺ and [H₅LF]⁴⁺, respectively) than those of the corresponding fluoride complex, due to their optimal fitting within the receptor cleft that allows for the formation of a strong anion⋯π interaction and favours anion de-solvation, improving the overall stability of the complexes. Among halides, I⁻ is definitively too large to be conveniently hosted by the receptor pocket, thus forming poorly stable complexes. More surprisingly, oxo-anions are not bound or very weakly bound by the protonated receptor, despite the known ability of charged oxygens to form O⁻⋯HN⁺ interactions, which generally make the complexes with polyammonium receptors of these anions more stable than those of Cl⁻, Br⁻ and I⁻. As a matter of fact, the size of oxo-anions hinders their encapsulation within the receptor cavity, inhibiting both the formation of strong anion⋯π contacts and anion desolvation upon complex formation.

Anion⋯π interactions not only enhance the binding ability of L toward Cl⁻ and, overall, Br⁻, making this receptor capable of forming complexes with similar or higher stability with respect to those of anion cryptate complexes, but also generate an optical signal via quenching of the acridinium emission.

The fluorescence sensing ability of L parallels its binding properties toward different anions. Differently from receptor L_D, the emission changes observed upon anion binding are likely due to the anion⋯π interactions, rather than to proton transfer processes. F⁻, Cl⁻ and Br⁻, which form the most stable complexes, show similar quenching of the emission, while I⁻ and oxo-anions poorly affect or do not affect the receptor emission.

As a whole, these results point out that L presents peculiar characteristics in the panorama of polyammonium receptors developed for anion binding. In fact, the insertion of the electron-poor large acridine moiety within a tailored polyammonium receptor architecture, with the aromatic N atom pointing out of the ring cavity, allows for the formation of strong anion⋯π contacts: an undoubted added value in the design of receptors able to firmly bind and optically signal in pure water the elusive Cl⁻ and Br⁻ anions. We believe that this approach can, in perspective, be used to develop new fluorescent receptors for halide anions in pure water, featuring strong binding and sensing ability and enhanced anion selectivity.

Author contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support from the Italian Ministero dell'Istruzione, Università e Ricerca within the PRIN project 2017EKCS3 and from the Cassa di Risparmio di Firenze Foundation, bando Ricerca e Innovazione 2020 is gratefully acknowledged.

References

1. (a) K. Bowman-James, A. Bianchi and E. García-España, Anion Coordination Chemistry, Wiley-VCH, New York, 2012; (b) J. L. Sessler, P. A. Gale and W. S. Cho, Anion Receptor Chemistry, The Royal Society of Chemistry, Cambridge, UK, 2006.
2. (a) L. K. Macreadie, A. M. Gilchrist, D. A. McNaughton, W. G. Ryder, M. Fares and P. A. Gale, Chem, 2022, 8, 46–118; (b) L. E. Santos-Figueroa, M. E. Moragues, E. Climent, A. Agostini, R. Martínez-Máñez and F. Sancenón, Chem. Soc. Rev., 2013, 42, 3489–3613; (c) N. Kaur, G. Kaur, U. A. Fegade, A. Singh, S. K. Sahoo, A. S. Kuwar and N. Singh, TrAC, Trends Anal. Chem., 2017, 95, 86–109; (d) P. A. Gale and C. Caltagirone, Coord. Chem. Rev., 2018, 354, 2–27; (e) R. Hein and P. D. Beer, Chem. Sci., 2022, 13, 7098–7125; (f) C. Guo, A. C. Sedgwick, T. Hirao and J. L. Sessler, Coord. Chem. Rev., 2021, 427, 213560; (g) D.-X. Wang and M. X. Wang, Acc. Chem. Res., 2020, 53, 1364–1380; (h) M. S. Taylor, Coord. Chem. Rev., 2020, 413, 213270; (i) T. L. Mako, J. M. Racicot and M. Levine, Chem. Rev., 2019, 119, 322–477; (j) P. Molina, F. Zapata and A. Caballero, Chem. Rev., 2017, 117, 9907–9972; (k) M. Langton, C. J. Serpell and P. D. Beer, Angew. Chem., Int. Ed., 2016, 55, 1974–1987; (l) A. Frontera, Coord. Chem. Rev., 2013, 257, 1716–1727; (m) C. Bazzicalupi, A. Bencini and V. Lippolis, Chem. Soc. Rev., 2010, 39, 3709–3728.
3. (a) S. Wu, Y. Wang, M. Iqbal, K. Mehmood, Y. Li, Z. Tang and H. Zhang, Environ. Pollut., 2022, 304, 119241; (b) R. S. Dhingra and M. Shah, Environ. Sci. Pollut. Res., 2021, 28, 60329–60345.
4. (a) C. Guan, J. Jiang, S. Pang, Y. Zhou, Y. Gao, J. Li and Z. Wang, Water Res., 2020, 176, 115725; (b) M. Flury and A. Papritz, J. Environ. Qual., 1993, 22, 747–758.
5. K. Watson, M. J. Farré and N. Knight, J. Environ. Manage., 2012, 110, 276–298.
6. (a) S. Peckham and N. Awofeso, Sci. World J., 2014, 293019; (b) S. Ayoob and A. K. Gupta, Crit. Rev. Environ. Sci. Technol., 2006, 36, 433–487.
7. (a) A. P. Davis, D. N. Sheppard and B. D. Smith, Chem. Soc. Rev., 2007, 36, 348–357; (b) D. L. Nelson and M. M. Cox, Lehninger Principles of Biochemistry, W. H. Freeman, NY, 5th edn, 2009.
8. D. Zak, M. Hupfer, Á. Cabezas, G. Jurasinski, J. Audet, A. Kleeberg, R. J. McInnes, S. M. Kristiansen, R. Petersen, H. Liu and T. Goldhammer, Earth-Sci. Rev., 2021, 212, 103446.
9. C. Ye, K. Lu, H. Song, Y. Mu, J. Chen and Y. A. Zhang, J. Environ. Sci., 2023, 123, 387–399.
10. K. E. Papathanasiou, M. Vassaki, A. Spinthaki, F.-E. G. Alatzoglou, E. Tripodianos, P. Turhanen and K. D. Demadis, Pure Appl. Chem., 2019, 91, 421–441.
11. J. J. Weeks Jr. and G. M. Hettiarachchi, J. Environ. Qual., 2019, 48, 1300–1313.
12. Bijay-Singh and E. Craswell, SN Appl. Sci., 2021, 3, 518.
13. D. L. Correll, J. Environ. Qual., 1998, 27, 261–266.
14. J. L. Atwood, K. T. Holman and J. W. Steed, Chem. Commun., 1996, 12, 1401–1407.
15. A. P. Davis and J. B. Joos, Coord. Chem. Rev., 2003, 240, 143–156.
16. P. D. Beer and P. A. Gale, Angew. Chem., Int. Ed., 2001, 40, 486–516.
17. L. Fabbrizzi, M. Licchelli, G. Rabaioli and A. Taglietti, Coord. Chem. Rev., 2000, 205, 85–108.
18. J. M. Llinares, D. Powell and K. Bowman-James, Coord. Chem. Rev., 2003, 240, 57–75.
19. V. McKee, J. Nelson and R. M. Town, Chem. Soc. Rev., 2003, 32, 309–325.
20. P. A. Gale and R. Quesada, Coord. Chem. Rev., 2006, 250, 3219–3244.
21. E. Macedi, A. Bencini, C. Caltagirone and V. Lippolis, Coord. Chem. Rev., 2020, 407, 213151.
22. P. Mateus, N. Bernier and R. Delgado, Coord. Chem. Rev., 2010, 254, 1726–1747.
23. C. A. Ilioudis, D. A. Tocher and J. W. Steed, J. Am. Chem. Soc., 2004, 126, 12395–12402.
24. L. Trembleau, T. A. D. Smith and M. H. Abdelrahman, Chem. Commun., 2013, 49, 5850–5852.
25. O. I. Shchukina, A. V. Zatirakha, A. S. Uzhel, A. D. Smolenkov and O. A. Shpigun, Anal. Chim. Acta, 2017, 964, 187–194.
26. C. De Stefano, C. Foti, A. Pettignano and S. Sammartano, Talanta, 2004, 64, 510–517.
27. C. Bazzicalupi, A. Bencini, A. Bianchi, A. Danesi, C. Giorgi, M. A. Martínez Lorente and B. Valtancoli, New J. Chem., 2006, 30, 959–965.
28. S. Salehzadeh and Y. Gholiee, Dalton Trans., 2015, 44, 19708–19716.
29. U. Manna, B. Nayak, Md. N. Hoque and G. Das, CrystEngComm, 2016, 18, 5036–5044.
30. C. Bazzicalupi, A. Bencini, C. Giorgi, B. Valtancoli, V. Lippolis and A. Perra, Inorg. Chem., 2011, 50, 7202–7216.
31. C. Bazzicalupi, A. Bencini, A. Bianchi, A. Danesi, C. Giorgi and B. Valtancoli, Inorg. Chem., 2009, 48, 2391–2398.
32. J. Pitarch-Jarque, K. Rissanen, S. Garcia-Granda, A. Lopera, M. P. Clares, E. Garcia-Espana and S. Blasco, New J. Chem., 2019, 43, 18915–18924.
33. K. Dabrowa, F. Ulatowski, D. Lichosyt and J. Jurczak, Org. Biomol. Chem., 2017, 15, 5927–5943.
34. P. Mateus, R. Delgado, V. Andre and M. T. Duarte, Org. Biomol. Chem., 2015, 13, 834–842.
35. D. Jana, G. Mani and C. Schulzke, Inorg. Chem., 2013, 52, 6427–6439.
36. G. Ambrosi, M. Formica, V. Fusi, L. Giorgi, E. Macedi, M. Micheloni, P. Paoli, R. Pontellini and P. Rossi, Chem. – Eur. J., 2011, 17, 1670–1682.
37. R. Kumar, T. Guchhait and G. Mani, Inorg. Chem., 2012, 51, 9029–9038.
38. V. Amendola, G. Bergamaschi, M. Boiocchi, R. Alberto and H. Braband, Chem. Sci., 2014, 5, 1820–1826.
39. S. A. Oshchepkov, T. A. Shumilova, S. R. Namashivaya, O. A. Fedorova, P. V. Dorovatovskii, V. N. Khrustalev and E. A. Kataev, J. Org. Chem., 2018, 83, 2145–2153.
40. A. M. Costero, J. Sanchis, S. Gil, V. Sanza and J. A. G. Williams, J. Mater. Chem., 2005, 15, 2848–2853.
41. Y. Lin, K. Du, M. R. Gau and I. J. Dmochowski, Chem. Sci., 2023, 14, 291–297.
42. W. A. Quinn, A. M. Saeed, D. R. Powell and Md. A. Hossain, J. Environ. Res. Public Health, 2010, 7, 2057–2070.
43. B. S. Morozov, S. S. R. Namashivaya, M. A. Zakharko, A. S. Oshchepkov and E. A. Kataev, ChemistryOpen, 2020, 9, 171–175.
44. M. E. Huston, E. U. Akkaya and A. W. Czarnik, J. Am. Chem. Soc., 1989, 111, 8735–8737.
45. A. S. Singh and S. S. Sun, J. Org. Chem., 2012, 77, 1880–1890.
46. C. H. Park and H. E. Simmons, J. Am. Chem. Soc., 1968, 90, 2431–2433.
47. B. Dietrich, B. Dilworth, J. M. Lehn, J. P. Souchez, M. Cesario, J. Guilhem and C. Pascard, Helv. Chim. Acta, 1996, 79, 569–587.
48. E. Graf and J. M. Lehn, J. Am. Chem. Soc., 1976, 98, 6403–6405.
49. (a) T. Fiala, K. Sleziakova, K. Marsalek, K. Salvadori and V. Sindelar, J. Org. Chem., 2018, 83, 1903–1912; (b) M. A. Yawer, V. Havel and V. Sindelar, Angew. Chem., Int. Ed., 2015, 54, 276–279.
50. M. Lisbjerg, B. M. Jessen, B. Rasmussen, B. E. Nielsen, A. Ø. Madsen and M. Pittelkow, Chem. Sci., 2014, 5, 2647–2650.
51. F. Sommer, Y. Marcus and S. Kubik, ACS Omega, 2017, 2, 3669–3680.
52. (a) M. J. Langton, S. W. Robinson, I. Marques, V. Félix and P. D. Beer, Nat. Chem., 2014, 6, 1039–1043; (b) A. Borissov, I. Marques, J. Y. C. Lim, V. Félix, M. D. Smith and P. D. Beer, J. Am. Chem. Soc., 2019, 141, 4119–4129.
53. K. Worm and F. P. Schmidtchen, Angew. Chem., Int. Ed. Engl., 1995, 34, 65–66.
54. Y. Chen, G. Wu, L. Chen, L. Tong, Y. Lei, L. Shen, T. Jiao and H. Li, Org. Lett., 2020, 22, 4878–4882.
55. S. Sudan, D. W. Chen, C. Berton, F. Fadaei-Tirani and K. Severin, Angew. Chem., Int. Ed., 2023, 62, e202218072.
56. S. Puccioni, C. Bazzicalupi, A. Bencini, C. Giorgi, B. Valtancoli, G. De Filippo, V. Lippolis, P. R. Salvi, G. Pietraperzia, R. Chelli and C. Gellini, J. Phys. Chem. A, 2013, 117, 3798–3808.
57. R. Chelli, G. Pietraperzia, A. Bencini, C. Giorgi, V. Lippolis, P. R. Salvi and C. Gellini, Phys. Chem. Chem. Phys., 2015, 17, 10813–10822.
58. C. Bazzicalupi, M. Chioccioli, C. Sissi, E. Porcù, C. Bonaccini, C. Pivetta, A. Bencini, C. Giorgi, B. Valtancoli, F. Melani and P. Gratteri, ChemMedChem, 2010, 5, 1995–2005.
59. (a) C. Estarellas, A. Bauzá, A. Frontera, D. Quinonero and P. M. Deyà, Phys. Chem. Chem. Phys., 2011, 13, 5696–5702; (b) A. Bauzá, T. J. Mooibroek and A. Frontera, ChemPhysChem, 2015, 16, 2496–2517.
60. E. T. Ryan, T. Xiang, K. P. Johnston and M. A. Fox, J. Phys. Chem. A, 1997, 101, 1827–1835.
61. R. M. Smith and A. E. Martell, NIST Stability Constants Database, version 4.0, National Institute of Standards and Technology, Washington, DC, 1997.
62. A. Bencini and V. Lippolis, Coord. Chem. Rev., 2012, 256, 149–169.
63. A. S. Alvarez, Dalton Trans., 2013, 42, 8617–8636.
64. M. Savastano, C. Bazzicalupi and A. Bianchi, Chem. – Eur. J., 2020, 26, 5994–6005.
65. (a) M. A. Spackman and P. G. Byrom, Chem. Phys. Lett., 1997, 267, 215–220; (b) J. J. McKinnon, M. A. Spackman and A. S. Mitchell, Acta Crystallogr., Sect. B: Struct. Sci., 2004, 60(6), 627–668.
66. M. A. Spackman and J. J. McKinnon, CrystEngComm, 2002, 4, 378–392.
67. Á. Martínez-Camarena, M. Savastano, C. Bazzicalupi, A. Bianchi and E. García-España, Molecules, 2020, 25, 3155.
68. S. L. Tan, M. M. Jotani and E. R. T. Tiekink, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2019, 75, 308–318.
69. J. J. Koenderink and A. J. Van Doorn, Image Vis. Comput., 1992, 10, 557–564.
70. M. Fujita, A. Ishida, S. Takamuku and S. Fukuzumi, J. Am. Chem. Soc., 1996, 118, 8566–8574.
71. T. Pedzinski, B. Marciniak and G. L. Hug, J. Photochem. Photobiol., A, 2002, 150, 21–30.
72. E. Giovannelli, M. Cioni, P. Procacci, G. Cardini, M. Pagliai, V. Volkov and R. Chelli, J. Chem. Theory Comput., 2017, 13, 5887–5899.
73. E. Giovannelli, P. Procacci, G. Cardini, M. Pagliai, V. Volkov and R. Chelli, J. Chem. Theory Comput., 2017, 13, 5874–5886.
74. G. Gran, Analyst, 1952, 77, 661–671.
75. P. Gans, A. Sabatini and A. Vacca, Talanta, 1996, 43, 1739–1753.
76. CrysAlis RED and Scakle3 Abspack, Version 1.171.32.29, Oxford Diffraction Ltd, Abingdon, Oxfordshire (U.K.).
77. A. Altomare, M. C. Burla, M. Camalli, G. L. Cascarano, C. Giacovazzo, A. Guagliardi, A. G. Moliterni, G. Polidori and R. Spagna, J. Appl. Crystallogr., 1999, 32, 115–119.
78. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
79. C. F. Macrae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235.
80. E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612.
81. R. Spackman, M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, D. Jayatilaka and M. A. Spackman, J. Appl. Crystallogr., 2021, 54, 1006–1011.
82. W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697.
83. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190.
84. V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins, 2006, 65, 712–725.
85. C. I. Bayly, P. Cieplak, W. D. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280.
86. K. P. Jensen and W. L. Jorgensen, J. Chem. Theory Comput., 2006, 2, 1499–1509.
87. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
88. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
89. M. Tuckerman, B. J. Berne and G. J. Martyna, J. Chem. Phys., 1992, 97, 1990–2001.
90. S. Marsili, G. F. Signorini, R. Chelli, M. Marchi and P. Procacci, J. Comput. Chem., 2010, 31, 1106–1116.
91. R. Chelli and G. F. Signorini, J. Chem. Theory Comput., 2012, 8, 830–842.

---

Footnotes

† Electronic supplementary information (ESI) available: Full-atom MD simulations technical details; summary of the crystallographic data; H-bond contacts in the crystal structures of 1–4; Hirshfeld surface percent composition in compounds 1 and 2; AMBER atom-types and atomic net charges of H₄L⁴⁺ and H₅L⁵⁺; details of the crystal packing of complexes 1–4; the ligand Hirshfeld surface in compound 2; plots of external vs. internal distances from the Hirshfeld surface of H₅L⁵⁺ (fingerprint plots) in 1 and 2; emission spectra of L in the presence of increasing amounts of Cl⁻, Br⁻, I⁻and H₂PO₄⁻; calculated and experimental equilibrium constants of the complexes; calculated ball and stick representations of H₄L⁴⁺ and H₅L⁵⁺; RMSD as a function of time calculated from a MD simulation of the [H₄LCl]³⁺ complex; RMSD as a function of time calculated from the MD simulations of [H₄LF]³⁺, [H₅LF]⁴⁺, [H₄LCl]³⁺ and [H₅ClF]⁴⁺; the calculated ball and stick representation of the conformations of [H₄LF]³⁺ and [H₅LF]⁴⁺; R distance and θ angle ranges used to define the conformations of the complexes; the two-dimensional distribution of R and θ and the corresponding calculated ball and stick representations for the conformations of [H₄LCl]³⁺ and [H₄L(SO₄)]²⁺. CCDC 2237482 (1), 2237483 (2), 2237484 (3) and 2237485 (4). For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3dt00682d

‡ These authors contributed equally.

---