 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Polarity-extended 8 − Neff rule for semiconducting main-group compounds with the TiNiSi-type of crystal structure†‡
Riccardo
Freccero
 *ab,
Yuri
Grin
*ab,
Yuri
Grin
 a and
Frank R.
Wagner
a and
Frank R.
Wagner
 *a
*a
aMax Planck Institute for Chemical Physics of Solids, Noethnitzer Str. 40, 01187 Dresden, Germany. E-mail: frank.wagner@cpfs.mpg.de
bDipartimento di Chimica e Chimica Industriale, Università degli Studi di Genova, I-16146 Genova, Italy. E-mail: riccardo.freccero@unige.it
First published on 18th May 2023
Abstract
Application of chemical bonding analysis in position-space techniques based on combined topological analysis of the electron density and electron-localizability indicator distributions has recently led to the formulation of a polarity-extended 8 − Neff rule for consistent inclusion of quantum chemically obtained polar-covalent bonding data into the classical 8 − N scheme for main-group compounds. Previous application of this scheme to semiconducting main-group compounds of the cubic MgAgAs type of structure with 8 valence electrons per formula unit (8 ve per f.u.) has shown a covalent bonding tendency preferring one zinc blende type partial structure over the other one, which seems to corroborate the classical Lewis picture of maximally four covalent bonds per main-group element. In contrast to the MgAgAs type, the orthorhombic TiNiSi type of structure displays a much higher geometrical flexibility to incorporate different kinds of metal atoms. The analysis of polar-covalent bonding in semiconducting 8 ve per f.u. containing main-group compounds AA′E of this structure type reveals a transition to non-Lewis type bonding scenarios of species E with up to ten polar-covalently bonded metal atoms. This kind of situation is consistently included into the extended 8 − Neff type bonding scheme. A systematic increase of partially covalent bonding from chalcogenides E16 to the tetrelides E14 is found, summing up to as much as 2 covalent bonds E14–A and E14–A′, and correspondingly remaining 4 lone pair type electrons on species E14. The familiar notion of this structure type consisting of a ‘[NiSi]’-type framework with ‘Ti’-type atoms filling the voids cannot be supported for the compounds investigated.
1. Introduction
Among ternary inorganic compounds, those with equiatomic composition ABC are very common. Hundreds of them crystallize in the cubic MgAgAs type (Pearson symbol cF12; space group F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m, No. 216) and the orthorhombic TiNiSi (oP12; Pnma, No. 62) type of structure.1,2 Depending on valence electron counts of constituent atoms, compounds assigned to these two structure types show semiconducting or metallic properties. Recently, the semiconducting representatives of the MgAgAs family (sometimes called half-Heusler phases or Nowotny–Juza phases if containing only main-group elements) attracted a lot of attention due to their possible thermoelectric application and quantum topological behaviors.3–6 Despite the structure relation between these two structural patterns is not simple (the suggested structural transformation mechanism includes three steps7), some of the 18 valence electron ABC compounds form polymorphs with these types of structure, e.g., TiGePt,7 HfGePt8 are semiconducting in the MgAgAs type of structure, but metallic in the TiNiSi type. The coordination numbers based on Brunner–Schwarzenbach (BS) procedure9 (see also Pearson data base1) in both atomic arrangements – Mg[6Ag, 4As; 0Mg]Ag[6Mg, 4′As; 0Ag]As[4Mg, 4′Ag; 0As] and Ti[6Ni, 6′Si; 6′′Ti]Ni[6Ti, 4Si; 2Ni]Si[5Ti, 4Ni; 0Si] (the superscript expression characterizes the number of atoms of each type belonging to the coordination environment of the respective central atom) – are rather different, such that a structural phase transition between them may be expected to significantly change physical properties. The maingroup compounds with 8 valence electrons per formula unit (8 ve per f.u.) can be formally described according to An+A′m+E(n+m)−. Here, A and A′ represent elements of groups 1, 2, and 13, E represents elements of groups 14 to 16, such that N0val(E) + n + m = 8, and non-metallic behavior can be expected in both structure types. In the MgAgAs type of compounds, this can be related to polar-covalent diatomic bonding connected with the 8 − N rule mainly within the 8 valence electrons containing 3∞[AgAs]2− partial structure of the zinc blende type.10 In the TiNiSi type, there is no such clear identification of a dominating polar-covalently 4-bonded partial structure incorporating the most electronegative Si-type species.
3m, No. 216) and the orthorhombic TiNiSi (oP12; Pnma, No. 62) type of structure.1,2 Depending on valence electron counts of constituent atoms, compounds assigned to these two structure types show semiconducting or metallic properties. Recently, the semiconducting representatives of the MgAgAs family (sometimes called half-Heusler phases or Nowotny–Juza phases if containing only main-group elements) attracted a lot of attention due to their possible thermoelectric application and quantum topological behaviors.3–6 Despite the structure relation between these two structural patterns is not simple (the suggested structural transformation mechanism includes three steps7), some of the 18 valence electron ABC compounds form polymorphs with these types of structure, e.g., TiGePt,7 HfGePt8 are semiconducting in the MgAgAs type of structure, but metallic in the TiNiSi type. The coordination numbers based on Brunner–Schwarzenbach (BS) procedure9 (see also Pearson data base1) in both atomic arrangements – Mg[6Ag, 4As; 0Mg]Ag[6Mg, 4′As; 0Ag]As[4Mg, 4′Ag; 0As] and Ti[6Ni, 6′Si; 6′′Ti]Ni[6Ti, 4Si; 2Ni]Si[5Ti, 4Ni; 0Si] (the superscript expression characterizes the number of atoms of each type belonging to the coordination environment of the respective central atom) – are rather different, such that a structural phase transition between them may be expected to significantly change physical properties. The maingroup compounds with 8 valence electrons per formula unit (8 ve per f.u.) can be formally described according to An+A′m+E(n+m)−. Here, A and A′ represent elements of groups 1, 2, and 13, E represents elements of groups 14 to 16, such that N0val(E) + n + m = 8, and non-metallic behavior can be expected in both structure types. In the MgAgAs type of compounds, this can be related to polar-covalent diatomic bonding connected with the 8 − N rule mainly within the 8 valence electrons containing 3∞[AgAs]2− partial structure of the zinc blende type.10 In the TiNiSi type, there is no such clear identification of a dominating polar-covalently 4-bonded partial structure incorporating the most electronegative Si-type species.
On the other hand, the TiNiSi-type structures can “simply” be considered as symmetry derivatives of the hexagonal hP3 AlB2 aristotype.11,12 However, in the REGa2−xNix compounds (RE = rare earth metal), a series of distorted derivatives of the AlB2 type was found by chemical substitution, i.e., x(AlB2) < x(CaIn2) < x(KHg2) < x(TiNiSi).11 Noteworthy, this series displays a cross transition CaIn2 → KHg2 between the hexagonal and the orthorhombic branch in the Bärnighausen tree13 of the AlB2 type.12 A mixed occupancy of the former boron sites by Ni and Ga was found in the first three structure types, and an ordered one in the TiNiSi type phase. Such substitution first leads to formation of a 3D network (AlB2 → CaIn2 type) with puckered [Ni, Ga] honeycomb nets, and further to the formation of a different type of 3D [Ni, Ga] framework (CaIn2 → KHg2 type) with the RE atoms inside its cavities. As a result, the TiNiSi structure could be geometrically described as being composed of a 3∞[NiSi] 4-connected network with Ti species located in the cavities. This description is only genealogical (keeping the 3D framework of the KHg2 “parent structure”), and is neither based on the analysis of interatomic distances, nor does it imply information about chemical bonding. Already the fact, that the driving force is a non-isoelectronic chemical substitution, indicates the influence of atomic interactions within the 3D network and between the network and the so-called filler atoms.
Thus, understanding of the factors tolerating the same structures occurring with non-isoelectronic combinations of elements, and appearance of geometrically closely related structures with such non-isoelectronic substitutions is a challenging issue for chemistry of intermetallic compounds. Families of compounds with many representatives, like the MgAgAs-type and TiNiSi-type compounds, constitute a rich playground for investigation of structure-bonding interrelations, which makes the present study on chemical bonding in the TiNiSi family a natural extension of the previous investigations on MgAgAs-type compounds.10
The structure-bonding relationships for some members of the TiNiSi and related KHg2 (=CeCu2) families were already investigated analyzing the geometric features (lattice parameters and unit cell volumes),14 or applying the quantum chemical tools, in particular the COHP technique.15,16 On the other hand, in the last years, for characterization of the bonding situation in intermetallic compounds, the combined analysis of the electron density ρ(r) and the ELI-D (electron localizability indicator) distribution YσD(r) in 3D space has been found to display valuable information. The complete partitioning of 3D space obtained in terms of ELI-D basins, identified as atomic core–shell regions, interatomic bond regions and lone-pair regions, is combined with the QTAIM atomic partitioning to yield quantitative information about polarity of bonding.10,17 This way, an extension of the 8 − N rule including polar-covalent bonding within the polyanionic network has been introduced.10a While the first systematic application has been on the highly symmetrical structures of the ternary maingroup Nowtny–Juza (MgAgAs type) phases – a ternary variant of anti-CaF2 type of structure, the present investigation aims to analyze binary and ternary compounds crystallizing in TiNiSi motif – a ternary variant of the anti-PbCl2 type of structure. In the following, the anti-PbCl2 and anti-CaF2 types of structures will be simply called PbCl2 and CaF2 types of structures, respectively, as is usually done in the literature.
2. Computational details
Electronic structure calculations for three A1A′1E16, four A2A′1E15, four A2A′2E14 and eleven A22E14 (seven with the TiNiSi and four with the CaF2 structure), compounds were performed with the all-electrons DFT-based FHI-aims package,18 using the PBE exchange–correlation functional.19 For all crystal structures, both lattice parameters and fractional coordinates were optimized (Table S1‡). The Brillouin zone sampling was effectuated with a (4, 8, 4) and (6, 6, 6) k-point mesh for the TiNiSi and CaF2 structure, respectively, and Gaussian smearing of 0.01 eV was employed. Predefined default “tight” basis sets were chosen, including scalar-relativistic effect for all electrons (ZORA approximation20).The obtained wave functions were used to calculate the electron density ρ(r) and the electron-localizability indicator (ELI-D21,22) YσD(r) on an equidistant grid of about 0.05 Bohr mesh size with the DGrid23 program. The subsequent topological analysis of both ρ(r) (QTAIM approach24) and ELI-D was performed with DGrid as well. In order to study the title compounds on the basis of the 8 − N rule extension in position-space,10a based on the QTAIM/ELI-D basin intersection technique, a penultimate shell correction (PSC0) of the valence basin populations25 was applied to each species assuming the (A1)+, (A2)2+, (E14)4+, (E15)5+ and (E16)6+ atomic core charges (Tables S2–S6 in the ESI‡). Results obtained without the application of the PSC0 corrections are available in Tables S7 and S9a–9c.‡ This way, the imprecisions of ELI-D valence electron counts for each atomic species are corrected, and the number of electrons in the valence region corresponds exactly to 8 ve per f.u. for each compound.
3. Results and discussion
3.1. Crystal chemistry
Three characteristic representatives of TiNiSi family, PbCl2 (Cl2 Cl1 Pb), TiNiSi itself and Co2Si (Co2 Co1 Si), clearly display the formation of a similar structural pattern realized by atoms with quite different chemical nature (Fig. 1). The coordination polyhedra of the most electronegative atomic species E are evaluated using the Brunner–Schwarzenbach (BS) scheme,9 a maximum-gap procedure to evaluate the coordination number without considering chemical knowledge about the selected compounds (Fig. 1). Already at this stage, some striking features of the TiNiSi family members become visible. While chemically different PbCl2 and TiNiSi show the same coordination number of CN = 9 (in most cases, see below) and a very similar coordination polyhedron for the interrelated Pb and Si positions, the Si species in Co2Si displays CN = 10 and a clearly different atomic coordination polyhedron. Indeed, Co2Si can be considered to belong to a different branch of the TiNiSi type, which is consistent with a detailed chemical bonding analysis.15,16 Moreover, being a further variant within the BS scheme, ht-SrLiAs also displays CN(As) = 10 (Fig. 2), which represents only a coordination extension of the normal CN = 9 scenario, while the coordination polyhedron of Si in Co2Si is clearly different from the one of As.In general, the compounds of the TiNiSi family can be grouped into those containing only main-group elements and those containing transition metals. Focusing on main-group representatives AA′E with 8 valence electron per formula unit (8 ve per f.u.) and considering the electronegativity (EN) differences between the components (e.g., Pauling or Sanderson scales), a chemical behavior as valence compounds following the 8 − N rule according to An+A′m+(0b)E(n+m)− with a certain electronic energy gap can be expected. With the focus on the 8 − N rule, the coordination of the E species constitutes the most important structural aspect. BS-type of coordination analysis of the E species for selected main-group representatives shows (Fig. 2), that they follow the scheme obtained above for TiNiSi and PbCl2 (Fig. 1). Note, that the sequence of metal atoms A, and A′ in these AA′E compounds is traditionally chosen according to the shortest distance to the atom type E, such that species A′ displaying the shortest distances d(E–A′) build up the 4-connected 3∞[A′E] network displayed in Fig. 1. In the distance histograms for species E for NaLiSe, CaLiAs, CaMgGe and Ca2Ge, the maximum gaps occur between the 9th and the 10th coordinating cation, and between the 10th and 11th neighbor in ht-SrLiAs (Fig. 2). The E coordination number of 4A′ + 5A = 9 is confirmed for most of the compounds studied, an exception being ht-SrLiAs with CN(As) = 4A′ + 6A = 10. Here, the 10th cationic neighbor is closer than the 11th neighbor being an anion. Note, that this 10th ligand A is always present also for other representatives (dashed line in Fig. 3a), only the position of the largest distance gap is different. Aiming at a better interpretation of distances and a preliminary chemical comparison between the structures, the sum of both ionic and covalent radii (I and C in Fig. 2, respectively) is shown as well. In the case of NaLiSe, CaLiAs and CaMgGe, some distances are located in the range between the covalent and the ionic ones, being always closer to the latter, however, some are even longer than the ionic one. With this procedure, the As–Li and Ge–Mg interactions seem to be more ionic than the Se–Li ones. This may be related to the applied approach estimating the ionic radii of Ge4− and As3−. Thus, slightly longer ‘ionic’ As–Li and Ge–Mg distances may be expected. The case of Ca2Ge is different: although the distances to four Ca ligands fall in the region between the ionic radii sum I and the gap, another five ones are located just before I with three Ca closer to the covalent radii sum C. This may suggest an increased covalent contribution of polar Ge–Ca bonding. Finally, and most importantly, it can be clearly seen from the BS plots (Fig. 2), that although the four distances d(E–A′) are always shorter than the five (or six) distances d(E–A) below the BS distance gap, their locations with respect to reference sums of covalent and ionic radii C and I, respectively, are rather similar, such that from distances alone a clear distinction between 3∞[A′E] network and A filler atoms depicted in Fig. 1 is not supported. Thus, the question arises, whether this picture can be supported from bond polarity analysis?
The main-group TiNiSi-type compounds display 8 valence electrons per formula unit. Assuming a Zintl-type bonding picture, a formal charge transfer from both A and A′ to E takes place, resulting in ionic interactions with no homopolar bonds and four lone pairs (lp) per E atom: [(0b)E16]2−; [(0b)E15]3−; [(0b)E14]4−. Despite the structural similarities and the analogous Zintl description, it is evident that the bonding situation for E components is not identical. Systematic changes are expected when moving from [E14]4−- to [E16]2−-containing phases. In particular, considering the gradual reduction of electronegativity difference (Δχ) and the transition from insulating A1A′1E16 (some of which are even colourless26) to semiconducting27–29 or poorly metallic (zero-gap semiconductor)30A22E14 and A2A′2E14 phases, a gradual transformation of ionic interactions towards heteropolar ones may be expected.
For the chemical bonding investigation of the TiNiSi family, the nature of the formal E “lone-pairs”10a,b,d with respect to eventual formation of E–A/A′ heteropolar bonds has to be carefully analyzed. For this purpose, the quantum chemical application of the polarity-extended 8 − N rule in position-space seems to be particularly appropriate since it can be successfully applied also when the coordination number of E is larger than 4, which is the case for the TiNiSi phases studied. Aiming to perform this comprehensive chemical investigation, eighteen representative AA′E compounds, among which seven are binaries and eleven ternaries, have been selected (Tables 1 and S1‡). For estimating the role of higher CN and symmetry lowering for the TiNiSi-type, binaries were also compared with results from a few selected high-symmetric CaF2-type representatives.
| AA′E | N bas(E) | Q eff/ELIBON | V QTAIM (Å3) | N eff(E) | N cb(E) | N lp(E) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | A′ | E | A | A′ | E | |||||
| a TiNiSi structure type. b CaF2 structure type. c In hypothetical CaF2 structure type. | ||||||||||
| NaLiSea | 4 | +0.81 | +0.85 | –1.66 | 10.22 | 4.09 | 45.53 | 7.66 | 0.34 | 3.66 |
| +1.00 | +1.00 | –2.00 | ||||||||
| NaLiTe a | 6 | +0.82 | +0.85 | –1.67 | 10.90 | 4.34 | 58.93 | 7.66 | 0.34 | 3.66 |
| +1.00 | +1.00 | –2.00 | ||||||||
| KNaSe a | 4 | +0.75 | +0.79 | –1.54 | 23.84 | 11.30 | 51.49 | 7.54 | 0.47 | 3.53 |
| +1.00 | +1.00 | –2.00 | ||||||||
| CaLiAs a | 6 | +1.32 | +0.83 | –2.15 | 15.34 | 3.97 | 43.03 | 7.14 | 0.86 | 3.14 |
| +2.00 | +1.00 | –3.00 | ||||||||
| CaLiSb a | 8 | +1.32 | +0.83 | –2.15 | 16.27 | 4.19 | 53.62 | 7.14 | 0.86 | 3.14 |
| +2.00 | +1.00 | –3.00 | ||||||||
| CaLiBi a | 8 | +1.30 | +0.82 | –2.12 | 16.97 | 4.37 | 57.55 | 7.12 | 0.88 | 3.12 |
| +2.00 | +1.00 | –3.00 | ||||||||
| SrLiAs a | 4 | +1.29 | +0.83 | –2.12 | 21.18 | 4.25 | 45.00 | 7.12 | 0.89 | 3.11 |
| +2.00 | +1.00 | –3.00 | ||||||||
| CaMgSi a | 4 | +1.28 | +1.37 | –2.65 | 15.63 | 8.61 | 44.66 | 6.65 | 1.35 | 2.65 |
| +2.00 | +2.00 | –4.00 | ||||||||
| CaMgGe a | 4 | +1.28 | +1.33 | –2.61 | 15.89 | 9.20 | 45.63 | 6.60 | 1.40 | 2.60 |
| +2.00 | +2.00 | –4.00 | ||||||||
| CaMgSn a | 7 | +1.29 | +1.29 | –2.58 | 16.78 | 10.15 | 55.01 | 6.58 | 1.44 | 2.56 |
| +2.00 | +2.00 | –4.00 | ||||||||
| SrMgGe a | 4 | +1.23 | +1.27 | –2.50 | 21.79 | 10.32 | 46.61 | 6.50 | 1.50 | 2.50 |
| +2.00 | +2.00 | –4.00 | ||||||||
| Ca2Si a | 3 | +1.25 | +1.20 | –2.45 | 17.64 | 16.57 | 48.72 | 6.43 | 1.57 | 2.43 |
| +2.00 | +2.00 | –4.00 | ||||||||
| Ca2Ge a | 3 | +1.24 | +1.19 | –2.43 | 17.97 | 16.91 | 49.83 | 6.42 | 1.59 | 2.41 |
| +2.00 | +2.00 | –4.00 | ||||||||
| Sr2Si a | 3 | +1.19 | +1.14 | –2.33 | 25.12 | 23.58 | 51.47 | 6.32 | 1.69 | 2.31 |
| +2.00 | +2.00 | –4.00 | ||||||||
| Sr2Ge a | 3 | +1.17 | +1.12 | –2.29 | 25.62 | 24.05 | 52.72 | 6.30 | 1.70 | 2.30 |
| +2.00 | +2.00 | –4.00 | ||||||||
| Ba2Si a | 4 | +1.01 | +0.95 | –1.96 | 34.64 | 32.74 | 47.23 | 5.96 | 2.04 | 1.96 |
| +2.00 | +2.00 | –4.00 | ||||||||
| Ba2Ge a | 4 | +0.99 | +0.94 | –1.93 | 35.34 | 33.42 | 48.46 | 5.93 | 2.07 | 1.93 |
| +2.00 | +2.00 | –4.00 | ||||||||
| Ba2Pb a | 4 | +0.98 | +0.94 | –1.92 | 37.97 | 36.03 | 61.91 | 5.92 | 2.08 | 1.92 |
| +2.00 | +2.00 | –4.00 | ||||||||
| Be2C b | 8 | +1.63 | – | –3.26 | 1.69 | – | 17.09 | 7.26 | 0.74 | 3.26 |
| +2.00 | –4.00 | |||||||||
| Mg2C b | 8 | +1.53 | – | –3.06 | 6.20 | – | 28.29 | 7.06 | 0.94 | 3.06 |
| +2.00 | –4.00 | |||||||||
| Mg2Sn b | 8 | +1.38 | – | –2.76 | 9.85 | – | 59.54 | 6.76 | 1.24 | 2.76 |
| +2.00 | –4.00 | |||||||||
| hyp-Ba2Geb,c | 6 | +1.01 | – | –2.02 | 37.17 | – | 53.93 | 6.02 | 1.98 | 2.02 |
| +2.00 | –4.00 | |||||||||
3.2. Chemical bonding analysis in position space
The computed QTAIM effective charges Qeff (Table 1) reveal, that species A and A′ play the role of cations and species E the counterbalancing anions, which is consistent with electronegativities χ(A) ≈ χ(A′) < χ(E). Keeping the cations and changing the E species, the effective charge transfer is found to be consistent with electronegativity differences Δχ. The difference between effective charges and oxidation states increases when reducing Δχ, which suggests that reduced charge transfer is caused by increased covalent interactions. This is analyzed and discussed in detail below.
The TiNiSi type of crystal structure is considered to be particularly suited for ternary compounds containing two kinds of metal atoms with different radii. Nevertheless, the sum of spherical atom volumes describing the shortest interatomic distances is always significantly lower than the volume of the unit cell. In contrast to atomic radii, effective atomic volumes (the quantum chemical realization of the Biltz volume increments32) completely describe the total volume of the structure, i.e. they represent an exhaustive partitioning of real space. The quantum chemically obtained volumes of QTAIM atoms (effective volumes) have been proven to be particularly useful to explain changes in unit cell dimensions as a function of composition for different classes of intermetallic compounds.31 QTAIM volumes for compounds AA′E listed in Table 1 fully agree with the expectations, showing that VQTAIM(A) > VQTAIM(A′). This result does not only hold for the investigated ternaries, but even for the same atom types occupying different Wyckoff sites in binary compounds.
The number, location and population of the ELI-D basins deliver the starting information about inter-atomic bonding. Already the numbers and locations of ELI-D basins in the valence region are not the same for all AA′E compounds studied (Table 1). Three different ELI-D topologies with 3 and 4 attractors were found for the seven binary and six ternary compounds (Fig. 3). The six ternaries share a very similar picture, with 4 attractors of three kinds located close to the contacts d1, d2 and d3 (Fig. 3a and b), which means along the three shortest E16–A′ (Li/Na), E15–A′ (Li) and E14–A′ (Mg) distances (Fig. 2). Other ELI-D topologies are found for the binaries A22E14. The phases Ca2E14, Sr2E14 display three ELI-D attractors located at the opposite side of d1 and d2 (Fig. 3c), indicated as d1* and d2*. For Ba2E14 (E = Si, Ge, Pb), a fourth attractor appears at the d3 opposed side, called d3* (Fig. 3d).
The remaining five AA′E compounds from the investigated group display a complicated picture with up to 10 ELI-D basins around the E atoms. Increasing the basis set helps reducing the number of basins, but still, with the best basis sets possible, i.e. without running into convergence problems, 6 to 8 weakly separated bond basins remained for this group of compounds (Table 1). This is not surprising; already for maingroup half-Heusler compounds the formation of 4 or 8 ELI-D valence basins has been reported.10a In the present case, this more complex behavior is caused by the low-symmetrical 9- or 10-coordination (Fig. 2) of the E species with increasing polarizability along E16 < E15 < E14. In addition, the coordinating metal atoms are of varying size and charge, i.e. of varying polarizing power. All this creates complex local bonding situations for these non-metallic compounds, which cannot be understood in terms of main-group atoms E with directed n 2-center 2-electron bonds and 4 − n 2-electron lone pairs originating from the Lewis model.34
Already for the compounds with initially 4 basins per E species, these basins display a high atomicity, i.e. a high number of intersecting QTAIM metal atoms A and A′. This indicates multiatomic instead of classical 2-atomic bonding. The splitting of the classically 4 basins per maingroup species into a larger number of ‘basin shivers’ (with each of them being less polyatomic), as observed for some investigated compounds, is therefore an alternative realization of the same bonding scenario in compounds belonging to the same structure family.
The number of QTAIM atoms intersecting a valence ELI-D basin defines its atomicity n, which is written in the form n a(iA, jA′, kE) (where ‘a’ stands for ‘atomicity’), with n = i + j + k denoting that a number of i atoms of type A, j atoms of type A′ and k atoms of type E intersect the corresponding ELI-D basin.36 In the case of lone pairs located at an E species, valence regions defined by the ELI-D basins are expected to completely belong to (anion) E, i.e. the basins should be monoatomic 1a(1E). This kinds of basins in solids are often found to be multiatomic, but with very tiny contributions of the remaining atoms A and A′ besides E such that p(BEi) ≈ 1. Such ELI-D basins are interpreted as effectively monoatomic (lone-pair like). When 1.0 > p(BEi) > 0.5, polar-covalent bonds are realized, i.e. species A and/or A′ are increasingly involved in covalent interactions with E, and basin atomicity is at least 2 or larger. This kind of scenario was actually found for all compounds investigated herein. The essence of the ELI-D/QTAIM polar bonding analysis in the framework of the polarity-extended 8 − Neff rule10 is the usage of bond fractions to decompose each homo- and hetero-polar bond into a number of covalent bonding electrons Ncbe (counted in form of atom E contributions to two-electron covalent bonds Ncb(E) = Ncbe(E), Table 1), and (hidden) lone-pair electrons Nlpe (counted as two-electron lone pairs Nlp(E) = Nlpe(E)/2, Table 1). With the access electron number  of atom E describing the number of electrons contained in all basins touching the core
of atom E describing the number of electrons contained in all basins touching the core  of atom E, and the valence electron population NELIval(E) part of the QTAIM atom E total electronic population Ntot(E), the following equations hold:
of atom E, and the valence electron population NELIval(E) part of the QTAIM atom E total electronic population Ntot(E), the following equations hold:
 | (1) |
| NELIval(E) = Ncb(E) + 2Nlp(E) | (2) |
Subtracting both equations yields
 | (3) |
If the access electron number 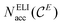 is equal to 8, the analogy with the 8 − N rule is evident.10a
is equal to 8, the analogy with the 8 − N rule is evident.10a
Through this type of polar bonding analysis, it is possible to overcome the limitation of the classical 8 − N approach, where only homopolar bondsing connecting the most electronegative species are described on the basis of the octet rule.10
The ELI-D core basins’ populations show significant deviations from the ideal core electron count expected according to the Periodic Table: E cores are underpopulated by about 0.25 electrons and alkaline-earth metals (except Mg) cores are overpopulated by 0.29 to 0.50 electrons. Values for each atom are listed in Tables S2–S5.‡ This leads to unfavourable deviations of the position-space valence electron count from the conceptual value of 8 valence electron per formula unit. Adjustment of the valence electron count in position space to exactly 8 ve per f.u. by the penultimate shell correction procedure (PSC0) introduced recently25 was applied here as well. The use of PSC0 for the populations of the ELI-D valence basins, has been found to yield a balanced description of the network–metal bonding for ternary La2MGe6 (M = Li, Mg, Al, Zn) compounds,25 and it turned out to be essential for the compounds studied herein as well (Tables 1 and S7‡). After PSC0 treatment, the corrected versions of 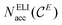 and NELIval(E) are obtained, namely
and NELIval(E) are obtained, namely  and NvalELI+(E), respectively, for which short-hand notations Nacc(E) and Neff(E) will be used in the text, where adequate.
and NvalELI+(E), respectively, for which short-hand notations Nacc(E) and Neff(E) will be used in the text, where adequate.
 | (4) |
| Neff (E) = NELI+val(E) | (5) |
With these notations, the polarity-extended 8 − N rule (eqn (3), with  ) takes the more compact form of an 8 − Neff rule:
) takes the more compact form of an 8 − Neff rule:
| Ncb(E) = 8 − Neff(E) | (6) |
The scenario of a fully ionic situation is described in terms of oxidation numbers calculated on the basis of electronegativity data for the present compounds. In the ELI-D based oxidation number (ELIBON) approach37 each basin's electron population is completely assigned to the atom with the majority ownership of the basin's electrons. Typically, it turns out, that this procedure is consistent with the usual assignment of all valence electrons to the most electronegative atom in the traditional oxidation state determination procedure. In the present cases this always led to exactly 8 valence electrons assigned to the E species (in this case NELIBON+val(E) = Nacc(E) = 8), i.e. PSC0-corrected ELIBON values of −(8 − N0val(E)), +N0val(A), and +N0val(A′) (with N0val(X) being the number of valence electrons of neutral atom X according to the periodic table) for species E, A, and A′, respectively (Table 1). The effective numbers of valence electrons Neff(E) (eqn (5)), decomposed into the number of two-electron covalent bonds Ncb and lone pairs Nlp, after the PSC0 treatment, are listed in Table 1 as well.
One advantage of the employed evaluation technique is, that it yields covalent bonding and lone pair electrons of species E as a sum over all polar bonds. For the homodesmic bonding situations of the AA′E compounds studied, i.e. all bonds A–E and A′–E are polar, the final results are not dependent on the specific number and locations of ELI-D basins for each compound. All ELI-D basins could have been even merged into one, and the QTAIM intersections with this one would still have yielded the same final results Nacc(E), Nval(E), Ncb(E), and Nlp(E). Thus, these values can be used for the systematic classification of the compounds according to varying bond polarity.
The results of polar bonding analysis for these complex ELI-D topologies shows regular trends (Fig. 4). In the formal, fully ionic picture 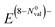 , each compound is located in the (0b, 4lp) point (left upper corner in Fig. 4, left). A gradual reduction of the Neff (E) is observed going from A1A′1E16 to A22E14, through A2A′1E15 and A2A′2E14, yielding an increase of the number of covalent bonds necessary to reach the octet. This trend leads to a certain clustering of four groups of compounds in different regions.
, each compound is located in the (0b, 4lp) point (left upper corner in Fig. 4, left). A gradual reduction of the Neff (E) is observed going from A1A′1E16 to A22E14, through A2A′1E15 and A2A′2E14, yielding an increase of the number of covalent bonds necessary to reach the octet. This trend leads to a certain clustering of four groups of compounds in different regions.
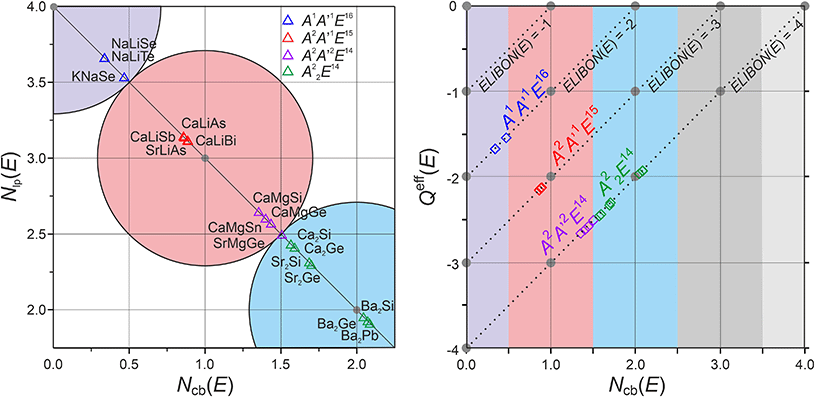 | ||
| Fig. 4 Polarity-extended 8 − Neff rule for TiNiSi-type compounds of maingroup elements. Location of the AA′E compounds according to their number of two-electron covalent bonds Ncb(E), lone pairs Nlb(E), and effective charges Qeff(E): (left) All compounds lie on the Ncb(E) + Nlb(E) = 4 line (black), i.e. with Nacc(E) = 8 they fulfil the 8 − Neff rule in position space representation (eqn (1)–(6)). Large grey circles delimit the domains of (0b, 4lp), (1b, 3lp) and (2b, 2lp) scenarios; (right) compounds of E14, E15, E16 lie on separate lines; the differently colored regions mark, from the left to the right, the domains of (0b, 4lp), (1b, 3lp), (2b, 2lp), (3b, 1lp) and (4b, 0lp) scenarios. | ||
The more salt-like chalcogenides NaLiSe, NaLiTe and KNaSe are located in the (0b, 4lp) domain, being the closest ones to the formal scenario. Although the coordination number of E is supposed to be nine (4A′ + 5A), the ELI-D valence region is always intersected by ten QTAIM cations (4A′ + 6A), which means that the first atom located after the BS distance gap (see Fig. 2, and the dashed black line in Fig. 3a) has to be considered as well. In the case of the three A1A′1E16 chalcogenides, the population of the intersected regions and the resulting bond fractions (Table S7a‡) are small enough to consider them as conceptually negligible. Hence, the four valence basins should be interpreted as effectively mono-atomic, i.e. of the lone-pair type. This is consistent with their location in the (0b, 4lp) domain.
The A2A′1E15 compounds have very similar Ncb(E) values ranging from 0.86 for CaLiAs, to 0.89 for ht-SrLiAs. Hence, they are located very close to the center of the (1b, 3lp) domain. The substitution of alkali with alkaline-earth species is mainly responsible for the reduced polarity resulting in a larger number of covalent bonds. The d1 and d2 basins are now six-atomic 6a(1E15, 1Li, 4A2) and the d3 one is five-atomic 5a(1E15, 1Li, 3A2). The border between the (1b, 3lp) and the (2b, 2lp) domains is populated by the A2A′2E14 tetrelides, with SrMgGe located exactly at the border (Ncb(Ge) = 1.50). The increased number of covalent bonds compared to the A2A′1E15 phases is mainly due to the substitution of Li by Mg (reduced bond polarity). From the ELI-D basin-atomicity point of view, the same scenario as for the A2A′1E15, but with larger metal contributions, is obtained for A2A2′E16. Finally, all the A22E14 binaries are found to be inside the (2b, 2lp) domain with Ba2E (E = Si, Ge, Pb) having Ncb ≈ 2 being those farthest away from the formal fully ionic description. This high number of covalent bonds is clearly realized via multiatomic basins: 6a–d1*(1E14, 5A) and 7a–d2*(1E14, 6A) for Ca2E and Sr2E; 6a–d1*(1E14, 5A), 6a–d2* (1E14, 5A) and 7a–d3*(1E14, 6A) for Ba2E (see Table S8b‡). The observed trend could be understood by a gradual reduction of the electronegativity difference between the E elements and the metal species A and A′. It leads to a reduced charge transfer with a consequent increase of the number of covalent bonds, realized in form of multiatomic interactions. However, within a group of compounds with the same anion, and similar ENs of the cations, the charge transfer does not strictly follow the electronegativity difference, probably because other factors, like the size difference between cations and anion, may play a role as well. For instance, focusing on the compounds A22E14, Ncb increases from Ca to Ba, i.e. it may be interpreted as increasing with Δχ. This should be digested with care, because ENs are very similar, e.g., the Allred–Rochow ones are equal to 1.0, Allen's ENs are 1.034 (Ca), 0.963 (Sr) and 0.881 (Ba) and Pauling ones are Ca 1.00 (Ca), 0.95 (Sr) and 0.89 (Ba). Unexpected trends of charge transfer are observed also for the QTAIM effective charges of A and A′ components: e.g. Qeff(Mg) ≈ 1.3, Qeff (Ba) ≈ 1.0, Qeff (Li) ≈ 0.8, and Qeff (K) ≈ 0.7. Supplementary calculations performed on A1Cl with A1 = Li–Cs, Mg2Ge and Ca2Ge (simulated also in the CaF2 structure) reveal the same trend, suggesting that this effect is not specific for the studied compounds and structures, and should be investigated in the future.
The difference Qeff(E)–ELIBON(E) between QTAIM effective charges for the E species and ELI-D based oxidation numbers increases in the following order: A1A′1E16 < A2A′1E15 < A2A′2E14 < A22E14. The trend represents the gradually increasing deviations from the ionic picture, which is accompanied by an increasing number of covalent bonding electrons Ncb(E). This can easily be seen by rewriting ELIBON(E) as a function of the number of access electrons  of E (eqn (4)),
of E (eqn (4)),
 | (7) |
 | (8) |
The difference Qeff(E) − ELIBON(E) is now seen to be directly related to the number of covalent bonding electrons Ncb(E) via the polarity extended 8 − Neff rule in position space eqn (3) and (6) with  , and NvalELI+(E) = Neff(E):
, and NvalELI+(E) = Neff(E):
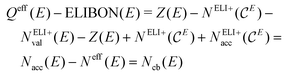 | (9) |
The linear relation Qeff(E) = Ncb(E) + ELIBON(E) depicted in Fig. 4 right introduces an alternative view on the scenario shown in Fig. 4 left. For each AA′E compound Qeff(E) is now depicted as a function of Ncb(E). Since the polarity-extended 8 − Neff rule is fulfilled for all of them, they find their location on different lines, depending on the ELIBON(E) value. As an example, ELIBON(E14) = –4, so all the A2A′2E14 and A22E14 compounds are located on the straight line in agreement with equation: Qeff(E14) = Ncb(E14) − 4. The two extreme situations are represented by points located on either the vertical or horizontal axes. Points on the vertical axis, i.e. with Ncb(E) = 0, have Qeff(E) = ELIBON(E) indicating a (0b, 4lp) bonding scenario where no covalent interactions occur. For all points on the upper horizontal axis, i.e. Qeff(E) = 0, the non-polar, completely covalent scenario is realized, the E species build up the number of homopolar bonds necessary to reach the octet stable configuration, i.e. (1b, 3lp) for E17, (2b, 2lp) for E16, (3b, 1lp) for E15 and (4b, 0lp) for E14. Reference for this behaviour could be elemental Cl2, Se, P and Ge, respectively. In Fig. 4 left, each classical (Ncb, 4 − Ncb) domain is indicated by a circle, all compounds studied lie on the same line Nlp = 4 − Ncb. Thus, it is possible to figure out the bonding scenario renouncing information about the nature of E. For example, if a A2A′1E15 type of compound had Ncb(E15) = 2, it would be located close to Ba2Si, Ba2Ge and Ba2Pb. In Fig. 4 right, the increasing number of covalent bonds is now shown as a function of the reducing effective charges, i.e. of the reduced charge transfer from A and A′ to E species. The compounds with different type of species E may have the same Ncb(E) but a different Qeff(E), being located on different lines depending on ELIBON(E).
The preference for a classically 4-coordinated partial structure found in this structure type is not the result of a general chemical-bonding preference, but of the symmetry-imposed restrictions of this structure type. This is consistent with the chemical bonding results for balanced A2A′2E14 compounds with the same structural features, which are obtained in the CaF2-type of structure. Since A = A′ in this structure type, the compounds automatically lie on the diagonal line Neff(A) = Neff(A′) in Fig. 5. Noteworthy, the size restrictions in the cubic CaF2 type of structure seem to be quite dominant, such that only a few main-group compounds are found to crystallize in this type, namely A22E14, A2 = Be, Mg, E14 = C, Si, Ge, Sn, Pb. The exemplarily chosen compounds Be2C, Mg2C, Mg2Sn, and hyp-Ba2Ge were evaluated in the same way as the TiNiSi-type ones (Table 1), where Ba2Ge, which is found experimentally in the TiNiSi-type of structure, was also optimized in the CaF2-type (denoted ‘hyp-Ba2Ge’) to allow for a direct comparison. As expected from electronegativity differences, the CaF2-type compounds display increasingly covalent contributions along Be2C, Mg2C, Mg2Sn, and hyp-Ba2Ge.
Answering the question, raised already from the BS analysis of the E species’ coordination, about the chemical relevance of the typical structure picture of the TiNiSi-type of structure given in Fig. 1, neither classical crystal chemistry nor bond-polarity analysis in the framework of 8 − Neff rule supports the usual notion of a 3∞[A′E] network with filler atoms A for the 8 ve per f.u. semiconducting compounds of the TiNiSi-type of structure. Nevertheless, such kind of structure diagrams are still useful in the framework of group–subgroup relations between crystal structures, because they visualize the genealogical evolvement of topological networks in the symmetry tree.
The results obtained for the highly coordinated E species raise a further important conceptual issue. With the E species coordination number of 9 or 10, the high covalency E–A and E–A′ especially of the A2A′2E14 compounds seems to contradict the notion, inherited from the Lewis picture, of maximally 4 covalent bonds for a main group species to the right of the Zintl line in a semiconducting compound. The present approach shows, that this is not the case, because the 9 or 10 polar-covalent bonds form in total <4 covalent bonds (Fig. 4), and this is quantitatively covered by the polarity-extended 8 − Neff rule in position space.
For (TiNiSi-type) Ba2Ge, the overall polarity is found to be slightly higher in the hypothetical CaF2 type, which is reflected also in the slightly higher electronic population and effective charges of Ge (−2.02 vs. −1.93). In the TiNiSi type, the 4-coordinating Ba′ species display in sum the higher covalent contributions Ga@Ba′4 than the 5-coordinating Ba species Ge@Ba5, which can be seen from Neff(A′) > Neff(A) in Fig. 5. This observation is also true for the other binary A22E14 compounds of the TiNiSi type being all located slightly to the left side of the diagonal line Neff(A′) = Neff(A) in Fig. 5. The increased covalency E–A′ is correlated with the shorter distances d(E–A′). The behaviour found for the binary TiNiSi representatives is just opposite to the one for the ternary representatives, where the Neff(A′) < Neff(A). This means, in these cases the less covalently bonded metal species is found to be always A′ showing the shorter distances d(E–A′) as well.
4. Conceptual analogies from the 8 − Neff rule between different bond scenarios
In the framework of the polarity-extended 8 − Neff rule applied to (so-called hyperelectronic) atomic species E with electron populations Neff(E) ≥ 4, similar valence electron populations Neff(E) correspond to similar number of covalent bonding cbe′ and hidden lone pair electrons lpe′, i.e. (cb′, lp′) coordinates. This is valid not only for compounds with purely covalent E–E bonding, but also for those with heteroatomic polar bonding E–A (species A have Neff(A) < 4) as well. Having the same (cb′, lp′) coordinate, the E species of compounds with different structure type and coordination are found to be related. This way, effectively 4-coordinated E species in semiconducting zinc blende and half-Heusler (MgAgAs) type of compounds are related to 8, 9 or 10-coordinated E species in semiconducting main group CaF2 and TiNiSi type of compounds. This conceptual correspondence between compounds with homopolar and heteropolar bonding was recently presented10a,b for heteropolar Lewis-type scenarios of compounds displaying 4 polar (4p scenario) effectively diatomic ELI-D valence basins of E, like AlP and LiAlGe (Fig. 6, middle). The correspondence was shown to exist between these and Zintl-type compounds with homonuclear polyanions of E showing a Lewis type of (m cb; (4 − m) lp) scenario. The same type of correspondence is now extended to the present compounds of study (Fig. 6, bottom), where the atomicity of the four valence basins (special cases with 4 basins were selected, s. Table 1) is always greater than 2 (due to the intersecting A and A′ atoms), and the BS coordination number of the E species is 9 or 10. Due the high number of QTAIM atoms intersecting ELI-D basins, the covalent part (blue squares) is always determined by more than one cationic species (Fig. 6 bottom). | ||
| Fig. 6 Conceptual equivalence (indicated by special arrow symbol) in the framework of polarity-extended 8 − Neff rule of nonpolar bonding situations displaying separated bonds and lone pairs (nb, (4 − n)lp) with polar bonding situations displaying the same amount of covalent bonding electrons and lone pairs (nb′, (4 − n)lp′) but being always mixed with each other in each polar bonding region. (top row) classically separated bonds and lone pairs in elemental structures Cl2 (left) and grey Se (right); (middle row) equivalence with 4 polar bonds (designated ‘4p’) in zinc blende (left) and MgAgAs (right) structure types with the corresponding nonpolar situations above them; (bottom row) equivalence with 10 polar bonded neighbours (designated ‘10p’) around 4 ELI-D basins in the TiNiSi type with the corresponding 4p and fully covalent situations above. Only the valence region of the central atom E is shown completely. QTAIM charges (superscript, Table 1) are rounded to integers; blue and green squares indicate the non-polar (covalent) and polar (lone pair) contributions to the valence basin populations, respectively; red lines constitute the border of the central atoms. | ||
A more complicated situation has been recently discussed for formally (3b)Ge and (2b)Ge species in La2MGe6 (M = Li, Mg, Al, Zn),25 realizing (3b; 1p) and (2b; 2p) instead of formal (3b, 1lp) and (2b, 2lp) scenarios, respectively. This means that, in addition to the expected 2-atomic Ge–Ge bonds ‘b’, the basins located in the lone-pair region were interpreted, as in the actual case, as polar bonds ‘p’ with the surrounding La and M atoms being actively involved, which yields effective bond atomicity always greater than two. These mixed-bonding cases, where even for La2MgGe6 with the nominally correct 8 − N electron count a metallic band structure has been obtained, were not ideally suited to represent the conceptual analogy with other bonding patterns obeyed by classical semiconducting valence compounds.
In the semiconducting compounds with exclusively (homodesmic) polar bonding studied herein, the polarity-extended 8 − Neff rule in position space is perfectly fulfilled. This invites for such a direct comparison, especially for those cases, where a number of four ELI-D basins around E were actually found in the analysis. While the displayed zinc blende/MgAgA-type scenario (Fig. 6 middle, left and right column) can be related to formally 4-bonded species (4b)E, the main-group TiNiSi-type scenario (Fig. 6 bottom, left and right column) is related to formally 0-(homo-)bonded species (0b)E with 4 lone pairs. The deviations found from this formal situation in the TiNiSi-type compounds represent continuous realizations between the two extremal bonding situations, 8 electrons in lone pairs leading to completely ionic bonding vs. 8 electrons in covalent bonding situations with significantly more than 4 partners, where the E species always possesses more than 50% of the electronic population of each E–A ELI-D basin. Notably, in the present scenario, there is no need for exactly 4 ELI-D basins representing 4 polar bonds in real space. As the final analysis results show, even in cases with a higher number of ELI-D basins surrounding species E, a consistent description of the polar bonding scenario within the polarity-extended 8 − Neff rule is obtained (Fig. 7, middle). An interesting difference is found between the polar-covalent Lewis type of 4p scenario, and the polar-covalent hyper-coordinated (with respect to the Lewis picture) 8p and 10p scenarios found in the CaF2 and TiNiSi type compounds investigated. In the 4p scenarios,10a the full range of possible scenarios from (0b, 4lp), (1b′, 3lp′), (2b′, 2lp′), (4b, 0lp) is possible, while the 8p and 10p scenarios are now observed to obey an upper boundary at (2b′, 2lp′), where the band gap closes as well. These hyper-coordinated scenarios with multi-atomic bonding must have a natural boundary within the present 8 − Neff scheme, because the most covalent variant 8p = (4b′, 0lp′) implying 8 neighbors being completely covalently bonded is clearly beyond the present scheme.10b The location of this kind of natural boundary in general, and its dependencies have to be investigated in future studies.
5. Conclusions
Chemical bonding analysis in position-space has been conducted for a series of 8 ve per f.u. semiconducting main-group representatives of the TiNiSi type of structure and a few related ones of the CaF2-type combining the ELI-D and QTAIM space partitioning methods (ELI-D/QTAIM basin intersection). The compounds investigated reveal large variations in the electron localizability picture, showing 3 to 8 local ELI-D maxima in the valence region of E species. The negatively charged E species are majority owners of all ELI-D valence basins intersected by 10 QTAIM cationic neighbor atoms A and A′. This amount is fairly consistent with the E species’ coordination number of 9 or 10 obtained from the BS scheme. The ELI-D based oxidation numbers (ELIBON) obtained for the quantum chemically computed bonding situation are identical to the formal ones E−(n+m) defined from formal charge transfer from the metal atoms leaving A+n and A′+m.All compounds studied are found to be in accord with the polarity-extended 8 − Neff rule, which is found valid also in non-classical situations of species E, where more than 4 coordinating atoms are involved (e.g., in polar multi-atomic bonding situations, Fig. 7) and more than 4 ELI-D bonding basins are connected to species E. Thus, the semiconducting main-group compounds AA′E with 8 ve per f.u. crystallizing in the TiNiSi structure family can be understood within a charge-compensated Zintl-like scheme Ax+A′y+ ((8 − Neff)b)E(x+y)−, with Neff(E) = N0val(E) + x + y ≤ 8, even for the non-integer charge transfers x and y obtained in the position-space bonding analysis. The total covalency in the compounds, as measured by the amount of covalent bonds Ncb of species E(x+y)− according to 8 − Neff(E), increases from chalcogenides towards tetrelides according to Ncb(E16) < Ncb(E15) < Ncb(E14). The increase is consistent with the associated EN(E) decrease, and is assisted by (i) decreasing initial electron count N0val(E), and (ii) by increasing covalent contributions from cationic species with higher formal charges. Compared to this, an eventually tiny overall EN increase of the metal atoms (A1, A′1) < (A2, A′1) < (A2, A′2) is found to be less important. Noteworthy, the most covalent polar-bonding situations (2b′, 2lp′) appearing with the E14 anions and large A2, A2′ cations are also those, where the band gap closes. It may hint, that the (2b′, 2lp′) situation may be an upper boundary for multiatomic polar-covalent bonding systems understandable within the charge-compensated Zintl scheme. Further studies of this interesting issue are necessary.
Noteworthy, neither the crystal chemical analysis, nor the bond-polarity analysis of the 8 ve per f.u. maingroup compounds of the TiNiSi-type studied support the familiar notion of a ‘[NiSi]’ = [A′E] type of network with filler atoms of type ‘Ti’ = A in the voids.
From a quite general point of view, two ways of application of the traditional 8 − N rule are found in the literature. One way starts with the sum formula of the compound and assignment of oxidation states for each atomic species. In a subsequent step the oxidation states of the species with N ≥ 4 valence electrons (ve) are interpreted as formal charges, for which the 8 − N rule yields the expected (predicted) number of homoatomic covalent bonds of these species.39 This way shows the predictive power of the 8 − N rule. The reverse way of working with this rule starts with the determination of the number of covalent bonds for each species in the already known crystal structure. The number of covalent bonds of each species with N ≥ 4 ve is then translated into a formal charge via the 8 − N rule, and the sum of all species’ formal charges is finally checked to be equal to zero. This way demonstrates the analytic power of the 8 − N rule.
As an example for both strategies, the zinc blende type compound AlP may be chosen. The 8 − N rule prediction would be based on Al+3 and P−3 oxidations states yielding Al3+ and non-bonded (with respect to homoatomic interactions) (0b)P3− species. In the analytic way of usage, the diamond-type of network implies Al–P bonds leading to (4b)Al1− (4b)P1+ species, which contradicts electronegativity differences, however. Of course, both variants are formally correct, and none of them is actually wrong, although both are unsatisfying.
The solution is given with the aid of the 8 − Neff rule based on QTAIM effective charges of about ± 2 (Fig. 6 middle, left column) as Al2+ (1b′)P2−. This way, the polarity-extended 8 − Neff rule could be considered to lose a part of the original predictive power by additionally opening the hitherto neglected polar-covalent bonding-scenario channel with equal importance as the homoatomic bonding one. On the other hand, it widens the analytical value of the 8 − Neff rule by inclusion of polar bonding scenarios into the mathematical description.
As an exemplary case, there seems to be a conceptual gap between the two competing MgAgAs and TiNiSi types of structures. The conceptual difference between them is caused by the identification of a diamond type of partial structure in the former, and the absence of such a tempting coordination in the latter. Thus, while the TiNiSi type main-group compounds are usually treated with the predictive type of approach, e.g. CaMgSn is formally considered39 as Ca2+ Mg2+ (0b)Sn4−, the MgAgAs type ones are often interpreted in the framework of the analytical type of approach emphasizing one covalently bonded zinc blende type partial structure,40i.e. a compound like LiAlGe is formally considered as Li+ (4b)Al− (4b)Ge0 and not as Li+ Al3+ Ge4−. The current study on TiNiSi type main-group compounds closes the conceptual gap between these and the MgAgAs type of main-group compounds by common analysis of polar-covalent bonding within the 8 − Neff scheme.
The present study yields a basic understanding of differences in nonmetal–metal coordination E@Mn from the viewpoint of bonding polarity for the polar multi-atomic bonds found already in the semiconducting main-group compounds, and forms a basis for a future interpretation of the TiNiSi type of compounds containing transition metals.
Conflicts of interest
There are no conflicts to declare.Note added after first publication
This article replaces the version published on 18th May 2023, which contained errors in Fig. 4.Acknowledgements
Open Access funding provided by the Max Planck Society.References
- P. Villars and K. Cenzual, Pearson's Crystal Data: Crystal Structure Database for Inorganic Compounds, Release 2021/22, ASM International, Materials Park, Ohio, USA Search PubMed.
- J. Dshemuchadse and W. Steurer, Intermetallics: structures, properties, and statistics, Oxford University Press, Oxford, United Kingdom, 2016 Search PubMed.
- R. J. Quinn and J.-W. G. Bos, Mater. Adv., 2021, 2, 6246–6266 RSC.
- I. Antonyshyn, F. R. Wagner, M. Bobnar, O. Sichevych, U. Burkhardt, M. Schmidt, M. König, K. Poeppelmeier, A. P. Mackenzie, E. Svanidze and Yu. Grin, Angew. Chem., Int. Ed., 2020, 59, 11136–11141 CrossRef CAS PubMed.
- W. Al-Sawai, H. Lin, R. S. Markiewicz, L. A. Wray, Y. Xia, S.-Y. Xu, M. Z. Hasan and A. Bansil, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 125208-1–125208-5 CrossRef.
- L. Müchler, F. Casper, B. Yan, S. Chadov and C. Felser, Phys. Status Solidi RRL, 2013, 7, 91–100 CrossRef.
- S.-V. Ackerbauer, A. Senyshyn, H. Borrmann, U. Burkhardt, A. Ormeci, H. Rosner, W. Schnelle, M. Gamza, R. Gumeniuk, R. Ramlau, E. Bischoff, J. C. Schuster, F. Weitzer, A. Leithe-Jasper, L. H. Tjeng and Yu. Grin, Chem. – Eur. J., 2012, 18, 6272–6283 CrossRef CAS PubMed.
- D. Bende, F. R. Wagner, O. Sichevych and Yu. Grin, Angew. Chem., Int. Ed., 2017, 56, 1313–1318 CrossRef CAS PubMed.
- G. O. Brunner and D. Schwarzenbach, Z. Kristallogr., 1971, 133, 127–133 CrossRef CAS.
- (a) D. Bende, F. R. Wagner and Yu. Grin, Inorg. Chem., 2015, 54, 3970–3978 CrossRef CAS PubMed; (b) F. R. Wagner, D. Bende and Yu. Grin, Dalton Trans., 2016, 45, 3236–3243 RSC; (c) D. Bende, Yu. Grin and F. R. Wagner, Chem. – Eur. J., 2014, 20, 9702–9708 CrossRef CAS PubMed; (d) D. Bende, Yu. Grin and F. R. Wagner, in Heusler Alloys, ed. C. Felser and A. Hirohata, Springer, 2016, pp. 133–156 Search PubMed.
- Yu. Grin and Ya. P. Yarmolyuk, Izv. AN SSSR Metally, 1983,(1), 192–195 CAS (in Russian); Yu. Grin and Ya. P. Yarmolyuk, Russ. Metall., 1983,(1), 161–164 Search PubMed (in English).
- R.-D. Hoffmann and R. Pöttgen, Z. Kristallogr., 2001, 216, 127–145 CAS.
- H. Bärnighausen, Commun. Math. Chem., 1980, 9, 139–175 Search PubMed.
- (a) W. Jeitschko, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1968, 24, 930–934 CrossRef CAS; (b) W. Jeitschko and R. O. Altmeyer, Z. Naturforsch., B: J. Chem. Sci., 1990, 45, 947–951 CrossRef CAS.
- G. Nuspl, K. Polborn, J. Evers, G. A. Landrum and R. Hoffmann, Inorg. Chem., 1996, 35, 6922–6932 CrossRef CAS PubMed.
- G. A. Landrum, R. Hoffmann, J. Evers and H. Boysen, Inorg. Chem., 1998, 37, 5754–5763 CrossRef CAS.
- F. R. Wagner, M. Kohout and Yu. Grin, J. Phys. Chem. A, 2008, 112, 9814–9828 CrossRef CAS PubMed.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef CAS.
- M. Kohout, Int. J. Quantum Chem., 2004, 97, 651–658 CrossRef CAS.
- F. R. Wagner, V. Bezugly, M. Kohout and Yu. Grin, Chem. – Eur. J., 2007, 13, 5724–5741 CrossRef CAS PubMed.
- M. Kohout, Program DGrid 5.0, Dresden, 2018 Search PubMed.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1999 Search PubMed.
- R. Freccero, P. Solokha, S. De Negri, A. Saccone, Yu. Grin and F. R. Wagner, Chem. – Eur. J., 2019, 25, 6600–6612 CrossRef CAS PubMed.
- K. Hippler, P. Vogt, R. Wortmann and H. Sabrowsky, Z. Naturforsch., B: J. Chem. Sci., 1989, 44, 1607–1609 CrossRef CAS.
- A. K. Chandran, V. K. Gudelli, P. C. Sreeparvathy and V. Kanchana, J. Solid State Chem., 2016, 243, 198–206 CrossRef CAS.
- X.-J. Feng, Yu. Prots, M. P. Schmidt, S. Hoffmann, I. Veremchuk, W. Schnelle, U. Burkhardt, J.-T. Zhao and Yu. Grin, Inorg. Chem., 2013, 52, 8971–8978 CrossRef CAS PubMed.
- D. M. Migas, L. Miglio, V. I. Shaposhnikov and V. E. Borisenko, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 205203-1–205203-7 CrossRef.
- A. K. Ganguli, A. M. Guloy and J. D. Corbett, J. Solid State Chem., 2000, 152, 474–477 CrossRef CAS.
- A. Baranov, M. Kohout, F. R. Wagner, Yu. Grin, R. Kniep and W. Bronger, Z. Anorg. Allg. Chem., 2008, 634, 2747–2753 CrossRef CAS.
- W. Biltz, Raumchemie der festen Stoffe, Verlag Leopold Voss, Leipzig, 1934 Search PubMed.
- F. R. Wagner and Yu. Grin, in Comprehensive Inorganic Chemistry III, ed. J. Reedijk and K. R. Poeppelmeier, Elsevier, Oxford, 2023, Vol. 3, pp. 222-237. DOI:10.1016/B978-0-12-823144-9.00189-8.
- G. N. Lewis, J. Am. Chem. Soc., 1916, 38, 762–785 CrossRef CAS.
- S. Raub and G. Jansen, Theor. Chem. Acc., 2001, 106, 223–232 Search PubMed.
- Q. Zheng, F. R. Wagner, A. Ormeci, Y. Prots, U. Burkhardt, M. Schmidt, W. Schnelle, Yu. Grin and A. Leithe-Jasper, Chem. – Eur. J., 2015, 21, 16285–16695 CrossRef.
- (a) I. Veremchuk, T. Mori, Yu. Prots, W. Schnelle, A. Leithe-Jasper, M. Kohout and Yu. Grin, J. Solid State Chem., 2008, 181, 1983–1991 CrossRef CAS; (b) P. Höhn, S. Agrestini, A. Baranov, S. Hoffmann, M. Kohout, F. Nitsche, F. R. Wagner and R. Kniep, Chem. – Eur. J., 2011, 17, 3347–3351 CrossRef PubMed.
- D. Menendez-Crespo, F. R. Wagner, E. Francisco, A. Martin-Pendas, Yu. Grin and M. Kohout, J. Phys. Chem. A, 2021, 125, 9011–9025 CrossRef CAS PubMed.
- A. K. Ganguli, A. M. Guloy and J. D. Corbett, J. Solid State Chem., 2000, 152, 474–477 CrossRef CAS.
- T. Graf, C. Felser and S. P. Parkin, Prog. Solid State Chem., 2011, 39, 1–50 CrossRef CAS.
Footnotes |
| † Dedicated to Eduard Zintl on the occasion of his 125th birthday. |
| ‡ Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dt00621b |
| This journal is © The Royal Society of Chemistry 2023 |





