DOI:
10.1039/D3DT00141E
(Paper)
Dalton Trans., 2023,
52, 3391-3402
Raman and NMR spectroscopic and theoretical investigations of the cubic laves-phases REAl2 (RE = Sc, Y, La, Yb, Lu)†
Received
16th January 2023
, Accepted 9th February 2023
First published on 13th February 2023
Abstract
The cubic Laves-phase aluminides REAl2 with RE = Sc, Y, La, Yb and Lu were prepared from the elements by arc-melting or using refractory metal ampoules and induction heating. They all crystallize in the cubic crystal system with space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and adopt the MgCu2 type structure. The title compounds were characterized by powder X-ray diffraction and spectroscopically investigated using Raman and 27Al and in the case of ScAl2 by 45Sc solid-state MAS NMR. In both, the Raman and NMR spectra, the aluminides exhibit only one signal due to the crystal structure. DFT calculations were used to calculate Bader charges illustrating the charge transfer in these compounds along with NMR parameters and densities of states. Finally, the bonding situation was assessed by means of ELF calculations rendering these compounds aluminides with positively charged REδ+ cations embedded in an [Al2]δ− polyanion.
m and adopt the MgCu2 type structure. The title compounds were characterized by powder X-ray diffraction and spectroscopically investigated using Raman and 27Al and in the case of ScAl2 by 45Sc solid-state MAS NMR. In both, the Raman and NMR spectra, the aluminides exhibit only one signal due to the crystal structure. DFT calculations were used to calculate Bader charges illustrating the charge transfer in these compounds along with NMR parameters and densities of states. Finally, the bonding situation was assessed by means of ELF calculations rendering these compounds aluminides with positively charged REδ+ cations embedded in an [Al2]δ− polyanion.
1 Introduction
Intermetallic aluminium compounds are an interesting class of materials, since they play a major role in the formation of high-strength aluminium alloys formed during precipitation hardening.1,2 In Mg–Cu–Al alloys for example, the so-called S-phase (MgCuAl2, Cmcm) forms during annealing.3–5 When searching the Pearson database,6 it becomes evident that Al forms binary compounds with almost every other element in the periodic table. Exceptions are the alkali-metals Na and heavier (Li compounds do exist), Cd and Hg, In and Tl as well as Pm and most of the actinides. The latter ones, however, are probably unknown due to a lack of accessibility. Amongst these, the alkaline-earth, group 3 and rare-earth metals and some of the actinides form compounds with the general formula MAl2 (Ca–Ba, Sc, Y, La–Nd, Sm–Lu, Th, U–Pu7–13) which adopt the cubic Laves-phase structure type MgCu2 (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). Having numerous isostructural compounds at hand enables the investigation of e.g. physical properties like their wear- and corrosion-resistance, their magnetic or superconductive, their low-temperature behaviour or their hydrogen storage capabilities also in dependence of the constituent elements.14–17 When drawing back to the MAl2 compounds, the compounds differ with respect to their unit cell parameter, but both crystallographic sites are special positions (M on 8b (3/8, 3/8, 3/8); Al on 16c (0,0,0)). Therefore, the sizes of the respective M atoms at least partially influence the lattice parameters. However, the elements differ significantly with respect to their electronegativities, and their valence electron configuration. In all cases, the Al atoms are more electronegative than the M atoms rendering these compounds aluminides. While the alkaline-earth atoms can supply a maximum of two electrons, elements of group 3 and the rare-earth atoms can supply up to three electrons. Exception of this rule are Eu and Yb, which are two electron metals in their elemental form.18,19 This in turn leads to differences in the respective negative charges on the Al atoms in the binary MAl2 compounds.
m). Having numerous isostructural compounds at hand enables the investigation of e.g. physical properties like their wear- and corrosion-resistance, their magnetic or superconductive, their low-temperature behaviour or their hydrogen storage capabilities also in dependence of the constituent elements.14–17 When drawing back to the MAl2 compounds, the compounds differ with respect to their unit cell parameter, but both crystallographic sites are special positions (M on 8b (3/8, 3/8, 3/8); Al on 16c (0,0,0)). Therefore, the sizes of the respective M atoms at least partially influence the lattice parameters. However, the elements differ significantly with respect to their electronegativities, and their valence electron configuration. In all cases, the Al atoms are more electronegative than the M atoms rendering these compounds aluminides. While the alkaline-earth atoms can supply a maximum of two electrons, elements of group 3 and the rare-earth atoms can supply up to three electrons. Exception of this rule are Eu and Yb, which are two electron metals in their elemental form.18,19 This in turn leads to differences in the respective negative charges on the Al atoms in the binary MAl2 compounds.
Solid-state Nuclear Magnetic Resonance (NMR) spectroscopy is a strong, site specific method for the characterization of compounds containing NMR active nuclei and known and used for several decades. Having 100% natural abundance the 27Al nucleus (I = 5/2) is an excellent candidate for NMR spectroscopic experiments, however, a medium-sized nuclear electric quadrupole moment (eQ = 0.15 × 10−28 m2) and a moderately high gyromagnetic ratio (γ = 6.976 × 107 rad T−1 s−1) can complicate the interpretation of its spectra.20,21 Still, 27Al (MAS-)NMR is nowadays a widely established technique for structural characterization in different material classes.22–26 Especially in the last twenty years it has been established as a versatile method for additional characterization of intermetallic compounds.27 And although this class of compounds has metallic character, the method can be used to gain a plethora of information such as validation of crystallographic structures, local environments, solid solutions and more. And although many ternary compounds have been characterized by NMR (e.g. the equiatomic ScTAl compounds,28 the ScT2Al Heusler phases,29 the gold compounds Na2Au3Al,30 AEAuX,31 AEAu2Al2,32 or the platinides Ba3Pt4Al433 or Sr2Pt3Al834) there is a significant lack of comparing studies about a larger group of isostructural compounds. As examples for the latter, the MTAl235,36 or the RE10TAl3 series37 should be mentioned.
Here, a combining study on the rare-earth aluminides REAl2 for the elements Sc, Y, La, Yb and Lu is presented. These aluminides are Pauli-paramagnetic (no localized magnetic moments, only conduction electrons) and exhibit only one crystallographic Al site, rendering them ideal candidates for systematic 27Al NMR studies. Individual studies on some of the compounds have already been reported before,38–41 however, a comparing work of the 27Al NMR data is missing and ScAl2 has not been characterized before. For this compound, in addition to 27Al also 45Sc NMR data could be obtained. Raman spectroscopic investigations were conducted on all prepared samples, which help to understand these compounds even further. Additionally, quantum-chemical calculations were carried out to help with the interpretation of the NMR data and to calculate Bader charges which can be used to analyse the anionic character of the [Al2]δ− network. The bonding situation was assessed using the electron localization function ELF.
2 Experimental
2.1 Synthesis
Aluminium pellets (99.99%, Onyxmet), scandium (99.98%; Onyxmet), yttrium (99.99%; Onyxmet), lanthanum (99.95%, Onyxmet), ytterbium (99.95%, Onyxmet) and lutetium (99.95%; Onyxmet) chunks were used for the reported syntheses. Lanthanum pieces were stored under an argon atmosphere, surface contaminations on the pieces were removed mechanically in an argon filled glovebox. The elements were weighed in the ideal stochiometric ratio of RE![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al = 1
Al = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and subsequently arc-melted in water-cooled copper crucibles in an argon atmosphere of about 800 mbar.42 The argon gas was purified over a titanium sponge (873 K), molecular sieve and silica gel prior to the use. The obtained buttons were remelted four to five times to improve the homogeneity. Powdered as-cast LuAl2 was loaded into a corundum crucible which was sealed in an evacuated silica tube and annealed at 1073 K for 48 h followed by cooling to RT within 48 h. The other samples were used without any further heat treatment. The ytterbium compound was synthesized in an arc-welded niobium ampoule43 due to the low boiling point of ytterbium metal (1496 K
2 and subsequently arc-melted in water-cooled copper crucibles in an argon atmosphere of about 800 mbar.42 The argon gas was purified over a titanium sponge (873 K), molecular sieve and silica gel prior to the use. The obtained buttons were remelted four to five times to improve the homogeneity. Powdered as-cast LuAl2 was loaded into a corundum crucible which was sealed in an evacuated silica tube and annealed at 1073 K for 48 h followed by cooling to RT within 48 h. The other samples were used without any further heat treatment. The ytterbium compound was synthesized in an arc-welded niobium ampoule43 due to the low boiling point of ytterbium metal (1496 K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18). The Nb ampoule was heated for 2 h to approximately 1200 K in an induction furnace (Trumpf Hüttinger, Truheat HF 5010) under argon atmosphere. All samples show metallic lustre, ground powders are grey and stable in air over months.
18). The Nb ampoule was heated for 2 h to approximately 1200 K in an induction furnace (Trumpf Hüttinger, Truheat HF 5010) under argon atmosphere. All samples show metallic lustre, ground powders are grey and stable in air over months.
2.2 X-ray diffraction
Powder X-ray diffraction (PXRD) patterns of the pulverized samples were recorded at room temperature on a D8-A25-Advance diffractometer (Bruker, Karlsruhe, Germany) in Bragg Brentano θ-θ-geometry (goniometer radius 280 mm) with Cu Kα-radiation (λ = 154.0596 pm). A 12 μm Ni foil working as Kβ filter and a variable divergence slit were mounted at the primary beam side. A LYNXEYE detector with 192 channels was used at the secondary beam side. Experiments were carried out in a 2θ range of 6–130° with a step size of 0.013° and a total scan time of 1 h. The recorded data was evaluated using the Bruker TOPAS 5.0 software.44
2.3 Solid-state NMR
27Al and 45Sc solid-state NMR spectra were recorded using a Bruker Avance III 400 WB spectrometer at 104.31 and 97.24 MHz using magic-angle spinning (MAS) conditions. The samples were used as fine powders. To reduce density and electrical conductivity, samples were mixed with dried sodium chloride in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 ratio. The diluted samples were loaded into a cylindrical ZrO2 rotor with a diameter of 4 mm and spun at the magic angle with 13 kHz. All experiments conducted were single-pulse with a typical pulse length of 0.83 μs and a relaxation delay of 1 s. Resonance shifts were referenced to 1 molar AlCl3 and ScCl3 solutions in H2O. The NMR spectra were recorded using the Bruker Topspin software,45 the analysis was performed with the help of the DMFit software.46
9 ratio. The diluted samples were loaded into a cylindrical ZrO2 rotor with a diameter of 4 mm and spun at the magic angle with 13 kHz. All experiments conducted were single-pulse with a typical pulse length of 0.83 μs and a relaxation delay of 1 s. Resonance shifts were referenced to 1 molar AlCl3 and ScCl3 solutions in H2O. The NMR spectra were recorded using the Bruker Topspin software,45 the analysis was performed with the help of the DMFit software.46
2.4 Raman measurements
For the acquisition of the Raman spectra, a Raman microscope LabRAM HR Evolution HORIBA Jobin Yvon A (Longmujeau, France) equipped with 532 and 633 nm Lasers (Melles Griot, IDEX Optics and Photonics, Albuquerque, USA) and an 1800 lines mm−1 grating and a 100er LWD objective was used.
2.5 Theoretical calculations
Density functional theory (DFT) calculations of the REAl2 series (RE = Sc, Y, La, Yb, Lu) were performed using the projector augmented wave method (PAW) of Blöchl47,48 coded in the Vienna ab initio simulation package (VASP).49,50 All VASP calculations employed the generalized gradient approximation (GGA) with exchange and correlation treated by Perdew–Burke–Enzerhof (PBE).51 The cut-off energy for the plane wave calculations was set to 500 eV and the Brillouin zone integration was carried out using 9 × 9 × 9 k-point meshes. NMR parameters were evaluated through the field gradient tensor calculations in VASP with the nuclear quadrupole moment of 146.6 mb for 27Al and –220 mb for 45Sc. The Bader charge analysis was based on VASP calculations with subsequent calculations using the Bader program developed by the Henkelman group.52–54 Chemical bonding was explored via Electron Localization Functions (ELF)55,56 obtained from the VASP calculations.
3 Results and discussion
3.1 Synthesis & X-ray diffraction
Phase pure samples, according to powder X-ray diffraction experiments, for all five rare-earth elements were obtained as described above. The diffraction patterns are shown in Fig. 1. The lattice parameters for the cubic compounds prepared in this work and from the literature are summarized in Table 1. As expected, the lattice parameters decrease with decreasing ionic radius57,58 of the rare-earth atoms and show an almost linear trend as it is expected due to the lanthanide contraction (Fig. 2). Exceptions from this trend are observed for EuAl2 and YbAl2. While the Eu atoms in EuAl2 exhibit a stable divalent state,59 YbAl2 was shown to be intermediate valent with a valence close to +2.4 at 300 K.60,61 Since both Eu2+ and Yb2+ are significantly larger compared to their trivalent counterparts (r(Eu2+) = 125 pm vs. r(Eu3+) = 107 pm and r(Yb2+) = 114 pm vs. r(Yb3+) = 99 pm; all given for CN = 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57,58), signficantly enlarged unit cells are observed for these two compounds.
57,58), signficantly enlarged unit cells are observed for these two compounds.
 |
| | Fig. 1 Powder X-ray diffraction pattern of the REAl2 compounds (RE = Sc, Y, La, Yb and Lu; top to bottom) crystallizing in the cubic MgCu2 type structure (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). The experimental data is shown as black dots, the fit as red line and the difference in blue. The green ticks indicate the Bragg positions. m). The experimental data is shown as black dots, the fit as red line and the difference in blue. The green ticks indicate the Bragg positions. | |
 |
| | Fig. 2 Lattice parameters of the REAl2 compounds (RE = Sc, Y, La–Nd, Sm–Lu) crystallizing in the cubic MgCu2 type structure (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) plotted versus their respective ionic radius for CN = 8. m) plotted versus their respective ionic radius for CN = 8. | |
Table 1 Lattice parameters, determined by Rietveld analysis from the recorded PXRD patterns of the cubic Laves-phases (MgCu2 type, Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) and from the literature
m) and from the literature
| Compound |
a/pm |
Ref. |
| ScAl2 |
757.98(1) |
This work |
| ScAl2 |
758.0 |
62
|
| YAl2 |
786.29(1) |
This work |
| YAl2 |
786.0 |
12
|
| LaAl2 |
814.85(1) |
This work |
| LaAl2 |
816.9 |
63
|
| CeAl2 |
809.0 |
63
|
| PrAl2 |
803.5 |
11
|
| NdAl2 |
799.9 |
11
|
| SmAl2 |
794.3 |
11
|
| EuAl2 |
812.5 |
64
|
| GdAl2 |
790.0 |
13
|
| TbAl2 |
786.7 |
13
|
| DyAl2 |
784.0 |
13
|
| HoAl2 |
781.3 |
13
|
| ErAl2 |
779.5 |
13
|
| TmAl2 |
778.0 |
64
|
| YbAl2 |
788.36(1) |
This work |
| YbAl2 |
787.7 |
64
|
| LuAl2 |
774.37(1) |
This work |
| LuAl2 – annealed |
774.24(1) |
This work |
| LuAl2 |
774.2 |
64
|
A more detailed analysis of the diffraction patterns indicates that all samples contain a certain degree of strain since they were used without annealing. The largest strain is observed for the samples of YAl2 and LuAl2, while ScAl2 for example shows almost no strain. The work of Yuan and coworkers reported,38 that a thermal treatment of the LuAl2 sample improves the qualitity of the NMR spectrum with respect to the line broadening and assymmetry of the central transition line shape, however, the resonance frequency and the quadrupolar coupling are not affected. This might indicate that their initial sample also contained certain amounts of strain. Subsequently, the as-cast LuAl2 sample from this work was annealed for 48 h at 1073 K, which led to a significant decrease of the strain.
3.2 Crystal chemistry
The REAl2 members (RE = Sc, Y, La, Yb, Lu) all crystallize in the cubic crystal system with space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and adopt the so-called cubic Laves-phase (MgCu2 type). The structure contains one RE and one Al site, with the Al atoms forming empty Al4 tetrahedra that are connected to other tetrahedra via all atoms forming a network (Fig. 3, left). The RE atoms reside in the cavities of this framework. When looking at the arrangement of the RE atoms, an arrangement similar to cubic diamond can be observed. In the following paragraph, the structure will be briefly discussed using ScAl2 as example. The Al atoms are surrounded by six Al and six Sc atoms in the shape of a compressed icosahedron (Fig. 3, right). The Al atoms form two opposing triangular faces while the six Sc atoms are located near the equatorial plane, forming an undulating six-membered ring. The Sc atoms exhibit a coordination number of 16 arranged as Frank-Kasper polyhedron (Sc@Sc4Al12; Fig. 3, middle). Due to the high site symmetries (Sc: 8b,
m and adopt the so-called cubic Laves-phase (MgCu2 type). The structure contains one RE and one Al site, with the Al atoms forming empty Al4 tetrahedra that are connected to other tetrahedra via all atoms forming a network (Fig. 3, left). The RE atoms reside in the cavities of this framework. When looking at the arrangement of the RE atoms, an arrangement similar to cubic diamond can be observed. In the following paragraph, the structure will be briefly discussed using ScAl2 as example. The Al atoms are surrounded by six Al and six Sc atoms in the shape of a compressed icosahedron (Fig. 3, right). The Al atoms form two opposing triangular faces while the six Sc atoms are located near the equatorial plane, forming an undulating six-membered ring. The Sc atoms exhibit a coordination number of 16 arranged as Frank-Kasper polyhedron (Sc@Sc4Al12; Fig. 3, middle). Due to the high site symmetries (Sc: 8b, ![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m; Al: 16c, .
3m; Al: 16c, .![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) and the symmetric coordination environment, one can derive that the asymmetry parameters ηQ for all 27Al and the 45Sc NMR spectra should be zero. At the same time, the nuclei of both Sc and Al exhibit a quadrupole moment. Therefore, the quadrupolar interaction of both nuclei is expected to be observed in their respective NMR spectra.
m) and the symmetric coordination environment, one can derive that the asymmetry parameters ηQ for all 27Al and the 45Sc NMR spectra should be zero. At the same time, the nuclei of both Sc and Al exhibit a quadrupole moment. Therefore, the quadrupolar interaction of both nuclei is expected to be observed in their respective NMR spectra.
 |
| | Fig. 3 (left) Unit cell of ScAl2 (MgCu2 type, Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) and coordination environments of the (middle) Sc (blue) and (right) Al (grey) atoms. Wyckoff positions and site symmetries as well as interatomic distances (in pm) are given. m) and coordination environments of the (middle) Sc (blue) and (right) Al (grey) atoms. Wyckoff positions and site symmetries as well as interatomic distances (in pm) are given. | |
3.3 Solid State NMR spectroscopy
All five 27Al MAS spectra recorded with single-pulse excitation experiments are shown in Fig. 4 (left). As described in the previous section, one resonance originating from one crystallographically independent Al site in the crystal structure is expected. All spectra show one sharp central line, originating from the |+1/2> ↔ |–1/2> transition. All of them also show a wide spinning side band manifold caused by the |±1/2> ↔ |±3/2> and |±3/2> ↔ |±5/2> transitions, which are observable due to quadrupolar interactions. All resonance lines are significantly shifted compared to an aqueous solution of Al3+ within a range of 200 up to 950 ppm. This is caused by the interaction of the magnetic moment of the active 27Al nuclei, the same is true for 45Sc, with the conduction electrons of the metallic material. This is known as the Knight shift. To analyse the spectra, in a first step all central transitions were fitted with simple Gaussian-Lorentz lines. As can be seen on the right part of Fig. 4, all line shapes can be described with a Gaussian-Lorentz fit in a satisfying fashion. However, in the spectra of YAl2, LuAl2 and YbAl2 the central transition shows a broad half-width and anisotropy with a shoulder on the left side.
 |
| | Fig. 4
27Al solid state MAS NMR spectra (black) of the REAl2 compounds (RE = Sc, Y, La, Yb, Lu) with simulations (red) of the central transition and the rotational sideband manifold (left). On the right site the central transition of each spectrum is shown. The asymmetric broadening is indicated by grey arrows. | |
Table 2 summarizes the relevant experimentally determined NMR parameters along with the ones from the DFT calculations. For some cases (RE = Y, La) the spectra could be simulated quite well using the values from DFT calculations. In these cases, the CQ parameters were not refined. Due to the cubic symmetry of the structure, the asymmetry parameter ηQ must be zero, which agrees with the result of the DFT calculations. From the resonance shifts δ gained by fitting the data, the Knight shift contribution δK can be calculated using the NMR parameters from the DFT calculations as described in the literature.27,65 Since all other contributions are small, they can be neglected as the Knight part dominates.
Table 2
27Al and 45Sc NMR parameters for the measured REAl2 compounds (RE = Sc, Y, La, Yb and Lu). Isotropic shift δ (±1 ppm), knight shift contribution δK, nuclear electric quadrupole coupling constants CQ (±0.05 MHz), electric field gradient asymmetry parameters ηQ (±0.05), chemical shift anisotropy (dCS parameter) (±5 ppm) and degrees of Gaussian (vs. Lorentzian) character of the central MAS signal
| Compound |
|
δ/ppm |
δ
K/ppm |
C
Q,theo/kHz |
C
Q,exp/kHz |
G/L |
dCS/ppm |
Lit. |
| ScAl2 |
27Al |
213 |
213 |
884 |
1618 |
0.53 |
43 |
This work |
|
45Sc |
2279 |
2279 |
0 |
92 |
0 |
–22 |
This work |
| YAl2 |
27Al |
336 |
343 |
3466 |
|
0.49 |
–17 |
This work |
|
27Al |
364 |
|
|
|
|
30 |
38
|
| LaAl2 |
27Al |
636 |
648 |
4626 |
|
0.53 |
–108 |
This work |
|
27Al |
600 |
|
|
4630/5139 |
|
0 |
38–40
|
| YbAl2 |
27Al |
924 |
926 |
2072 |
2488 |
0.21 |
–188 |
This work |
|
27Al |
1100 |
|
|
2300/2580 |
|
|
39 and 41 |
| LuAl2 |
27Al |
379 |
381 |
2034 |
2794 |
0.65 |
–14 |
This work |
|
27Al |
386 |
|
|
2840 |
|
48/32 |
38
|
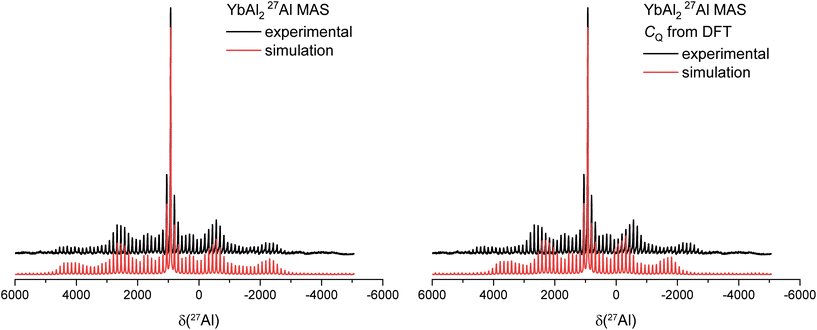
For all spectra the theoretical values of CQ obtained from DFT calculations were used to simulate the spectra in the first place. In the cases of Sc, Yb and Lu the theoretical values did not match the experimental spectra well, here a better fit was found using the DMFit simulation program.46Fig. 5 (left) exemplarily shows the 27Al MAS spectrum for YbAl2, where the intensity profile simulated based on the DFT-calculated CQ does not match to the recorded spectrum, while Fig. 5 (right) shows the results from the fit. For quadrupolar coupling constants >3 MHz it is more difficult up to impossible to determine the CQ parameter via the analysis of the experimental sideband spinning pattern because it extends over a too large spectral region which exceeds the available spectral bandwidth.33 At the same time, it also becomes clear that a determination of CQ from the line shape of the central transition is not possible because it is featureless and can be described well with a Gaussian-Lorentz simulation (Fig. 5). This is also the case for the La and Y compounds. Here, the quadrupolar coupling parameters obtained via DFT calculations were used and no refinement was performed. Finally, one can observe that the spinning sideband pattern intensities are asymmetric to the central transition. This indicates that chemical shift anisotropy (CSA) is present.
 |
| | Fig. 5
27Al MAS spectrum of YbAl2 fitted with an experimental determined value of CQ (left) versus the CQ value obtained by DFT calculations (right). | |
It should be noted that the samples of YAl2, YbAl2 and LuAl2 show a shoulder to the left side of the central transition. Similar asymmetric line broadening of the central transition of the YAl2 and LuAl2 spectra is also observed in the literature.38 That observation is consistent with the fact that significant strain is observed in the PXRD patterns for all compounds (vide supra). To overcome the influence of strain within the structure, the arc-melted sample of LuAl2 was exemplarily heat treated and reinvestigated by NMR. It should be mentioned that the influence of annealing was already investigated in the literature.38Fig. 6 shows a comparison of the 27Al MAS spectra of as-cast LuAl2 and after annealing. It can be observed that the anisotropically broadened central transition is still present, but the line width of the transition gets smaller (by a factor of 2) after the thermal treatment. This observation is in line with the reduction in strain in the PXRD pattern.
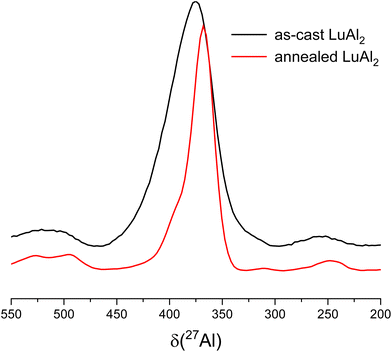 |
| | Fig. 6 Comparison of the central transition in the 27Al MAS spectra of as-cast (black) and annealed (red) LuAl2. | |
The 27Al and 45Sc spectra of ScAl2 are shown in Fig. 7. For the 45Sc MAS NMR also one sharp central line, originating from the |+1/2> ↔ |–1/2> transition is observed, a potential spinning side band manifold is caused by the |±1/2> ↔ |±3/2>, |±3/2> ↔ |±5/2> and |±5/2> ↔ |±7/2> transitions, which are observable due to quadrupolar interactions.66 The DFT calculations on ScAl2 suggest a CQ and ηQ of zero, but simulations of the observed spinning sideband manifold give a rather small value of CQ = 92 kHz. A possible explanation for the difference between experiment and theory in this case could be that the DFT calculations are performed with a non-defective, perfect structure, which is not true for as synthesized compounds. Here disorder and strain can play a significant role. And even if ScAl2 exhibits a rather small strain as refined from the powder X-ray diffraction data, NMR as a local probe can visualize even these small influences. This observation can also explain, why the calculated CQ parameters in most cases are smaller than the experimental values (Table 2). The same is true for the 27Al MAS spectrum for ScAl2, here the experimental CQ value is double the size of the theoretical one (Table 2), similar to what has been observed for YbAl2 (vide supra).
 |
| | Fig. 7
27Al (left) and 45Sc (right) MAS spectrum of ScAl2 (black) along with the fitted spectra (red). | |
Of these five compounds, YAl2, LaAl2, YbAl2 and LuAl2 have already been investigated by 27Al NMR investigations.38–41 For these, a full characterization, along with partial quantum chemical investigations has been conducted and the results from the literature have been compiled in Table 2 along with the results of this study. The resonance shifts of the central transitions are in good (YAl2 and LuAl2) to fair (LaAl2) agreement with the ones reported by Yuan et al.,38 while the quadrupolar coupling constants CQ are a good match. For YbAl2, only the quadrupolar coupling constants CQ had been reported before by Jaccarino39 and Barnes,41 which is in good agreement with the results reported here. In contrast, for ScAl2, no investigations regarding the resonance shift and the quadrupolar coupling have been reported. Here, only the Knight shift contribution and an estimate of the s-electron densities have been reported.67
3.4 Raman spectroscopy
Raman spectroscopic measurements of the title compounds have been conducted using crystallites of the polycrystalline sample under a Raman microscope 532 nm and 633 nm laser excitation. All five compounds show one band in the measured range of 10 to 900 cm−1 (Fig. 8) originating from the respective intermetallic compound. The bands around 100 cm−1 could be assigned to water. According to the investigations of Güntherodt et al.,68 the Γ25′ (T2g) Raman-active mode in the cubic Laves-phase is caused by the rare-earth atoms (8b site) with their diamond-type arrangement. They investigated different REAl2 compounds (RE = La, Ce, Eu, Gd, Dy, Yb) and observed modes with peak maxima ranging from 95 for YbAl2 to 118 cm−1 for GdAl2 (Table 3). Their data could be confirmed for the cases of LaAl2, YbAl2 and LuAl2 and furthermore extended by the measurements of ScAl2 and YAl2 with maxima at 199 and 157–160 cm−1 and half-width values of 6 and 5 cm−1, respectively. The positions for LaAl2 and YbAl2 as well as half-widths for LuAl2 agree with the ones in the literature.68 A striking feature, however, is that EuAl2 and YbAl2 exhibit by far the lowest wavenumbers. This nicely correlates with their formal oxidation state being divalent (EuAl2) and intermediate valent (YbAl2). The amplitudes of the YbAl2 oscillation are weak; the cause could be the superposition with water vibrations as well as the intermediate valence state. YbAl2 shows an asymmetric broadening of the band in direction to smaller wavenumbers and Güntherodt et al., observed a half width of 10 cm−1.68 Analogously, a shoulder at 108 cm−1 was detected for LuAl2 next to the main band at 112 cm−1. Since here no intermediate valence behaviour is possible, this feature might be caused by the significant strain in the material.
 |
| | Fig. 8 Raman spectra of REAl2 (RE = Sc, Y, Lu, La, Yb), the arrows mark the shoulders at RE = Lu, Yb. | |
Table 3 Raman bands of REAl2 compounds, measurements conducted in this study are the average of 6 measurements, respectively, at room temperature
| RE |
Position T2g/cm−1 |
FWHM/cm−1 |
Reference |
Position T2g/cm−1 |
FWHM/cm−1 |
Ref. |
| FWHM: Full width at half maximum. |
| Sc |
198–199 |
6.3 |
This work |
|
|
|
| Y |
157–160 |
5.4 |
This work |
|
|
|
| Gd |
|
|
|
118 |
4 |
68
|
| Dy |
|
|
|
117 |
5 |
68
|
| Sm |
|
|
|
115 |
|
69
|
| Lu |
111–112 |
3.4 |
This work |
|
|
|
| 108 (shoulder) |
3.8 |
This work |
|
|
|
| La |
110–112 |
4.9 |
This work |
112 |
5 |
68
|
| Ce |
|
|
|
109 |
7 |
68
|
| Yb |
96–97 |
2.7 |
This work |
95 |
10 |
68
|
| Eu |
|
|
|
96 |
4 |
68
|
Like with the NMR resonances, the Raman bands observed for the different REAl2 members show significant differences. When the Raman bands are plotted versus the unit cell parameter a (Fig. 9), two trends are observed. For the members of group 3, the Raman bands shift almost linearly within the group from Sc (200 cm−1) to Y (158 cm−1) to La (110 cm−1). In contrast, within the lanthanide series there are only small variations, with the exceptions of EuAl2 and YbAl2. The latter, however, exhibit divalent Eu2+ or intermediate valent Yb2.4+ cations, hence, the unusually large lattice parameters and low Raman shifts. The differences could be explained by the electron configurations. While Sc, Y and La are rather transition metals, the other elements are f-elements and exhibit electron configurations of [Xe] 4fn with n ≥ 1.
 |
| | Fig. 9 Raman shifts plotted versus the lattice parameters of the REAl2 compounds. The almost linear trend within group 3 is highlighted by the blue dashed line. The lanthanide compounds are highlighted by the green box. | |
3.5 Quantum chemistry
The electronic structures of the title compounds were analysed using density functional theory (DFT) calculations. The electron density of states (DOS) curves of REAl2 (RE = Sc, Y, La, Yb, Lu) and the partial s-electron DOS (p-DOS) of the Al atoms in each compound are plotted in Fig. 10. There is a substantial density of states at the Fermi level for all five compounds, indicating metallic behaviour, in line with the silvery shiny metallic appearance. The calculated Bader effective charges for REAl2 (RE = Sc, Y, La, Yb, Lu) are listed in Table 4. In all five compounds, the RE atoms have positive, while the Al atoms have negative charges, rendering them aluminides. The effective charges on the RE atoms are significantly smaller than +3 indicating weak ionic bonding between the REδ+ cations and the [Al2]δ− polyanionic network. When looking at the trend of the Pauling electronegativities (EN)18 (Sc: χ = 1.36; Y: χ = 1.22; La: χ = 1.1; Yb: χ = 1.1; Lu: χ = 1.27) one would expect larger positive effective charges of La and Yb, compared to Sc, Y and Lu, contrary to the Bader charges (Table 4). To better understand the chemical bonding in REAl2, electron localization functions have been examined and the results are shown in Fig. 11 and 12. Fig. 11 shows a high electron localization between nearest neighbour Al atoms, signalling covalent Al–Al interactions, which form the [Al2]δ− network. This is also supported by the iso-surface plotted in Fig. 12. It is worth noting that the electron localization is not evenly distributed around the Al–Al bond but prefers the side of bond facing the RE atom, which may be caused by the orbital overlap between Al and the RE atoms indicating partial multi-centre bonding. There is a high electron localization between La (or Yb) and the Al atoms in LaAl2 (or YbAl2), indicating stronger La–Al (Yb–Al) covalent interactions (weaker ionic interactions respectively) compared to those in ScAl2, YAl2 and LuAl2, providing an explanation for the small effective positive charges on La (or Yb), however, being in contrast with the EN. It is possible that the 5d orbitals in LaAl2 can overlap more with Al s/p orbitals, resulting in stronger covalent La–Al interactions, or, as suggest before, multi-centre bonding takes place. For YbAl2, based on the DOS in Fig. 10, the 4f orbital is right below the Fermi level, which might contribute to the Yb–Al orbital overlap and leading to strong Yb–Al covalent interactions. In addition, Yb is a so-called two-electron metal, despite Sc, Y, La and Lu being three-electron metals. Therefore, a reduced Bader charge on the Yb atoms is expected from this point of view. However, YbAl2 is an intermediate valent compound60,61 and exhibits partial Yb3+ character, making the bonding situation even more complicated.
 |
| | Fig. 10 (A) Total density of states and (B) Al s-electron partial density of states (per Al atom) of REAl2 (RE = Sc, Y, La, Yb, Lu) from non-spin-polarized DFT calculations, dotted line indicates Fermi level. | |
 |
| | Fig. 11 Electron localization function (ELF) plots of the (110) plane for REAl2 (RE = Sc, Y, La, Yb, Lu). Purple and grey spheres represent RE and Al atoms, respectively. | |
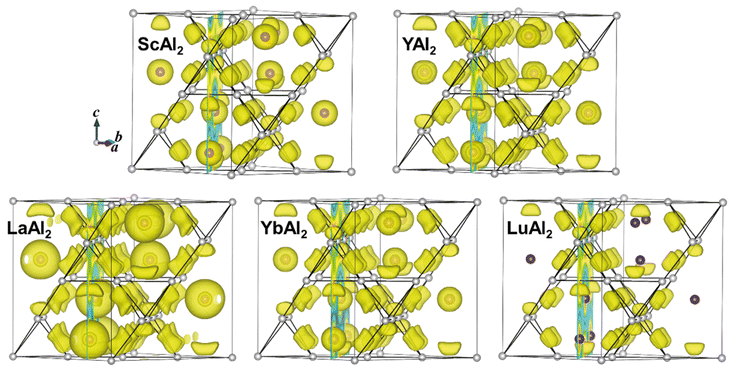 |
| | Fig. 12 Electron localization functions (ELF) plots for REAl2 (RE = Sc, Y, La, Yb, Lu) at iso-surface level of 0.70. Purple and grey spheres represent RE and Al atoms, respectively. | |
Table 4 Bader charges and s-electron densities (DOS per Al atom, states/eV) of the Al atoms at the Fermi level in the REAl2 series (RE = Sc, Y, La, Yb, Lu) obtained from non-spin-polarized DFT calculations
| REAl2 |
ScAl2 |
YAl2 |
LaAl2 |
YbAl2 |
LuAl2 |
| Charge on RE |
+1.23 |
+1.25 |
+0.97 |
+1.08 |
+1.14 |
| Charge on Al |
−0.61 |
−0.62 |
−0.48 |
−0.54 |
−0.57 |
| DOS per Al atom |
0.00670 |
0.00851 |
0.0144 |
0.0511 |
0.0102 |
Fig. 13 finally shows the correlation between the s-electron DOS of the Al atoms at the Fermi level plotted versus the calculated Knight shift contribution δK. As for the Raman measurements, also a correlation between the two and three electron metals can be observed. In YbAl2, a significantly, almost by a factor of 10, larger s-electron DOS at EF is observed leading to a dramatic shift in the 27Al NMR signal. Within the close-shell compounds, an almost linear increase of the Knight shift δKversus the s-electron DOS is visible.
 |
| | Fig. 13 Al atom s-electron pDOS at EF plotted versus δK. The green and blue boxes indicate the formally two and three electron metals. | |
4 Conclusion
The close-shell rare-earth aluminides REAl2 with RE = Sc, Y, La and Lu as well as intermediate valent YbAl2 (all cubic MgCu2 type) were synthesized from the elements and structurally characterized by powder X-ray diffraction. All compounds are X-ray pure; however, significant strain could be observed for the Y, Yb and Lu compounds. Annealing of LuAl2 decreased the strain. 27Al solid-state MAS NMR spectra were recorded for all compounds and in addition, 45Sc solid-state MAS NMR spectroscopic investigations for ScAl2 were conducted. All 27Al spectra exhibit a single central transition, in line with one crystallographic Al site, the same is true for the 45Sc spectrum. However, in agreement with the PXRD investigations, the main transitions of YAl2, YbAl2 and LuAl2 show an asymmetry which is probably caused by the strain of the material. Comparing investigations of annealed LuAl2 show a significantly sharper signal. The spectra were fitted using NMR parameters obtained from quantum-chemical calculations, however, not for all compounds the calculated values are in line with the experimentally observed ones, again caused by the internal strain. Raman spectra collected of all title compounds also show the strain inherent to the material. A comparison of the Raman shifts with respect to the structural data shows that the shift in the Raman signals can be explained by the variations in the interatomic distances and the electronic situation of the respective RE element. Finally, the bonding situation within the REAl2 members was assessed using Bader charge calculations and electron localization function (ELF). Bader charges clearly indicate the formation of aluminides due to the negatively charged [Al2]δ− framework, in line with the Pauling electronegativities. The peculiarities in the Bader charges can be attributed to the oxidation state of the RE atoms and a multi-centre bond formation. A comparison of the s-electron density at EF with the Knight shift contribution to the 27Al NMR resonance shows a linear dependency for the close-shell atoms, Yb, however, differs, due to the intermediate valence state.
Author contributions
All authors have accepted responsibility for the entire content of this submitted manuscript and approved the submission.
Conflicts of interest
The authors declare no conflicts of interest regarding this article.
Acknowledgements
Instrumentation and technical assistance for this work were provided by the Service Center X-ray Diffraction, with financial support from Saarland University and German Science Foundation (project number INST 256/349-1) and by the Service Center NMR with financial support from Saarland University and German Research Foundation DFG. We thank the San Diego Supercomputer Center (SDSC) for providing computing resources. Funding has been provided by the Deutsche Forschungsgemeinschaft DFG (JA 1891-10-1).
References
-
O. Janka, Metallic light-weight alloys: Al, Ti, Mg, in Applied Inorganic Chemistry, ed. R. Pöttgen, T. Jüstel and C. Strassert, De Gruyter, 2022, pp. 158–173 Search PubMed.
-
F. Ostermann, Anwendungstechnologie Aluminium, Springer Vieweg, Berlin, Heidelberg, 2014 Search PubMed.
- R. Kilaas, V. Radmilovic and U. Dahmen, Mater. Res. Soc. Symp. Proc., 2001, 589, 273–278 CrossRef CAS.
- B. Heying, R.-D. Hoffmann and R. Pöttgen, Z. Naturforsch., 2005, 60b, 491–494 CrossRef.
- S. J. Andersen, C. D. Marioara, J. Friis, S. Wenner and R. Holmestad, Adv. Phys.: X, 2018, 3, 1479984 Search PubMed.
-
P. Villars and K. Cenzual, Pearson's Crystal Data: Crystal Structure Database for Inorganic Compounds, ASM International®, Materials Park, Ohio, USA, 2023 Search PubMed.
- H. Nowotny, E. Wormnes and A. Mohrnheim, Z. Metallkd., 1940, 32, 39–42 CAS.
- R. E. Rundle and A. S. Wilson, Acta Crystallogr., 1949, 2, 148–150 CrossRef CAS.
- O. J. C. Runnalls, JOM, 1953, 5, 1460–1462 CrossRef CAS.
- O. J. C. Runnalls, Can. J. Chem., 1956, 34, 133–145 CrossRef CAS.
- A. Iandelli, Natl. Phys. Lab. (U. K.), Symp., 1951, 3F2–3F11 Search PubMed.
- V. B. Compton and B. T. Matthias, Acta Crystallogr., 1959, 12, 651–654 CrossRef CAS.
- J. H. Wernick and S. Geller, Trans. Metall. Soc. AIME, 1960, 218, 866–868 CAS.
- F. Stein and A. Leineweber, J. Mater. Sci., 2021, 56, 5321–5427 CrossRef CAS.
- E. Bauer, E. Gratz and G. Adam, J. Phys. F: Met. Phys., 1986, 16, 493 CrossRef CAS.
- A. T. Burkov, M. Vedernikov and E. Gratz, Physica B Condens. Matter, 1992, 176, 263–274 CrossRef CAS.
- A. K. Pathak, D. Paudyal, K. A. Gschneidner and V. K. Pecharsky, J. Appl. Phys., 2014, 115, 17E109 CrossRef.
-
J. Emsley, The Elements, Clarendon Press, Oxford University Press, Oxford, New York, 1998 Search PubMed.
-
J. Donohue, The Structures of the Elements, Wiley, New York, 1974 Search PubMed.
- R. K. Harris, E. D. Becker, S. M. Cabral de Menezes, P. Granger, R. E. Hoffman and K. W. Zilm, Pure Appl. Chem., 2008, 80, 59–84 CrossRef CAS.
- N. J. Stone, At. Data Nucl. Data Tables, 2016, 112, 1–28 CrossRef.
- A. Putnis, Phys. Chem. Miner., 1996, 23, 247–247 CrossRef CAS.
- M. Haouas, F. Taulelle and C. Martineau, Prog. Nucl. Magn. Reson. Spectrosc., 2016, 95, 11–36 CrossRef PubMed.
- A. T. Bell, Colloids Surf., A, 1999, 158A, 221–234 CrossRef.
-
G. Engelhardt, Characterization of Zeolite Catalysts and Related Materials by Multinuclear Solid-State NMR Spectroscopy, In Surface Science: Principles and Current Applications, ed. R. J. MacDonald, E. C. Taglauer and K. R. Wandelt, Springer Berlin Heidelberg, Berlin, Heidelberg, 1996, pp. 321–330 Search PubMed.
- A. L. Blumenfeld and J. J. Fripiat, Magn. Reson. Chem., 1999, 37, S118–S125 CrossRef CAS.
- C. Benndorf, H. Eckert and O. Janka, Acc. Chem. Res., 2017, 50, 1459–1467 CrossRef CAS PubMed.
- M. Radzieowski, C. Benndorf, S. Haverkamp, H. Eckert and O. Janka, Z. Naturforsch., 2016, 71b, 553–566 CrossRef.
- C. Benndorf, O. Niehaus, H. Eckert and O. Janka, Z. Anorg. Allg. Chem., 2015, 168–175 CrossRef CAS.
- F. Stegemann, C. Benndorf, Y. Zhang, M. Bartsch, H. Zacharias, B. P. T. Fokwa, H. Eckert and O. Janka, Inorg. Chem., 2017, 56, 1919–1931 CrossRef CAS PubMed.
- C. Benndorf, F. Stegemann, S. Seidel, L. Schubert, M. Bartsch, H. Zacharias, B. Mausolf, F. Haarmann, H. Eckert, R. Pöttgen and O. Janka, Chem. – Eur. J., 2017, 23, 4187–4196 CrossRef CAS PubMed.
- F. Stegemann, C. Benndorf, Y. Zhang, M. Bartsch, H. Zacharias, B. P. T. Fokwa, H. Eckert and O. Janka, Z. Anorg. Allg. Chem., 2017, 643, 1379–1390 CrossRef CAS.
- F. Stegemann, C. Benndorf, T. Bartsch, R. S. Touzani, M. Bartsch, H. Zacharias, B. P. T. Fokwa, H. Eckert and O. Janka, Inorg. Chem., 2015, 54, 10785–10793 CrossRef CAS PubMed.
- F. Stegemann, T. Block, S. Klenner, Y. Zhang, B. P. T. Fokwa, C. Doerenkamp, H. Eckert and O. Janka, Eur. J. Inorg. Chem., 2021, 2021, 3832–3845 CrossRef CAS.
- F. Stegemann, T. Block, S. Klenner, Y. Zhang, B. P. T. Fokwa, A. Timmer, H. Mönig, C. Doerenkamp, H. Eckert and O. Janka, Chem. – Eur. J., 2019, 25, 10735–10747 CrossRef CAS PubMed.
- M. Radzieowski, F. Stegemann, C. Doerenkamp, S. F. Matar, H. Eckert, C. Dosche, G. Wittstock and O. Janka, Inorg. Chem., 2019, 58, 7010–7025 CrossRef CAS PubMed.
- C. Benndorf, H. Eckert and O. Janka, Dalton Trans., 2017, 46, 1083–1092 RSC.
- C. C. Yuan, Y. F. Yang, X. K. Xi, J. Cui and J. F. Xiang, Solid State Nucl. Magn. Reson., 2012, 41, 28–31 CrossRef CAS PubMed.
- V. Jaccarino, B. T. Matthias, M. Peter, H. Suhl and J. H. Wernick, Phys. Rev. Lett., 1960, 5, 251–253 CrossRef CAS.
- K. Betsuyaku and H. Harima, J. Magn. Magn. Mater., 2001, 226–230, 199–201 CrossRef CAS.
- R. G. Barnes, W. H. Jones and T. P. Graham, Phys. Rev. Lett., 1961, 6, 221–223 CrossRef CAS.
- R. Pöttgen, T. Gulden and A. Simon, GIT Labor-Fachz., 1999, 43, 133–136 Search PubMed.
- R. Pöttgen, A. Lang, R.-D. Hoffmann, B. Künnen, G. Kotzyba, R. Müllmann, B. D. Mosel and C. Rosenhahn, Z. Kristallogr., 1999, 214, 143–150 Search PubMed.
-
Bruker AXS Inc., Topas, Version 5, Karlsruhe, Germany, 2014 Search PubMed.
-
Bruker Corp., Topspin, Version 2.1, Karlsruhe, 2008 Search PubMed.
- D. Massiot, F. Fayon, M. Capron, I. King, S. Le Calvé, B. Alonso, J.-O. Durand, B. Bujoli, Z. Gan and G. Hoatson, Magn. Reson. Chem., 2002, 40, 70–76 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908 CrossRef CAS PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- A. Savin, R. Nesper, S. Wengert and T. F. Fässler, Angew. Chem., 1997, 109, 1892–1918 CrossRef.
- B. Silvi and A. Savin, Nature, 1994, 371, 683–686 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., 1976, A32, 751 CrossRef CAS.
- R. D. Shannon and C. T. Prewitt, Acta Crystallogr., 1969, B25, 925 CrossRef.
- A. Gleissner, W. Potzel, J. Moser and G. M. Kalvius, Phys. Rev. Lett., 1993, 70, 2032–2035 CrossRef CAS PubMed.
- A. Iandelli and A. Palenzona, J. Less-Common Met., 1972, 29, 293–297 CrossRef CAS.
- E. E. Havinga, K. H. J. Buschow and H. J. van Daal, Solid State Commun., 1973, 13, 621–627 CrossRef CAS.
- V. N. Rechkin, L. K. Lamikhov and T. I. Samsonova, Sov. Phys. Crystallogr., 1964, 9, 325–327 Search PubMed.
- H. N. Nowotny, Z. Metallkd., 1942, 34, 22–24 CAS.
- S. E. Haszko, Trans. Metall. Soc. AIME, 1960, 218, 958 CAS.
- S. Engel, E. C. J. Gießelmann, L. E. Schank, G. Heymann, K. Brix, R. Kautenburger, H. P. Beck and O. Janka, Inorg. Chem., 2023 DOI:10.1021/acs.inorgchem.2c04391.
- H. Eckert and R. Pöttgen, Z. Anorg. Allg. Chem., 2010, 636, 2232–2243 CrossRef CAS.
- E. P. Chock, R. A. B. Devine, S. A. Dodds, R. Orbach and L. Tippie, J. Phys. F: Met. Phys., 1977, 7, 1097–1102 CrossRef CAS.
- G. Güntherodt, A. Jayaraman, G. Batlogg, M. Croft and E. Melczer, Phys. Rev. Lett., 1983, 51, 2330–2332 CrossRef.
- J. Su and C. Zhu, Mater. Res. Bull., 2003, 38, 2025–2029 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Stefan
Engel
a,
Stefan
Engel
 a,
Weronika
Kostusiak
bc,
Yuemei
Zhang
a,
Weronika
Kostusiak
bc,
Yuemei
Zhang
 b,
Petra
Herbeck-Engel
d,
Guido
Kickelbick
b,
Petra
Herbeck-Engel
d,
Guido
Kickelbick
 a and
Oliver
Janka
a and
Oliver
Janka
 *a
*a
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and adopt the MgCu2 type structure. The title compounds were characterized by powder X-ray diffraction and spectroscopically investigated using Raman and 27Al and in the case of ScAl2 by 45Sc solid-state MAS NMR. In both, the Raman and NMR spectra, the aluminides exhibit only one signal due to the crystal structure. DFT calculations were used to calculate Bader charges illustrating the charge transfer in these compounds along with NMR parameters and densities of states. Finally, the bonding situation was assessed by means of ELF calculations rendering these compounds aluminides with positively charged REδ+ cations embedded in an [Al2]δ− polyanion.
m and adopt the MgCu2 type structure. The title compounds were characterized by powder X-ray diffraction and spectroscopically investigated using Raman and 27Al and in the case of ScAl2 by 45Sc solid-state MAS NMR. In both, the Raman and NMR spectra, the aluminides exhibit only one signal due to the crystal structure. DFT calculations were used to calculate Bader charges illustrating the charge transfer in these compounds along with NMR parameters and densities of states. Finally, the bonding situation was assessed by means of ELF calculations rendering these compounds aluminides with positively charged REδ+ cations embedded in an [Al2]δ− polyanion.![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). Having numerous isostructural compounds at hand enables the investigation of e.g. physical properties like their wear- and corrosion-resistance, their magnetic or superconductive, their low-temperature behaviour or their hydrogen storage capabilities also in dependence of the constituent elements.14–17 When drawing back to the MAl2 compounds, the compounds differ with respect to their unit cell parameter, but both crystallographic sites are special positions (M on 8b (3/8, 3/8, 3/8); Al on 16c (0,0,0)). Therefore, the sizes of the respective M atoms at least partially influence the lattice parameters. However, the elements differ significantly with respect to their electronegativities, and their valence electron configuration. In all cases, the Al atoms are more electronegative than the M atoms rendering these compounds aluminides. While the alkaline-earth atoms can supply a maximum of two electrons, elements of group 3 and the rare-earth atoms can supply up to three electrons. Exception of this rule are Eu and Yb, which are two electron metals in their elemental form.18,19 This in turn leads to differences in the respective negative charges on the Al atoms in the binary MAl2 compounds.
m). Having numerous isostructural compounds at hand enables the investigation of e.g. physical properties like their wear- and corrosion-resistance, their magnetic or superconductive, their low-temperature behaviour or their hydrogen storage capabilities also in dependence of the constituent elements.14–17 When drawing back to the MAl2 compounds, the compounds differ with respect to their unit cell parameter, but both crystallographic sites are special positions (M on 8b (3/8, 3/8, 3/8); Al on 16c (0,0,0)). Therefore, the sizes of the respective M atoms at least partially influence the lattice parameters. However, the elements differ significantly with respect to their electronegativities, and their valence electron configuration. In all cases, the Al atoms are more electronegative than the M atoms rendering these compounds aluminides. While the alkaline-earth atoms can supply a maximum of two electrons, elements of group 3 and the rare-earth atoms can supply up to three electrons. Exception of this rule are Eu and Yb, which are two electron metals in their elemental form.18,19 This in turn leads to differences in the respective negative charges on the Al atoms in the binary MAl2 compounds.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al = 1
Al = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and subsequently arc-melted in water-cooled copper crucibles in an argon atmosphere of about 800 mbar.42 The argon gas was purified over a titanium sponge (873 K), molecular sieve and silica gel prior to the use. The obtained buttons were remelted four to five times to improve the homogeneity. Powdered as-cast LuAl2 was loaded into a corundum crucible which was sealed in an evacuated silica tube and annealed at 1073 K for 48 h followed by cooling to RT within 48 h. The other samples were used without any further heat treatment. The ytterbium compound was synthesized in an arc-welded niobium ampoule43 due to the low boiling point of ytterbium metal (1496 K
2 and subsequently arc-melted in water-cooled copper crucibles in an argon atmosphere of about 800 mbar.42 The argon gas was purified over a titanium sponge (873 K), molecular sieve and silica gel prior to the use. The obtained buttons were remelted four to five times to improve the homogeneity. Powdered as-cast LuAl2 was loaded into a corundum crucible which was sealed in an evacuated silica tube and annealed at 1073 K for 48 h followed by cooling to RT within 48 h. The other samples were used without any further heat treatment. The ytterbium compound was synthesized in an arc-welded niobium ampoule43 due to the low boiling point of ytterbium metal (1496 K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18). The Nb ampoule was heated for 2 h to approximately 1200 K in an induction furnace (Trumpf Hüttinger, Truheat HF 5010) under argon atmosphere. All samples show metallic lustre, ground powders are grey and stable in air over months.
18). The Nb ampoule was heated for 2 h to approximately 1200 K in an induction furnace (Trumpf Hüttinger, Truheat HF 5010) under argon atmosphere. All samples show metallic lustre, ground powders are grey and stable in air over months.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 ratio. The diluted samples were loaded into a cylindrical ZrO2 rotor with a diameter of 4 mm and spun at the magic angle with 13 kHz. All experiments conducted were single-pulse with a typical pulse length of 0.83 μs and a relaxation delay of 1 s. Resonance shifts were referenced to 1 molar AlCl3 and ScCl3 solutions in H2O. The NMR spectra were recorded using the Bruker Topspin software,45 the analysis was performed with the help of the DMFit software.46
9 ratio. The diluted samples were loaded into a cylindrical ZrO2 rotor with a diameter of 4 mm and spun at the magic angle with 13 kHz. All experiments conducted were single-pulse with a typical pulse length of 0.83 μs and a relaxation delay of 1 s. Resonance shifts were referenced to 1 molar AlCl3 and ScCl3 solutions in H2O. The NMR spectra were recorded using the Bruker Topspin software,45 the analysis was performed with the help of the DMFit software.46
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57,58), signficantly enlarged unit cells are observed for these two compounds.
57,58), signficantly enlarged unit cells are observed for these two compounds.

![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) plotted versus their respective ionic radius for CN = 8.
m) plotted versus their respective ionic radius for CN = 8.![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) and from the literature
m) and from the literature
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and adopt the so-called cubic Laves-phase (MgCu2 type). The structure contains one RE and one Al site, with the Al atoms forming empty Al4 tetrahedra that are connected to other tetrahedra via all atoms forming a network (Fig. 3, left). The RE atoms reside in the cavities of this framework. When looking at the arrangement of the RE atoms, an arrangement similar to cubic diamond can be observed. In the following paragraph, the structure will be briefly discussed using ScAl2 as example. The Al atoms are surrounded by six Al and six Sc atoms in the shape of a compressed icosahedron (Fig. 3, right). The Al atoms form two opposing triangular faces while the six Sc atoms are located near the equatorial plane, forming an undulating six-membered ring. The Sc atoms exhibit a coordination number of 16 arranged as Frank-Kasper polyhedron (Sc@Sc4Al12; Fig. 3, middle). Due to the high site symmetries (Sc: 8b,
m and adopt the so-called cubic Laves-phase (MgCu2 type). The structure contains one RE and one Al site, with the Al atoms forming empty Al4 tetrahedra that are connected to other tetrahedra via all atoms forming a network (Fig. 3, left). The RE atoms reside in the cavities of this framework. When looking at the arrangement of the RE atoms, an arrangement similar to cubic diamond can be observed. In the following paragraph, the structure will be briefly discussed using ScAl2 as example. The Al atoms are surrounded by six Al and six Sc atoms in the shape of a compressed icosahedron (Fig. 3, right). The Al atoms form two opposing triangular faces while the six Sc atoms are located near the equatorial plane, forming an undulating six-membered ring. The Sc atoms exhibit a coordination number of 16 arranged as Frank-Kasper polyhedron (Sc@Sc4Al12; Fig. 3, middle). Due to the high site symmetries (Sc: 8b, ![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m; Al: 16c, .
3m; Al: 16c, .![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) and the symmetric coordination environment, one can derive that the asymmetry parameters ηQ for all 27Al and the 45Sc NMR spectra should be zero. At the same time, the nuclei of both Sc and Al exhibit a quadrupole moment. Therefore, the quadrupolar interaction of both nuclei is expected to be observed in their respective NMR spectra.
m) and the symmetric coordination environment, one can derive that the asymmetry parameters ηQ for all 27Al and the 45Sc NMR spectra should be zero. At the same time, the nuclei of both Sc and Al exhibit a quadrupole moment. Therefore, the quadrupolar interaction of both nuclei is expected to be observed in their respective NMR spectra.












