Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Synthesis and lewis acidity of fluorinated triaryl borates†
Mashael M.
Alharbi‡
 ab,
Yara
van Ingen‡
ab,
Yara
van Ingen‡
 a,
Alberto
Roldan
a,
Alberto
Roldan
 a,
Tanja
Kaehler
*a and
Rebecca L.
Melen
a,
Tanja
Kaehler
*a and
Rebecca L.
Melen
 *a
*a
aCardiff Catalysis Institute, School of Chemistry, Cardiff University, Main Building, Park Place, Cardiff, CF10 3AT, Cymru/Wales, UK. E-mail: KaehlerT@cardiff.ac.uk; MelenR@cardiff.ac.uk
bDepartment of Chemistry, King Faisal University, College of Science, P.O. Box 400, Al-Ahsa 31982, Saudi Arabia
First published on 14th January 2023
Abstract
A series of fluorinated triaryl borates B(OArF)3 (ArF = 2-FC6H4, 3-FC6H4, 4-FC6H4, 2,4-F2C6H3, 3,5-F2C6H3, 2,3,4-F3C6H2, 2,4,6-F3C6H2, 3,4,5-F3C6H2) have been prepared and isolated from the reactions of the mono-, di-, or tri-fluorophenol with BCl3. The Lewis acidity of these borates has been determined by NMR spectroscopic and theoretical methods and compared to their well-established borane counterpart.
Introduction
Since 1923,1 when Gilbert Lewis first suggested the concept of Lewis acids and bases, Lewis acids have been employed in all areas of chemistry in both the laboratory and on industrial scale. They are commonly employed to activate substrates both stoichiometrically and catalytically through adduct formation, lowering the LUMO of the reactive species. From a bond activation perspective, there is a strong correlation between the strength of a Lewis acid and substrate activation. However, this is not always observed when looking at an entire catalytic cycle.2 Nevertheless, there has been a drive to develop strong Lewis acids for applications in catalysis. One particular area where strong Lewis acids have been developed is for applications in frustrated Lewis pair (FLP) chemistry.3–7 The strength of a Lewis acid can be quantified by several means, including NMR spectroscopy and computational methods.8 The Gutmann–Beckett9,10 and Childs11 methods rely on adding an internal probe Et3PO or crotonaldehyde (CA) and measuring the change in chemical shift (Δδ) in the 31P (Et3PO) or 1H (H3 atom of CA) NMR spectra respectively. Computational methods to quantify the Lewis acidity often investigate the fluoride ion affinity (FIA) or the hydride ion affinity (HIA).8,12 The latter being better probe for softer Lewis acids. Most often, the strength of a Lewis acid is defined by its FIA value, and a molecule with an FIA stronger than SbF5 (501 kJ mol−1) is considered a Lewis superacid.8First synthesised in the 1960s,13 B(C6F5)3 is one of the most commonly used Lewis acids in FLP chemistry.3–7,14,15 However, with an FIA of 452 kJ mol−1, B(C6F5)3 falls short of being classified as a Lewis superacid.16 The heavier group 13 analogue Al(C6F5)3 with an FIA of 530 kJ mol−1, on the other hand, is a Lewis superacid.17 Much research has focused on making derivatives of E(C6F5)3 (E = B, Al) with different fluorine or chlorine substitution patterns on the aryl rings (ArF or ArCl).18 Adding an electronegative oxygen or nitrogen spacer before the halogenated aryl ring has been shown to increase the Lewis acidity (Scheme 1). For example, Sundermeyer reported an Al(N(C6F5)2)3 FIA Lewis acidity of 555 kJ mol−1.19 Other notable aluminium Lewis superacids include Krossing's Al(OC(CF3)3)3 (FIA = 547 kJ mol−1)16 and Beckmann's Al(OC(C6F5)3)3 (FIA = 555 kJ mol−1).20 Relating to this study, B(OC6F5)3 was first reported in 1992 by Naumann.21 Britovsek later prepared the intermediate borinic [(C6F5)2BOC6F5] and boronic [C6F5B(OC6F5)2] acids and analysed their Lewis acidity from Gutmann–Beckett method (Δδ Et3PO = 33.6, 34.1 ppm, respectively).22 The increased Lewis acidity of the boron centre when including an O-atom spacer is attributed to the reduced pπ–pπ bonding between the oxygen and the boron centre due to the high electron-withdrawing nature of the C6F5 groups. Surprisingly, the FIA for B(OC6F5)3 is 419 kJ mol−1, significantly lower than its borane counterpart B(C6F5)3.12 In contrast, the reported Gutmann–Beckett value of Δδ = 34.5 ppm (ref. 22) for B(OC6F5)3 showed a higher Lewis acidity when compared to Δδ = 25.5 ppm for B(C6F5)3.21
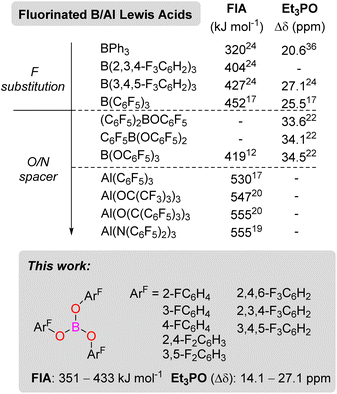 | ||
| Scheme 1 Group 13 Lewis acids and their Lewis acidities from Fluoride Ion Affinity and Gutmann–Beckett (Et3PO) metrics. | ||
This discrepancy between computational and experimental methods for the Lewis acidity when including an O/N-atom spacer has not previously been investigated to the best of our knowledge. Previous studies in our laboratory have focused on synthesising E(ArF)3 compounds where ArF ≠ C6F5.23,24 These derivatives have sometimes shown increased catalytic activity and/or stability, for example, for B(3,4,5-F3C6H2)3 (Scheme 1).23–27 In the present study, we were interested in synthesising a series of B(OArF)3 derivatives of varying Lewis acidities.
The fluorinated triaryl borates 1–8 were synthesised by the general procedure from the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometric reaction of mono-, di-, or tri-fluorophenol with BCl3. The fluorinated triaryl borate products were then purified by crystallisation from a concentrated solution in pentane at −35 °C and washed with either cold pentane or CH2Cl2 to give the products in 74–91% yields (Scheme 2). All the compounds showed similar 11B NMR chemical shifts for the boron environment, with a broad peak appearing between δ = 15.7–17.7 ppm in the 11B NMR spectrum (Table 1), in good agreement with previously reported B(OPh)328 (δ = 16.5 ppm) and B(OC6F5)329 (δ = 15 ppm).
1 stoichiometric reaction of mono-, di-, or tri-fluorophenol with BCl3. The fluorinated triaryl borate products were then purified by crystallisation from a concentrated solution in pentane at −35 °C and washed with either cold pentane or CH2Cl2 to give the products in 74–91% yields (Scheme 2). All the compounds showed similar 11B NMR chemical shifts for the boron environment, with a broad peak appearing between δ = 15.7–17.7 ppm in the 11B NMR spectrum (Table 1), in good agreement with previously reported B(OPh)328 (δ = 16.5 ppm) and B(OC6F5)329 (δ = 15 ppm).
| Compound | 11Ba (ppm) | Et3PO 31Pa (ppm) | Et3PO Δδa (ppm) | CA 1Ha (ppm) | CA Δδa (ppm) | FIAb (kJ mol−1) | HIAb (kJ mol−1) | GEIc (eV) |
|---|---|---|---|---|---|---|---|---|
| a In CDCl3. b PBEh-3c//M06-2X/def2-QZVPP level. c B3LYP/def2-TZVP level. d Not determined. | ||||||||
| 1 | 16.5 | 76.3 | 23.8 | 6.87 | 0.02 | 351 | 339 | 0.88 |
| 2 | 15.9 | 74.5 | 22.0 | —d | —d | 368 | 340 | 1.19 |
| 3 | 16.3 | 66.6 | 14.1 | 6.87 | 0.02 | 359 | 329 | 1.09 |
| 4 | 16.7 | 76.2 | 23.7 | —d | —d | 376 | 360 | 1.24 |
| 5 | 15.6 | 78.9 | 26.4 | 6.87 | 0.02 | 404 | 377 | 1.31 |
| 6 | 16.5 | 79.6 | 27.1 | 6.88 | 0.03 | 402 | 374 | 1.30 |
| 7 | 17.7 | 79.6 | 27.1 | 6.88 | 0.03 | 372 | 347 | 1.23 |
| 8 | 15.7 | 79.1 | 26.6 | 6.88 | 0.03 | 433 | 414 | 1.45 |
| B(OC6F5)3 | 1529 | 80.922 | 34.522 | 7.2533 | 0.4022 | 431 | 411 | 1.81 |
| B(OPh)3 | 16.528 | 69.422 | 23.022 | 6.8822 | 0.0322 | 350 | 323 | 0.81 |
| B(C6F5)3 | 5921 | 78.033 | 25.533 | 7.9033 | 1.0533 | 454 | 497 | 3.65 |
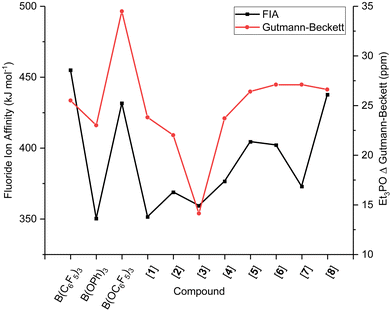
With a series of fluorinated borates in hand, we next investigated their Lewis acidity and compared them to literature reported B(OC6F5)3, B(OPh)3, and B(C6F5)3. Firstly, we analysed the Lewis acidity by use of the Gutmann–Beckett method. Et3PO (0.6 equiv.) was added to an NMR tube containing PPh3 as internal standard, and the fluorinated triaryl borates 1–8 (1.0 equiv.) in CDCl3 to generate Et3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O → B(OArF)3. The 31P NMR chemical shift (δ ppm) was measured as well as the change in 31P NMR chemical shift between the free phosphine oxide (δ = 52.5 ppm) and the adduct (Δδ) (Table 1). The Lewis acidity was found to decrease in the order 6 = 7 > 8 > 5 > 1 > 4 > 2 > 3, from which it can be deduced that reducing the number of electron withdrawing F-atoms decreases the Lewis acidity, however there appeared to be little correlation for the substitution pattern. When comparing the synthesised borates to previously reported borates and boranes, the following trend is observed; B(OC6F5)3 > 8, 7, 6, 5 > B(C6F5)3 ≫ B(OPh)3. These results align with Britovsek's findings, i.e., introducing an O-atom spacer increases Lewis acidity and verifies the importance of tuning acidity through fluorine substitutions.22
O → B(OArF)3. The 31P NMR chemical shift (δ ppm) was measured as well as the change in 31P NMR chemical shift between the free phosphine oxide (δ = 52.5 ppm) and the adduct (Δδ) (Table 1). The Lewis acidity was found to decrease in the order 6 = 7 > 8 > 5 > 1 > 4 > 2 > 3, from which it can be deduced that reducing the number of electron withdrawing F-atoms decreases the Lewis acidity, however there appeared to be little correlation for the substitution pattern. When comparing the synthesised borates to previously reported borates and boranes, the following trend is observed; B(OC6F5)3 > 8, 7, 6, 5 > B(C6F5)3 ≫ B(OPh)3. These results align with Britovsek's findings, i.e., introducing an O-atom spacer increases Lewis acidity and verifies the importance of tuning acidity through fluorine substitutions.22
The Lewis acidity of compounds 1–8 was also experimentally determined via the Childs method using CA as the Lewis base. However, only slight differences in the chemical shift of the H3 atom of CA in the 1H NMR spectra were observed, Δδ = 0.02–0.03 ppm, when comparing fluorination patterns of the borates (Table 1). A comparison of the change in chemical shift (Δδ) of CA for the perfluorinated borate B(OC6F5)3, at 0.40 ppm, to the perfluorinated borane B(C6F5)3, at 1.05 ppm, suggests that the borane is a stronger Lewis acid than the borate from the Childs method, a difference with the Gutmann–Beckett method. An expression of the Gutmann–Beckett and Childs metrics as percentages of B(C6F5)3 are presented in Table 2. The hard soft acid base theory (HSAB) introduced by Pearson invokes the charge density and polarizability of an acid or base, and can be used to make qualitative predictions of acids and bases and how they may prefer to react.30–32 Et3PO is considered hard due to its highly polarised P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, whereas CA is softer, hence the greater Δδ upon adduct formation of the borate with Et3PO than CA would suggest that the borate is a harder Lewis acid than the borane. A key step in both these experimental Lewis acidity metrics is the pyramidalisation of the boron centre from trigonal planar to tetrahedral upon adduct formation with a Lewis base. The introduction of an O-spacer likely affects the ease of pyramidalization from two perspectives: the steric changes upon a larger distance between the B atom to the phenyl ring in borates when compared to boranes, as well as the attractive dispersion effects between the Lewis base and the O and fluorinated phenyl groups in the ligand sphere of the B centre. The smaller fluoride and hydride bases were considered to further probe these effects through the use of fluoride and hydride ion affinity (FIA/HIA) metrics.
O bond, whereas CA is softer, hence the greater Δδ upon adduct formation of the borate with Et3PO than CA would suggest that the borate is a harder Lewis acid than the borane. A key step in both these experimental Lewis acidity metrics is the pyramidalisation of the boron centre from trigonal planar to tetrahedral upon adduct formation with a Lewis base. The introduction of an O-spacer likely affects the ease of pyramidalization from two perspectives: the steric changes upon a larger distance between the B atom to the phenyl ring in borates when compared to boranes, as well as the attractive dispersion effects between the Lewis base and the O and fluorinated phenyl groups in the ligand sphere of the B centre. The smaller fluoride and hydride bases were considered to further probe these effects through the use of fluoride and hydride ion affinity (FIA/HIA) metrics.
| Compound | Et3PO Δδ | CA Δδ | FIA | HIA | GEI |
|---|---|---|---|---|---|
| B(C6F5)3 | 100% | 100% | 100% | 100% | 100% |
| B(OC6F5)3 | 135% | 38% | 94% | 82% | 49% |
| 7 | 78% | 2% | 81% | 76% | 33% |
| 8 | 104% | 2% | 95% | 83% | 39% |
Fluoride and hydride ion affinity (FIA/HIA) are computationally derived metrics of Lewis acidity, defined as the enthalpy of the reaction (or pairing) of a Lewis acid with a Lewis base (F− or H−, respectively). Since the FIA of a Lewis acid considers the hard Lewis base F−, this represents hard Lewis acidity, whilst the soft H− base, and consequently HIA of a Lewis acid, reflects soft Lewis acidity properties.
Both fluoride and hydride anions are small and lack directionality as a base upon coordination to an acid, a key difference in the pyramidalisation step to the bases considered in the Gutmann–Beckett and Childs metrics. Hence, the FIA/HIA values consider Lewis acidity with limited to no influence of effects of steric interactions or π-interactions, as highlighted by Greb in previous work on ion affinity metrics.12,34
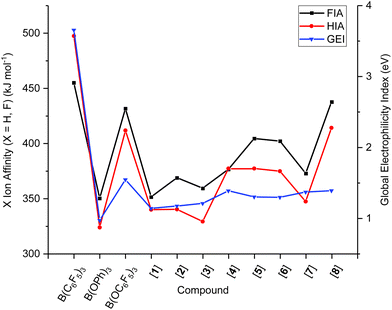
To determine the FIAs/HIAs, single point calculations at the M06-2X+D3(0)/def2-QZVPP level of theory35–37 were performed on the compounds optimised geometries at PBEh-3c,38 previously VSEPR-optimised. Isodesmic affinities were obtained through anchoring the enthalpies to reference systems (see ESI, section S6.2 for details†).12,39 A general trend of increasing FIA and HIA is observed with an increasing number F-substituents, giving 1, 3, 2 < 4, 5 < 6 < B(OC6F5)3 < 8. When the same number of F-atoms are present,40meta-substitution of fluorine induces higher FIA and HIAs than para- than ortho-substitution giving a trend of 1, 3 < 2, 4 < 5, and 7 < 6 < 8. Interestingly, 7 with a 2,4,6-F substitution has a lower Lewis acidity than compounds 4 and 5 which only have two F-atoms on the ArF rings. Likewise, the 3,4,5-F substitution in 8 gives higher FIA and HIA values than B(OC6F5)3, at 433 and 431 kJ mol−1 (FIA) compared to 414 and 411 kJ mol−1 (HIA), respectively. In both cases, the presence of two ortho-F atoms appears to diminish the Lewis acidity.
Surprisingly, and in contrast to the Gutmann–Beckett and Childs methods, the FIA and HIA of borate B(OC6F5)3 are significantly lower than that of borane B(C6F5)3 (Table 2). As mentioned, the pyramidalisation of the boron centre is required for acid–base adduct formation, one that is unaffected by steric and dispersion effects of the Lewis base in the FIA and HIA metrics. The slightly lower Lewis acidity in FIA and HIA than for Gutmann–Beckett and Childs metrics for the borates, hence, suggest that the Lewis acid strength in the experimental methods is governed by either steric or dispersion effects or a combination of the two, as a result of the introduction of the O-spacer and its resultant ligand sphere interaction with the Lewis base. The two most widely accepted and applied metrics, FIA and Gutmann–Beckett are compared in Fig. 1, showing opposing strengths of Lewis acidity for the borates than the boranes.
A comparison between the hard FIA and soft HIA, by representing these strengths relative to B(C6F5)3, show again that the borate is a harder Lewis acid than the borane (Table 2) the FIA of B(OC6F5)3 is 94%, and the HIA is 82%. Furthermore, the inverse of HIA is hydride donor ability,41 and the involvement of electrophilic boron centres in stoichiometric and catalytic transformation of basic substrates often relies on a balance between Lewis acidity and hydride donor ability, hence the softer HIA is relevant in context other than Lewis acidity strength.
Another computational comparison of Lewis acidity is given by the global electrophilicity index (GEI).42,43 This index considers intrinsic Lewis acidity, independent from the coordination of a Lewis base, as a measure of the Lewis acid's ability to accept electrons by considering the HOMO and LUMO energy levels in the form of chemical hardness42 and Mulliken electronegativity44–46 (see ESI, section S6.3†). In this work, the Lewis acids were re-optimised at the B3LYP/def2-TZVP theory level,47,48 and the EHOMO and ELUMO were taken as the energies of corresponding Kohn–Sham orbitals.
In B(C6F5)3, the LUMO is formed of a 2p-orbital that is orthogonal to the trigonal plane of the borane (Fig. 3A); in comparison, B(OC6F5)3 does not exhibit a localised 2p-orbital as the LUMO (Fig. 3B). Instead, a delocalised orbital situated across the B–O–C atoms is observed, seemingly a distortion from the vacant 2p-orbital of the B atom as a likely result of a degree of pπ–pπ donation from O to B (Fig. 3B). The LUMO+1 of B(OC6F5)3 does display a p-orbital perpendicular to the trigonal plane (Fig. 3C), yet most of the LUMO and LUMO+1 is localised on the ligand-sphere. Analysis of the unoccupied orbitals for all optimised borates showed that the most localised p-orbital on the B atom is in the LUMO+1, hence GEI values were calculated with the LUMO+1 for the borates (see ESI, Table S5† for a comparison), as has been done previously by Chitnis and co-workers.49 The GEI values for the varying substitution patterns follow the same general trend as for FIA and HIA (Fig. 2). A lower GEI value (Table 2) for B(OC6F5)3 in comparison to B(C6F5)3 is consistent with the computed LUMO+1 of B(OC6F5)3 lying at a higher energy than the LUMO of B(C6F5)3 (see ESI, Table S5†).
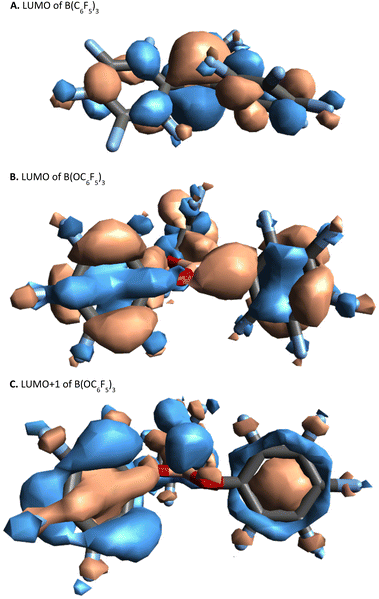 | ||
| Fig. 3 Visual representation (side-view) of the: LUMO of B(C6F5)3, top; the LUMO of B(OC6F5)3, middle; and the LUMO+1 of B(OC6F5)3 bottom, calculated at B3LYP/def2-TZVP level of theory (top-view can be found in the ESI, section S6.4†). | ||
An intrinsic Lewis acidity scale like GEI has benefits as it is readily available at low computational cost. However, whilst giving relevant insight into the unoccupied orbitals of the Lewis acid that participate in reactivity with a Lewis base, it in fact does not reflect the reactivity, and hence must be treated with some caution. Furthermore, computational metrics such as presented FIA and HIA were shown to give some insight into hard and soft characteristics of Lewis acids when compared to each other. These affinity metrics can be used to describe the strength of a Lewis acid from a theoretical perspective but the Lewis base lacks directionality.
Compounds 1, 7, and 8 could be recrystallised from CH2Cl2 and their structures determined by single crystal X-ray diffraction (Fig. 4). The three-component positional disorder could be resolved for 1, of which the major component is displayed in Fig. 1. As a result, the structural parameters of 1 will not be discussed. For compounds 7 and 8, the boron centre occupies a trigonal planar geometry, with the boron atom lying merely 0.019 (7) and 0.012 Å (8) out of the O3-plane. This slight deviation implies higher planarity than exhibited in B(OC6F5)3 (0.03 Å)22 and is comparable to that of B(OC6H5)3 (0.014 Å),50 as would be expected for lower F-substitution.
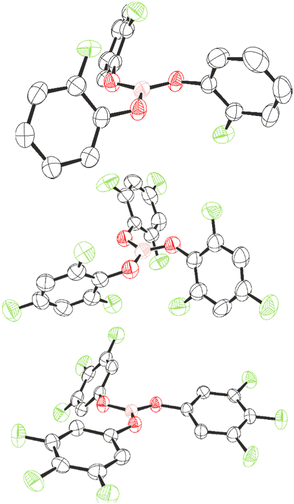 | ||
| Fig. 4 Crystal structures of 1 (top), 7 (middle), and 8 (bottom). Thermal ellipsoids shown at 50%. H atoms omitted for clarity. Carbon: black; oxygen: red; fluorine: light green; boron: pink. | ||
Varying Lewis acidity is expected from a pπ–pπ donation from oxygen to boron reflected by the coplanarity between B and O, with a higher contribution reducing Lewis acidity. We assessed this by comparing the torsion angle between O1–O2–O3 and B–O–C planes of 7 and 8, and that of B(OC6F5)3 and B(OC6H5)3. Torsion angles in 8 are smaller (B–O1 = 4°, B–O2 = 5°, B–O3 = 4°) than in B(OC6F5)3, for which Britovsek observed one larger torsion angle (B–O1 = 5°, B–O2 = 21°, B–O3 = 7°),22 consistent with an extent of pπ–pπ donation in 8, and thus higher Lewis acidity than B(OC6F5)3. For 7, the torsion angles are larger than in 8 (B–O1 = 11°, B–O2 = 9°, B–O3 = 6°) and approach those observed in B(OC6H5)3 (B–O1 = 14°, B–O2 = 14°, B–O3 = 15°).50 The differences are consistent with a lower Lewis acidity of 7 and B(OC6H5)3 compared to 8 and B(OC6F5)3. However, it must be noted that a key feature that determines structural parameters is the crystal packing within the unit cell, which is in part determined by π–π and F–π interactions. As such, the torsion angles and inclination angles must be treated with some level of caution. The inclination angles of the phenyl rings compared to the BO3 plane are larger and more uniform in 7 (69°, 64°, and 64°) than in 8 (21°, 11°, and 55°). The larger inclination angle for 7 is likely a result of steric effects of the ortho-F atoms.
Conclusions
In conclusion, we have demonstrated a simple synthesis of a series of fluorinated triaryl borates (B(OArF)3), for which Lewis acidity was determined by NMR (Gutmann–Beckett and Childs) methods as well as by computational means (HIA, FIA, and GEI). The Lewis acids were found to be stronger Lewis acids than the archetypical fluorinated boranes from Gutmann–Beckett, yet weaker when comparing their frontier orbitals by computational methods. Evidence for pπ–pπ donation from oxygen to boron was seen in the borate-delocalised LUMO and trends in structural analysis of the torsion angles for 7 and 8. The application of these compounds in Lewis acid catalysis and frustrated Lewis pair chemistry is the focus of our future studies.Author contributions
MA performed the experimental work. YVI performed the calculations and the crystal structure analysis. YVI, TK, and RLM wrote the manuscript. RLM directed the project, and AR directed the computer simulations. MA, YVI, and TK wrote the ESI.† All authors proofread and edited the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
MA acknowledges financial support from the Saudi Ministry of Education and the Deanship of Scientific Research at King Faisal University, Saudi Arabia (Grant No. 1591). TK and RLM would like to thank the EPSRC (EP/R026912/1). YVI is grateful to Mr Vladimir Y. Vladimirov for guidance with calculations. YVI and AR acknowledge Supercomputing Wales for access to the Hawk HPC facility, part-funded by the European Regional Development Fund via the Welsh Government. Information about the data that underpins the results presented in this article can be found in the Cardiff University data catalogue at http://doi.org/10.17035/d.2023.0237563437.References
- G. N. Lewis, Valence and the Structure of Atoms and Molecules, The Chemical Catalog Company, New York, 1923 Search PubMed.
- S. Woodward, Tetrahedron, 2002, 58, 1017–1050 CrossRef CAS.
- D. W. Stephan, J. Am. Chem. Soc., 2015, 137, 10018–10032 CrossRef CAS PubMed.
- D. W. Stephan, Science, 2016, 354, 1248 CrossRef CAS PubMed.
- J. Lam, K. M. Szkop, E. Mosaferi and D. W. Stephan, Chem. Soc. Rev., 2019, 48, 3592–3612 RSC.
- D. W. Stephan, Chem, 2020, 6, 1520–1526 CAS.
- D. W. Stephan, J. Am. Chem. Soc., 2021, 143, 20002–20014 CrossRef CAS PubMed.
- L. Greb, Chem. – Eur. J., 2018, 24, 17881–17896 CrossRef CAS PubMed.
- U. Mayer, V. Gutmann and W. Gerger, Chem. Mon., 1975, 106, 1235–1257 CrossRef CAS.
- M. A. Beckett, G. C. Strickland, J. R. Holland and K. Sukumar Varma, Polymer, 1996, 37, 4629–4631 CrossRef CAS.
- R. F. Childs, D. L. Mulholland and A. Nixon, Can. J. Chem., 1982, 60, 809–812 CrossRef CAS.
- P. Erdmann, J. Leitner, J. Schwarz and L. Greb, ChemPhysChem, 2020, 21, 987–994 CrossRef CAS PubMed.
- A. G. Massey and A. J. Park, J. Organomet. Chem., 1964, 2, 245–250 CrossRef CAS.
- G. Erker, Dalton Trans., 2005, 1883–1890 RSC.
- J. R. Lawson and R. L. Melen, Inorg. Chem., 2017, 56, 8627–8643 CrossRef CAS PubMed.
- H. Böhrer, N. Trapp, D. Himmel, M. Schleep and I. Krossing, Dalton Trans., 2015, 44, 7489–7499 RSC.
- L. O. Müller, D. Himmel, J. Stauffer, G. Steinfeld, J. Slattery, G. Santiso-Quiñones, V. Brecht and I. Krossing, Angew. Chem., Int. Ed., 2008, 47, 7659–7663 CrossRef PubMed.
- J. L. Carden, A. Dasgupta and R. L. Melen, Chem. Soc. Rev., 2020, 49, 1706–1725 RSC.
- J. F. Kögel, D. A. Sorokin, A. Khvorost, M. Scott, K. Harms, D. Himmel, I. Krossing and J. Sundermeyer, Chem. Sci., 2018, 9, 245–253 RSC.
- J. F. Kögel, A. Y. Timoshkin, A. Schröder, E. Lork and J. Beckmann, Chem. Sci., 2018, 9, 8178–8183 RSC.
- D. Naumann, H. Butler and R. Gnann, Z. Anorg. Allg. Chem., 1992, 618, 74–76 CrossRef CAS.
- G. J. P. Britovsek, J. Ugolotti and A. J. P. White, Organometallics, 2005, 24, 1685–1691 CrossRef CAS.
- T. Kaehler and R. L. Melen, Cell Rep. Phys. Sci., 2021, 2, 100595 CrossRef CAS.
- D. M. C. Ould, J. L. Carden, R. Page and R. L. Melen, Inorg. Chem., 2020, 59, 14891–14898 CrossRef CAS PubMed.
- Q. Yin, Y. Soltani, R. L. Melen and M. Oestreich, Organometallics, 2017, 36, 2381–2384 CrossRef CAS.
- J. R. Lawson, L. C. Wilkins and R. L. Melen, Chem. – Eur. J., 2017, 23, 10997–11000 CrossRef CAS PubMed.
- J. L. Carden, L. J. Gierlichs, D. F. Wass, D. L. Browne and R. L. Melen, Chem. Commun., 2019, 55, 318–321 RSC.
- B. Wrackmeyer, Annual Reports on NMR Spectroscopy, Elsevier, London, 1988 Search PubMed.
- A. Sundararaman and F. Jäkle, J. Organomet. Chem., 2003, 681, 134–142 CrossRef CAS.
- R. G. Pearson, J. Am. Chem. Soc., 1963, 85, 3533–3539 CrossRef CAS.
- R. G. Pearson, J. Chem. Educ., 1968, 45, 581 CrossRef CAS.
- R. G. Pearson, J. Chem. Educ., 1968, 45, 643 CrossRef CAS.
- I. B. Sivaev and V. I. Bregadze, Coord. Chem. Rev., 2014, 270–271, 75–88 CrossRef CAS.
- P. Erdmann and L. Greb, ChemPhysChem, 2021, 22, 935–943 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- F. Weigend, F. Furche and R. Ahlrichs, J. Chem. Phys., 2003, 119, 12753–12762 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- P. Erdmann and L. Greb, ChemPhysChem, 2021, 22, 935–943 CrossRef CAS PubMed.
- C. Lewis, B. Fluoroarylboranes, M. M. Morgan, A. J. V. Marwitz, W. E. Piers and M. Parvez, Organometallics, 2013, 32, 317 CrossRef.
- Z. M. Heiden and A. P. Lathem, Organometallics, 2015, 34, 1818–1827 CrossRef CAS.
- R. G. Parr, L. v. Szentpály and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS.
- A. R. Jupp, T. C. Johnstone and D. W. Stephan, Dalton Trans., 2018, 47, 7029–7035 RSC.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef CAS.
- R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, J. Chem. Phys., 1978, 68, 3801–3807 CrossRef CAS.
- R. S. Mulliken, J. Chem. Phys., 1934, 2, 782–793 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- K. M. Marczenko, S. Jee and S. S. Chitnis, Organometallics, 2020, 39, 4287–4296 CrossRef CAS.
- I. M. Malkowsky, R. Frohlich, U. Griesbach, H. Pütter and S. R. Waldvogel, Eur. J. Inorg. Chem., 2006, 1690–1697 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental procedures, NMR spectra, DFT data, and X-ray data. CCDC 2208652 (1) 2208553 (7) and 2208552 (8). For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2dt04095f |
| ‡ Both authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2023 |