A “gold standard” computational proof for the existence of gold(III) aurophilicity

Abstract

The existence of aurophilic gold(III)⋯gold(III) interactions has for a long time been neglected due to structural arguments and comparison with the aurophilicity of gold(I) compounds. We show with calculations at the CCSD(T) level of theory that the [Au^III(CH₃)₃(NH₃)]₂ dimer has a metallophilic dispersion interaction between the gold(III) atoms of 10.5 kJ mol⁻¹. The aurophilic interaction is illustrated by topological QTAIM calculations and IRI analysis.

---

The concept of metallophilicity encompasses attractive van der Waals interactions between pairs, strings, or clusters of closed- (d¹⁰, s²d¹⁰) or seemingly closed-shell (d⁸) late transition metals that originate from the relativistic mass increase of the s electrons. Among metallophilic interactions, aurophilicity has a privileged status due to its noticeable strength of 30–50 kJ mol⁻¹ that affects the crystalline structure and bulk properties of gold(I)-containing materials.^1–3 The character of the interaction is supported by ever-growing irrefutable structural evidence and by computational simulation at post-Hartree–Fock (HF) and density functional theory (DFT) levels that consider van der Waals interactions.⁴ A gold⋯gold distance of less than twice its van der Waals radius is considered aurophilic. The radius proposed by Bondi for gold, 1.62 Å, is usually chosen,⁵ although longer values have been reported, such as Allinger's 2.43 Å.^6,7

Whereas the existence of the aurophility between gold(I) atoms (Au^I⋯Au^I; [Au^I]: [Xe] 4f¹⁴5d¹⁰) is now out of debate, there is still room for doubts regarding the presence of analogous aurophilicity between gold(III) atoms (Au^III⋯Au^III; [Au^III]: [Xe] 4f¹⁴5d⁸). There is still no consensus in the scientific community on its existence.⁸ Two factors are thought to prevent the formation of Au^III⋯Au^III interactions: (i) the depletion of electron density, since gold(III) is a hard Pearson acid, whereas gold(I) is a soft one, and (ii) the relativistic effects of gold(III) are less pronounced as compared to gold(I).⁹

However, this reasoning is only enough for explaining the weaker interaction between Au^III⋯Au^III as compared to the Au^I⋯Au^I one but not to rule out its existence. In our opinion, the different orbital structure (d⁸vs. d¹⁰) and coordination environment (square planar vs. linear) of gold(III) may not prevent the existence of dispersive forces like aurophilicity. Moreover, the contribution of relativistic effects to the aurophilic attraction is not fundamental, accounting for only 22–27% of the total interaction energy.^10,11 There are some experimental and computational results that support our claim that Au^III⋯Au^III interactions contribute to the stabilization of gold(III) dimers and polymers, even though they are weaker and overruled by other secondary interactions. The following studies suggest that there is a weak van der Waals-type interaction between the gold(III) atoms:

(i) Mendizabal and Pyykkö calculated at the second order Møller–Plesset (MP2) level of theory a stabilizing interaction of −34.94 or −56.75 kJ mol⁻¹ between the two molecules of the [Au^IIICl₃(PH₃)]₂ dimer when the dipole moments of the monomers were perpendicular or antiparallel, respectively. There was an attraction of −20.71 kJ mol⁻¹ even at the HF level, when the molecules were oriented in a perpendicular fashion.¹²

(ii) In 2005, Klapötke et al. prepared a series of ammonium tetraazidoaurate(III) (Q[Au^III(N₃)₄]; Q = NMe₄, NMe₂H₂, NH₄) complexes. The crystal structure of (NMe₄)[Au^III(N₃)₄] has one-dimensional chains of anions linked by Au^III⋯Au^III contacts, whose bond distances are 3.507(3), 3.584(3) Å.¹³ However, an attractive nature of such contacts was not obtained in molecular structure optimizations of a [Au^III(N₃)₄]₂²⁻ dimer at the DFT level using the B3LYP functional. The dimer dissociated.

(iii) A year later, Doerrer et al. synthesized up to eleven double salts of [Pt^II(tpy)X]⁺ and [Au^III(bpy)X₂]⁺ (tpy = 2,2′:6′,2′′-terpyridine; bpy = 2,2′-bipyridine; X = Cl, Br, CN) cations that were prepared by anion metathesis in aqueous solution.¹⁴ Among them, the crystal structures of [Au^III(bpy)Cl₂][Au^IIIBr₄] and [Au^III(bpy)Br₂][Au^IIIBr₄] with the gold(III)-gold(III) ion pairs are noteworthy, since they have Au^III (cation)⋯Au^III (anion) distances of 3.518(1) Å and ca. 3.54 Å, respectively. The quality of [Au^III(bpy)Br₂][Au^IIIBr₄] was unpublishable. A similar study was reported in 2015 by Haukka et al. including quantum theory of atoms in molecules (QTAIM) calculations of the topology of the charge density.⁷ The authors proposed a combination of structural measurements and bond critical point (BCP) descriptors to identify Au^III⋯Au^III aurophilicity. They also report Au^III⋯Au^III interaction energies at the DFT/PBE0 level of theory in the range 3.6–9.3 kJ mol⁻¹.

(iv) Extremely short intramolecular Au^III⋯Au^III distances ranging between 2.984–3.080 Å were obtained by Bessonov et al. for the molecular structure of doubly supported dimethylgold(III) carboxylates ([{Au^III(CH₃)₂}₂(μ-OC(R)O)₂]; R = H, CF₃, C(CH₃)₃, Ph).¹⁵

(v) Che et al. contributed to the search for these interactions with the article from 2012 where they prepared [Au^III(C^N^N)(C≡CC₆H₄-4-NMe₂)](PF₆) (C^N^N = 6-phenyl-2,2′-bipyridine) with the shortest unsupported Au^III⋯Au^III distance to date of 3.495 Å.¹⁶

The gold(III) ions of examples (ii) and (v) would not be expected to aggregate by Au^III⋯Au^III contacts based on Coulomb repulsion, and therefore gold(III) aurophilicity is reasonably invoked in these cases. Also note that in examples (iii) and (iv) the presumed gold(III) aurophilic interaction is assisted by Coulomb attraction and ligand support, respectively.

Here, we demonstrate that at the “gold standard” level of theory i.e., at the coupled cluster singles and doubles level with a perturbative treatment of the triples (CCSD(T)) in combination with the def2-TZVP basis sets,¹⁷ the Au^III⋯Au^III interactions explain a part of the total interaction energy between neutral gold(III) complexes.

For achieving a clearer-as-possible description of the Au^III⋯Au^III interaction without losing chemical representativeness, we have built a very simple dimer model by substituting the C₃N donor atoms of the well-known bis-orthometallated [Au^III(C^N^C)(alkynyl)] complexes¹⁸ with methyl and ammonia ligands, respectively. The small size of [Au^III(CH₃)₃(NH₃)]₂ (Fig. 1, inset; molecule 1) allows us to employ correlated ab initio levels of theory such as RI-MP2/def2-TZVP and CCSD(T)/def2-TZVP. The computational details are given in the ESI.† The molecular structure of 1 optimized at the RI-MP2/def2-TZVP level has been employed in the calculations of the interaction energies. The potential energy curves (PECs) have been obtained by stretching the Au^III⋯Au^III distance to the selected values, without reoptimization of the rest of the dimer. The counterpoise-corrected RHF, RI-MP2 and CCSD(T) interaction energies (ΔE_int, eqn (S1)†) as functions of the Au^III⋯Au^III distance (R) are plotted in Fig. 1. The equilibrium distances (R_e) and interaction energies (ΔE_int(R_e)) derived from fitting the points to the Herschbach–Laurie four-parameter function (eqn (S2)†) are given in Table 1.

Fig. 1 The total interaction energy as a function of the Au^III⋯Au^III distance for molecule 1, calculated at the RHF (black), RI-MP2 (red) and CCSD(T) (green) levels of theory. Inset: RI-MP2/def2-TZVP optimized structure of molecule 1; colour code: C, grey; H, white; Au, yellow; N, blue.

Table 1 Gold(III)⋯Gold(III) Equilibrium Distances (R_e in Å) and Interaction Energies (ΔE_int in kJ mol⁻¹) of Molecule 1 at the RHF, RI-MP2 and CCSD(T) levels of theory^a

Level of theory	R e	−ΔEint(Re)
		Total	Au^III⋯[ligand]	[ligand]⋯[ligand]	Au^III⋯Au^III
a −ΔEint(Au^III⋯Au^III) = ΔEint(total) − 2 × ΔEint(Au^III⋯[ligand]) + ΔEint([ligand]⋯[ligand]).
RHF	4.11	15.9	—	—	—
RI-MP2	3.48	56.6	25.3	10.7	16.7
CCSD(T)	3.59	45.1	23.1	11.6	10.5

---

The PECs are markedly different depending on the chosen level of theory. In other words, the PEC depends on how electron correlation is considered in the computational framework. At the RHF level that does not consider electron correlation, the interaction curve is non-bonding and flat at long distances, although an overall binding of the dimer (ΔE_int < 0) is found at distances longer than ca. 3.48 Å. This finding agrees with the results obtained by Mendizabal and Pyykkö for antiparallel [Au^IIICl₃(PH₃)]₂, and the same explanation based on long-range dipole–dipole attraction may be invoked here. When electron correlation is considered an interaction minimum is predicted, suggesting a dispersive origin for the intermolecular attraction. Whereas both RI-MP2 and CCSD(T) predict a minimum, RI-MP2 calculations find it at a shorter distance of 3.48 Å as compared to 3.59 Å at the CCSD(T) level. The binding energy of 56.64 kJ mol⁻¹ obtained at the RI-MP2 level is also somewhat larger than the one of 45.05 kJ mol⁻¹ calculated at CCSD(T) level, which is in line with the notion that MP2 overestimates van der Waals interaction energies. The total interaction energy between the monomers of 1 can be approximated to the sum of Au^III⋯Au^III, twice Au^III⋯[ligand], and [ligand]⋯[ligand] contributions {[ligand] = [(CH₃)₃(NH₃)]}. The contribution from the Au^III⋯[ligand] interactions to the total interaction energy has been partially removed by subtracting twice that calculated for a monomer of 1 and the saturated ligands of the other monomer at the RI-MP2 and CCSD(T) Au^III⋯Au^III equilibrium distances, respectively. The extra [ligand]⋯[ligand] interaction energy removed in this way has been restored by adding that of the saturated ligands of [(CH₄)₃(NH₃)]₂ (see Fig. S1 and the ESI for further details†). Correcting for Au^III⋯[ligand] and [ligand]⋯[ligand] interaction leads to an approximate attractive interaction energy of 16.7 (RI-MP2) and 10.5 kJ mol⁻¹ (CCSD(T)) when considering only the Au^III⋯Au^III interactions.

We have repeated this procedure with Klapötke's anionic [Au^III(N₃)₄]₂²⁻ dimer (molecule 2)¹³ and with a theoretical cationic {cis-[Au^III(CH₃)₂(NH₃)₂]}₂²⁺ dimer (molecule 3) as a model of the interaction found in [Au^III(C^N^N)(C≡CC₆H₄-4-NMe₂)](PF₆),¹⁶ as proofs of concept. Due to the larger size of 2 and the repulsive character of the interaction found within 3 (vide infra), we only report results obtained at the RHF/def2-TZVP and RI-MP2/def2-TZVP levels of theory. We also found that optimizing the bound dimer of 2 at the RI-DFT/B3LYP-D3(BJ)/def2-TZVP level of theory results in its dissociation. However, if the same calculation is done at the RI-MP2/def2-TZVP level, a short Au^III⋯Au^III distance of 3.09 Å is obtained (Fig. S2,† inset). The PECs of 2 are repulsive at all distances due to the coulombic force between the anions, but an MP2 minimum at ca. 3.21 Å is found (Fig. S2†). Thus, Au^III⋯Au^III interactions may play a role in directing the crystal packing of [NMe₄][Au^III(N₃)₄]. However, the free optimization of 3 at the same level of theory as 2 led to the complete dissociation of the dimer. A starting structure was therefore obtained by fixing the Au^III⋯Au^III distance during the optimization. The absence of a minimum in the PECs of 3 (Fig. S3†) shows that cation-cation repulsion overcomes gold(III) aurophilicity if no other interligand interactions are present.

The RI-DFT/PBE0-D3(BJ)/def2-TZVP interaction energy (ΔE_int)s§ between the gold(III) monomers of molecule 1 has been decomposed into:

ΔE_int = ΔE_ele + ΔE_ex-rep + ΔE_orb + ΔE_corr + ΔE_disp

where ΔE_ele is the quasiclassical electrostatic interaction, ΔE_ex-rep is the Pauli exchange repulsion, ΔE_orb is the orbital relaxation, ΔE_corr is the correlation interaction, and ΔE_disp is the additional van der Waals interaction energy obtained with the D3(BJ) correction. The relative contribution of each attractive energy contribution to the total interaction energy, except the repulsive ΔE_ex-rep, is plotted in Fig. 2 as a function of the Au^III⋯Au^III distance. For a plot of the absolute values see Fig. S4.† Note that, at the Au^III⋯Au^III equilibrium distance of 3.40–3.60 Å, the correlation contribution has its maximum and surpasses that for orbital relaxation. Thus, the inter-dimer attraction arises from dispersion interaction and from electrostatic interaction as obtained at the RHF level.

Fig. 2 Relative contribution of ΔE_ele (black), ΔE_orb (green), ΔE_corr (blue) and ΔE_disp (pink) to the stabilization of molecule 1.

The CCSD(T) electron density of molecule 1 has been examined using QTAIM¹⁹ and topological calculations with the interaction region indicator (IRI) analysis method.²⁰ The relationship between the QTAIM (3, −1) BCPs, bond paths i.e., the maximal gradient path connecting two BCPs, and sign(λ₂) × ρ_e-weighted IRI isosurfaces in a single image is a powerful tool for gaining visual insight into the covalent and non-covalent interactions. Fig. 3 shows how molecule 1 is bound by attractive, van der Waals, and repulsive interactions and their strength. A BCP is found in the bond path connecting the two gold(III) atoms with an electron density (ρ_e(BCP)) of 0.0055 e ų. Its Laplacian (∇²[ρ_e(BCP)]) is 0.0136. The ρ_e(BCP) value between gold(III)–gold(III) ion pairs is even one order of magnitude smaller than the one reported by Haukka et al.,⁷ overruling any covalent character of the modelled interaction. Moreover, the positive ∇²[ρ_e(BCP)] value indicates reduction and expansion of the electron density as in closed-shell bonds.²¹ The expected region for van der Waals interactions between the ligands are depicted in the IRI isosurface as a bright green area around the corresponding BCPs. More importantly, an area with similar characteristics (electron-poor, attractive character) coinciding with the gold(III)⋯gold(III) intermetallic axis is also seen in Fig. 3. The physical meaning of bond paths has been controversial because some authors incorrectly assigned them to chemical bonds.²² It should be stressed that bond paths do not reflect chemical bonds of Lewis type but they provide a much broader concept of bonded interactions including the van der Waals ones.²³ Thus, the bond path connecting the two gold(III) atoms is the ultimate topological proof of the existence of a van der Waals-type interaction acting between the metals, which can be consequently addressed as gold(III) aurophilicity. A similar IRI isosurface and QTAIM bond path between the gold(III) atoms is seen for molecule 2 in Fig. S5 in the ESI.†

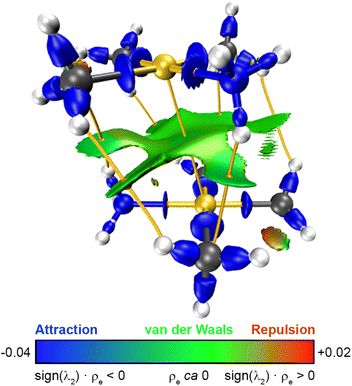Fig. 3 The QTAIM (3, −1) BCPs (orange dots), bond paths (yellow strings) and the IRI isosurface (isovalue = 1.0) are superimposed for molecule 1. The RGB colour scale refers to the IRI isosurface (adapted from ref. 16). Colour code: C, grey; H, white; Au, yellow, N, blue.

To conclude, we believe that the lack of structural evidence of gold(III) aurophilicity is partly a consequence of the current interests in gold(III) chemistry, which focusses on the production of phosphors and the tailoring of their emission energies by pre- and post-synthetic modifications.^8,18 Strongly σ-donating ligands consisting of large aromatic polycyclic pincers are needed and routinely employed for achieving luminescence. As expected, π-stacking interactions are the most important supramolecular motif that overrules Au^III⋯Au^III interactions. We hope that this communication will pave the way for accepting gold(III) aurophilicity as a weak metallophilic interaction and that it stimulates further experimental research on this less developed topic.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The research has been supported by MCIN/AEI/10.13039/501100011033 through project PID2019-104379RB-C22, and by The Academy of Finland through project 340583. DB acknowledges Universidad de La Rioja for the concession of a Margarita Salas post-doctoral scholarship financed by the Spanish Ministerio de Universidades and the European Union-NextGenerationEU program. This work used the Beronia cluster (Universidad de La Rioja), which is supported by FEDER-MINECO grant number UNLR-094E-2C-225. The authors also acknowledge CSC-IT Center for Science, Finland and the Finnish Grid and Cloud Infrastructure (persistent identifier urn:nbn:fi:research-infras-2016072533) for computational resources.

JML, MM and MEO designed the project. DS and MM provided the computational resources. DB and FR conducted the calculations. All authors have contributed to the text of the final version of the manuscript. DB and FR contributed equally.

References

1. N. Mirzadeh, S. H. Privér, A. J. Blake, H. Schmidbaur and S. K. Bhargava, Chem. Rev., 2020, 120, 7551–7591.
2. H. Schmidbaur and A. Schier, Chem. Soc. Rev., 2012, 41, 370–412.
3. H. Schmidbaur and A. Schier, Chem. Soc. Rev., 2008, 37, 1931–1951.
4. P. Pyykkö, Angew. Chem., Int. Ed., 2004, 43, 4412–4456.
5. A. Bondi, J. Phys. Chem., 1964, 68, 441–451.
6. N. L. Allinger, X. Zhou and J. Bergsma, J. Mol. Struct.: THEOCHEM, 1994, 312, 69–83.
7. A. N. Chernyshev, M. V. Chernysheva, P. Hirva, V. Y. Kukushkin and M. Haukka, Dalton Trans., 2015, 44, 14523–14531.
8. L. Rocchigiani and M. Bochmann, Chem. Rev., 2021, 121, 8364–8451.
9. P. Schwerdtfeger, P. D. W. Boyd, S. Brienne and A. K. Burrell, Inorg. Chem., 1992, 31, 3411–3422.
10. P. Pyykko, N. Runeberg and F. Mendizabal, Chem. – Eur. J., 1997, 3, 1451–1457.
11. N. Runeberg, M. Schütz and H.-J. Werner, J. Chem. Phys., 1999, 110, 7210–7215.
12. F. Mendizabal and P. Pyykkö, Phys. Chem. Chem. Phys., 2004, 6, 900–905.
13. T. M. Klapötke, B. Krumm, J.-C. Galvez-Ruiz and H. Nöth, Inorg. Chem., 2005, 44, 9625–9627.
14. R. Hayoun, D. K. Zhong, A. L. Rheingold and L. H. Doerrer, Inorg. Chem., 2006, 45, 6120–6122.
15. A. A. Bessonov, N. B. Morozova, N. V. Kurat'eva, I. A. Baidina, N. V. Gel'fond and I. K. Igumenov, Russ. J. Coord. Chem., 2008, 34, 73–80.
16. W. Lu, K. T. Chan, S.-X. Wu, Y. Chen and C.-M. Che, Chem. Sci., 2012, 3, 752–755.
17. J. Řezáč and P. Hobza, J. Chem. Theory Comput., 2013, 9, 2151–2155.
18. C. Bronner and O. S. Wenger, Dalton Trans., 2011, 40, 12409–12420.
19. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
20. T. Lu and Q. Chen, Chem.: Methods, 2021, 1, 231–239.
21. R. Bianchi, G. Gervasio and D. Marabello, Inorg. Chem., 2000, 39, 2360–2366.
22. R. F. W. Bader, J. Phys. Chem. A, 2009, 113, 10391–10396.
23. R. F. W. Bader, J. Phys. Chem. A, 1998, 102, 7314–7323.

---

Footnotes

† Electronic supplementary information (ESI) available: Computational details, interaction energy calculations on molecules 1–3, EDA of molecule 1, IRI analysis of molecule 2, Cartesian coordinates of molecules 1–3, [Au^III(CH₃)₃(NH₃)]⋯ [(CH₄)₃(NH₃)] and [(CH₄)₃(NH₃)]₂. See DOI: https://doi.org/10.1039/d2dt03731a

‡ These authors contributed equally.

§ The energy decomposition analysis (EDA) is currently implemented in TURBOMOLE v.7.5.1 at the RHF and DFT levels of theory only.

---